Abstract
The real-life assembly production often has transportation between fabrication and assembly, and the capacity of transportation machine is often considered; however, the previous works are mainly about two-stage distributed assembly scheduling problems. In this study, a distributed energy-efficient assembly scheduling problem (DEASP) with transportation capacity is investigated, in which dedicated parallel machines with symmetry under the given conditions, transportation machines and an assembly machine are used. An adaptive imperialist competitive algorithm (AICA) is proposed to minimize makespan and total energy consumption. A heuristic and an energy-saving rule are used to produce initial solutions. An adaptive assimilation with adaptive global search and an adaptive revolution are implemented, in which neighborhood structures are chosen dynamically, and revolution probability and search times are decided by using the solution quality. The features of the problem are also used effectively. Computational experiments are conducted on a number of instances. The computational results demonstrate that the new strategies of AICA are effective and efficient and AICA can provide promising results for the considered DEASP.
1. Introduction
In recent years, single factory or centralized production has been continuously replaced by multi-factory production or distributed manufacturing with the further development of globalization. Distributed manufacturing enables manufacturers to be closer to their customers and suppliers, to produce and market their products more effectively, to respond to market changes more quickly, to achieve better product quality, lower production cost and reduced management risk. As an important part of manufacturing systems, scheduling is shifted from single factory scheduling to distributed scheduling with the change of mode of production. Distributed scheduling problems have received much attention in the past decade [1,2,3,4,5].
Assembly scheduling problem (ASP) is an effective way to balance batch production and production flexibility, and has attracted much attention after the pioneering works of Lee et al. [6] and Potts et al. [7], along with a number of related works that have been obtained. In recent years, Framinan et al. [8] described ASP as , where and indicate machine environments of the fabrication stage and the assembly stage, respectively, and provided a full review of the previous works and the future topics. Komaki et al. [9] implemented a consolidated survey of ASP and proposed salient research opportunities. Assembly production systems are also shifted from single factory to multiple factories in recent years, and the distributed assembly scheduling problem (DASP) has been considered extensively.
As stated by Framinan et al. [8], two-stage ASP with layout, in which m dedicated parallel machines are for fabrication and one assembly machine is for assembly, has been extensively considered, and various methods including exact method, heuristic and meta-heuristic have been successfully used [10,11,12,13,14]. Meta-heuristics have become the main method because meta-heuristic performs better than an exact algorithm on large-scale ASP and often can produce better results than heuristics.
Allahverdi and Al-Anzi [15] presented tabu search (TS) and particle swarm optimization (PSO) for the problem for the first time. Shokrollahpour et al. [16]) proposed an imperialist competitive algorithm (ICA) for a bi-objective problem. Navaei et al. [17] handled the problem with sequence-dependent setup time (SDST) at two stages and developed four hybrid meta-heuristics with ICA, simulated annealing (SA) and heuristic. In the hybrid algorithm, SA and ICA are presented to find a sequence of jobs at the first stage, and a heuristic and SA are developed to assign addressed jobs to assembly machines at the second stage. Kazemi et al. [18] studied the problem with batching and delivery by a ICA and a hybrid ICA with the dominance relations. For two-stage ASP with layout, Wu et al. [11] developed some dominance propositions with a lower bound used in a branch-and-bound algorithm and presented six versions of hybrid PSO algorithms to find approximate solutions, they also presented four meta-heuristic including genetic algorithm (GA), cloud theory-based SA and iterated greedy [12], and Wang et al. [19] provided some dominance rules and opposition-based PSO to solve the problem with a cumulated learning effect.
Unlike two-stage ASP with layout, three-stage ASP with the above layout is not considered fully, in which the transportation stage is added between the fabrication stage and assembly stage. Hatami et al. [20] presented a mathematical model and two meta-heuristics, namely TS and SA, for the problem with SDST. Shoaardebili and Fattahi [21] developed two multi-objective meta-heuristics based on SA and GA for the problem with SDST and machine availability. Komaki et al. [22] proposed an improved discrete cuckoo optimization algorithm, which incorporates novel features such as clustering, egg laying and immigration of the cuckoos based on a discrete representation scheme.
As a typical distributed scheduling problem, DASP in multiple factories is considered fully. For DASP with F factories, each of which has layout, Xiong et al. [23] developed some hybrid algorithms named hybrid GA with reduced variable neighborhood search and a hybrid discrete differential evolution with reduced variable neighborhood search to minimize total completion time. Deng et al. [24] presented a mixed integer linear programming model and a competitive memetic algorithm based on a ring-based neighborhood structure and some knowledge-based local search operators to minimize makespan. Zhang and Xing [25] proposed a memetic social spider optimization algorithm with two improvement techniques, problem-special local search and self-adaptive restart strategy to minimize total completion time. Lei et al. [26] developed a cooperated teaching–learning-based optimization algorithm with class cooperation to minimize the makespan. A DASP with F processing factories and an assembly factory has also been investigated [27,28,29,30,31,32,33]; however, the above works mainly deal with two stages: the fabrication and assembly stages, and seldom focus on a DASP with three stages: fabrication, transportation and assembly.
As stated above, the previous works are mainly about two-stage ASP with layout. It is often assumed that the time for collecting and transporting components to the assembly stage is negligible. However, in many realistic situations, the collecting and transporting time is considerably large and cannot be ignored, in this case, transportation as a middle stage should be added between the fabrication stage and the assembly stage; moreover, the neglecting of transportation results in more loss in multiple factories. In the existing works [22], transportation time is frequently adopted and the capacity of the transportation machine is hardly included; on the other hand, although energy-efficient scheduling has been well-studied in various environments, it is hardly investigated in an assembly production environment. Generally, the energy efficiency of multiple factories is more important than that of a single factory, so it is necessary to deal with a distributed energy-efficient assembly scheduling problem (DEASP) with three stages.
ICA is inspired by the sociopolitical behaviors and has a good neighborhood search ability, effective global search property, good convergence rate, minor chance of trapping into local optima and flexible structure [34]. It has been used to solve various production scheduling problems [17,18,35,36,37,38,39,40,41,42]. Regarding distributed scheduling, Marandi and Fatemi Ghomi [43] studied distributed scheduling together with a vehicle routing problem and developed an improved ICA after a mathematical model was provided. Lei et al. [41] proposed a ICA with memory and new revolution for distributed unrelated parallel machine scheduling. Li et al. [44] presented a ICA with empire cooperation for solving a fuzzy DASP with layout. Its search ability and advantages are tested and proved. ICA is used to solve ASP; however, to the best of our knowledge, it is not applied to deal with a DEASP. The above features and extensive applications of ICA to scheduling problems motivate us to cope with the DEASP by ICA.
In this study, a DEASP with three stages is considered, in which assignment of the transportation machine is done based on capacity. An adaptive imperialist competitive algorithm (AICA) is proposed to minimize the makespan and total energy consumption simultaneously. A heuristic and an energy-saving rule are used to produce initial solutions. An adaptive assimilation with an adaptive global search is implemented. An adaptive revolution is given, in which neighborhood structures are chosen dynamically, and revolution probability and search times are decided based on solution quality. A number of experiments are conducted. The computational results demonstrate that the new strategies of AICA are effective and efficient and AICA can provide promising results for the considered DEASP.
The remainder of the paper is organized as follows. Problem description is given in Section 2 followed by an introduction to ICA in Section 3. Section 4 shows the proposed AICA for the problem. Numerical experiments on AICA are reported in Section 5, the conclusions are summarized in the final section and some topics of future research are provided.
2. Problem Description
A DEASP with three stages is described below. n independent jobs are produced in F homogeneous factories with different sites. Each factory f has m dedicated parallel machines for fabrication, h identical transportation machines and an assembly machine . Each has capacity Q and is used to move components of one job at a time. There is a set V of d different processing speeds for machines and . .
It is often assumed that energy consumption increases and processing time decreases when a job is processed on a machine at a higher speed [45]. This assumption is also used on assembly time. Machines and have two modes: working mode and stand-by mode. () is the energy consumption per unit time in working mode and () is the energy consumption per unit idle time on machine (). indicates energy consumption for a back and forth trip of a transportation machine and is time of a back and forth trip.
Each job has m components . is the weight of . These components are first processed on machines at the fabrication stage, then they are collected and transferred by transportation machine to the assembly machine and assembled together, and then the job is obtained. Each job has the same processing and assembly times in each factory. and indicate processing time on machine and assembly time for . and are setup times for fabrication of and assembly of . When transports the components of a job, the total weight of the components cannot exceed Q.
The following constraints are considered.
- All machines are available at time 0.
- Each machine can fabricate, transport or assemble at most one job at a time.
- Each job can be fabricated, transported or assembled at most one machine at a time.
- is used to move components of at most one job at a time.
The problem consists of a factory assignment sub-problem, speed selection used to decide speed of machines for fabrication and assembly, and scheduling sub-problem. There are strong coupled relations among them. The factory assignment notably affects results of the scheduling sub-problem, and optimal solutions can be obtained after the solutions of three sub-problems are effectively combined together.
The scheduling sub-problem in a factory is a three-stage ASP with layout, the time complexity of which is . Obviously, the time complexity of DEASP is notably greater than that of ASP because of factory assignment, so the problem is NP-hard because the ASP is NP-hard [8]. On the other hand, in the general parallel machine scheduling with makespan, symmetry exists, that is, two jobs on the same machines are exchanged, and makespan is not changed. In a DEASP with layout, symmetry on the fabrication stage is still kept when the maximum completion times of jobs and at the fabrication stage are not changed, that is, the last fabricated components of two jobs are not swapped with any other components, for and , their all components except the last one on the same parallel machine still have symmetry.
A DEASP with three stages is a multi-objective optimization problem with makespan and total energy consumption and all the above described constraints.
where is completion time of job , denotes maximum completion time of all jobs, , and are total energy consumption at fabrication stage, transportation stage and assembly stage, respectively.
where indicates the total number of back and forth trips of , is 1 if works at speed at time t and 0 otherwise. is 1 if is idle at time t and 0 otherwise, is 1 if works at speed at time t and 0 otherwise, is 1 if is idle at time t and 0 otherwise.
Table 1 shows an example with 2 factories, 8 jobs and 4 components of each. , , data on energy consumption and transportation are shown in Section 5. A schedule of the example is shown in Figure 1. In this Figure, take job as an example, 8 on denotes the k-th component of , 8 on denotes the movement of components by , 8 on indicates that is assembled on . , , , so , , , , as a result, .

Table 1.
Processing data of the example.
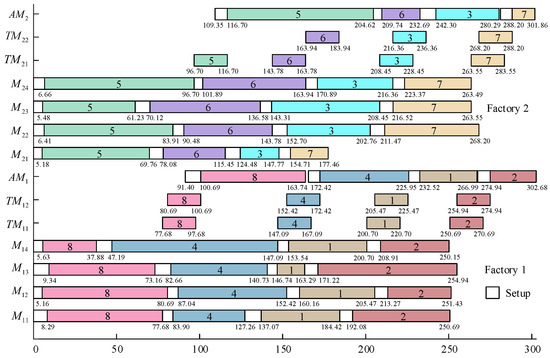
Figure 1.
A schedule of the example.
3. Introduction to ICA
In ICA, a country represents a solution of the problem, and solutions in population P are categorized into two parts: imperialists and colonies, the former are some of the best solutions in P and the latter are all solutions of P except imperialists.
ICA is shown below.
- (1)
- Initialization. Randomly produce an initial population P and calculate the cost of each solution in P.
- (2)
- Initial empires. Choose solutions with the smallest cost as imperialists, calculate the normalized cost and the number of colonies and randomly allocate colonies for each imperialist k.
- (3)
- Assimilation. In each empire, each colony moves toward its imperialist and is replaced with the newly generated solution if possible.
- (4)
- Revolution. Perform revolution according to revolution probability .
- (5)
- Exchange. In each empire, compare each colony with its imperialist and replace the imperialist with the colony with a smaller cost than its imperialist.
- (6)
- Imperialist competition. Calculate total cost , normalized total cost and power for each empire k, construct the following vector , decide an empire g with the biggest and allocate the weakest colony of the weakest empire into empire g.
- (7)
- If the termination condition is not met, go to (3); otherwise, stop the search.Where is a random number following uniform distribution in [0,1].
With respect to cost, the smaller the cost of a solution is, the better the solution is. When a new solution is better than a colony in assimilation and revolution, the colony is replaced with the new solution; otherwise, the colony is kept invariant. , , , and are defined by Hosseini and Khaled [34].
When ICA is used to solve production scheduling, the equation used in assimilation is hard to produce feasible solutions, so ICA is often discretized [38,39,40,41].
4. AICA for DEASP with Three Stages
To solve DEASP, a heuristic and an energy-saving rule are used to produce initial solutions, and adaptive search mechanisms are added into assimilation and revolution. These steps of AICA are described in the following.
4.1. Coding and Decoding
Lei et al. [26] proposed a representation method for DASP with layout. Based on this representation, a coding method is adopted to describe solution of DEASP in this study.
For DEASP with three stages, an assignment and scheduling string and a speed selection string are used, where is the number of all allocated jobs in factory f, , , , , is the chosen speed of used to fabricate the k-th component of . is the speed of assembly machine for .
The decoding procedure is shown below. The first string is divided into F segments, for segment of factory f, start with job , for each job , assign its m components on m machines at fabrication stage sequentially and deal with its fabrication on with speed , then transfer them to assembly machine by , and complete assembly on assembly machine on speed , where .
About the allocation of transportation machine, for job allocated in factory f, (1) choose transportation machine with earliest available time for . If more than one transportation machines with the same , a transportation machine with the smallest subscript is chosen. If more than one is required, the above steps are repeated until all required transportation machines are decided; (2) at the fabrication stage, each fabricated component of is loaded into according to first completion first transportation rule; if the sum of weight of all loaded components exceeds Q when a component is loaded, it is added into another transportation machine.
For the example in Table 1, a solution is and and the obtained schedule is shown in Figure 1. In Figure 1, needs two machines and , which are selected sequentially. Components 1, 3 and 4 of are loaded into , when component 2 is added, the capacity is exceeded, so component 2 is moved by ; moreover, is just used to transfer component 2 and does not move the components of other jobs.
4.2. Initialization and Initial Empires
Heuristic 1 is shown below. Suppose that all jobs processed on a two-machine flow shop, the processing time of on the first machine is and the processing time on the second machine is , then apply NEH and obtain a permutation of all jobs.
Heuristic 2 is described as follows. A job permutation is first obtained by using heuristic 1, then start with the first job on the permutation, for each job, decide a new factory and a new position on the assignment and scheduling string that can lead to the smallest makespan.
An energy-saving rule is used. For each factory , decide the smallest speed of each fabrication machine and assembly machine for each job under the condition that the makespan is kept invariant.
N initial solutions are produced. For solution , randomly produce a speed selection string, and then apply heuristic 2 and the energy-saving rule sequentially. For solution , each is first set to be , then heuristic 2 is used to produce an assignment and scheduling string and energy-saving rule is applied to adjust speeds of fabrication and assembly. For solution , produce speed selection string by letting each be and construct an assignment and scheduling string by using heuristic 2. Other initial solutions are randomly produced.
After population P with N initial solutions is produced, non-dominated sorting and crowding distance computation are done according to Deb et al. [46]; then, for each solution , its rank value and crowding distance are obtained, and its normalized cost is defined; solutions with the biggest are chosen as imperialists and other solutions are colonies; finally, compute and for each imperialist k and randomly select solutions as colonies of imperialist k.
where indicates crowding distance of , is set to 2 for boundary solution, is rank value of , the set is the set of all imperialists, , is a function that gives the nearest integer of x, indicates power of imperialist k.
initial empires are produced. The normalized total cost of empire k is defined by
where is a real number and often set to be 0.1, indicates the set of all colonies possessed by imperialist k.
4.3. Adaptive Assimilation
Assimilation is often executed by making each colony move toward its imperialist, and the movement is implemented by global search operator between colony and its imperialist [40,47]. In this study, an adaptive assimilation is proposed, in which assimilation probability of is computed by
The detailed steps of adaptive assimilation are shown below.
- (1)
- Let , decide the weakest empire g with the smallest .
- (2)
- For each colony , if random number , then if and rank value of its imperialist is greater than 1, then randomly select an imperialist l with rank value of 1; otherwise, directly use imperialist k; if , then execute order crossover (OX) between and the chosen imperialist; otherwise, implement a two-point crossover between and the selected imperialist, a new solution z is obtained, if z is not dominated by , z substitutes for and update external archive .
- (3)
- , if , go to step (2); otherwise, stop the assimilation.Where is obtained by sorting all solutions in P in the ascending order of makespan and is computed by sorting all solutions in the ascending order of . Archive is used to store non-dominated solutions produced by AICA.
OX [24] acts on assignment and scheduling string, and two-point crossover is performed on a speed selection string.
When is used to update , is included into , all solutions of are compared and all dominated solutions are removed from .
In the above assimilation, colony is given according to its rank value, the colony of the weakest empire may choose the imperialist of other empires, and OX and two-point crossover are chosen by . If , two crossovers are selected with the same probability, if , then the speed selection string (assignment and scheduling string) is given higher priority than the assignment and scheduling string (speed selection string) to diminish (). The above selection on two crossovers is done because of the following features of the problem: the makespan is mainly decided by the assignment and scheduling string and has a high correlation with the speed selection string.
These adaptive mechanisms are seldom adopted in the previous ICAs [38,39,47]. They can result in good exploration ability and high search efficiency because of the usage of adaptive and the above features.
4.4. Adaptive Revolution
Revolution is about an unexpected change in characteristics of some colonies. In general, a colony for revolution is chosen according to revolution probability, and the revolution of the chosen colony is implemented by using neighborhood search [40]. In this study, an adaptive revolution is presented, in which revolution probability and search times R are defined adaptively and an adaptive multiple neighborhood search is proposed based on eight neighborhood structures.
Revolution probability is often set to be 0.1 in many ICAs. When of is greater than 5, has bad convergence performance and low solution quality, its and , these settings are used to make execute global search mainly; on the contrary, when of is 1, lower and higher are also applied to make execute a neighborhood search mainly, thus, these adaptive settings on and can effectively make a good balance between exploration and exploitation. Adaptive revolution is shown below. In each empire , for each colony , if random number , then execute an adaptive multiple neighborhood search.
An adaptive multiple neighborhood search of is described as follows.
- (1)
- Decide factory with biggest completion time and factory with biggest energy consumption
- (2)
- Let , repeat the following steps until :
If, then , repeat the following steps until : produce ; , if z is not dominated by , then replace with z and update ; otherwise, .
Otherwise, if, then define , , let , repeat the following steps until : produce , if z is not dominated by , then replace with z and renew ; otherwise, .
Otherwise, let , repeat the following steps until : generate , if z is not dominated by , then z substitutes for and is used to renew ; otherwise, .
is applied to produce new solutions by removing a randomly chosen job from factory to a randomly chosen factory . In , a factory is randomly selected and a job from factory and a job randomly chosen from factory f are swapped. is shown below. Two randomly selected jobs from factory are exchanged.
Insertion and swap in are done in the assignment and scheduling string, for example, job in factory 2 and in factory 1 are exchanged, then the assignment and scheduling string becomes .
After assembly of job is finished on , if is idle in a time interval, then is a type-II job; otherwise, is a type-I job. In Figure 1, job is type-I and is type-II.
– make full use of the feature of the DEASP. is done in the following way. In factory , decide the last type-II job , randomly decide a job after , for the last fabricated component of , if the fabrication speed is , then the speed becomes . is similar to . In , are selected as done in , then if the assembly speed of is , then the new speed is . In Figure 1, , is the last type-II job, is decided, the speed of the last fabricated component or the assembly speed increases, and makespan can diminish likely.
is shown below. Randomly select a type-II job that is not in factory and let its assembly speed diminish to . is used to reduce fabrication speed of the first fabricated component for a randomly chosen type-II job not in factory . is similar to . In , a type-I job is randomly selected and a job is considered, which meets the following condition: if on assignment and scheduling string, then the fabrication speed of the first fabricated component of is reduced as done in . When – are used, the reduction of speed can lead to smaller and a fixed makespan, as a result, a dominating solution z can be generated.
4.5. Algorithm Description
The detailed steps of AICA are shown below.
- (1)
- Initialization. Produce initial population P by using heuristics and random way.
- (2)
- Sort all solutions in the ascending order of makespan and , respectively, and obtain , , and for each .
- (3)
- Execute adaptive assimilation.
- (4)
- Perform adaptive revolution and exchange imperialist and colony if possible in each empire.
- (5)
- Implement imperialist competition.
- (6)
- If the termination condition is not met, go to (2); otherwise, stop the search.
Flow chart of AICA is shown in Figure 2.
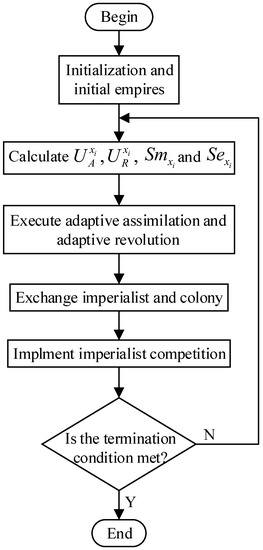
Figure 2.
Flow chart of AICA.
When the imperialist competition is done, the normalized total cost in Equation (9) is used to compute , and the winning empire is decided and the weakest colony of the weakest empire is moved to the winning empire, as done in Section 3.
AICA has some different features from the previous ICAs [18,39,40,41,42]. Adaptive assimilation is implemented by using adaptive assimilation probability and adaptive global search based on the characteristics of the problem. In adaptive revolution, is decided by solution quality, and an adaptive multiple neighborhood search with adaptive parameter R is adopted; moreover, features of DEASP are also used in assimilation and revolution.
5. Computational Experiments
Extensive experiments are conducted to test the performance of AICA for the considered DEASP. All experiments are implemented by using Microsoft Visual Studio 2019 C++ and run on a desktop computer with i5-7200U CPU 2.50 GHz 8 GB RAM.
5.1. Instances, Comparative Algorithms and Metrics
Overall, 127 instances are used and denoted as [23]. The related data are shown as follows. , , , , , , , , , .
Wang et al. [48] proposed a multi-objective whale swarm algorithm (MOWSA) to solve a distributed permutation flow shop scheduling problem with the objectives of makespan and energy consumption. Li et al. [49] handled energy-efficient scheduling of distributed permutation flow shop with total flow time and total energy consumption and presented an improved non-dominated sorting genetic algorithm-II (INSGA-II). In recent years, a competitive memetic algorithm (CMA) has been applied to solve distributed two-stage ASP [24], multi-objective distributed permutation flow shop scheduling [20] and carbon-efficient scheduling of distributed flow shop with makespan and carbon emissions [50]. In this study, CMA [51] is chosen to compare with AICA.
The above algorithms can be directly applied to solve our DEASP after fabrication, transportation and assembly are executed in the decoding procedure; moreover, these algorithms deal with two objectives: a time-related objective and an energy-related objective, so they are chosen as comparative algorithms.
ICA is obtained by deleting adaptive mechanisms from AICA, that is, the difference between AICA and ICA just lies in that and . The comparisons between AICA and ICA are used to show the effect of adaptive mechanisms.
Metric [52] is applied to compare the approximate Pareto optimal set, respectively, obtained by algorithms. measures the fraction of members of B that are dominated by members of L.
Metric [53] is the ratio of the number of the elements in the set to , where the reference set is composed of the non-dominated solutions in the union of non-dominated sets of all algorithms.
Metric [50] calculated as follows is used to evaluate the distribution of the obtained non-dominated solutions. The smaller the metric is, the more uniformly the solutions are distributed.
where is the Euclid distance in the objective space between solution and its nearest solution and .
5.2. Parameters Settings
AICA has following parameters: N, , , and stopping condition. We first tested stopping condition and found that AICA can converge well when seconds CPU times reaches. We also found that seconds CPU times also can be used as stopping condition of comparative algorithms.
Taguchi method [54] is used to decide the settings for other parameters. We select instance . The levels of each parameter are shown in Table 2. AICA with each combination runs 10 times independently for the chosen instance. The orthogonal array is in Table 3 and the related results on each level are listed in Table 4.

Table 2.
Parameters and their levels.

Table 3.
The orthogonal .

Table 4.
Related results on level of parameters.
The results of and ratio are shown in Figure 3, in which ratio is defined as . When the metrics are computed, all archives of an algorithm obtained in 10 runs are formed into a non-dominated set and the algorithms are compared to each other according to their non-dominated set.
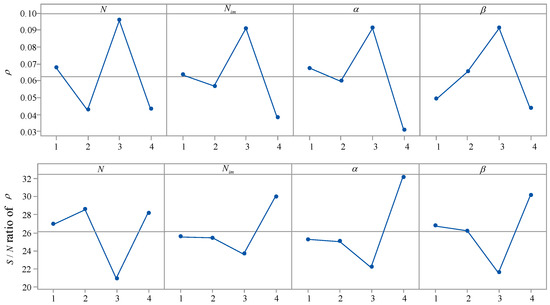
Figure 3.
Main effects plot for means and ratio.
It can be found from Figure 3 that AICA with the combination , , and can obtain better results than AICA with other combinations, so the above combination is adopted.
ICA has the same parameters with AICA.
We directly use parameter settings of three comparative algorithms except the stopping condition and test these settings for each comparative algorithm. The computational results show that those settings of each comparative algorithm are still effective, and comparative algorithms with those settings can produce better results than MOWSA, INSGA-II and CMA with other settings.
5.3. Results and Discussions
Five algorithms are tested and compared, which are AICA, ICA, MOWSA, INSGA-II and CMA. Each algorithm randomly runs 10 times for each instance. The corresponding results of all algorithms are shown in Table 5, Table 6, Table 7 and Table 8, and small scale examples are listed in Table A1, Table A2 and Table A3, in which A, I, C, M and N indicate AICA, ICA, CMA, MOWSA and INSGA-II, respectively. Figure 4 describes the box plot of five algorithms and Figure 5 shows non-dominated solutions produced by all algorithms.

Table 5.
Computational results of five algorithms on .

Table 6.
Computational results of five algorithms on .

Table 7.
Computational results of five algorithms on .

Table 8.
Computational results of five algorithms on .

Figure 4.
Box plot of five algorithms.
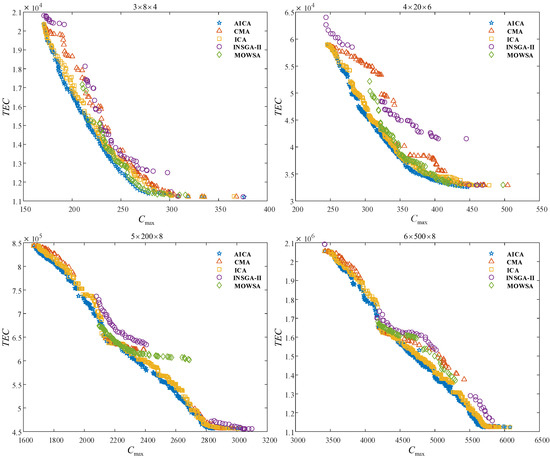
Figure 5.
Distribution of non-dominated solutions of five algorithms.
As shown in Table 5 and Table A3, AICA produces better results than ICA. is less than on nearly all instances and is greater than 0.6 on more than 100 instances, that is, most of non-dominated solutions of ICA are dominated by the non-dominated set of AICA. On the other hand, of AICA is bigger than that of ICA on 124 instances and bigger than that of ICA by at least 0.4 on nearly all instances. The above analyses show that AICA performs better than ICA.
It can be found from Table 8 and Table A3 that AICA possesses smaller than ICA on 116 instances. Non-dominated solutions of AICA are distributed more uniformly than those of ICA. Figure 4 also reveals the difference between AICA and ICA on . The notable performance between AICA and ICA demonstrates that adaptive mechanisms really have a positive impact on the performance of AICA.
As stated in Table 5, Table 6 and Table 7, AICA has smaller than on all instances; moreover, is less than 0.1 on most of the instances. Very few members of the non-dominated set of AICA are dominated by those of the non-dominated set of CMA. of CMA is smaller than 0.1 on nearly all instances and 0 on about 15 instances, that is, CMA cannot provide any members or very few members for . AICA has better convergence performance than CMA. This conclusion also can be drawn from Figure 4 and Figure 5.
When AICA is compared with MOWSA and INSGA-II, it can be found that AICA also converges better than these two comparative algorithms. is 0 on most of the instances, and is less than on more than 100 instances. of AICA is bigger than that of MOWSA and that of INSGA-II on nearly all instances.
With respect to , AICA has a bigger value than its three comparative algorithms on very few instances, that is, the non-dominated solutions of AICA are distributed more uniformly than those of INSGA-II, CMA and MOWSA. The conclusion on can also be found from Figure 4 and Figure 5.
AICA has adaptive mechanisms to decide and adaptively based on solution quality and adaptive multiple neighborhood search considering the features of the problem. Higher and smaller are given to solutions with bigger and vice versa. Neighborhood structures are dynamically selected according to features on two objectives, as a result, exploration and exploitation can be balanced well and search efficiency is improved greatly, thus, AICA can provide notably better results than its comparative algorithms and is a very competitive algorithm for solving DEASP with three stages.
6. Conclusions
Transportation is an important stage in real-life assembly production systems; however, the previous works are mainly about DASP with two stages. In this study, DEASP with fabrication, transportation and assembly is considered, and a new algorithm called AICA is proposed to minimize makespan and total energy consumption simultaneously. A heuristic and an energy-saving rule are used to produce initial solutions. Adaptive assimilation with adaptive global search and an adaptive revolution are implemented, in which neighborhood structures are chosen dynamically, and revolution probability and search times are decided based on solution quality. Features of the problem are also used in assimilation and revolution. A number of computational experiments are conducted. The computational results demonstrate that the new strategies of AICA are effective and efficient and AICA can provide promising results for a DEASP with three stages.
A DEASP with three stages does not attract sufficient attention. We will continue to cope with this problem with various processing constraints such as factory eligibility, which is an extended version of machine eligibility. DEASPs with other layouts, for example, layout, is also our future topic. We will also pay attention to DEASP with uncertainty. New optimization mechanisms such as the usage of machine learning are added into meta-heuristics such as imperialist competitive algorithm for obtaining high quality solutions. In recent years, there are some works on the integration of machine learning and meta-heuristics and the effectiveness of the integration is proved. These are also our main future works.
Author Contributions
Conceptualization, D.L.; methodology, J.L.; software, J.L.; validation, D.L.; formal analysis, D.L.; investigation, D.L.; resources, J.L.; data curation, J.L.; writing—original draft preparation, D.L.; writing—review and editing, D.L.; visualization, J.L.; supervision, D.L.; project administration, D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (No. 61573264).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DEASP | distributed energy-efficient assembly scheduling problem |
| ICA | imperialist competitive algorithm |
| AICA | adaptive imperialist competitive algorithm |
| ASP | Assembly scheduling problem |
| DASP | distributed assembly scheduling problem |
| TS | tabu search |
| PSO | particle swarm optimization |
| SDST | sequence-dependent setup time |
| SA | simulated annealing |
| GA | genetic algorithm |
| DEASP | distributed energy-efficient assembly scheduling problem |
| n | the total number of jobs |
| F | the total number of factories |
| m | the total number of machines at the first stage in each factory |
| h | the total number of transportation machines in each factory |
| d | the total number of speeds for each machine |
| the i-th job in set | |
| the k-th dedicated parallel machine in the f-th factory | |
| the l-th transportation machine in the f-th factory | |
| the assembly machine in the f-th factory | |
| Q | the capacity of transportation machine |
| V | the set of speeds for each machine |
| the energy consumption of per unit time in working mode | |
| the energy consumption of per unit time in working mode | |
| the energy consumption of per unit idle time | |
| the energy consumption of per unit idle time | |
| the energy consumption for a back and forth trip of a transportation machine | |
| the time for a back and forth trip of a transportation machine | |
| the k-th component of job | |
| the weight of | |
| processing time on machine for | |
| assembly time on machine for | |
| setup time for fabrication of | |
| setup time for assembly of | |
| completion time of job | |
| completion time of all jobs | |
| total energy consumption at fabrication stage | |
| total energy consumption at transportation stage | |
| total energy consumption at assembly stage | |
| the total number of back and forth trips of | |
| is 1 if works at speed at time t and 0 otherwise | |
| is 1 if is idle at time t and 0 otherwise | |
| is 1 if works at speed at time t and 0 otherwise | |
| is 1 if is idle at time t and 0 otherwise | |
| P | population |
| the number of imperialists | |
| the number of colonies for imperialist k | |
| the normalized cost for imperialist k | |
| the total cost for empire k | |
| the normalized total cost for empire k | |
| the power for empire k | |
| random number | |
| the number of all allocated jobs in factory f | |
| the g-th job in factory f | |
| the chosen speed of used to fabricate the k-th component of | |
| the speed of assembly machine for | |
| the earliest available time of transportation machine for | |
| the i-th solution in population P | |
| the rank value of | |
| the crowding distance of | |
| the set of all imperialists | |
| the number of colonies | |
| power of imperialist k | |
| the set of all colonies possessed by imperialist k | |
| the assimilation probability of | |
| OX | order crossover |
| sort results in ascending order of makespan for | |
| sort results in ascending order of TEC for | |
| archive | |
| the factory with biggest completion time | |
| the factory with biggest energy consumption | |
| MOWSA | multi-objective whale swarm algorithm |
| INSGA-II | improved non-dominated sorting genetic algorithm-II |
| CMA | competitive memetic algorithm |
| the non-dominated solution set in the union of non-dominated sets of all algorithms | |
| the Euclid distance in the objective space between and its nearest solution |
Appendix A

Table A1.
Computational results about small-scale instances of five algorithms on .
Table A1.
Computational results about small-scale instances of five algorithms on .
| Instance | (A,C) | (C,A) | (A,M) | (M,A) | (A,N) | (N,A) | (A,I) | (I,A) |
|---|---|---|---|---|---|---|---|---|
| 2 × 8 × 2 | 0.615 | 0.147 | 0.345 | 0.329 | 0.827 | 0.154 | 0.850 | 0.161 |
| 2 × 8 × 3 | 0.891 | 0.057 | 0.366 | 0.213 | 0.938 | 0.036 | 0.743 | 0.258 |
| 2 × 8 × 4 | 0.859 | 0.052 | 0.425 | 0.165 | 1.000 | 0.000 | 0.656 | 0.294 |
| 2 × 10 × 2 | 0.581 | 0.145 | 0.049 | 0.459 | 0.902 | 0.047 | 0.539 | 0.401 |
| 2 × 10 × 3 | 0.566 | 0.182 | 0.320 | 0.286 | 0.794 | 0.143 | 0.626 | 0.355 |
| 2 × 10 × 4 | 0.585 | 0.197 | 0.453 | 0.071 | 0.916 | 0.059 | 0.593 | 0.283 |
| 2 × 12 × 2 | 0.654 | 0.210 | 0.479 | 0.107 | 0.572 | 0.239 | 0.534 | 0.403 |
| 2 × 12 × 3 | 0.660 | 0.095 | 0.073 | 0.439 | 0.897 | 0.061 | 0.502 | 0.481 |
| 2 × 12 × 4 | 0.500 | 0.230 | 0.090 | 0.540 | 0.930 | 0.010 | 0.667 | 0.275 |
| 3 × 8 × 2 | 0.451 | 0.265 | 0.375 | 0.197 | 0.955 | 0.029 | 0.623 | 0.382 |
| 3 × 8 × 3 | 0.738 | 0.176 | 0.419 | 0.304 | 1.000 | 0.000 | 0.824 | 0.287 |
| 3 × 8 × 4 | 0.974 | 0.034 | 0.833 | 0.162 | 1.000 | 0.007 | 0.792 | 0.216 |
| 3 × 10 × 2 | 0.794 | 0.138 | 0.349 | 0.344 | 1.000 | 0.000 | 0.873 | 0.094 |
| 3 × 10 × 3 | 0.986 | 0.032 | 0.317 | 0.372 | 0.987 | 0.000 | 0.869 | 0.229 |
| 3 × 10 × 4 | 0.753 | 0.106 | 0.565 | 0.245 | 1.000 | 0.005 | 0.734 | 0.191 |
| 3 × 12 × 2 | 0.590 | 0.102 | 0.247 | 0.404 | 0.877 | 0.060 | 0.702 | 0.235 |
| 3 × 12 × 3 | 0.526 | 0.142 | 0.309 | 0.278 | 1.000 | 0.006 | 0.547 | 0.341 |
| 3 × 12 × 4 | 0.753 | 0.103 | 0.391 | 0.210 | 1.000 | 0.004 | 0.695 | 0.262 |
| 4 × 8 × 2 | 0.544 | 0.270 | 0.348 | 0.327 | 0.945 | 0.028 | 0.714 | 0.312 |
| 4 × 8 × 3 | 0.983 | 0.051 | 0.434 | 0.182 | 1.000 | 0.010 | 0.813 | 0.253 |
| 4 × 8 × 4 | 0.843 | 0.148 | 0.352 | 0.344 | 1.000 | 0.041 | 0.725 | 0.344 |
| 4 × 10 × 2 | 0.464 | 0.215 | 0.339 | 0.331 | 0.986 | 0.015 | 0.556 | 0.485 |
| 4 × 10 × 3 | 0.812 | 0.087 | 0.526 | 0.150 | 0.836 | 0.044 | 0.729 | 0.300 |
| 4 × 10 × 4 | 0.917 | 0.071 | 0.500 | 0.264 | 1.000 | 0.007 | 0.632 | 0.336 |
| 4 × 12 × 2 | 0.606 | 0.124 | 0.187 | 0.352 | 0.947 | 0.026 | 0.723 | 0.202 |
| 4 × 12 × 3 | 0.464 | 0.145 | 0.382 | 0.295 | 1.000 | 0.000 | 0.495 | 0.430 |
| 4 × 12 × 4 | 0.706 | 0.102 | 0.514 | 0.194 | 1.000 | 0.000 | 0.571 | 0.369 |

Table A2.
Computational results about small-scale instances of five algorithms on .
Table A2.
Computational results about small-scale instances of five algorithms on .
| Instance | A | C | M | N | I | Instance | A | C | M | N | I |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 × 8 × 2 | 0.517 | 0.000 | 0.367 | 0.041 | 0.075 | 3 × 10 × 4 | 0.721 | 0.000 | 0.168 | 0.000 | 0.112 |
| 2 × 8 × 3 | 0.604 | 0.000 | 0.359 | 0.000 | 0.036 | 3 × 12 × 2 | 0.443 | 0.000 | 0.389 | 0.000 | 0.168 |
| 2 × 8 × 4 | 0.497 | 0.000 | 0.420 | 0.000 | 0.083 | 3 × 12 × 3 | 0.521 | 0.000 | 0.318 | 0.000 | 0.161 |
| 2 × 10 × 2 | 0.225 | 0.000 | 0.519 | 0.000 | 0.257 | 3 × 12 × 4 | 0.705 | 0.000 | 0.172 | 0.000 | 0.123 |
| 2 × 10 × 3 | 0.520 | 0.000 | 0.309 | 0.046 | 0.126 | 4 × 8 × 2 | 0.641 | 0.023 | 0.250 | 0.000 | 0.086 |
| 2 × 10 × 4 | 0.444 | 0.047 | 0.325 | 0.026 | 0.158 | 4 × 8 × 3 | 0.520 | 0.000 | 0.439 | 0.000 | 0.041 |
| 2 × 12 × 2 | 0.329 | 0.008 | 0.386 | 0.041 | 0.236 | 4 × 8 × 4 | 0.492 | 0.000 | 0.344 | 0.000 | 0.164 |
| 2 × 12 × 3 | 0.290 | 0.100 | 0.338 | 0.010 | 0.262 | 4 × 10 × 2 | 0.385 | 0.000 | 0.333 | 0.009 | 0.274 |
| 2 × 12 × 4 | 0.451 | 0.013 | 0.405 | 0.008 | 0.122 | 4 × 10 × 3 | 0.675 | 0.006 | 0.135 | 0.055 | 0.129 |
| 3 × 8 × 2 | 0.468 | 0.000 | 0.377 | 0.000 | 0.156 | 4 × 10 × 4 | 0.654 | 0.008 | 0.211 | 0.000 | 0.128 |
| 3 × 8 × 3 | 0.603 | 0.017 | 0.314 | 0.000 | 0.066 | 4 × 12 × 2 | 0.524 | 0.042 | 0.296 | 0.011 | 0.127 |
| 3 × 8 × 4 | 0.704 | 0.000 | 0.173 | 0.000 | 0.123 | 4 × 12 × 3 | 0.505 | 0.011 | 0.242 | 0.000 | 0.242 |
| 3 × 10 × 2 | 0.689 | 0.000 | 0.277 | 0.000 | 0.034 | 4 × 12 × 4 | 0.605 | 0.005 | 0.174 | 0.000 | 0.215 |
| 3 × 10 × 3 | 0.556 | 0.000 | 0.350 | 0.006 | 0.087 |

Table A3.
Computational results about small-scale instances of five algorithms on .
Table A3.
Computational results about small-scale instances of five algorithms on .
| Instance | A | C | M | N | I | Instance | A | C | M | N | I |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 × 8 × 2 | 4.120 | 5.756 | 5.587 | 5.999 | 4.967 | 3 × 10 × 4 | 5.493 | 6.068 | 6.826 | 5.881 | 5.929 |
| 2 × 8 × 3 | 4.082 | 6.263 | 5.519 | 6.226 | 4.466 | 3 × 12 × 2 | 5.355 | 6.516 | 6.073 | 6.095 | 5.995 |
| 2 × 8 × 4 | 5.139 | 6.650 | 6.861 | 5.128 | 5.164 | 3 × 12 × 3 | 5.857 | 8.270 | 6.836 | 7.123 | 5.721 |
| 2 × 10 × 2 | 4.808 | 5.934 | 5.920 | 5.241 | 5.056 | 3 × 12 × 4 | 5.432 | 8.058 | 7.382 | 6.498 | 5.520 |
| 2 × 10 × 3 | 4.930 | 5.457 | 6.427 | 5.849 | 5.392 | 4 × 8 × 2 | 4.445 | 6.412 | 7.836 | 7.399 | 4.935 |
| 2 × 10 × 4 | 4.886 | 6.957 | 6.071 | 6.078 | 5.210 | 4 × 8 × 3 | 5.911 | 7.121 | 6.335 | 7.736 | 6.329 |
| 2 × 12 × 2 | 4.827 | 5.963 | 5.308 | 5.278 | 4.467 | 4 × 8 × 4 | 6.267 | 7.260 | 8.231 | 6.272 | 6.602 |
| 2 × 12 × 3 | 5.075 | 6.657 | 7.564 | 5.835 | 5.850 | 4 × 10 × 2 | 4.312 | 5.652 | 6.570 | 5.739 | 5.224 |
| 2 × 12 × 4 | 4.929 | 5.313 | 6.860 | 6.301 | 5.069 | 4 × 10 × 3 | 5.286 | 6.124 | 7.761 | 9.027 | 5.651 |
| 3 × 8 × 2 | 4.458 | 6.127 | 5.661 | 5.736 | 4.388 | 4 × 10 × 4 | 5.084 | 7.875 | 9.246 | 7.138 | 5.886 |
| 3 × 8 × 3 | 5.373 | 7.853 | 8.213 | 7.627 | 5.798 | 4 × 12 × 2 | 5.258 | 6.336 | 5.996 | 7.926 | 5.642 |
| 3 × 8 × 4 | 5.722 | 7.255 | 6.784 | 8.571 | 6.434 | 4 × 12 × 3 | 5.380 | 7.949 | 7.429 | 7.629 | 5.625 |
| 3 × 10 × 2 | 4.421 | 6.282 | 5.901 | 5.998 | 5.142 | 4 × 12 × 4 | 5.502 | 7.244 | 8.106 | 6.810 | 6.007 |
| 3 × 10 × 3 | 4.994 | 7.129 | 7.022 | 6.815 | 5.245 |
References
- Mou, J.; Duan, P.; Gao, L.; Liu, X.; Li, J. An effective hybrid collaborative algorithm for energy-efficient distributed permutation flow-shop inverse scheduling. Future Gener. Comput. Syst. 2022, 128, 521–537. [Google Scholar] [CrossRef]
- Mao, J.Y.; Pan, Q.K.; Miao, Z.H.; Gao, L.; Chen, S. A hash map-based memetic algorithm for the distributed permutation flowshop scheduling problem with preventive maintenance to minimize total flowtime. Knowl. Based Syst. 2022, 242, 108413. [Google Scholar] [CrossRef]
- Han, X.; Han, Y.Y.; Zhang, B.; Qin, H.X.; Li, J.Q.; Liu, Y.P.; Gong, D.W. An effective iterative greedy algorithm for distributed blocking flowshop scheduling problem with balanced energy costs criterion. Appl. Soft Comput. 2022, 129, 109502. [Google Scholar] [CrossRef]
- Li, Y.Z.; Pan, Q.K.; Ruiz, R.; Sang, H.Y. A referenced iterated greedy algorithm for the distributed assembly mixed no-idle permutation flowshop scheduling problem with the total tardiness criterion. Knowl. Based Syst. 2022, 239, 108036. [Google Scholar] [CrossRef]
- Rossi, F.L.; Nagano, M.S. Heuristics and iterated greedy algorithms for the distributed mixed no-idle flowshop with sequence-dependent setup times. Comput. Ind. Eng. 2021, 157, 107337. [Google Scholar] [CrossRef]
- Lee, C.Y.; Cheng, T.C.E.; Lin, B.M.T. Minimizing the makespan in the 3-machine assembly-type flow shop scheduling problem. Manag. Sci. 1993, 39, 616–625. [Google Scholar] [CrossRef]
- Potts, C.N.; Sevast’janov, S.V.; Strusevich, V.A.; Wassenhove, L.N.V.; Zwaneveld, C.M. The two-stage assembly scheduling problem: Complexity and approximation. Oper. Res. 1995, 43, 346–355. [Google Scholar] [CrossRef]
- Framinan, J.M.; Perez-Gonzalez, P.; Fernandez-Viagas, V. Deterministic assembly scheduling problems: A review and classification of current-type scheduling models and solution procedures. Eur. J. Oper. Res. 2019, 273, 401–417. [Google Scholar] [CrossRef]
- Komaki, G.M.; Sheikh, S.; Malakooti, B. Flow shop scheduling problems with assembly operations: A review and new trends. Int. J. Prod. Res. 2019, 57, 2926–2955. [Google Scholar] [CrossRef]
- Framinan, J.M.; Perez-Gonzalez, P. The 2-stage assembly flowhop scheduling problem with total completion time: Efficient constructive heuristic and metaheuristic. Comput. Oper. Res. 2017, 88, 237–246. [Google Scholar] [CrossRef]
- Wu, C.-C.; Chen, J.Y.; Lin, W.C.; Lai, K.; Liu, S.C.; Yu, P.W. A two-stage three-machine assembly flow shop scheduling with learning consideration to minimize the flowtime by six hybrids of particle swarm optimization. Swarm Evol. Comput. 2018, 41, 97–110. [Google Scholar] [CrossRef]
- Wu, C.-C.; Bai, D.Y.; Azzouz, A.; Chung, I.H.; Said, L.B. A brand-and-bound algorithm and four meta-heuristics for minimizing total completion time for a two-stage assembly flow-shop scheduling problem with learning consideration. Eng. Optimiz. 2020, 52, 1009–1036. [Google Scholar] [CrossRef]
- Luo, J.C.; Liu, Z.Q.; Xing, K.Y. Hybrid branch and bound algorithms for the two-stage assembly scheduling problem with seperated setup times. Int. J. Prod. Res. 2019, 57, 1398–1412. [Google Scholar] [CrossRef]
- Talens, C.; Fernandez-Viagas, V.; Perez-Gonzalez, P.; Framinan, J.M. New efficient constructive heuristics for the two-stage multi-machine assembly scheduling problem. Comput. Ind. Eng. 2020, 140, 106223. [Google Scholar] [CrossRef]
- Allahverdi, A.; Al-Anzi, F.S. Evolutionary heuristics and an algorithm for the two-stage assembly scheduling problem to minimize makespan with setup times. Int. J. Prod. Res. 2006, 44, 4713–4735. [Google Scholar] [CrossRef]
- Shokrollahpour, E.; Zandieh, M.; Dorri, B. A novel imperialist competitive algorithm for bi-criteria scheduling of the assembly flowshop problem. Int. J. Prod. Res. 2011, 49, 3087–3103. [Google Scholar] [CrossRef]
- Naderi, B.; Yazdani, M. A model and imperialist competitive algorithm for hybrid flow shops with sublots and setup times. J. Manuf. Syst. 2014, 33, 647–653. [Google Scholar] [CrossRef]
- Kazemi, H.; Mazdeh, M.M.; Rostami, M. The two stage assembly flow-shop scheduling problem with batching and delivery. Eng. Appl. Artif. Intell. 2017, 63, 98–107. [Google Scholar] [CrossRef]
- Wang, D.J.; Qiu, H.X.; Wu, C.C.; Lin, W.C.; Lai, K.J.; Cheng, S.-R. Dominance rule and opposition-based particle swarm optimization for two-stage assembly scheduling with time cumulated learning effect. Soft Comput. 2019, 23, 9617–9628. [Google Scholar] [CrossRef]
- Hatami, S.; Ebrahimnejad, S.; Tavakkoli-Moghaddam, R.; Maboudian, Y. Two meta-heuristics for three-stage asseembly flowshop scheduling with sequence-depdent setup times. Int. J. Adv. Manuf. Tech. 2010, 50, 1153–1164. [Google Scholar] [CrossRef]
- Shoaardebili, N.; Fattahi, P. Multi-objective meta-heuristics to solve three-stage assembly flow shop scheduling problem with machine availability constraints. Int. J. Prod. Res. 2015, 53, 944–968. [Google Scholar] [CrossRef]
- Komaki, G.M.; Teymourian, E.; Kayvanfar, V.; Booyavi, Z. Improved discrete cuckoo optimization algorithm for the three-stage assembly flowshop scheduling problem. Comput. Ind. Eng. 2017, 105, 158–173. [Google Scholar] [CrossRef]
- Xiong, F.L.; Xing, K.Y.; Wang, F.; Lei, H.; Han, L.B. Minimizing the total completion time in a distributed two stage assembly system with setup times. Comput. Oper. Res. 2014, 47, 92–105. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L.; Wang, S.Y.; Zheng, X.L. A competitive memetic algorithm for the distributed two-stage assembly flow-shop scheduling problem. Int. J. Prod. Res. 2016, 54, 3561–3577. [Google Scholar] [CrossRef]
- Zhang, G.H.; Xing, K.Y. Memetic social spider optimization algorithm for scheduling two-stage assembly flowshop in a distributed environment. Comput. Ind. Eng. 2018, 125, 423–433. [Google Scholar] [CrossRef]
- Lei, D.M.; Su, B.; Li, M. Cooperated teaching-learning-based optimisation for distributed two-stage flow shop scheduling. Int. J. Prod. Res. 2020, 59, 1–14. [Google Scholar] [CrossRef]
- Hatami, S.; Ruiz, R.; Andrés-Romano, C. Heuristic and metaheuristics for the distributed assembly permutaiton flowshop scheduling problem with sequence dependent setup times. Int. J. Prod. Econ. 2015, 169, 76–88. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, S. An effective hybrid biogeography-based optimization algorithm for the distributed assembly permutation flow-shop scheduling problem. Comput. Ind. Eng. 2016, 97, 128–136. [Google Scholar] [CrossRef]
- Shao, W.S.; Pi, D.C.; Shao, Z.S. Local search methods for a distributed assembly no-idle flow shop scheduling problem. IEEE Syst. J. 2019, 13, 1945–1956. [Google Scholar] [CrossRef]
- Pan, Q.K.; Gao, L.; Li, X.Y.; Jose, F.M. Effective constructive heuristics and meta-heuristics for the distributed assembly permutation flowshop scheduling problem. Appl. Soft Comput. 2019, 81, 105492. [Google Scholar] [CrossRef]
- Ferone, D.; Hatami, S.; González-Neira, E.M.; Juan, A.A.; Festa, P. A biased-randomized iterated local search for the distributed assembly permutation flow-shop problem. Int. J. Prod. Res. 2020, 27, 1368–1391. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Zhao, J.L.; Wang, L.; Tang, J.X. An optimal block knowledge driven backtracking search algorithm for distributed assembly no-wait flow shop scheduling problem. Appl. Soft Comput. 2021, 111, 107750. [Google Scholar] [CrossRef]
- Huang, Y.Y.; Pan, Q.K.; Huang, J.P.; Suganthan, P.N.; Gao, L. An improved iterated greedy algorithm for the distributed assembly permutation flow shop scheduling problem. Comput. Ind. Eng. 2021, 152, 107021. [Google Scholar] [CrossRef]
- Hosseini, S.; Khaled, A.A. A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research. Appl. Soft Comput. 2014, 24, 1078–1094. [Google Scholar] [CrossRef]
- Goldansaz, S.M.; Jolai, F.; Anaraki, A.H.Z. A hybrid imperialist competitive algorithm for minimizing makespan in a multi-processor open shop. Appl. Math. Model. 2013, 37, 9603–9616. [Google Scholar] [CrossRef]
- Seidgar, H.; Kiani, M.; Abedi, M.; Fazlollahtabar, H. An efficient imperialist competitive algorithm for scheduling in the two-stage assembly flow shop problem. Int. J. Prod. Res. 2014, 52, 1240–1256. [Google Scholar] [CrossRef]
- Navaei, J.; Fatemi Ghomi, S.M.T.; Jolai, F.; Mozdgir, A. Heuristics for an assembly flow-shop with non-identical assembly machines and sequence dependent setup times to minimize sum of holding and delay costs. Comput. Oper. Res. 2014, 44, 52–65. [Google Scholar] [CrossRef]
- Zandieh, M.; Khatami, A.R.; Rahmati, S.H.A. Flexible job shop scheduling under condition-based maintenance: Improved version of imperialist competitive algorithm. Appl. Soft Comput. 2017, 58, 449–464. [Google Scholar] [CrossRef]
- Li, M.; Lei, D.M.; Cai, J.C. Two-level imperialist competitive algorithm for energy-efficient hybrid flow shop scheduling problem with relative importance of objectives. Swarm Evol. Comput. 2019, 49, 34–43. [Google Scholar] [CrossRef]
- Lei, D.M.; Li, M.; Wang, L. A two-Phase meta-heuristic for multiobjective flexible job shop scheduling problem with total energy consumption threshold. IEEE Trans Cybern. 2019, 49, 1097–1109. [Google Scholar] [CrossRef]
- Lei, D.M.; Yuan, Y.; Cai, J.C.; Bai, D.Y. An imperialist competitive algorithm with memory for distributed parallel machines scheduling. Int. J. Prod. Res. 2020, 58, 597–614. [Google Scholar] [CrossRef]
- Guo, J.; Lei, D.M.; Li, M. Two-phase imperialist competitive algorithm for energy-efficient flexible job shop scheduling. J. Intell. Fuzzy Syst. 2021, 40, 12125–12137. [Google Scholar] [CrossRef]
- Marandi, F.; Fatemi Ghomi, S.M.T. Integrated multi-factory production and distributed scheduling applying vehicle routing approach. Int. J. Prod. Res. 2019, 57, 722–748. [Google Scholar] [CrossRef]
- Li, M.; Su, B.; Lei, D.M. A novel imperialist competitive algorithm for fuzzy distributed assembly flow shop scheduling. J. Intell. Fuzzy Syst. 2021, 40, 4545–4561. [Google Scholar] [CrossRef]
- Ding, J.Y.; Song, S.J.; Wu, C. Carbon-efficient scheduling of flow shops by multi-objective optimization. Eur. J. Oper. Res. 2016, 248, 758–771. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transac. Evolut. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Karimi, S.; Ardalan, Z.; Naderi, B.; Mohammadi, M. Scheduling flexible job-shops with transportation times: Mathematical models and a hybrid imperialist competitive algorithm. Appl. Math. Model. 2017, 41, 667–682. [Google Scholar] [CrossRef]
- Wang, G.C.; Gao, L.; Li, X.Y.; Li, P.G.; Tasgetiren, M.F. Energy-efficient distributed permutation flow shop scheduling problem using a multi-objective whale swarm algorithm. Swarm Evol. Comput. 2020, 57, 100716. [Google Scholar]
- Li, Y.Z.; Pan, Q.K.; Gao, K.Z.; Tasgetiren, M.F.; Zhang, B. A green scheduling algorithm for the distributed flowshop problem. Appl. Soft Comput. 2021, 109, 107526. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L. A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem. Swarm Evol. Comput. 2017, 32, 121–131. [Google Scholar] [CrossRef]
- Deng, J.; Wang, L.; Wu, C.G.; Wang, J.J.; Zheng, X.L. A competitive memetic algorithm for carbon-efficient scheduling of distributed flow-shop. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2016; pp. 92–98. [Google Scholar]
- Zitzler, E.; Thiele, L. Multi-objective evolutionary algorithms: A comparative case study and the strength pareto approach. IEEE Transac. Evolut. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Lei, D.M. Pareto archive particle swarm optimization for multi-objective fuzzy job shop scheduling problems. Int. J. Adv. Manuf. Tech. 2008, 37, 157–165. [Google Scholar] [CrossRef]
- Taguchi, G. Introduction to Quality Engineering; Asian Productivity Organization: Tokyo, Japan, 1986. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).