Variable Matrix-Type Step-Size Affine Projection Sign Algorithm for System Identification in the Presence of Impulsive Noise
Abstract
1. Introduction
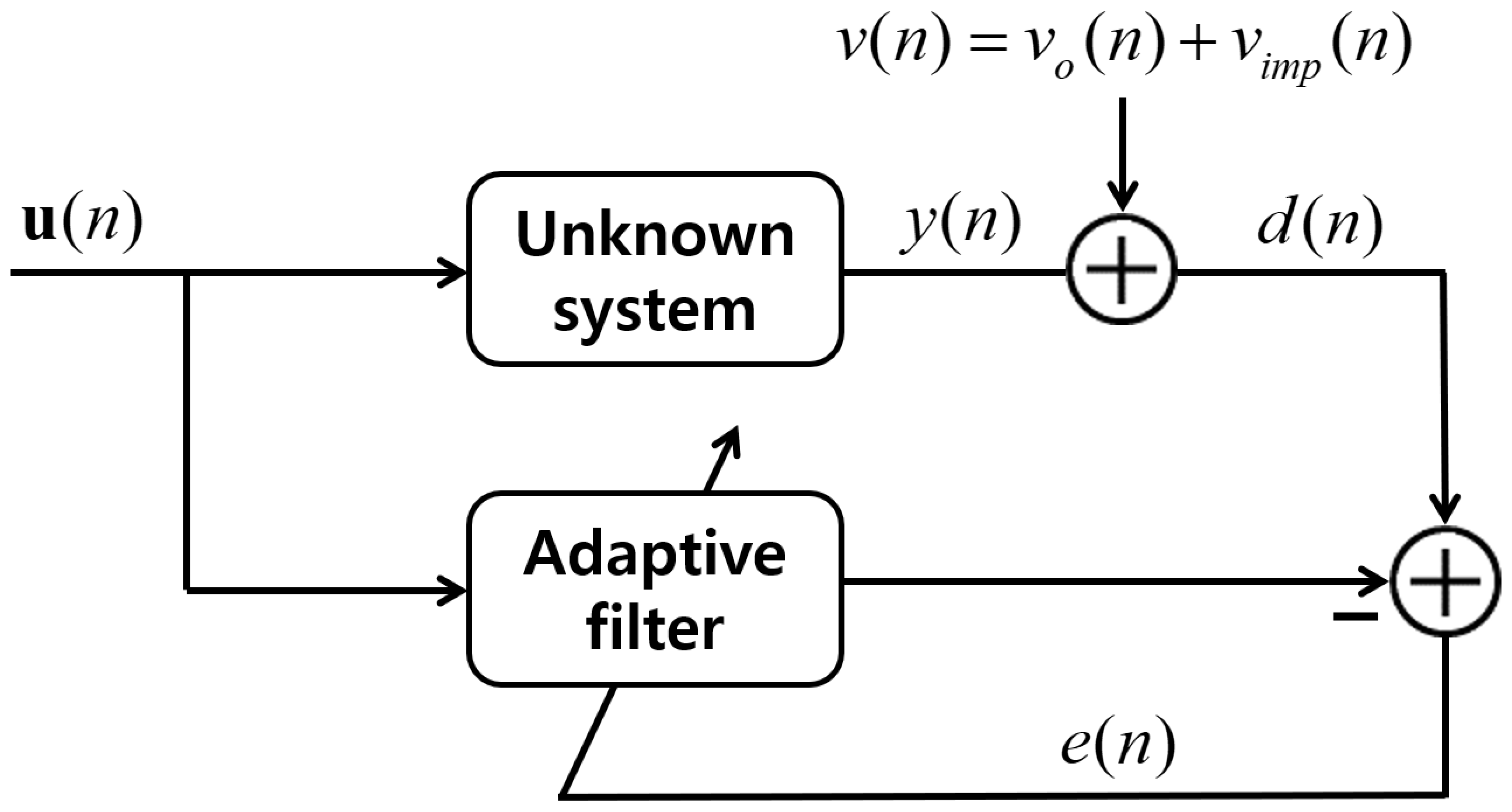
2. Original APSA
3. Variable Matrix-Type Step-Size APSA
3.1. Optimal Matrix-Type Step Size
3.2. Practical Considerations
3.3. Reset Algorithm for a Sudden Change in the System
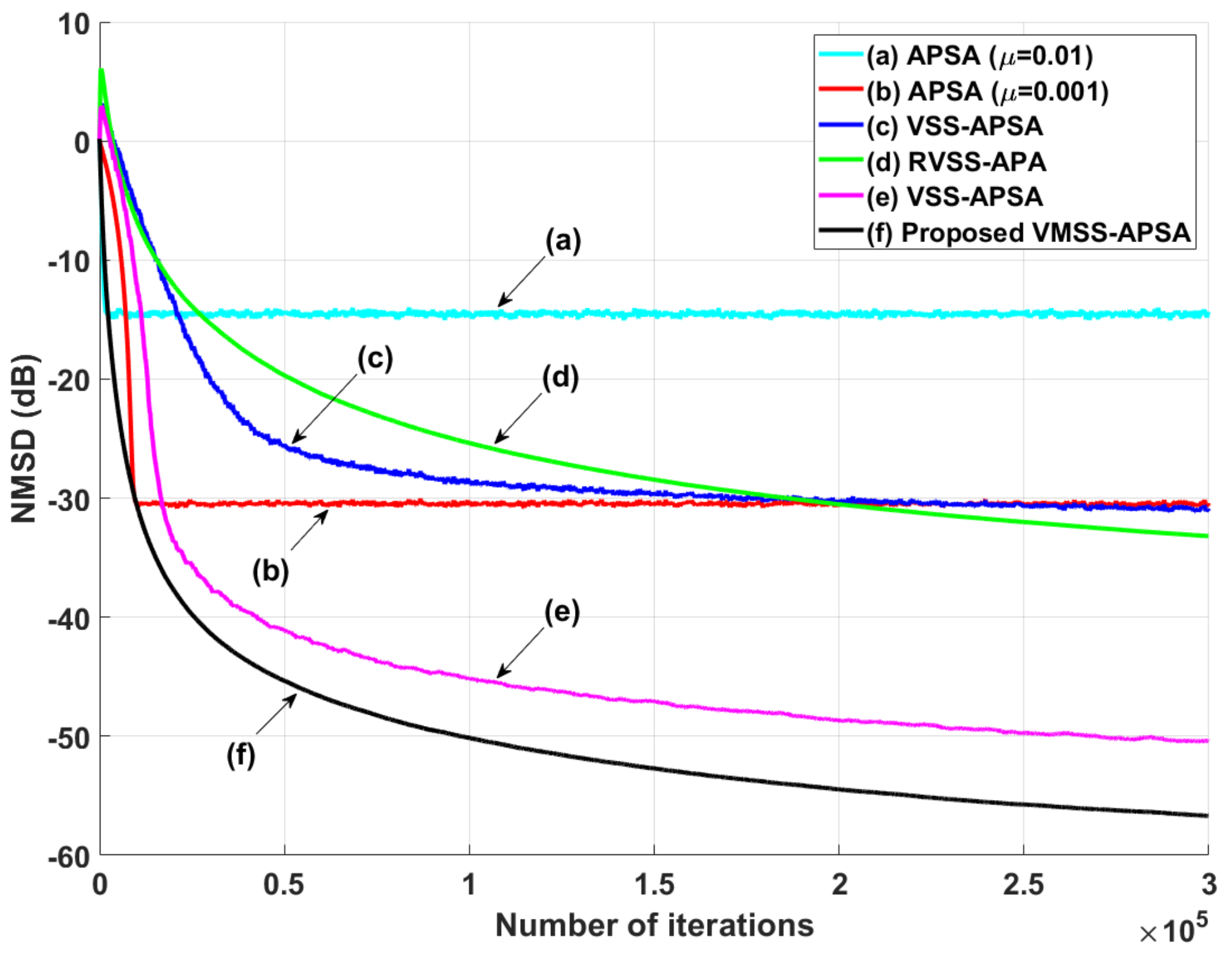
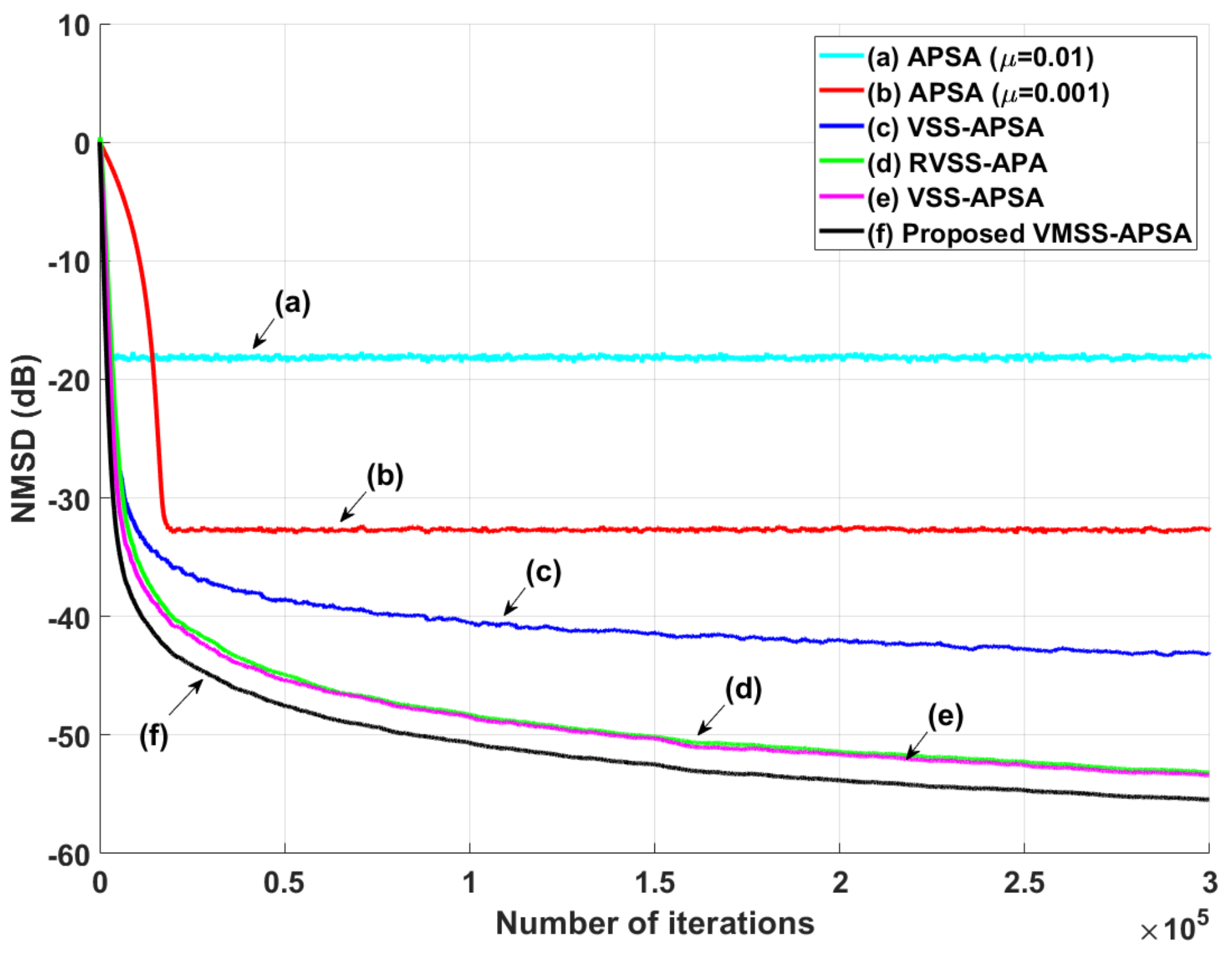
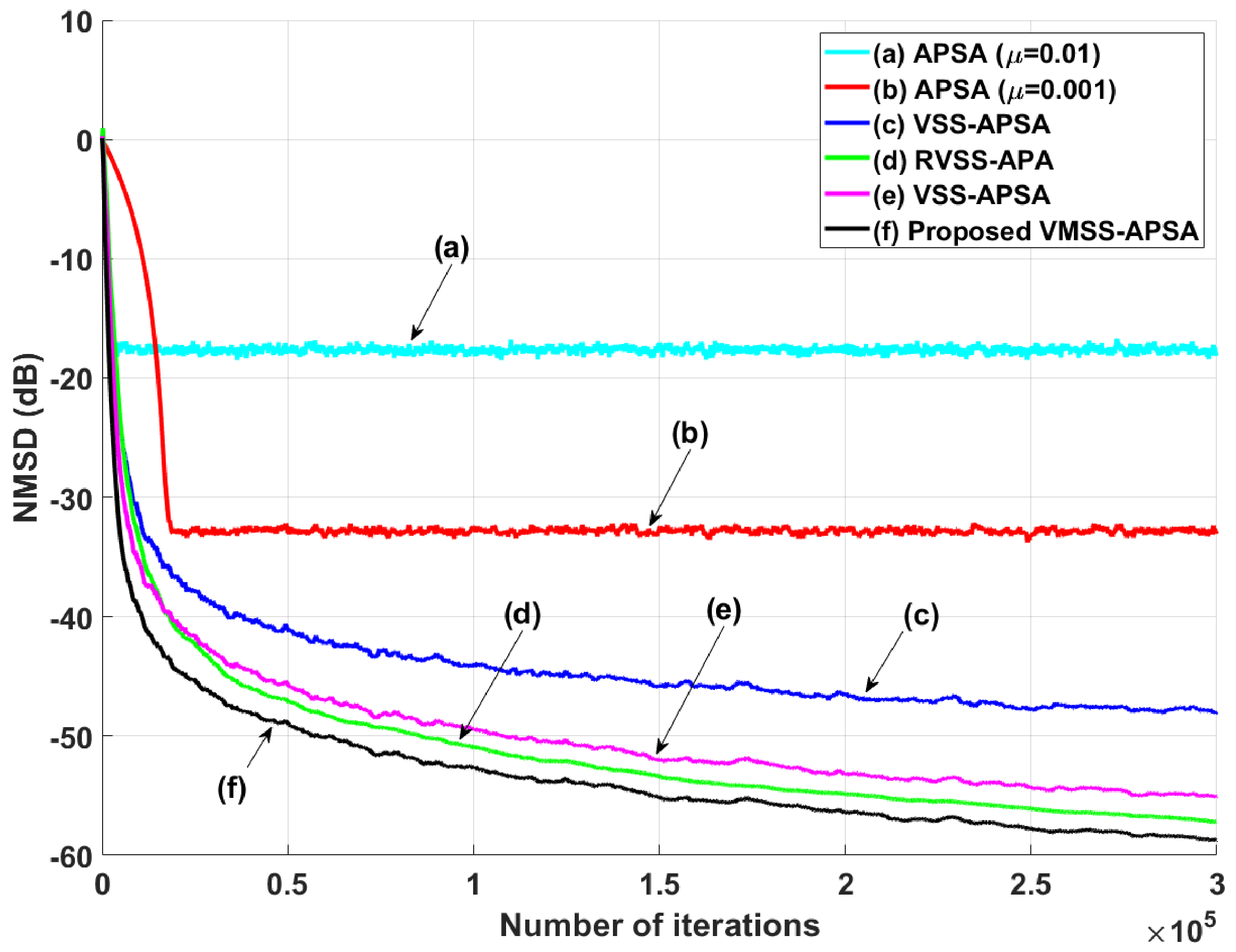
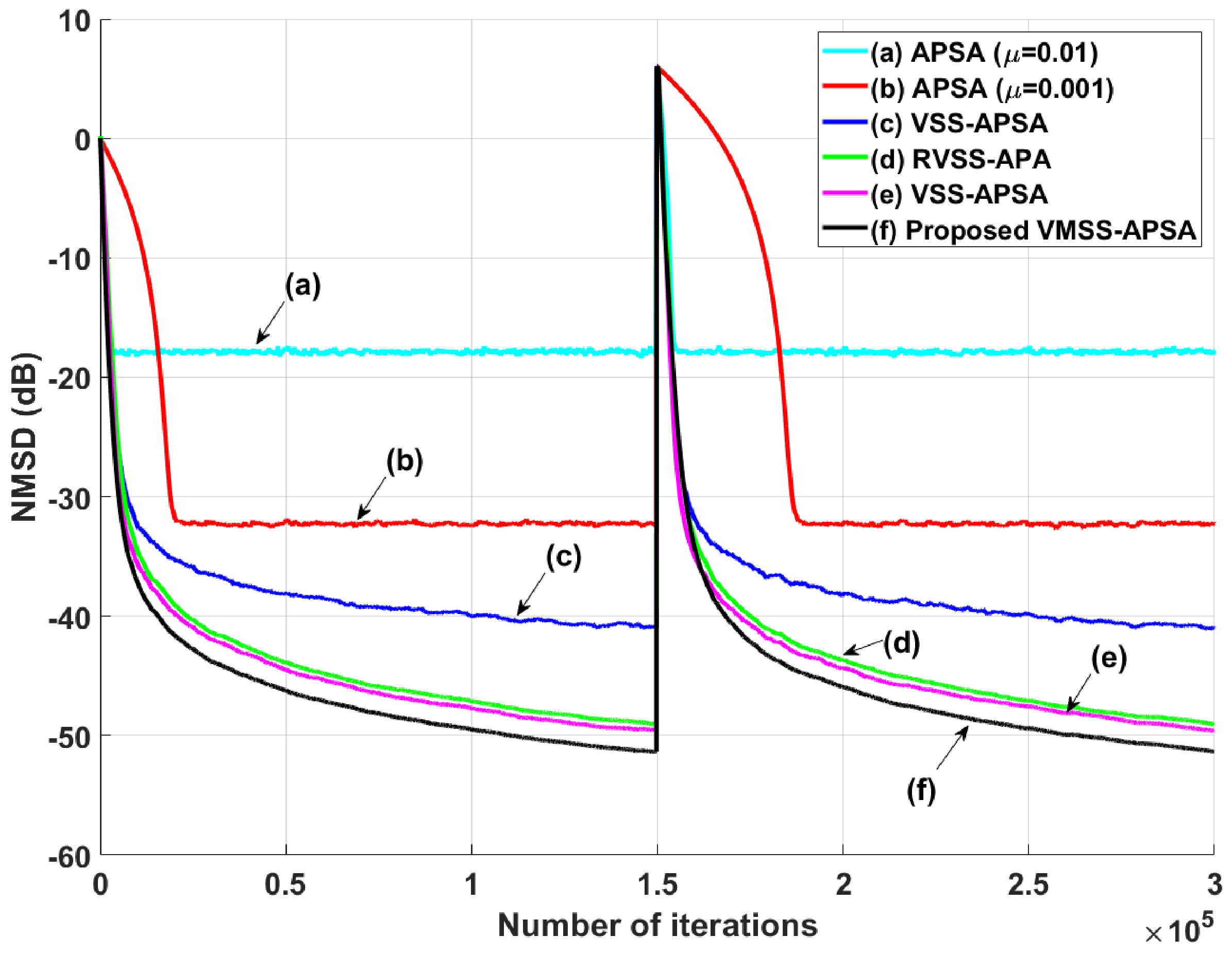
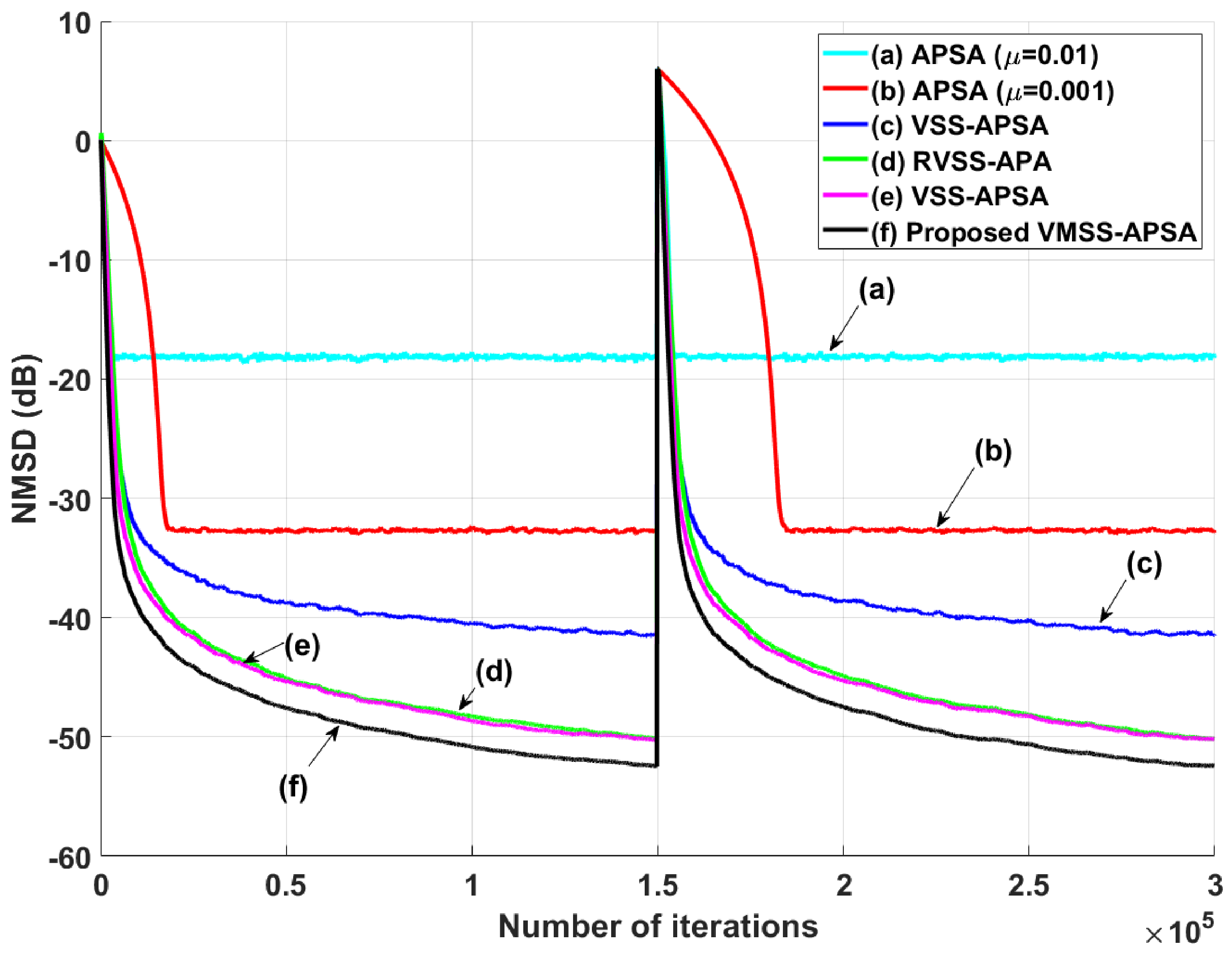
4. Simulation Results
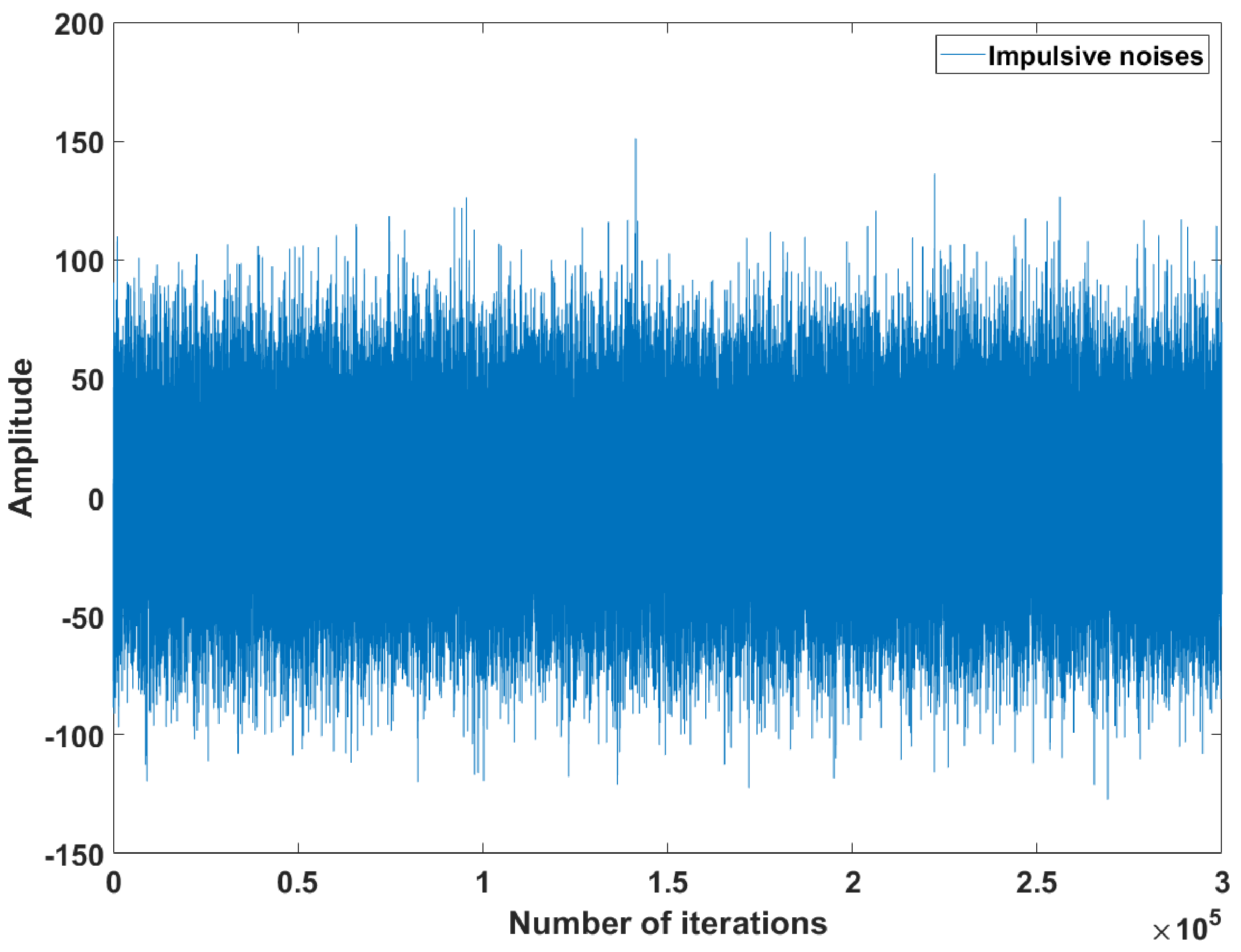
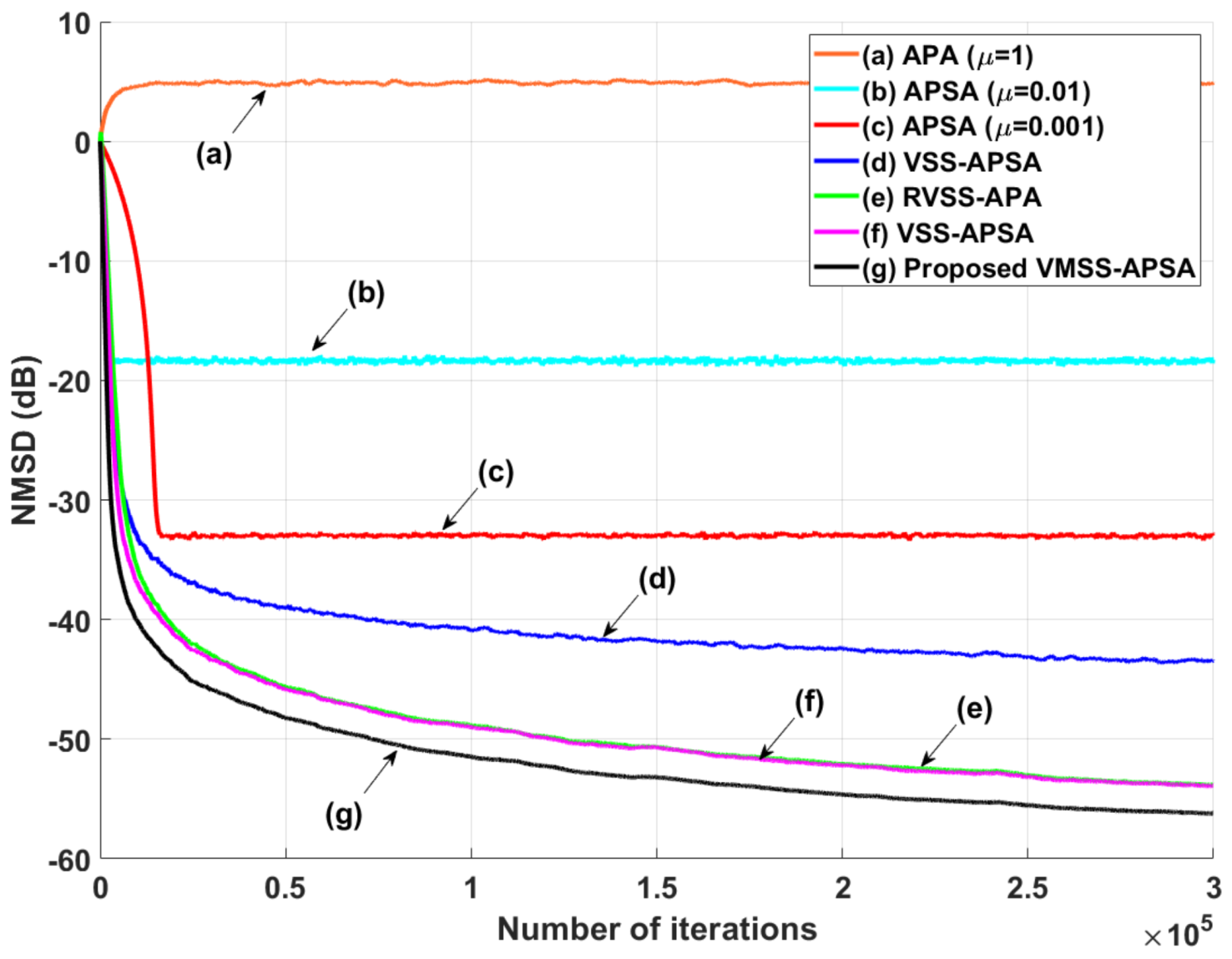
4.1. System Identification Scenarios under Impulsive Noise
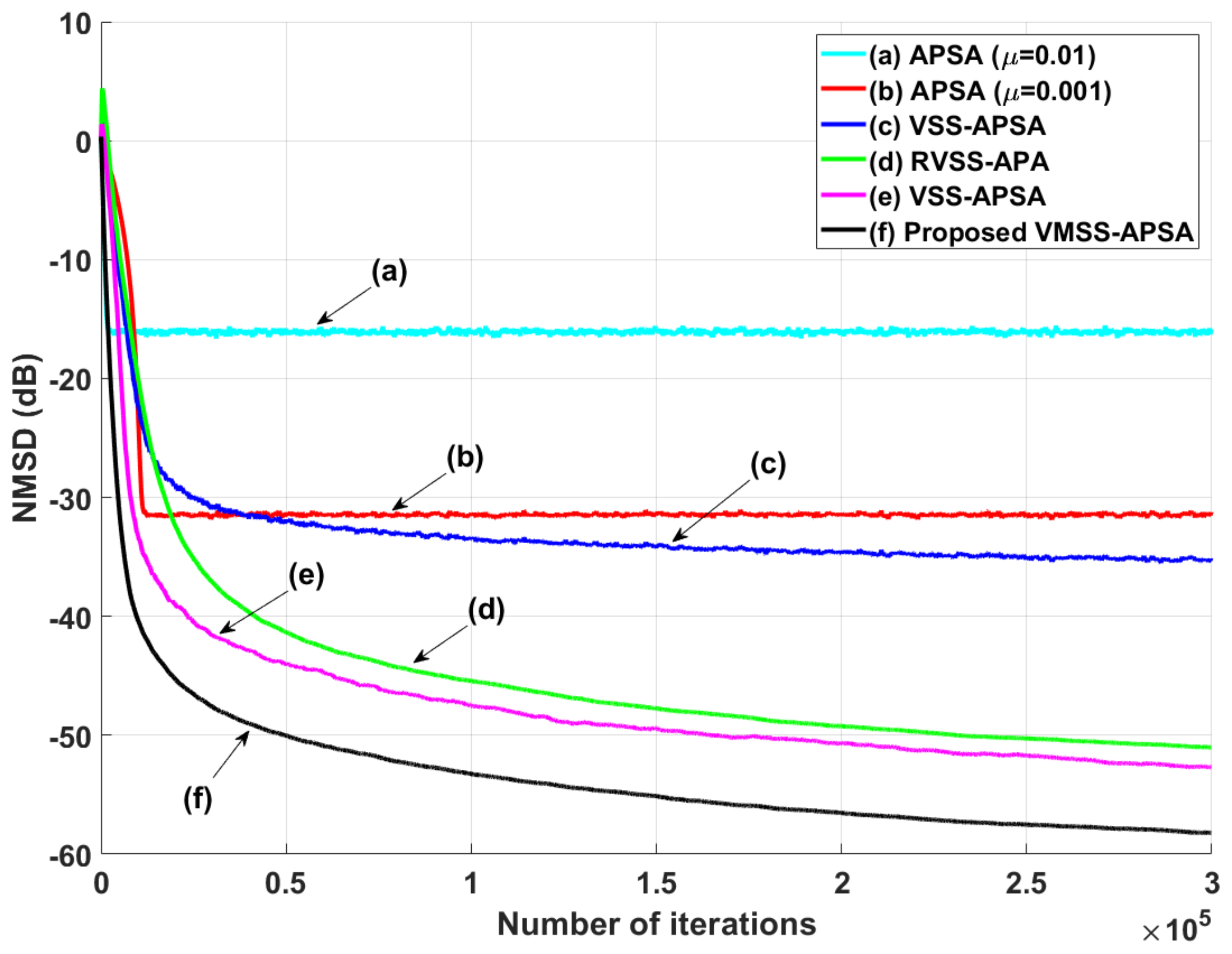
4.2. System Sudden-Change Scenarios
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiang, M.; Xia, Y.; Mandic, D.P. Performance Analysis of Deficient Length Quaternion Least Mean Square Adaptive Filters. IEEE Trans. Signal Process. 2019, 68, 65–80. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, H. A Novel Method for Online Extraction of Small-Angle Scattering Pulse Signals from Particles Based on Variable Forgetting Factor RLS Algorithm. Sensors 2021, 21, 5759. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, Y.; Sun, L. A Proportionate Normalized Maximum Correntropy Criterion Algorithm with Correntropy Induced Metric Constraint for Identifying Sparse Systems. Symmetry 2018, 10, 683. [Google Scholar] [CrossRef]
- Dogariu, L.-M.; Stanciu, C.L.; Elisei-Iliescu, C.; Paleologu, C.; Benesty, J.; Ciochina, S. Tensor-Based Adaptive Filtering Algorithms. Symmetry 2021, 13, 481. [Google Scholar] [CrossRef]
- Kumar, K.; Pandey, R.; Karthik, M.L.N.S.; Bhattacharjee, S.S.; George, N.V. Robust and sparsity-aware adaptive filters: A Review. Signal Process. 2021, 189, 108276. [Google Scholar] [CrossRef]
- Long, X.; Zhao, H.; Hou, X.; Quan, W. A variable regularization parameter widely linear complex-valued NLMS algorithm: Performance analysis and wind prediction. Signal Process. 2022, 201, 108731. [Google Scholar] [CrossRef]
- Yu, Y.; Huang, Z.; Zakharov, Y.; Lamare, R.C. Sparsity-Aware Robust Normalized Subband Adaptive Filtering Algorithms With Alternating Optimization of Parameters. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 3934–3938. [Google Scholar] [CrossRef]
- Abadi, M.S.E.; Msgarani, H.; Khademiyan, S.M. Robust Variable Step-Size Affine Projection Sign Algorithm Against Impulsive Noises. Circuits Syst. Signal Process. 2019, 39, 1471–1488. [Google Scholar] [CrossRef]
- Yu, Y.; Lu, L.; Zahkhav, Y.; Lamare, R.C.; Chen, B. Robust Sparsity-Aware RLS Algorithms With Jointly-Optimized Parameters Against Impulsive Noise. IEEE Signal Process. Lett. 2022, 29, 1037–1041. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Zakharov, Y.V.; Li, Y.; Chen, B. Affine-Projection Lorentzian Algorithm for Vehicle Hands-Free Echo Cancellation. IEEE Trans. Veh. Technol. 2021, 70, 2561–2575. [Google Scholar] [CrossRef]
- Yi, Y.; He, H.; Lamare, R.C.; Chen, B. General Robust Subband Adaptive Filtering: Algorithms and Applications. IEEE/ACM Trans. Audio Speech Lang. Process. 2022, 30, 2128–2140. [Google Scholar]
- Ozeki, K.; Umeda, T. An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electron. Commun. Jpn. 1984, 67, 19–27. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, Y.; Huang, X.; Jin, Z. A Sparsity-Aware Variable Kernel Width Proportionate Affine Projection Algorithm for Identifying Sparse Systems. Symmetry 2019, 11, 1218. [Google Scholar] [CrossRef]
- Li, G.; Wang, G.; Dai, Y.; Sun, Q.; Yang, X.; Zhang, H. Affine projection mixed-norm algorithms for robust filtering. Signal Process. 2021, 187, 108153. [Google Scholar] [CrossRef]
- Shin, J.; Kim, J.; Kim, T.K.; Yoo, J. Lp-Norm-like Affine Projection Sign Algorithm for Sparse System to Ensure Robustness against Impulsive Noise. Symmetry 2021, 13, 1916. [Google Scholar] [CrossRef]
- Shao, T.; Zheng, Y.R.; Benesty, J. An affine projection sign algorithm robust against impulsive interference. IEEE Signal Process. Lett. 2010, 17, 327–330. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, Y.R.; Grant, S.L. Proportionate affine projection sign algorithm for network echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2273–2284. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Choi, H.; Park, P. Improved affine projection sign algorithm for sparse system identification. Electron. Lett. 2012, 48, 927–929. [Google Scholar] [CrossRef]
- Kim, J.H.; Chang, J.-H.; Nam, S.W. Affine projection sign algorithm with l1 minimization-based variable step-size. Signal Process. 2014, 105, 376–380. [Google Scholar] [CrossRef]
- Shin, J.; Yoo, J.; Park, P. Variable step-size affine projection sign algorithm. Electron. Lett. 2012, 48, 483–485. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Park, P. Variable step-size affine projection sign algorithm. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 274–278. [Google Scholar]
- Rey Vega, L.; Rey, H.; Benesty, J. A robust variable step-size affine projection algorithm. Signal Process. 2010, 90, 2806–2810. [Google Scholar] [CrossRef]
- Rey Vega, L.; Rey, H.; Benesty, J.; Tressens, S. A new robust variable step-size NLMS algorithm. IEEE Trans. Signal Process. 2008, 56, 1878–1893. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Park, P. Variable step-size sign algorithm against impulsive noises. IET Signal Process. 2015, 9, 506–510–176. [Google Scholar] [CrossRef]
- Shin, J.; Yoo, J.; Park, P. Variable step-size sign subband adaptive filter. IEEE Signal Process. Lett. 2013, 20, 173–176. [Google Scholar] [CrossRef]
- Yoo, J.; Shin, J.; Park, P. A band-dependent variable step-size sign subband adaptive filter. Signal Process. 2014, 104, 407–411. [Google Scholar] [CrossRef]
- Tiglea, D.G.; Candido, R.; Silva, M.T.M. A Variable Step Size Adaptive Algorithm With Simple Parameter Selection. IEEE Signal Process. Lett. 2022, 29, 1774–1778. [Google Scholar] [CrossRef]
- Zou, Y.; Chan, S.; Ng, T. A recursive least m-estimate (RLM) adaptive filter for robust filtering in impulse noise. IEEE Signal Process. Lett. 2000, 7, 324–326. [Google Scholar] [CrossRef]


| Initialization values: , |
|---|
| Parameter setting: |
| BEGIN |
| FOR to M DO |
| IF |
| ELSE |
| END |
| ENDFOR |
| END |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shin, J.; Park, B.Y.; Lee, W.I.; Yoo, J. Variable Matrix-Type Step-Size Affine Projection Sign Algorithm for System Identification in the Presence of Impulsive Noise. Symmetry 2022, 14, 1985. https://doi.org/10.3390/sym14101985
Shin J, Park BY, Lee WI, Yoo J. Variable Matrix-Type Step-Size Affine Projection Sign Algorithm for System Identification in the Presence of Impulsive Noise. Symmetry. 2022; 14(10):1985. https://doi.org/10.3390/sym14101985
Chicago/Turabian StyleShin, Jaewook, Bum Yong Park, Won Il Lee, and Jinwoo Yoo. 2022. "Variable Matrix-Type Step-Size Affine Projection Sign Algorithm for System Identification in the Presence of Impulsive Noise" Symmetry 14, no. 10: 1985. https://doi.org/10.3390/sym14101985
APA StyleShin, J., Park, B. Y., Lee, W. I., & Yoo, J. (2022). Variable Matrix-Type Step-Size Affine Projection Sign Algorithm for System Identification in the Presence of Impulsive Noise. Symmetry, 14(10), 1985. https://doi.org/10.3390/sym14101985






