Stability Analysis of an Upwind Difference Splitting Scheme for Two-Dimensional Saint–Venant Equations
Abstract
1. Introduction
2. The Proposed Methods
2.1. Formulation of the Problem
2.2. A Special Form of the Saint–Venant Equations
2.3. Upwind Implicit Difference Scheme
3. Results
3.1. Stability of the Difference Scheme
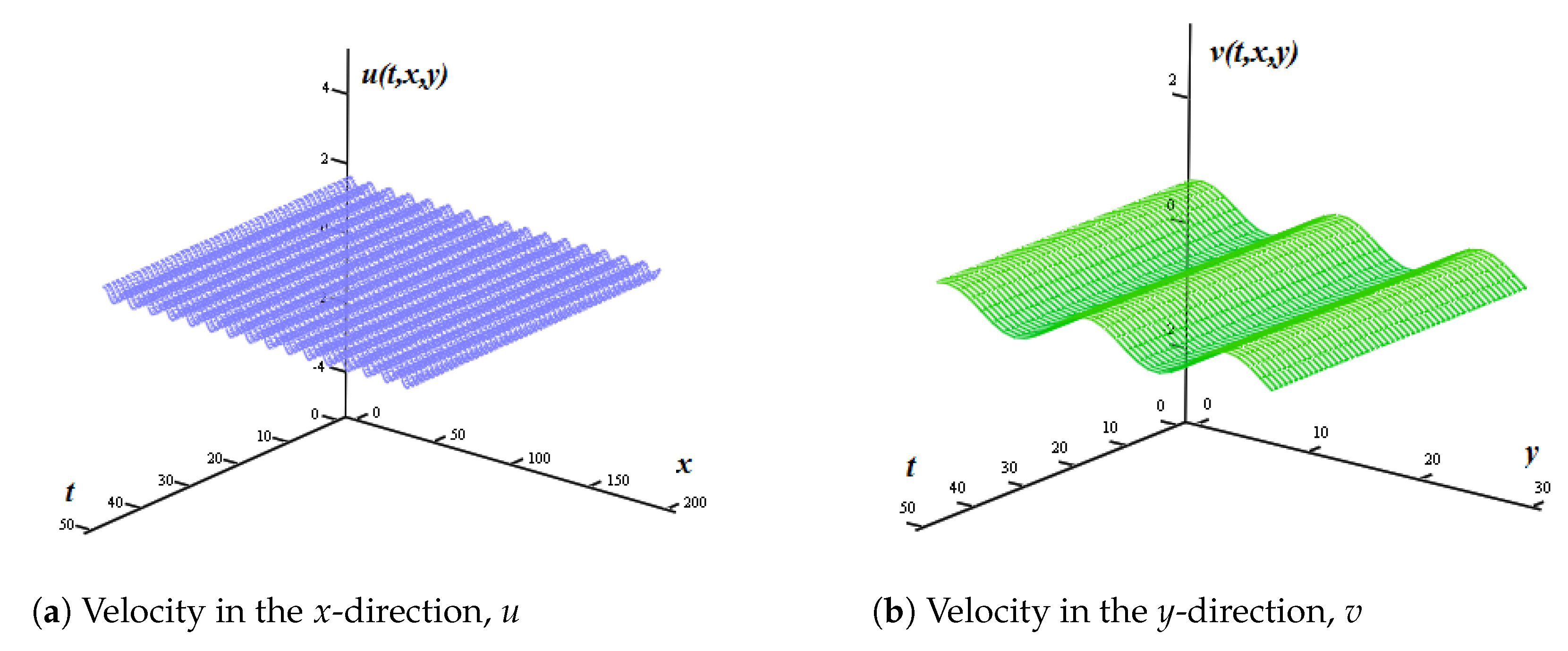
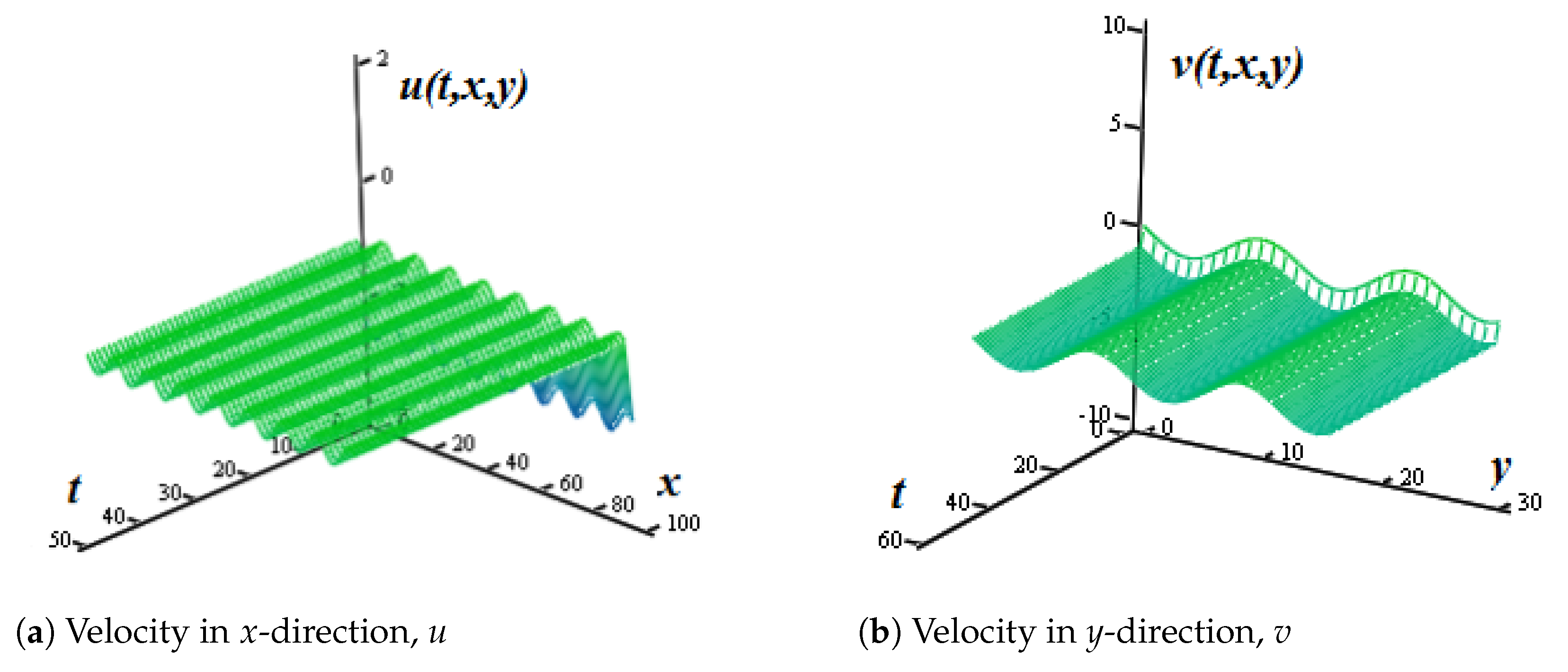
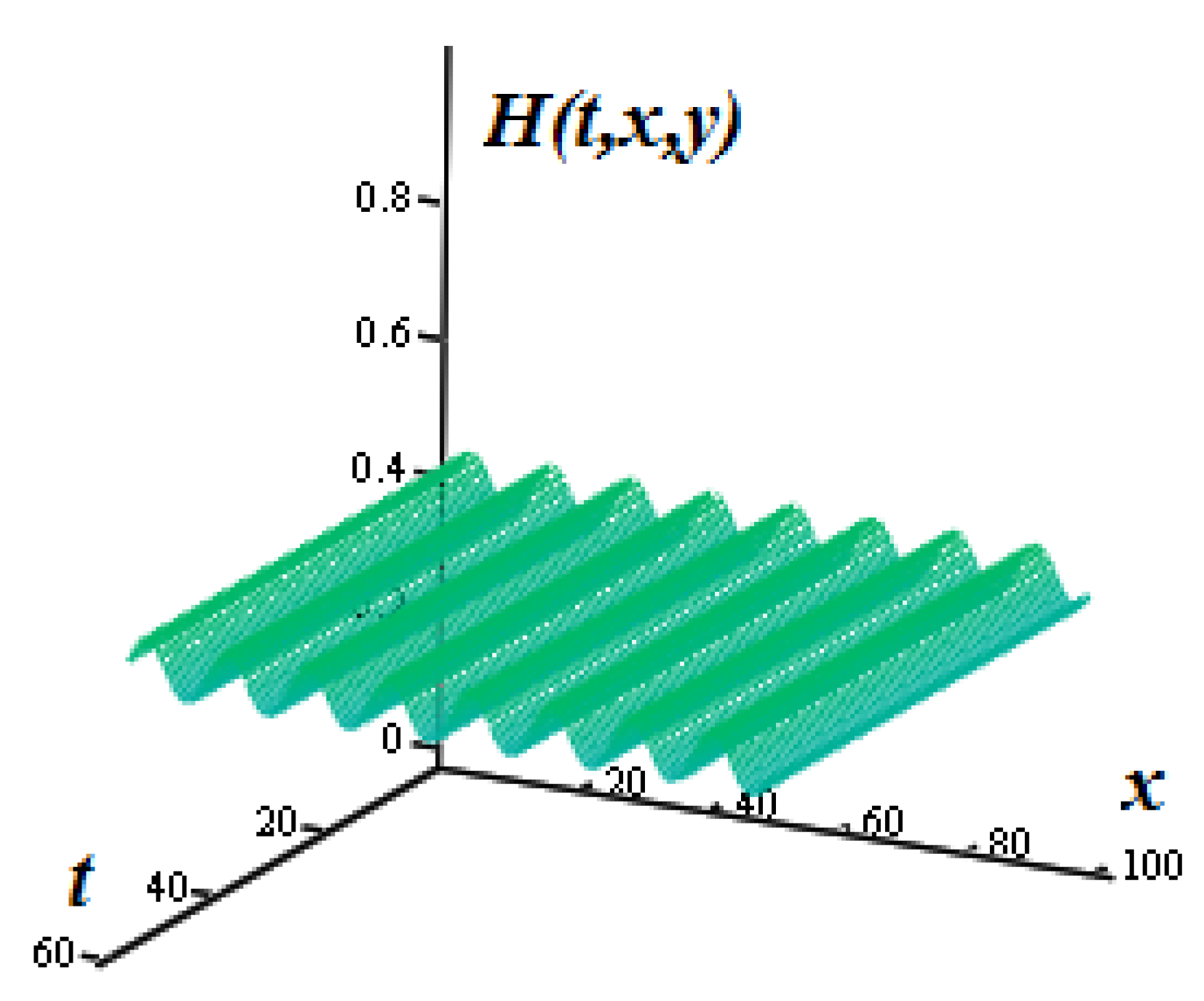
3.2. Numerical Example 1
3.3. Numerical Example 2
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kader, M.; Badé, R.; Saley, B. Study of the 1D Saint-Venant Equations and Application to the Simulation of a Flood Problem. J. Appl. Math. Phys. 2020, 8, 1193. [Google Scholar]
- Zendrato, N.; Chrysanti, A.; Yakti, B.; Adityawan, M. Application of Finite Difference Schemes to 1D St. Venant for Simulating Weir Overflow. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 147, p. 03011. [Google Scholar]
- Ersoy, M.; Lakkis, O.; Townsend, P. A Saint-Venant Model for Overland Flows with Precipitation and Recharge. Math. Comput. Appl. 2021, 26, 1. [Google Scholar]
- Vasiliev, O.F.; Godunov, S.K.; Pritvits, N.A.; Temnoeva, T.A.; Fryazinova, I.L.; Shugrin, S.M. Numerical method for calculating the propagation of long waves in open channels and its application to the flood problem. Dokl. AN SSSR 1963, 151, 525–527. [Google Scholar]
- Shugrin, S.M. On inhomogeneous difference schemes. J. Comput. Math. Phys. 1966, 6, 184–185. [Google Scholar]
- Whitham, G.B. The effects of hydraulic resistance in thedam-break problem. Proc. R. Soc. Lond. Ser. A 1955, 227, 399–407. [Google Scholar]
- Dressler, R.F. Comparison of theories and experiments for thehydraulic dam-break wave. Int. Assoc. Sci. Hydrol. 1954, 3, 319–328. [Google Scholar]
- Montuori, C.; Cimini, G.B.; Favali, P. Teleseismic tomography of the southern Tyrrhenian subduction zone: New results from sea floor and land recordings. J. Geophys. Res. 2007, 112, B03311. [Google Scholar] [CrossRef]
- Vasiliev, O.F.; Gladyshev, M.T.; Sudobicher, V.G. Numerical solution of problems on flows with discontinuous waves in open channels. Numer. Methods Contin. Mech. 1970, 1, 3. [Google Scholar]
- Sanders, B.F. High-resolution and non-oscillatory solution of the St. Venant equations in non-rectangular and non-prismatic channels. J. Hydraul. Res. 2010, 3, 321–330. [Google Scholar]
- Diagne, A.; Tang, S.; Diagn, M.; Krstic, M. State Feedback Stabilization of the Linearized Bilayer Saint-Venant Model. IFAC Int. Fed. Autom. Control. 2016, 49, 130–135. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. Numerical solution of the Saint-Venant equations by an efficient hybrid finite-volume/finite-difference method. J. Hydrodyn. 2018, 30, 189–202. [Google Scholar] [CrossRef]
- Yang, Z.; Bai, F.; Xiang, K. A lattice Boltzmann model for the open channel flows described by the Saint-Venant equations. R. Soc. Open Sci. 2019, 6, 190439. [Google Scholar] [CrossRef]
- Gracia, N.; Suharjito; Viska, N. Saint-Venant Model Analysis of Trapezoidal Open Channel Water Flow Using Finite Difference Method. In Proceedings of the 4th International Conference on Computer Science and Computational Intelligence, 2019, Procedia Computer Science, Yogyakarta, Indonesia, 12–13 September 2019; Volume 157, pp. 6–15. [Google Scholar]
- Bastin, G.; Coron, J.-M. Stability and Boundary Stabilization of 1-D Hyperbolic Systems. Prog. Nonlinear Differ. Equ. Their Appl. 2016, 88, 280. [Google Scholar]
- Bastin, G.; Coron, J.-M. A quadratic Lyapunov function for hyperbolic density-velocity systems with nonuniform steady states. Syst. Control. Lett. 2017, 104, 66–71. [Google Scholar] [CrossRef]
- Coron, J.-M.; Bastin, G. Dissipative boundary conditions for one-dimensional quasi-linear hyperbolic systems: Lyapunov stability for the C1-norm. SIAM J. Control Optim. 2015, 53, 1464–1483. [Google Scholar] [CrossRef]
- Coron, J.-M.; Novel, B.A.; Bastin, G. A Lyapunov approach to control irrigation canals modeled by Saint-Venant equations. In Proceedings of the CD-Rom, Karlsruhe, Germany, 31 August–3 September 1999; Paper F1008-5, ECC99. pp. 3178–3183. [Google Scholar]
- Coron, J.-M.; Hu, L.; Olive, G. Finitetime boundary stabilization of general linear hyperbolic balance laws via Fredholm backstepping transformation. Automatica 2017, 84, 95–100. [Google Scholar] [CrossRef]
- Coron, J.-M.; Vazquez, R.; Krstic, M.; Bastin, G. Local exponential H2 stabilization of a 2×2 quasilinear hyperbolic system using backstepping. SIAM J. Control. Optim. 2013, 51, 2005–2035. [Google Scholar] [CrossRef]
- Diagne, A.; Diagne, M.; Tang, S.; Krstic, M. Backstepping stabilization of the linearized Saint-Venant-exner model. Autom. J. IFAC 2017, 76, 345–354. [Google Scholar] [CrossRef]
- Hayat, A.; Shang, P. A quadratic Lyapunov function for Saint-Venant equations with arbitrary friction and space-varying slope. Automatica 2019, 100, 52–60. [Google Scholar] [CrossRef]
- Jane, A. Accurate and Efficient Numerical Solutions for the Saint Venant Equations of Open Channel Flow; University of Nottingham: Nottingham, UK, 1999. [Google Scholar]
- Sleigh, P.A. The St Venant Equations School of Civil Engineering; University of Leeds: Leeds, UK, 2000. [Google Scholar]
- Aldrighetti, E. Computational Hydraulic Techniques for the Saint Venant Equations in Arbitrarily Shaped Geometry; Università degli Studi di Trento: Trento, Italy, 2007. [Google Scholar]
- Giovangigli, V.; Tran, B. Mathematical Analysis of a Saint-Venant Model with Variable Temperature. Math. Model. Methods Appl. Sci. 2010, 20, 1251–1297. [Google Scholar] [CrossRef]
- Lin, M.F. Modeling and Control Design of River Systems. Modelling and Control Design of River Systems. Ph.D. Thesis, Department of Electrical and Electronic Engineering, University of Melbourne, Melbourne, Australia, 2012. [Google Scholar]
- Aloev, R.; Khudayberganov, M.U.; Blokhin, A.M. Construction and research of adequate computational models for quasilinear hyperbolic systems. Numer. Algebr. Control. Optim. 2018, 8, 287–299. [Google Scholar]
- Aloev, R.; Eshkuvatov, Z.K.; Khudayberganov, M.U.; Long, N. A discrete analogue of energy integral for a difference scheme for quasilinear hyperbolic systems. Appl. Math. 2018, 9, 789–805. [Google Scholar] [CrossRef]
- Aloev, R.; Berdyshev, A.; Akbarova, A.; Baishemirov, Z. Development of an algorithm for calculating stable solutions of the Saint-Venant equation using an upwind implicit difference scheme. East.-Eur. J. Enterp. Technol. 2021, 4, 47–56. [Google Scholar] [CrossRef]
- Khoperskov, A.; Khrapov, S. A numerical simulation of the shallow water flow on a complex topography. In Numerical Simulations in Engineering and Science; IntechOpen: London, UK, 2018; pp. 237–254. [Google Scholar]
- Kovyrkina, O.A.; Ostapenko, V.V. On the construction of high-accuracy combined difference schemes. Dokl. Math. 2018, 478, 517–522. [Google Scholar] [CrossRef]
- Shokin, Y.I.; Rychkov, A.D.; Khakimzyanov, G.S.; Chubarov, L.B. A combined computational algorithm for solving the problem of long surface waves runup on the shore. Russ. J. Numer. Anal. Math. Model. 2016, 31, 217–227. [Google Scholar] [CrossRef]
- Shokin, S.A.; Rychkov, A.D.; Chubarov, L.B. Numerical modeling of tsunami wave run-up on the coast using the large-particle method. Math. Model. 2015, 27, 99–112. [Google Scholar]
- Lich, T.G.; Luat, L.K. Boundary conditions for the two-dimensional Saint-Venant equation system. Appl. Math. Model. 1992, 16, 498–502. [Google Scholar] [CrossRef]
- Lich, T.G.; Cuong, L.V.; Son, N.M. Calculation of the horizontal two-dimensional unsteady flow by the method of characteristics. Vietnam J. Mech. 2003, 25, 49–64. [Google Scholar] [CrossRef][Green Version]
- Kulikovskii, A.G.; Pogorelov, N.V.; Semenov, A.Y. Mathematical Problems of Numerical Solution of Hyperbolic Systems of Equations; Fizmatlit: Moscow, Russia, 2001. [Google Scholar]
- Burguete, J.; García-Navarro, P.; Murillo, J. Numerical boundary conditions for globally mass conservative methods to solve the shallow-water equations and applied to river flow. Int. J. Numer. Methods Fluids 2006, 51, 585–615. [Google Scholar] [CrossRef]
- Castro, M.J.; Ortega, S.; Pares, C. Well-balanced methods for the shallow water equations in spherical coordinates. Comput. Fluids 2017, 157, 196–207. [Google Scholar] [CrossRef]
- Berthon, C.; Chalons, C. A fully well-balanced, positive and entropy-satisfying Godunov-type method for the shallow-water equations. Math. Comput. 2016, 85, 1281–1307. [Google Scholar] [CrossRef]
- Godunov, S.K. Equations of Mathematical Physics, 2nd ed.; Nauka, USSR: Moscow, Russia, 1976. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berdyshev, A.; Aloev, R.; Bliyeva, D.; Dadabayev, S.; Baishemirov, Z. Stability Analysis of an Upwind Difference Splitting Scheme for Two-Dimensional Saint–Venant Equations. Symmetry 2022, 14, 1986. https://doi.org/10.3390/sym14101986
Berdyshev A, Aloev R, Bliyeva D, Dadabayev S, Baishemirov Z. Stability Analysis of an Upwind Difference Splitting Scheme for Two-Dimensional Saint–Venant Equations. Symmetry. 2022; 14(10):1986. https://doi.org/10.3390/sym14101986
Chicago/Turabian StyleBerdyshev, Abdumauvlen, Rakhmatillo Aloev, Dana Bliyeva, Sardor Dadabayev, and Zharasbek Baishemirov. 2022. "Stability Analysis of an Upwind Difference Splitting Scheme for Two-Dimensional Saint–Venant Equations" Symmetry 14, no. 10: 1986. https://doi.org/10.3390/sym14101986
APA StyleBerdyshev, A., Aloev, R., Bliyeva, D., Dadabayev, S., & Baishemirov, Z. (2022). Stability Analysis of an Upwind Difference Splitting Scheme for Two-Dimensional Saint–Venant Equations. Symmetry, 14(10), 1986. https://doi.org/10.3390/sym14101986





