Certain New Development to the Orthogonal Binary Relations

Abstract

In this study, inspired by the concept of B-metric-like space (BMLS), we introduce the concept of orthogonal B-metric-like space (OBMLS) via a hybrid pair of operators. Additionally, we establish the concept of orthogonal dynamic system (ODS) as a generalization of the dynamic system (DS), which improves the existing results for analysies such as those presented here. By applying this, some new refinements of the $F_{\perp }$-Suzuki-type ($F_{\perp }$-ST) fixed-point results are presented. These include some tangible instances, and applications in the field of nonlinear analysis are given to highlight the usability and validity of the theoretical results.

1. Introduction and Preliminaries

Fixed point theory (FPT) and its applications provide an important framework for the study of symmetry in mathematics [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. The literature contains many extensions of the concept of FPT in metric spaces (MSs) and its topological structure. Matthews [18] introduced the notion of partial metric space (PMS) and proved that the Banach contraction theorem (BCT) (or contraction theorem) can be generalized to the partial metric context for applications in program verification. The concept of b-metric space (BMS) was introduced and studied by Czerwik [19]. Recently, Amini-Harandi [20] introduced the notion of metric-like space (MLS). Afterward, Alghamdi et al. [21] introduced the notion of BMLS, which is an interesting generalization of PMS and MLS. While examining this with the PMS, they ascertain that every PMS is an BMLS, but the converse does not need to be true, showing that a BMLS is more general structure than the PMS and MLS.

The contraption of DS is a strong formalistic apparatus, associated with a large-spectrum analysis of multistage decision-making problems (MDMP). Such problems appear and are congruent in essentially all human activities. Unfavorably, for explicit reasons, the analysis of MDMP is difficult. MDMP are characteristic of all DS in which the associated variables are state and decision variables (see more, [22,23]). In recent years, Klim and Wardowski [24], discuss the idea of DS instead of the Picard iterative sequence in the context of fixed-point theory. Their objective was further exploited by numerous researchers in many ways (see more details in [25]).

Recently, Gordji et al. [26] established the new idea of an orthogonality behavior in the context of metric spaces (MSs) and provided some new fixed-point theorems for the Banach contraction theorem (BCT) in the MSs class that is endowed with this new type of orthogonal binary relation ⊥.

The main objective of this manuscript is to introduce and investigate a new concept of OBMLS and ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$ for hybrid pairs of mappings. Some new, related, multi-valued $F_{\perp }$ -ST fixed-point theorems are established with respect to ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$. Our investigation is completed by tangible examples and applications in ordinary differential equations and nonlinear fractional differential equations.

Hereinafter, we recall the definition of the orthogonal set (briefly $\widehat{O}$-set) and some related fixed-point results.

Definition 1.

[26] A $\widehat{O}$-set is a pair $(\mathbb{C},\perp )$ where $\perp \subseteq \mathbb{C}\times \mathbb{C}$ form a binary relation and $\mathbb{C}$ is a non-empty set; therefore, we have

$$\exists {\breve{e}}_0\in \mathbb{C}\mathit{such}\mathit{that}\breve{e}\perp {\breve{e}}_0(\mathit{or}{\breve{e}}_0\perp \breve{e})\forall \breve{e}\in \mathbb{C}.$$

Example 1.

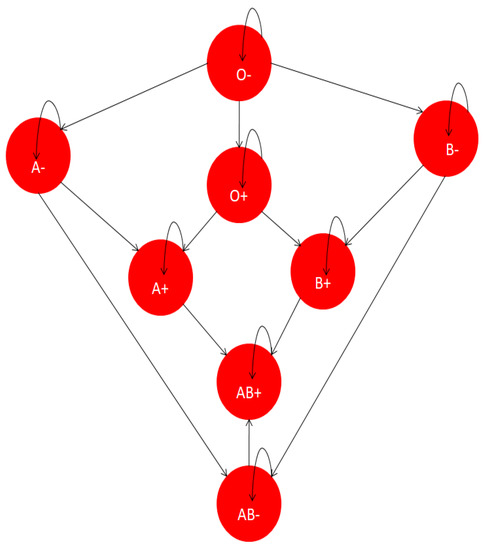
Define ⊥ on $\mathbb{C}\ne \varphi$ by $\breve{e}\perp \widehat{e}$, where we consider $\mathbb{C}$ to be the collection of all people in the world. Let $\breve{e}$ provide blood to $\widehat{e}$. Based on Figure 1, if ${\widehat{e}}_0$ is a body in so that his/her blood group type is O-negative, we can write ${\widehat{e}}_0\perp \widehat{e}$∀$\widehat{e}\in \mathbb{C}$. This implies that $\left(\mathbb{C},\perp \right)$ is an $\widehat{O}$-set. According to this fashion, in the $\widehat{O}$ set, ${\widehat{e}}_0$ is not unique. Note that, in this logical example, ${\widehat{e}}_0$ may be a body with the blood group type $AB$-positive. Therefore, we write $\widehat{e}\perp {\widehat{e}}_0$∀$\widehat{e}\in \mathbb{C}$.

Figure 1. Orthogonal blood groups relations.

Definition 2.

[26] A sequence $\left\{{\widehat{e}}_n\right\}$ on $\left(\mathbb{C},\perp \right)$ is known as orthogonal sequence ($\widehat{O}$-sequence) if the following condition holds true

$$\forall \kappa \in \mathbb{N},{\widehat{e}}_{\kappa }\perp {\widehat{e}}_{\kappa +1}(\mathit{or}{\widehat{e}}_{\kappa +1}\perp {\widehat{e}}_{\kappa }).$$

Definition 3.

[26] The triplet pair $\left(\mathbb{C},\perp ,d\right)$ is known as orthogonal MS ($\widehat{O}$-MS) if $\left(\mathbb{C},\perp \right),$ is an $\widehat{O}$-set and $\left(\mathbb{C},d\right)$ is an MS.

Theorem 1.

[26] Let triplet pair $\left(\mathbb{C},\perp ,d\right)$ be an $\widehat{O}$-complete MS (complete MS not needed) and $0<\delta <1$. Let $\mu :\mathbb{C}\to \mathbb{C}$, such that the following conditions hold true:

(i) 

${\widehat{O}}_{\perp }$—continuous;

(ii) 

${\widehat{O}}_{\perp }$—contraction mapping endowed with Lipschitz constant;

(iii) 

${\widehat{O}}_{\perp }$—preserving. Then, μ possesses a unique fixed point. Moreover, $\lim {\mu }^i\left(\breve{e}\right)=\breve{e}$∀$n\in \mathbb{C}$.

Alghamdi et al. [21] introduced the notion of b-metric-like space as follows:

Definition 4.

A BMLS on a non-empty set $\mathbb{C}$ is a function $\xi :\mathbb{C}\times \mathbb{C}\to {\check{R}}^{+}\cup \left\{0\right\}$ such that, for each ${\breve{e}}_1,{\breve{e}}_2,{\breve{e}}_3\in \mathbb{C}$ with $s\ge 1$, we have

(${\xi }_i$)

if $\xi \left({\breve{e}}_1,{\breve{e}}_2\right)=0$ implies ${\breve{e}}_1={\breve{e}}_2$;

(${\xi }_{ii}$)

$\xi \left({\breve{e}}_1,{\breve{e}}_2\right)=\xi \left({\breve{e}}_2,{\breve{e}}_1\right)$;

(${\xi }_{iii}$)

$\xi \left({\breve{e}}_1,{\breve{e}}_3\right)\le s[\xi \left({\breve{e}}_1,{\breve{e}}_2\right)+\xi \left({\breve{e}}_2,{\breve{e}}_3\right)]$.

The pair $\left(\mathbb{C},\xi \right)$ is known as a BMLS.

Definition 5.

Let $\left(\mathbb{C},\zeta \right)$ be a BMLS. Then, we have

(i) 

a sequence $\left\{{\breve{e}}_n\right\}$ of $\mathbb{C}$ converges to a point $\breve{e}\in \mathbb{C}$ iff

$$\underset{n\to \infty }{\lim }\xi \left(\breve{e},{\breve{e}}_n\right)=\xi \left(\breve{e},\breve{e}\right).$$

(ii) 

a sequence $\left\{{\breve{e}}_n\right\}$ of BMLS $\left(\mathbb{C},\xi \right)$ is known as a Cauchy-sequence, iff ${\lim }_{n,m\to \infty }\xi \left({\breve{e}}_n,{\breve{e}}_m\right)$ exists (and is finite).

(iii) 

a BMLS $\left(\mathbb{C},\xi \right)$ is known as complete if every Cauchy-sequence $\left\{{\breve{e}}_n\right\}\in \mathbb{C}$ converges and is endowed with $\tau \left(\xi \right)$ to $\breve{e}\in \mathbb{C}$, such that ${\lim }_{n,m\to \infty }\xi \left({\breve{e}}_n,{\breve{e}}_m\right)=\xi \left(\breve{e},\breve{e}\right)={\lim }_{n\to \infty }\xi \left(\breve{e},{\breve{e}}_n\right)$.

Nadler [27] developed the concept of Hausdorff metric (HM) and improved the BCT for multi-valued operators instead of single-valued operators. Herein, we investigate the concept of HM-like in light of HM, as follows. Let $\left(\mathbb{C},\xi \right)$ be a BMLS. For ${\breve{e}}_1\in \mathbb{C}$ and $V_1\subseteq \mathbb{C}$, let ${\xi }_b\left({\breve{e}}_1,V_1\right)=\inf \left\{\xi \left({\breve{e}}_1,{\breve{e}}_2\right):{\breve{e}}_2\in V_2\right\}.$ Define $\widehat{H}:CB\left(\mathbb{C}\right)\times CB\left(\mathbb{C}\right)\to \left[0,+\infty \right)$ by

$$\widehat{H}\left(V_1,V_2\right)=\max \left\{\underset{{\breve{e}}_1\in V_1}{\sup }{\xi }_b({\breve{e}}_1,V_2),\underset{{\breve{e}}_2\in V_2}{\sup }{\xi }_b({\breve{e}}_1,V_1)\right\}$$

for each $V_1,V_2\in CB\left(\mathbb{C}\right).$$CB\left(\mathbb{C}\right)$ denotes the family of all non-empty closed and bounded-subsets of $\mathbb{C}$ and $CL\left(\mathbb{C}\right)$ denotes the family of all non-empty closed-subsets of $\mathbb{C}$.

Theorem 2.

Let $(\mathbb{C},ð)$ be a complete MS and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ is known as Nadler contraction mapping, if $\sigma \in [0,1)$ exists in such a way that

$$\widehat{H}(\mu {\breve{e}}_1,\mu {\breve{e}}_2)\le \sigma ð({\breve{e}}_1,{\breve{e}}_2)\forall {\breve{e}}_1,{\breve{e}}_2\in \mathbb{C}.$$

Then, μ possesses at least one fixed point (see more details in [27]).

In 2012, Wardowski [28] developed the concept of a contraction operator known as an F-contraction and improved the Banach contraction theorem (BCT) via F-contraction, which is the real generalization of BCP. Then, the concept of F-contraction was advanced to the case of non-linear F-contractions with a dynamic system, justifying that F-contractions with a dynamic system have a more general structure than the F-contraction (see more details in [24]).

Definition 6.

[28] Let ${\nabla }_{ϝ}$ be the set of mapping $F:{\check{R}}^{+}⟶\check{R}$, satisfying each of the following axioms $\left(F_i\right)$, $\left(F_{ii}\right)$ and $\left(F_{iii}\right)$:

($F_i$)

∀${\breve{e}}_1,{\breve{e}}_2\in {\check{R}}^{+}$ such that

$${\breve{e}}_1<{\breve{e}}_2\Rightarrow F\left({\breve{e}}_1\right)<F\left({\breve{e}}_2\right).$$

($F_{ii}$)

∀$\left\{{\breve{e}}_a\right\}\in {\check{R}}^{+},$ we have

$$\underset{a⟶\infty }{\lim }{\breve{e}}_a=0\iff \underset{a⟶\infty }{\lim }F\left({\breve{e}}_a\right)=-\infty \forall a\in N.$$

($F_{iii}$)

$0<\varpi <1$ exists such that ${\lim }_{\beta \to 0}{\beta }^{\varpi }F\left(\beta \right)=0$. Let $\mathbb{C},b)$ be an MS and $\rho :\mathbb{C}\to \mathbb{C}$ is known as F-contraction, if $\tau \in {\check{R}}^{+}-\left\{0\right\}$ exists such that

$$ð(\rho {\breve{e}}_1,\rho {\breve{e}}_2)>0\Rightarrow \tau +F\left(ð(\rho {\breve{e}}_1,\rho {\breve{e}}_2)\right)\le F\left(ð({\breve{e}}_1,{\breve{e}}_2)\right)\mathit{for}\mathit{each}{\breve{e}}_1,{\breve{e}}_2\in \mathbb{C}.$$

We provide some related examples of mappings belonging to ${\nabla }_{ϝ}$ as follows:

Example 2.

[28] Let ${\nabla }_{ϝ}$ be the set of mappings $F_1,F_2,F_3,F_4:{\check{R}}^{+}⟶\check{R}$ defined by:

(1) 

$F_1\left(\breve{e}\right)=\ln \breve{e}$∀$\breve{e}>0$;

(2) 

$F_2\left(\breve{e}\right)=\breve{e}+ln\breve{e}$∀$\breve{e}>0$;

(3) 

$F_3\left(\breve{e}\right)=-\frac{1}{\sqrt{\breve{e}}}$∀$\breve{e}>0$;

(4) 

$F_4\left(\breve{e}\right)$$=\ln ({\breve{e}}^2+\breve{e})$∀$\breve{e}>0$.

Now, we recall the following basic concept of the dynamic system (DS):

Definition 7.

Let $\mu :\mathbb{C}\to C\left(\mathbb{C}\right)$ be a mapping. A set

$$\check{D}\left(\mu ,{\breve{e}}_0\right)=\left\{{\left({\breve{e}}_a\right)}_{a\ge 0}:{\breve{e}}_a\in \mu {\breve{e}}_{a-1}\forall a\in N\right\}.$$

known as DS $\check{D}\left(\mu ,{\breve{e}}_0\right)$ of μ with respect to the starting point ${\breve{e}}_0$. ${\breve{e}}_0\in \mathbb{C}$ is arbitrary and fixed. In light of $\check{D}\left(\mu ,{\breve{e}}_0\right),$${\left({\breve{e}}_a\right)}_{a\in N-\left\{0\right\}}$ onward has the form $\left({\breve{e}}_a\right)$ (see more in [24]).

We now recall some basic concepts of F-contraction with respect to the dynamic system (DS), as follows:

Theorem 3.

[24] Let $\mu :\mathbb{C}\to C\left(\mathbb{C}\right)$ be a multi-valued F-contraction with respect to a $\check{D}\left(\mu ,{\breve{e}}_0\right)$, if there is a function $\tau :{\check{R}}^{+}⟶\check{R}$, such that

$$d({\breve{e}}_a,{\breve{e}}_{a+1})>0\Rightarrow \tau \left(d({\breve{e}}_{a-1},{\breve{e}}_a)\right)+Fd({\breve{e}}_a,{\breve{e}}_{a+1})\le Fd({\breve{e}}_{a-1},{\breve{e}}_a)\forall a\in \mathbb{N}.$$

Assume that there are ${\breve{e}}_a\in \check{D}(\mu ,{\breve{e}}_0)$, such that $\lim {\inf }_{l\to a^{+}}\tau \left(l\right)>0$ for each $a\ge 0$ and a mapping $\mathbb{C}\ni {\breve{e}}_a⟼d({\breve{e}}_a,\mu {\breve{e}}_a)$ is $\check{D}(\mu ,{\breve{e}}_0)$ a dynamic lower semi-continuous mapping. Then, μ has a fixed point.

2. Main Results

First, to provide our new definition as a generalization of B-metric-like spaces:

Definition 8.

An OBMLS on a non-empty set $\mathbb{C}$ with $s\ge 1$ is a function $\zeta :\mathbb{C}\times \mathbb{C}\to {\check{R}}^{+}\cup \left\{0\right\}$ such that, for each ${\breve{e}}_1,{\breve{e}}_2,{\breve{e}}_3\in \mathbb{C}$ with respect to orthogonal relation (${\breve{e}}_1\perp {\breve{e}}_2\perp {\breve{e}}_3)$, if the following conditions hold:

(${\zeta }_i$)

if $\zeta \left({\breve{e}}_1,{\breve{e}}_2\right)=0$ implies ${\breve{e}}_1={\breve{e}}_2;$

(${\zeta }_{ii}$)

$\zeta \left({\breve{e}}_1,{\breve{e}}_2\right)=\zeta \left({\breve{e}}_2,{\breve{e}}_1\right);$

(${\zeta }_{iii}$)

$\zeta \left({\breve{e}}_1,{\breve{e}}_3\right)\le s[\zeta \left({\breve{e}}_1,{\breve{e}}_2\right)+\zeta \left({\breve{e}}_2,{\breve{e}}_3\right)].$

The pair $\left(\mathbb{C},\zeta \right)$ is known as an OBMLS.

Example 3.

Let $\mathbb{C}=\left\{0,1,2,3\right\}$ and $\zeta :\mathbb{C}\times \mathbb{C}\to {\check{R}}^{+}\cup \left\{0\right\}$ is given by

$$\begin{array}{ccccc}\zeta (0,0)=0& \zeta (1,1)=2& \zeta (2,2)=2& \zeta (3,3)=2& \zeta (0,1)=\frac{1}{5}\\ \zeta (0,2)=\frac{1}{5}& \zeta (0,3)=\frac{1}{5}& \zeta (1,2)=1& \zeta (1,3)=1& \zeta (2,3)=4\end{array}$$

$\forall {\breve{e}}_1,{\breve{e}}_2\in \mathbb{C}$ with respect to $\zeta \left({\breve{e}}_1,{\breve{e}}_2\right)=\zeta \left({\breve{e}}_2,{\breve{e}}_1\right)$ and ${\breve{e}}_1\perp {\breve{e}}_2$ if, and only if, ${\breve{e}}_1{\breve{e}}_2\ne 0.$ Then, $\left(\mathbb{C},\zeta \right)$ is an OBMLS with $s=2.$ The above example is not BMLS since $\zeta \left(1,2\right)=1>0.8=2[ð\left(1,0\right)+ð\left(0,2\right)].$

Remark 1.

Every BMLS is OBMLS, but the converse does not generally hold true.

The fashions of convergence, Cauchy sequence and completeness criteria are same as in BMLS. The term Hausdorff metric can easily be amplified to the case of an OBMLS.

Let $\left(\mathbb{C},\zeta \right)$ be an OBMLS. For ${\breve{e}}_1\in \mathbb{C}$ and $V_1\subseteq \mathbb{C}$, let ${\zeta }_b\left({\breve{e}}_1,V_2\right)=\inf \left\{\zeta \left({\breve{e}}_1,{\breve{e}}_2\right):{\breve{e}}_2\in V_2\right\}.$ Define $H_O:CB\left(\mathbb{C}\right)\times CB\left(\mathbb{C}\right)\to \left[0,+\infty \right)$ as by

$$H_O\left(V_1,V_2\right)=\max \left\{\underset{{\breve{e}}_1\in V_1}{\sup }{\zeta }_b({\breve{e}}_1,V_2),\underset{{\breve{e}}_2\in V_2}{\sup }{\zeta }_b({\breve{e}}_1,V_1)\right\}$$

for each $V_1,V_2\in CB\left(\mathbb{C}\right).$

In the following, the concept of ODS, ODS for a hybrid pair of mappings and its ⊥-preservation are introduced, and some elementary facts about these concepts are discussed.

Definition 9.

Let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$, ${\breve{e}}_0\in \mathbb{C}$ be a fixed point. A set

$${\check{D}}_{\perp }(\mu ,{\breve{e}}_0)=\left\{{\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha +1}{(\mathit{or}{\breve{e}}_{\alpha +1}\perp {\breve{e}}_{\alpha })}_{\alpha \in \mathbb{N}-\left\{0\right\}}:{\breve{e}}_{\alpha }\in \mu {\breve{e}}_{\alpha -1}\forall \alpha \in \mathbb{N}\right\}$$

is known as the ODS of μ with ${\breve{e}}_0$. Herein, ODS ${\check{D}}_{\perp }(\mu ,{\breve{e}}_0)$ and onward has the form ${\mu }_{\perp }\left({\breve{e}}_{\alpha }\right)$.

Definition 10.

Let $\rho :\mathbb{C}\to \mathbb{C}$ and let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$, ${\breve{e}}_0\in \mathbb{C}$ be a fixed point. A set

$${\check{D}}_{\perp }(\rho ,\mu ,{\breve{e}}_0)=\left\{{\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha +1}{(\mathit{or}{\breve{e}}_{\alpha +1}\perp {\breve{e}}_{\alpha })}_{\alpha \in \mathbb{N}-\left\{0\right\}}:{\breve{e}}_{\alpha +1}=\rho {\breve{e}}_{\alpha }\in \mu {\breve{e}}_{\alpha -1}\forall \alpha \in \mathbb{N}\right\}$$

is known as the ODS of ρ and μ with ${\breve{e}}_0$. Moreover, ODS ${\check{D}}_{\perp }(\rho ,\mu ,{\breve{e}}_0)$ and onward has the form ${\rho }_{\perp }\left({\breve{e}}_{\alpha }\right)$.

Example 4.

Define $\rho :[0,\infty )\to [0,\infty )$ and $\mu :[0,\infty )\to CB\left(\right[0,\infty \left)\right)$ as by $\rho \left(\breve{e}\right)={\breve{e}}^2$ and $\mu \left(\breve{e}\right)=[\breve{e}+2,\infty )$, respectively. The sequence $\left\{{\breve{e}}_{\alpha }\right\}$, as given by ${\breve{e}}_{\alpha }=\sqrt{{\breve{e}}_{\alpha -1}+2}$, is an ρ iterative sequence of μ with a starting point of $0.$

Definition 11.

Let $\left(\mathbb{C},\perp \right)$ be an $\widehat{O}$-set and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ are called the ⊥-preserving of μ if $\mu {\breve{e}}_{\alpha }\perp \mu {\breve{e}}_{\alpha +1}$ whenever ${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha +1}$ for $\alpha \in \mathbb{N}$.

Definition 12.

Let $\left(\mathbb{C},\perp \right)$ be an $\widehat{O}$-set and $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ are called the ⊥-preserving of a hybrid pair of mappings if $\rho {\breve{e}}_{\alpha }\perp \rho {\breve{e}}_{\alpha +1}\subseteq \mu {\breve{e}}_{\alpha }\perp \mu {\breve{e}}_{\alpha +1}$ whenever ${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha +1}$ for $\alpha \in \mathbb{N}$.

The first main result of this exposition is given as follows.

Definition 13.

Let $\left(\mathbb{C},\zeta ,s,\perp \right)$ be an OBMLS. Let $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ are called a hybrid pair of mappings of $F_{\perp }$-ST-I contraction with ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$, if for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right)$ such that

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha }),$$

implying that

$$\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0\Rightarrow \tau \left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\leqq F\left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(1)

$$\begin{array}{ccc}\hfill \widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })& =& {\sigma }_1(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })+{\sigma }_2({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})+{\sigma }_3({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha })\hfill \\ & & +\frac{{\sigma }_4({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })}{2s}+\frac{{\sigma }_5({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha -1})}{2s}\hfill \end{array}$$

∀${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha -1}$(or ${\breve{e}}_{\alpha -1}\perp {\breve{e}}_{\alpha })\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$, where $0\leqq {\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4,{\sigma }_5\leqq 1$ such that ${\sigma }_1+{\sigma }_2+{\sigma }_3+{\sigma }_4+{\sigma }_5=1$ and $1-{\sigma }_3-{\sigma }_5>0$.

Remark 2.

In our investigation, we examine that the following property does not hold true:

$$\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0,\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })>0foreach\alpha \in \mathbb{N}$$

(2)

then, there exist some ${\alpha }_0\in \mathbb{N}$, such that $\zeta (\rho {\breve{e}}_{{\alpha }_0},\rho {\breve{e}}_{{\alpha }_{0+1}})>0$ and $\zeta (\rho {\breve{e}}_{{\alpha }_0},\rho {\breve{e}}_{{\alpha }_0})=0$. Therefore, we obtain

$$\rho {\breve{e}}_{{\alpha }_{0-1}}=\rho {\breve{e}}_{{\alpha }_0}\in \mu {\breve{e}}_{{\alpha }_{0-1}},$$

which implies the existence of a common fixed point of the pair $(\rho ,\mu ).$ Therefore, considering the $\check{D}(\mu ,\rho ,{\breve{e}}_0)$, satisfying Equation (2) does not depress the generality of our investigation.

Theorem 4.

Let $(\mathbb{C},\zeta ,s,\perp )$ be an $\widehat{O}$-complete OBMLS. Let $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ are called a hybrid pair of mappings of the $F_{\perp }$-ST-I contraction with respect to ODS $\check{D}(\mu ,\rho ,{\breve{e}}_0).$ Assume that:

(O1) 

: If, in addition, the hybrid pair of mapping $(\rho ,\mu )$ are ⊥-preserving;

(O2) 

: There is ${\breve{e}}_w\in {\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$ such that, for each $l\ge 0$$\lim {\inf }_{k\to l^{+}}\tau \left(k\right)>0;$

(O3) 

: If, moreover, $F_{\perp }$ is super-additive, i.e., for ${\breve{e}}_1,{\breve{e}}_2,{\widehat{v}}_3,{\widehat{v}}_4\in {\check{R}}^{+}$, we have

$$F({\widehat{v}}_1{\breve{e}}_1+{\widehat{v}}_2{\breve{e}}_2)\le {\widehat{v}}_{2}F\left({\breve{e}}_1\right)+{\widehat{v}}_{2}F\left({\breve{e}}_2\right).$$

Then, ρ and μ have a common fixed point in $\left(\mathbb{C},\perp \right).$

Proof. 

Owing to the fact that the pair $\left(\mathbb{C},\perp \right)$ is an $\widehat{O}$-set, then there is ${\breve{e}}_0\in \mathbb{C}$, such that $\breve{e}\perp {\breve{e}}_0$ (or ${\breve{e}}_0\perp \breve{e}$) $\forall \breve{e}\in \mathbb{C}$. It follows that ${\breve{e}}_0\perp \rho {\breve{e}}_0$ (or $\rho {\breve{e}}_0\perp {\breve{e}}_0$). Upon setting ${\breve{e}}_1=\rho {\breve{e}}_0,$${\breve{e}}_2=\rho {\breve{e}}_1,···,$${\breve{e}}_{\alpha +1}=\rho {\breve{e}}_{\alpha }$$\forall \alpha \in \mathbb{N}\cup \left\{0\right\}.$ In case there is ${\breve{e}}_{{\alpha }_0}={\breve{e}}_{{\alpha }_{0+1}}$ for some $\alpha \in \mathbb{N}$, then our proof of 4 proceeds as follows. Therefore, without loss, we may assume that ${\breve{e}}_{\alpha }\ne {\breve{e}}_{\alpha +1}$$\forall \alpha \in \mathbb{N}$; thus, we have $\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0$ for each $\alpha \in \mathbb{N}-\left\{0\right\}.$ Since the hybrid pair of mapping $(\rho ,\mu )$ are ⊥-preserving, we can write

$${\check{D}}_{\perp }(\rho ,\mu ,{\breve{e}}_0)=\left\{{\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha +1}{(\mathit{or}{\breve{e}}_{\alpha +1}\perp {\breve{e}}_{\alpha })}_{\alpha \in \mathbb{N}\cup \left\{0\right\}}:{\breve{e}}_{\alpha +1}=\rho {\breve{e}}_{\alpha }\in \mu {\breve{e}}_{\alpha -1}\forall \alpha \in \mathbb{N}\right\}.$$

Thus, $\left\{{\breve{e}}_{\alpha }\right\}$ is an ODS $\check{D}(\mu ,\rho ,{\breve{e}}_0)$. Since $F_{\perp }$-ST-I is a contraction operator, we have

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\forall \alpha \in \mathbb{N}.$$

(3)

Therefore, (1), results in the following:

$$\begin{array}{ccc}\hfill F(\zeta ({\breve{e}}_{\alpha +1},{\breve{e}}_{\alpha +2})& =& F\left[\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})\right)+{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha })\right)\hfill \\ & & +\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })\right)}{2s}+\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha -1})\right)]}{2s}\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})\right)+{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha })\right)\hfill \\ & & +\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })\right)}{2s}+\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha -1})\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\hfill \\ & & +\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha +1})\right)}{2s}+\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha })\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\hfill \\ & & +\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha +1})\right)}{2s}+\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha })\right)}{2s}].\hfill \end{array}$$

(4)

Next, we certify the following inequality

$$\zeta ({\breve{e}}_{\alpha +1},{\breve{e}}_{\alpha +2})<\zeta ({\breve{e}}_{\alpha },{\breve{e}}_{\alpha +1})\forall \alpha \in \mathbb{N}.$$

(5)

Based on the contrary, we assume that there exist $r\in \mathbb{N}$ in such a way that $\zeta ({\breve{e}}_{r+1},{\breve{e}}_{r+2})\geqq \zeta ({\breve{e}}_r,{\breve{e}}_{r+1})$. Then, in view of (4) we have:

$$\begin{array}{ccc}\hfill F\left(\zeta ({\breve{e}}_{r+1},{\breve{e}}_{r+2})\right)& =& F\left[\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{r-1},\mu {\breve{e}}_{r-1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_r,\mu {\breve{e}}_r)\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{r-1},\mu {\breve{e}}_r)\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_r,\mu {\breve{e}}_{r-1})\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{r-1},\mu {\breve{e}}_{r-1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_r,\mu {\breve{e}}_r)\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{r-1},\mu {\breve{e}}_r)\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_r,\mu {\breve{e}}_{r-1})\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)+\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_{r+1})\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_r)\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)+\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_{r+1})\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_r)\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)+\frac{s{\sigma }_4(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)+\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1}))}{2s}\hfill \\ & & +\frac{2s{\sigma }_5\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)+\frac{s{\sigma }_4(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)+\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1}))}{2s}\hfill \\ & & +\frac{2s{\sigma }_5\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)\hfill \\ & & +{\sigma }_4\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1}))+{\sigma }_5\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1})\right)\hfill \\ & & +{\sigma }_4\zeta (\rho {\breve{e}}_r,\rho {\breve{e}}_{r+1}))+{\sigma }_5\left(\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)\right)].\hfill \end{array}$$

Since $F_{\perp }$ is super-additive, we can obtain

$$F\left[\left(1-{\sigma }_3-{\sigma }_4\right)\left(\zeta ({\breve{e}}_{r+1},{\breve{e}}_{r+2})\right)\right]\leqq F\left[\left({\sigma }_1+{\sigma }_2+{\sigma }_5\right)\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r))\right]-\tau \left(\widehat{C}({\breve{e}}_{r-1},{\breve{e}}_r)\right),$$

By appealing to the above fashion, we have

$$F\left[\left(\zeta ({\breve{e}}_{r+1},{\breve{e}}_{r+2})\right)\right]\leqq F\left[\zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r))\right]-\frac{\tau \left(\widehat{C}({\breve{e}}_{r-1},{\breve{e}}_r)\right)}{1-{\sigma }_3-{\sigma }_4},$$

which, by virtue of $\left(F_i\right)$, implies that $\zeta ({\breve{e}}_{r+1},{\breve{e}}_{r+2})\leqq \zeta (\rho {\breve{e}}_{r-1},\rho {\breve{e}}_r)$, which contradicts this. Hence, (5) holds true. In light of the above observations, $\zeta ({\breve{e}}_r,{\breve{e}}_{r+1})$ is a decreasing sequence in R and and is bounded from below. Assuming that there is $\mathsf{\Omega }\geqq 0$, such that

$$\mathsf{\Omega }=\underset{\alpha \to \infty }{\lim }\zeta ({\breve{e}}_{\alpha },{\breve{e}}_{\alpha +1})=\inf \left\{\zeta ({\breve{e}}_{\alpha },{\breve{e}}_{\alpha +1}):\alpha \in \mathbb{N}\right\}.$$

(6)

We now need to prove that $\mathsf{\Omega }=0$. We assume, based on the contrary, that $\mathsf{\Omega }>0.$ For a given $\epsilon >0$, there exist a number of $\sigma \in \mathbb{N}$, in such a way that

$$\zeta ({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})<\mathsf{\Omega }+\epsilon .$$

(7)

By virtue of $\left(F_i\right),$ we can write:

$$F\left(\zeta ({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})\right)<F(\mathsf{\Omega }+\epsilon ).$$

(8)

By referencing (3), we have

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\sigma -1},\mu \rho {\breve{e}}_{\sigma -1})\leqq \zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma }).$$

(9)

Since the hybrid pair of mappings $(\rho ,\mu )$ of $F_{\perp }$-ST-I provide a contraction operatror, we can obtain:

$$\begin{array}{ccc}\hfill F\left(\zeta ({\breve{e}}_{\sigma +1},{\breve{e}}_{\sigma +2})\right)& =& F\left[\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\sigma -1},\mu {\breve{e}}_{\sigma -1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{\sigma },\mu {\breve{e}}_{\sigma })\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\sigma -1},\mu {\breve{e}}_{\sigma })\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_{\sigma },\mu {\breve{e}}_{\sigma -1})\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\sigma -1},\mu {\breve{e}}_{\sigma -1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{\sigma },\mu {\breve{e}}_{\sigma })\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\sigma -1},\mu {\breve{e}}_{\sigma })\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_{\sigma },\mu {\breve{e}}_{\sigma -1})\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)+\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma +1})\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma })\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)+\frac{{\sigma }_4\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma +1})\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma })\right)}{2s}].\hfill \end{array}$$

Owing to the above hypothesis, this, in turn, yields:

$$\begin{array}{ccc}\hfill F\left(\zeta ({\breve{e}}_{\sigma +1},{\breve{e}}_{\sigma +2})\right)& \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)+\frac{s{\sigma }_4(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })+\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1}))}{2s}\hfill \\ & & +\frac{2s{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)}{2s}]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)+\frac{s{\sigma }_4(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })+\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1}))}{2s}\hfill \\ & & +\frac{2s{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)}{2s}]\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)\hfill \\ & & +{\sigma }_4\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1}))+{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)]\hfill \\ & & -\tau [{\sigma }_1\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)+{\sigma }_3\left(\zeta (\rho {\breve{e}}_{\sigma },\rho {\breve{e}}_{\sigma +1})\right)\hfill \\ & & +{\sigma }_4\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma }))+{\sigma }_5\left(\zeta (\rho {\breve{e}}_{\sigma -1},\rho {\breve{e}}_{\sigma })\right)]\hfill \end{array}$$

Since $F_{\perp }$ is super-additive, we can write

$$F\left[(1-{\sigma }_3)\zeta ({\breve{e}}_{\sigma +1},{\breve{e}}_{\sigma +2})\right]\leqq F\left[({\sigma }_1+{\sigma }_2+{\sigma }_4+{\sigma }_5)\zeta ({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})\right]-\tau \left(\widehat{C}({\breve{e}}_{\sigma -1},{\breve{e}}_{\sigma })\right).$$

(10)

By given condition ${\sigma }_1+{\sigma }_2+{\sigma }_3+{\sigma }_4+{\sigma }_5=1$, we get

$$F\left(\zeta ({\breve{e}}_{\sigma +1},{\breve{e}}_{\sigma +2})\right)\leqq F\left(\zeta ({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})\right)-\frac{\tau \left(\widehat{C}({\breve{e}}_{\sigma -1},{\breve{e}}_{\sigma })\right)}{1-{\sigma }_3}.$$

(11)

Again, in light of $F_{\perp }$-ST-I contraction, we obtain

$$F\left(\zeta ({\breve{e}}_{\sigma +2},{\breve{e}}_{\sigma +3})\right)\leqq F\left(\zeta ({\breve{e}}_{\sigma +1},{\breve{e}}_{\sigma +2})\right)-\frac{\tau \left(\widehat{C}({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})\right)}{1-{\sigma }_3}.$$

Continuing these steps, we can write

$$\begin{array}{ccc}\hfill F\left(\zeta ({\breve{e}}_{\sigma +\alpha },{\breve{e}}_{\sigma +\left(\alpha +1\right)})\right)& \leqq & F\left(\zeta ({\breve{e}}_{\sigma +\left(\alpha -1\right)},{\breve{e}}_{\sigma +\alpha })\right)-\frac{\tau \left(\widehat{C}({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +1})\right)}{1-{\sigma }_3}\hfill \\ & \leqq & F\left(\zeta ({\breve{e}}_{\sigma +\left(\alpha -2\right)},{\breve{e}}_{\sigma +\left(\alpha -1\right)})\right)-\frac{\tau \left(\widehat{C}({\breve{e}}_{\sigma -1},{\breve{e}}_{\sigma })\right)}{1-{\sigma }_3}\hfill \\ & & ···\hfill \\ & \leqq & F\left(\zeta ({\breve{e}}_{\sigma },{\breve{e}}_{\sigma +\alpha })\right)-\frac{n\tau \left(\widehat{C}({\breve{e}}_{\sigma -1},{\breve{e}}_{\sigma })\right)}{1-{\sigma }_3}\hfill \\ & <& F(M+\epsilon )-\frac{n\tau \left(\widehat{C}({\breve{e}}_{\sigma -1},{\breve{e}}_{\sigma })\right)}{1-{\sigma }_3}.\hfill \end{array}$$

(12)

Following $\alpha \to \infty$, along with $\left(F_{ii}\right)$, we have ${\lim }_{\alpha \to \infty }F\left(\zeta ({\breve{e}}_{\sigma +\alpha },{\breve{e}}_{\sigma +\left(\alpha +1\right)})\right)=-\infty$. Additionally, in view of $\left(F_{ii}\right)$, we have

$$\underset{\alpha \to \infty }{\lim }F\left(\zeta ({\breve{e}}_{\sigma +\alpha },{\breve{e}}_{\sigma +\left(\alpha +1\right)})\right)=0.$$

Therefore, there is ${\alpha }_1\in \mathbb{N}$ such that $\zeta ({\breve{e}}_{\sigma +\alpha },{\breve{e}}_{\sigma +\left(\alpha +1\right)})<\mathsf{\Omega }$∀$\alpha >{\alpha }_1$, which is a contradiction. Therefore, we can write:

$$\underset{\alpha \to \infty }{\lim }\zeta ({\breve{e}}_{\alpha },{\breve{e}}_{\alpha +1})=0=\mathsf{\Omega }.$$

(13)

Now, we show that:

$$\underset{\alpha ,m\to \infty }{\lim }\zeta ({\breve{e}}_{\alpha },{\breve{e}}_m)=0.$$

(14)

Supposing, on the contrary, that for $\epsilon >0$ there are sequences $y\left(\alpha \right)$ and $z\left(\alpha \right)$ in $\mathbb{N}$, we have

$$\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})\geqq \epsilon ,\zeta ({\breve{e}}_{y_{\left(\alpha \right)-1}},{\breve{e}}_{z_{\left(\alpha \right)}})<\epsilon ,y\left(\alpha \right)>z\left(\alpha \right)>\alpha (\forall \alpha \in \mathbb{N}).$$

(15)

Therefore, we have

$$\begin{array}{ccc}\hfill \zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})& \leqq & s\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)-1}})+s\zeta ({\breve{e}}_{y_{\left(\alpha \right)-1}},{\breve{e}}_{z_{\left(\alpha \right)}})\hfill \\ & <& s\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)-1}})+s\epsilon \hfill \end{array}$$

(16)

By (13), there is ${\alpha }_2\in \mathbb{N}$, such that

$$\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)-1}})<\epsilon ,\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)+1}})<\epsilon ,\zeta ({\breve{e}}_{z_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)+1}})<\epsilon (\mathrm{for}\mathrm{each}n>n_2,$$

(17)

which, together with (16), yields,

$$\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})<2s\epsilon (\forall \alpha >{\alpha }_2),$$

(18)

implies

$$F\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})<F\left(2s\epsilon \right)(\mathrm{for}\mathrm{each}\alpha >{\alpha }_2).$$

(19)

In view of (15) and (17), we have

$$\frac{1}{2s}\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)+1}})<\frac{\epsilon }{2s}<\epsilon \leqq \zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})(\forall \alpha >{\alpha }_2).$$

(20)

Applying triangle inequality, we find that

$$ϵ\leqq \zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)}})\leqq s\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)+1}})+s^2\zeta ({\breve{e}}_{y_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)+1}})+s^2\zeta ({\breve{e}}_{z_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)}}).$$

(21)

Next, we proceed to the limitas $\alpha \to \infty$ in (21) and make use of (13); then, we have

$$\frac{ϵ}{s^2}\leqq \underset{\alpha \to \infty }{\lim }\inf \zeta ({\breve{e}}_{y_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)+1}}).$$

There also exist ${\alpha }_3\in \mathbb{N}$ such that $\zeta ({\breve{e}}_{y\left(\alpha \right)+1},{\breve{e}}_{z\left(\alpha \right)+1})>0$ for each $\alpha >{\alpha }_3.$ Further, since the hybrid pair of mappings $(\rho ,\mu )$ are ⊥-preserving, in addition to being ⊥-transitive, we can write

$${\breve{e}}_{y_{\left(\alpha \right)}}\perp {\breve{e}}_{z_{\left(\alpha \right)}}(\mathit{or}{\breve{e}}_{z_{\left(\alpha \right)}}\perp {\breve{e}}_{y_{\left(\alpha \right)}}).$$

Following the $F_{\perp }$-ST-I contraction, we find that:

$$\begin{array}{ccc}\hfill F\left(\zeta ({\breve{e}}_{y_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)+1}})\right)& =& F(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)},\rho {\breve{e}}_{z\left(\alpha \right)})\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)-1})\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{y\left(\alpha \right)-1},\mu {\breve{e}}_{y\left(\alpha \right)-1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{z\left(\alpha \right)-1},\mu {\breve{e}}_{z\left(\alpha \right)-1})\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{y\left(\alpha \right)-1},\mu {\breve{e}}_{z\left(\alpha \right)-1})\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(\rho {\breve{e}}_{z\left(\alpha \right)-1},\mu {\breve{e}}_{y\left(\alpha \right)-1})\right)}{2s}]-\tau \left(\widehat{C}({\breve{e}}_{y\left(\alpha \right)-1},{\breve{e}}_{z\left(\alpha \right)-1})\right)\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)-1})\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{y\left(\alpha \right)})\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)})\right)\hfill \\ & & +\frac{{\sigma }_4(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)})+\left(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)},\rho {\breve{e}}_{z\left(\alpha \right)-1})\right)}{2}\hfill \\ & & +\frac{{\sigma }_5({\zeta }_b(\rho {\breve{e}}_{z\left(\alpha \right)-1},\rho {\breve{e}}_{y\left(\alpha \right)})+\zeta (\rho {\breve{e}}_{y\left(\alpha \right)},\rho {\breve{e}}_{y\left(\alpha \right)-1}))]}{2}\hfill \\ & & -\tau \left(\widehat{C}({\breve{e}}_{y\left(\alpha \right)-1},{\breve{e}}_{z\left(\alpha \right)-1})\right)\hfill \\ & \leqq & F[{\sigma }_1\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)-1})\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{y\left(\alpha \right)})\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)})\right)\hfill \\ & & +\frac{{\sigma }_4(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)+1})+\left(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)+1},\rho {\breve{e}}_{z\left(\alpha \right)})\right)}{2}\hfill \\ & & +\frac{{\sigma }_5(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)-1},\rho {\breve{e}}_{y\left(\alpha \right)+1})+\zeta (\rho {\breve{e}}_{y\left(\alpha \right)+1},\rho {\breve{e}}_{y\left(\alpha \right)}))]}{2}\hfill \\ & & -\tau \left(\widehat{C}({\breve{e}}_{y\left(\alpha \right)-1},{\breve{e}}_{z\left(\alpha \right)-1})\right).\hfill \end{array}$$

(22)

In the light of (17), (18) and (19), implies (22)

$$\begin{array}{ccc}\hfill F\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)},\rho {\breve{e}}_{z\left(\alpha \right)})\right)& \le & F[\left({\sigma }_1\left(2s\epsilon \right)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)-1},\rho {\breve{e}}_{y\left(\alpha \right)})\right)\hfill \\ & & +{\sigma }_3\left(\zeta (\rho {\breve{e}}_{z\left(\alpha \right)-1},\rho {\breve{e}}_{z\left(\alpha \right)})\right)\hfill \\ & & +\frac{{\sigma }_4(s\epsilon +\epsilon )}{2}+\frac{{\sigma }_5(s\epsilon +\epsilon ))}{2}]\hfill \\ & & -\tau \left(\widehat{C}({\breve{e}}_{y\left(\alpha \right)-1},{\breve{e}}_{z\left(\alpha \right)-1})\right)\hfill \end{array}$$

(23)

for $\alpha >\max \left\{{\alpha }_2,{\alpha }_3\right\}.$ Taking the limit as $\alpha \to \infty$ in Equation (23), we have

$$\underset{\alpha \to \infty }{\lim }F\left(\zeta (\rho {\breve{e}}_{y\left(\alpha \right)},\rho {\breve{e}}_{z\left(\alpha \right)})\right)=-\infty .$$

which, by virtue of ($F_{ii}$), implies that ${\lim }_{\alpha \to \infty }$$\zeta (\rho {\breve{e}}_{y\left(\alpha \right)},\rho {\breve{e}}_{z\left(\alpha \right)})=0$. Therefore, from (21), we have

$$\begin{array}{ccc}\hfill \underset{\alpha \to \infty }{\lim }\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})& \leqq & \underset{\alpha \to \infty }{\lim }(s\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{y_{\left(\alpha \right)+1}})+s^2\zeta ({\breve{e}}_{y_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)+1}})\hfill \\ & & +s^2\zeta ({\breve{e}}_{z_{\left(\alpha \right)+1}},{\breve{e}}_{z_{\left(\alpha \right)}}))\hfill \\ & =& 0\hfill \end{array}$$

which implies that ${\lim }_{\alpha \to \infty }\zeta ({\breve{e}}_{y_{\left(\alpha \right)}},{\breve{e}}_{z_{\left(\alpha \right)}})=0$ is a contradiction. Hence, (14) holds true. Therefore, $\left\{{\breve{e}}_{\alpha }\right\}$ is a $\widehat{O}$-Cauchy sequence in $\left(\mathbb{C},\perp \right).$ Since $\mathbb{C}$ is a $\widehat{O}$-complete OBMLS, there is a point $c\in \mathbb{C}$, such that

$$\zeta (c,c)=\underset{\alpha \to \infty }{\lim }\zeta ({\breve{e}}_{\alpha },c)=\underset{\alpha ,m\to \infty }{\lim }\zeta ({\breve{e}}_{\alpha },{\breve{e}}_m)=0$$

(24)

Now, we further prove that for each $\alpha \in \mathbb{N}$

$$\frac{1}{2s}\zeta ({\breve{e}}_{\alpha },{\breve{e}}_{\alpha +1})<\zeta ({\breve{e}}_{\alpha },c)\mathit{or}\frac{1}{2s}\zeta ({\breve{e}}_{\alpha +1},{\breve{e}}_{\alpha +2})<\zeta ({\breve{e}}_{\alpha +1},c).$$

(25)

Assuming that there is ${\alpha }_0\in \mathbb{N}$, such that

$$\frac{1}{2s}\zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_0+1})\geqq \zeta ({\breve{e}}_{\alpha },c)\mathrm{and}\frac{1}{2s}\zeta ({\breve{e}}_{{\alpha }_{0+1}},{\breve{e}}_{{\alpha }_{0+2}})\geqq \zeta ({\breve{e}}_{{\alpha }_{0+1}},c)$$

(26)

From (5) and (26), we have

$$\begin{array}{ccc}\hfill \zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_0+1})& \leqq & s\zeta ({\breve{e}}_{{\alpha }_0},c)+s\zeta (c,{\breve{e}}_{{\alpha }_0+1})\hfill \\ & \leqq & \frac{1}{2s}s\zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_0+1})+\frac{1}{2s}s\zeta ({\breve{e}}_{{\alpha }_0+1},{\breve{e}}_{{\alpha }_o+2})\hfill \\ & \leqq & \frac{1}{2}\zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_0+1})+\frac{1}{2}\zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_o+1})\hfill \\ & \leqq & \zeta ({\breve{e}}_{{\alpha }_0},{\breve{e}}_{{\alpha }_0+1}),\hfill \end{array}$$

a contradiction. Hence, (25) holds true. Furthermore, we can see that

$$\begin{array}{ccc}\hfill F\left(\zeta (\rho {\breve{e}}_{\alpha +1},\rho c)\right)& \leqq & F[\left({\sigma }_1\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)+{\sigma }_2{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha }))\hfill \\ & & +{\sigma }_3\left({\zeta }_b(c,\mu c)\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu c)\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(c,\mu {\breve{e}}_{\alpha })\right)}{2s}]-\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},c)\right).\hfill \end{array}$$

(27)

or

$$\begin{array}{ccc}\hfill F\left(\zeta (\rho {\breve{e}}_{\alpha +2},\rho c)\right)& \leqq & F\left[\right({\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha },c)\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(c,\mu c)\right)+\frac{{\sigma }_4\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu c)\right)}{2s}\hfill \\ & & +\frac{{\sigma }_5\left({\zeta }_b(c,\mu {\breve{e}}_{\alpha +1})\right)}{2s}]-\tau \left(\widehat{C}({\breve{e}}_{\alpha },c)\right).\hfill \end{array}$$

(28)

Let us now consider (27) that holds true, From (27), we have

$$\begin{array}{ccc}\hfill F(\zeta (\rho {\breve{e}}_{\alpha },\rho c)& \leqq & F\left[\right({\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)+{\sigma }_2\left({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })\right)\hfill \\ & & +{\sigma }_3\left({\zeta }_b(c,\mu c)\right)+\frac{{\sigma }_4}{2}\left(\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)\hfill \\ & & +\zeta (c,\rho c))+\frac{{\sigma }_5}{2}\left(\zeta (c,\rho {\breve{e}}_{\alpha -1})\right)\hfill \\ & & +\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })\left)\right]-\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},c)\right).\hfill \end{array}$$

This implies

$$\begin{array}{ccc}\hfill F(\zeta (\rho {\breve{e}}_{\alpha },\rho c)& \leqq & F\left[\right({\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha -1})\right)\hfill \\ & & +{\sigma }_3\left(\zeta (c,\rho c)\right)+\frac{{\sigma }_4}{2}\left(\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)\hfill \\ & & +\zeta (c,\rho c))+\frac{{\sigma }_5}{2}\left(\zeta (c,\rho {\breve{e}}_{\alpha -1})\right)\hfill \\ & & +\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha -1})\left)\right]-\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},c)\right).\hfill \end{array}$$

(29)

From (13) and (24), there exists ${\alpha }_4\in \mathbb{N}$ for some ${\epsilon }^{*}>0$, such that

$$\zeta (c,\rho {\breve{e}}_{\alpha -1})<{\epsilon }^{*},\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha -1})<{\epsilon }^{*},\alpha >{\alpha }_4.$$

(30)

Therefore, (29) and (30)$canbecaluclatedasfollows$

$$\begin{array}{ccc}\hfill F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho c)\right)& \le & F\left[\right({\sigma }_1\left(\zeta (\rho {\breve{e}}_{\alpha -1},c)\right)+{\sigma }_2\left(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha +1})\right)\hfill \\ & & +{\sigma }_3\left(\zeta (c,\rho c)\right)+\frac{{\sigma }_4}{2}({\epsilon }^{*}+\zeta (c,\rho c))\hfill \\ & & +\frac{{\sigma }_5}{2}{\epsilon }^{*}]-\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},c)\right)\hfill \end{array}$$

(31)

$\alpha >{\alpha }_4.$. As a consequence of these facts, the lateral limit as $\alpha \to \infty ,$${\lim }_{\alpha \to \infty }F(\zeta (\rho {\breve{e}}_{\alpha },\rho c)=-\infty$, which implies

$$\underset{\alpha \to \infty }{\lim }\zeta (\rho {\breve{e}}_{\alpha },\rho c)=0.$$

(32)

Furthermore, $\zeta (c,\rho c)\leqq s\zeta (c,\rho {\breve{e}}_{\alpha })+s\zeta (\rho {\breve{e}}_{\alpha },\rho c)$. Following $\alpha \to \infty ,$ and using (24) and (32), we can obtain $\zeta (c,\rho c)=0.$ Thus, clearly, $c=\rho c\in \mu c$ has a common fixed point of a hybrid pair of mappings $(\rho ,\mu ).$ □

From the above developments, we have found some important corollaries:

Corollary 1.

Let $(\mathbb{C},\zeta ,s,\perp )$ be an $\widehat{O}$-complete OBMLS. Let $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be known as a hybrid pair of mappings of $F_{\perp }$-ST-II contractions with ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :[0,\infty )\to [0,\infty )$, such that

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha }),$$

implies

$$\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\leqq F\left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(33)

$$\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })={\sigma }_1(\zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha })+{\sigma }_2({\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})+{\sigma }_3\left({\zeta }_b(\rho {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha })\right)$$

∀${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha -1}$(or ${\breve{e}}_{\alpha -1}\perp {\breve{e}}_{\alpha })\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$, $\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0$, where $0\leqq {\sigma }_3<1$ and $0\le {\sigma }_1,{\sigma }_2\le 0$, such that ${\sigma }_1+{\sigma }_2+{\sigma }_3=1$. Assume that (O1), (O2) and (O3) holds true. Then, ρ and μ has a common fixed point in $\left(\breve{e},\perp \right).$

Corollary 2.

Let $(\mathbb{C},\zeta ,s,\perp )$ be an $\widehat{O}$-complete OBMLS. Let $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be called a hybrid pair of mappings of $F_{\perp }$-ST-III contraction via ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right),$ such that

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha }),$$

implies

$$\tau \left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\leqq F\left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(34)

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$ and $\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0$. Assume that (O1) and (O2) hold true. Then, ρ and μ have a common fixed point in $\left(\mathbb{C},\perp \right).$

Corollary 3.

Let$\left(\mathbb{C},\zeta ,s,\perp \right)$ be an $\widehat{O}$-complete OBMLS. Let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be a $F_{\perp }$-ST-1V contraction mapping involving ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right)$, such that

$$\frac{1}{2s}{\zeta }_b({\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })\leqq \zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha +1}),$$

then this implies

$$\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})\right)\leqq F\left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(35)

$$\begin{array}{ccc}\hfill \widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })& =& {\sigma }_1(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })+{\sigma }_2({\zeta }_b({\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})+{\sigma }_3({\zeta }_b({\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha })+\frac{{\sigma }_4({\zeta }_b({\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })}{2s}\hfill \\ & & +\frac{{\sigma }_5({\zeta }_b({\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha -1})}{2s}\hfill \end{array}$$

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,{\breve{e}}_0)$, $H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})>0$, where $0\leqq {\sigma }_1,{\sigma }_2,{\sigma }_3,{\sigma }_4,{\sigma }_5\leqq 1$, such that ${\sigma }_1+{\sigma }_2+{\sigma }_3+{\sigma }_4+{\sigma }_5=1$ and $1-{\sigma }_3-{\sigma }_5>0$. Assume that (O1), (O2) and (O3) hold true. Then, μ has a fixed point in $\left(\mathbb{C},\perp \right).$

Corollary 4.

Let$\left(\mathbb{C},\zeta ,s,\perp \right)$ be an $\widehat{O}$-complete OBMLS. Let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be known as $F_{\perp }$-ST-V contraction mapping via ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right),$ such that

$$\frac{1}{2s}{\zeta }_b({\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha })\leqq \zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha +1})$$

implies

$$\tau \left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})\right)\leqq F\left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(36)

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,{\breve{e}}_0)$ and $H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})>0$. Assume that (O1) and (O2) hold true. Then, μ has a fixed point in $\left(\mathbb{C},\perp \right).$

Corollary 5.

Let$\left(\mathbb{C},\zeta ,s,\perp \right)$ be an $\widehat{O}$-complete OBMLS. Let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be called an $F_{\perp }$-type-VI contraction mapping with ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right),$ such that

$$\tau \left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})\right)\leqq F\left(\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

(37)

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,{\breve{e}}_0)$ and $H(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})>0$. Assume that (O1) and (O1) hold true. Then, μ has a fixed point in $\left(\mathbb{C},\perp \right).$

Corollary 6.

Let$\left(\mathbb{C},\zeta ,s,\perp \right)$ be an $\widehat{O}$-complete OBMLS. Let $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ be called an $F_{\perp }$-ST-VII contraction mapping via ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$, $\tau :\left[0,\infty \right)\to \left[0,\infty \right)$ and $\mathsf{\Phi }:\kappa \to \kappa$ form a non-negative Lebesgue integrable operator, which is summable on each compact subset of κ such that

$$\frac{1}{2s}{\zeta }_b({\breve{e}}_{\alpha -1},\mu {\breve{e}}_{\alpha -1})\leqq \eta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha +1}),$$

this implies

$$H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})>0\Rightarrow \tau \left(\zeta \left({\epsilon }_{\alpha -1},{\epsilon }_{\alpha }\right)\right)+F\left({\int }_0^{H_O(\mu {\breve{e}}_{\alpha },\mu {\breve{e}}_{\alpha +1})}\mathsf{\Phi }\left(s\right)\delta s\right)\le F\left({\int }_0^{\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })}\mathsf{\Phi }\left(s\right)\delta s\right)$$

(38)

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,{\breve{e}}_0)$ and ∀ given $ϵ>0$, so that ${\int }_0^{ϵ}\mathsf{\Phi }\left(s\right)\delta s>0$. Suppose that (O1) and (O2) hold true. Then, μ has a fixed point in $\left(\mathbb{C},\perp \right).$

Corollary 7.

Let$\left(\mathbb{C},\zeta ,s,\perp \right)$ be an $\widehat{O}$-complete OBMLS. Let $\rho :\mathbb{C}\to \mathbb{C}$ and $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right)$ are called a hybrid pair of mappings of $F_{\perp }$-ST-VIII contraction via ODS. If, for some $F_{\perp }\in {\nabla }_{ϝ}$, $\tau :\left[0,\infty \right)\to \left[0,\infty \right)$ and $\mathsf{\Phi }:\kappa \to \kappa$ a non-negative Lebesgue integrable operator, which is summable on each compact subset of κ such that

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha }),$$

implies

$$\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0\Rightarrow \tau \left(\zeta \left({\epsilon }_{\alpha -1},{\epsilon }_{\alpha }\right)\right)+F\left({\int }_0^{\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})}\mathsf{\Phi }\left(s\right)\delta s\right)\le F\left({\int }_0^{\zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })}\mathsf{\Phi }\left(s\right)\delta s\right)$$

(39)

∀${\breve{e}}_{\alpha }\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$ and ∀ given $ϵ>0$ so that ${\int }_0^{ϵ}\mathsf{\Phi }\left(s\right)\delta s>0$. Suppose that (O1) and (O2) hold true. Then, ρ and μ has a common fixed point in $\left(\mathbb{C},\perp \right).$

In the following, the first main tangible example of this exposition is given.

Example 5.

Let $\mathbb{C}={\check{R}}^{+}\cup \left\{0\right\}$, and let $\zeta :\mathbb{C}\times \mathbb{C}\to {\check{R}}^{+}\cup \left\{0\right\}$ be define $\zeta \left({\breve{e}}_1,{\breve{e}}_2\right)={\left(\max \left\{{\breve{e}}_1,{\breve{e}}_2\right\}\right)}^2$∀${\breve{e}}_1,{\breve{e}}_2\in \mathbb{C}.$ Define the binary relation ⊥ on $\mathbb{C}$ by $\breve{e}\perp y$ if $\breve{e},y\in [3,n+4]$ for some $n\in \mathbb{N}$ or $\breve{e}=0.$ Then, clearly, $\left(\breve{e},\zeta ,s,\perp \right)$ is a $\widehat{O}$-complete OBMLS. The mappings $\rho :\mathbb{C}\to \mathbb{C}$, $\mu :\mathbb{C}\to CB\left(\mathbb{C}\right),$$F:{\check{R}}^{+}\to \check{R}$ and $\tau :{\check{R}}^{+}\to {\check{R}}^{+}$ to be considered here are as follows:

$$\rho \breve{e}=\left\{\begin{array}{c}0,\mathrm{if}\breve{e}=0;\hfill \\ \breve{e}+1,\mathrm{if}\breve{e}\in [1,2];\hfill \\ \breve{e}-1,\mathrm{if}\breve{e}\in [2,\infty ),\hfill \end{array}\right.$$

$$\mu \breve{e}=\left\{\begin{array}{c}\left\{0\right\},\mathrm{if}\breve{e}=0;\hfill \\ \frac{\breve{e}}{2},\infty ),\mathrm{if}\breve{e}\in [1,\infty ),\hfill \end{array}\right.$$

Define $F:{\check{R}}^{+}\to \check{R}$ and $\tau :{\check{R}}^{+}\to {\check{R}}^{+}$ by $F\breve{e}=\ln \left(\breve{e}\right)$ and

$${\tau }_{\breve{e}}=\left\{\begin{array}{c}\ln \left(1\right)\mathrm{for}\breve{e}=0;\hfill \\ \ln \left(\frac{3}{2}\right)\mathrm{for}\breve{e}\in (0,\infty ).\hfill \end{array}\right.$$

Let $\breve{e}\in \breve{e}$ and ⊥-sequence $\left\{{\breve{e}}_{\alpha }\right\}\to \breve{e}$ be as defined by ${\breve{e}}_{\alpha }=\sqrt{{\breve{e}}_{\alpha -1}+2}$ in $\check{D}(\mu ,\rho ,0);$ then, the following cases hold true:

Case 1: Let ${\breve{e}}_{\alpha }=0$∀$n\in \mathbb{N};$ then, $\breve{e}=0$ and $\rho {\breve{e}}_{\alpha }=0=\rho \breve{e}.$

Case 2: Let ${\breve{e}}_{\alpha }\ne 0$ for some $n\in \mathbb{N};$ then, there exists $m\in \mathbb{N}$, such that $\breve{e}\in [3,n+4]$ and $\rho {\breve{e}}_{\alpha }=\rho \breve{e}.$ Therefore, the hybrid pair of mappings ρ and μ are ⊥-continuous on $\check{D}(\mu ,\rho ,0)$ but not continuous on $\check{D}(\mu ,\rho )$. Taking ${\breve{e}}_{\alpha -1}=1,$${\breve{e}}_{\alpha }=2,$${\sigma }_1=\frac{1}{2},$${\sigma }_2={\sigma }_3=\frac{1}{4},$${\sigma }_4={\sigma }_5=\frac{1}{12}$, then

$$\frac{1}{2}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\geqq \zeta ({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha +1}),$$

which implies

$$\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\geqq F\left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

∀${\breve{e}}_{\alpha }\in \check{D}(\rho ,\mu ,0).$ Hence, Theorem (4) is not satisfied. Clearly, the hybrid pair of mapping $(\rho ,\mu )$ is ⊥-preserving. Taking ${\sigma }_1=\frac{1}{2},$${\sigma }_2={\sigma }_3=\frac{1}{4},$${\sigma }_4={\sigma }_5=\frac{1}{12},$${\breve{e}}_{\alpha }=0$ and ${\breve{e}}_{\alpha -1}\in [1,\infty )$ with respect to ${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha -1}$(or ${\breve{e}}_{\alpha -1}\perp {\breve{e}}_{\alpha })$, we can easily obtain

$$\frac{1}{2s}{\zeta }_b(\rho {\breve{e}}_{\alpha -1},\mu \rho {\breve{e}}_{\alpha -1})\leqq \zeta (\rho {\breve{e}}_{\alpha -1},\rho {\breve{e}}_{\alpha }),$$

implying that

$$\tau \left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)+F\left(\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})\right)\leqq F\left(\widehat{C}({\breve{e}}_{\alpha -1},{\breve{e}}_{\alpha })\right)$$

∀${\breve{e}}_{\alpha },{\breve{e}}_{\alpha -1}\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$ with respect to ${\breve{e}}_{\alpha }\perp {\breve{e}}_{\alpha -1}$ or ${\breve{e}}_{\alpha -1}\perp {\breve{e}}_{\alpha })\in \check{D}(\mu ,\rho ,{\breve{e}}_0)$ and $\zeta (\rho {\breve{e}}_{\alpha },\rho {\breve{e}}_{\alpha +1})>0.$ Therefore, all the required conclusions of Theorem (4) are fulfilled and 0 is a common fixed point of ρ and μ.

In the following, some applications in the context of ordinary differential equations and nonlinear fractional differential equations are designed with respect to the integral boundary value conditions, which are given to highlight the usability and validity of the theoretical results.

3. Application to Ordinary Differential Equations

In this section, we investigate an application of Corollary (5) to establish the existence of solutions to ordinary differential equations (ODE) under the influence of complex valued mearurable functions and orthogonal binary relations ⊥. This is in effect for our purpose. First, we recall that the space $L^P(\Delta ,A,\kappa )$ consists of of all complex valued measurable functions $\delta$ underlying space $\Delta$ for each $1\le P\le \infty$, such that

$${\int }_{\Delta }{\left|\delta \left(y\right)\right|}^{P}d\kappa \left(y\right),$$

(40)

where A is called the $\sigma$-algebra of mearurable sets and $\kappa$ is the measure scale. Taking $P=1$, the space $L^1(\Delta ,A,\kappa )$ consists of all integrable functions $\delta$ on $\Delta$ and defines the $L^1$ norm of $\delta$ by

$${∥\delta ∥}_1={\int }_{\Delta }\left|\delta \left(y\right)\right|d\kappa \left(y\right).$$

(41)

Now, we consider the following differential equations:

$$\left\{\begin{array}{c}\frac{d\mu }{dr}={{\rm Y}}(r,\mu \left(r\right)),r\in I=[0,L];\hfill \\ \mu \left(0\right)=\eta ,\eta \ge 1,\hfill \end{array}\right.$$

(42)

where $L>0$ and ${{\rm Y}}:I\times \check{R}\to \check{R}$ is an integrable functions satisfying the following axioms:

($O_a$)

: ${{\rm Y}}(h,P),$ for each $P\ge 0$ and $h\in I;$

($O_b$)

: ∀$y,y^{\prime }\in L^1(I,A,\kappa )$ with respect to $y\left(h\right)y^{\prime }\left(h\right)\ge y\left(h\right)$ or $y\left(h\right)y^{\prime }\left(h\right)\ge y^{\prime }\left(h\right)$ for each $h\in I,$ there exists $\delta \in L^1(I,A,\kappa )$ and $\tau :\left[0,\infty \right)\to \left[0,\infty \right),$ such that

$${(\left|{{\rm Y}}(h,y(h\left)\right)\right|+\left|{{\rm Y}}(h,y^{\prime }\left(h\right))\right|)}^2\le \frac{\left|\delta \left(h\right)\right|}{{(1+\tau \sqrt{\delta \left(h\right)})}^2}{(\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|)}^2$$

(43)

and

$$\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|\le \delta \left(h\right)e^{\breve{e}\left(h\right)}$$

where $\breve{e}\left(h\right)={\int }_0^h\left|\delta \left(y\right)\right|d\left(y\right).$ Define a mappings $d:\Delta \times \Delta \to {\check{R}}^{+}$ by

$$d(y,y^{\prime })=\underset{r\in I}{\sup }{\left(\left|y\left(r\right)\right|+\left|y^{\prime }\left(r\right)\right|\right)}^2{e}^{-\breve{e}\left(r\right)}.$$

(44)

Thus, $(\Delta ,d)$ is an OBMLS with $s=2$. The ⊥-continuous mapping ${{{\rm Y}}}^{\prime }:\Delta \to CB(\Delta )$ to be considered here are as follows. Let us say that

$$\left({{{\rm Y}}}^{\prime }y\right)\left(r\right)\in \eta +{\int }_0^r{{\rm Y}}(h,y\left(h\right))dh.$$

(45)

In addition, the following relation of such objects is useful. Let us define the orthogonality binary relation ⊥ on $\Delta$ by

$$y\perp y^{\prime }\mathrm{iff}y\left(r\right)y^{{}^{\prime }}\left(r\right)\ge y\left(r\right)\mathit{or}y\left(r\right)y^{{}^{\prime }}\left(r\right)\ge y^{{}^{\prime }}\left(r\right)\forall r\in I.$$

(46)

Further, we are now in the position to state the second main result of this exposition as follows:

Theorem 5.

If assumptions (40)–(46) $\left(O_a\right)$ and $\left(O_b\right)$ are satisfied, then the differential Equation (42) has a solution, as follows:

$$\Delta =\left\{\mu \in C(I,\check{R}):\mu \left(r\right)>0\forall r\in I\right\}.$$

Proof. 

Since $\breve{e}\left(r\right)={\int }_0^r\left|\delta \left(h\right)\right|dh$, we have ${\breve{e}}^{\prime }\left(r\right)=\left|\delta \left(r\right)\right|$ for almost everywhere $r\in I$. Now, we can see that ${{{\rm Y}}}^{\prime }$ is ⊥-preserving. $Forall$$y,y^{\prime }\in \Delta$ with $y\perp y^{\prime }$ and $r\in I$, we have

$$\left({{{\rm Y}}}^{\prime }y\right)\left(r\right)\in \eta +{\int }_0^r{{\rm Y}}(h,y\left(h\right))dh\ge 1.$$

(47)

Therefore, it follows that $\left({{{\rm Y}}}^{\prime }y\right)\left(r\right)\left({{{\rm Y}}}^{\prime }{y}^{\prime }\right)\left(r\right)\ge \left({{{\rm Y}}}^{\prime }y\right)\left(r\right)$ and so $\left({{{\rm Y}}}^{\prime }y\right)\left(r\right)\perp \left({{{\rm Y}}}^{\prime }{y}^{\prime }\right)\left(r\right).$ Hence, ${{{\rm Y}}}^{\prime }$ is ⊥-preserving. Next, we prove that ${{{\rm Y}}}^{\prime }$ is $F_{\perp }$-contraction. Let $y,y^{\prime }\in \Delta$ with $y\perp y^{\prime }$ and ${{{\rm Y}}}^{\prime }y\perp {{{\rm Y}}}^{\prime }{y}^{\prime }.$$Forall$$h\in I,$ we have

$$\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|\le \delta \left(h\right)e^{\breve{e}\left(h\right)}$$

(48)

and, therefore,

$$d(y,y^{\prime })=\underset{r\in I}{\sup }{\left(\left|y\left(r\right)\right|+\left|y^{\prime }\left(r\right)\right|\right)}^2{e}^{-\breve{e}\left(r\right)}\le \delta \left(h\right).$$

(49)

It follows that

$${(1+\tau \sqrt{d(y,y^{\prime })})}^2\le {(1+\tau \sqrt{\delta \left(h\right)})}^2$$

(50)

Owing to (49) and ($O_b$), we have

$$\begin{array}{ccc}\hfill {(\left|{{{\rm Y}}}^{\prime }y\left(h\right)\right|+\left|{{{\rm Y}}}^{\prime }{y}^{\prime }\left(h\right)\right|)}^2& \le & {\int }_0^r{(\left|{{\rm Y}}(h,y(h\left)\right)\right|+\left|{{\rm Y}}(h,y(h\left)\right)\right|)}^{2}dh\hfill \\ & \le & {\int }_0^r\frac{\left|\delta \left(h\right)\right|}{{(1+\tau \sqrt{\delta \left(h\right)})}^2}{(\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|)}^{2}dh\hfill \\ & \le & {\int }_0^r\frac{\left|\delta \left(h\right)\right|}{{(1+\tau \sqrt{\delta \left(h\right)})}^2}{(\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|)}^2{e}^{-\breve{e}\left(r\right)}{e}^{\breve{e}\left(r\right)}dh\hfill \\ & \le & \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}{\int }_0^r\delta \left(h\right)e^{\breve{e}\left(h\right)}dh\hfill \\ & \le & \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}(e^{\breve{e}\left(r\right)}-1)\hfill \\ & \le & \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}(e^{\breve{e}\left(r\right)}-1)e^{-\breve{e}\left(r\right)}\hfill \\ & \le & \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}(1-e^{-\breve{e}\left(r\right)})\hfill \\ & \le & \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}(1-e^{-{∥\delta ∥}_1}).\hfill \end{array}$$

Thus, it follows that

$$d({{{\rm Y}}}^{\prime }y,{{{\rm Y}}}^{\prime }{y}^{\prime })\le \frac{d(y,y^{\prime })}{{(1+\tau \sqrt{d(y,y^{\prime })})}^2},$$

which implies

$$\frac{{(1+\tau \sqrt{d(y,y^{\prime })})}^2}{d(y,y^{\prime })}\le \frac{1}{d({{{\rm Y}}}^{\prime }y,{{{\rm Y}}}^{\prime }{y}^{\prime })}$$

(51)

From (51), we can obtain

$$\tau -\frac{1}{\sqrt{d({{{\rm Y}}}^{\prime }y,{{{\rm Y}}}^{\prime }{y}^{\prime })}}\le -\frac{1}{d(y,y^{\prime })}$$

(52)

Setting $F\left(y\right)=-\frac{1}{\sqrt{y}},$ it follows that ${{{\rm Y}}}^{\prime }$ is an $F_{\perp }$-contraction. Thus, all the required hypotheses of Corollary (5) are satisfied and we have shown that Equation (42) has at least one solution. □

4. Application to Nonlinear Fractional Differential Equations

In this section, we developed an application of Corollary (5) to establish the existence of solutions to nonlinear fractional differential equations (NFDE) via orthogonal binary relations ⊥ (see more [29,30,31,32]). First, we recall the existence of solutions for the NFDE

$${}_{\widehat{c}}{\check{D}}^{\eta }\left(p\left(\breve{e}\right)\right)=\phi (\breve{e},p\left(\breve{e}\right))(1<\breve{e}<1,\eta \in (1,2])$$

(53)

with the integral boundary value conditions (IBVC)

$$p\left(0\right)=0,p\left(1\right)={\int }_0^{\beta }p\left(s\right)ds(0<\beta <1),$$

(54)

Where we can denote that the ${}_{\widehat{c}}{\check{D}}^{\eta }$ Caputo fractional derivative (CFD) of the order $\eta$ and $p:I(=[0,1])\times \check{R}\to \check{R}$ is a continuous function. Here, $({\Lambda },$${∥∥}_{\infty }),$${\Lambda }(=\widehat{C}(I,\check{R}))$ is the Banach space of continuous functions from I into R, endowed with the supremum norm ${∥p∥}_{\infty }={\sup }_{\breve{e}\in I}\left|p\left(\breve{e}\right)\right|.$ Mappings $d:{\Lambda }\times {\Lambda }\to {\check{R}}^{+}$ are defined by

$$d(y,y^{\prime })=\underset{r\in I}{\sup }{\left(\left|y\left(r\right)\right|+\left|y^{\prime }\left(r\right)\right|\right)}^2{e}^{-\breve{e}\left(r\right)}.$$

(55)

Thus, $(\Delta ,d)$ is a BMLS with $s=2$. The Caputo fractional differential equation (CFDE) can be defined with respect to order ${}_{\widehat{c}}{\check{D}}^{\eta }\left(\gamma \left(\breve{e}\right)\right)$ by

$${}_{\widehat{c}}{\check{D}}^{\eta }\left(\gamma \left(\breve{e}\right)\right)=\frac{1}{{\Gamma }\left(j-\eta \right)}{\int }_0^{\breve{e}}{\left(\breve{e}-s\right)}^{j-\eta -1}{\gamma }^{\left(j\right)}\left(s\right)ds$$

(56)

where $j-1<\eta <j,$$j=\left[\eta \right]+1$, the family $\left[\eta \right]$ represents ${\check{R}}^{+},$${\Gamma }$ represents the Gamma function and $\gamma :{\check{R}}^{+}\to \check{R}$ is a continuous function. Moreover, the Riemann–Liouville fractional derivatives (RLFD) of order $\eta$, for a continuous function $\gamma$, is defined by

$${\check{D}}^{\eta }\left(\gamma \left(\breve{e}\right)\right)=\frac{1}{{\Gamma }\left(j-\eta \right)}\frac{d^j}{d{\breve{e}}^j}{\int }_0^{\breve{e}}\frac{1}{{\left(\breve{e}-s\right)}^{\eta -j+1}}{\gamma }^{\left(j\right)}\left(s\right)ds(j=\left[\eta \right]+1).$$

(57)

We are now in the position to state the third main result of this exposition as follows:

Theorem 6.

Suppose that there exists a function $\lambda :\check{R}\times \check{R}\to \check{R}$, such that

($O_i$)

: ∀$y,y^{\prime }\in {\Lambda },$ with respect to $y\left(h\right)y^{\prime }\left(h\right)\ge y\left(h\right)$ or $y\left(h\right)y^{\prime }\left(h\right)\ge y^{\prime }\left(h\right)$ for each $h\in I,$ there exist $\tau :\left[0,\infty \right)\to \left[0,\infty \right),$ such that

$${(\left|\lambda (h,y(h\left)\right)\right|+\left|\lambda (h,y^{\prime }\left(h\right))\right|)}^2\le \frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left(h\right)\right|+\left|y^{\prime }\left(h\right)\right|)}^2{e}^{-\tau }$$

(58)

($O_{ii}$)

: there exists $y_0\in {\Lambda },$ such that $\lambda (y_0\left(h\right),P{y}_0\left(h\right))$ for each $h\in I,$ where the ⊥-continuous operator $\mathsf{\Phi }:{\Lambda }\to CB\left({\Lambda }\right)$ is defined by

$$\mathsf{\Phi }p\left(r\right)\in \left\{\begin{array}{c}\frac{1}{{\Gamma }\left(\eta \right)}{\int }_0^r{\left(r-\breve{e}\right)}^{\eta -1}\phi (\breve{e},p\left(\breve{e}\right))d\breve{e}\\ -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\eta -1}\phi (\breve{e},p\left(\breve{e}\right))d\breve{e}\\ +\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{\left(\breve{e}-{\breve{e}}_1\right)}^{\eta -1}\phi ({\breve{e}}_1,p\left({\breve{e}}_1\right))d{\breve{e}}_1\right)d\breve{e}\end{array}\right.$$

(59)

for $p\in {\Lambda }$ and $r\in \left[0,1\right].$

($O_{iii}$)

: for each $h\in I$ and $y,y^{\prime }\in {\Lambda },$ such that $\lambda (y\left(h\right),y^{\prime }\left(h\right))>0,$ implies $\lambda (\mathsf{\Phi }y\left(h\right),\mathsf{\Phi }{y}^{\prime }\left(h\right))>0.$

Under the assumptions (53)–(59), and if $\left(O_i\right)$-$\left(O_{iii}\right)$ are satisfied, then the NFDE (53) possesses at least one solution.

Proof. 

Define the orthogonality binary relation ⊥ on ${\Lambda }$ by

$$y\perp y^{\prime }\mathrm{iff}y\left(r\right)y^{{}^{\prime }}\left(r\right)\ge y\left(r\right)\mathit{or}y\left(r\right)y^{{}^{\prime }}\left(r\right)\ge y^{{}^{\prime }}\left(r\right)\forall r\in I.$$

(60)

Now, we prove that $\mathsf{\Phi }$ is ⊥-preserving. ∀$y,y^{\prime }\in \Delta$ with $y\perp y^{\prime }$ and $r\in I$, we have

$$\mathsf{\Phi }p\left(r\right)\in \left\{\begin{array}{c}\frac{1}{{\Gamma }\left(\eta \right)}{\int }_0^r{\left(r-\breve{e}\right)}^{\eta -1}\phi (\breve{e},p\left(\breve{e}\right))d\breve{e}\\ -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\eta -1}\phi (\breve{e},p\left(\breve{e}\right))d\breve{e}\\ +\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{\left(\breve{e}-{\breve{e}}_1\right)}^{\eta -1}\phi ({\breve{e}}_1,p\left({\breve{e}}_1\right))d{\breve{e}}_1\right)d\breve{e}\end{array}\right.\ge 1.$$

(61)

Therefore, it follows that $\left(\mathsf{\Phi }y\right)\left(r\right)\left(\mathsf{\Phi }{y}^{\prime }\right)\left(r\right)\ge \left(\mathsf{\Phi }y\right)\left(r\right)$, and so $\left(\mathsf{\Phi }y\right)\left(r\right)\perp \left(\mathsf{\Phi }{y}^{\prime }\right)\left(r\right).$ Hence, $\mathsf{\Phi }$ is ⊥-preserving. Next, we prove that $\mathsf{\Phi }$ is an $F_{\perp }$-contraction. Let $y,y^{\prime }\in {\Lambda }$ with $y\perp y^{\prime }$ and $\mathsf{\Phi }y\perp \mathsf{\Phi }{y}^{\prime }.$ For each $h\in I$, and owing to ⊥-continuous operator $\mathsf{\Phi },$ one can write:

$$\begin{array}{ccc}& & {\left(\left|\mathsf{\Phi }y\left(h\right)|+|\mathsf{\Phi }{y}^{\prime }\left(h\right)\right|\right)}^2\hfill \\ & =& \left(\left|\frac{1}{{\Gamma }\left(\alpha \right)}{\int }_0^r{\left(r-\breve{e}\right)}^{\alpha -1}\phi \left(\breve{e},p\left(\breve{e}\right)\right)d\breve{e}\right.\right.\hfill \\ & & -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\alpha \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\alpha -1}\phi (\breve{e},p\left(\breve{e}\right))d\breve{e}\hfill \\ & & \left.+\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\alpha \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{\left(\breve{e}-{\breve{e}}_1\right)}^{\alpha -1}\phi ({\breve{e}}_1,p\left({\breve{e}}_1\right))d{\breve{e}}_1\right)d\breve{e}\right|\hfill \\ & & +\left|\frac{1}{{\Gamma }\left(\alpha \right)}{\int }_0^r{\left(r-\breve{e}\right)}^{\alpha -1}\phi \left(\breve{e},p^{\prime }\left(\breve{e}\right)\right)d\breve{e}\right.\hfill \\ & & -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\alpha \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\alpha -1}\phi (\breve{e},p^{\prime }\left(\breve{e}\right))d\breve{e}\hfill \\ & & {\left.\left.+\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\alpha \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{\left(\breve{e}-{\breve{e}}_1\right)}^{\alpha -1}\phi ({\breve{e}}_1,p^{\prime }\left({\breve{e}}_1\right))d{\breve{e}}_1\right)d\breve{e}\right|\right)}^2\hfill \end{array}$$

This, in turn, yields (owing to the above hypothesis):

$$\begin{array}{ccc}& & {\left(\left|\mathsf{\Phi }y\left(h\right)|+|\mathsf{\Phi }{y}^{\prime }\left(h\right)\right|\right)}^2\hfill \\ & \le & \frac{1}{{\Gamma }\left(\alpha \right)}{\int }_0^r{|r-\breve{e}|}^{\alpha -1}{\left(\left|\phi \left(\breve{e},p\left(\breve{e}\right)\right)|+|\phi \left(\breve{e},p^{\prime }\left(\breve{e}\right)\right)\right|\right)}^{2}d\breve{e}\hfill \\ & & -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\alpha \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\alpha -1}\left(\right|\phi (\breve{e},p\left(\breve{e}\right))|+|\phi (\breve{e},p\left(\breve{e}\right)){\left|\right)}^{2}d\breve{e}\hfill \\ & & +\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}|\breve{e}-{\breve{e}}_1{|}^{\alpha -1}\left(\right|\phi ({\breve{e}}_1,p\left({\breve{e}}_1\right))|+|\phi ({\breve{e}}_1,p\left({\breve{e}}_1\right)){\left|\right)}^{2}d{\breve{e}}_1\right)d\breve{e}\hfill \\ & \le & \frac{1}{{\Gamma }\left(\eta \right)}{\int }_0^r{|r-\breve{e}|}^{\alpha -1}\frac{{\Gamma }\left(\alpha +1\right)}{5}{(\left|y\left(\breve{e}\right)\right|+\left|y^{\prime }\left(\breve{e}\right)\right|)}^2{e}^{-\tau }d\breve{e}\hfill \\ & & -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\alpha -1}\frac{{\Gamma }\left(\alpha +1\right)}{5}{(\left|y\left(\breve{e}\right)\right|+\left|y^{\prime }\left(\breve{e}\right)\right|)}^2{e}^{-\tau }d\breve{e}\hfill \\ & & +\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{|\breve{e}-{\breve{e}}_1|}^{\eta -1}\frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }d{\breve{e}}_1\right)d\breve{e}\hfill \\ & \le & \frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }(\frac{1}{{\Gamma }\left(\eta \right)}{\int }_0^1{|r-\breve{e}|}^{\eta -1}d\breve{e}\hfill \\ & & -\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^1{\left(1-\breve{e}\right)}^{\eta -1}d\breve{e}+\frac{2r}{\left(2-{\sigma }^2\right){\Gamma }\left(\eta \right)}{\int }_0^{\sigma }\left({\int }_0^{\breve{e}}{|\breve{e}-{\breve{e}}_1|}^{\eta -1}d{\breve{e}}_1\right)d\breve{e})\hfill \\ & \le & \frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }(\frac{r^{\alpha }}{\eta }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{1}{\alpha }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{{\sigma }^{\alpha +1}}{\eta \left(\eta +1\right)})\hfill \\ & \le & \frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }\underset{r\in (0,1)}{\sup }(\frac{r^{\eta }}{\eta }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{1}{\eta }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{{\sigma }^{\eta +1}}{\eta \left(\eta +1\right)})\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill {\left(\left|\mathsf{\Phi }y\left(h\right)|+|\mathsf{\Phi }{y}^{\prime }\left(h\right)\right|\right)}^2& \le & \frac{{\Gamma }\left(\eta +1\right)}{5}{(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }\hfill \\ & & \underset{r\in (0,1)}{\sup }(\frac{r^{\eta }}{\eta }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{1}{\eta }+\frac{2r}{\left(2-{\sigma }^2\right)}\frac{{\sigma }^{\eta +1}}{\eta \left(\eta +1\right)})\hfill \end{array}$$

Thus, $forall$$y,y^{\prime }\in {\Lambda }$ with respect to $y\perp y^{\prime }$, $\mathsf{\Phi }y\perp \mathsf{\Phi }{y}^{\prime }$ and $\lambda (y\left(h\right),y^{\prime }\left(h\right))>0$ for each $h\in I,$ we have

$${\left(\left|\mathsf{\Phi }y\left(h\right)|+|\mathsf{\Phi }{y}^{\prime }\left(h\right)\right|\right)}^2\le {(\left|y\left({\breve{e}}_1\right)\right|+\left|y^{\prime }\left({\breve{e}}_1\right)\right|)}^2{e}^{-\tau }.$$

(62)

or

$$H_O(\mathsf{\Phi }y,\mathsf{\Phi }{y}^{\prime })\le e^{-\tau }d(y,y^{\prime }).$$

By applying this to logarithm, we can write

$$\ln \left(H_O(\mathsf{\Phi }y,\mathsf{\Phi }{y}^{\prime })\right)\le \ln \left(e^{-\tau }d(y,y^{\prime })\right)$$

and, hence, we can easily obtain, with the setting of $F\left(y\right)=\ln \left(y\right)$$,\forall$$y\in R$

$$\tau \left(d(y,y^{\prime })\right)+F\left(H_O(\mathsf{\Phi }y,\mathsf{\Phi }{y}^{\prime })\right)\le F\left(d(y,y^{\prime })\right).$$

Thus, due to assumptions (53)–(59), all the required hypotheses of Corollary (5) are satisfied. Therefore, Equation (53) possesses at least one solution. □

Example 6.

Let CFDE, with respect to order η${}_{\widehat{c}}{\check{D}}^{\eta }$ and its IBVB, be written as follows:

$${}_{\widehat{c}}{\check{D}}^{\frac{3}{2}}\left(p\left(\breve{e}\right)\right)=\frac{1}{{\left(\breve{e}+3\right)}^2}\frac{\left|p\left(\breve{e}\right)\right|}{1+\left|p\left(\breve{e}\right)\right|},(\breve{e}\in [0,1])$$

(63)

and

$$p\left(0\right)=0,p\left(1\right)={\int }_0^{\frac{3}{4}}p\left(s\right)ds,$$

(64)

where $\eta =\frac{3}{2},$ $\beta =\frac{3}{4}$ and $\phi (\breve{e},p\left(\breve{e}\right))=\frac{1}{{\left(\breve{e}+3\right)}^2}\frac{\left|p\left(\breve{e}\right)\right|}{1+\left|p\left(\breve{e}\right)\right|}.$ Furthermore, $|\phi (\breve{e},p)|\le \frac{1}{7},$ $K=\frac{{\Gamma }\left(\eta +1\right)}{5}$ and therefore, after setting for

$$\tau \left(\breve{e}\right)=\breve{e}.\ln \left(\frac{101}{100}\right),\mathit{for}\breve{e}\in (0,\infty ).$$

(65)

Therefore, we can apply Corollary (5). Hence, there is a solution to Equation (63) in Λ, along with the conditions (64).

5. Open Problems

In this section, we pose some challenging questions for researchers.

Problem I: Clearly, the limit of the convergent sequence is not necessarily unique in BMLS. Can the limit of a convergent sequence be unique in OBMLS?

Problem II: Can Theorem (1) be proved by the Semi-$F_{\perp }$-contraction?

6. Conclusions

In conclusion, this manuscript deals with the new concept of OBMLS to approximate the fixed-point results for a hybrid pair of mappings that are are introduced and studied. In addition, a new ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$ is provided and determined via a hybrid pair of mappings. A new multi-valued $F_{\perp }$ Suzuki-type contractive condition is proposed in an OBMLS under the influence of ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$. Finally, our investigation is completed with tangible examples and applications to ordinary differential equations and nonlinear fractional differential equations in the field of nonlinear analysis.

Some potential future works are as follows:

(i)

Discuss the possibility of applying multi-valued $F_{\perp }$ Suzuki-type fixed-point results with respect to ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$ to the context of fuzzy mapping;

(ii)

Discuss the possibility of an orthogonal B-metric-like space with respect to ODS ${\check{D}}_{\perp }(\mu ,\rho ,{\breve{e}}_0)$ in the context of an orthogonal fuzzy B-metric-like space.