Counting Non-Convex 5-Holes in a Planar Point Set

Abstract

Let S be a set of n points in the general position, that is, no three points in S are collinear. A simple k-gon with all corners in S such that its interior avoids any point of S is called a k-hole. In this paper, we present the first algorithm that counts the number of non-convex 5-holes in S. To our best knowledge, prior to this work there was no known algorithm in the literature except a trivial brute force algorithm. Our algorithm runs in time $O(T+Q)$, where T denotes the number of 3-holes, or empty triangles, in S and Q that denotes the number of non-convex 4-holes in S. Note that $T+Q$ ranges from $\mathsf{\Omega }\left(n^2\right)$ to $O\left(n^3\right)$, while its expected number is $\mathsf{\Theta }(n^{2}logn)$ when the points in S are chosen uniformly and independently at random from a convex and bounded body in the plane.

1. Introduction

Let S be a set of n points in the plane that are in general position; that is, no three points in S are collinear. For each $k\ge 3$, a k-gon in S is a simple polygon with k corners that are members of S. A k-hole in S is an empty k-gon, that is, its interior does not contain any point in S, so is an empty k-gon. In this paper, we focus on the number of k-holes in S for a fixed $k\ge 3$, and address the problem of counting non-convex k-holes in a given set S, in particular for $k=5$.

The problem of counting or enumerating k-gons or k-holes has been studied for decades by many researchers. It is obvious that counting objects of a particular type is not as hard as enumerating them, since we can count them by enumeration. Dobkin et al. [1] in 1990 presented an algorithm that enumerates all convex k-holes in time $O(h_3\left(S\right)+k·h_k\left(S\right))$, where $h_k\left(S\right)$ denotes the number of k-holes in S. This algorithm, in particular, for $k=3,4$ takes time $O\left(h_k\left(S\right)\right)$, proportional to the number of reported k-holes. Rote et al. [2] studied the problem of counting convex k-gons in S and presented an $O\left(n^{k-2}\right)$-time algorithm. This was improved to $O\left(k{n}^3\right)$ time for $k\ge 6$ by Mitchell et al. [3] after Rote and Woeginger [4]. Mitchell et al. [3] also solved the problem of counting convex k-holes in the same time $O\left(k{n}^3\right)$, and it was very recent that the second author improved this to $O\left(k{h}_3\left(S\right)\right)$ time [5]. The number $h_3\left(S\right)$ of empty triangles in S ranges between $\mathsf{\Omega }\left(n^2\right)$ and $O\left(n^3\right)$, while the expected value of $h_3\left(S\right)$ is proven to be $\mathsf{\Theta }\left(n^2\right)$ if the points in S are uniformly chosen from a convex and bounded body in the plane [6,7].

1.1. Our Contribution and Approach

The problem of counting non-convex k-holes, however, has not received enough attention for a long time. Very recently, the authors showed how to count non-convex 4-holes in S in $O\left(h_3\left(S\right)\right)$ time [8].

In this paper, we continue our efforts, and present an algorithm that precisely counts non-convex 5-holes in a given set S. Our main contribution is summarized by the following theorem.

Theorem 1.

Let S be a set of n points, no three of which are collinear. The number of non-convex 5-holes in S can be computed in $O(h_3\left(S\right)+{\widehat{h}}_4\left(S\right))$ time, where $h_3\left(S\right)$ denotes the number of empty triangles in S and ${\widehat{h}}_4\left(S\right)$ denotes the number of non-convex 4-holes in S.

To our best knowledge, prior to this work, there was no known algorithm that counts non-convex k-holes in a given set S of points for $k\ge 5$ in the literature, except a trivial exhaustive enumeration algorithm taking $O\left(n^{k+1}\right)$ time. Our algorithm takes $O(h_3\left(S\right)+{\widehat{h}}_4\left(S\right))$ time, where ${\widehat{h}}_4\left(S\right)$ denotes the number of non-convex 4-holes in S. The number ${\widehat{h}}_4\left(S\right)$ of non-convex 4-holes in S varies from 0 to $O\left(n^3\right)$ [9], while its expected number has been known to be $\mathsf{\Theta }(n^{2}logn)$ by Fabilia-Monroy et al. [10] when the points in S were chosen uniformly at random from a convex and bounded body. Hence, our algorithm is expected to run in $O(n^{2}logn)$ time for random points S, while its worst-case running time is bounded by $O\left(n^3\right)$. See the below and

Table 1. The current best bounds on the minimum, maximum, and expected numbers of convex and non-convex k-holes, denoted by $h_k\left(S\right)$ and ${\widehat{h}}_k\left(S\right)$, and their total number ${\overline{h}}_k\left(S\right)$ in a set S of n points in general position. For the expected number of k-holes, the n points in S are assumed to be chosen uniformly and independently at random from a convex and bounded body.

		Minimum		Maximum		Expected
$k=3$	$h_3$	$n^2-O\left(n\right)$, $1.6196n^2+o\left(n\right)$	[11]	$\left(\genfrac{}{}{0pt}{}{n}{3}\right)=\mathsf{\Theta }\left(n^3\right)$	[easy]	$\mathsf{\Theta }\left(n^2\right)$	[6]
$k=4$	$h_4$	$\frac{1}{2}{n}^2-O\left(n\right)$, $1.9397n^2+o\left(n\right)$	[11]	$\left(\genfrac{}{}{0pt}{}{n}{4}\right)=\mathsf{\Theta }\left(n^4\right)$	[easy]	$\mathsf{\Theta }\left(n^2\right)$	[10]
	${\widehat{h}}_4$	0	[easy]	$\mathsf{\Theta }\left(n^3\right)$	[9]	$\mathsf{\Theta }(n^{2}logn)$	[10]
	${\overline{h}}_4$	$\mathsf{\Omega }\left(n^2\right)$, $O(n^{2}logn)$	[9,10,12]	$\left(\genfrac{}{}{0pt}{}{n}{4}\right)=\mathsf{\Theta }\left(n^4\right)$	[9]	$\mathsf{\Theta }(n^{2}logn)$	[10]
$k\ge 5$	$h_k$	$\left\{\begin{array}{cc}\mathsf{\Omega }\left(n{log}^{4/5}n\right),O\left(n^2\right)\hfill & k=5\hfill \\ \mathsf{\Omega }\left(n\right),O\left(n^2\right)\hfill & k=6\hfill \\ 0\hfill & k\ge 7\hfill \end{array}\right.$	[11,13,14]	$\left(\genfrac{}{}{0pt}{}{n}{k}\right)=\mathsf{\Theta }\left(n^k\right)$	[easy]	$O\left(n^2\right)$	[7]
	${\widehat{h}}_k$	0	[easy]	$\mathsf{\Theta }\left(n^{k-1}\right)$	[12]	$O\left(n^{k-1}\right)$	[12]
	${\overline{h}}_k$	$\mathsf{\Omega }\left(n^2\right)$,$O\left(n^{\frac{k+1}{2}}{log}^{k-3}n\right)$	[12]	$\left(\genfrac{}{}{0pt}{}{n}{k}\right)=\mathsf{\Theta }\left(n^k\right)$	[12]	$O\left(n^{k-1}\right)$	[12]

for more details on the known bounds on the number $h_k\left(S\right)$ of convex k-holes and the number ${\widehat{h}}_k\left(S\right)$ of non-convex k-holes for each $k\ge 3$.

In order to count 5-holes in S, we start with a simple fact that any pentagon is decomposed into three triangles. Conversely, a 5-hole can be obtained by attaching three empty triangles that are adjacent side by side. Of these three triangles, the one adjacent to the other two is called a middle triangle of the pentagon. We give a classification of middle triangles of 5-holes into four types according to the relative positions of the other two triangles, and reveal a crucial relation between the number of diagonals of 5-holes and the types of middle triangles. This observation enables us several different ways of counting 5-holes with multiplicity, together with the structural properties of 3-holes (i.e., empty triangles) and 4-holes known by the previous paper [8]. In turn, we obtain a system of linear equations of a constant number of variables, and the number of non-convex 5-holes in S can be computed by solving the system.

1.2. Related Work

Combinatorial and algorithmic studies on k-gons and k-holes were initiated by Erdős and Szekeres [15] in 1935, and are still being continued by many researchers today.

In 1935, Erdős and Szekeres asked the least number $N\left(k\right)$ for $k\ge 3$ such that any set of $N\left(k\right)$ points in general position in ${\mathbb{R}}^2$ contains a convex k-gon [15,16]. This problem is known as the Erdős–Szekeres problem. It is proven that $N\left(4\right)=5$, $N\left(5\right)=9$ [15], and $N\left(6\right)=17$ [17]. The exact value of $N\left(k\right)$ for $k\ge 7$ is unknown. Erdős and Szekeres [15] also proved an upper bound $N\left(k\right)\le \left(\genfrac{}{}{0pt}{}{2k-4}{k-2}\right)+1$ and conjectured that $N\left(k\right)=2^{k-2}+1$ for each $k\ge 2$. Note that the conjecture holds for $k\le 6$. Erdős and Szekeres later proved a matching lower bound $N\left(k\right)\ge 2^{k-2}+1$ in 1961 [16]. Suk [18] in 2017 made a breakthrough $N\left(k\right)\le 2^{k+O(k^{2/3}logk)}$. Currently, the best upper bound is $N\left(k\right)\le 2^{k+O\left(\sqrt{klogk}\right)}$ due to Holmsen et al. [19].

In 1978, Erdős also posed an empty version of the Erdős–Szekeres problem which asks the least number $H\left(k\right)$ for $k\ge 3$ such that any set of $H\left(k\right)$ points in general position contains a convex k-hole [20]. Some known results on $H\left(k\right)$ are as follows: $H\left(3\right)=3$ and $H\left(4\right)=5$ are easy to see, $H\left(5\right)=10$ is proved by Harborth [21], $H\left(6\right)$ is bounded [22,23], and Horton [13] proved that $H\left(k\right)$ for $k\ge 7$ is unbounded and undefined.

As a variant of the Erdős–Szekeres problem, the possible number of convex k-gons and k-holes in a set of n points has been studied extensively in the literature. Here, we introduce only results on the number of k-holes; for more results on k-gons, we refer to survey papers by Morris and Soltan [24,25].

It is not difficult to see that the maximum possible number of convex k-holes is achieved when the points in S are in a convex position so that $h_k\left(S\right)\le \left(\genfrac{}{}{0pt}{}{n}{k}\right)=\mathsf{\Theta }\left(n^k\right)$. Thus, most of the research has focused on their minimum possible numbers and expected numbers when the points in S are chosen uniformly from a certain convex shape in the plane. For the minimum and expected number of convex k-holes, currently, the best bounds are summarized in Table 1. Some important bounds are as follows. Note that $h_k\left(S\right)$ can be zero for any $k\ge 7$ and some sets S of any size n by Horton [13]. Bárány and Füredi [6] showed that the minimum of $h_k\left(S\right)$ over all sets S of n points is $\mathsf{\Theta }\left(n^2\right)$ for $k\in \{3,4\}$ and is between $\mathsf{\Omega }\left(n\right)$ and $O\left(n^2\right)$ for $k\in \{5,6\}$. There has been constant effort to improve the hidden constants in the $O(·)$ and $\mathsf{\Omega }(·)$. For more history, see Bárány and Valtr [11], Valtr [26], Dumistrescu [27], Pinchasi, Radoičić, and Sharir [28], and references therein. A recent breakthrough was due to Aichholzer et al. [14] who showed that the minimum possible number of convex 5-holes is at least $\mathsf{\Omega }\left(n{log}^{4/5}n\right)$. Bárány and Füredi [6] showed that the expected value of $h_3\left(S\right)$ is $\mathsf{\Theta }\left(n^2\right)$ when the points in S are chosen uniformly from a unit square. Recently, Balko et al. [7] extended this result to any higher-dimensional space and any convex body of unit measure from which points are chosen uniformly at random.

Despite a huge amount of results on convex k-gons and k-holes, it was relatively recent that the first nontrivial bounds on the minimum and maximum numbers of non-convex k-gons and k-holes were proven. Aichholzer et al. [9] and Aichholzer et al. [12] established several new bounds on the maximum/minimum possible number of non-convex k-gons and k-holes for $k\le 4$. Let ${\widehat{h}}_k\left(S\right)$ be the number of non-convex k-holes in S, and let ${\overline{h}}_k\left(S\right):=h_k\left(S\right)+{\widehat{h}}_k\left(S\right)$ be the number of k-holes in S, regardless of being convex or non-convex. Specifically, they showed that the minimum of ${\overline{h}}_k\left(S\right)$ is between $\mathsf{\Omega }\left(n^2\right)$ and $O\left(n^{\frac{k+1}{2}}{log}^{k-3}n\right)$ and the maximum of ${\widehat{h}}_k\left(S\right)$ is $\mathsf{\Theta }\left(n^{k-1}\right)$ for each $k\ge 4$. Fabila-Monroy et al. [10] proved that the expected number of ${\widehat{h}}_4\left(S\right)$ is $12n^{2}logn+o(n^{2}logn)$ when the points in S are chosen uniformly from a convex and bounded body. This also improves the upper bound of the minimum number of ${\overline{h}}_4\left(S\right)$ to $O(n^{2}logn)$. Again, see Table 1 for the current best bounds on the minimum, maximum, and expected numbers of ${\widehat{h}}_k\left(S\right)$ and ${\overline{h}}_k\left(S\right)$.

1.3. Organization of the Paper

The rest of the paper is organized as follows. Section 2 introduces some necessary preliminaries and facts on empty triangles and empty quadrilaterals, that is, 3-holes and 4-holes known in the literature, for further discussion on our algorithm that counts 5-holes. Section 3 is devoted to provide crucial properties of 5-holes in terms of their middle triangles. Our counting algorithm is described and analyzed in Section 4. We finally conclude this paper with remarks and open problems in Section 5.

2. Preliminaries

Throughout the paper, we consider a standard orthogonal coordinate system in the plane ${\mathbb{R}}^2$ with the x- and y-coordinates, from which we may say that a point is to the left, to the right, below, or above another point in a normal sense. For any two points $p,q\in {\mathbb{R}}^2$, the line segment joining p and q will be denoted by $\overline{pq}$.

A polygon with k corners is represented by a cyclic sequence of its corners $p_1{p}_2\dots p_k$. When we write any polygon by its corner sequence $p_1{p}_2\dots p_k$, it is imposed that the corners are traversed in counterclockwise order. A diagonal of a polygon is a segment between its two nonadjacent corners that does not stick out of the polygon. Any convex k-gon has $\left(\genfrac{}{}{0pt}{}{k}{2}\right)=k(k-1)/2$ distinct diagonals, while any non-convex k-gon has a strictly smaller number of those.

Let S be a given set of n points in general position in the plane so that no three points in S are collinear. For any $k\ge 3$, let $h_k:=h_k\left(S\right)$, ${\widehat{h}}_k:={\widehat{h}}_k\left(S\right)$, and ${\overline{h}}_k:={\overline{h}}_k\left(S\right)$ for simplicity. For any $p\in S$, let $S_p$ be the cyclic array consisting of points in $S\backslash \left\{p\right\}$ in counterclockwise order around p. The sorted cyclic arrays $S_p$ for all $p\in S$ can be obtained in total $O\left(n^2\right)$ time by constructing the arrangement of n lines dual to the points in S and traversing the arrangement. See Dobkin et al. [1] and Rote et al. [2].

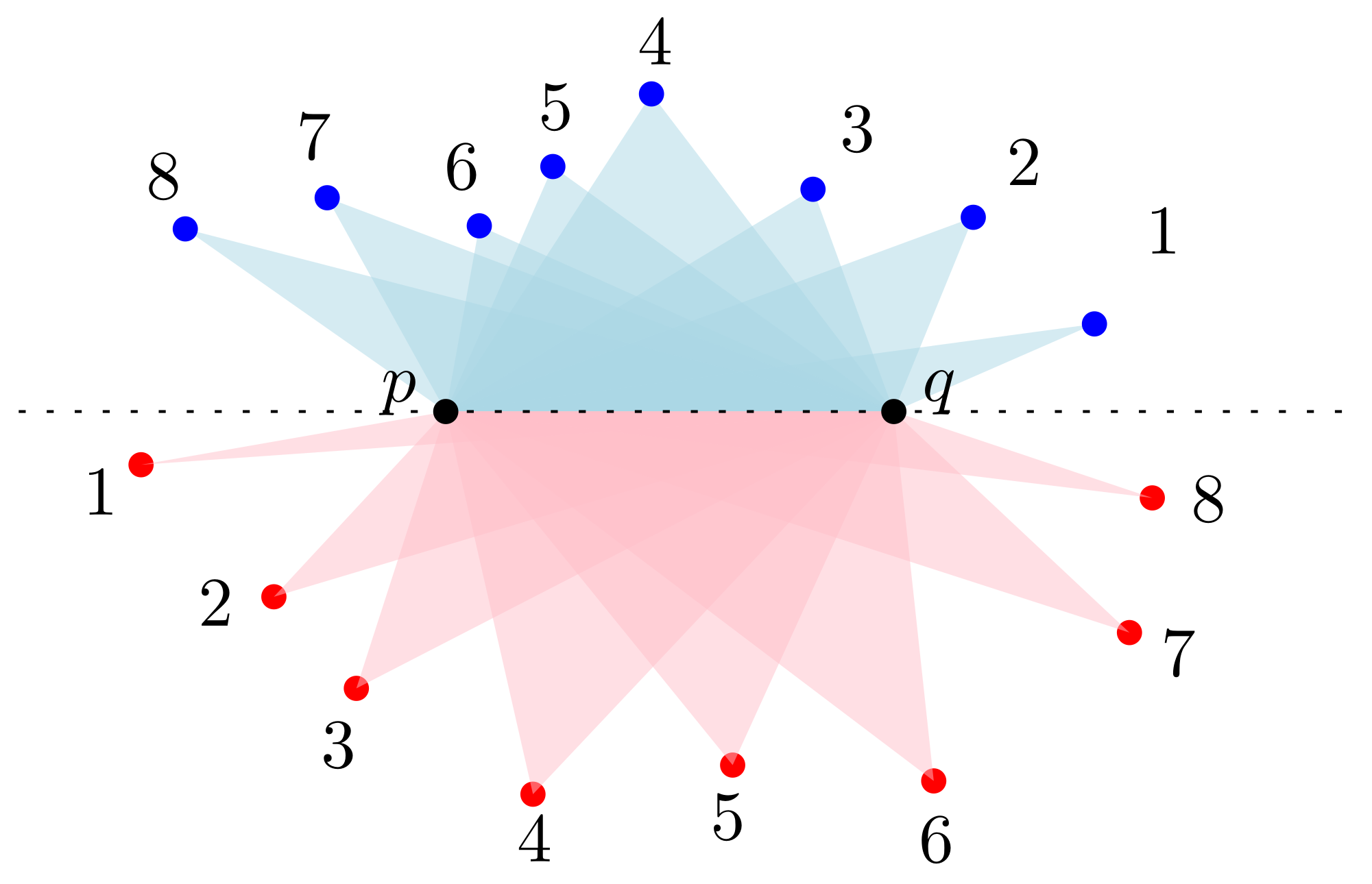
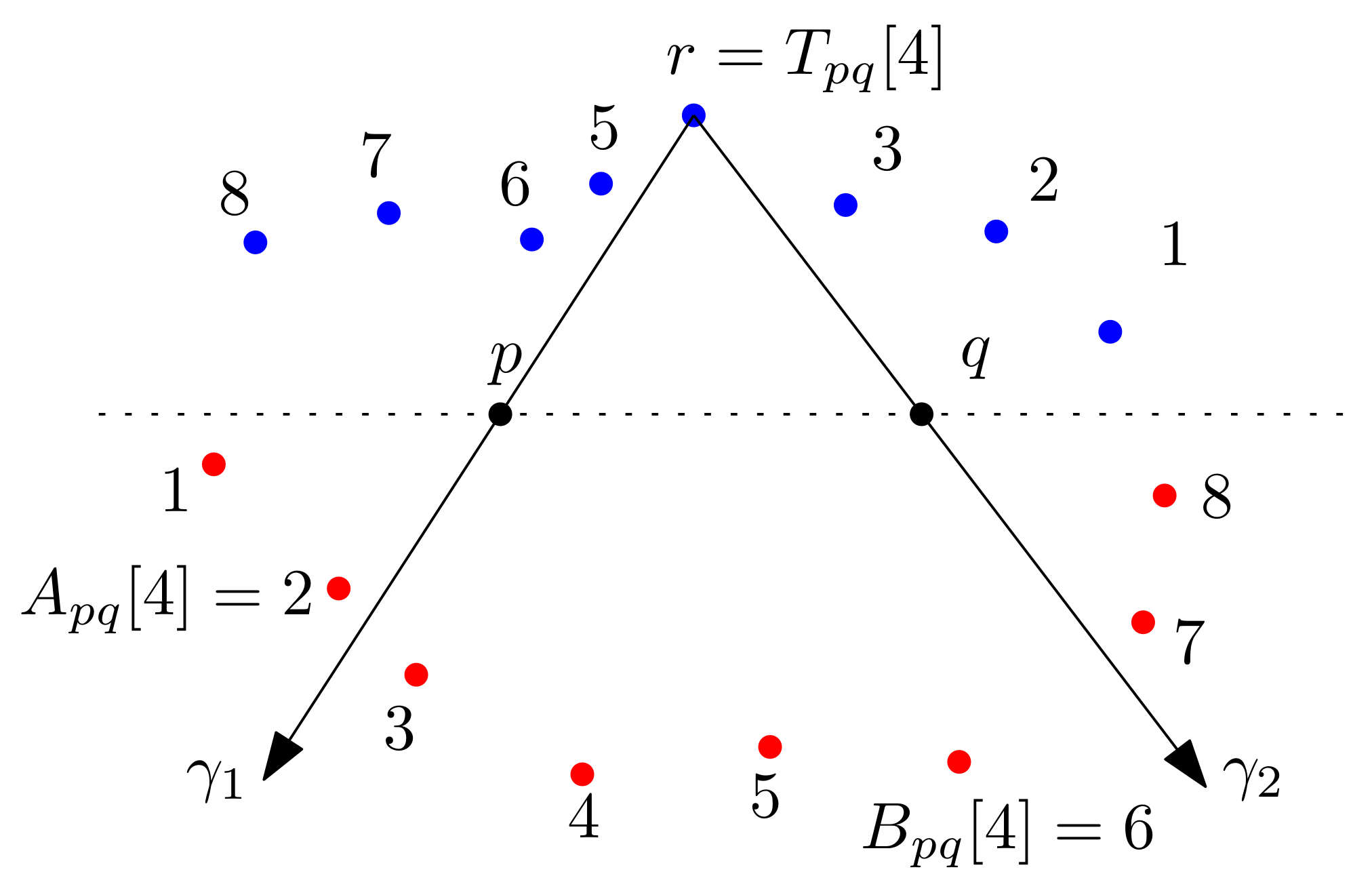
2.1. Empty Triangles and Their Structures

For any two distinct points $p,q\in S$, let $T_{pq}$ be the set of all points $r\in S\backslash \{p,q\}$ such that the triangle $pqr$ is empty, and we obtain p, q, and r in this order when we traverse the boundary of the triangle in the counterclockwise direction from p. Similarly, let $T_{qp}$ be the set of all points $r\in S\backslash \{p,q\}$ such that the triangle $qpr$ is empty, and we obtain q, p, and r in this order when we traverse the boundary of the triangle in the counterclockwise direction from q. Note that $T_{pq}$ and $T_{qp}$ are separated by the line through p and q, and that $T_{pq}\cup T_{qp}$ consists of all points $r\in S$ such that the triangle constructed with $\overline{pq}$ and a third corner r is empty. See Figure 1 for an illustration.

The following is an immediate identity by a common counting technique.

Lemma 1.

It holds that ${\sum }_{p\in S}{\sum }_{q\in S_p}\left|T_{pq}\right|=3h_3$.

Proof. 

Consider any empty triangle $abc$ in S. Then, the triangle $abc$ is involved in exactly three sets $T_{ab}$, $T_{bc}$, and $T_{ca}$ in such a way that $c\in T_{ab}$, $a\in T_{bc}$, and $b\in T_{ca}$. Hence, in the sum ${\sum }_{p\in S}{\sum }_{q\in S_p}\left|T_{pq}\right|$, each empty triangle is counted exactly three times, so we have the claimed equation.    □

The authors have proved the following in a previous paper [8].

Lemma 2 

(Sung and Bae [8]). For any pair $(p,q)\in S\times S$ with $p\ne q$, the points in $T_{pq}$ appear in the same counterclockwise order, both around p and q. For all such pairs $(p,q)$, the points in $T_{pq}$ can be computed and sorted in this order in total $O\left(h_3\right)$ time into a sorted array.

By an abuse of notation, we shall mean by $T_{pq}$ the sorted array of itself obtained by the above lemma. Additionally, for any positive integer i, let $T_{pq}\left[i\right]$ denote the i-th point in the array $T_{pq}$. In Figure 1, the points in $T_{pq}$ and $T_{qp}$ and their indices are depicted.

2.2. Empty Quadrilaterals

Fix two points $p,q\in S$ with $p\ne q$, and any point $r=T_{pq}\left[i\right]$ in $T_{pq}$. Consider the two directed rays emanating from r towards p and q, respectively, denoted by ${\gamma }_1$ and ${\gamma }_2$, respectively. We associate with $T_{pq}\left[i\right]$ the following: Let $A_{pq}\left[i\right]$ be the largest index $j_1$ of $T_{qp}$ such that $T_{qp}\left[j_1\right]$ lies on the right side of ${\gamma }_1$, or $A_{pq}\left[i\right]=0$ if there is no point in $T_{qp}$ on the right side of ${\gamma }_1$; let $B_{pq}\left[i\right]$ be the largest index $j_2$ of $T_{qp}$ such that $T_{qp}\left[j_2\right]$ lies on the right side of ${\gamma }_2$, or $B_{pq}\left[i\right]=0$ if there is no point in $T_{qp}$ on the right side of ${\gamma }_2$. See Figure 2 for an illustration. These values are essential to count the number of convex and non-convex 4-holes, as shown in the Ref. [8], in which all these values can be computed in $O\left(h_3\right)$ time.

Lemma 3 

(Sung and Bae [8]). Let $p,q\in S$ with $p\ne q$ be fixed. For any $1\le i\le |T_{pq}|-1$, it holds that $A_{pq}[i+1]\ge A_{pq}\left[i\right]$ and $B_{pq}[i+1]\ge B_{pq}\left[i\right]$. The values of $A_{pq}\left[i\right]$ and $B_{pq}\left[i\right]$ for all $1\le i\le |T_{pq}|$ can be computed in $O\left(\right|T_{pq}|+|T_{qp}\left|\right)$ time.

Consider an empty triangle $pqr$ in S with $r\in T_{pq}$. Any 4-hole with $pq$ as a diagonal can be obtained by gluing $pqr$ and another empty triangle $qps$ with $s\in T_{qp}$ along the side $pq$. The resulting 4-hole $psqr$ can be either convex or non-convex. The authors have shown the following. Let i be such that $r=T_{pq}\left[i\right]$, and j be such that $s=T_{qp}\left[j\right]$. Then the 4-hole $psqr$ is convex if, and only if $A_{pq}\left[i\right]<j\le B_{pq}\left[i\right]$. This directly provides a way of counting 4-holes having $\overline{pq}$ as a diagonal, being separately convex and non-convex.

Lemma 4 

(Sung and Bae [8]). Let $p,q\in S$ with $p\ne q$ be fixed. Then, $psqr$ is a 4-hole for $r,s\in S$ with a diagonal $\overline{pq}$ if, and only if $r\in T_{pq}$ and $s\in T_{qp}$. Moreover, if $r=T_{pq}\left[i\right]$ and $s=T_{qp}\left[j\right]$ for indices $1\le i\le |T_{pq}|$ and $1\le j\le |T_{qp}|$, then the following hold:

(i) 

The 4-hole $psqr$ is convex if, and only if $A_{pq}\left[i\right]<j\le B_{pq}\left[i\right]$.

(ii) 

The 4-hole $psqr$ is non-convex if, and only if $j\le A_{pq}\left[i\right]$ or $j>B_{pq}\left[i\right]$.

Therefore, the number of convex 4-holes $psqr$ for fixed $p,q\in S$ and $r=T_{pq}\left[i\right]$ is exactly $B_{pq}\left[i\right]-A_{pq}\left[i\right]$, and the number of those that are non-convex is exactly $|T_{qp}|-(B_{pq}\left[i\right]-A_{pq}\left[i\right])$.

The statements in Lemma 4 can also be verified in Figure 2. Consider the example depicted in Figure 2 in which $i=4$ and $r=T_{pq}\left[4\right]$. Then, any convex 4-hole of the form $psqr$ should choose $s\in T_{qp}$ to be between the two rays ${\gamma }_1$ and ${\gamma }_2$, so if $s=T_{qp}\left[j\right]$, then j must be between $A_{pq}\left[4\right]+1$ and $B_{pq}\left[4\right]$. On the other hand, non-convex 4-holes are constructed by choosing $s=T_{qp}\left[j\right]$ with $1\le j\le A_{pq}\left[4\right]$ or $B_{pq}\left[4\right]<j\le \left|T_{qp}\right|$.

Lemma 4 provides a way of counting convex and non-convex 4-holes, by iterating all $p,q\in S$ and $r\in T_{pq}$.

Lemma 5.

It holds that

$$\begin{array}{cc}\hfill h_4& =\frac{1}{4}\sum _{p\in S}\sum _{q\in S_p}\sum _{1\le i\le |T_{pq}|}(B_{pq}\left[i\right]-A_{pq}\left[i\right])and\hfill \\ \hfill {\widehat{h}}_4& =\frac{1}{2}\sum _{p\in S}\sum _{q\in S_p}\left(|T_{pq}|·|T_{qp}|-\sum _{1\le i\le |T_{pq}|}(B_{pq}\left[i\right]-A_{pq}\left[i\right])\right).\hfill \end{array}$$

Proof. 

The above equations immediately follow from Lemma 4.    □

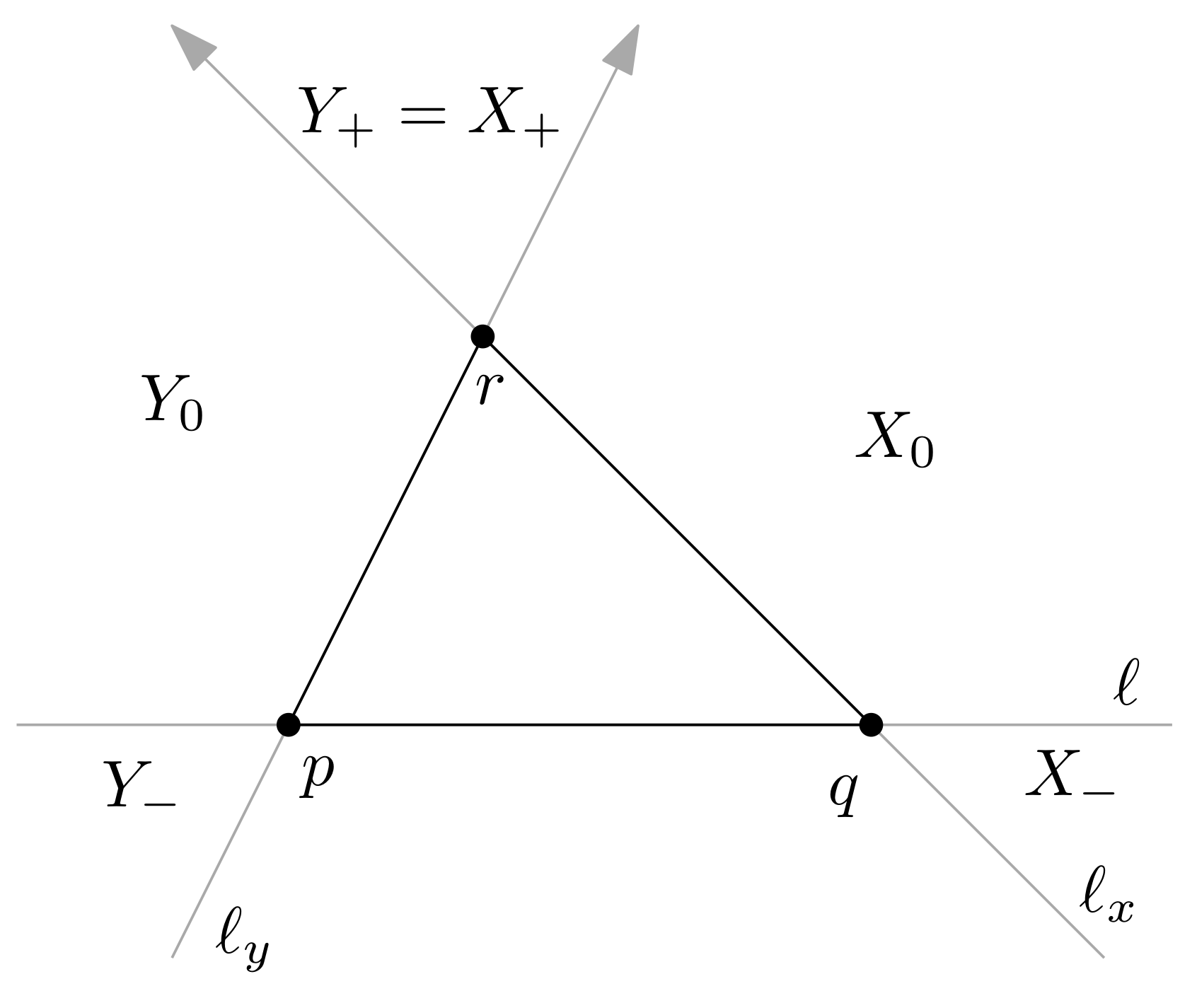
3. Middle Triangles of Empty Pentagons

It is obvious and well-known that any simple k-gon, being either convex or non-convex, can be decomposed into exactly $k-2$ triangles by cutting it along two non-crossing diagonals. Such a decomposition is called a triangulation of a polygon. Any pentagon, hence, admits a triangulation of exactly three triangles. This implies that any simple pentagon has at least two diagonals. More generally, we observe the following.

Lemma 6.

Let P be any simple pentagon. The number of diagonals of any simple pentagon is between two and five. Moreover, a simple pentagon has five diagonals if, and only if it is convex.

Proof. 

As discussed above, any simple pentagon admits a triangulation of three triangles. Therefore, there must be at least two diagonals.

For each corner v of any simple pentagon, it is adjacent to two other corners, so there are, at most, two corners that can be joined with v by diagonals. This implies that the maximum number of diagonals of a simple pentagon is five, and this can be achieved only when it is convex.    □

In any triangulation of a pentagon P, there must be a triangle bounded by two diagonals of the pentagon P. Such a triangle in P is called a middle triangle of P. In general, a simple pentagon has at least one middle triangle as it has a triangulation, while it may not be unique.

Consider an empty pentagon, or a 5-hole, P in the given set S of points. Let $pqr$ be a middle triangle of P such that $\overline{qr}$ and $\overline{rp}$ are diagonals of P and $\overline{pq}$ is a side of P. Then, $pqr$ is an empty triangle in S and P can be written as $P=pqxry$ where $x,y\in S$ are the other two corners of P. The two triangles $pry$ and $qxr$ are also empty, and hence we have that $x\in T_{rq}$ and $y\in T_{pr}$.

Assume without loss of generality that $\overline{pq}$ is horizontal and r is above the line ℓ extending $\overline{pq}$. Let ${\ell }_y$ be the directed line through p and towards r, and ${\ell }_x$ be the directed line through q and towards r. Observe that y lies in the left side of ${\ell }_y$ and x lies in the right side of ${\ell }_x$, since P is a simple pentagon. Let X be the half-plane on the left side of ${\ell }_x$ and Y be the half-plane on the right side of ${\ell }_y$. Hence, we have $x\in X$ and $y\in Y$.

These regions X and Y are further partitioned as follows: The region X is partitioned into three regions $X_{+}$, $X_0$, and $X_{-}$ by two lines ${\ell }_x$ and ℓ such that $X_{+}=X\cap Y$, $X_{-}$ is the region below ℓ, and $X_0=X\backslash (X_{+}\cup X_{-})$. Analogously, Y is partitioned into three regions $Y_{+}$, $Y_0$, and $Y_{-}$ by ${\ell }_y$ and ℓ such that $Y_{+}=X_{+}=X\cap Y$, $Y_{-}$ is the region below ℓ, and $Y_0=Y\backslash (Y_{+}\cup Y_{-})$. See Figure 3 for an illustration.

We classify each middle triangle $pqr$ of a 5-hole $P=pqxry$ into one of the following four types, depending on the locations of x and y. We say that the middle triangle $pqr$ of P is of:

(a)

type 00 if $x\in X_0$ and $y\in Y_0$,

(b)

type $0-$ if either $x\in X_0$ and $y\in Y_{-}$, or $x\in X_{-}$ and $y\in Y_0$,

(c)

type $0+$ if either $x\in X_0$ and $y\in Y_{+}$, or $x\in X_{+}$ and $y\in Y_0$, or

(d)

type $+-$, otherwise, if $x\in X_{+}\cup X_{-}$ and $y\in Y_{+}\cup Y_{-}$.

We observe fundamental properties of a 5-hole that has a middle triangle of each specific type.

Lemma 7.

Let $P=pqxry$ be any 5-hole in S such that $pqr$ is a middle triangle of P. Let d be the number of diagonals and m be the total number of middle triangles of P. Then, the following holds according to the type of $pqr$.

(a) 

If $pqr$ is of type 00, then either $d=5$ or $d=4$.

• If $d=5$, then $m=5$ and the other four middle triangles are all of type 00.
• If $d=4$, then $m=3$ and the other two middle triangles are all of type $0-$.

(b) 

If $pqr$ is of type $0-$, then either $d=4$ or $d=3$.

• If $d=4$, then $m=3$ and the other two middle triangles are of type $0-$ and 00, respectively.
• If $d=3$, then $m=2$ and the other middle triangle is of type $0+$.

(c) 

If $pqr$ is of type $0+$, then $d=3$ and $m=2$. The other middle triangle is of type $0-$.

(d) 

If $pqr$ is of type $+-$, then $d=2$ and $m=1$.

Proof. 

Consider each of the four types of the middle triangle $pqr$ of 5-hole $P=pqxry$. See Figure 4 for illustrations.

(a)

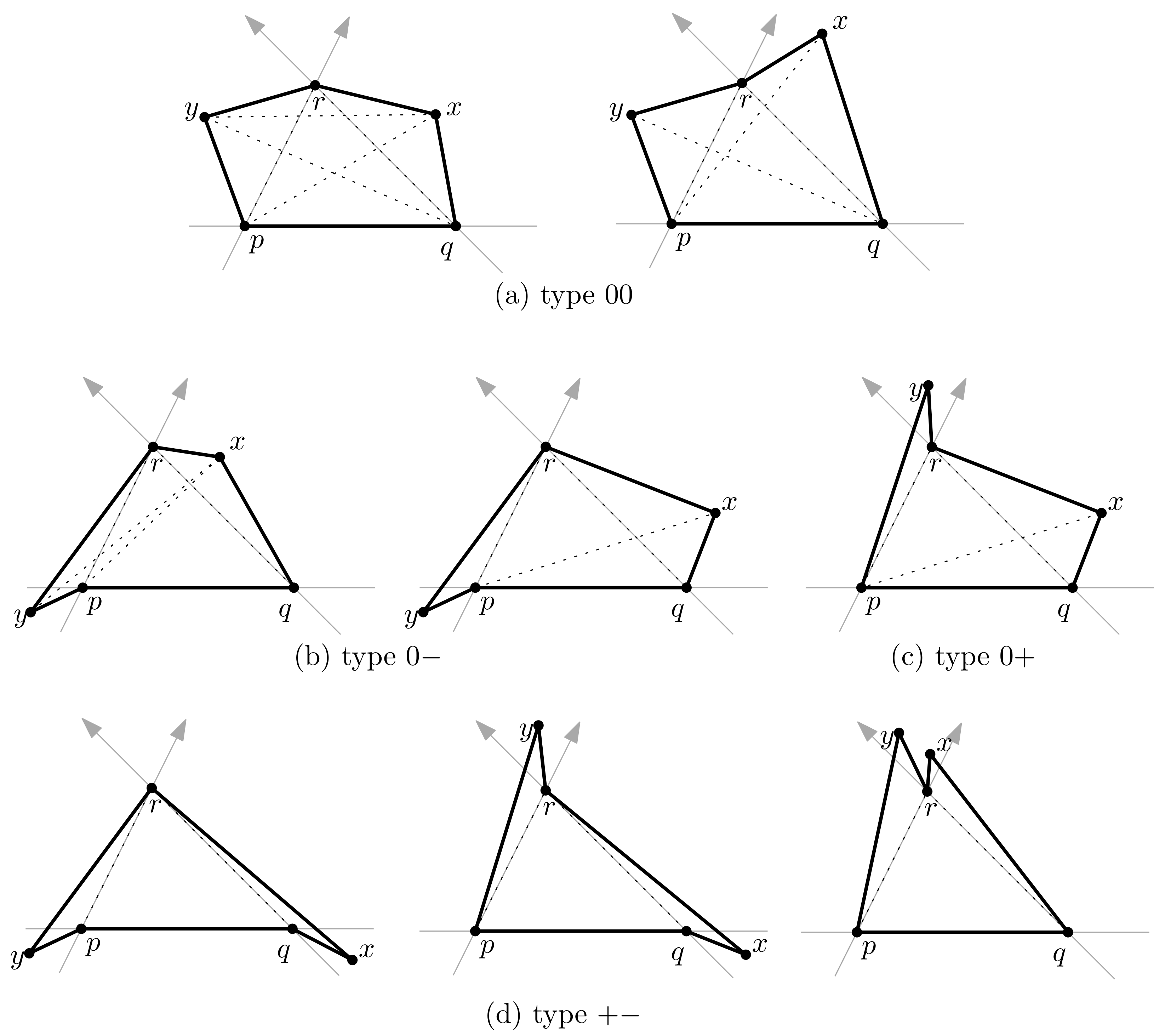
Suppose that $pqr$ is of type 00, so we have $x\in X_0$ and $y\in Y_0$. In this case, by Lemma 4, both 4-holes $pqry$ and $pqxr$ are convex, so both $\overline{yq}$ and $\overline{xp}$ are diagonals of 5-hole $P=pqxry$. There are two cases: either $\overline{xy}$ is a diagonal or not.

• If $\overline{xy}$ is a diagonal, then there are $d=5$ diagonals of P, including $\overline{rp}$ and $\overline{rq}$, and $m=5$ middle triangles of P: $pqr$, $qxy$, $xrp$, $ryq$ and $ypx$. Observe that all these five middle triangles are of type 00. See the left figure of Figure 4a.
• If $\overline{xy}$ is not a diagonal, then P has four diagonals, and three middle triangles: $pqr$, $xrp$, and $ryq$. Observe that $xrp$ and $ryq$ are of type $0-$, while $pqr$ is of type 00. See the right figure of Figure 4a.

(b)

Suppose that $pqr$ is of type $0-$, so either $x\in X_0$ and $y\in Y_{-}$, or $x\in X_{-}$ and $y\in Y_0$. We assume the former case without loss of generality since the other case is symmetric. In this case, by Lemma 4, 4-hole $pqxr$ is convex while 4-hole $pqry$ is non-convex, so $\overline{xp}$ is a diagonal of P but $\overline{yq}$ is not. There are two cases: either $\overline{xy}$ is a diagonal or not.

• If $\overline{xy}$ is a diagonal of P, then P has four diagonals and three middle triangles: $pqr$, $xrp$, and $ypx$. Observe that $pqr$ and $ypx$ are of type $0-$, while $xrp$ is of type 00 type. See the left figure of Figure 4b.
• If $\overline{xy}$ is not a diagonal of P, then P has three diagonals and two middle triangles $pqr$ and $xrp$. Observe that $xrp$ is of type $0+$, while $pqr$ is of type $0-$. See the right figure of Figure 4b.

(c)

Suppose that $pqr$ is of type $0+$, so either $x\in X_0$ and $y\in Y_{+}$, or $x\in X_{+}$ and $y\in Y_0$. We assume the former case without loss of generality, since the other case is symmetric. Similarly to the above case, the 4-hole $pqxr$ is convex while the 4-hole $pqry$ is non-convex, so $\overline{xp}$ is a diagonal of P but $\overline{yq}$ is not. In this case, however, $\overline{xy}$ is always not a diagonal of P, since both x and y lie in a common side of the line through q and r. Thus, P has three diagonals and two middle triangles $pqr$ and $xrp$. Observe that $xrp$ is of type $0-$, while $pqr$ is of type $0+$. See Figure 4c.

(d)

Suppose that $pqr$ is of type $+-$, so $x\in X_{+}\cup X_{-}$ and $y\in Y_{+}\cup Y_{-}$. Then, none of the segments $\overline{xp}$ and $\overline{yq}$ can be a diagonal of P, as both 4-holes $pqxr$ and $pqry$ are non-convex by Lemma 4. Additionally, observe that the segment $\overline{xy}$ cannot be a diagonal of P, either, by the following reason: if $x\in X_{+}$ or $y\in Y_{+}$, then corner r of P is a reflex vertex and, otherwise, if $x\in X_{-}$ and $y\in Y_{-}$, then both p and q are reflex vertices of P. See Figure 4d. Therefore, the pentagon P has exactly two diagonals $\overline{pr}$ and $\overline{qr}$, and only one middle triangle $pqr$ of type $+-$.

This completes the proof of the lemma.    □

From Lemma 7 and its proof, we further observe the following properties of 5-holes, depending on the number of its diagonals.

Lemma 8.

Let P be any 5-hole in S and d be the number of its diagonals.

(i) 

If $d=5$, then P is convex and has five middle triangles of type 00.

(ii) 

If $d=4$, then P has three middle triangles, two of which are of type $0-$ and the third of which is of type 00.

(iii) 

If $d=3$, then P has two middle triangles, one of which is of type $0+$ and the other of which is of type $0-$.

(iv) 

If $d=2$, then P has a unique middle triangle of type $+-$.

Proof. 

Let $P=pqxry$ be any 5-hole such that $pqr$ is a middle triangle, and let d be the number of its diagonals. By Lemma 6, we have $2\le d\le 5$. We consider each case of $d=2,3,4,5$.

First, assume that $d=5$. By Lemma 7, the middle triangle $pqr$ is of type 00, as, otherwise, there is no possibility that P has $d=5$ diagonals. Again by Lemma 7 (a), we know that P has five middle triangles all of which are of type 00.

Second, assume that $d=4$. Then, by Lemma 7, we have that $pqr$ is either of type 00 or type $0-$. In the former case, Lemma 7 (a) states that P has two more middle triangles all of which are of type $0-$. In the latter case, Lemma 7 (b) states that P has two more middle triangles, one of which is of type 00, and the other, which is of type $0-$. We hence conclude that a 5-hole P with $d=4$ diagonals has three middle triangles, two of which are of type $0-$ and the third of which is of type 00, in either case.

Next, assume that $d=3$. Then, by Lemma 7, we have that $pqr$ is either of type $0-$ or type $0+$. In the former case, Lemma 7 (b) states that P has one more middle triangle of type $0+$. In the latter case, Lemma 7 (c) states that P has one more middle triangle of type $0-$. Thus, a 5-hole P with $d=3$ diagonals has two middle triangles, one of which is of type $0-$, and the other of which is of type $0+$.

Finally, assume that $d=2$. In this case, from Lemma 7, we know that $pqr$ must be of type $+-$, and it is the unique middle triangle.    □

The above lemma suggests a natural way of classification of pentagons according to the number of diagonals and middle triangles. In the following section, we describe our algorithm that counts the number of 5-holes with d diagonals separately for $d\in \{2,3,4,5\}$ in a given set S of points, so it separately counts convex and non-convex 5-holes in S.

4. Counting Empty Pentagons

Let S be a given set of n points in general position, as declared above. For $d\in \{2,3,4,5\}$, denote by $z_d$ the number of 5-holes in S that have d diagonals. By Lemma 6, the number of convex 5-holes in S is $h_5=h_5\left(S\right)=z_5$, and the number of non-convex 5-holes is ${\widehat{h}}_5={\widehat{h}}_5\left(S\right)=z_2+z_3+z_4$.

In this section, we describe an algorithm that precisely computes $z_d$ for each $d\in \{2,3,4,5\}$. Our algorithm indeed counts the number of middle triangles of 5-holes in S in several different ways, resulting in a sufficient number of linear equations on $\{z_2,z_3,z_4,z_5\}$. Hence, we can finally solve the system of linear equations to specify the values of $z_d$ for all $d\in \{2,3,4,5\}$.

More specifically, for each empty triangle $pqr$, we count the number of 5-holes that have $pqr$ as a middle triangle of a specific type. This can be done by attaching two other empty triangles to $pqr$ along shared sides.

4.1. Attaching Two Empty Triangles to a Middle Triangle

As discussed in Section 3, any 5-hole can be partitioned into three empty triangles, one of which is a middle triangle. Conversely, we can construct all 5-holes by considering all possible ways of attaching two empty triangles to a tentative middle triangle along shared sides.

For our purposes, we consider each pair $(p,q)\in S\times S$ with $p\ne q$. For each $i\in \{1,\dots ,|T_{pq}\left|\right\}$, let $r=T_{pq}\left[i\right]$. Then, consider the empty triangle $pqr$ and all the pairs of empty triangles $rqx$ and $pry$ that share sides $\overline{qr}$ and $\overline{pr}$, respectively. Note that $x\in T_{rq}$ and $y\in T_{pr}$ by definition. The union $pqr\cup rqx\cup pry$ is clearly a 5-hole $pqxry$ such that $pqr$ is a middle triangle, unless $rqx$ and $pry$ overlap. This simply implies that the number of those 5-holes $pqxry$ is $|T_{rq}|·|T_{pr}|$, minus the number of pairs $(x,y)\in T_{rq}\times T_{pr}$ such that $rqx$ and $pry$ overlap.

We can even think of those 5-holes $pqxry$ such that $pqr$ is a middle triangle of a specific type. Specifically, for each $p,q\in S$ and $r\in T_{pq}$, we define $Z_{00}(p,q;r)$ to be the number of pairs $(x,y)\in T_{pr}\times T_{rq}$ such that $x\in X_0$ and $y\in Y_0$; $Z_{0+}(p,q;r)$ to be the number of those pairs $(x,y)$ such that either $x\in X_0$ and $y\in Y_{+}$, or $x\in X_{+}$ and $y\in Y_0$; $Z_{0-}(p,q;r)$ to be the number of those pairs $(x,y)$ such that either $x\in X_0$ and $y\in Y_{-}$, or $x\in X_{-}$ and $y\in Y_0$; and $Z_{+-}(p,q;r)$ to be the number of those pairs $(x,y)$ such that either $x\in X_{+}\cup X_{-}$ and $y\in Y_{+}\cup Y_{-}$, where the six regions $X_{+},X_0,X_{-},Y_{+},Y_0,Y_{-}$ are as defined in Section 3. See Figure 3.

These quantities are indeed the potential number of 5-holes $pqxry$ for fixed $p,q\in S$ and $r\in T_{pq}$ such that the triangle $pqr$ is a middle triangle of each specified type, while they count all those pairs $(x,y)$ without considering whether $rqx$ and $pry$ overlap or not.

One good point for the quantities is that they can be computed quite easily. Let $X_{-},X_0,X_{+}=Y_{+},Y_0,Y_{-}$ be the five regions defined for a fixed $p,q,r$ as in Section 3; see Figure 3. From the definition of the arrays $A_{qr}$, $B_{qr}$, $A_{rp}$, $B_{rp}$, we observe that the following relation between the region where x or y lies and their indices in $T_{rq}$ and $T_{pr}$, respectively. See Figure 5 for an illustration.

Lemma 9.

Let $P=pqxry$ be any 5-hole in S such that $pqr$ is a middle triangle of P. Denote by $i_p$ and $i_q$ the indices such that $p=T_{qr}\left[i_p\right]$ and $q=T_{rp}\left[i_q\right]$, and by $j_x$ and $j_y$ the indices such that $x=T_{rq}\left[j_x\right]$ and $y=T_{pr}\left[j_y\right]$. We then have

$$\left\{\begin{array}{cc}x\in X_{-}\hfill & iff1\le j_x\le A_{qr}\left[i_p\right]\hfill \\ x\in X_0\hfill & iff{A}_{qr}\left[i_p\right]<j_x\le B_{qr}\left[i_p\right]\hfill \\ x\in X_{+}\hfill & iff{B}_{qr}\left[i_p\right]<j_x\le \left|T_{rq}\right|\hfill \end{array}\right.and\left\{\begin{array}{cc}y\in Y_{-}\hfill & iff{B}_{rp}\left[i_q\right]<j_y\le \left|T_{pr}\right|\hfill \\ y\in Y_0\hfill & iff{A}_{rp}\left[i_q\right]<j_y\le B_{rp}\left[i_q\right]\hfill \\ y\in Y_{+}\hfill & iff1\le j_y\le A_{rp}\left[i_q\right]\hfill \end{array}\right..$$

Proof. 

Recall the definition of $A_{qr}\left[i_p\right]$ and $B_{qr}\left[i_p\right]$: $A_{qr}\left[i_p\right]$ is the largest index $j_1$ of $T_{rq}$ such that $T_{rq}\left[j_1\right]$ lies on the right side of the directed line through p towards q; $B_{qr}\left[i_p\right]$ is the largest index $j_2$ of $T_{rq}$ such that $T_{rq}\left[j_2\right]$ lies on the right side of the directed line through p towards r.

Hence, we have $x\in X_{-}$ if, and only if $1\le j_x\le j_1=A_{qr}\left[i_p\right]$; $x\in X_0$ if, and only if $A_{qr}\left[i_p\right]=j_1<j_x\le j_2=B_{qr}\left[i_p\right]$; $x\in X_{+}$ if, and only if $B_{qr}\left[i_p\right]=j_2<j_x\le \left|T_{rq}\right|$. This proves the first part of the lemma. The second part for the range of $j_y$ can be seen in a symmetric and analogous way.    □

Lemma 9 directly implies the following.

Lemma 10.

For any $p,q\in S$ with $p\ne q$ and $r\in T_{pq}$, the following equations hold:

$$\begin{array}{cc}\hfill Z_{00}(p,q;r)& =(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])·(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right]),\hfill \\ \hfill Z_{0-}(p,q;r)& =(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])·\left(\right|T_{pr}|-B_{rp}\left[i_q\right])+A_{rq}\left[i_p\right]·(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right]),\hfill \\ \hfill Z_{0+}(p,q;r)& =(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])·A_{rp}\left[i_q\right]+\left(\right|T_{rq}|-B_{qr}\left[i_p\right])·(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right]),and\hfill \\ \hfill Z_{+-}(p,q;r)& =\left(|T_{rq}|-(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])\right)·\left(|T_{pr}|-(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right])\right),\hfill \end{array}$$

where $i_p$ and $i_q$ denote the indices in arrays $T_{qr}$ and $T_{rp}$, respectively, such that $p=T_{qr}\left[i_p\right]$ and $q=T_{rp}\left[i_q\right]$.

Proof. 

By Lemma 9, we get the number of points $x\in T_{rq}$ in each of the three regions $X_{-}$, $X_0$, and $X_{+}$ as follows. The number of $x\in T_{rq}$ such that $x\in X_{-}$ is exactly $A_{qr}\left[i_p\right]$; the number of $x\in T_{rq}$ such that $x\in X_0$ is exactly $B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right]$; and the number of $x\in T_{rq}$ such that $x\in X_{+}$ is exactly $|T_{rq}|-B_{qr}\left[i_p\right]$.

Similarly, the number of $y\in T_{pr}$ such that $y\in Y_{-}$ is exactly $|T_{pr}|-B_{rp}\left[i_q\right]$; the number of $y\in T_{pr}$ such that $y\in Y_0$ is exactly $B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right]$; and the number of $y\in T_{pr}$ such that $y\in Y_{+}$ is exactly $A_{rp}\left[i_q\right]$.

This directly implies the lemma.    □

Remember that the four quantities $Z_{00}(p,q;r)$, $Z_{0-}(p,q;r)$, $Z_{0+}(p,q;r)$, and $Z_{+-}(p,q;r)$ count the number of pairs $(x,y)$ with $x\in T_{rq}$ and $y\in T_{pr}$ without considering whether the corresponding triangles $qxr$ and $pry$ overlap or not. In the following, we characterize a necessary and sufficient condition when the two triangles overlap. For any ordered triple $(a,b,c)$ of distinct points in the plane, we say that $(a,b,c)$ makes a left turn if c lies on the left side of the directed line through a towards b.

Lemma 11.

Let $p,q\in S$ and $r\in T_{pq}$ be fixed. Let $x\in T_{rq}$ and $y\in T_{pr}$. The triangles $qxr$ and $pry$ overlap if, and only if $x\in X_{+}$, $y\in Y_{+}$, and $(x,r,y)$ makes a left turn.

Proof. 

First, we observe that if $qxr$ and $pry$ overlap, then $x\in X_{+}$ and $y\in Y_{+}$. Assume for this purpose that $x\in X_0\cup X_{-}$. Then, the triangle $qxr$ and the point y are separated by the line through p and r. This implies that $qxr$ and $pry$ cannot overlap. Symmetrically, we have that $qxr$ and $pry$ cannot overlap if $y\in Y_0\cup Y_{-}$. Hence, if $qxr$ and $pry$ overlap, then $x\in X_{+}$ and $y\in Y_{+}$.

Then, suppose that $x\in X_{+}$ and $y\in Y_{+}$. For any $x\in X_{+}$ and $y\in Y_{+}$, it holds that $y\notin qxr$ and $x\notin pry$ since $qxr$ and $pry$ are empty triangles. This implies that $qxr$ and $pry$ overlap if, and only if $(x,r,y)$ makes a left turn. See Figure 6. This concludes the lemma.    □

The above lemma implies the following: On one hand, the three quantities $Z_{00}(p,q;r)$, $Z_{0-}(p,q;r)$, and $Z_{0+}(p,q;r)$ are indeed the number of 5-holes of the form $pqxry$ with $x\in T_{rq}$ and $y\in T_{pr}$ such that $pqr$ is a middle triangle of type 00, $0-$, and $0+$, respectively. On the other hand, the quantity $Z_{+-}(p,q;r)$, however, may not be the same as the number of 5-holes of the form $pqxry$ with $x\in T_{rq}$ and $y\in T_{pr}$ such that $pqr$ is a middle triangle of type $+-$, since it may count the cases of pairs $(x,y)$ that cause an overlap of $qxr$ and $pry$. We let $\chi (p,q;r)$ be the number of such pairs $(x,y)$, so $Z_{+-}(p,q;r)-\chi (p,q;r)$ is equal to the number of 5-holes $pqxry$ such that $pqr$ is a middle triangle of type $+-$.

Lemma 12.

Let $p,q\in S$ and $r\in T_{pq}$ be fixed. The value of $\chi (p,q;r)$ can be precisely computed in time $O\left(\right|T_{rq}|-B_{qr}\left[i_p\right]+A_{rp}\left[i_q\right]+1)$, provided that the indices $i_p$ and $i_q$ such that $p=T_{qr}\left[i_p\right]$ and $q=T_{rp}\left[i_q\right]$ are known.

Proof. 

Here, we describe an algorithm that computes $\chi (p,q;r)$. This can be done by linearly scanning two sorted arrays $T_{rq}$ and $T_{pr}$ in limited ranges.

More precisely, we initially set an index variable $j_x$ to be $B_{qr}\left[i_p\right]+1$, and another $j_y$ to be 1. Additionally, prepare a counter-variable c, initially being zero. We perform the following while $j_x\le \left|T_{rq}\right|$ and $j_y\le A_{rp}\left[i_q\right]$: If $(T_{rq}\left[j_x\right],r,T_{pr}\left[j_y\right])$ makes a left turn, then increase c by $|T_{rq}|-j_x+1$ and increase $j_y$ by 1; otherwise, if $(T_{rq}\left[j_x\right],r,T_{pr}\left[j_y\right])$ makes a right turn, then increase $j_x$ by 1.

Since either $j_x$ or $j_y$ increases by one after every iteration, the total running time is bounded by $O\left(\right|T_{rq}|-B_{qr}\left[i_p\right]+A_{rp}\left[i_q\right])$ plus a constant $O\left(1\right)$; hence, $O\left(\right|T_{rq}|-B_{qr}\left[i_p\right]+A_{rp}\left[i_q\right]+1)$, as claimed. Note that $|T_{rq}|-B_{qr}\left[i_p\right]+A_{rp}\left[i_q\right]$ can be zero.

The correctness of this algorithm is guaranteed by Lemma 11 and the observation that if $(T_{rq}\left[j_x\right],r,T_{pr}\left[j_y\right])$ makes a left turn, then so does $(T_{rq}\left[j_x^{\prime }\right],r,T_{pr}\left[j_y\right])$ for all $j_x\le j_x^{\prime }\le \left|T_{rq}\right|$.    □

Now, consider the sum of each of these values over all $p,q\in S$ and $r\in T_{pq}$. Define

$$\begin{array}{cc}\hfill Z_{00}& :=\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}{Z}_{00}(p,q;r),\hfill \\ \hfill Z_{0-}& :=\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}{Z}_{0-}(p,q;r),\hfill \\ \hfill Z_{0+}& :=\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}{Z}_{0+}(p,q;r),\hfill \\ \hfill Z_{+-}& :=\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}{Z}_{+-}(p,q;r),\mathrm{and}\hfill \\ \hfill \chi & :=\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}\chi (p,q;r).\hfill \end{array}$$

We then have the following system of linear equations for $z_2,z_3,z_4,z_5$.

Lemma 13.

It holds that

$$Z_{00}=z_4+5z_5,Z_{0-}=z_3+2z_4,Z_{0+}=z_3,and{Z}_{+-}=z_2+\chi .$$

Proof. 

The lemma can be shown directly from Lemmas 8, 10 and 11.

By Lemma 11, for each $p,q\in S$ and $r\in T_{pq}$, $Z_{00}(p,q;r)$, $Z_{0-}(p,q;r)$, and $Z_{0+}(p,q;r)$ count the number of 5-holes such that $pqr$ is a middle triangle of type 00, $0-$, and $0+$, respectively. This implies that their sums $Z_{00}$, $Z_{0-}$, and $Z_{0+}$ count all middle triangles of type 00, $0-$, and $0+$, respectively, of all 5-holes in S.

Consider every 5-hole in S. Then, Lemma 8 implies the following:

(a)

Every 5-hole with five diagonals contributes 5 counts in $Z_{00}$, every 5-hole with four diagonals contributes 1 count in $Z_{00}$, and none of those with three or less diagonals contributes in $Z_{00}$.

(b)

Every 5-hole with four diagonals contributes 2 counts in $Z_{0-}$, every 5-hole with three diagonals contributes 1 count in $Z_{0-}$, and the others contribute nothing in $Z_{0-}$.

(c)

Every 5-hole with three diagonals contributes 1 count in $Z_{0+}$ and the others contribute nothing in $Z_{0+}$.

(d)

Every 5-hole with two diagonal contributes 1 count in $Z_{+-}$.

Therefore, the first three equations are derived by Lemma 11, as discussed above.

In order to conclude the fourth equation, Lemma 11 implies that $Z_{+-}(p,q;r)-\chi (p,q;r)$ is exactly the number of 5-holes such that $pqr$ is a middle triangle of type $+-$. Therefore, we have $Z_{+-}=z_2+\chi$.    □

4.2. Algorithm

Now, we are ready to describe our algorithm that precisely computes the values of $z_2$, $z_3$, $z_4$, and $z_5$. A high-level description of our algorithm is shown in Algorithm 1. Our algorithm consists of two phases: the preprocessing phase and the main computation phase. In the main computation phase, it computes the values of $Z_{00}$, $Z_{0-}$, $Z_{0+}$, $Z_{+-}$, and $\chi$ as defined above, and solve the system of equations shown in Lemma 13 to obtain the values of $z_2$, $z_3$, $z_4$, and $z_5$. In the preprocessing phase, we prepare some data structures for efficient processing of the main computation phase.

Algorithm 1 Count5Holes

1: Compute all empty triangles in S and sorted arrays $S_p$ for all $p\in S$. 2: Compute sorted arrays $T_{pq}$, $A_{pq}$, and $B_{pq}$ for all $p,q\in S$ with $p\ne q$. 3: Build the dictionary D. 4: Compute $Z_{00}$, $Z_{0-}$, $Z_{0+}$, $Z_{+-}$, and $\chi$. 5: Let $z_2\leftarrow Z_{+-}-\chi$, $z_3\leftarrow Z_{0+}$, $z_4\leftarrow (Z_{0-}-z_3)/2$ and $z_5\leftarrow (Z_{00}-z_4)/5$. 6: return$(z_2,z_3,z_4,z_5)$

In the preprocessing phase, we start with enumerating all empty triangles in S by the algorithm of Dobkin et al. [1]. As discussed above, their algorithm takes $O\left(h_3\right)$ time. In the same time bound, we can specify the sorted arrays $T_{pq}$ by Lemma 2.

Additionally, we build a dictionary structure D on the set of all empty triangles that maps each empty triangle $pqr$ to a triple $(i_p,i_q,i_r)$ of indices such that $p=T_{qr}\left[i_p\right]$, $q=T_{rp}\left[i_q\right]$, and $r=T_{pq}\left[i_r\right]$. The dictionary structure D can be implemented by a hash table with a perfect hash function since the set of keys is static, and hence, the access to any key entry can be done in $O\left(1\right)$ time [29,30]. Using the dictionary D, one can know in $O\left(1\right)$ time the position of each point of any empty triangle $pqr$ in the sorted arrays $T_{qr}$, $T_{rp}$ and $T_{pq}$, respectively. The following lemma shows how to prepare the dictionary structure.

Lemma 14.

The dictionary D can be built in $O\left(h_3\right)$ time.

Proof. 

After computing all empty triangles in S, we initialize D on the set of all empty triangles that maps each triangle to a triple $(0,0,0)$.

In order to update the triples of indices correctly, we iterate all pairs $(p,q)\in S\times S$ with $p\ne q$ and linearly scan the sorted array $T_{pq}$. For each $i\in \{1,\dots ,|T_{pq}\left|\right\}$, access the entry of $pqr$ where $r=T_{pq}\left[i\right]$ and update the corresponding index $i_r$ in the triple to be the value of i. By Lemma 1, it takes $O\left(h_3\right)$ time. □

Then, we compute the values of $A_{pq}\left[i\right]$ and $B_{pq}\left[i\right]$ for all $i\in \{1,\dots ,|T_{pq}\left|\right\}$ and all pairs $(p,q)$ by Lemma 3.

In summary, in the preprocessing phase, we build sorted arrays $T_{pq}$ with associated arrays $A_{pq}$ and $B_{pq}$ for all pairs $(p,q)\in S\times S$ with $p\ne q$, and the dictionary D. All these data structures are built in total $O\left(h_3\right)$ time.

Now, we describe the main computation step, in which we compute the values of $Z_{00}$, $Z_{0-}$, $Z_{0+}$, $Z_{+-}$, and $\chi$. This can be done simply by iterating all $p\in S$, $q\in S_p$, and $i\in \{1,\dots ,|T_{pq}\left|\right\}$ and compute the values of $Z_{00}(p,q;r)$, $Z_{0-}(p,q;r)$, $Z_{0+}(p,q;r)$, $Z_{+-}(p,q;r)$ and $\chi (p,q;r)$ by Lemmas 10 and 12. In conclusion, $Z_{00}$, $Z_{0-}$, $Z_{0+}$, and $Z_{+-}$ can be computed in $O\left(h_3\right)$ time, while $\chi$ can be computed in $O(h_3+{\widehat{h}}_4)$ time.

Lemma 15.

The values of $Z_{00}$, $Z_{0-}$, $Z_{0+}$, and $Z_{+-}$ can be computed in $O\left(h_3\right)$ time, after the preprocessing phase is done.

Proof. 

For a fixed triple $(p,q,r)$ with $p\in S$, $q\in S_p$ and $r\in T_{pq}$, it takes $O\left(1\right)$ time to specify the triple of indices $(i_p,i_q,i_r)$ such that $p=T_{qr}\left[i_p\right]$, $q=T_{rp}\left[i_q\right]$, and $r=T_{pq}\left[i_r\right]$ by the dictionary D. Hence, we can compute in $O\left(1\right)$ time the values of $Z_{00}(p,q;r)$, $Z_{0-}(p,q;r)$, $Z_{0+}(p,q;r)$, and $Z_{+-}(p,q;r)$ by Lemma 10, using the arrays $T_{rq}$, $A_{qr}$, $B_{qr}$, $T_{pr}$, $A_{rp}$, and $B_{rp}$ obtained from the preprocessing phase.

Finally, observe that we have $O\left(h_3\right)$ of such triples $(p,q,r)$, since it forms an empty triangle $pqr$. Hence, the values of $Z_{00}$, $Z_{0-}$, $Z_{0+}$, and $Z_{+-}$ can be computed in $O\left(h_3\right)$ time. □

Lemma 16.

The value of χ can be precisely computed in $O(h_3+{\widehat{h}}_4)$ time.

Proof. 

We compute $\chi (p,q;r)$ for all $r\in T_{pq}$ and all pairs $p,q\in S$, and their sum $\chi$. By definition, we have

$$\chi =\sum _{p\in S}\sum _{q\in S_p}\sum _{r\in T_{pq}}\chi (p,q;r)=\sum _{pqr:\mathrm{empty}}(\chi (p,q;r)+\chi (q,r;p)+\chi (r,p;q)).$$

By Lemma 12, and in order to compute $\chi (p,q;r)+\chi (q,r;p)+\chi (r,p;q)$ for a fixed empty triangle $pqr$, we spend time

$$O\left(\right(|T_{rq}|-B_{qr}\left[i_p\right]+A_{rp}\left[i_q\right])+(|T_{pr}|-B_{rp}\left[i_q\right]+A_{pq}\left[i_r\right])+(|T_{qp}|-B_{pq}\left[i_r\right]+A_{qr}\left[i_p\right])+1),$$

which is equal to

$$O\left(\right|T_{qp}|+|T_{pr}|+|T_{rq}|-(B_{pq}\left[i_r\right]-A_{pq}\left[i_r\right])-(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right])-(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])+1)$$

by rearranging the terms. Thus, the total running time is the sum of the above terms over all empty triangles $pqr$.

First, observe that if we expand the sum

$$S_1:=\sum _{pqr:\mathrm{empty}}\left(\right|T_{qp}|+|T_{pr}|+|T_{rq}\left|\right),$$

then the term $|T_{q^{\prime }{p}^{\prime }}|$ for any $p^{\prime },q^{\prime }\in S$ with $p^{\prime }\ne q^{\prime }$ appears exactly $|T_{p^{\prime }{q}^{\prime }}|$ times. This is because each occurrences of the term $|T_{q^{\prime }{p}^{\prime }}|$ corresponds to an empty triangle of the form $p^{\prime }{q}^{\prime }{r}^{\prime }$ for some $r^{\prime }\in T_{p^{\prime }{q}^{\prime }}$. Hence, we have that

$$S_1=\sum _{p\in S}\sum _{q\in S_p}|T_{pq}|·|T_{qp}|.$$

Now, consider the sum

$$S_2:=\sum _{pqr:\mathrm{empty}}((B_{pq}\left[i_r\right]-A_{pq}\left[i_r\right])+(B_{rp}\left[i_q\right]-A_{rp}\left[i_q\right])+(B_{qr}\left[i_p\right]-A_{qr}\left[i_p\right])).$$

If we expand this sum $S_2$, then the term $B_{p^{\prime }{q}^{\prime }}\left[i\right]-A_{p^{\prime }{q}^{\prime }}\left[i\right]$ appears exactly once for any $p^{\prime },q^{\prime }\in S$ with $p^{\prime }\ne q^{\prime }$ and any $1\le i\le |T_{p^{\prime }{q}^{\prime }}|$. This implies that

$$S_2=\sum _{p\in S}\sum _{q\in S_p}\sum _{1\le i\le |T_{pq}|}(B_{pq}\left[i\right]-A_{pq}\left[i\right]).$$

Putting it all together, The total running time to compute the value of $\chi$ is

$$\begin{array}{cc}\hfill & O\left(S_1-S_2+\sum _{pqr:\mathrm{empty}}1\right)\hfill \\ \hfill & =O\left(\sum _{p\in S}\sum _{q\in S_p}|T_{pq}|·|T_{qp}|-\sum _{p\in S}\sum _{q\in S_p}\sum _{1\le i\le |T_{pq}|}(B_{pq}\left[i\right]-A_{pq}\left[i\right])+h_3\right)\hfill \\ \hfill & =O\left(\sum _{p\in S}\sum _{q\in S_p}\left(|T_{pq}|·|T_{qp}|-\sum _{1\le i\le |T_{pq}|}(B_{pq}\left[i\right]-A_{pq}\left[i\right])\right)+h_3\right)\hfill \\ \hfill & =O(h_3+{\widehat{h}}_4),\hfill \end{array}$$

where ${\widehat{h}}_4$ denotes the number of non-convex 4-holes in S, by Lemma 5. □

Finally, we apply Lemma 13 to compute each of $z_2$, $z_3$, $z_4$, and $z_5$, as described in Line 6 of Algorithm 1.

The running time of our algorithm is bounded by $O(h_3+{\widehat{h}}_4)$, as follows: We spend $O\left(h_3\right)$ time for the preprocessing step. To compute $Z_{00}$, $Z_{0-}$, $Z_{0+}$, and $Z_{+-}$, it takes $O\left(h_3\right)$ time by Lemma 15, while we spend $O(h_3+{\widehat{h}}_4)$ time to compute $\chi$, as analyzed in Lemma 16. The last step computing $z_2$, $z_3$, $z_4$, and $z_5$ takes only $O\left(1\right)$ time.

Therefore, we conclude Theorem 1 stated in Section 1.

5. Concluding Remarks

In this paper, we presented the first algorithm that counts non-convex 5-holes in a given set S of n points in general position. Our counting algorithm took $O(h_3\left(S\right)+{\widehat{h}}_4\left(S\right))$ time, proportional to the number of empty triangles and non-convex 4-holes in S. Note that $\mathsf{\Omega }\left(n^2\right)\le h_3\left(S\right)\le O\left(n^3\right)$ and $0\le {\widehat{h}}_4\left(S\right)\le O\left(n^3\right)$, while their expected numbers were $\mathsf{\Theta }\left(n^2\right)$ and $\mathsf{\Theta }(n^{2}logn)$, respectively, when S was randomly chosen from a convex and bounded body in the plane. See Table 1 for more details.

One natural question is about the extension of our algorithmic results to non-convex k-holes for $k\ge 6$. It seems to us that it is not urgent to generalize our algorithmic approach even to the case of 6-holes. Specifically, a pentagon was decomposed into three triangles in such a way that two were attached to the middle one, while a polygon with $k\ge 6$ corners was decomposed into $k-2\ge 4$ triangles, and the number of methods to attach $k-2$ triangles grew exponentially in k. Moreover, the number of cases in which these attached triangles overlapped also grew rapidly as k increased.

Another open question is about the true computational complexity of counting convex or non-convex k-holes. Both variants of the maximum-width empty annulus problem had a lower bound of $\mathsf{\Omega }(nlogn)$ by reducing from the maximum gap problem. There was a huge gap between the lower bound $\mathsf{\Omega }(nlogn)$ and the running times of our algorithms. Thus, can one find an algorithm that counts k-holes for $k=3,4,5$ in $o\left(n^3\right)$ time in the worst case, or prove a better lower bound of $\omega (nlogn)$? In particular, we are unaware of any algorithm that counts the number $h_3\left(S\right)$ of empty triangles faster than $O\left(h_3\left(S\right)\right)=O\left(n^3\right)$.