Geometric Morphometrics of Bilateral Asymmetry in Eunotia bilunaris (Eunotiales, Bacillariophyceae) as a Tool for the Quantitative Assessment of Teratogenic Deviations in Frustule Shapes
Abstract
1. Introduction
2. Materials and Methods
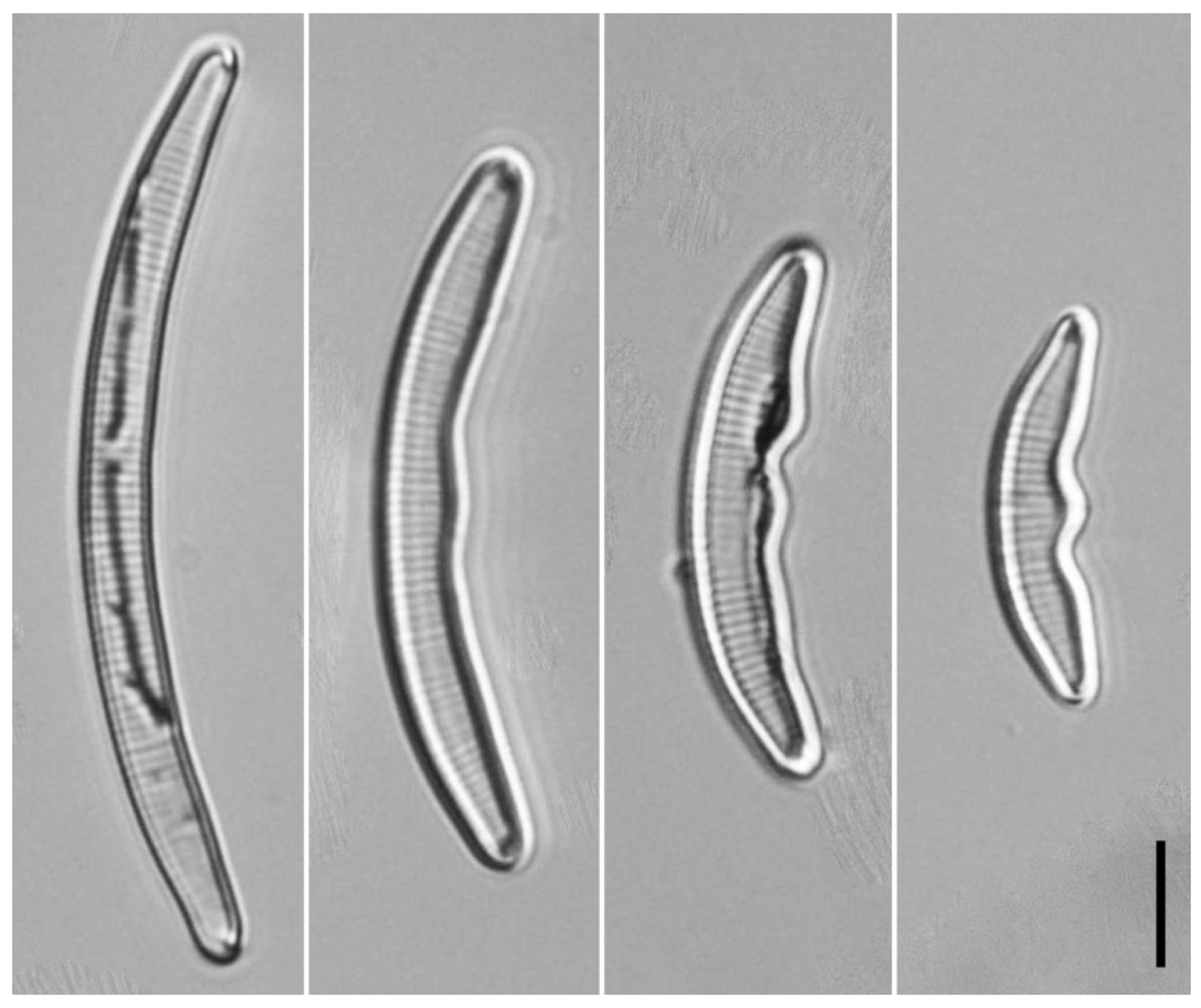
2.1. Sampling and Data Acquisition
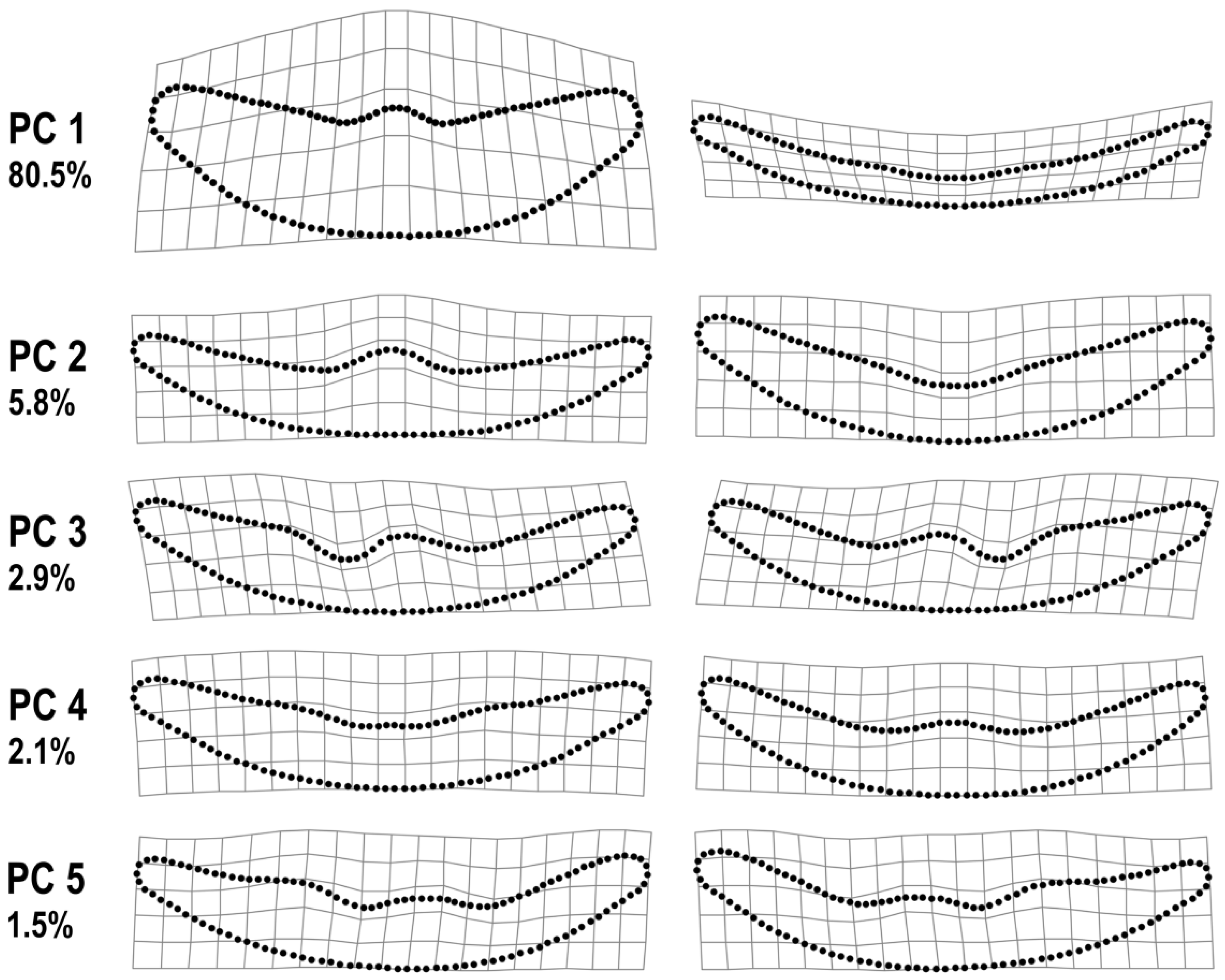
2.2. Geometric Morphometrics
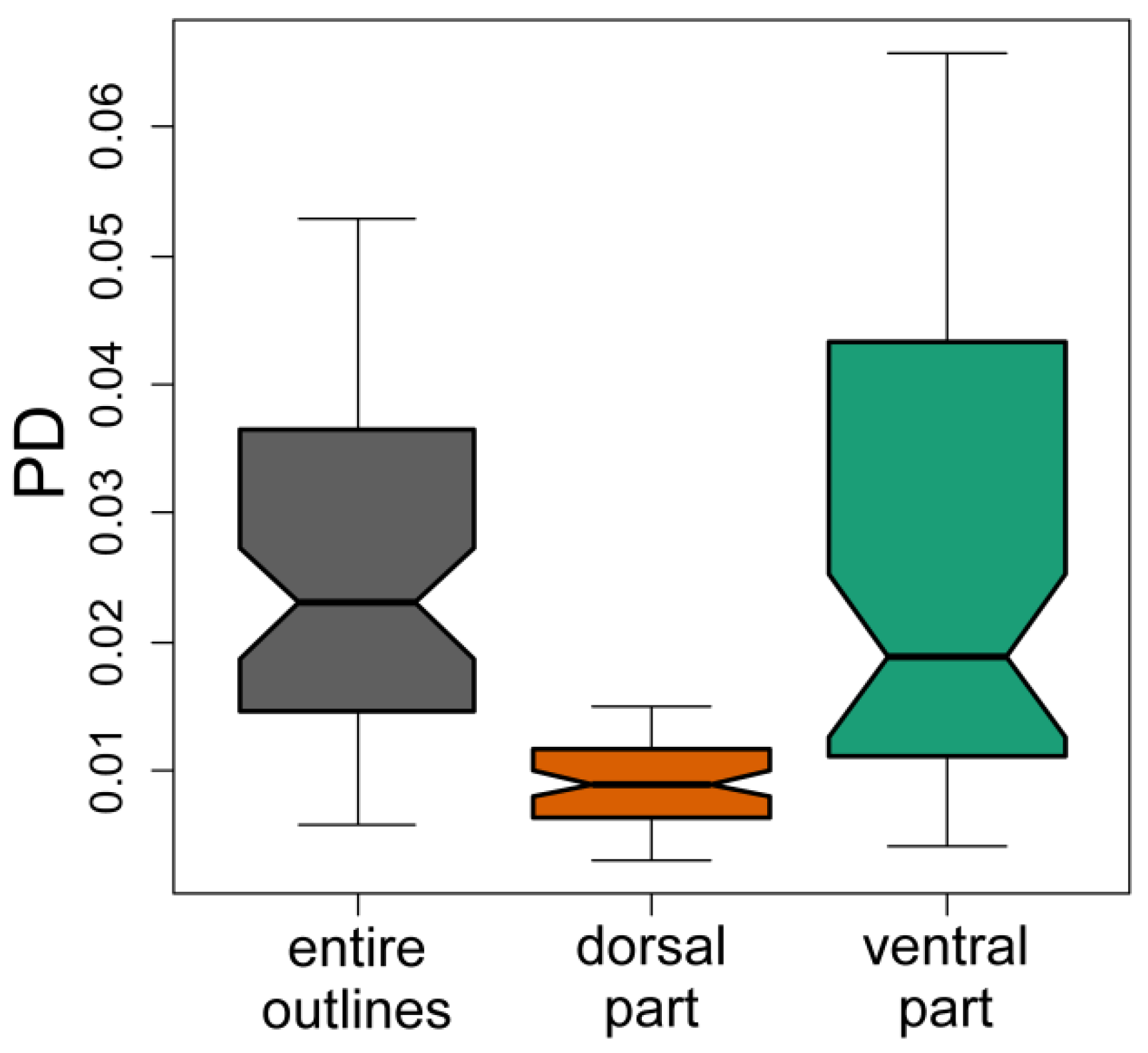
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malviya, S.; Scalco, E.; Audic, S.; Vincent, F.; Veluchamy, A.; Poulain, J.; Wincker, P.; Iudicone, D.; de Vargas, C.; Bittner, L.; et al. Insights into Global Diatom Distribution and Diversity in the World’s Ocean. Proc. Nat. Acad. Sci. USA 2016, 113, 1516–1525. [Google Scholar] [CrossRef]
- Round, F.E.; Crawford, R.M.; Mann, D.G. The Diatoms. Biology and Morphology of the Genera; Cambridge University Press: Cambridge, UK, 1990; p. 747. [Google Scholar]
- Sienkiewicz, S.; Gąsiorowski, M. The Evolution of a Mining Lake—From Acidity to Natural Neutralization. Sci. Total Environ. 2016, 557, 343–354. [Google Scholar] [CrossRef] [PubMed]
- Falasco, E.; Bona, F.; Badino, G.; Hoffmann, L.; Ector, L. Diatom Teratological Forms and Environmental Alterations: A Review. Hydrobiologia 2009, 623, 1–35. [Google Scholar] [CrossRef]
- Falasco, E.; Ector, L.; Wetzel, C.E.; Badino, G.; Bona, F. Looking Back, Looking Forward: A Review of the New Literature on Diatom Teratological Forms (2010–2020). Hydrobiologia 2021, 848, 1675–1753. [Google Scholar] [CrossRef]
- Cattaneo, A.; Couillard, Y.; Wunsam, S.; Courcelles, M. Diatom Taxonomic and Morphological Changes as Indicators of Metal Pollution and Recovery in Lac Dufault (Quebec, Canada). J. Paleolimnol. 2004, 32, 163–175. [Google Scholar] [CrossRef]
- Furey, P.C.; Lowe, R.L.; Johansen, J.R. Teratology in Eunotia Taxa in the Great Smoky Mountains National Park and Description of Eunotia macroglossa sp. nov. Diat. Res. 2009, 24, 273–290. [Google Scholar] [CrossRef]
- Morin, S.; Cordonier, A.; Lavoie, I.; Arini, A.; Blanco, S.; Duong, T.T.; Tornés, E.; Bonet, B.; Corcoll, N.; Faggiano, L.; et al. Consistency in Diatom Response to Metal-contaminated Environments. In Emerging and Priority Pollutants in Rivers; Guasch, H., Ginebreda, A., Geiszinger, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 117–146. [Google Scholar]
- Smith, T.; Manoylov, K. Diatom Deformities from an Acid Mine Drainage Site at Friendship Hills National Historical Site, Pennsylvania. J. Fresh. Ecol. 2007, 22, 521–527. [Google Scholar] [CrossRef]
- Grabowska, M.; Hindák, F.; Hindáková, A. Phototrophic Microflora of Dystrophic Lake Sęczek, Masuria, Poland. Oceanol. Hydrobiol. Stud. 2014, 43, 337–345. [Google Scholar] [CrossRef]
- Millan, F.; Izere, C.; Breton, V.; Voldoire, O.; Biron, D.G.; Wetzel, C.E.; Miallier, D.; Allain, E.; Ector, L.; Beauger, A. The Effect of Natural Radioactivity on Diatom Communities in Mineral Springs. Bot. Lett. 2020, 167, 95–113. [Google Scholar] [CrossRef]
- Dziengo-Czaja, M.; Matuszak, J.A. Teratological Forms of Diatoms (Bacillariophyceae) as Indicators of Water Pollution in the Western Part of Puck Bay (Southern Baltic Sea). Oceanol. Hydrobiol. Stud. 2008, 37, 119–132. [Google Scholar] [CrossRef]
- Sienkiewicz, E.; Gąsiorowski, M. Natural Evolution of Artificial Lakes Formed in Lignite Excavations based on Diatom, Geochemical and Isotopic Data. J. Paleolimnol. 2019, 62, 1–13. [Google Scholar] [CrossRef]
- Olenici, A.; Blanco, S.; Borrego-Ramos, M.; Momeu, L.; Baciu, C. Exploring the Effects of Acid Mine Drainage on Diatom Teratology using Geometric Morphometry. Ecotoxicology 2017, 26, 1018–1030. [Google Scholar] [CrossRef] [PubMed]
- Olenici, A.; Baciu, C.; Blanco, S.; Morin, S. Naturally and Environmentally Driven Variations in Diatom Morphology: Implications for Diatom-based Assessment of Water Quality. In Modern Trends in Diatom Identification. Fundamentals and Applications; Cristóbal, G., Blanco, S., Bueno, G., Eds.; Springer: Cham, Switzerland, 2020; pp. 39–52. [Google Scholar]
- Cerisier, A.; Vedrenne, J.; Lavoie, I.; Morin, S. Assessing the Severity of Diatom Deformities using Geometric Morphometry. Bot. Lett. 2019, 166, 32–40. [Google Scholar] [CrossRef]
- Savriama, Y.; Klingenberg, C.P. Beyond Bilateral Symmetry: Geometric Morphometric Methods for any Type of Symmetry. BMC Evol. Biol. 2011, 11, 280. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.P. Analyzing Fluctuating Asymmetry with Geometric Morphometrics: Concepts, Methods, and Applications. Symmetry 2015, 7, 843–934. [Google Scholar] [CrossRef]
- Woodard, K.; Kulichová, J.; Poláčková, T.; Neustupa, J. Morphometric Allometry of Representatives of Three Naviculoid Genera throughout their Life Cycle. Diat. Res. 2016, 31, 231–242. [Google Scholar] [CrossRef]
- Potapova, M.; Hamilton, P.B. Morphological and Ecological Variation within the Achnanthidium minutissimum (Bacillariophyceae) Species Complex. J. Phycol. 2007, 43, 561–575. [Google Scholar] [CrossRef]
- Veselá, J.; Neustupa, J.; Pichrtová, M.; Poulíčková, A. Morphometric Study of Navicula Morphospecies (Bacillariophyta) with Respect to Diatom Life Cycle. Fottea 2009, 9, 307–316. [Google Scholar] [CrossRef]
- Woodard, K.; Neustupa, J. Morphometric Asymmetry of Frustule Outlines in the Pennate Diatom Luticola poulickovae (Bacillariophyceae). Symmetry 2016, 8, 150. [Google Scholar] [CrossRef]
- Kulichová, J.; Urbánková, P. Symmetric and Asymmetric Components of Shape Variation in the Diatom Genus Frustulia (Bacillariophyta). Symmetry 2020, 12, 1626. [Google Scholar] [CrossRef]
- Mann, D.G. Symmetry and Cell Division in Raphid Diatoms. Ann. Bot. 1983, 52, 573–581. [Google Scholar] [CrossRef]
- Mann, D.G. Protoplast Rotation, Cell Division and Frustule Symmetry in the Diatom Navicula bacillum. Ann. Bot. 1984, 53, 295–302. [Google Scholar] [CrossRef]
- Cox, E.J. Ontogeny, Homology, and Terminology—Wall Morphogenesis as an Aid to Character Recognition and Character State Definition for Pennate Diatom Systematics. J. Phycol. 2012, 48, 1–31. [Google Scholar] [CrossRef]
- Kociolek, J.P.; Williams, D.M.; Stepanek, J.; Liu, Q.; Liu, Y.; You, Q.; Karthick, B.; Kulikovskiy, M. Rampant Homoplasy and Adaptive Radiation in Pennate Diatoms. Plant Ecol. Evol. 2019, 152, 131–141. [Google Scholar] [CrossRef]
- Fazlutdinova, A.; Gabidullin, Y.; Allaguvatova, R.; Gaysina, L. Diatoms in Volcanic Soils of Mutnovsky and Gorely Volcanoes (Kamchatka Peninsula, Russia). Microorganisms 2021, 9, 1851. [Google Scholar] [CrossRef]
- The GIMP Development Team. 2014. Available online: https://www.gimp.org (accessed on 31 October 2021).
- Rohlf, F.J. The tps Series of Software. Hystrix Ital. J. Mammal. 2015, 26, 9–12. [Google Scholar]
- Adams, D.C.; Otárola-Castillo, E. Geomorph: An R Package for the Collection and Analysis of Geometric Morphometric Shape Data. Meth. Ecol. Evol. 2013, 4, 393–399. [Google Scholar] [CrossRef]
- Adams, D.C.; Collyer, M.; Kaliontzopoulou, A. Package “Geomorph”. 2020. Available online: https://cran.r-project.org/web/packages/geomorph/geomorph.pdf (accessed on 31 October 2021).
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape Analysis of Symmetric Structures: Quantifying Variation among Individuals and Asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.M.; Shadrina, E.G.; Trofimov, I.E. Fluctuating Asymmetry, Developmental Noise and Developmental Stability: Future Prospects for the Population Developmental Biology Approach. Symmetry 2020, 12, 1376. [Google Scholar] [CrossRef]
- McManus, H.A.; Lewis, L.A.; Schultz, E.T. Distinguishing Multiple Lineages of Pediastrum duplex with Morphometrics and a Proposal for Lacunastrum gen. nov. J. Phycol. 2011, 47, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Neustupa, J. Patterns of Symmetric and Asymmetric Morphological Variation in Unicellular Green Microalgae of the Genus Micrasterias (Desmidiales, Viridiplantae). Fottea 2013, 13, 53–63. [Google Scholar] [CrossRef]
- Lenarczyk, J.; McManus, H.A. Testing the Boundaries of the Green Algal Species Pediastrum alternans (Chlorophyceae) Using Conventional, Geometric Morphometric and Phylogenetic Methods. Phycologia 2016, 55, 515–530. [Google Scholar] [CrossRef]
- Neustupa, J. Asymmetry and Integration of Cellular Morphology in Micrasterias compereana. BMC Evol. Biol. 2017, 17, 1. [Google Scholar] [CrossRef] [PubMed]
- Lenarczyk, J. Evolution of Morphological Variability and Modularity in Single Cells of Algal Colonies: A Case Study Pseudopediastrum (Hydrodictyaceae, Sphaeropleales, Chlorophyceae). Phycologia 2019, 58, 180–191. [Google Scholar] [CrossRef]
- Neustupa, J.; Woodard, K. Geometric Morphometrics Reveals Increased Symmetric Shape Variation and Asymmetry Related to Lead Exposure in the Freshwater Green Alga Micrasterias compereana. Ecol. Indic. 2020, 111, 106054. [Google Scholar] [CrossRef]
- Rohlf, F.J.; Slice, D. Extensions of the Procrustes Method for the Optimal Superimposition of Landmarks. Syst. Zool. 1990, 39, 40–59. [Google Scholar] [CrossRef]
- MacLeod, N. Morphometrics: History, Development Methods and Prospects. Zool. Syst. 2017, 42, 4–33. [Google Scholar]
- MacLeod, N. Use of Landmark and Outline Morphometrics to Investigate Thecal Form Variation in Crushed Gogiid Echinoderms. Palaeoworld 2015, 24, 408–429. [Google Scholar]
- Neustupa, J.; Nemcova, Y. Morphological Allometry Constrains Symmetric Shape Variation, but not Asymmetry, of Halimeda tuna (Bryopsidales, Ulvophyceae) Segments. PLoS ONE 2018, 13, e0206492. [Google Scholar]
- Zelditch, M.L.; Swiderski, D.L.; Sheets, D.H. Geometric Morphometrics for Biologists: A Primer, 2nd ed.; Elsevier Academic Press: London, UK, 2012; p. 478. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Multimodel Inference: Understanding AIC and BIC in Model Selection. Sociol. Meth. Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Dryden, I.L. Shapes: Statistical Shape Analysis. R Package Version 1.2.6. 2021. Available online: https://CRAN.R-project.org/package=shapes (accessed on 2 November 2021).
- R Core Team. R: A Language and Environment for Statistical Computing. 2021. Available online: https://www.r-project.org/ (accessed on 2 November 2021).
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological Statistics Software Package for Education and Data Analysis. Palaeont. Electron. 2001, 4, 1–9. [Google Scholar]
- Cox, J.D. Deformed Diatoms. Proc. Am. Soc. Micr. 1890, 12, 178–183. [Google Scholar] [CrossRef]
- Jahn, R.; Kusber, W.H. Algae of the Ehrenberg Collection: 1. Typification of 32 Names of Diatom Taxa Described by C. G. Ehrenberg. Willdenowia 2004, 34, 577–595. [Google Scholar] [CrossRef][Green Version]
- Mann, D.G.; Chepurnov, V.A.; Idei, M. Mating System, Sexual Reproduction, and Auxosporulation in the Anomalous Raphid Diatom Eunotia (Bacillariophyta). J. Phycol. 2003, 39, 1067–1084. [Google Scholar] [CrossRef]
- Geitler, L. Der Formwechsel der Pennaten Diatomeen (Kieselalgen). Arch. Protistenkd. 1932, 78, 1–226. [Google Scholar]
- English, J.D.; Potapova, M.G. Ontogenetic and Interspecific Valve Shape Variation in the Pinnatae Group of the Genus Surirella and the Description of S. lacrimula sp. nov. Diat. Res. 2012, 27, 9–27. [Google Scholar] [CrossRef]
- Vanormelingen, P.; Chepurnov, V.A.; Mann, D.G.; Sabbe, K.; Vyverman, W. Genetic Divergence and Reproductive Barriers among Morphologically Heterogeneous Sympatric Clones of Eunotia bilunaris sensu lato (Bacillariophyta). Protist 2008, 159, 73–90. [Google Scholar] [CrossRef] [PubMed]
- Falasco, E.; Bona, F.; Ginepro, M.; Hlúbiková, D.; Hoffmann, L.; Ector, L. Morphological Abnormalities of Diatom Silica Walls in Relation to Heavy Metal Contamination and Artificial Growth Conditions. Water SA 2009, 35, 595–606. [Google Scholar] [CrossRef][Green Version]
- Kulichová, J.; Neustupa, J.; Vrbová, K.; Levkov, Z.; Kopalová, K. Asymmetry in Luticola species. Diatom Res. 2019, 34, 67–74. [Google Scholar] [CrossRef]
- Lavoie, I.; Hamilton, P.B.; Morin, S.; Tiam, S.K.; Kahlert, M.; Gonçalves, S.; Falasco, E.; Fortin, C.; Gontero, B.; Heudre, D.; et al. Diatom Teratologies as Biomarkers of Contamination: Are all Deformities Ecologically Meaningful? Ecol. Indic. 2017, 82, 539–550. [Google Scholar] [CrossRef]
- Fernández, M.R.; Martín, G.; Corzo, J.; De La Linde, A.; García, E.; López, M.; Sousa, M. Design and Testing of a New Diatom-based Index for Heavy Metal Pollution. Arch. Environ. Contam. Toxicol. 2018, 74, 170–192. [Google Scholar] [CrossRef] [PubMed]
- Wishkerman, A.; Hamilton, P.B. Shape outline extraction software (DiaOutline) for elliptic Fourier analysis application in morphometric studies. Appl. Plant Sci. 2018, 6, e1204. [Google Scholar] [CrossRef] [PubMed]
- Coquillé, N.; Morin, S. Fitness of Teratological Morphotypes and Heritability of Deformities in the Diatom Gomphonema gracile. Ecol. Indic. 2019, 106, 105442. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woodard, K.; Neustupa, J. Geometric Morphometrics of Bilateral Asymmetry in Eunotia bilunaris (Eunotiales, Bacillariophyceae) as a Tool for the Quantitative Assessment of Teratogenic Deviations in Frustule Shapes. Symmetry 2022, 14, 42. https://doi.org/10.3390/sym14010042
Woodard K, Neustupa J. Geometric Morphometrics of Bilateral Asymmetry in Eunotia bilunaris (Eunotiales, Bacillariophyceae) as a Tool for the Quantitative Assessment of Teratogenic Deviations in Frustule Shapes. Symmetry. 2022; 14(1):42. https://doi.org/10.3390/sym14010042
Chicago/Turabian StyleWoodard, Katerina, and Jiri Neustupa. 2022. "Geometric Morphometrics of Bilateral Asymmetry in Eunotia bilunaris (Eunotiales, Bacillariophyceae) as a Tool for the Quantitative Assessment of Teratogenic Deviations in Frustule Shapes" Symmetry 14, no. 1: 42. https://doi.org/10.3390/sym14010042
APA StyleWoodard, K., & Neustupa, J. (2022). Geometric Morphometrics of Bilateral Asymmetry in Eunotia bilunaris (Eunotiales, Bacillariophyceae) as a Tool for the Quantitative Assessment of Teratogenic Deviations in Frustule Shapes. Symmetry, 14(1), 42. https://doi.org/10.3390/sym14010042






