Abstract
Neutron stars are perfect candidates to investigate the effects of a modified gravity theory, since the curvature effects are significant and more importantly, potentially testable. In most cases studied in the literature in the context of massive scalar-tensor theories, inflationary models were examined. The most important of scalar-tensor models is the Higgs model, which, depending on the values of the scalar field, can be approximated by different scalar potentials, one of which is the inflationary. Since it is not certain how large the values of the scalar field will be at the near vicinity and inside a neutron star, in this work we will answer the question, which potential form of the Higgs model is more appropriate in order for it to describe consistently a static neutron star. As we will show numerically, the non-inflationary Higgs potential, which is valid for certain values of the scalar field in the Jordan frame, leads to extremely large maximum neutron star masses; however, the model is not self-consistent, because the scalar field approximation used for the derivation of the potential, is violated both at the center and at the surface of the star. These results shows the uniqueness of the inflationary Higgs potential, since it is the only approximation for the Higgs model, that provides self-consistent results.
1. Introduction
The next two decades will possibly bring sensational observational results to the cosmology, theoretical physics and theoretical astrophysics community. All of these observations are related to gravitational wave detections, either stochastic inflationary gravitational waves, such as the LISA [1,2] and DECIGO [3,4], or ordinary astrophysical originating gravitational waves. With regard to astrophysical sources of gravitational waves, neutron stars are in the epicenter of current theoretical and experimental research. This is because neutron stars (NSs) [5,6,7,8,9] are superstars among stars, a wide range of physics research areas must be used to describe these accurately, such as nuclear and high energy physics [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24], modified gravity can also describe NSs [25,26,27,28,29,30,31,32,33,34,35,36,37], and theoretical astrophysics [38,39,40,41,42,43,44,45,46,47,48,49]. Four decades passed since the first observation of a NS, and to date serious questions remain regarding the inner structure and physics of NSs. The equation of state (EoS) of nuclear matter is still a mystery in addition to the fundamental question whether general relativity (GR) or modified gravity [50,51,52,53,54,55,56,57] controls the physics of the star. A particularly appealing form of modified gravity is scalar-tensor gravity, and many works on NSs in the context of scalar-tensor gravity already exist in the literature [58,59,60,61,62,63,64,65,66,67,68,69,70,71]. Also scalar-tensor gravity is popular in cosmological contexts too [72,73,74,75,76,77,78,79,80,81,82,83,84], where viable inflationary models can be realized. The model with the highest importance in scalar-tensor gravity is the Higgs model, since the Higgs boson is the first fundamental (elementary) scalar elementary particle that has ever been observed [85]. The Higgs inflationary potential is capable of producing a viable inflationary era [76] and this occurs for a specific range of values of the scalar field and the non-minimal coupling constant to the Ricci scalar, usually denoted as . In a previous work we studied NSs in the context of scalar-tensor theories, using the inflationary Higgs potential [34]. In this work we extend our work to account for different limiting values of the scalar field and the combined non-minimal coupling of the form . We shall be interested in values in Geometrized units. In this approximation, we shall derive the Einstein frame potential and the relevant conformal transformation function . Accordingly, we shall derive the corresponding Tolman–Oppenheimer–Volkoff (TOV) equations in the Einstein frame, for static NSs, and we shall solve these numerically, assuming piecewise polytropic EoSs [86,87]. We shall find the relations for static NSs. Our results indicate an important fact, that the only correct description of the Higgs potential for static NSs is the one we developed in Ref. [34]. The results of the current article indicate that the maximum masses of NSs exceed the 3 limit, but the approximation fails to hold true at the center and at the surface of the NSs. This result indicates how unique is the inflationary Higgs potential, for providing a self-consistent neutron star phenomenology.
2. Non-Inflationary Higgs Scalar-Tensor Gravity in the Einstein Frame and Static NSs Phenomenology
We are interested in extracting the Einstein frame counterpart theory of the Jordan frame Higgs theory, and we shall do so by using a conformal transformation, see [58,79,88,89,90,91] for details on conformal transformations. The Jordan frame action of the Higgs model as it appears in cosmological contexts [76], in Geometrized units () is the following,
where is the non-minimal coupling function and is the potential, defined as follows,
where denotes the Jordan frame scalar field. In addition, , , g and denote the metric tensor, the action for the matter fluids, the determinant of the metric tensor and the Ricci scalar in the Jordan frame.
Performing the conformal transformation , where the function is defined as,
and the Einstein frame action in terms of the canonical scalar field reads,
where the “tilde” denotes quantities evaluated in the Einstein frame. Specifically, , , and denote the metric tensor, the action for the matter fluids, the determinant of the metric tensor and the Ricci scalar in the Einstein frame.
Also the Einstein frame potential is,
and when expressed in terms of this is written as,
Using relation between the Einstein frame canonical scalar field and the Jordan frame scalar field ,
and combined with Equation (2), we get,
For the Higgs inflationary potential, the field values approximations are the following
however, we shall use another approximation relevant in Higgs potential physics, namely [76],
which is equivalent to the following two approximations,
Thus, integrating the above we get the final relation between and ,
At leading order the function reads,
thus, at leading order . Moreover, the potential as function of is,
For phenomenological reasoning [76], we shall choose with . With regard to the EoS, we shall use a piecewise polytropic EoS, the details of which can be found in [34].
For , the requirement (13) can in principle be satisfied, but the constraint of Equation (12) is not necessarily satisfied. As we will show, this is the case for the non-inflationary Higgs potential, and we shall verify this numerically. For the study we shall consider static NSs, which are described by a spherically symmetric static spacetime of the form,
where denotes the gravitational mass of the stellar object confined inside a radius r.
For Geometrized units (), the TOV equations for the spherically symmetric spacetime are,
The TOV equations must be solved numerically subject to the following initial conditions,
where , , are the pressure of the NS, the value of the function and the value of the scalar field at the center of the NS. The values of and at the center of the star, shall be obtained using a double shooting method, in order for the optimal values of them to be obtained. The requirement for obtaining the optimal values is the scalar field values to vanish at numerical infinity, which proves to be the same numerically as in the inflationary Higgs potential, namely km in the Einstein frame, see [34]. In addition, for the derivation of the gravity we need to consider the ADM Jordan frame mass and the Jordan frame radius. Denoting with the Einstein frame radius at large distances, and , the Jordan frame mass is related to the Einstein frame mass as follows,
with and , and is the Jordan frame radius. The Einstein frame radius of the star can be obtained by the numerical code by using the condition , so it is basically determined by the condition that the pressure of the star vanishes at the surface of the star. Accordingly, by finding we can obtain the Jordan frame radius R using the relation , where is the value of the scalar field at the surface of the star. Finally and important note is to verify numerically the validity of the approximation (12) in the Jordan frame. For the numerical analysis, we shall use a freely available PYTHON code pyTOV-STT [92], and we shall derive the solutions for both the interior and the exterior of the NS, using the “LSODA” numerical method. The EoSs we shall use are the WFF1 [93], the SLy [94], and the APR EoS [95]. Let us proceed to the results of our analysis, and we start off with the graphs for all the EoSs which we present in Figure 1. The purple curve corresponds to the WFF1 EoS, while the red and blue to the SLy and APR EoSs respectively. From the graphs it is apparent that for the non-inflationary Higgs model, the maximum masses are comparably higher with regard to the GR ones. In addition, in Table 1 we present all the maximum masses for all the EoSs corresponding to the alternative Higgs model. As it can be seen in Table 1, the maximum masses for the alternative Higgs model are quite elevated compared to the GR ones. In addition, the GW170817 constraint which indicates that the radius corresponding to the maximum NS mass must be larger than is satisfied km.
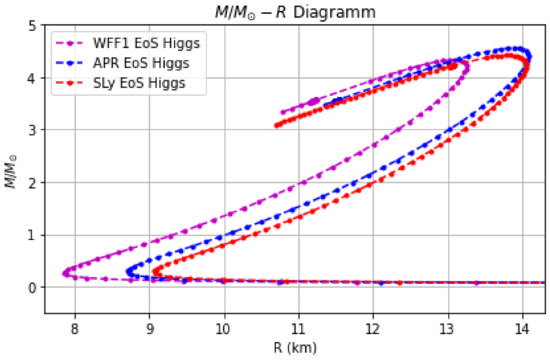
Figure 1.
graphs for the alternative non-inflationary Higgs model for the WFF1 EoS (purple curve), the APR EoS (blue curve), and the SLy EoS (red curve). The y-axis is expressed in units, with M denoting the Jordan frame ADM mass, and the x-axis is the circumferential radius.

Table 1.
Maximum Masses and the of Static NS for the non-Inflationary Higgs Model and for GR.
The results are deemed quite interesting; however, the non-inflationary Higgs model has inherent issues with the approximation (12) as we proved numerically. Particularly it is not satisfied neither at the center nor at the surface of the star. This feature can be clearly seen in Figure 2, where we present the values of in the Jordan frame for all the EoS for the surface scalar field values. The same applies for the values of the scalar field in the center of the star. Therefore, to our original question whether inflationary scalar potentials or other approximations must be used for static NSs phenomenology, the answer seems to be that only inflationary potentials provide consistent results.
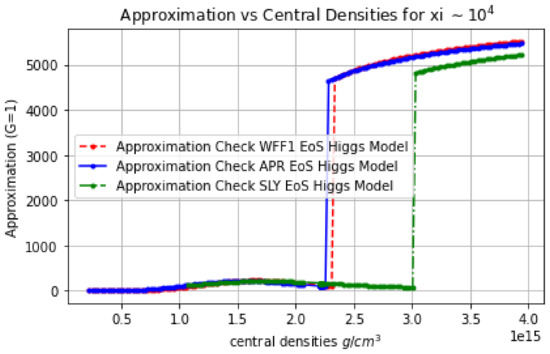
Figure 2.
The quantity (y-axis) in Geometrized units, versus the central densities in CGS units, for , for the WFF1 (red curve), APR (blue curve) and Sly (green curve) EoSs. As it can be seen the constraint (12) is not satisfied.
3. Concluding Remarks
In the field of cosmology, there exist several massive scalar field theories which can potentially play an important role for describing NSs phenomenology. From these theories, the most important is the Higgs inflationary theory in its various forms. Specifically, depending on the scalar field values, the Higgs potential can take various forms, each of which may describe a different era in the cosmological theory. Thus, the question is which approximate Higgs potential can describe in a viable and consistent static NS phenomenology. In this paper we addressed this question for the most fundamental of all the scalar field cosmologies, the Higgs inflationary theory. We considered the theory in the Jordan frame and upon conformally transforming it, we derived the Einstein frame theory. Accordingly, assuming a specific range for for the scalar field values, we derived the appropriate quantities which are relevant for studying static NSs in the Einstein frame. For a static spherically symmetric spacetime we derived the TOV equations and we numerically solved them using a double shooting method for optimizing the results. The numerical analysis yielded the Einstein frame masses and radii of the static NS, and also the Einstein frame values of the scalar field, from which we found the corresponding Jordan frame quantities. We constructed the graphs and we investigated the validity of the approximations holding true for the non-inflationary Higgs model. As we showed, the maximum masses for the alternative Higgs model are quite elevated, compared with the GR case; however, for all the EoSs studies, the approximation we assumed for deriving the theory break down. Thus, although the theory provides interesting result, the inherent structure of it is not correct and consistent. This indicates strongly the suitability of inflationary potentials for studying NSs phenomenology, regardless how well motivated other forms of potentials might be. Moreover, it seems that the approximations for the scalar field values used for deriving the inflationary potentials, are well respected on the surface, center and at numerical infinity of the NS. Hence, in conclusion the Higgs potential that is used for inflationary phenomenology is the only suitable for describing consistently NSs.
We need to note with regard to the EoSs we used, that we used the PAR, and more importantly the WFF1, known as FPS EoS, and the SLy, which both are known to provide a unified description of the crust and core of NSs. However, all these EoSs are to date rather old (nearly 20 years old); thus, it is compelling to incorporate to the analysis more timely and to date EoSs, such as the BSk24 [96,97].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
I am grateful to the referee 3 of the manuscript who pointed out the timely BSk24, which I intend to incorporate in my code for the piecewise polytropic EoS.
Conflicts of Interest
The author declares no conflict of interest.
References
- Baker, J.; Bellovary, J.; Bender, P.L.; Berti, E.; Caldwell, R.; Camp, J.; Conklin, J.W.; Cornish, N.; Cutler, C.; DeRosa, R.; et al. The Laser Interferometer Space Antenna: Unveiling the Millihertz Gravitational Wave Sky. arXiv 2019, arXiv:1907.06482. [Google Scholar]
- Smith, T.L.; Caldwell, R. LISA for Cosmologists: Calculating the Signal-to-Noise Ratio for Stochastic and Deterministic Sources. Phys. Rev. D 2019, 100, 104055. [Google Scholar] [CrossRef] [Green Version]
- Seto, N.; Kawamura, S.; Nakamura, T. Possibility of direct measurement of the acceleration of the universe using 0.1-Hz band laser interferometer gravitational wave antenna in space. Phys. Rev. Lett. 2001, 87, 221103. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron stars 1: Equation of state and structure, Astrophys. Space Sci. Libr. 2007, 326, 1–619. [Google Scholar]
- Friedman, J.L.; Stergioulas, N. Rotating Relativistic Stars; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef] [Green Version]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lattimer, J.M.; Prakash, M. The physics of neutron stars. Science 2004, 304, 536–542. [Google Scholar] [CrossRef] [Green Version]
- Olmo, G.J.; Rubiera-Garcia, D.; Wojnar, A. Stellar structure models in modified theories of gravity: Lessons and challenges. Phys. Rept. 2020, 876, 1–75. [Google Scholar] [CrossRef]
- Lattimer, J.M. The nuclear equation of state and neutron star masses. Ann. Rev. Nucl. Part. Sci. 2012, 62, 485–515. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.W.; Gandolfi, S. Connecting Neutron Star Observations to Three-Body Forces in Neutron Matter and to the Nuclear Symmetry Energy. Phys. Rev. Lett. 2012, 108, 081102. [Google Scholar] [CrossRef]
- Horowitz, C.J.; Perez-Garcia, M.A.; Berry, D.K.; Piekarewicz, J. Dynamical response of the nuclear ’pasta’ in neutron star crusts. Phys. Rev. C 2005, 72, 35801. [Google Scholar]
- Watanabe, G.; Iida, K.; Sato, K. Thermodynamic properties of nuclear ’pasta’ in neutron star crusts. Nucl. Phys. A 2003, 676, 455–473. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Chen, L.W.; Li, B.A.; Ma, H.R. Nuclear constraints on properties of neutron star crusts. Astrophys. J. 2009, 697, 1549–1568. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef] [Green Version]
- de Jesús Mendoza-Temis, J.; Wu, M.R.; Martínez-Pinedo, G.; Langanke, K.; Bauswein, A.; Janka, H.T. Nuclear robustness of the r process in neutron-star mergers. Phys. Rev. C 2015, 92, 55805. [Google Scholar] [CrossRef] [Green Version]
- Ho, W.C.G.; Elshamouty, K.G.; Heinke, C.O.; Potekhin, A.Y. Tests of the nuclear equation of state and superfluid and superconducting gaps using the Cassiopeia A neutron star. Phys. Rev. C 2015, 91, 15806. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the nuclear equation of state from the existence of a ~2.6 M⊙ neutron star: The GW190814 puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Buschmann, M.; Co, R.T.; Dessert, C.; Safdi, B.R. X-ray Search for Axions from Nearby Isolated Neutron Stars. Phys. Rev. Lett. 2021, 126, 21102. [Google Scholar] [CrossRef]
- Safdi, B.R.; Sun, Z.; Chen, A.Y. Detecting Axion Dark Matter with Radio Lines from Neutron Star Populations. Phys. Rev. D 2019, 99, 123021. [Google Scholar] [CrossRef] [Green Version]
- Hook, A.; Kahn, Y.; Safdi, B.R.; Sun, Z. Radio Signals from Axion Dark Matter Conversion in Neutron Star Magnetospheres. Phys. Rev. Lett. 2018, 121, 241102. [Google Scholar] [CrossRef] [Green Version]
- Edwards, T.D.P.; Kavanagh, B.J.; Visinelli, L.; Weniger, C. Transient Radio Signatures from Neutron Star Encounters with QCD Axion Miniclusters. Phys. Rev. Lett. 2021, 127, 131103. [Google Scholar] [CrossRef] [PubMed]
- Nurmi, S.; Schiappacasse, E.D.; Yanagida, T.T. Radio signatures from encounters between Neutron Stars and QCD-Axion Minihalos around Primordial Black Holes. arXiv 2021, arXiv:2102.05680. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Extended Gravity Description for the GW190814 Supermassive Neutron Star. Phys. Lett. B 2020, 811, 135910. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Farinelli, R.; Odintsov, S.D. Mass-radius relation for neutron stars in f(R) gravity. Phys. Rev. D 2016, 93, 23501. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Extreme neutron stars from Extended Theories of Gravity. JCAP 2015, 2015, 1. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Maximal neutron star mass and the resolution of the hyperon puzzle in modified gravity. Phys. Rev. D 2014, 89, 103509. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D. Further stable neutron star models from f(R) gravity. JCAP 2013, 2013, 40. [Google Scholar] [CrossRef] [Green Version]
- Arapoglu, A.S.; Deliduman, C.; Eksi, K.Y. Constraints on Perturbative f(R) Gravity via Neutron Stars. JCAP 2011, 2011, 20. [Google Scholar] [CrossRef] [Green Version]
- Astashenok, A.V.; Odintsov, S.D. Rotating Neutron Stars in F(R) Gravity with Axions. Mon. Not. Roy. Astron. Soc. 2020, 498, 3616. [Google Scholar] [CrossRef]
- Lobato, R.V.; Carvalho, G.A.; Bertulani, C.A. Neutron stars in f(R,Lm) gravity with realistic equations of state: Joint-constrains with GW170817, massive pulsars, and the PSR J0030+0451 mass-radius from NICER data. Eur. Phys. J. C 2021, 81, 1013. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Universal inflationary attractors implications on static neutron stars. Class. Quant. Grav. 2021, 38, 175005. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Neutron Stars in Scalar-tensor Gravity with Higgs Scalar Potential. arXiv 2021, arXiv:2104.01982. [Google Scholar]
- Odintsov, S.D.; Oikonomou, V.K. Neutron stars phenomenology with scalar–tensor inflationary attractors. Phys. Dark Univ. 2021, 32, 100805. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Causal limit of neutron star maximum mass in f(R) gravity in view of GW190814. Phys. Lett. B 2021, 816, 136222. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Capozziello, S.; Odintsov, S.D.; Oikonomou, V.K. Novel stellar astrophysics from extended gravity. EPL 2021, 134, 59001. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. Phys. Rev. D 2016, 93, 65044. [Google Scholar] [CrossRef] [Green Version]
- Khadkikar, S.; Raduta, A.R.; Oertel, M.; Sedrakian, A. Maximum mass of compact stars from gravitational wave events with finite-temperature equations of state. Phys. Rev. C 2021, 103, 55811. [Google Scholar] [CrossRef]
- Sedrakian, D.M.; Hayrapetyan, M.V.; Shahabasyan, M.K. Gravitational radiation of slowly rotating neutron stars. Astrophysics 2006, 49, 194–200. [Google Scholar] [CrossRef]
- Sedrakian, A. Axion cooling of neutron stars. II. Beyond hadronic axions. Phys. Rev. D 2019, 99, 43011. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Guo, G.; Lien, J.H.; Lin, Y.H.; Wu, M.R. Compact Dark Objects in Neutron Star Mergers. arXiv 2020, arXiv:2012.11908. [Google Scholar]
- Vretinaris, S.; Stergioulas, N.; Bauswein, A. Empirical relations for gravitational-wave asteroseismology of binary neutron star mergers. Phys. Rev. D 2020, 101, 84039. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Blacker, S.; Vijayan, V.; Stergioulas, N.; Chatziioannou, K.; Clark, J.A.; Bastian, N.U.F.; Blaschke, D.B.; Cierniak, M.; Fischer, T. Equation of state constraints from the threshold binary mass for prompt collapse of neutron star mergers. Phys. Rev. Lett. 2020, 125, 141103. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef] [Green Version]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [Green Version]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using gravitational-wave observations and quasi-universal relations to constrain the maximum mass of neutron stars. Astrophys. J. Lett. 2018, 852, L25. [Google Scholar] [CrossRef]
- Nathanail, A.; Most, E.R.; Rezzolla, L. GW170817 and GW190814: Tension on the maximum mass. Astrophys. J. Lett. 2021, 908, L28. [Google Scholar] [CrossRef]
- Köppel, S.; Bovard, L.; Rezzolla, L. A General-relativistic Determination of the Threshold Mass to Prompt Collapse in Binary Neutron Star Mergers. Astrophys. J. Lett. 2019, 872, L16. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1. [Google Scholar] [CrossRef] [Green Version]
- Capozziello, S.; De Laurentis, M. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity: A Survey of Gravitational Theories for Cosmology and Astrophysics; Springer: Dordrecht, The Netherland, 2010; p. 170. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115. [Google Scholar] [CrossRef] [Green Version]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59. [Google Scholar] [CrossRef] [Green Version]
- de la Cruz-Dombriz, A.; Saez-Gomez, D. Black holes, cosmological solutions, future singularities, and their thermodynamical properties in modified gravity theories. Entropy 2012, 14, 1717. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413. [Google Scholar] [CrossRef] [Green Version]
- Dimopoulos, K. Introduction to Cosmic Inflation and Dark Energy; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Pani, P.; Berti, E. Slowly rotating neutron stars in scalar-tensor theories. Phys. Rev. D 2014, 90, 24025. [Google Scholar] [CrossRef] [Green Version]
- Staykov, K.V.; Doneva, D.D.; Yazadjiev, S.S.; Kokkotas, K.D. Slowly rotating neutron and strange stars in R2 gravity. JCAP 2014, 2014, 6. [Google Scholar] [CrossRef] [Green Version]
- Horbatsch, M.; Silva, H.O.; Gerosa, D.; Pani, P.; Berti, E.; Gualtieri, L.; Sperhake, U. Tensor-multi-scalar theories: Relativistic stars and 3 + 1 decomposition. Class. Quant. Grav. 2015, 32, 204001. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.B.; Berti, E.; Crispino, L.C.B. Slowly rotating anisotropic neutron stars in general relativity and scalar–tensor theory. Class. Quant. Grav. 2015, 32, 145008. [Google Scholar] [CrossRef]
- Doneva, D.D.; Yazadjiev, S.S.; Stergioulas, N.; Kokkotas, K.D. Rapidly rotating neutron stars in scalar-tensor theories of gravity. Phys. Rev. D 2013, 88, 84060. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Gao, Y.; Shao, L. Strong-field effects in massive scalar-tensor gravity for slowly spinning neutron stars and application to X-ray pulsar pulse profiles. Phys. Rev. D 2020, 102, 64057. [Google Scholar] [CrossRef]
- Salgado, M.; Sudarsky, D.; Nucamendi, U. On spontaneous scalarization. Phys. Rev. D 1998, 58, 124003. [Google Scholar] [CrossRef] [Green Version]
- Shibata, M.; Taniguchi, K.; Okawa, H.; Buonanno, A. Coalescence of binary neutron stars in a scalar-tensor theory of gravity. Phys. Rev. D 2014, 89, 84005. [Google Scholar] [CrossRef] [Green Version]
- Savaş Arapoğlu, A.; Yavuz Ekşi, K.; Emrah Yükselci, A. Neutron star structure in the presence of nonminimally coupled scalar fields. Phys. Rev. D 2019, 99, 64055. [Google Scholar] [CrossRef] [Green Version]
- Ramazanoğlu, F.M.; Pretorius, F. Spontaneous Scalarization with Massive Fields. Phys. Rev. D 2016, 93, 64005. [Google Scholar] [CrossRef] [Green Version]
- Altaha Motahar, Z.; Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Axial quasinormal modes of scalarized neutron stars with massive self-interacting scalar field. Phys. Rev. D 2019, 99, 104006. [Google Scholar] [CrossRef] [Green Version]
- Chew, X.Y.; Dzhunushaliev, V.; Folomeev, V.; Kleihaus, B.; Kunz, J. Rotating wormhole solutions with a complex phantom scalar field. Phys. Rev. D 2019, 100, 44019. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Scen Khoo, F.; Kunz, J. Ultra-long-lived quasi-normal modes of neutron stars in massive scalar-tensor gravity. EPL 2020, 130, 50002. [Google Scholar] [CrossRef]
- Altaha Motahar, Z.; Blázquez-Salcedo, J.L.; Kleihaus, B.; Kunz, J. Scalarization of neutron stars with realistic equations of state. Phys. Rev. D 2017, 96, 64046. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Shaposhnikov, M. Higgs inflation at the critical point. Phys. Lett. B 2014, 734, 249–254. [Google Scholar] [CrossRef]
- Garcia-Bellido, J.; Rubio, J.; Shaposhnikov, M.; Zenhausern, D. Higgs-Dilaton Cosmology: From the Early to the Late Universe. Phys. Rev. D 2011, 84, 123504. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.; Magnin, A.; Shaposhnikov, M.; Sibiryakov, S. Higgs inflation: Consistency and generalisations. JHEP 2011, 2011, 16. [Google Scholar] [CrossRef] [Green Version]
- Bezrukov, F.L.; Shaposhnikov, M. The Standard Model Higgs boson as the inflaton. Phys. Lett. B 2008, 659, 703–706. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.S.; Sahni, V.; Toporensky, A.V. Initial conditions for Inflation in an FRW Universe. Phys. Rev. D 2018, 98, 83538. [Google Scholar] [CrossRef] [Green Version]
- Steinwachs, C.F.; Kamenshchik, A.Y. Non-minimal Higgs Inflation and Frame Dependence in Cosmology. AIP Conf. Proc. 2013, 1514, 161–164. [Google Scholar]
- Rubio, J. Higgs inflation. Front. Astron. Space Sci. 2019, 5, 50. [Google Scholar] [CrossRef]
- Kaiser, D.I. Primordial spectral indices from generalized Einstein theories. Phys. Rev. D 1995, 52, 4295–4306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gundhi, A.; Steinwachs, C.F. Scalaron-Higgs inflation. Nucl. Phys. B 2020, 954, 114989. [Google Scholar] [CrossRef]
- Cervantes-Cota, J.L.; Dehnen, H. Induced gravity inflation in the standard model of particle physics. Nucl. Phys. B 1995, 442, 391–412. [Google Scholar] [CrossRef] [Green Version]
- Kamada, K.; Kobayashi, T.; Takahashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized Higgs inflation. Phys. Rev. D 2012, 86, 23504. [Google Scholar] [CrossRef] [Green Version]
- Schlogel, S.; Rinaldi, M.; Staelens, F.; Fuzfa, A. Particlelike solutions in modified gravity: The Higgs monopole. Phys. Rev. D 2014, 90, 44056. [Google Scholar] [CrossRef] [Green Version]
- Füzfa, A.; Rinaldi, M.; Schlögel, S. Particlelike distributions of the Higgs field nonminimally coupled to gravity. Phys. Rev. Lett. 2013, 111, 121103. [Google Scholar] [CrossRef] [Green Version]
- Aad, G.; Abajyan, T.; Abbott, B.; Abdallah, J.; Khalek, S.A.; Abdelalim, A.A.; Abdinov, O.; Aben, R.; Abi, B.; ATLAS Collaboration. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Read, J.S.; Lackey, B.D.; Owen, B.J.; Friedman, J.L. Constraints on a phenomenologically parameterized neutron-star equation of state. Phys. Rev. D 2009, 79, 124032. [Google Scholar] [CrossRef] [Green Version]
- Read, J.S.; Markakis, C.; Shibata, M.; Uryu, K.; Creighton, J.D.E.; Friedman, J.L. Measuring the neutron star equation of state with gravitational wave observations. Phys. Rev. D 2009, 79, 124033. [Google Scholar] [CrossRef]
- Faraoni, V. Cosmology in Scalar-Tensor Gravity; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Faraoni, V. Conformally coupled inflation. Galaxies 2013, 1, 96–106. [Google Scholar] [CrossRef] [Green Version]
- Buck, M.; Fairbairn, M.; Sakellariadou, M. Inflation in models with Conformally Coupled Scalar fields: An application to the Noncommutative Spectral Action. Phys. Rev. D. 2010, 82, 43509. [Google Scholar] [CrossRef] [Green Version]
- Faraoni, V.; Gunzig, E.; Nardone, P. Conformal transformations in classical gravitational theories and in cosmology. Fund. Cosmic Phys. 1999, 20, 121. [Google Scholar]
- Nikolaos Stergioulas. Available online: https://github.com/niksterg (accessed on 14 January 2021).
- Wiringa, R.B.; Fiks, V.; Fabrocini, A. Equation of state for dense nucleon matter. Phys. Rev. C. 1988, 38, 1010–1037. [Google Scholar] [CrossRef]
- Douchin, F.; Haensel, P. A unified equation of state of dense matter and neutron star structure. Astron. Astrophys. 2001, 380, 151. [Google Scholar] [CrossRef] [Green Version]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. The Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels–Montreal functionals—I. Role of symmetry energy. Mon. Not. Roy. Astron. Soc. 2019, 481, 2994–3026. [Google Scholar] [CrossRef] [Green Version]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y. Unified equations of state for cold nonaccreting neutron stars with Brussels-Montreal functionals. II. Pasta phases in semiclassical approximation. Phys. Rev. C 2020, 101, 015802. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).