Abstract
We show that the Higgs and confinement phases of a gauge Higgs theory, with the Higgs field in the fundamental representation of the gauge group, are distinguished both by a broken or unbroken realization of the global center subgroup of the gauge group, and by the type of confinement in each phase. This is color confinement in the Higgs phase, and a stronger property, which we call “separation-of-charge” confinement, in the confining phase.
1. Introduction
In this article we would like to address two very old questions in gauge field theory, for which we will propose new answers. The first question is: What is meant by a “spontaneously broken gauge theory,” in view of Elitzur’s theorem [1], the work of Osterwalder and Seiler [2], Fradkin and Shenker [3], Banks and Rabinovici [4], and the fact that all physical particles in, e.g., an SU(2) gauge Higgs theory, are color singlets [5,6]. The second question is: What is meant by the word “confinement” in a theory (such as QCD) with matter in the fundamental representation of the gauge group? In such theories, the order parameters associated with pure gauge theories, i.e., non-vanishing string tension, ‘t Hooft loops, Polyakov loops, and vortex free energies have apparently non-confining behavior.
Starting with the first question, most discussions of the Higgs mechanism begin with a “Mexican hat” potential of some kind, and the Higgs field is expanded around one of the minima of this potential, i.e., , where the particular minimum is selected by fixing to a unitary gauge. When this replacement for is inserted back into the action, some or all of the gauge vector bosons acquire a mass. However, then we may ask: in what sense is this spontaneous symmetry breaking? Unitary gauge, for the U(1) and SU(2) groups, is a complete gauge fixing; once has been fixed, all gauge freedom has been removed. Thus, there is no gauge symmetry left to break, spontaneously or otherwise. Yet, one often speaks of a Higgs mechanism (“spontaneous gauge symmetry breaking”) occurring in such theories. Thus, perhaps, at least in connection with this issue, we should avoid gauge fixing? However, in the absence of gauge fixing, a local gauge symmetry cannot break spontaneously, as we know from Elitzur’s famous theorem. What about a middle way, i.e., choose some gauge, e.g., Coulomb, Landau, or axial gauge, which leaves a global subgroup (a “remnant” symmetry) of the gauge group unfixed? A global symmetry can break spontaneously. This is perfectly consistent with Elitzur’s theorem, and some textbooks and review articles (e.g., [7,8]) do define “spontaneous gauge symmetry breaking” in this way. The problem with this idea is that the location of the transition line is gauge-dependent [9]. This is seen in Figure 1, where transition lines for the breaking of the global remnant symmetry were computed in SU(2) gauge Higgs theory in both Coulomb and Landau gauges. (There are also suggestions that photons, or in general massless gauge bosons, are the Goldstone bosons of a spontaneously broken remnant gauge symmetry that exists in covariant gauge, i.e., it is the massless phase which is the phase of a spontaneously broken gauge symmetry. See Guendelman [10] and references therein.)
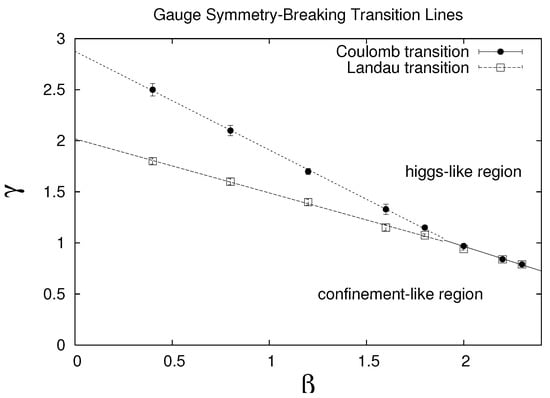
Figure 1.
The location of remnant global gauge symmetry breaking in Landau and Coulomb gauges, in the coupling plane, for the SU(2) gauge Higgs theory in (4). Figure from ref. [9].
A second reason to doubt that there is any essential distinction between the Higgs and confinement phases is the theorem proven by Osterwalder and Seiler [2] (see also the closely related work of Banks and Rabinovici [4]), whose consequences were elaborated by Fradkin and Shenker [3]. This theorem states that in a lattice gauge Higgs theory with the Higgs in the fundamental representation, there is no thermodynamic phase transition which isolates the Higgs from the confinement-like region; one can always follow a path from a point in the one region of the phase diagram to the other, without encountering a thermodynamic singularity. A third good reason, pointed out by Frölich, Morchio and Strocchi [5], ‘t Hooft [6], and Susskind (cf. [4]), is that physical particles in the so-called “Higgs” phase are created by local color singlet operators acting on the vacuum, as in the confinement region. We will refer to a gauge theory in which all asymptotic particle states are color singlet objects as color (or “C”) confinement. According to this definition, both the Higgs and confining regions of an SU(2) gauge Higgs theory, and QCD, are C confining theories.
Then is there any meaning to the word “confinement” beyond C confinement? In a pure gauge theory, of course there is. There is the area law for Wilson loops, the vanishing of the Polyakov line order parameter, the formation of stable color electric flux tubes between static sources, and the consequent linear rise of the static quark potential with quark-antiquark separation. In such theories, the confinement phase can be identified as the phase of unbroken center symmetry (distinct from the gauge symmetry). However, in a gauge theory with matter in the fundamental representation, none of these properties hold, at least not exactly or asymptotically. There is no global center symmetry distinct from the gauge symmetry; long flux tubes are unstable due to string-breaking by matter fields, and the linearly rising potential eventually goes flat.
In view of all these facts, we believe that the informed consensus on the two questions we have raised is as follows:
- Confinement, in a gauge + matter theory, can only mean that all of the particles in the asymptotic spectrum are color neutral; i.e., confinement is C confinement. Both the confining and the Higgs regions of a gauge Higgs theory are C confining.
- There is no such thing as a “spontaneously broken gauge symmetry,” at least none that has any physical meaning. In a gauge Higgs theory, the “Higgs” and “confinement” regions of the phase diagram are part of the same Higgs-confinement phase.
In our opinion, these consensus views are both wrong.
In the next section, we point out that the Higgs phase of a gauge Higgs theory is closely analogous to a spin glass, that the relevant symmetry which is spontaneously broken is a global symmetry which transforms the Higgs field but does not transform the gauge field, and that this symmetry contains, at a minimum, the global center subgroup of the gauge group. This symmetry is distinct from the quite different center symmetry, of which the order parameter is the Polyakov line. We will construct a gauge invariant order parameter, modeled after the Edwards–Anderson order parameter [11] for a spin glass, which can detect the spontaneous breaking of this global subgroup of the gauge symmetry. This order parameter does not depend, not even implicitly, on a gauge choice. In the following Section 3, we introduce the concept of separation-of-charge (S) confinement, which is a stronger condition than color confinement, and which generalizes the concept of confinement in pure gauge theories to theories with dynamical matter and string-breaking. We will explain how, in the absence of a massless phase, the phase of unbroken global center gauge symmetry is the S confining phase, while the spin glass (aka Higgs) phase is a C confining phase, in which this global symmetry is spontaneously broken.
This article is a review, and we concentrate on simply describing our main results. The interested reader will find detailed derivations in the cited references.
2. The Higgs Phase as a Spin Glass
The Edwards–Anderson model of a spin glass is an Ising model with random couplings among spins, i.e.,
where , the sum is (usually) over nearest neighbors, and the are a set of random couplings between sites with probability distributions . There is obviously a global symmetry in the limit. However, after the sum over random couplings, we have in this limit. Despite this fact, there is still a way to detect the spontaneous breaking of the global symmetry. Following [11], let us define
where is called the Edwards–Anderson order parameter. Its expectation value is non-zero in the spin glass phase, indicating spontaneous symmetry breaking of the global symmetry, despite the fact that .
The gauge Higgs analogy to a spin glass is shown in Table 1. In a gauge Higgs theory, the Higgs field plays the role of spin, and the gauge link variables play the role of random couplings. As in a spin glass, , and for similar reasons. However, this is not the end of the story, as regards spontaneous symmetry breaking.

Table 1.
Analogies between spin glass and gauge Higgs theories.
We will define a custodial symmetry to be a group whose elements transform the Higgs field, but do not transform the gauge field. It is clear that this group contains, at a minimum, the global center subgroup of the gauge group. Let us begin from the continuum action of a gauge Higgs theory
On the lattice, for the SU(2) group, and taking the limit, we may write
where is an SU(2) group-valued field. The possibility of expressing as a group-valued field is special to SU(2), and the custodial symmetry transformations are
This global SU(2) custodial group of course contains as a subgroup, which is indistinguishable from the global subgroup of the gauge group. For larger SU(N) gauge groups, the custodial group may contain only the global center subgroup of the gauge group.
Now, to make correspondence with the Edwards–Anderson treatment, let us first define
where the are energy eigenstates, with the corresponding wave functionals in Schrödinger representation. The thermal expectation value of some operator is given by the standard expression
However, the relationship between thermal expectation values in quantum statistical mechanics, and the Euclidean path integral, is given by
where S is the Euclidean action of the gauge Higgs theory, and it is understood that there is a finite time extension (=1/) and periodic boundary conditions in the Euclidean path integral. Comparing the bottom lines of the last two equations, and making the identification of the fields in three-space in Equation (7) with the fields on a time slice in Equation (8), we arrive at
We next introduce
with an SU(2)-valued field. The term proportional to h is added for formal reasons, since the proper definition of spontaneous symmetry breaking requires first introducing a small explicit breaking term, then taking the infinite volume limit, followed by . We then define
where
Equation (11) for gauge Higgs theory should be compared with the Edwards–Anderson order parameter in (2). The term proportional to h is introduced in such a way (involving ) that it does not break local gauge invariance, cf. [12].
We still have to specify , but there is only one possibility. We must have, for the thermal average of an operator on a time slice,
Since is the standard thermal average of on a time slice in a gauge Higgs theory, we need to have
Both and are gauge invariant, even at finite h, and we are mainly interested in the zero temperature limit.
We now have a gauge invariant criterion for the spontaneous breaking of custodial symmetry:
which is entirely analogous to the Edwards–Anderson criterion for the spontaneous symmetry breaking of global symmetry in a spin glass:
In the case of gauge Higgs theory, our claim is that the phase of broken symmetry is the Higgs phase.
2.1. Two Theorems
Now let be any physical gauge condition imposed on spacelike links, separately on each timeslice. We will call this an F-gauge. Examples include Coulomb gauge, the Laplacian version [13] of Coulomb gauge, and axial gauge. We can prove two theorems relating in physical F-gauges to our spin wave order parameter .
Theorem 1.
In any physical F gauge
Theorem 2.
There exists at least one physical F gauge, call it , which saturates the bound:
Custodial symmetry breaking is therefore a necessary condition for in any F-gauge, and a sufficient condition for in some F-gauge. For proofs of these statements, see [12].
2.2. Numerical Evaluation
can be evaluated numerically by lattice Monte Carlo, and for practical purposes, one can dispense with the complicated term in (11) proportional to h. In that case, (11) simplifies to
Once we put the expressions in this form, we can forget about the spin glass analogy and simply regard the calculation as evaluating the vacuum expectation of a gauge invariant operator , which depends only on spacelike links on the timeslice, and which happens to have an involved definition which itself involves a path integral. Then, the order parameter can be computed with no difficulty at any , via a “Monte Carlo within a Monte Carlo” procedure. Figure 2a shows how this is done. The procedure is to update both the link and scalar field variables as usual, for e.g., 100 sweeps, generating configurations drawn from the usual probability distribution . However, the computation of the order parameter at each data taking “sweep” (better to call it an “event”) is also done by Monte Carlo simulation. Each data taking event involves sweeps over the lattice, where the spacelike link variables on one time slice, say , are held fixed, while all other field variables are updated. During these sweeps, we evaluate the average value at each site on the timeslice, and from there, we compute as defined in (19). Averaging over many of these data taking events, with different held fixed, gives us an estimate for using sweeps in each procedure. On general statistical grounds,
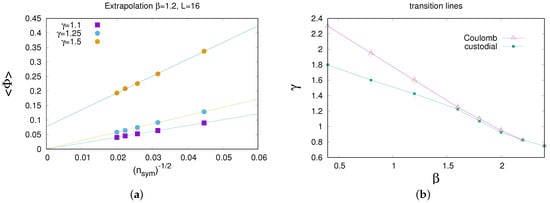
Figure 2.
(a) Extrapolation of to above () and below () the custodial symmetry breaking transition at , in SU(2) gauge Higgs theory. The lattice volume is ; error bars are smaller than the symbol sizes. (b) The custodial symmetry breaking/spin glass transition line joins the filled squares; the Coulomb gauge transition line, joining the open triangles, lies entirely within the broken custodial symmetry phase, as it must from Theorem 1. Figures from ref. [12].
Having computed at a variety of values, the last step is to extrapolate the data to , as shown in Figure 2a. At couplings inside the unbroken phase, the data extrapolates to zero. In the broken phase, extrapolates to a non-zero value. (Of course, on a finite lattice, the order parameter always vanishes for , and what that means numerically is that, without the explicit term breaking term proportional to h, for large enough, eventually the data points would depart from the extrapolated line derived from the lower values, and fall to zero. However, this departure towards zero, in the broken phase, would occur at ever larger values of , as the lattice volume is increased.) One can estimate the point at which the transition from a zero to non-zero value occurs, and this is the transition point. The figure shows some sample extrapolations in SU(2) gauge Higgs theory at several values, on a lattice, with is held fixed at . By this procedure, one arrives at a transition line (green data points) shown in Figure 2b. The upper line is the transition line for spontaneous breaking of the “remnant” symmetry, which is left unfixed in Coulomb gauge. This line lies above the breaking of custodial symmetry determined by the order parameter , in conformity with Theorem 1, i.e., custodial symmetry may be broken where remnant symmetry in an F-gauge (such as Coulomb) is unbroken, but not the other way around. (One should keep in mind that is really the expectation value of a highly non-local quantity, namely , where is the gauge transformation to the F-gauge.)
The gauge invariant order parameter gives us an unambiguous criterion for the breaking of custodial symmetry, which includes, at a minimum, the global center symmetry of the gauge group. We have suggested that the phase of broken custodial symmetry is the Higgs phase, but that only makes sense if there is a genuine physical distinction which corresponds to this criterion. One might object on a priori grounds that the Osterwalder–Seiler theorem [2] (see also Banks and Rabinovici [4], and Fradkin and Shenker [3]) already rules out any such essential distinction, but one should be a little wary of this argument. We already know of examples where there exist distinct phases of many-body systems which are not separated by a thermodynamic transition. One example is the roughening transition in Yang–Mills theory. In the rough phase, the width of flux tubes grows logarithmically with quark–antiquark separation, and the static quark potential contains a term of stringy origin. Neither of these features hold outside the rough phase. Another example is the Kertesz line in the Ising model in an external field [14], which has to do with a percolation transition in the random cluster formulation of the model. The point here is that the analysis of a local observable like the free energy does not rule out non-analytic behavior in non-local observables, and such observables can be physically important. So, our next task is to explain what, precisely, is the physical distinction between the broken and unbroken phases of custodial symmetry, and why these deserve to be called the Higgs and confinement phases, respectively.
3. Separation of Charge Confinement
We return to this question: What is the meaning of the word “confinement”, when there are matter fields in the fundamental representation of the gauge group? We know that both the Higgs and confinement phases have C confinement, since all asymptotic particle states are color neutral in both phases. Yet, there would appear to be some qualitative differences. In the Higgs phase of an SU(2) gauge Higgs theory, as we know from both perturbation theory and experiment:
- There are only Yukawa forces.
- There are no linear Regge trajectories.
- There is no flux tube formation, even as metastable states.
By contrast, in a theory like QCD, there is a linear potential and flux tube formation up to the point of string breaking, and it is the flux tube formation which is responsible for the observed linear Regge trajectories. These features are also expected to arise somewhere in the phase diagram of any gauge theory with matter in the fundamental representation, and they serve to physically distinguish the Higgs from the confinement phase. However, can we make that distinction precise?
Let us start with a (superficially) silly question: what is the binding energy of the proton? Or the J/, or any hadron. Obviously, unlike the hydrogen atom, we cannot ionize a proton, or quarkonium, at least experimentally, and compare the energies of the bound and ionized states. Instead of an isolated quark and antiquark, we instead obtain a bunch of color neutral hadrons (Figure 3) with integer electric charges. (Figure 3 and Figure 4 of course picture a mesonic quark–antiquark state, but the picture is similar for baryonic states.)
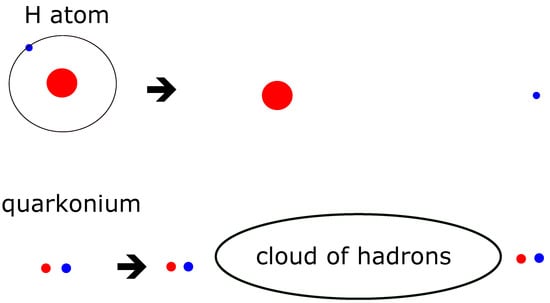
Figure 3.
Unlike Hydrogen, where the ionization energy can be measured experimentally, there is no experimental procedure for creating an “ionized” hadron. There are, however, physical states (see next figure) in the Hilbert space which do correspond to widely separated but interacting quarks.
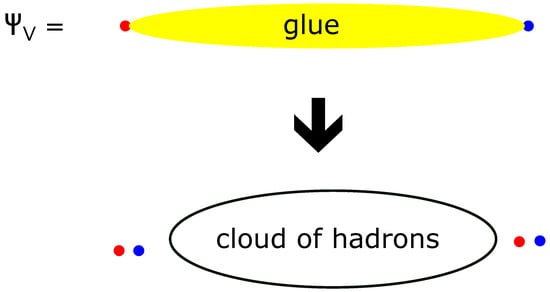
Figure 4.
Decay of a state with widely separated quark-antiquark color charges and fractional electric charge into a set of color neutral hadrons of integer electric charge. The property of S confinement is related to the energy of the color charge separated state , in the limit of color charge separation . Figure from [15].
However, there are, nonetheless, physical states in the Hilbert space which do correspond to isolated (“ionized”) quarks, separated by a large distance. Such states would be difficult to realize experimentally, but they do exist in the Hilbert space. For a system, such states have the form
where is the ground state, are color indices, and is a gauge bi-covariant operator which is a functional of only the gauge field, transforming as
In QCD, there would be a fractional electric charge at , and an opposite fractional electric charge at , with no electric charge in between. Of course, the system would very rapidly decay into integer-charged hadrons (Figure 4). Let be the energy expectation value above the vacuum energy ,
of a state of the form (21).
Definition 1.
A gauge theory has the property of separation-of-charge confinement if the following condition is satisfied:
for any choice of bi-covariant operator , which is a functional of only the gauge field A.
It is crucial, in this definition, that depends only on the gauge field, not on any matter fields, otherwise it would be easy to constuct a V operator that would violate the S condition, e.g.,
In that case,
corresponds to two color singlet (static quark + Higgs) states, only weakly interacting at large separations. Operators V of this kind, which depend on the matter fields, are excluded; the idea is to study the energy of physical states with large separations R of static color charges unscreened by matter fields. This also means that the lower bound on , unlike in pure gauge theories, is not the lowest energy of a state containing a static quark–antiquark pair. It is the lowest energy of such states when color screening by matter is excluded.
The S (separation of charge) condition is a much stronger condition than C confinement, and in our opinion, it is the natural generalization, to gauge theories with matter fields, of the linearly rising static quark potential as a confinement criterion in pure gauge theories. S confinement presumably holds in QCD. What about gauge Higgs theories?
First, we ask whether S confinement exists anywhere in the phase diagram except at (pure gauge theory). The answer is yes. We can show [16] that gauge-Higgs theory is S confining at least in the region
This is based on strong-coupling expansions and a theorem (Gershgorim) in linear algebra. Then, does S confinement hold everywhere in the phase diagram? Here, the answer is no. We can construct V operators which violate the S-confinement criterion when is large enough [17]. This means that there must exist a transition between S and C confinement. The question is whether this transition coincides with the spontaneous breaking of custodial symmetry.
3.1. No S Confinement in the Higgs (Spin Glass) Phase
On the lattice, is determined from the lattice logarithmic time derivative
where the timelike link variables arise after integrating out the static quark fields. In the Higgs phase, according to the previous theorems, there is always an F-gauge in which . This also implies . Let be the gauge transformation to that gauge, and choose
Then, evaluating in that F-gauge, we have
which demonstrates the absence of S confinement in the spin glass phase.
Let us define
Here, the operators which act on the vacuum in both the charged and neutral states are fully gauge invariant; the difference is in how that invariance is implemented in each case. In the neutral state, gauge invariance is imposed locally by color screening, with the color charge of the quarks neutralized by the scalar field. By contrast, gauge invariance in the charged state is implemented via an intrinsically non-local operator, the V operator, analogous to dressing an electron/positron pair with an electric dipole field, or running a color electric flux tube between a quark/antiquark pair.
Now consider, in (31), taking the limit. This leaves an isolated charged fermion at in the charged state, and a neutral hadron at in the neutral state. Let and evaluate the overlap in the Higgs phase
This means that there is no essential distinction between the states that we have labeled as “charged” and “neutral.” That is a consequence of broken global gauge symmetry, with the corollary that the vacuum is not an eigenstate of zero charge, as discussed further below.
An isolated color charged particle is the source of a long-range color electric field, and this is ruled out if the theory is massive. In the absence of a massless sector, both the Higgs and confinement phases are C confining, and we have just established that the Higgs phase is not S confining. So, confinement in the Higgs phase is only C confinement.
3.2. The Symmetric Phase
This time, we have
where
Since custodial symmetry is unbroken for gauge configurations drawn from the probability distribution , it follows that for such configurations, in the symmetric phase at ,
Therefore
Note that this result holds for all V operators (all isolated charges) in the symmetric phase, independent of any gauge choice. This is a consequence of the invariance of the ground state, and it means that in the symmetric phase, unlike in the broken phase, there is a sharp distinction between charged states and color neutral states.
Expanding on this point, consider the limit in (31), with states expressed in Schrödinger representation
An example of is , where is the gauge transformation to an F-gauge. Then, although is a physical state and therefore satisfies the Gauss Law constraint, i.e., is invariant under infinitesimal gauge transformations, it transforms covariantly under the global subgroup of the gauge group. Explicitly, under a global gauge transformation
we have, in the symmetric phase,
Under the same transformation, is invariant. It follows that in the symmetric phase
and of course, this is true for the overlap of any state which transforms covariantly under with any state invariant under this global group. This really serves, in the symmetric phase, as a definition of what we mean by a physical state containing an isolated charge. These are physical states which transform covariantly under the subgroup, and are therefore orthogonal to all neutral states, which are invariant under all elements of the gauge group. Again, we stress that this sharp distinction between states with isolated charge, and neutral states, is a consequence of unbroken symmetry, and the invariance of the ground state.
Things are different in the broken (Higgs, spin glass) phase. In this phase, according to Theorem 2, one can always find an F-gauge where
However, under a global transformation
so of course (41) implies that cannot be invariant under the global subgroup; i.e., the global center symmetry is spontaneously broken. It follows that states and are not necessarily orthogonal, even though the operators which create these states have different transformation properties. In the example shown above, choosing , we have
and there are always F-gauges, in the Higgs phase, where the right-hand side is non-zero. (There are also F-gauges in the Higgs phase where , but this simply means that where this is true, the operator , operating on the vacuum, creates a state of infinite energy, and is for this reason orthogonal to the vacuum. For further discussion of this point, cf. [12].) The conclusion is that in the broken phase, unlike the symmetric phase, there is no unambiguous distinction between a state with an isolated color charge, and a color neutral state.
States such as , in the unbroken phase in the limit, may be of either finite or infinite energy. If there are no charged states of finite energy above the vacuum energy, then the system is in an S confinement phase. If, on the other hand, there do exist charged finite energy states, orthogonal to all neutral states, then states of this kind will necessarily appear in the spectrum. The system cannot then be in a C confining phase, where there are no charged particles in the spectrum. Nor can it be in an S confining phase, where isolated charges are all states of infinite energy. The remaining possibility is a massless phase. So, the phase of unbroken custodial symmetry is either S confining, or massless. This is consistent with the fact that in all F-gauges in the symmetric phase, so there exists no sensible perturbative expansion of around a non-zero expectation value, and no Brout–Englert–Higgs mechanism in the symmetric phase, at least not one that can be seen in any physical F-gauge.
In dimensions, an SU(2) gauge Higgs theory (Higgs in the fundamental representation) does not have a massless phase. In dimensions, there is such a phase, isolated from the confinement and Higgs phases by thermodynamic transitions, and it has recently been checked by Ward [18] that throughout the massless phase and across the massless to confinement transition as we have predicted. The massless to Higgs transition, on the other hand, is a custodial symmetry breaking transition, and it is also seen that the order parameter becomes finite across this transition line, as expected.
The conclusion is that the spin glass phase is a C confinement (Higgs) phase, while the phase of unbroken custodial symmetry may be either a massless or an S confining phase. In the absence of a massless phase, as in SU(2) gauge Higgs theory in dimensions, the transition from the symmetric to the spin glass phase coincides with the transition from S confinement to C confinement.
3.3. Examples
It is useful to check numerically, in some examples, that
- The charged and neutral states defined in (31) are orthogonal in the confinement phase, and have finite overlap in the Higgs phase, as a consequence of unbroken vs. broken symmetry;
- The energy of any charged state diverges with charge separation in the confinement phase, regardless of , but it is always possible to find operators , such that the resulting state has finite energy in the same limit in the Higgs phase.
This will be illustrated in SU(3) gauge Higgs theory. However, before proceeding to those results, let us look at the simplest possible example of a state with an isolated charge, namely pure QED with a static charge (and no dynamical charges) at the point . The lowest energy state of this kind was written down long ago by Dirac [19]:
where
It is easy to check that satisfies the Gauss Law. However, let be an arbitrary U(1) gauge transformation, and we separate out the zero mode . Then,
and therefore
So, transforms covariantly under the global center subgroup (which is U(1)) of the U(1) gauge group; this is the hallmark of a physical state, in an infinite volume, containing an isolated charge. The vacuum state is invariant under such transformations, simply because it depends only on the gauge field, which is itself invariant under those global transformations. This means that is a charged state, and of course it is finite energy (apart from the usual UV divergence which is regulated on the lattice).
The operator is an example of what we have elsewhere [17] called a “pseudomatter” field; this is a field which transforms like a matter field in the fundamental representation, except that it is invariant under transformations in the global center subgroup of the gauge group. Any gauge transformation to an F-gauge can be decomposed into N pseudomatter fields , and vice versa:
In particular, the operator defined earlier is precisely the gauge transformation to Coulomb gauge in an abelian theory. This operator dresses a static charge with a surrounding Coulomb field. Another example, in an SU(N) lattice gauge theory, is any eigenstate of the covariant Laplacian operator
where
The use of low-lying eigenstates of the lattice Laplacian operator is essential in the construction of the Laplacian–Landau gauge introduced by Vink and Weise [13], which is free of Gribov copies.
Now, let us consider an SU(3) lattice gauge Higgs theory, with action
and we impose for simplicity a unimodular constraint on the Higgs field. Let us define
where
and where the is a pseudomatter operator corresponding to the eigenstate of the lattice Laplacian operator with the smallest eigenvalue. The energy expectation values of the charged and neutral states are then given by Equation (28), using the operators in (53) above, and these we have computed numerically in [15]. The results obtained in the confinement phase at , and in the Higgs phase at are shown in Figure 5. Note that in these plots, taken from [15], the charged and neutral states are labeled
for reasons given in that reference.
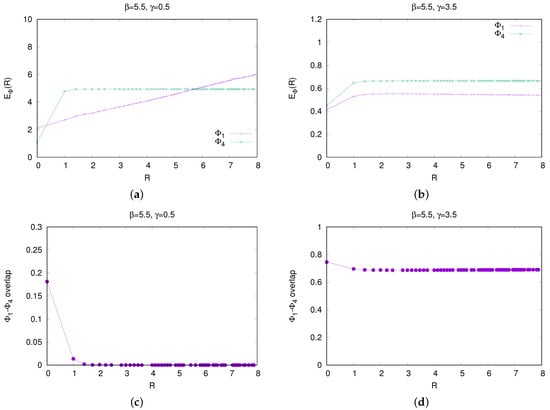
Figure 5.
Contrasting properties of charged () and neutral () fermion–antifermion states in the confinement and Higgs phases of an SU(3) gauge Higgs theory. (a) Energy expectation value vs. separation R of the and states in the confined phase, . (b) Same as subfigure (a), but in the Higgs phase at . (c) Overlap vs. R of normalized charge () and neutral () states in the confined phase, at . (d) Same as subfigure (c), but in the Higgs phase at . Figures from ref. [15].
These plots illustrate the statements made about the distinction between different types of confinement in the Higgs and confinement phases. The confined phase is S confining. Hence, the energy of any charged state, created with any operator, will diverge at quark separation . The energy of a neutral state (in this case, the charges of the quarks are neutralized by the Higgs fields), will be finite in the same limit. This is all clearly seen in Figure 5a. The overlap of charged and neutral states vanishes in the confinement phase (a prediction of Equation (36)), as we see in Figure 5c. Things are different in the Higgs phase. In this case, the energies of both the charged and neutral states go to a finite constant as , as seen in Figure 5b, meaning that the Higgs phase is not a phase of S confinement, and in Figure 5d, we see that the overlap between the two states is substantial (this time a prediction of Equation (32)) in the same limit, due to the fact that the global center subgroup of the SU(3) gauge group is spontaneously broken, and there is no longer any essential distinction between charged and neutral states, so long as those states satisfy the required Gauss Law constraint.
3.4. QCD as a Symmetric Phase
Since our discussion has focused on gauge Higgs theory, it is natural to ask how it applies to a theory like QCD, where the matter in the fundamental representation of the gauge group is fermionic, and we would expect that the global center subgroup of the gauge group is unbroken. Although this question has not yet been addressed numerically, we believe that it could be addressed in the following way: After integrating out the fermionic degrees of freedom, one ends up with a fermionic determinant, which in turn can be expressed in terms of pseudofermion fields, which are in fact scalar fields in the fundamental representation. This is how QCD can be simulated numerically, via the hybrid Monte Carlo algorithm. The pseudofermion action is, of course, non-local, but apart from computation time, we see no difficulty in principle in applying the numerical approach outlined in Section 2.2 to QCD, where we would expect in the appropriate limit. If so, then according to our criteria, QCD is in the phase of S confinement; i.e., the confinement phase.
4. Conclusions
In this article, we have argued that, contrary to the general consensus, there really is an essential distinction to be made between the confinement and Higgs phases of a gauge Higgs theory, and that these phases are distinguished by confinement type, and by the broken or unbroken realization of a global center subgroup of the gauge group. In this respect, which is not in contradiction to Elitzur’s theorem, the Higgs phase really is a phase of spontaneously broken gauge symmetry, and this breaking is detected by a gauge invariant order parameter closely analogous to the Edwards–Anderson order parameter for a spin glass. In fact, we believe that it is sensible to view the Higgs phase as a kind of spin glass phase of a gauge Higgs theory.
The general consensus is also that the word “confinement,” in a gauge theory with matter in the fundamental representation, can only mean that the asymptotic particle spectrum is color neutral, which is a property we call C (color) confinement. This property holds in both the Higgs and confinement phases, but not, of course, in a massless phase. However, we have shown that there is a stronger variety of confinement which exists in the confinement phase, and which distinguishes that phase physically from the Higgs phase. This is the property of S (separation of charge) confinement, associated with the formation of metastable color electric flux tubes, and it is the natural extension of confinement criteria in a pure gauge theory to theories with matter fields. As outlined here, and in more detail in ref. [12], the transition line between S and C confinement coincides with the transition from the unbroken to the broken phase of the global center subgroup of local gauge symmetry.
Author Contributions
Conceptualization, methodology, investigation, software, writing—review and editing, J.G. and K.M.; writing—original draft preparation, funding aquisition, J.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research is supported by the U.S. Department of Energy under Grant No. DE-SC0013682.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elitzur, S. Impossibility of Spontaneously Breaking Local Symmetries. Phys. Rev. 1975, D12, 3978–3982. [Google Scholar] [CrossRef]
- Osterwalder, K.; Seiler, E. Gauge Field Theories on the Lattice. Ann. Phys. 1978, 110, 440. [Google Scholar] [CrossRef]
- Fradkin, E.H.; Shenker, S.H. Phase Diagrams of Lattice Gauge Theories with Higgs Fields. Phys. Rev. 1979, D19, 3682–3697. [Google Scholar] [CrossRef]
- Banks, T.; Rabinovici, E. Finite Temperature Behavior of the Lattice Abelian Higgs Model. Nucl. Phys. B 1979, 160, 349–379. [Google Scholar] [CrossRef]
- Frohlich, J.; Morchio, G.; Strocchi, F. Higgs phenomenon without a symmetry breaking order parameter. Nucl. Phys. 1981, B190, 553–582. [Google Scholar] [CrossRef]
- Hooft, G.T. Which Topological Features of a Gauge Theory Can Be Responsible for Permanent Confinement? NATO Sci. Ser. B 1980, 59, 117–133. [Google Scholar] [CrossRef]
- Duncan, A. The Conceptual Framework of Quantum Field Theory; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Kibble, T.W.B. Spontaneous symmetry breaking in gauge theories. Phil. Trans. Roy. Soc. Lond. A 2014, 373, 20140033. [Google Scholar] [CrossRef]
- Caudy, W.; Greensite, J. On the ambiguity of spontaneously broken gauge symmetry. Phys. Rev. 2008, D78, 025018. [Google Scholar] [CrossRef]
- Guendelman, E.I. Zero Energy Gauge Fields and the Phases of a Gauge Theory. Int. J. Mod. Phys. A 1990, 5, 2783–2798. [Google Scholar] [CrossRef]
- Edwards, S.F.; Anderson, P.W. Theory of spin glasses. J. Phys. F Met. Phys. 1975, 5, 965–974. [Google Scholar] [CrossRef]
- Greensite, J.; Matsuyama, K. Higgs phase as a spin glass and the transition between varieties of confinement. Phys. Rev. D 2020, 101, 054508. [Google Scholar] [CrossRef]
- Vink, J.C.; Wiese, U.J. Gauge fixing on the lattice without ambiguity. Phys. Lett. 1992, B289, 122–126. [Google Scholar] [CrossRef][Green Version]
- Kertesz, J. Existence of weak singularities when going around the liquid-gas critical point. Physica 1989, A161, 58–62. [Google Scholar] [CrossRef]
- Greensite, J. Excitations of elementary fermions in gauge Higgs theories. Phys. Rev. D 2020, 102, 054504. [Google Scholar] [CrossRef]
- Greensite, J.; Matsuyama, K. What symmetry is actually broken in the Higgs phase of a gauge-Higgs theory? Phys. Rev. 2018, D98, 074504. [Google Scholar] [CrossRef]
- Greensite, J.; Matsuyama, K. Confinement criterion for gauge theories with matter fields. Phys. Rev. 2017, D96, 094510. [Google Scholar] [CrossRef]
- Ward, D. The Higgs phase as a spin glass phase in D = 5 dimensional SU(2) gauge Higgs theory. arXiv 2021, arXiv:2112.12220. [Google Scholar]
- Dirac, P.A.M. Gauge invariant formulation of quantum electrodynamics. Can. J. Phys. 1955, 33, 650. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).