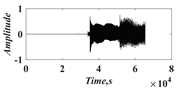
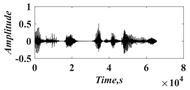
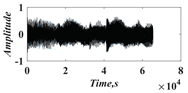
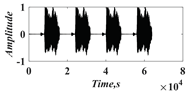
1. Introduction
With the rapid development of the internet, wireless voice communication technology was widely applied in real-life, and in the process of data transmission there is the risk of information leakage; therefore, audio information encryption research is of great significance. Many traditional encryption algorithms are widely used in audio encryption and achieved good encryption results, such as Advanced Encryption Standard (AES) [
1,
2], Data Encryption Standard (DES) [
3,
4] and S-box algorithm [
5,
6], etc., Although these algorithms have perfect encryption technology, some algorithms still have some defects and cannot fully ensure the security of encryption. The main disadvantage of AES is that it uses a static S-box in the whole algorithm, which damages the security of AES and may be subject to different algebraic attacks. Therefore, to overcome this shortcoming, Amandeep S. [
7] and others proposed a dynamic S-box AES encryption algorithm. Because the chaotic system has the characteristics of ergodicity, initial value sensitivity, and strong pseudo-random sequence, many scholars proposed to encrypt plaintext information by combining the AES algorithm with the chaotic system, and the results were satisfactory. Alireza A. [
8] et al. Proposed to encrypt the image by combining the chaotic sequence with the improved AES algorithm. The experimental results show that this encryption method reduces the time complexity of the algorithm, increases the keyspace of the algorithm, and significantly improves security. The chaotic system has made an important contribution to the encryption scheme. Therefore, in recent years, chaotic systems were widely used in encryption algorithms [
9,
10,
11]. Abdelfatah R.I. [
9] proposed a multichaotic mapping audio encryption scheme, and the novel features of this algorithm are as follows: adaptive scrambling and cryptographic feedback are used to realize global scrambling and deep diffusion, respectively. At the same time, four different audio encryption technologies are combined in the same scheme to make it more secure. Shah D. et al. [
10] proposed that Mobius transform was used as the source to generate a strong S-box substitution network and Henon chaotic map to perform pixel-level displacement. However, the Henon chaotic map has a low dimension, and its keyspace is limited. To solve this problem, Zhao H. et al. [
11] proposed an adaptive symmetric Henon chaotic map, which has the characteristics of wide parameter range and high complexity. Therefore, it has a larger keyspace and is more suitable for encryption algorithms. Farsana F.J. et al. [
12] introduced a modified discrete Henon map, which can weaken the correlation between adjacent samples. At the same time, an improved super-Lorenz chaotic system was proposed to iterate and fill the silent period in speech conversation, and a dynamic key flow mechanism was designed to enhance the correlation between Ming and ciphertext. Some audio encryption schemes meet the security requirements of the design by enhancing the complexity of the algorithm but increasing the difficulty of data processing and the time of audio encryption, such as Naskar P.K. et al. [
13] proposed an audio encryption algorithm based on DNA Encoding and Channel Shuffling, which overcomes the inefficient algorithm of multiple rounds. However, due to the adoption of an encryption scheme based on traditional mathematical methods, the timeliness of the encryption algorithm is reduced. Of course, in the existing research, there is no lack of many encryption algorithms that were decoded. Saeed N. et al. [
14] found the loopholes through simulation, obtained the key of the algorithm, and decoded an image encryption algorithm related to chaotic mapping. This is a good example.
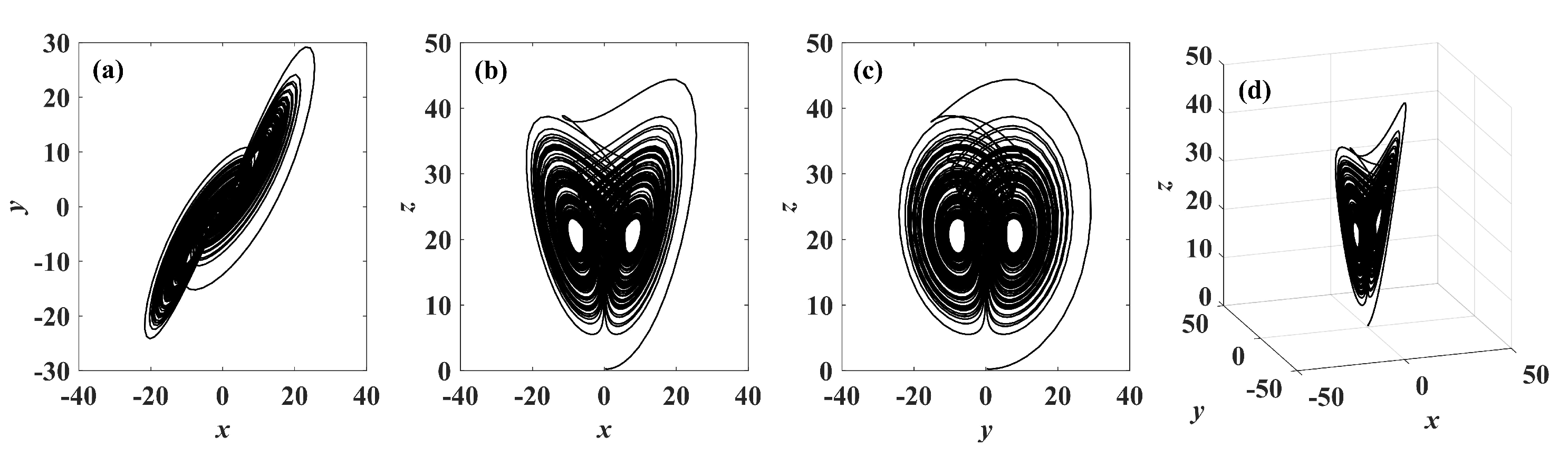
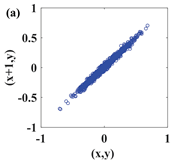
A memristor is a kind of nonlinear element with memory function and nanoscale size. It can be used as a nonlinear part of a chaotic system and has rich dynamic behaviors, which significantly improves the randomness and complexity of chaotic system signals [
15]. Because the memristor is a controllable nonlinear device, in some systems, the chaotic attractors of the even and singular vortices can be obtained only by changing the parameters of the memristor. Therefore, the memristor chaotic system can provide a complex, variable, and reliable pseudo-random cipher generator for the encryption algorithm and can effectively avoid the degradation of the chaotic system dynamics.
Bao B.C. [
16] designed and studied a chaotic circuit based on memristor. The active double-ended memristor circuit is used to replace Chua’s diode. The circuit is directly extended from Chua’s oscillator to obtain a new chaotic system. The results show that the introduction of memristor makes the dynamic behavior of the system more complex. Ma Xujiong [
17] proposed a chaotic circuit with memristor, mode resistance capacitor, and linear inductor established the dimensionless mathematical model of the circuit and found that 19 different types of chaotic attractors will be generated in the circuit. Compared with that of the traditional chaotic attractors, the circuit has rich dynamic characteristics and good application prospects in the field of secure communication. Chen J.J. [
18] designed an image encryption algorithm of a new hyperchaotic system based on memristor, which can produce complex chaotic attractors. The experimental results show that the circuit simulation and numerical simulation results of the system always proved the feasibility, effectiveness, and ability to produce chaotic behavior of the system. Combined with the proposed image encryption scheme, the security analysis shows that the scheme is not easy to crack and can resist all kinds of attacks. Peng G. [
19] proposed a new modal memristor chaotic system, realized its circuit simulation, and applied it to image encryption. The application scope of the memristor is far beyond these. For example, Kamal F.M. [
20] designed a new fractional nonautonomous chaotic circuit model by introducing a fractional element memristor circuit; Akgul A. [
21] proposed a new fractional-order chaotic circuit with memristor and linear inductor. To show the application advantages of the proposed chaotic system, it also realized the synchronization of fractional-order chaotic system and applied it to secure communication system for the first time. In addition, in their latest research, Yan D. [
22] also proposed a chaotic attractor based on the combination of fractal transformation and memristor chaotic system. The main advantage of the system is that multiple rolling attractors and extended chaotic attractors can be generated only by modifying system parameters, and various circular chaotic attractors can be generated in combination with classical Julia fractal. Its attractor has complex dynamic behavior [
23], which is very suitable for all kinds of secure communication fields.
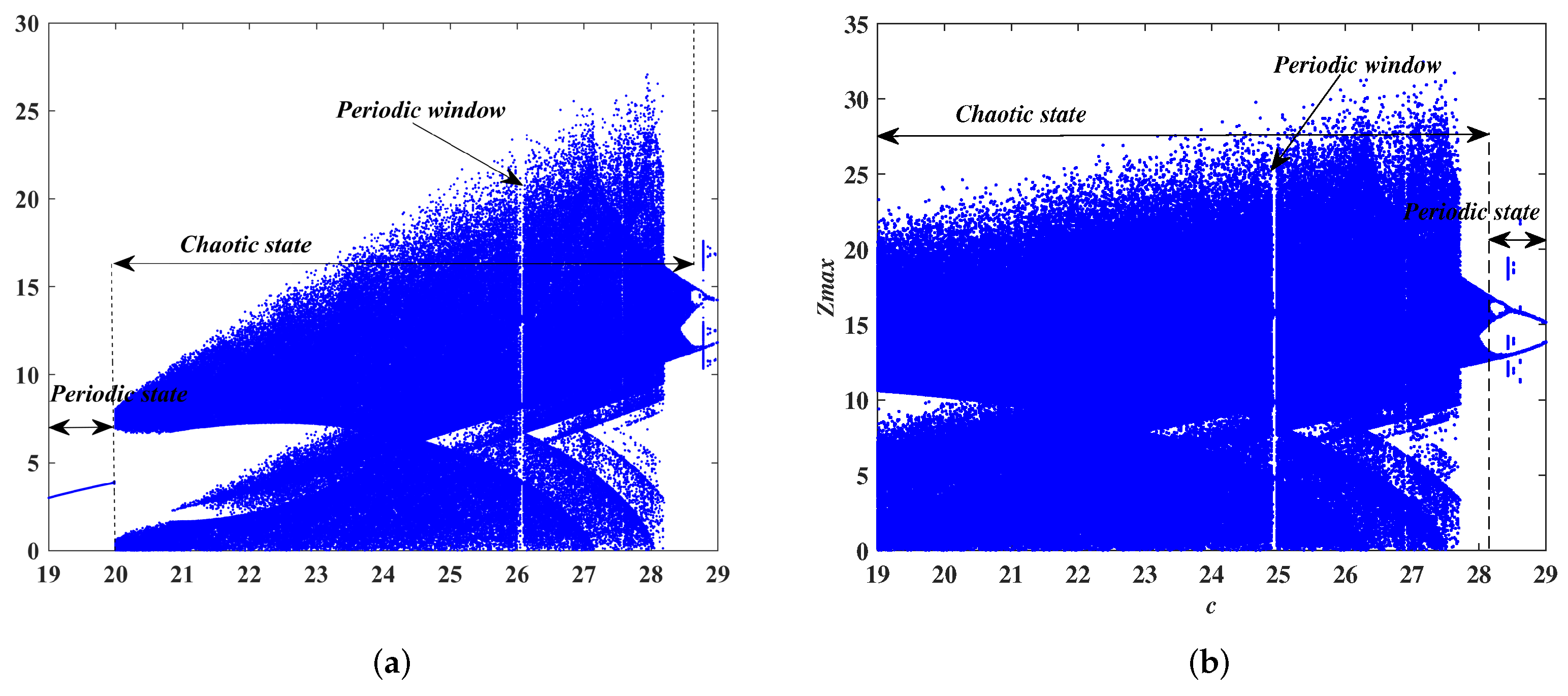
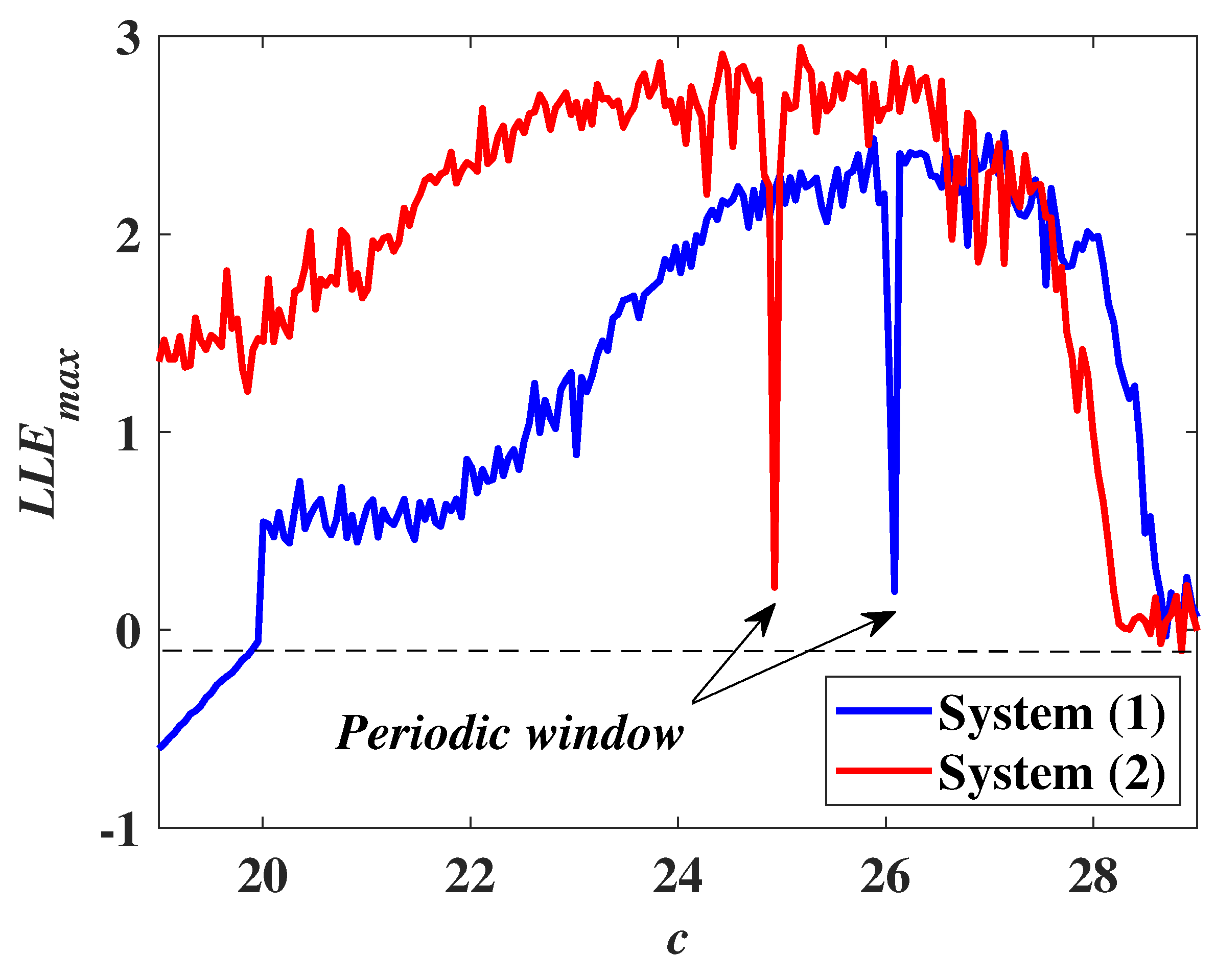
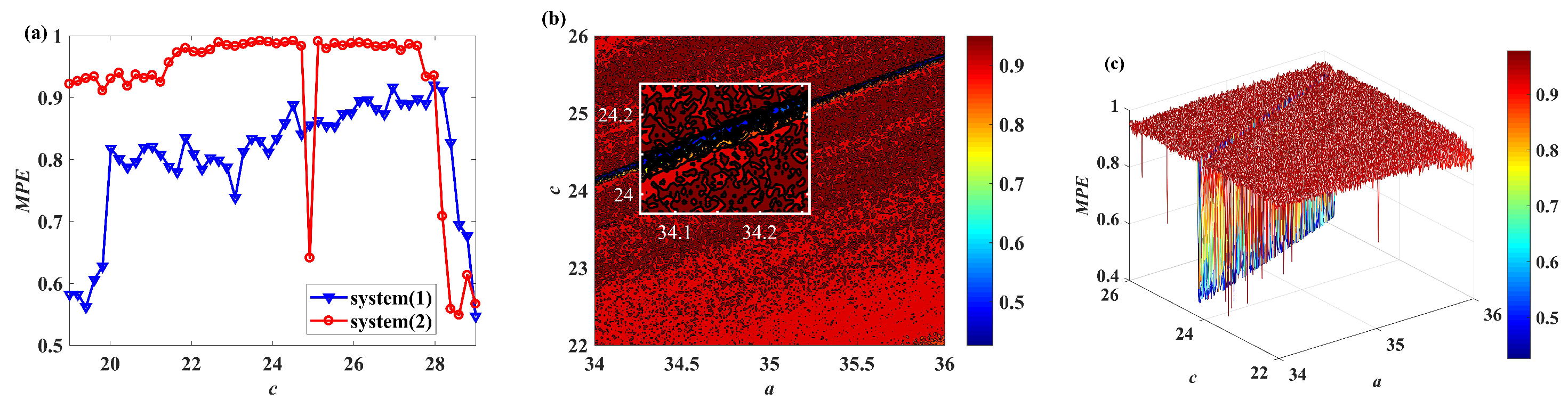
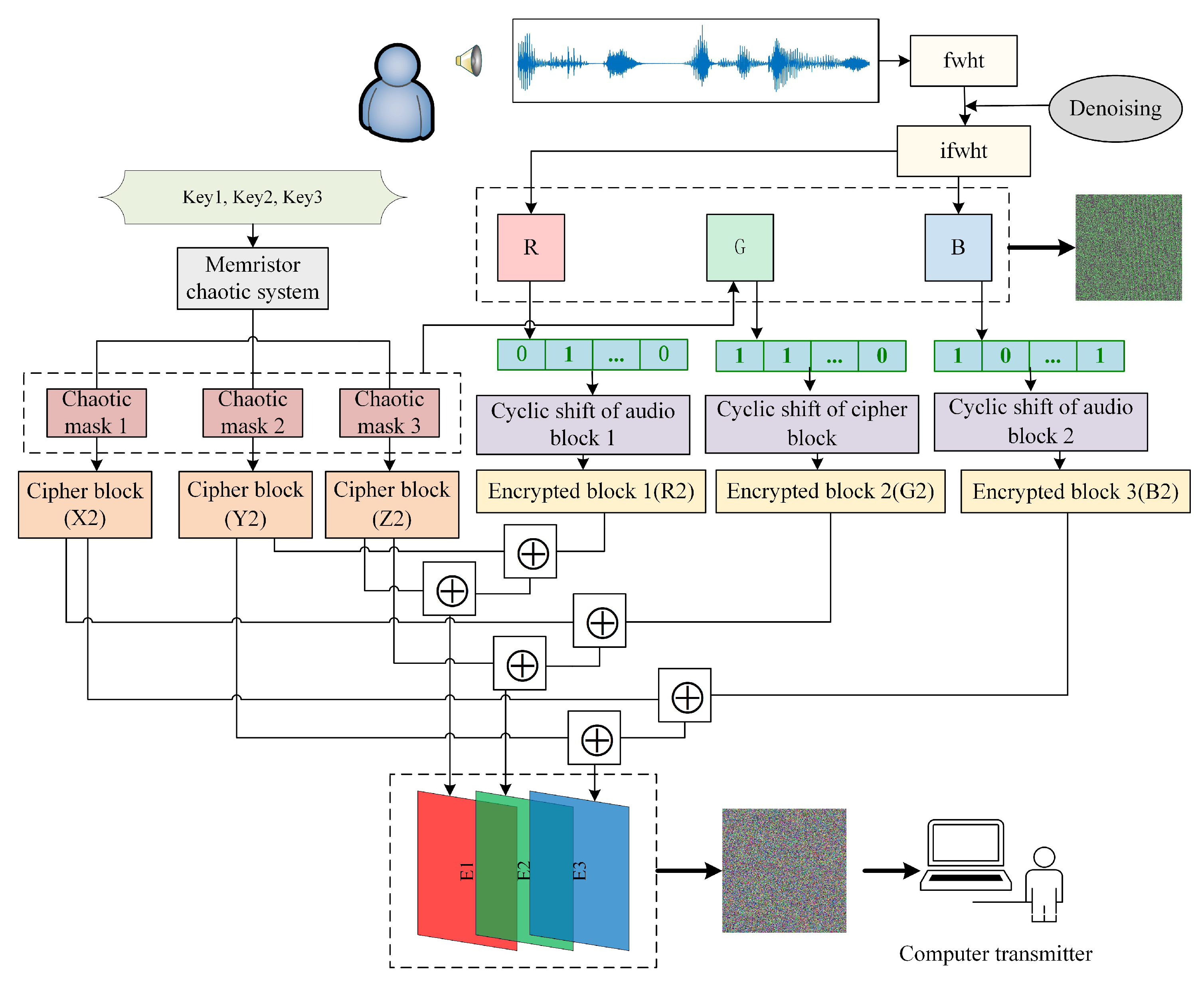
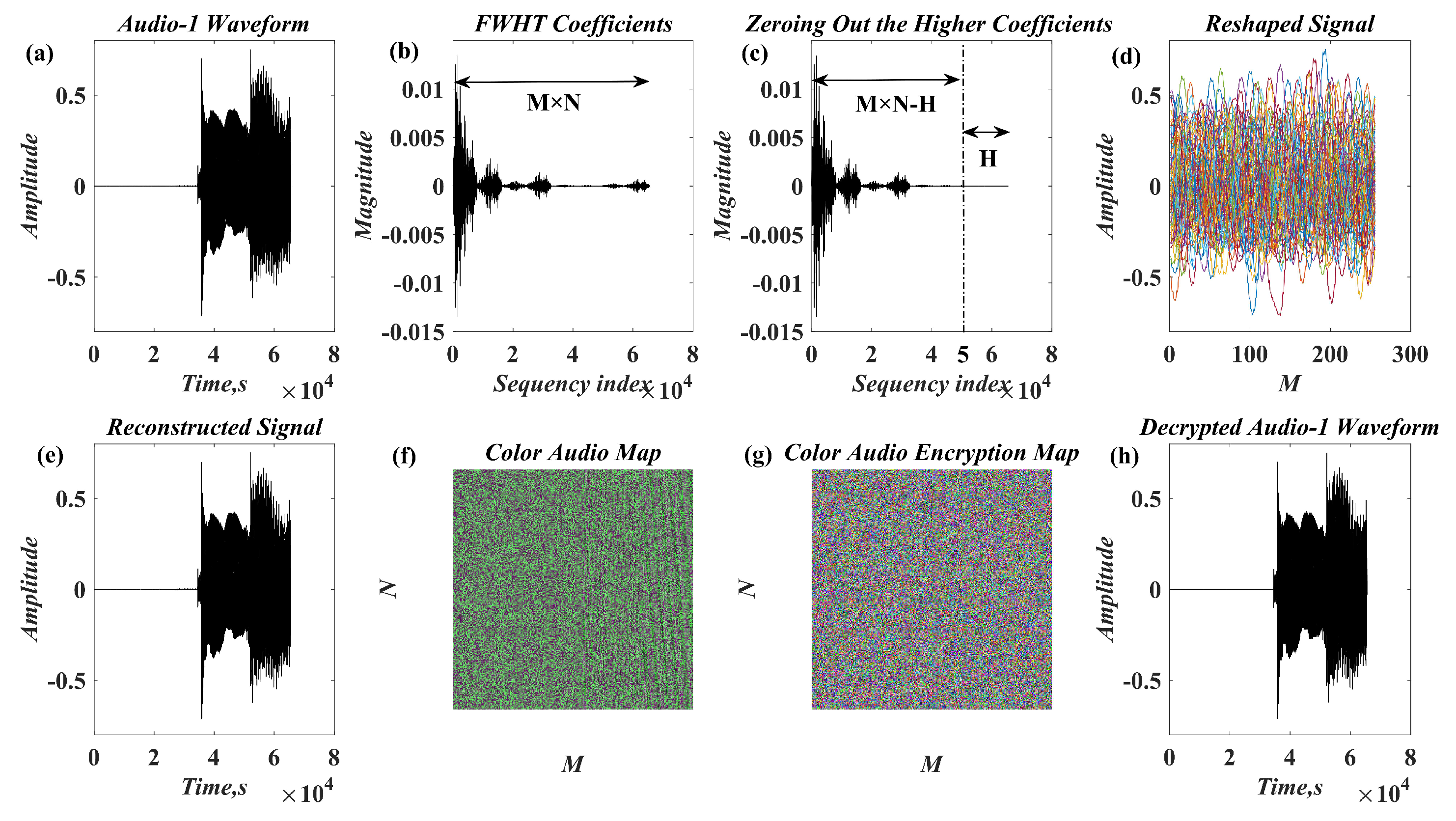
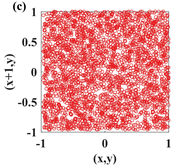
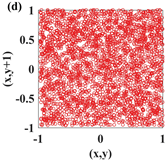
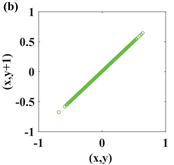
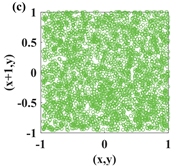
In recent years, with the in-depth study of memristor chaotic system, it is more and more widely used in encryption algorithms. To improve the security and efficiency of digital speech encryption algorithm, an audio encryption algorithm based on Chen memristor chaotic system is proposed in this paper. To further improve the security of the traditional scrambling and diffusion encryption framework, a special audio encryption method is proposed. The Fast Walsh–Hadamard Transform is used for adaptive compression, denoising, and reconstruction of the audio signal. The high complexity chaotic mask block is used as the filling layer, and the dual-channel audio signal is cleverly transformed into a color audio image. To make the encryption algorithm highly correlated with plaintext audio, the audio’s stored byte information is taken as the parameter of interactive channel shuffling operation, and the cipher block is used for overlapping diffusion encryption to obtain ciphertext audio. Ciphertext audio is transmitted in the form of a noise image so that the algorithm has two protective barriers, which can effectively reduce the risk of ciphertext audio information being intercepted and cracked in the transmission process. In addition, compared with that of Chen chaotic system, the Chen memristor chaotic system has a larger bifurcation interval in the range of parameter c, which means that it has a larger keyspace and can resist violent attacks. The encryption scheme not only solves the security problems of simple scrambling and diffusion operation but also improves the efficiency of the encryption algorithm.
Our contributions are as follows:
(1) The Chen memristor chaotic system has a larger chaotic parameter interval and can produce pseudo-random sequences with high complexity, which is more difficult to predict than general chaotic signals.
(2) A method of skillfully transforming the audio signals into image information is proposed.
(3) We propose an audio encryption algorithm based on interactive channel shuffling and overlapping diffusion. Experimental simulation shows that the algorithm has high security.
The rest of this paper is organized as follows: in
Section 2, a new memristor chaotic system model is proposed and the correlation dynamics are analyzed; in
Section 3, an encryption algorithm for compressing and denoising audio signals and transforming them into image information is proposed. In the algorithm, interactive channel shuffling and overlapping diffusion are also designed; in
Section 4, the experimental simulation and security analysis of the encryption algorithm is carried out; and
Section 5 summarizes and discusses the full text.
5. Conclusions
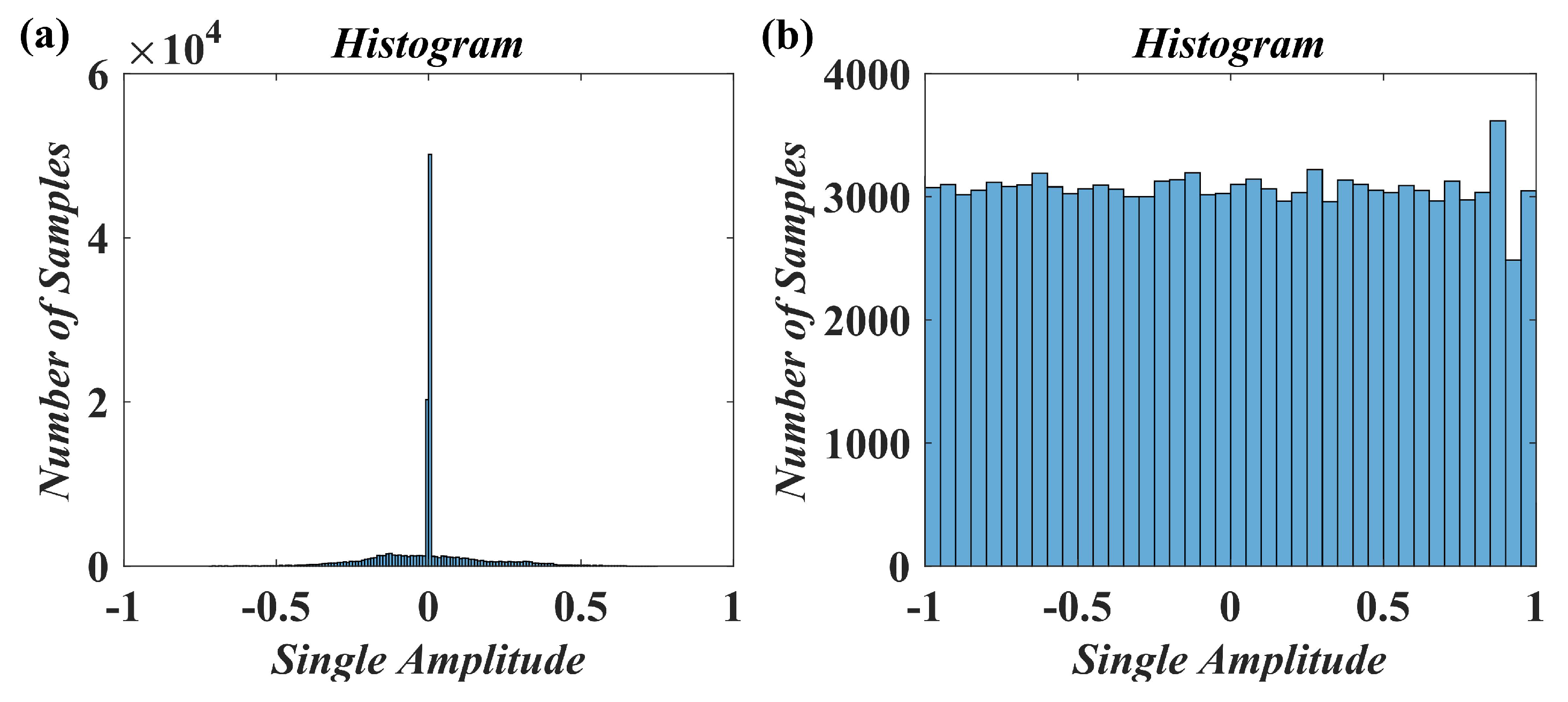
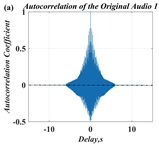
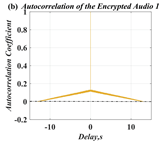
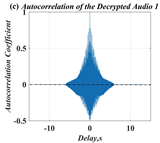
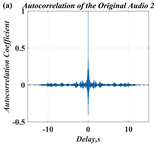
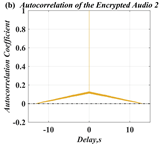
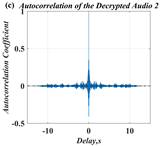
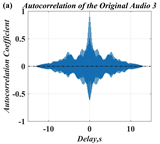
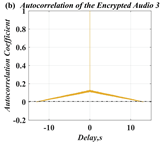
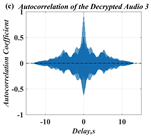
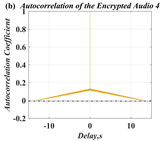
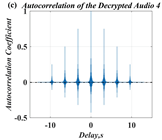
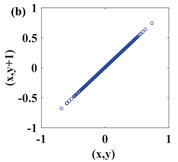
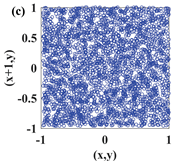
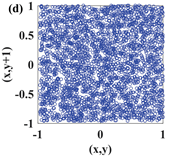
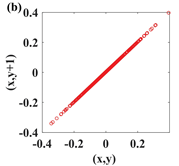
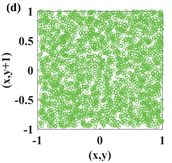
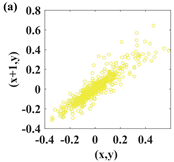
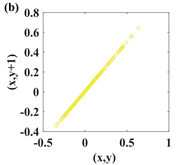
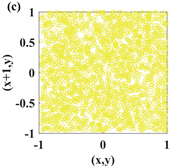
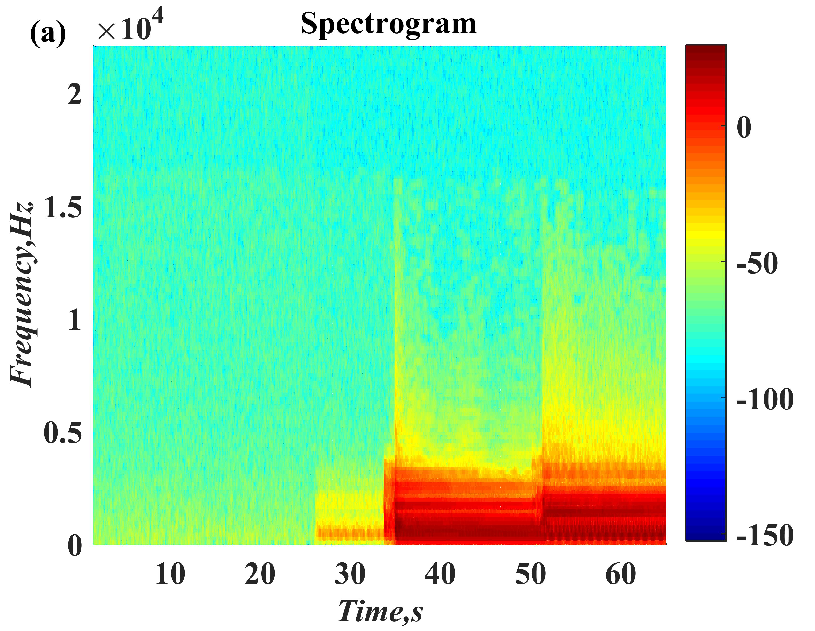
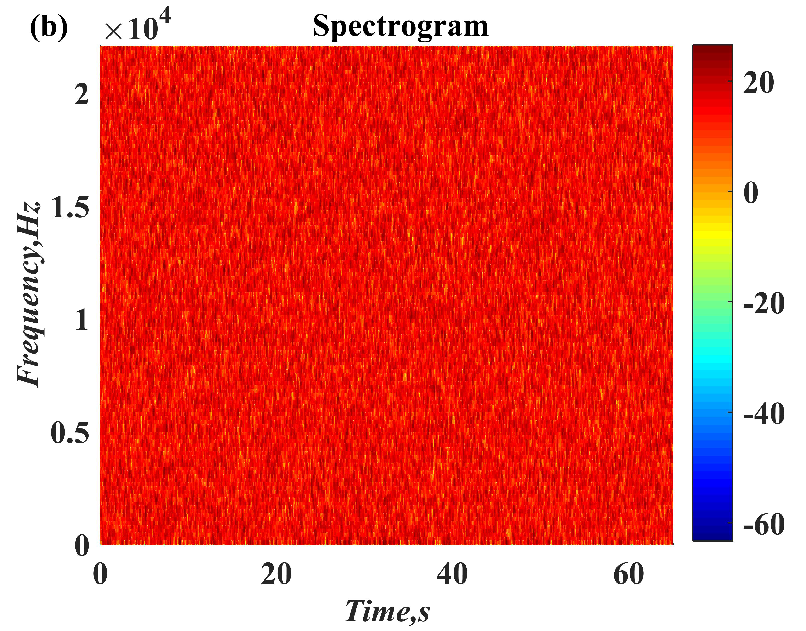
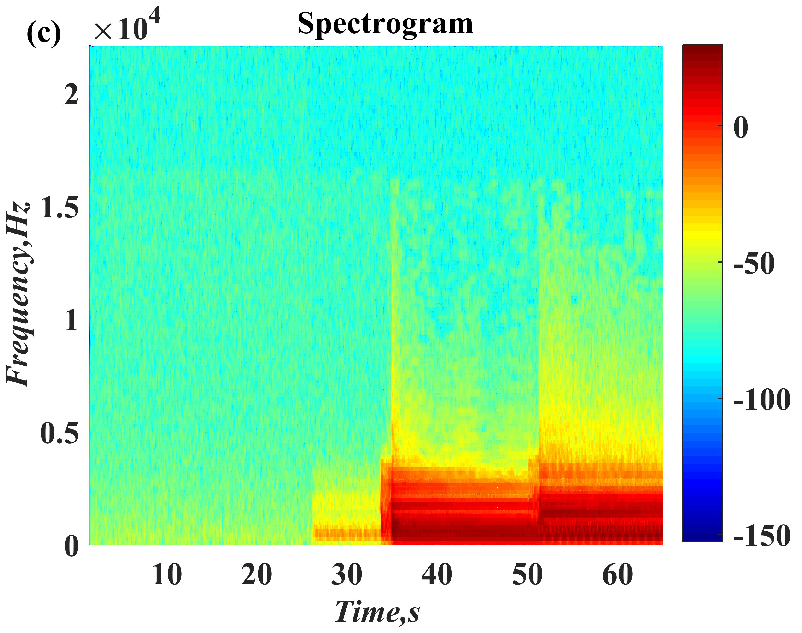
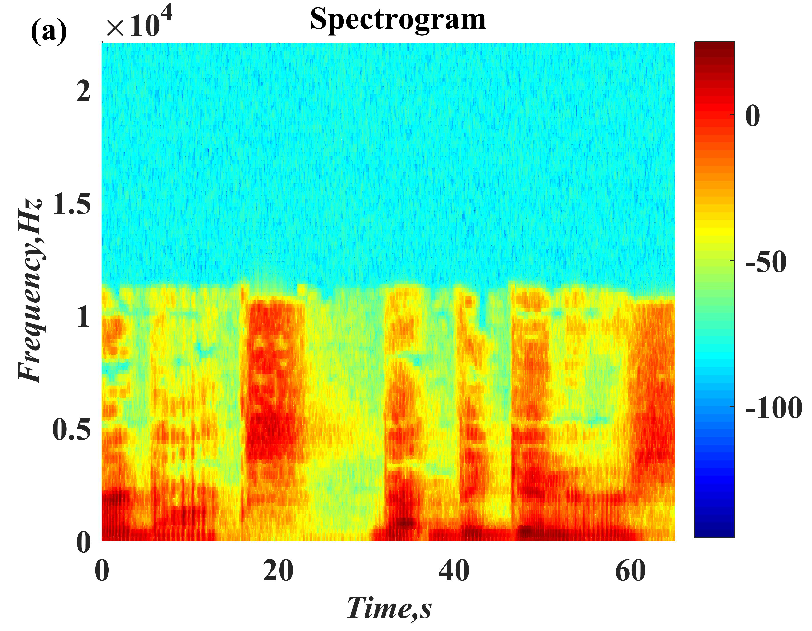
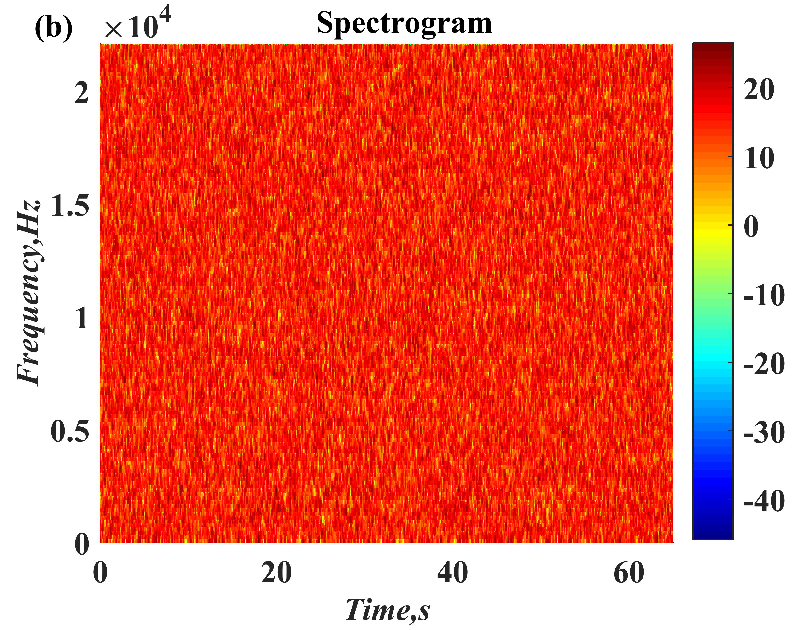
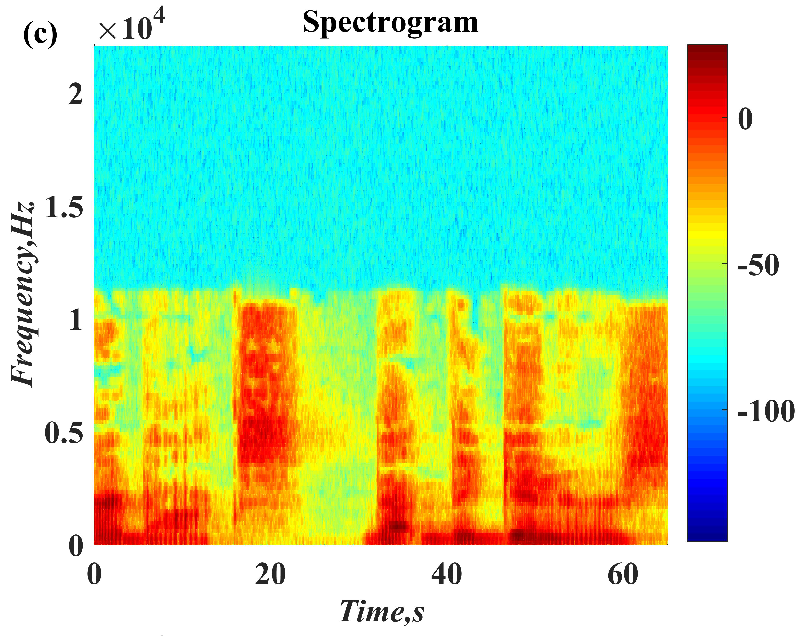
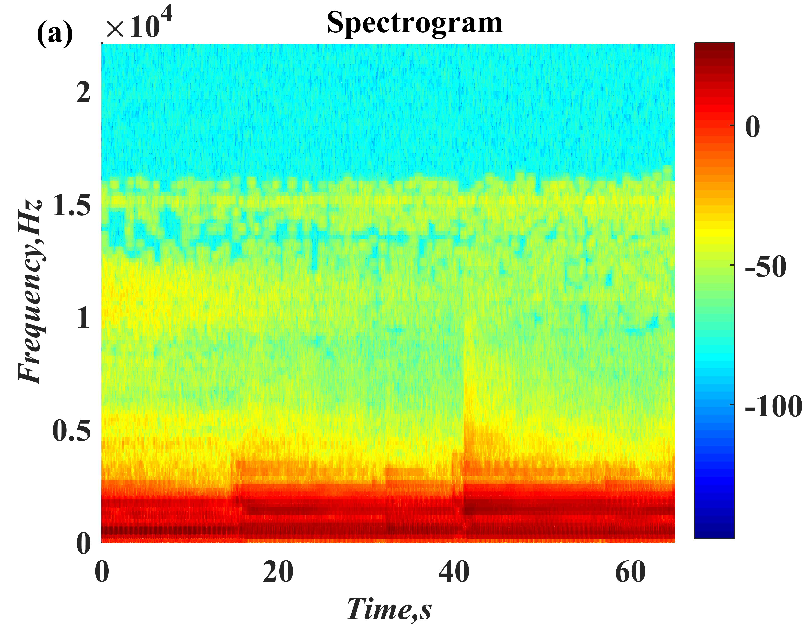
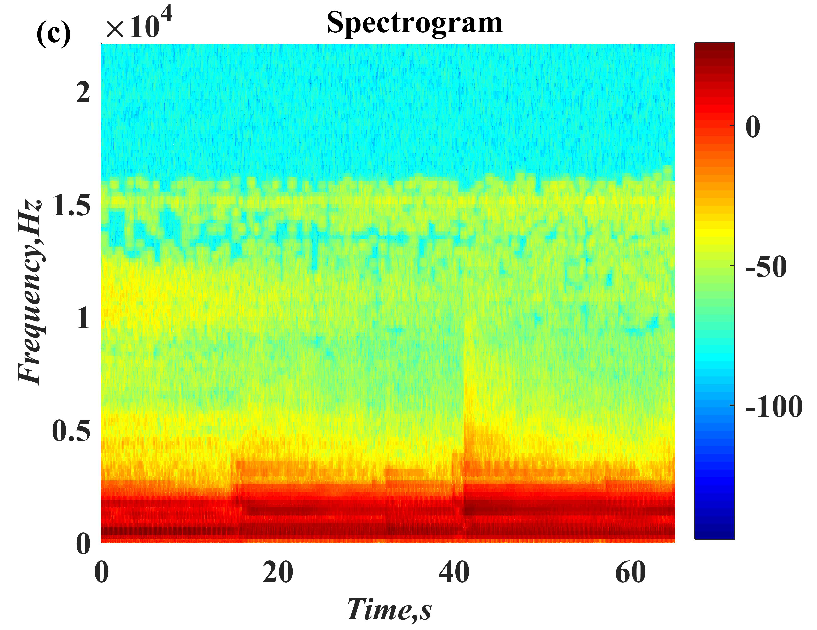
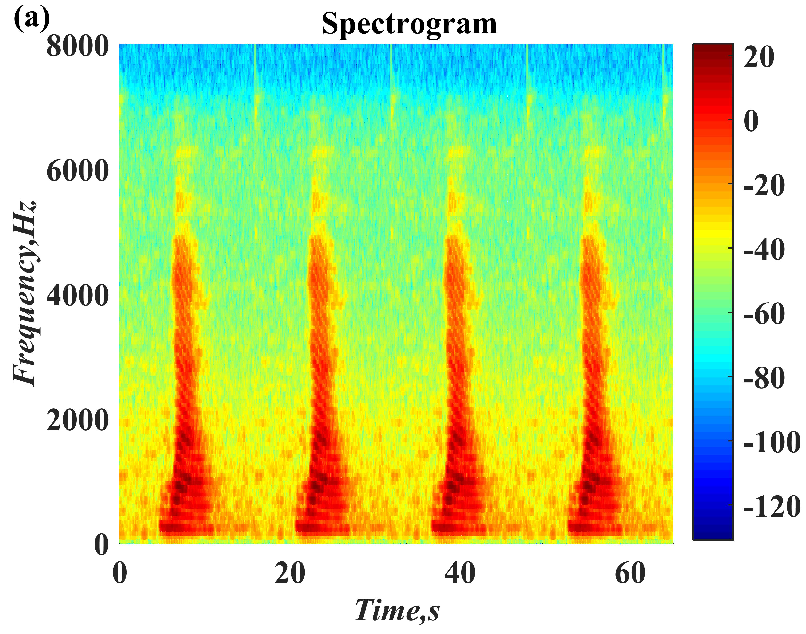
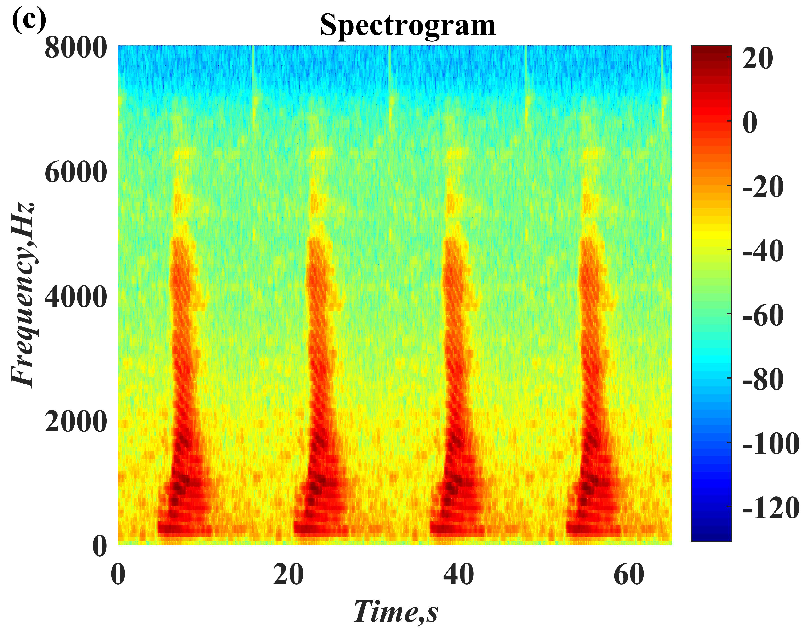
In this paper, a digital audio encryption scheme based on a new Chen memristor chaotic system is proposed to resist various traditional signal attacks. Chen memristor chaotic system based on magnetron titanium dioxide memristor enhances the robustness of the original chaotic system, expands the parameter range of the system effectively, and further increases the keyspace of the algorithm. In addition, the Fast Walsh–Hadamard Transform (FWHT) is introduced to adaptively compress, denoise, and reconstruct the audio signal, which effectively reduces the audio redundancy and the overall cost of computer storage and running time. In the stage of interactive channel shuffling and overlapping diffusion encryption associated with plaintext, the user holding the correct key can start the encryption algorithm to skillfully convert the 1D audio signal into a 2D digital image matrix for encryption, so that the algorithm has a double-layer security effect. In this paper, four different types of audio files are tested to verify the feasibility and effectiveness of the encryption algorithm. Experimental results show that the performance of the algorithm is better than the above audio encryption algorithm. At the same time, it also provides a certain reference for the application of the combination of adaptive audio compression denoising theory and chaos theory in the field of communication security.
In some audio encryption algorithms, the ciphertext audio is usually stored and transmitted in the form of noise. Assuming that the attacker has access to the decryption system (i.e., select ciphertext attack), but the decryption key is safely embedded in the device and cannot be obtained, at this time, the key can be inferred by decrypting a large number of selected ciphertexts and using the generated plaintext. In future work, we intend to further study the enhanced chaotic system. Multiple chaotic systems are used as the cipher generator of the algorithm to make it have a huge keyspace. Secondly, transform the transmission form of ciphertext audio to provide the algorithm with higher security.