SMGen: A Generator of Synthetic Models of Biochemical Reaction Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Reaction-Based Models
2.2. SMGen
- System connectivity: a biochemical network can be represented as an undirected graph with a single connected component, where the nodes represent the molecular species, and the edges correspond to the species interactions. This representation easily allows for ensuring the system connectivity, a property that is strictly required to guarantee that each species , with , will be involved in at least one reaction , with .To be more precise, as a first step, an undirected graph with a single connected component is built. This undirected graph is randomly generated by using edges and by taking into account the maximum number of reactants and products, obtaining a connected biochemical reaction network. It is worth noting that a graph with a single connected component can be built if and only if the following condition is met:where and are the maximum number of reactants and products, respectively. As a second step, starting from the initial undirected graph, the stoichiometric matrices are generated. The stoichiometric matrices can be viewed and treated as a Petri net [37,38] that, in turn, can be considered as a bipartite graph. Then, the stoichiometric matrices are randomly updated by adding and removing connections among the species, always taking into consideration the maximum number of reactants and products. Note that the initial connections, which correspond to the edges of the initial undirected graph, are never removed to ensure that all the species are involved in at least one reaction, maintaining the whole biochemical network connected. We designed an algorithm (see Algorithm A1) that builds the graph, composed of a single connected component, with the minimum number of edges that are needed to connect all the nodes.
- Maximum number of reactants and products: for each reaction , with , the number of reactants and the number of products cannot be arbitrarily large but has to be lower than or equal to a user-defined value (i.e., and ). Stated otherwise, the maximum order of the generated reactions should be fixed. SMGen does not explicitly account for conservation conditions during the generation of the RBMs; however, it can generate reactions that are akin to, e.g., protein modifications or conformational changes, thus resulting in two biochemical species whose sum is constant during the simulation.
- Linear independence: to ensure that each reaction , with , is endowed with plausible characteristics of a real biochemical reaction, the vectors of the stoichiometric coefficients of the reactants and products involved in must be linearly independent. An example of an unrealistic reaction consists in increasing or decreasing the amount of a species starting from one molecule of the species itself, e.g., , with . Since the linear independence is evaluated between the reactants and the products of each reaction, it is related to the number of species and reactions. Thus, it could happen that when the number of species is much higher than the number of reactions it is not possible to build a graph with a single connected component. In such a case, duplicated reactions or linear-dependent vectors between reactants and products of some reactions will occur. On the contrary, it is always possible to build a graph, composed of a single connected component, when the number of reactions is much higher than the number of species.
- Reaction discreteness: each reaction , with , must appear only once in the network; that is, duplicated reactions are not allowed.
- the number of species N and the number of reactions M;
- the maximum number of reactants and products and that might appear in any reaction;
- the probability distribution that is used to initialize the species amounts (to be chosen among uniform, normal, logarithmic, or log-normal distributions). Note that all species amounts are initialized using the same distribution probability;
- the minimum and maximum values and for the initial species amounts (to be specified either as number of molecules or concentrations);
- the probability distribution that is used to set the values of the kinetic constants (to be chosen among uniform, normal, logarithmic, or log-normal distributions). Note that all kinetic constants are generated using the same distribution probability;
- the minimum and maximum values and for the kinetic constants;
- the total number of RBMs that the user wants to generate;
- the mean and standard deviation values and for the initial amounts—as well as the mean and standard deviation values and for the kinetic constants—must also be provided if the normal or log-normal distributions are selected.

- Proc manages the GUI;
- Proc is the main process that orchestrates the computation;
- Proc, with , are the worker processes.

- the user interacts with the GUI, managed by Proc, to fill in all the required values for the parameters necessary to create the RBMs;
- Proc sends the values of all parameters to the main process (Proc), which allocates the resources and distributes the work to the workers (Proc, with );
- each worker (Proc, with ) generates an RBM. As soon as a worker terminates its execution, it communicates to the main process that the RBM has been created. If necessary, the main process assigns the generation of other RBMs to idle workers. When all the required RBMs are obtained, the workers enter in the death state, while the main process waits for further instructions from Proc.
| Algorithm 1 SMGen: workflow of a single worker execution. |
| 1: function generator() 2: ## Algorithm A1 3: GRAPH_GEN(N) 4: ## Algorithm A2 5: STOICH_MATRICES_GEN() 6: 7: for to M do 8: for to N do 9: if then 10: 11: if then 12: 13: ## Algorithm A3 14: STOICH_COEFFICIENTS_GEN() 15: ## Algorithm A4 16: LINEAR_INDEPENDENCE_MATRIX() 17: ## Algorithm A5 18: UNIQUE_REACTIONS() 19: while are not empty do 20: 21: ## Algorithm A6 22: CORRECTION_REACTIONS() 23: ## Algorithm A7 24: LINEAR_INDEPENDENCE_REACTION() 25: ## Algorithm A5 26: UNIQUE_REACTIONS() 27: ## Algorithm A8 28: AMOUNTS_GEN() 29: ## Algorithm A9 30: KINETIC_CONSTANTS_GEN() the instructions shown in lines 6–12 are required to build the structure of the initial graph of the reactions. |
- Given the parameters provided by the user, the graph representing the species and their interactions is randomly initialized (line 3 of Algorithm 1; see Algorithm A1).
- The adjacency matrix of the graph generated in Step 1 is converted into the stoichiometric matrices and (line 5 of Algorithm 1; see Algorithm A2). Note that the instructions in lines 6–17 of Algorithm 1 are required to build the data structure of the initial graph, which is then modified.
- The stoichiometric coefficients are randomly generated (line 19 of Algorithm 1; see Algorithm A3).
- For each reaction , with , the linear independence between the reactants and products is verified (line 21 of Algorithm 1; see Algorithm A4).
- The uniqueness of each reaction in the RBM is verified (line 23 of Algorithm 1; see Algorithm A5).
- Any error in the RBM identified in the previous steps is corrected (line 27 of Algorithm 1; see Algorithm A6); the linear independence and the uniqueness of the reactions in the modified RBM are iteratively verified (lines 29 and 31 of Algorithm 1; see Algorithms A5 and A7, respectively).
- The initial amounts of the species are generated according to the chosen probability distribution (line 33 of Algorithm 1; see Algorithm A8). If a species appears only as a reactant in the whole RBM, its amount is set to remain unaltered. The rationale behind this is double: on the one hand, we avoid the possibility of creating reactions that could be applied at most once, which is a highly improbable situation in biological systems; on the other hand, we mimic the non-limiting availability of some biochemical resources, for instance, it might be used to reproduce the execution of in vitro experiments where some species are continually introduced in the systems to keep their amount constant [40].
- The kinetic constants of the reactions are generated according to the chosen probability distribution (line 35 of Algorithm 1; see Algorithm A9).
| Symbol | Description |
|---|---|
| M | Number of reactions composing the RBM |
| N | Number of species involved in the RBM |
| Maximum number of the reactants | |
| Maximum number of the products | |
| Array of the initial amounts | |
| Array of the kinetic constants | |
| Stoichiometric matrix of the reagents | |
| Stoichiometric matrix of the products | |
| Adjacency matrix of the graph of the reactions | |
| Probability distribution for the initial amounts | |
| Minimum value of the initial amounts | |
| Maximum value of the initial amounts | |
| Mean of the normal and log-normal distributions for the initial amounts | |
| Standard deviation of the normal and log-normal distributions for the initial amounts | |
| Probability distribution for the kinetic constants | |
| Minimum value of the kinetic constants | |
| Maximum value of the kinetic constants | |
| Mean of the normal and log-normal distributions for the initial amounts | |
| Standard deviation of the normal and log-normal distributions for the kinetic constants amounts | |
| ⊙ | The concatenation operator |
3. Results
- we set the number of species , and then we varied the number of reactions ;
- we set the number of reactions , and then we varied the number of species ;
- we varied both the maximum numbers of reactants and products in .
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Algorithms
| Algorithm A1 Random initialization of the graph of reactions. |
|
| Algorithm A2 Conversion of the adjacency matrix into the stoichiometric matrices and . |
|
| Algorithm A3 Generation of the random stoichiometric coefficients. |
|
| Algorithm A4 Checking the linear independence between stoichiometric matrices. |
|
| Algorithm A5 Checking if the generated reactions are unique. |
|
| Algorithm A6 Random correction of the repeated reactions. |
|
| Algorithm A7 Checking the linear independence between reactants or products. |
|
| Algorithm A8 Random initialization of the amounts of the species. |
|
| Algorithm A9 Random generation of kinetic constants of the reactions. |
|
Appendix B. Analysis of the Properties of the RBMs Generated by SMGen
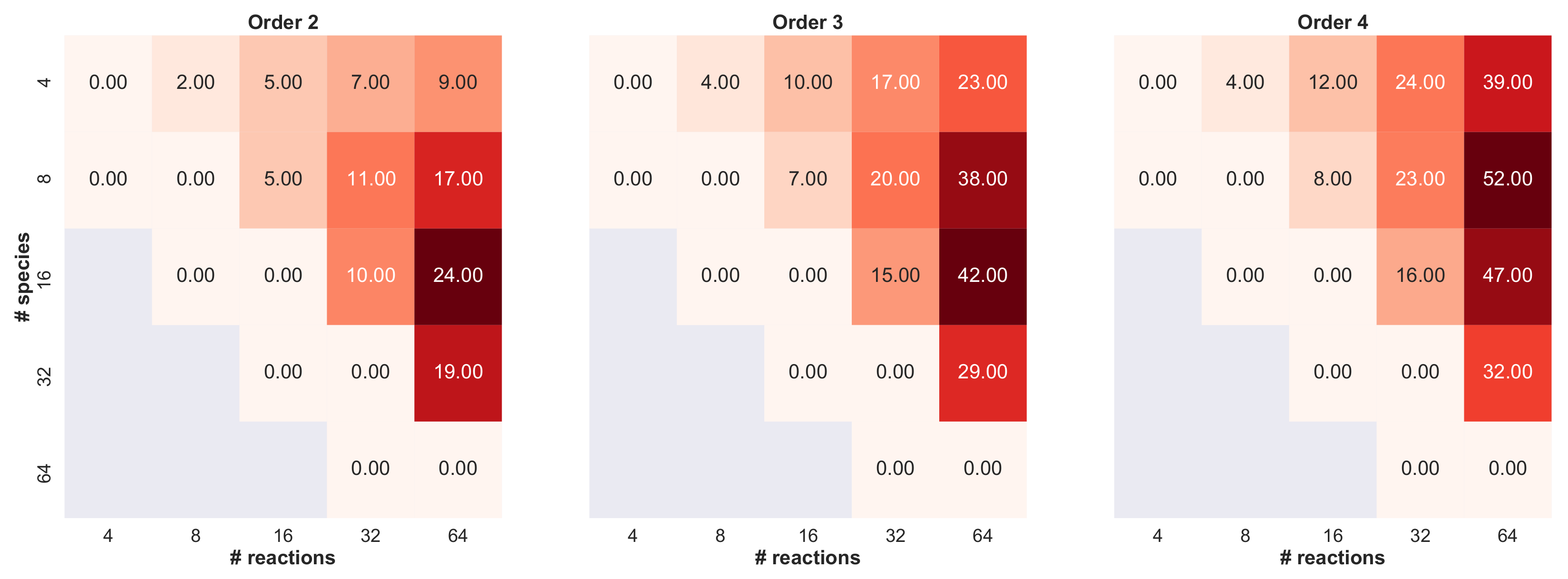
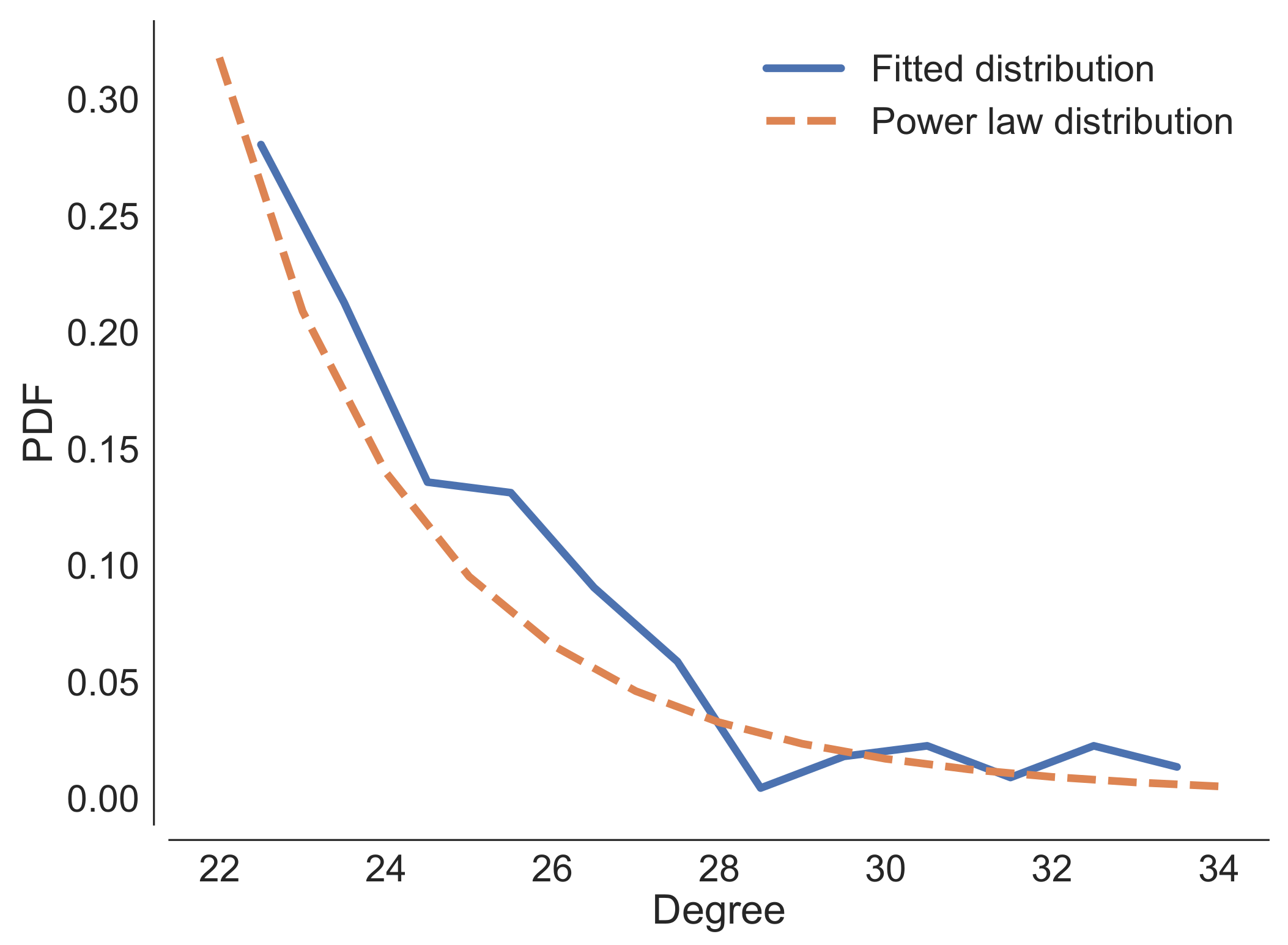

References
- Aldridge, B.B.; Burke, J.M.; Lauffenburger, D.A.; Sorger, P.K. Physicochemical modelling of cell signalling pathways. Nat. Cell Biol. 2006, 8, 1195–1203. [Google Scholar] [CrossRef]
- Szallasi, Z.; Stelling, J.; Periwal, V. System Modeling in Cellular Biology: From Concepts to Nuts and Bolts; The MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Nobile, M.S.; Tangherloni, A.; Rundo, L.; Spolaor, S.; Besozzi, D.; Mauri, G.; Cazzaniga, P. Computational Intelligence for Parameter Estimation of Biochemical Systems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Munsky, B.; Hlavacek, W.S.; Tsimring, L.S. Quantitative Biology: Theory, Computational Methods, and Models; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M.S. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. 2019, 81, 105494. [Google Scholar] [CrossRef]
- Kitano, H. Systems biology: A brief overview. Science 2002, 295, 1662–1664. [Google Scholar] [CrossRef] [PubMed]
- Chou, I.C.; Voit, E.O. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar] [CrossRef] [PubMed]
- Somogyi, E.T.; Bouteiller, J.M.; Glazier, J.A.; König, M.; Medley, J.K.; Swat, M.H.; Sauro, H.M. libRoadRunner: A high performance SBML simulation and analysis library. Bioinformatics 2015, 31, 3315–3321. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A complex pathway simulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef]
- Moraru, I.I.; Schaff, J.C.; Slepchenko, B.M.; Blinov, M.; Morgan, F.; Lakshminarayana, A.; Gao, F.; Li, Y.; Loew, L.M. Virtual Cell modelling and simulation software environment. IET Syst. Biol. 2008, 2, 352–362. [Google Scholar] [CrossRef]
- Li, H.; Petzold, L. Efficient parallelization of the stochastic simulation algorithm for chemically reacting systems on the graphics processing unit. Int. J. High Perform. Comput. Appl. 2010, 24, 107–116. [Google Scholar]
- Zhou, Y.; Liepe, J.; Sheng, X.; Stumpf, M.P.; Barnes, C. GPU accelerated biochemical network simulation. Bioinformatics 2011, 27, 874–876. [Google Scholar] [CrossRef] [PubMed]
- Komarov, I.; D’Souza, R.M.; Tapia, J. Accelerating the Gillespie τ-leaping method using graphics processing units. PLoS ONE 2012, 7, e37370. [Google Scholar]
- Komarov, I.; D’Souza, R.M. Accelerating the Gillespie exact stochastic simulation algorithm using hybrid parallel execution on graphics processing units. PLoS ONE 2012, 7, e46693. [Google Scholar] [CrossRef]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Mauri, G. GPU-accelerated simulations of mass-action kinetics models with cupSODA. J. Supercomput. 2014, 69, 17–24. [Google Scholar] [CrossRef]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Pescini, D.; Mauri, G. cuTauLeaping: A GPU-powered tau-leaping stochastic simulator for massive parallel analyses of biological systems. PLoS ONE 2014, 9, e91963. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sumiyoshi, K.; Hirata, K.; Hiroi, N.; Funahashi, A. Acceleration of discrete stochastic biochemical simulation using GPGPU. Front. Physiol. 2015, 6, 42. [Google Scholar] [CrossRef] [PubMed]
- Tangherloni, A.; Nobile, M.; Besozzi, D.; Mauri, G.; Cazzaniga, P. LASSIE: Simulating large-scale models of biochemical systems on GPUs. BMC Bioinform. 2017, 18, 246. [Google Scholar] [CrossRef] [PubMed]
- Tangherloni, A.; Nobile, M.S.; Cazzaniga, P.; Capitoli, G.; Spolaor, S.; Rundo, L.; Mauri, G.; Besozzi, D. FiCoS: A fine-and coarse-grained GPU-powered deterministic simulator for biochemical networks. PLoS Comput. Biol. 2021, 17, e1009410. [Google Scholar] [CrossRef]
- Glont, M.; Nguyen, T.V.N.; Graesslin, M.; Hälke, R.; Ali, R.; Schramm, J.; Wimalaratne, S.M.; Kothamachu, V.B.; Rodriguez, N.; Swat, M.J.; et al. BioModels: Expanding horizons to include more modelling approaches and formats. Nucleic Acids Res. 2018, 46, D1248–D1253. [Google Scholar] [CrossRef] [PubMed]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels—15 years of sharing computational models in life science. Nucleic Acids Res. 2020, 48, D407–D415. [Google Scholar] [CrossRef]
- Besozzi, D.; Cazzaniga, P.; Pescini, D.; Mauri, G.; Colombo, S.; Martegani, E. The role of feedback control mechanisms on the establishment of oscillatory regimes in the Ras/cAMP/PKA pathway in S. cerevisiae. EURASIP J. Bioinform. Syst. Biol. 2012, 2012, 10. [Google Scholar] [CrossRef] [PubMed]
- Cazzaniga, P.; Nobile, M.S.; Besozzi, D.; Bellini, M.; Mauri, G. Massive exploration of perturbed conditions of the blood coagulation cascade through GPU parallelization. BioMed Res. Int. 2014, 2014, 863298. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pescini, D.; Cazzaniga, P.; Besozzi, D.; Mauri, G.; Amigoni, L.; Colombo, S.; Martegani, E. Simulation of the Ras/cAMP/PKA pathway in budding yeast highlights the establishment of stable oscillatory states. Biotechnol. Adv. 2012, 30, 99–107. [Google Scholar] [CrossRef]
- Renz, A.; Widerspick, L.; Dräger, A. Genome-Scale Metabolic Model of Infection with SARS-CoV-2 Mutants Confirms Guanylate Kinase as Robust Potential Antiviral Target. Genes 2021, 12, 796. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.W.; Allen, J.W.; Green, W.H.; West, R.H. Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms. Comput. Phys. Commun. 2016, 203, 212–225. [Google Scholar] [CrossRef]
- Khanshan, F.S.; West, R.H. Developing detailed kinetic models of syngas production from bio-oil gasification using Reaction Mechanism Generator (RMG). Fuel 2016, 163, 25–33. [Google Scholar] [CrossRef]
- Lok, L.; Brent, R. Automatic generation of cellular reaction networks with Moleculizer 1.0. Nat. Biotechnol. 2005, 23, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Städter, P.; Schälte, Y.; Schmiester, L.; Hasenauer, J.; Stapor, P.L. Benchmarking of numerical integration methods for ODE models of biological systems. Sci. Rep. 2021, 11, 2696. [Google Scholar] [CrossRef] [PubMed]
- Garrido, A. Symmetry in complex networks. Symmetry 2011, 3, 1–15. [Google Scholar] [CrossRef]
- Ohlsson, F.; Borgqvist, J.; Cvijovic, M. Symmetry structures in dynamic models of biochemical systems. J. R. Soc. Interface 2020, 17, 20200204. [Google Scholar] [CrossRef]
- Keating, S.M.; Waltemath, D.; König, M.; Zhang, F.; Dräger, A.; Chaouiya, C.; Bergmann, F.T.; Finney, A.; Gillespie, C.S.; Helikar, T.; et al. SBML Level 3: An extensible format for the exchange and reuse of biological models. Mol. Syst. Biol. 2020, 16, e9110. [Google Scholar] [CrossRef]
- Besozzi, D.; Cazzaniga, P.; Mauri, G.; Pescini, D. BioSimWare: A software for the modeling, simulation and analysis of biological systems. In International Conference on Membrane Computing; Springer: Berlin, Germany, 2010; pp. 119–143. [Google Scholar]
- Chellaboina, V.; Bhat, S.P.; Haddad, W.M.; Bernstein, D.S. Modeling and analysis of mass-action kinetics. IEEE Control Syst. 2009, 29, 60–78. [Google Scholar]
- Voit, E.O.; Martens, H.A.; Omholt, S.W. 150 years of the mass action law. PLoS Comput. Biol. 2015, 11, e1004012. [Google Scholar] [CrossRef]
- Nelson, D.L.; Lehninger, A.L.; Cox, M.M. Lehninger Principles of Biochemistry, 5th ed.; Macmillan: London, UK, 2008. [Google Scholar]
- Chaouiya, C.; Remy, E.; Thieffry, D. Petri net modelling of biological regulatory networks. J. Discrete Algorithms 2008, 6, 165–177. [Google Scholar] [CrossRef]
- Davidrajuh, R. Detecting Existence of Cycles in Petri Nets. In Proceedings of the International Joint Conference SOCO’16-CISIS’16-ICEUTE’16, San Sebastián, Spain, 9–21 October 2016; pp. 376–385. [Google Scholar]
- Tangherloni, A.; Spolaor, S.; Rundo, L.; Nobile, M.S.; Cazzaniga, P.; Mauri, G.; Liò, P.; Merelli, I.; Besozzi, D. GenHap: A novel computational method based on genetic algorithms for haplotype assembly. BMC Bioinform. 2019, 20, 172. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.J.; Ramakrishnan, N.; Cao, Y. Reconstructing chemical reaction networks: Data mining meets system identification. In Proceedings of the 14th ACM International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; pp. 142–150. [Google Scholar]
- Dalcín, L.; Paz, R.; Storti, M. MPI for Python. J. Parallel Distrib. Comput. 2005, 65, 1108–1115. [Google Scholar] [CrossRef]
- Gropp, W.D.; Gropp, W.; Lusk, E.; Skjellum, A. Using MPI: Portable Parallel Programming With the Message-Passing Interface; MIT Press: Cambridge, MA, USA, 1999; Volume 1. [Google Scholar]
- Vaidyanathan, S. Dynamics and control of Brusselator chemical reaction. Int. J. ChemTech Res. 2015, 8, 740–749. [Google Scholar]
- Cornish-Bowden, A. One hundred years of Michaelis–Menten kinetics. Perspect. Sci. 2015, 4, 3–9. [Google Scholar] [CrossRef]
- Hill, A.V. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. J. Physiol. 1910, 40, 4–7. [Google Scholar]
- Dimitrova, T.; Petrovski, K.; Kocarev, L. Graphlets in multiplex networks. Sci. Rep. 2020, 10, 1928. [Google Scholar] [CrossRef]
- Doria-Belenguer, S.; Youssef, M.K.; Böttcher, R.; Malod-Dognin, N.; Pržulj, N. Probabilistic graphlets capture biological function in probabilistic molecular networks. Bioinformatics 2020, 36, i804–i812. [Google Scholar] [CrossRef] [PubMed]
- Pržulj, N. Biological network comparison using graphlet degree distribution. Bioinformatics 2007, 23, e177–e183. [Google Scholar] [CrossRef]
- Wong, E.; Baur, B.; Quader, S.; Huang, C.H. Biological network motif detection: Principles and practice. Brief. Bioinform. 2012, 13, 202–215. [Google Scholar] [CrossRef] [PubMed]
- Stone, L.; Simberloff, D.; Artzy-Randrup, Y. Network motifs and their origins. PLoS Comput. Biol. 2019, 15, e1006749. [Google Scholar] [CrossRef] [PubMed]
- Kim, W.; Li, M.; Wang, J.; Pan, Y. Biological network motif detection and evaluation. BMC Syst. Biol. 2011, 5, S5. [Google Scholar] [CrossRef] [PubMed]
- Prill, R.J.; Iglesias, P.A.; Levchenko, A. Dynamic properties of network motifs contribute to biological network organization. PLoS Biol. 2005, 3, e343. [Google Scholar] [CrossRef]
- Feinberg, M. Foundations of Chemical Reaction Network Theory; Springer: Berlin, Germany, 2019. [Google Scholar]
- Arita, M. Scale-freeness and biological networks. J. Biochem. 2005, 138, 1–4. [Google Scholar] [CrossRef]
- Wang, Y.; Christley, S.; Mjolsness, E.; Xie, X. Parameter inference for discretely observed stochastic kinetic models using stochastic gradient descent. BMC Syst. Biol. 2010, 4, 99. [Google Scholar] [CrossRef] [PubMed]
- Totis, N.; Tangherloni, A.; Beccuti, M.; Cazzaniga, P.; Nobile, M.S.; Besozzi, D.; Pennisi, M.; Pappalardo, F. Efficient and settings-free calibration of detailed kinetic metabolic models with enzyme isoforms characterization. In Proceedings of the International Meeting on Computational Intelligence Methods for Bioinformatics and Biostatistics, Caparica, Portugal, 6–8 September 2018; pp. 187–202. [Google Scholar]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef] [PubMed]
- Kline, M.P.; Morimoto, R.I. Repression of the heat shock factor 1 transcriptional activation domain is modulated by constitutive phosphorylation. Mol. Cell. Biol. 1997, 17, 2107–2115. [Google Scholar] [CrossRef] [PubMed]

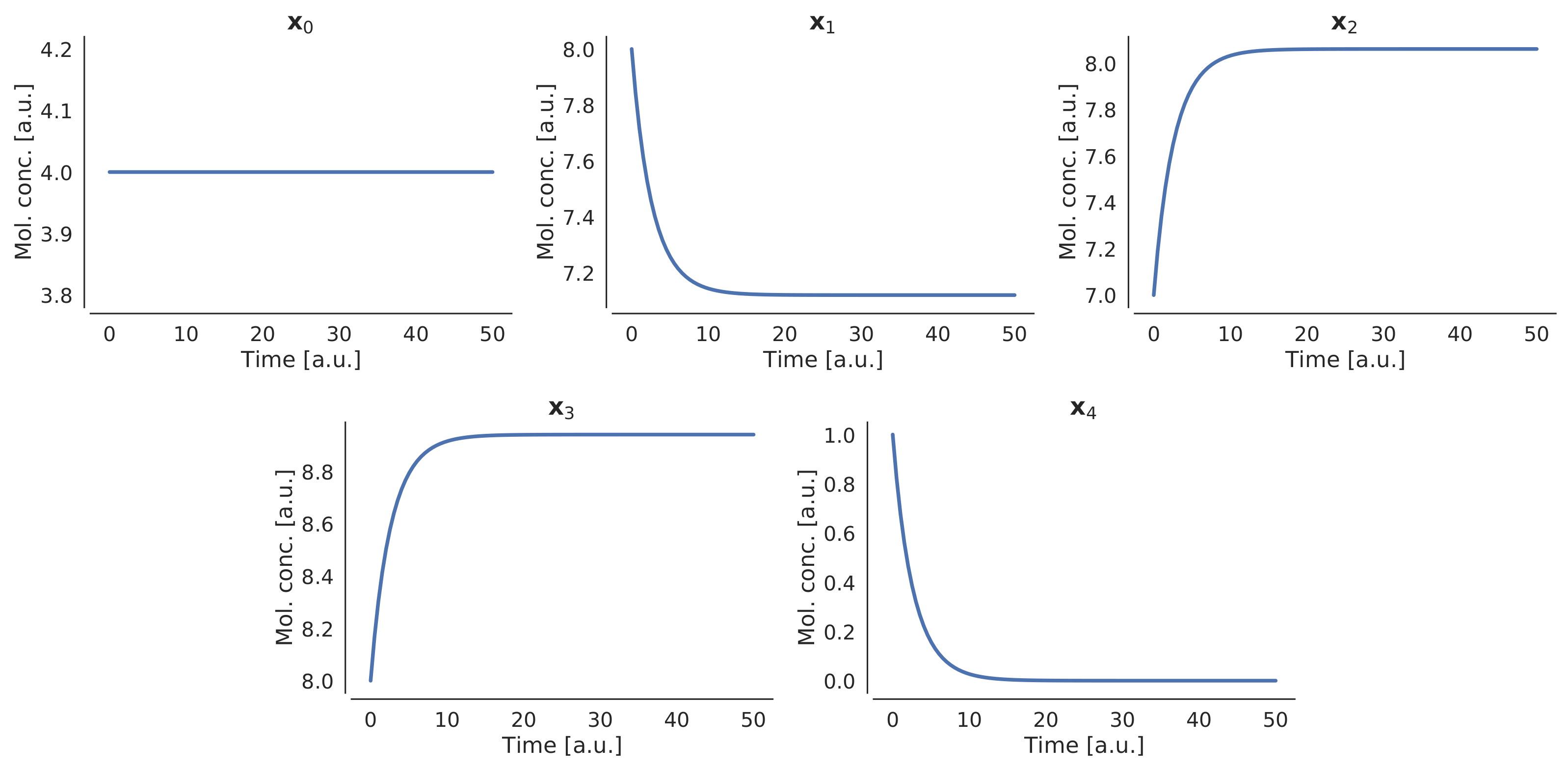


| No. | Reagents | Products | Constant |
|---|---|---|---|
| Species | Initial Amount |
|---|---|
| 4 | |
| 8 | |
| 7 | |
| 8 | |
| 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riva, S.G.; Cazzaniga, P.; Nobile, M.S.; Spolaor, S.; Rundo, L.; Besozzi, D.; Tangherloni, A. SMGen: A Generator of Synthetic Models of Biochemical Reaction Networks. Symmetry 2022, 14, 119. https://doi.org/10.3390/sym14010119
Riva SG, Cazzaniga P, Nobile MS, Spolaor S, Rundo L, Besozzi D, Tangherloni A. SMGen: A Generator of Synthetic Models of Biochemical Reaction Networks. Symmetry. 2022; 14(1):119. https://doi.org/10.3390/sym14010119
Chicago/Turabian StyleRiva, Simone G., Paolo Cazzaniga, Marco S. Nobile, Simone Spolaor, Leonardo Rundo, Daniela Besozzi, and Andrea Tangherloni. 2022. "SMGen: A Generator of Synthetic Models of Biochemical Reaction Networks" Symmetry 14, no. 1: 119. https://doi.org/10.3390/sym14010119
APA StyleRiva, S. G., Cazzaniga, P., Nobile, M. S., Spolaor, S., Rundo, L., Besozzi, D., & Tangherloni, A. (2022). SMGen: A Generator of Synthetic Models of Biochemical Reaction Networks. Symmetry, 14(1), 119. https://doi.org/10.3390/sym14010119









