Model-Free Non-Cascade Integral Sliding Mode Control of Permanent Magnet Synchronous Motor Drive with a Fast Reaching Law
Abstract
:1. Introduction
2. Ultra-Local Model of PMSM
3. Design of Dual Disturbance Observers
3.1. Design of Matched Disturbance Observer
3.2. Design of Mismatched Disturbance Observer
4. Design of Non-Cascade Integral Sliding Mode Control with a Fast Reaching Law
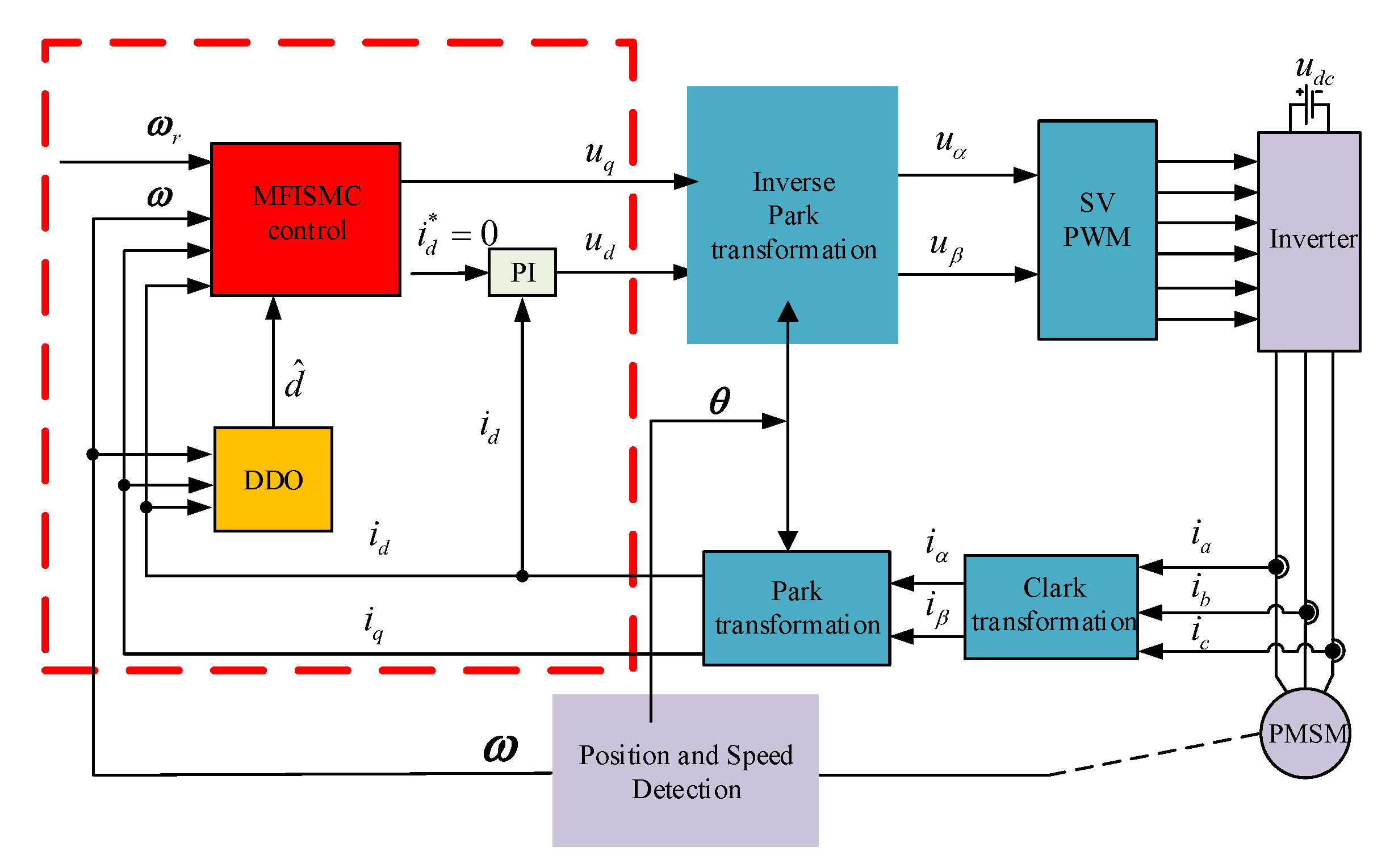
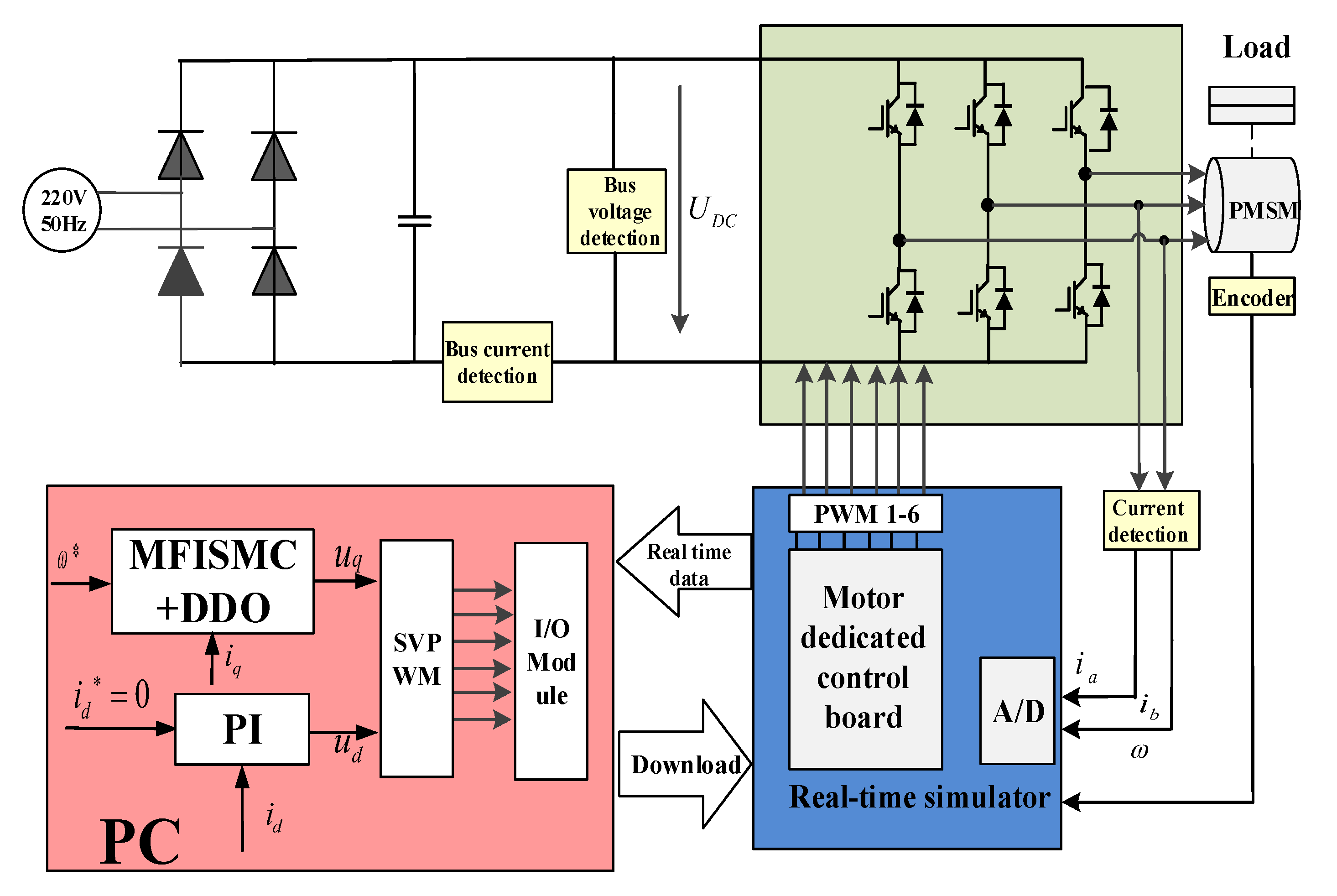
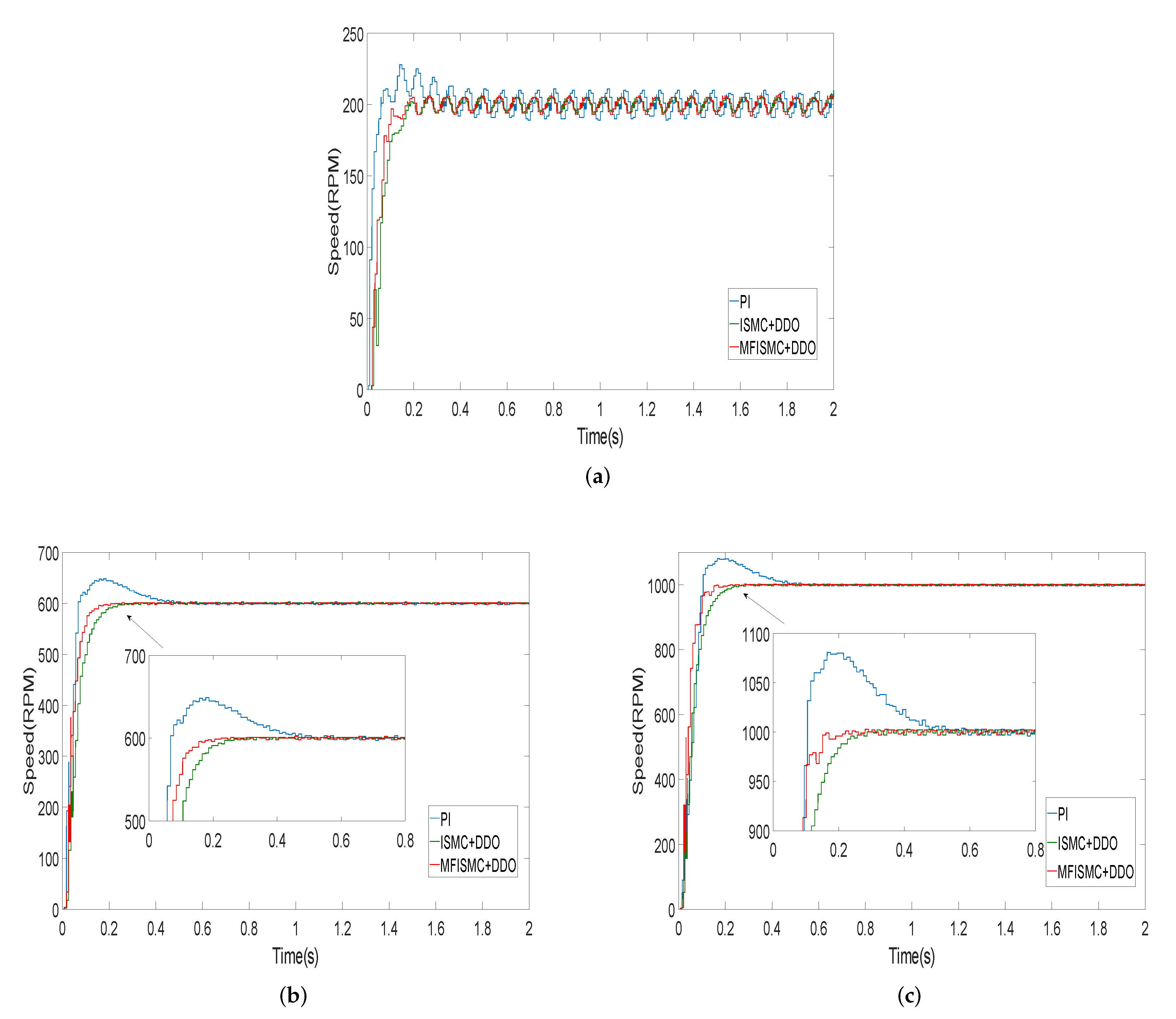
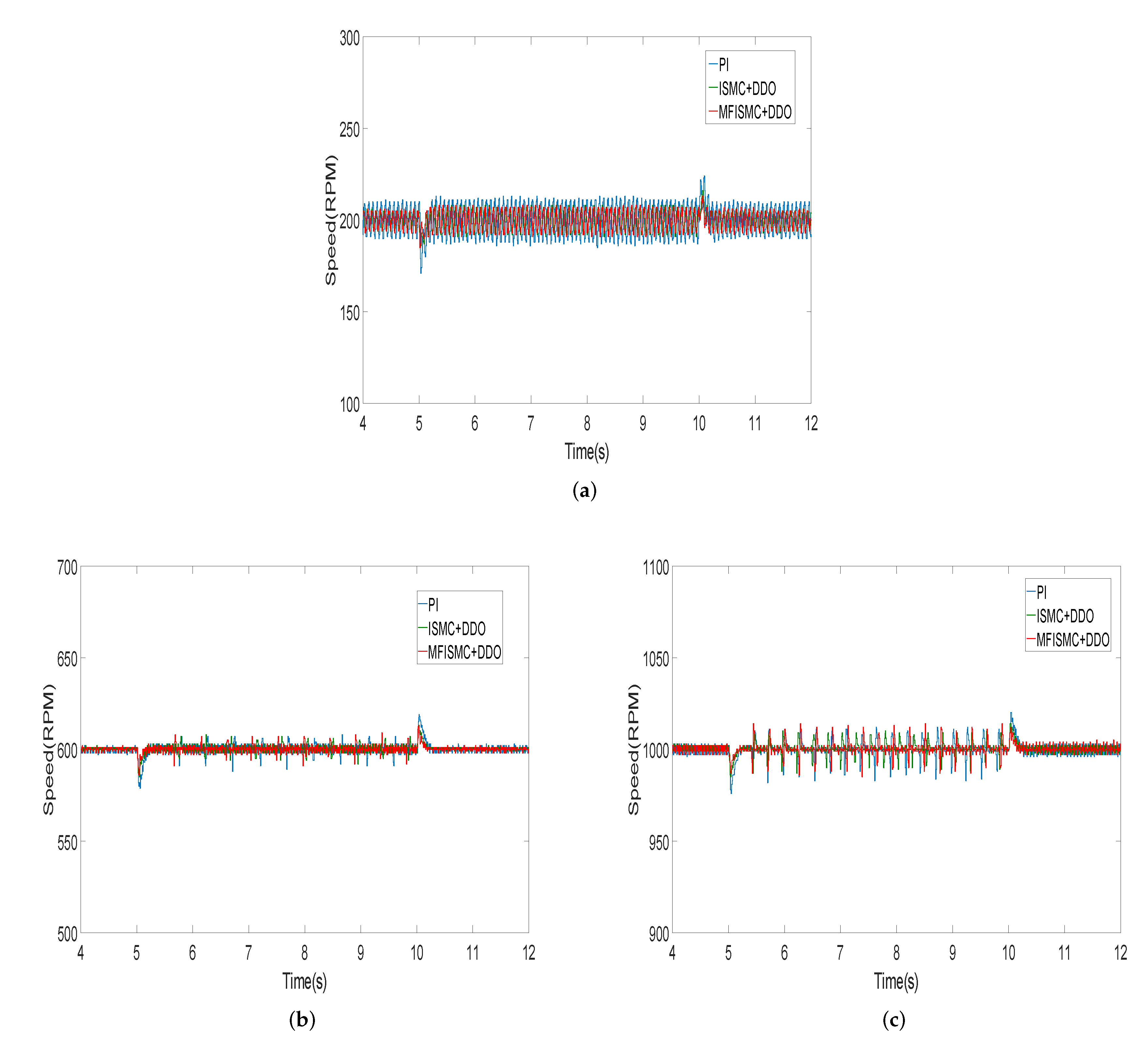
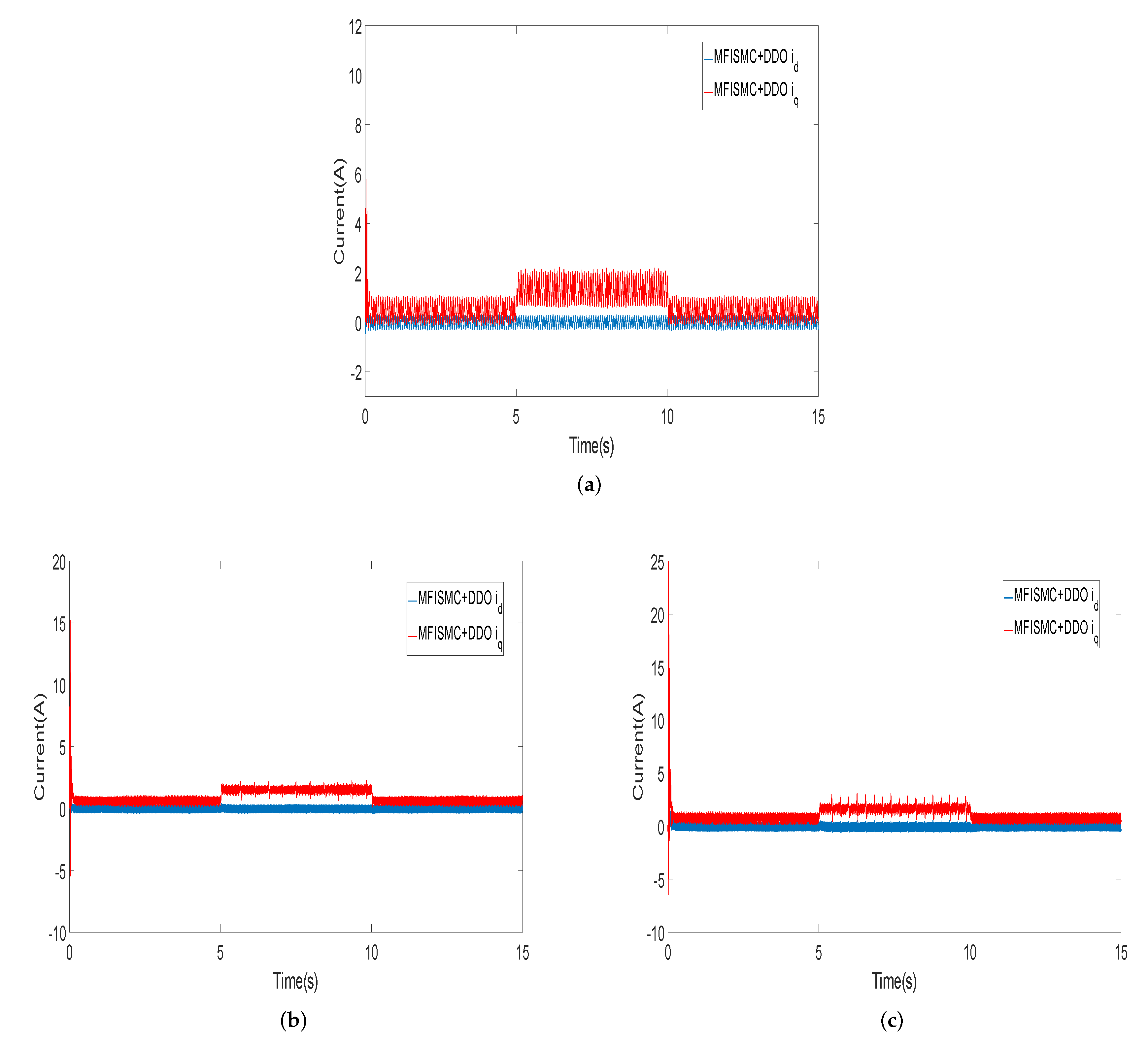
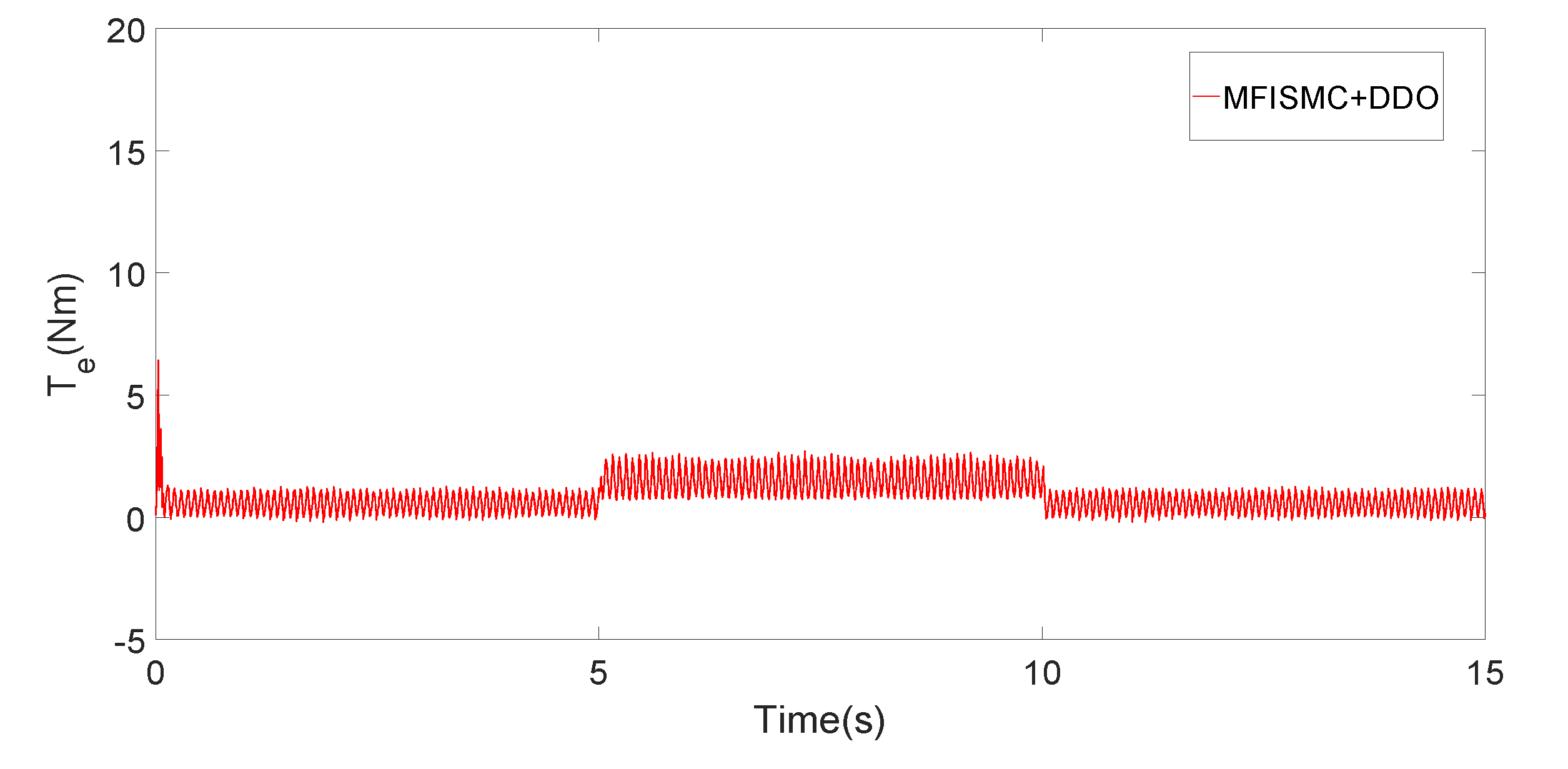
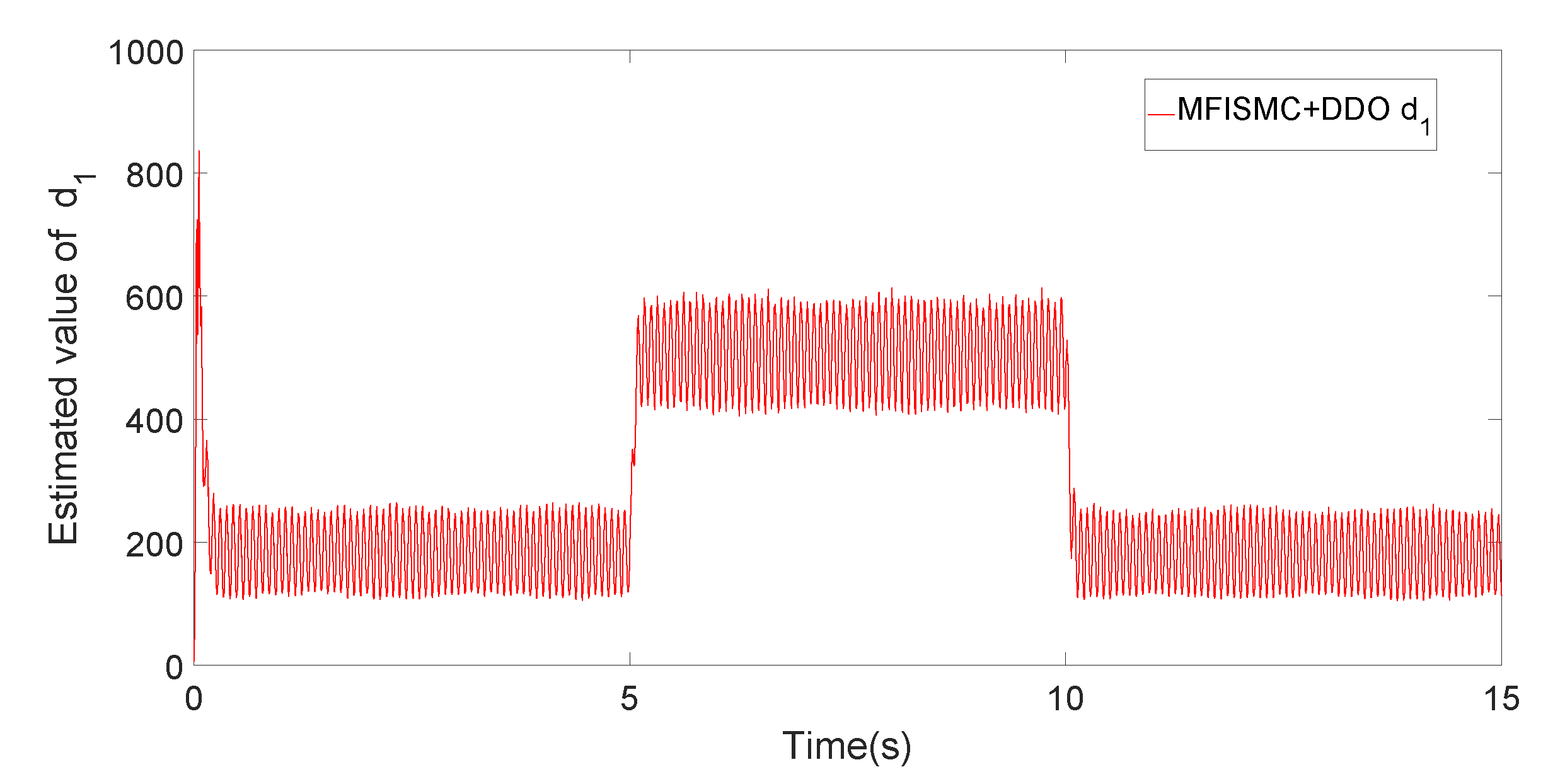
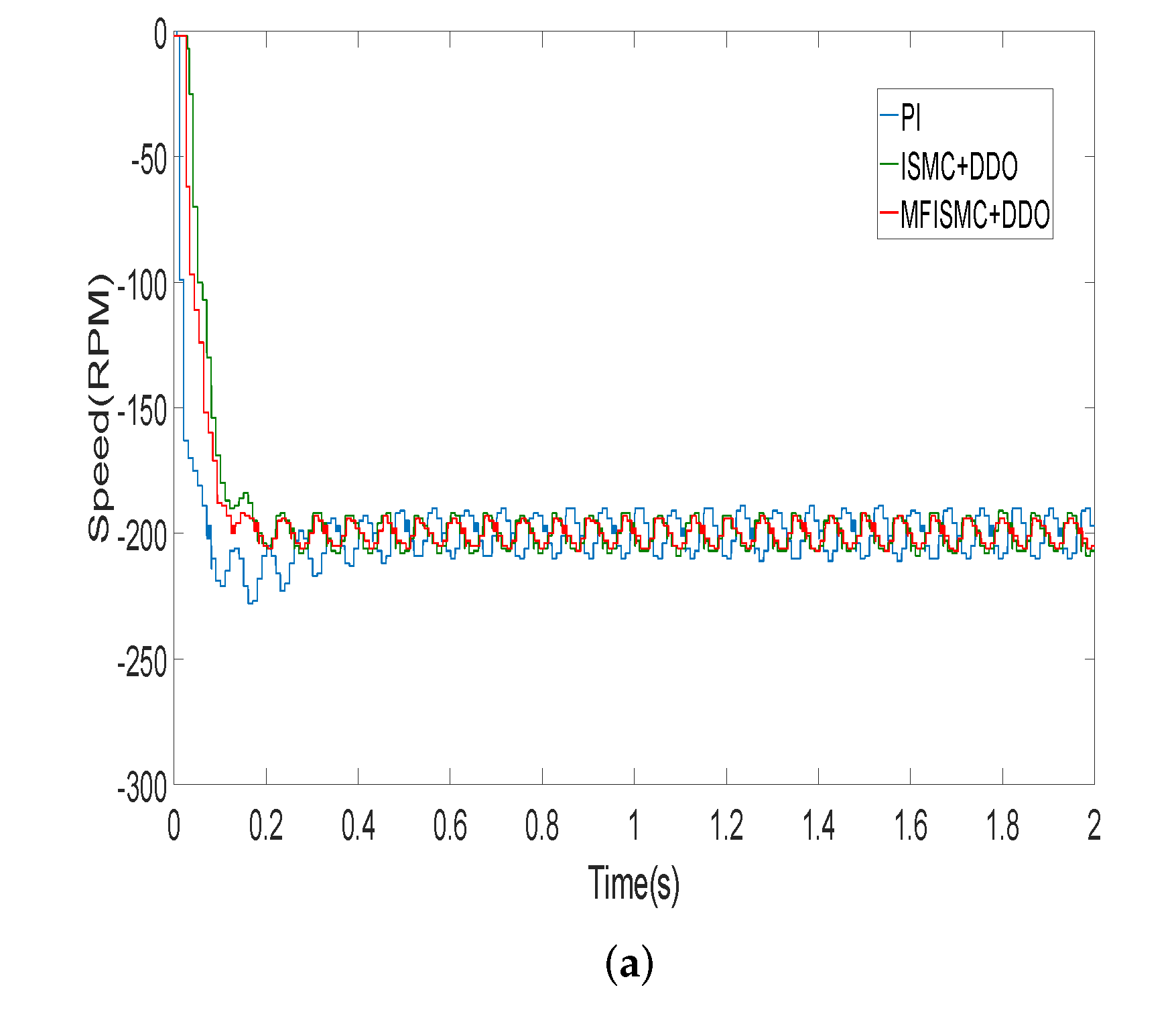
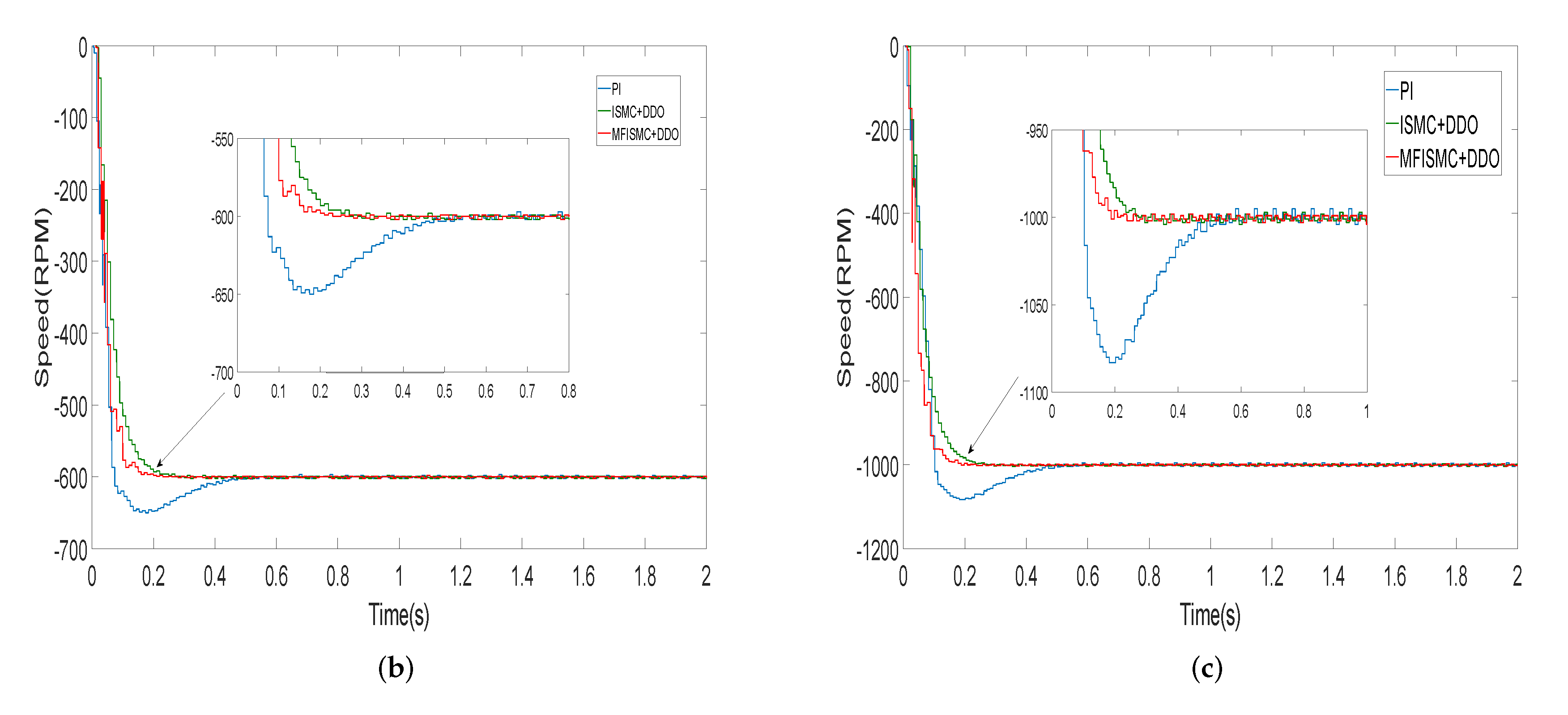
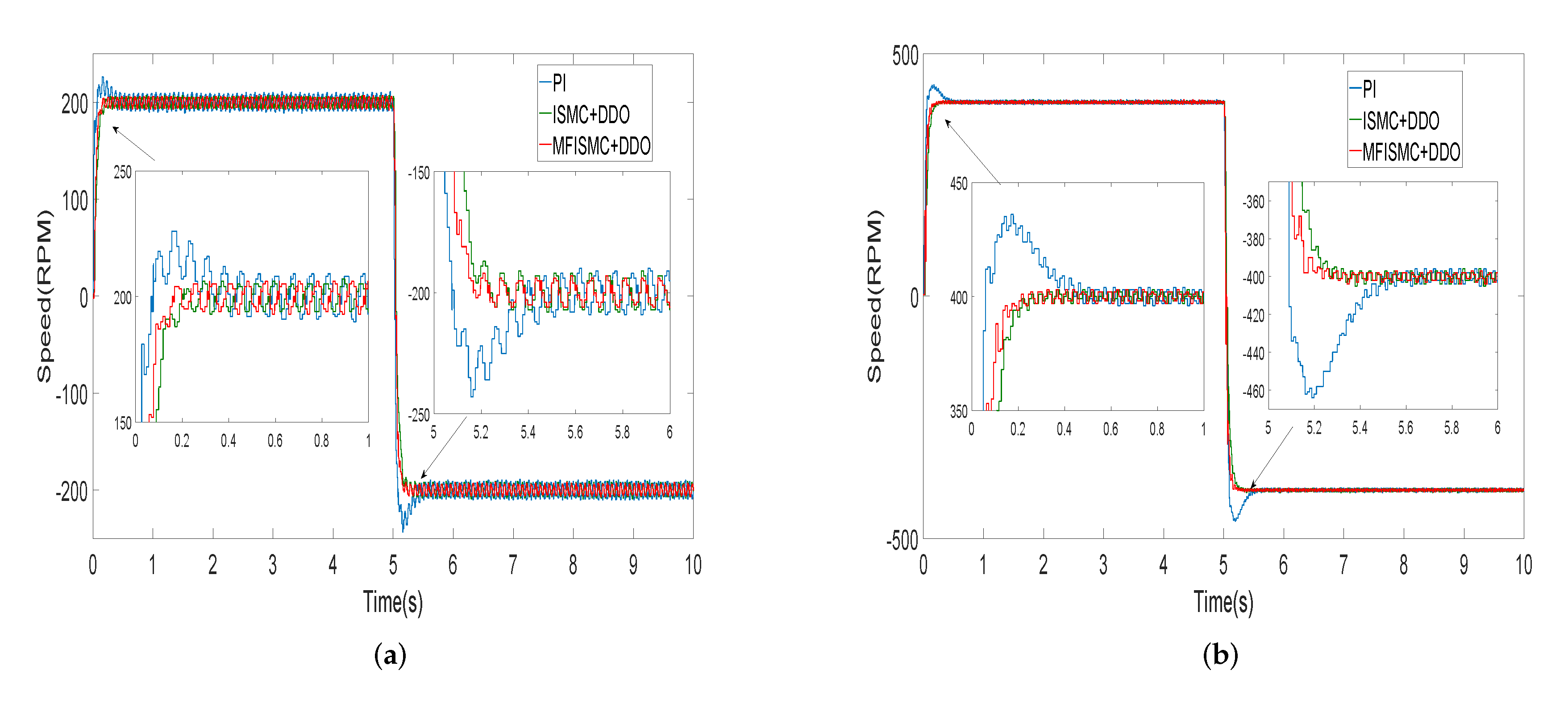
5. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cai, B.; Zhao, Y.; Liu, H.; Xie, M. Data-Driven Fault Diagnosis Methodology in Three-Phase Inverters for PMSM Drive Systems. IEEE Trans. Power Electron. 2017, 32, 5590–5600. [Google Scholar] [CrossRef]
- Yan, Y.; Wang, S.; Xia, C.; Wang, H.; Shi, T. Hybrid Control Set-Model Predictive Control for Field-Oriented Control of VSI-PMSM. IEEE Trans. Energy Convers 2016, 31, 1622–1633. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H. Continuous adaptive integral-type sliding mode control based on disturbance observer for PMSM drives. Nonlinear Dyn. 2021, 104, 1429–1441. [Google Scholar] [CrossRef]
- Xu, W.; Jiang, Y.; Mu, C. Novel Composite Sliding Mode Control for PMSM Drive System Based on Disturbance Observer. IEEE Trans. Appl. Supercond. 2016, 26, 1–5. [Google Scholar] [CrossRef]
- Liu, S.; Liu, C.; Huang, Y.; Zhao, H. Model Predictive Two-Target Current Control for OW-PMSM. IEEE Trans. Power Electron. 2021, 36, 3224–3235. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Yu, H.; Yu, J. Model-free adaptive discrete-time integral terminal sliding mode control for PMSM drive system with disturbance observer. IET Electr. Power Appl. 2020, 14, 1756–1765. [Google Scholar] [CrossRef]
- Morawiec, M. The Adaptive Backstepping Control of Permanent Magnet Synchronous Motor Supplied by Current Source Inverter. IEEE Trans. Ind. Inform. 2013, 9, 1047–1055. [Google Scholar] [CrossRef]
- Utkin, V. Variable structure systems with sliding modes. IEEE Trans. Autom. Control 1977, 22, 212–222. [Google Scholar] [CrossRef]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51–56. [Google Scholar] [CrossRef]
- Teng, Q.; Xu, R.; Han, X. Integral Sliding Mode-Based Model Predictive Current Control With Low Computational Amount for Three-Level Neutral-Point-Clamped Inverter-Fed PMSM Drives. IEEE Trans. Energy Convers. 2020, 35, 2249–2260. [Google Scholar] [CrossRef]
- Gao, W.; Hung, J.C. Variable structure control of nonlinear systems: A new approach. IEEE Trans. Ind. Electron. 1993, 40, 45–55. [Google Scholar]
- Mishra, J.P.; Yu, X.; Jalili, M.; Feng, Y. On fast terminal sliding-mode control design for higher order systems. In Proceedings of the IECON 2016-42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016; pp. 252–257. [Google Scholar]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Yu, X. Sliding-Mode Control for Systems With Mismatched Uncertainties via a Disturbance Observer. IEEE Trans. Ind. Electron. 2013, 60, 160–169. [Google Scholar] [CrossRef]
- Dong, S.; Chen, G.; Liu, M.; Wu, Z. Cooperative neural-adaptive fault-tolerant output regulation for heterogeneous nonlinear uncertain multiagent systems with disturbance. Sci. China Inf. Sci. 2021, 64, 1–12. [Google Scholar] [CrossRef]
- Dai, C.; Guo, T.; Yang, J.; Li, S. A Disturbance Observer-Based Current-Constrained Controller for Speed Regulation of PMSM Systems Subject to Unmatched Disturbances. IEEE Trans. Ind. Electron. 2021, 68, 767–775. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, H.; Feng, N.; Wang, Y. Non-cascade backstepping sliding mode control with three-order extended state observer for PMSM drive. IET Power Electron. 2020, 13, 307–316. [Google Scholar] [CrossRef]
- Qu, L.; Qiao, W.; Qu, L. An Extended-State-Observer-Based Sliding-Mode Speed Control for Permanent-Magnet Synchronous Motors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1605–1613. [Google Scholar] [CrossRef]
- Nguyen, N.; Oh, H.; Kim, Y.; Moon, J. Disturbance observer-based continuous finite-time sliding mode control against matched and mismatched disturbances. Complexity 2020, 2020, 1–14. [Google Scholar] [CrossRef]
- Liu, X.; Yu, H.; Yu, J.; Zhao, L. Combined Speed and Current Terminal Sliding Mode Control With Nonlinear Disturbance Observer for PMSM Drive. IEEE Access 2018, 6, 29594–29601. [Google Scholar] [CrossRef]
- Wang, F.; He, L. FPGA-Based Predictive Speed Control for PMSM System Using Integral Sliding-Mode Disturbance Observer. IEEE Trans. Ind. Electron. 2021, 68, 972–981. [Google Scholar] [CrossRef]
- Han, S.; Zhou, J.; Chen, Y.; Zhang, Y.; Tang, G.; Wang, L. Active Fault-Tolerant Control for Discrete Vehicle Active Suspension via Reduced-Order Observer. IEEE Trans. Syst. Man Cybern. Syst. 2020. [Google Scholar] [CrossRef]
- Michel, F.; Cédric, J. Model-free control. Int. J. Control 2013, 86, 2228–2252. [Google Scholar]
- Xu, D.; Shi, Y.; Ji, Z. Model-Free Adaptive Discrete-Time Integral Sliding-Mode-Constrained-Control for Autonomous 4WMV Parking Systems. IEEE Trans. Ind. Electron. 2018, 65, 834–843. [Google Scholar] [CrossRef]
- Navarro-Alarcón, D.; Liu, Y.; Romero, J.G.; Li, P. Model-Free Visually Servoed Deformation Control of Elastic Objects by Robot Manipulators. IEEE Trans. Robot. 2013, 29, 1457–1468. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Zhang, H. Model-free Deadbeat Predictive Current Control of a Surface-Mounted Permanent Magnet Synchronous Motor Drive System. J. Power Electron. 2018, 18, 103–115. [Google Scholar]
- Zhang, Y.; Jin, J.; Huang, L. Model-Free Predictive Current Control of PMSM Drives Based on Extended State Observer Using Ultralocal Model. IEEE Trans. Ind. Electron. 2021, 68, 993–1003. [Google Scholar] [CrossRef]
- Mao, J.; Li, H.; Yang, L.; Zhang, H.; Liu, L.; Wang, X.; Tao, J. Non-cascaded Model-free Predictive Speed Control of SMPMSM Drive System. IEEE Trans. Energy Convers. 2021. [Google Scholar] [CrossRef]
- Prior, G.; Krstic, M. Quantized-Input Control Lyapunov Approach for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Control. Syst. Technol. 2013, 21, 1784–1794. [Google Scholar] [CrossRef]
- Mohammed, S.A.Q.; Nguyen, A.T.; Choi, H.H.; Jung, J.W. Improved iterative learning control strategy for surface-mounted permanent magnet synchronous motor drives. IEEE Trans. Ind. Electron. 2020, 67, 10134–10144. [Google Scholar] [CrossRef]
- Apte, A.; Thakar, U.; Joshi, V. Disturbance observer based speed control of PMSM using fractional order PI controller. IEEE/CAA J. Autom. Sin. 2019, 6, 316–326. [Google Scholar] [CrossRef]
- Li, S.; Zhou, M.; Yu, X. Design and Implementation of Terminal Sliding Mode Control Method for PMSM Speed Regulation System. IEEE Trans. Ind. Inform. 2013, 9, 1879–1891. [Google Scholar] [CrossRef]
- Ginoya, D.; Shendge, P.; Phadke, S. Sliding mode control for mismatched uncertain systems using an extended disturbance observer. IEEE Trans. Ind. Electron. 2014, 61, 1983–1992. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. Constrained state feedback speed control of pmsm based on model predictive approach. IEEE Trans. Ind. Electron. 2016, 63, 3867–3875. [Google Scholar] [CrossRef]
- Preindl, M.; Bolognani, S. Model predictive direct speed control with finite control set of pmsm drive systems. IEEE Trans. Power Electron. 2013, 28, 1007–1015. [Google Scholar] [CrossRef]
- Guo, T.; Sun, Z.; Wang, X.; Li, S.; Zhang, K. A simple current constrained controller for permanent-magnet synchronous motor. IEEE Trans. Ind. Informatics 2019, 15, 1486–1495. [Google Scholar] [CrossRef]
- Pan, J.; Li, W.; Zhang, H. Control Algorithms of Magnetic Suspension Systems Based on the Improved Double Exponential Reaching Law of Sliding Mode Control. Int. J. Control. Autom. Syst. 2018, 16, 2878–2887. [Google Scholar] [CrossRef]

| Description | Value | Unit |
|---|---|---|
| rated speed | 1000 | RPM |
| rated power | 1.5 | KW |
| moment of inertia | 0.0027 | kg·m |
| permanent magnet flux | 0.32 | Wb |
| line resistance | 1.84 | |
| line inductance | 6.65 | mH |
| number of pole pairs | 4 |
| Speed (RPM) | Control Scheme | Speed Fluctuation (RPM) | Adjustment Time (s) | ||
|---|---|---|---|---|---|
| Load Up | Load Down | Load Up | Load Down | ||
| 200 | MFISMC + DDO | −15 | +13 | 0.12 | 0.21 |
| ISMC + DDO | −14 | +16 | 0.15 | 0.21 | |
| PI | −29 | + 24 | 0.19 | 0.25 | |
| 600 | MFISMC + DDO | −14 | +13 | 0.12 | 0.16 |
| ISMC + DDO | −15 | +13 | 0.14 | 0.19 | |
| PI | −21 | +19 | 0.25 | 0.24 | |
| 1000 | MFISMC + DDO | −13 | +14 | 0.20 | 0.19 |
| ISMC + DDO | −15 | +14 | 0.23 | 0.21 | |
| PI | −24 | +20 | 0.28 | 0.24 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Liu, X. Model-Free Non-Cascade Integral Sliding Mode Control of Permanent Magnet Synchronous Motor Drive with a Fast Reaching Law. Symmetry 2021, 13, 1680. https://doi.org/10.3390/sym13091680
Li T, Liu X. Model-Free Non-Cascade Integral Sliding Mode Control of Permanent Magnet Synchronous Motor Drive with a Fast Reaching Law. Symmetry. 2021; 13(9):1680. https://doi.org/10.3390/sym13091680
Chicago/Turabian StyleLi, Tong, and Xudong Liu. 2021. "Model-Free Non-Cascade Integral Sliding Mode Control of Permanent Magnet Synchronous Motor Drive with a Fast Reaching Law" Symmetry 13, no. 9: 1680. https://doi.org/10.3390/sym13091680
APA StyleLi, T., & Liu, X. (2021). Model-Free Non-Cascade Integral Sliding Mode Control of Permanent Magnet Synchronous Motor Drive with a Fast Reaching Law. Symmetry, 13(9), 1680. https://doi.org/10.3390/sym13091680





