Canonical Correlations and Nonlinear Dependencies

Abstract

Canonical correlation analysis (CCA) is the default method for investigating the linear dependence structure between two random vectors, but it might not detect nonlinear dependencies. This paper models the nonlinear dependencies between two random vectors by the perturbed independence distribution, a multivariate semiparametric model where CCA provides an insight into their nonlinear dependence structure. The paper also investigates some of its probabilistic and inferential properties, including marginal and conditional distributions, nonlinear transformations, maximum likelihood estimation and independence testing. Perturbed independence distributions are closely related to skew-symmetric ones.

1. Introduction

Canonical correlation analysis is a multivariate statistical method purported to analyze the correlation structure between two random vectors

$$\mathbf{x}=\left(\begin{array}{c}{X}_1\\ \dots \\ X_p\end{array}\right)\mathrm{and}\mathbf{y}=\left(\begin{array}{c}{Y}_1\\ \dots \\ Y_q\end{array}\right).$$

It obtains the linear transformations

$$\mathbf{z}=\mathbf{Ax}=\left(\begin{array}{c}{Z}_1\\ \dots \\ Z_p\end{array}\right)\mathrm{and}\mathbf{w}=\mathbf{By}=\left(\begin{array}{c}{W}_1\\ \dots \\ W_q\end{array}\right).$$

where the only nonnull correlations are those between components of $\mathbf{z}$ and $\mathbf{w}$ with the same indices, that is

$$\left(\begin{array}{c}{Z}_1\\ W_1\end{array}\right),\dots ,\left(\begin{array}{c}{Z}_r\\ W_r\end{array}\right)\mathrm{with}r=min\left(p,q\right).$$

The random vector ${\left(Z_1,W_1\right)}^{\top }$ is the first canonical pair and the correlation between its components, that is, the first canonical correlation is the highest among all correlations between a projection of $\mathbf{x}$ and a projection of $\mathbf{y}$. Similarly, the random vector ${\left(Z_i,W_i\right)}^{\top }$ is the i-th canonical pair and the correlation between its components, that is, the i-th canonical correlation is the highest among all correlations between a projection of $\mathbf{x}$ and a projection of $\mathbf{y}$, which are orthogonal to the previous canonical pairs, for $i\in \{2,\dots ,r\}$.

Canonical correlation analysis is particularly appropriate when the joint distribution of the vectors $\mathbf{x}$ and $\mathbf{y}$ is multivariate normal but it often performs poorly when the data are nonnormal [1]. The problem has been addressed nonparametrically [2], semiparametrically [1] and parametrically [3]. In this paper we introduce a semiparametric model to investigate the nonlinear dependence structure by means of canonical correlations. Kernel canonical correlation analysis (KCCA) and distance canonical correlation analysis (DCCA) play a prominent role among nonparametric generalizations of CCA aimed at addressing nonlinear dependencies (see, e.g., [4,5]).

The main contributions of the paper are as follows. Firstly, it defines the perturbed independence distribution as a statistical model for the joint distribution of two random vectors. The proposed model is somewhat reminiscent of copula models, in that the parameters addressing the dependence structure between two random vectors do not appear in the marginal distributions of the vectors themselves; however, the generating mechanism of perturbed independence distributions is very different from those of ordinary copulas.

Secondly, the perturbed independence model allows for flexible and tractable modeling of the nonlinear dependence structure between two random vectors, since the conditional distribution of a random vector with respect to the other is skew-symmetric. The proposed model provides a parametric interpretation of KCCA and DCCA, which are commonly regarded as nonparametric multivariate methods.

Thirdly, some appealing properties of canonical correlation analysis that hold true in the normal case still hold true in the perturbed independence case. For example, the first (second) component of a canonical pair is independent from the second (first) component of any other canonical pair. Further, if the marginal distributions of the two given vectors are normal, any canonical pair is independent of any other canonical pair.

Fourthly, the paper investigates the bivariate perturbed independence models within the framework of positive and negative association. In particular, it shows that the canonical pairs obtained from a perturbed independence distribution have the desirable properties of being positive quadrant dependent, under mild assumptions on the perturbing function.

The rest of the paper is structured as follows. Section 2 defines perturbed independence distributions and states some of their probabilistic and inferential properties. Section 3 connects perturbed independence distributions, canonical correlation analysis, positive dependence orderings and ordinal measures of association. Section 4 uses both theoretical and empirical results to find nonlinear transformations that increase correlations. Appendix A contains all proofs.

2. Model

This section defines the perturbed independence model, states its invariance properties and the independence properties of its canonical pairs. The theoretical results are illustrated with the bivariate distribution $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ introduced by [6,7], where $\varphi \left(·\right)$ and $\Phi \left(·\right)$ denote the probability and the cumulative density functions of a standard normal distribution, while $\lambda$ is a real value. Ref. [8] thoroughly investigated its properties and proposed some generalizations.

A p-dimensional random vector $\mathbf{x}$ is centrally symmetric (simply symmetric, henceforth) if there is a p-dimensional real vector $\mathbf{\xi }$ such that $\mathbf{x}-\mathbf{\xi }$ and $\mathbf{\xi }-\mathbf{x}$ are identically distributed ([9]). A real-valued function $\pi \left(·\right)$ is a skewing function (also known as perturbing function) if it satisfies the equality $\pi \left(-\mathbf{a}\right)=1-\pi \left(\mathbf{a}\right)$ and the inequalities $0\le \pi \left(\mathbf{a}\right)\le 1$ for any real vector $\mathbf{a}$ [10]. The probability density function of a perturbed independence model is twice the product of two symmetric probability density functions and a skewing function evaluated at a bilinear function of the outcomes. A more formal definition follows.

Definition 1.

Let the joint distribution of the random vectors $\mathbf{x}$ and $\mathbf{y}$ be

$$f\left(\mathbf{x},\mathbf{y}\right)=2h\left(\mathbf{x}-\mathbf{\mu }\right)k\left(\mathbf{y}-\mathbf{\nu }\right)\pi \left\{{\left(\mathbf{y}-\mathbf{\nu }\right)}^{\top }\mathsf{\Psi }\left(\mathbf{x}-\mathbf{\mu }\right)\right\},$$

where $h\left(·\right)$ is the pdf of a p-dimensional, centrally symmetric distribution, $k\left(·\right)$ is the pdf of a q-dimensional, centrally symmetric distribution, Ψ is a $q\times p$ matrix and $\pi \left(·\right)$ is a function satisfying $0\le \pi \left(-a\right)=1-\pi \left(a\right)\le 1$ for any real value a. We refer to this distribution as to a perturbed independence model, with components $h\left(·\right)$ and $k\left(·\right)$, location vectors $\mathbf{\mu }$ and $\mathbf{\nu }$, perturbing function $\pi \left(·\right)$ and association matrix Ψ.

In the bivariate distribution $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$, both components coincide with the normal pdf, both location vectors coincide with the origin, the perturbing function is the standard normal cdf and the association matrix is the scalar parameter $\lambda$.

Random numbers having a perturbed independence distribution can be generated in a very simple way. For the sake of simplicity, we illustrate it in the simplified case where $\mathbf{\mu }$ and $\mathbf{\nu }$ are null vectors and $\pi \left(·\right)$ is a cumulative distribution function of a distribution symmetric at the origin. First, generate the vectors $\mathbf{u}$ and $\mathbf{v}$ from the densities $h\left(·\right)$ and $k\left(·\right)$. Second, generate the scalar r from the distribution whose cumulative density function is $\pi \left(·\right)$. Third, let the vector $\mathbf{w}$ be ${\left({\mathbf{u}}^{\top },{\mathbf{v}}^{\top }\right)}^{\top }$ if the bilinear form ${\mathbf{u}}^{\top }\mathsf{\Psi }\mathbf{v}$ is greater than r and either ${\left(-{\mathbf{u}}^{\top },{\mathbf{v}}^{\top }\right)}^{\top }$ or ${\left({\mathbf{u}}^{\top },-{\mathbf{v}}^{\top }\right)}^{\top }$ in the opposite case. Then, the distribution of $\mathbf{w}$ is perturbed independence with components $h\left(·\right)$ and $k\left(·\right)$, null location vectors, perturbing function $\pi \left(·\right)$ and association matrix $\mathsf{\Psi }$.

The bivariate distribution $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ might be generated as follows. First, generate three mutually independent, standard normal random numbers U, W and Z. Second, set X equal to U and Y equal to W if the product $\lambda UW$ is greater than Z. Otherwise, set X equal to $-U$ and Y equal to W. Then the joint distribution of X and Y is $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$.

A p-dimensional probability density function $2g\left(\mathbf{a}-\mathbf{\xi }\right)\pi \left(\mathbf{a}-\mathbf{\xi }\right)$ is skew-symmetric with kernel $g\left(·\right)$ (i.e., a probability density function symmetric at the origin), location vector $\mathbf{\xi }$ and skewing function function $\pi \left(·\right)$. The function $g\left(·\right)$ would be more precisely denoted by $g_p\left(·\right)$, since it depends on the dimension of the corresponding random vector. However, we use $g\left(·\right)$ instead of $g_p\left(·\right)$ to relieve the notational burden. Ref. [11] discuss hypothesis testing on $g\left(·\right)$ for any choice of function $\pi \left(·\right)$. The most widely studied skew-symmetric distributions are the linearly skewed distributions, where the skewing function depends on $\mathbf{a}-\mathbf{\xi }$ only through its linear function ${\mathbf{\alpha }}^{\top }\left(\mathbf{a}-\mathbf{\xi }\right)$, as it happens for the multivariate skew-normal case. [12], as well as [13], investigated their inferential properties. Ref. [14] used them to motivate kurtosis-based projection pursuit.

In the notation of the above definition, the first part of the following theorem states that the marginal distributions of $\mathbf{x}$ and $\mathbf{y}$ are $h\left(\mathbf{x}-\mathbf{\mu }\right)$ and $k\left(\mathbf{y}-\mathbf{\nu }\right)$. Thus, perturbed independent distributions separately model the marginal distributions and the association between two random vectors, and constitute an alternative to copulas. The second part of the following theorem states that the conditional distribution of a component with respect to the other is linearly skewed. Hence, the association between the two components has an analytical form, which has been thoroughly investigated.

Theorem 1.

Let the random vectors $\mathbf{x}$ and $\mathbf{y}$ have a perturbed independence distribution with components $h\left(·\right)$, $k\left(·\right)$ and location vectors $\mathbf{\mu }$, $\mathbf{\nu }$. Then the following statements hold true.

• The marginal probability density functions of $\mathbf{x}$ and $\mathbf{y}$ are $h\left(\mathbf{x}-\mathbf{\mu }\right)$ and $k\left(\mathbf{y}-\mathbf{\nu }\right)$.
• The conditional probability density functions of $\mathbf{x}$ given $\mathbf{y}$ and $\mathbf{y}$ given $\mathbf{x}$ are skew-symmetric with kernels $h\left(·\right)$ and $k\left(·\right)$, while the associated location vectors are $\mathbf{\mu }$ and $\mathbf{\nu }$.

The marginal distributions of $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ are standard normal: $X~N\left(0,1\right)$ and $Y~N\left(0,1\right)$. The conditional distributions are skew-normal: the probability density functions of $X|Y=y~\mathcal{SN}\left(\lambda y\right)$ and of $Y|X=x~\mathcal{SN}\left(\lambda x\right)$ are $2\varphi \left(x\right)\Phi \left(\lambda xy\right)$ and $2\varphi \left(y\right)\Phi \left(\lambda xy\right)$. The sign of the correlation between X and Y is the same as the sign of $\lambda$ but the two random variables are nonlinearly dependent [7]:

$$\mathrm{E}\left(X|Y=y\right)=\sqrt{\frac{2}{\pi }}\frac{\lambda y}{\sqrt{1+{\lambda }^2{y}^2}},\mathrm{E}\left(Y|X=x\right)=\sqrt{\frac{2}{\pi }}\frac{\lambda x}{\sqrt{1+{\lambda }^2{x}^2}}.$$

There is a close connection between order statistics and either skew-normal distributions or their generalizations. For example, any linear combination of the minimum and the maximum of a bivariate, exchangeable and elliptical random vector is skew-elliptical [15]. In particular, any skew-normal distribution might be represented as the maximum or the minimum of a bivariate, normal and exchangeable random vector. At present, it is not clear whether there exists a meaningful connection between order statistics and perturbed independence distributions, which would ease both the interpretation and the application of these distributions.

The mean vector $\mathbf{m}$ and the covariance matrix $\mathbf{S}$ of the $n\times d$ data matrix $\mathbf{X}$ are statistically independent, if the rows of $\mathbf{X}$ are a random sample from a multivariate normal distribution. As a direct consequence, the components of the pairs $\left({\mathbf{m}}_1,{\mathbf{S}}_2\right)$ and $\left({\mathbf{m}}_2,{\mathbf{S}}_1\right)$ are statistically independent, too, where ${\mathbf{m}}_1$ and ${\mathbf{S}}_1$ (${\mathbf{m}}_2$ and ${\mathbf{S}}_2$) are the mean vector and the covariance matrix of ${\mathbf{X}}_1$ (${\mathbf{X}}_2$), that is the data matrix whose columns coincide with the first $0<p<d$ (the last $d-p$) columns of $\mathbf{X}$. The same property holds true for perturbed independence models, as a corollary of the following theorem.

Theorem 2.

Let the random vectors $\mathbf{x}$ and $\mathbf{y}$ have the perturbed independence distribution with location vectors $\mathbf{\mu }$ and $\mathbf{\nu }$. Then any even function of $\mathbf{x}-\mathbf{\mu }$ is independent of $\mathbf{y}$. Similarly, any even function of $\mathbf{y}-\mathbf{\nu }$ is independent of $\mathbf{x}$.

Let the joint distribution of the random variables X and Y be $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$. Then Y and $X^2$ are mutually independent. Similarly, X and $Y^2$ are mutually independent.

The components of the canonical covariates $\mathbf{z}={\left(Z_1,\dots ,Z_p\right)}^{\top }$ and $\mathbf{w}={\left(W_1,\dots ,W_q\right)}^{\top }$ are uncorrelated when their indices differ:

$$\rho \left(Z_i,Z_j\right)=\rho \left(W_i,W_j\right)=\rho \left(Z_i,W_j\right)=0\mathrm{when}i\ne j.$$

A p-dimensional random vector $\mathbf{v}$ is said to be sign-symmetric if there is a p-dimensional real vector $\mathbf{u}$ such that $\mathbf{v}-\mathbf{u}$ and $\mathbf{U}\left(\mathbf{v}-\mathbf{u}\right)$ are identically distributed, where $\mathbf{U}$ is any $p\times p$ diagonal matrix whose diagonal elements are either 1 or $-1$ [9]. For example, spherical random vectors are sign-symmetric. The following theorem shows that the canonical covariates belonging to different canonical vectors and with different indices are independent, if the joint distribution of the original variables is perturbed independence with sign-symmetric components.

Theorem 3.

Let the random vectors $\mathbf{x}\in {\mathbb{R}}^p$ and $\mathbf{y}\in {\mathbb{R}}^q$ have a perturbed independence distribution with sign-symmetric components. Further, let $\mathbf{z}={\left(Z_1,\dots ,Z_p\right)}^{\top }$ and $\mathbf{w}={\left(W_1,\dots ,W_q\right)}^{\top }$ be the canonical covariates of $\mathbf{x}$ and $\mathbf{y}$. Then $Z_i$ and $W_j$ are independent when $i\ne j$.

Under normal sampling, the components of different canonical pairs are statistically independent. The following corollary of the above theorem shows that the same property still holds true when the original variables have a perturbed independence distribution with normal components.

Corollary 1.

Let the random vectors $\mathbf{x}\in {\mathbb{R}}^p$ and $\mathbf{y}\in {\mathbb{R}}^q$ have a perturbed independence distribution with normal components. Further, let $\mathbf{z}={\left(Z_1,\dots ,Z_p\right)}^{\top }$ and $\mathbf{w}={\left(W_1,\dots ,W_q\right)}^{\top }$ the canonical covariates of $\mathbf{x}$ and $\mathbf{y}$. Then the variables $Z_i$, $Z_j$, $W_i$ and $W_j$ are pairwise independent when $i\ne j$.

As remarked by [16], the default measures of multivariate skewness and kurtosis are those introduced by [17]. Mardia’s skewness is the sum of all squared, third-order, standardized moments, while Mardia’s kurtosis is the fourth moment of the Mahalanobis distance of the random vector from its mean.

Mardia’s kurtosis of $2\varphi \left(x_1\right)\varphi \left(x_2\right)\Phi \left(\lambda x_1{x}_2\right)$ is

$$\frac{8+4E^2\left(XY\right)}{{\left\{1-E^2\left(XY\right)\right\}}^2},$$

so that it increases with the squared correlation between X and Y ([18]).

It is tempting to generalize $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ by letting

$$2\Phi \left(\lambda \underset{i=1}{\prod ^p}{x}_i\right)\underset{i=1}{\prod ^p}\varphi \left(x_i\right),$$

as performed in [6,7]. Unfortunately, this model does not preserve the nonlinear associations between pairs of its components. For example, the joint bivariate marginals of the trivariate distribution $2\varphi \left(x\right)\varphi \left(y\right)\varphi \left(z\right)\Phi \left(\lambda xyz\right)$ are bivariate, standard normal random vectors [19]. Other generalizations of $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ have been proposed by [8].

Let $f_{\mathbf{xy}}$ be the joint probability density function of the p-dimensional random vector $\mathbf{x}$ and of the q-dimensional random vector $\mathbf{y}$. Further, let $f_{\mathbf{x}}$ and $f_{\mathbf{y}}$ be the marginal probability density functions of $\mathbf{x}$ and $\mathbf{y}$. The distance covariance between $\mathbf{x}$ and $\mathbf{y}$ with respect to the weight function w is

$${\mathcal{V}}^2\left(\mathbf{x},\mathbf{y},w\right)={\int }_{{\mathbb{R}}^{p+q}}{\left|f_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s}\right)-f_{\mathbf{x}}\left(\mathbf{t}\right)f_{\mathbf{y}}\left(\mathbf{s}\right)\right|}^{2}w\left(\mathbf{t},\mathbf{s}\right)d\mathbf{t}d\mathbf{s},$$

where $\mathbf{t}\in {\mathbb{R}}^p$, $\mathbf{s}\in {\mathbb{R}}^q$ and $w\left(\mathbf{t},\mathbf{s}\right)\ge 0$ [20]. If the joint distribution of $\mathbf{x}$ and $\mathbf{y}$ is a perturbed independence model with components $h\left(·\right)$ and $k\left(·\right)$, location vectors $\mathbf{\mu }$ and $\mathbf{\nu }$, perturbing function $\pi \left(·\right)$ and association matrix $\mathsf{\Psi }$ we have

$$\begin{array}{c}{f}_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s};\mathbf{\mu },\mathbf{\nu },\mathsf{\Psi }\right)=2h\left(\mathbf{t}-\mathbf{\mu }\right)k\left(\mathbf{s}-\mathbf{\nu }\right)\pi \left\{{\left(\mathbf{s}-\mathbf{\nu }\right)}^{\top }\mathsf{\Psi }\left(\mathbf{t}-\mathbf{\mu }\right)\right\},\\ \\ f_{\mathbf{x}}\left(\mathbf{t};\mathbf{\mu }\right)=h\left(\mathbf{t}-\mathbf{\mu }\right),f_{\mathbf{y}}\left(\mathbf{s};\mathbf{\nu }\right)=k\left(\mathbf{s}-\mathbf{\nu }\right),\pi \left(-a\right)=1-\pi \left(a\right).\end{array}$$

A little algebra leads to the identities

$$\begin{array}{c}{f}_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s}\right)-f_{\mathbf{x}}\left(\mathbf{t}\right)f_{\mathbf{y}}\left(\mathbf{s}\right)=2h\left(\mathbf{t}-\mathbf{\mu }\right)k\left(\mathbf{s}-\mathbf{\nu }\right)\pi \left\{{\left(\mathbf{s}-\mathbf{\nu }\right)}^{\top }\mathsf{\Psi }\left(\mathbf{t}-\mathbf{\mu }\right)\right\}-h\left(\mathbf{t}-\mathbf{\mu }\right)k\left(\mathbf{s}-\mathbf{\nu }\right)=\\ \\ h\left(\mathbf{t}-\mathbf{\mu }\right)k\left(\mathbf{s}-\mathbf{\nu }\right)\left[2\pi \left\{{\left(\mathbf{s}-\mathbf{\nu }\right)}^{\top }\mathsf{\Psi }\left(\mathbf{t}-\mathbf{\mu }\right)\right\}-1\right]=\frac{f_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s};\mathbf{\mu },\mathbf{\nu },\mathsf{\Psi }\right)-f_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s};\mathbf{\mu },\mathbf{\nu },-\mathsf{\Psi }\right)}{2}.\end{array}$$

Hence, for perturbed independence models, the distance covariance is just half the difference between $f_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s};\mathbf{\mu },\mathbf{\nu },\mathsf{\Psi }\right)$ and $f_{\mathbf{xy}}\left(\mathbf{t},\mathbf{s};\mathbf{\mu },\mathbf{\nu },-\mathsf{\Psi }\right)$, which is the probability density functions of

$$\left(\begin{array}{c}\hfill \mathbf{x}\\ \hfill \mathbf{y}\end{array}\right)\mathrm{and}\left(\begin{array}{c}\hfill \mathbf{x}\\ \hfill -\mathbf{y}\end{array}\right).$$

In particular, if the joint distribution of the random variables X and Y is $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ we have

$$f_{XY}\left(t,s\right)-f_X\left(t\right)f_Y\left(s\right)=\varphi \left(x\right)\varphi \left(y\right)\left\{\Phi \left(\lambda xy\right)-\Phi \left(-\lambda xy\right)\right\}.$$

3. Concordance

This section investigates the bivariate perturbed independence models within the framework of positive and negative association. In particular, it shows that the canonical pairs obtained from a perturbed independence distribution have the desirable properties of being positive quadrant dependent, under mild assumptions on the perturbing function. The seminal paper by [21] started a vast literature on dependence orderings and their connections with ordinal measures of association. For the sake of brevity, here we mention only some thorough reviews of the concepts in this section: [22,23,24,25,26,27].

Two random variables are said to be either concordant, positively associated or positively dependent if larger (smaller) outcomes of one of them often occur together with larger (smaller) outcomes of the other random variable. Conversely, two random variables are said to be either discordant, negatively associated or negatively dependent if larger (smaller) outcomes of one of them often occur together with smaller (larger) outcomes of the other random variable. For example, financial returns from different markets are known to be positively dependent (see, e.g., [28,29,30]). The degree of concordance or discordance is assessed with ordinal measures of association, of which the most commonly used are Pearson’s correlation (simply correlation, for short), Spearman’s rho and Kendall’s tau.

The correlation is the best known measure of ordinal association. The correlation between two random variables X and Y is

$$\rho \left(X,Y\right)=\frac{\mathrm{E}\left\{\left(X-{\mu }_X\right)\left(Y-{\mu }_Y\right)\right\}}{\sqrt{\mathrm{E}\left\{{\left(X-{\mu }_X\right)}^2\right\}·\mathrm{E}\left\{{\left(Y-{\mu }_Y\right)}^2\right\}}},$$

where ${\mu }_X$ and ${\mu }_Y$ are the expectations of X and Y. The ordinal association between two random variables might be decomposed into a linear component and a nonlinear component. The liner component refers to the tendency of the random variables to deviate from their means in a proportional way. The correlation only detects and measures the linear component of the ordinal association. When the nonlinear component is not negligible, the information conveyed by the correlation needs to be integrated with information from other measures of ordinal association.

Spearman’s rho, also known as Spearman’s correlation, between the random variables X and Y is the correlation between the two variables after being transformed according to their marginal cumulative distribution functions:

$${\rho }_S\left(X,Y\right)=\rho \left\{F_X\left(X\right),F_Y\left(Y\right)\right\},$$

where $F_X\left(·\right)$ and $F_Y\left(·\right)$ are the marginal cumulative distribution functions of X and Y. Its sample counterpart is the correlation between the observed ranks. Spearman’s rho is a measure of ordinal association detecting both linear and nonlinear dependence. It is also more robust to ouliers than the Pearson’s correlation.

Kendall’s tau, also known as Kendall’s correlation, between two random variables is the difference between their probability of concordance and their probability of discordance. The former (latter) is the probability that the difference between the first components of two independent outcomes from a bivariate distribution have the same sign of (a different sign than) the difference between the second components of the same pairs. More formally, Kendall’s tau between the random variables X and Y is

$$\tau \left(X,Y\right)=Pr\left\{\left(X_1-X_2\right)\left(Y_1-Y_2\right)>0\right\}-Pr\left\{\left(X_1-X_2\right)\left(Y_1-Y_2\right)<0\right\},$$

where ${\left(X_1,Y_1\right)}^{\top }$ and ${\left(X_2,Y_2\right)}^{\top }$ are two independent outcomes from the bivariate random vector ${\left(X,Y\right)}^{\top }$. Just like Spearman’s rho, Kendall’s tau is an ordinal measure of association detecting linear as well as nonlinear dependence and is more robust to outliers than Pearson’s correlation.

Unfortunately, Pearson’s correlation, Spearman’s rho and Kendall’s tau might take different signs, thus making it difficult to measure ordinal association. In order to prevent this from happening, it is convenient to impose some constraints on the bivariate distribution. The distribution of a bivariate random vector ${\left(X,Y\right)}^{\top }$ is said to be positively quadrant dependent (PQD) if its joint cdf is greater or equal than the product of the marginal cdf:

$$F_{X,Y}\left(x,y\right)\ge F_X\left(x\right)·F_Y\left(y\right)$$

for any two real values x and y. Similarly, the distribution of a bivariate random vector ${\left(X,Y\right)}^{\top }$ is said to be negatively quadrant dependent (PQD) if its joint cdf is either smaller or equal than the product of the marginal cdf:

$$F_{X,Y}\left(x,y\right)\le F_X\left(x\right)·F_Y\left(y\right)$$

for any two real values x and y. Pearson’s correlation, Spearman’s rho and Kendall’s tau of PQD (NQD) distributions are either null or have positive (negative) signs.

Independent random variables are special cases of PQD and NQD random variables. In order to rule this case out, the PQD and NQD condition can be made more restrictive that the above inequalities needs to be strict for measurable sets of x and y values. For example, a strictly positive quadrant dependent pair of random variables satisfies the inequality

$$F_{X,Y}\left(x,y\right)>F_X\left(x\right)·F_Y\left(y\right)$$

for any two real values x and y belonging to given interval of positive length. Pearson’s correlation, Spearman’s rho and Kendall’s tau of strictly positive (negative) quadrant dependent distributions have positive (negative) signs. As shown in the following theorem, a bivariate perturbed independence model is strictly positive (negative) quadrant dependent if the perturbing function is a cumulative density function and the association parameter is a positive (negative) scalar.

Theorem 4.

Let the joint distribution of the random variables X and Y be perturbed independent with components $h\left(·\right)$ and $k\left(·\right)$, perturbing function $\pi \left(·\right)$ and association parameter λ: $f\left(x,y\right)=2h\left(x\right)k\left(y\right)\pi \left(\lambda xy\right)$. Further, let $\pi \left(·\right)$ be the cumulative density function of a symmetric distribution. Then the random variables X and Y are strictly positive (negative) quadrant dependent when λ is positive (negative).

The joint distribution $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ of the bivariate random vector ${\left(X,Y\right)}^{\top }$ introduced in the previous section fulfills the assumptions in Theorem 5. In particular, if the association parameter $\lambda$ is positive, the random variables X and Y are strictly positive quadrant dependent:

$$F_{X,Y}\left(a,b\right)={\int }_{-\infty }^b{\int }_{-\infty }^{a}2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)dxdy>\Phi \left(a\right)\Phi \left(b\right)=F_X\left(a\right)F_Y\left(b\right),$$

for any two real values a and b. As a direct consequence, their Pearson’s correlation $\rho \left(X,Y\right)$, their Spearman’s rho ${\rho }_S\left(X,Y\right)$ and their Kendall’s tau $\tau \left(X,Y\right)$ are positive.

Pearson’s correlation between the components of a canonical pair is nonnegative. However, within a nonparametric framework, their Spearman’s rho and their Kendall’s tau can take any sign. When Pearson’s correlation between the components of a canonical pair is positive but their Spearman’s rho and their Kendall’s tau are negative, the former ordinal association measure becomes quite unreliable and canonical correlation analysis provides little insight into the dependence structure. This problem does not occur under a perturbed independence model satisfying the assumptions stated in the following theorem.

Theorem 5.

Let ${\left(Z_1,W_1\right)}^{\top }$, …, ${\left(Z_r,W_r\right)}^{\top }$, with $r=min\left(p,q\right)$ the canonical pairs obtained from a perturbed independence distribution, and let their density be

$$2\pi \left(\underset{i=1}{\sum ^r}{\lambda }_i{z}_i{w}_i\right)\left\{\stackrel{r}{\prod _{i=1}}{h}_i\left(z_i\right)\right\}\left\{\stackrel{r}{\prod _{i=1}}{k}_i\left(w_i\right)\right\},$$

where $\pi \left(·\right)$ is a strictly increasing perturbing function. Then the joint distribution of the i-th canonical pair is a bivariate perturbed independence model:

$$2h_i\left(z_i\right)k_i\left(w_i\right)G\left({\lambda }_i{z}_i{w}_i\right),$$

where $G\left(·\right)$ is a strictly increasing perturbing function.

We illustrate the above theorem with the perturbed independence distribution

$$2{\varphi }_p\left(\mathbf{x};{\Sigma }_{\mathbf{x}}\right){\varphi }_p\left(\mathbf{y};{\Sigma }_{\mathbf{y}}\right)F\left({\mathbf{y}}^{\top }\mathsf{\Psi }\mathbf{x}\right),$$

where ${\varphi }_q\left(·;\Omega \right)$ is the q-dimensional normal density with null mean vector and covariance matrix $\Sigma$, $F\left(·\right)$ is the cdf of a continuous distribution symmetric at the origin and $\mathsf{\Psi }$ is a symmetric $p\times p$ matrix. The distribution of the canonical variates $\mathbf{z}=\mathbf{Ax}={\left(Z_1,...,Z_p\right)}^{\top }$ and $\mathbf{w}=\mathbf{By}={\left(W_1,...,W_q\right)}^{\top }$ is

$$2{\varphi }_{2p}\left(\mathbf{z},\mathbf{w};{\mathbf{I}}_{2p}\right)F\left(\underset{i=1}{\sum ^p}{\lambda }_i{z}_i{w}_i\right),$$

which fulfills the assumptions in Theorem 6. Then the joint distribution of the i-th canonical pair ${\left(Z_i,W_i\right)}^{\top }$ is

$$2\varphi \left(z_i\right)\varphi \left(w_i\right)G_i\left({\lambda }_i{z}_i{w}_i\right),$$

where $\varphi \left(·\right)$ is the pdf of a univariate, standard normal distribution and $G_i\left(·\right)$ is the cdf of a continuous distribution symmetric at the origin. By Theorem 5 and since the i-th canonical correlation $\rho \left(Z_i,W_i\right)$ is nonnegative, the association parameter ${\lambda }_i$, Kendall’s tau $\tau \left(Z_i,W_i\right)$ and Spearman’s rho ${\rho }_S\left(Z_i,W_i\right)$ are nonnegative, too. Moreover, if $\rho \left(Z_i,W_i\right)$ is positive, the association parameter ${\lambda }_i$, Kendall’s tau $\tau \left(Z_i,W_i\right)$ and Spearman’s rho ${\rho }_S\left(Z_i,W_i\right)$ are positive, too.

4. Nonlinearity

As a desirable property, CCA decomposes the covariance matrix between the p-dimensional random vector $\mathbf{x}$ and the q-dimensional random vector $\mathbf{y}$ into linear combinations of the covariances between uncorrelated linear functions of $\mathbf{x}$ and $\mathbf{y}$. Ref. [31] thoroughly investigate the interpretation of CCA within the framework of linear dependence. The first output of CCA are the linear combinations of $\mathbf{x}$ and $\mathbf{y}$, which are maximally correlated:

$$\underset{\mathbf{a}\in {\mathbb{R}}_0^p,\mathbf{b}\in {\mathbb{R}}_0^q}{max}corr\left({\mathbf{a}}^{\top }\mathbf{x},{\mathbf{b}}^{\top }\mathbf{y}\right),$$

where ${\mathbb{R}}_0^p$ and ${\mathbb{R}}_0^q$ are the sets of p-dimensional and q-dimensional nonnull, real vectors.

As mentioned in the Introduction and in the previous section, both the interpretability and the usefulness of CCA are severely diminished by nonlinear dependencies between $\mathbf{x}$ and $\mathbf{y}$. A solution would be looking for the linear and nonlinear transformations of $\mathbf{x}$ and $\mathbf{y}$, which are maximally correlated:

$$\underset{g_1,g_2\in \mathbb{G}}{max}\underset{\mathbf{a}\in {\mathbb{R}}_0^p,\mathbf{b}\in {\mathbb{R}}_0^q}{max}corr\left\{g_1\left({\mathbf{a}}^{\top }\mathbf{x}\right),g_2\left({\mathbf{b}}^{\top }\mathbf{y}\right)\right\},$$

where $\mathbb{G}$ is the set of all real valued monotonic functions. In the general case, the maximization needs to be performed simultaneously with respect to the nonlinear functions $g_1\left(·\right)$, $g_2\left(·\right)$ and the real vectors $\mathbf{a}$, $\mathbf{b}$, thus being difficult to compute and difficult to interpret. Ref. [1] addressed the problem by proposing the Gaussian copula model, where the components of $\mathbf{x}$ and $\mathbf{y}$ have a joint distribution that is multivariate normal, after being transformed according to monotonic and nonlinear functions. However, these monotonic transformations do not have a clear interpretation and they are not guaranteed to increase the correlations.

Perturbed independence models do not suffer from these limitations. Firstly, the monotonic transformations have a simple interpretation, being the expectations of one variable conditioned with respect to the other. Secondly, the same transformations are guaranteed to increase the correlations, under mild assumptions. These statements are made more precise in the following theorem.

Theorem 6.

Let the joint distribution of the random variables X and Y be perturbed independent with null location parameters, nonnull association parameter and increasing perturbing function. Finally, let $\mathit{X}$ and $\mathit{Y}$ have finite second moments. Then the conditional expectation $g\left(X\right)=E\left(Y|X\right)$ is a monotone, odd and nonlinear function, while the correlation between Y and X is smaller than the correlation between $\mathit{Y}$ and $g\left(X\right)$.

We illustrate the above theorem with the distribution $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$ of the bivariate random vector ${\left(X,Y\right)}^{\top }$ introduced in Section 1. The conditional expectations of Y and X with respect to the outcomes x of X and y of Y are

$$\mathrm{E}\left(Y|X=x\right)=\frac{\lambda x\sqrt{2/\pi }}{\sqrt{1+{\lambda }^2{x}^2}}\mathrm{and}\mathrm{E}\left(X|Y=y\right)=\frac{\lambda y\sqrt{2/\pi }}{\sqrt{1+{\lambda }^2{y}^2}},$$

so that the nonlinear function of X and Y maximally correlated with Y and X are

$$g_1\left(X\right)=\mathrm{E}\left(Y|X\right)=\frac{\lambda X\sqrt{2/\pi }}{\sqrt{1+{\lambda }^2{X}^2}}\mathrm{and}{g}_2\left(Y\right)=\mathrm{E}\left(X|Y\right)=\frac{\lambda Y\sqrt{2/\pi }}{\sqrt{1+{\lambda }^2{Y}^2}}.$$

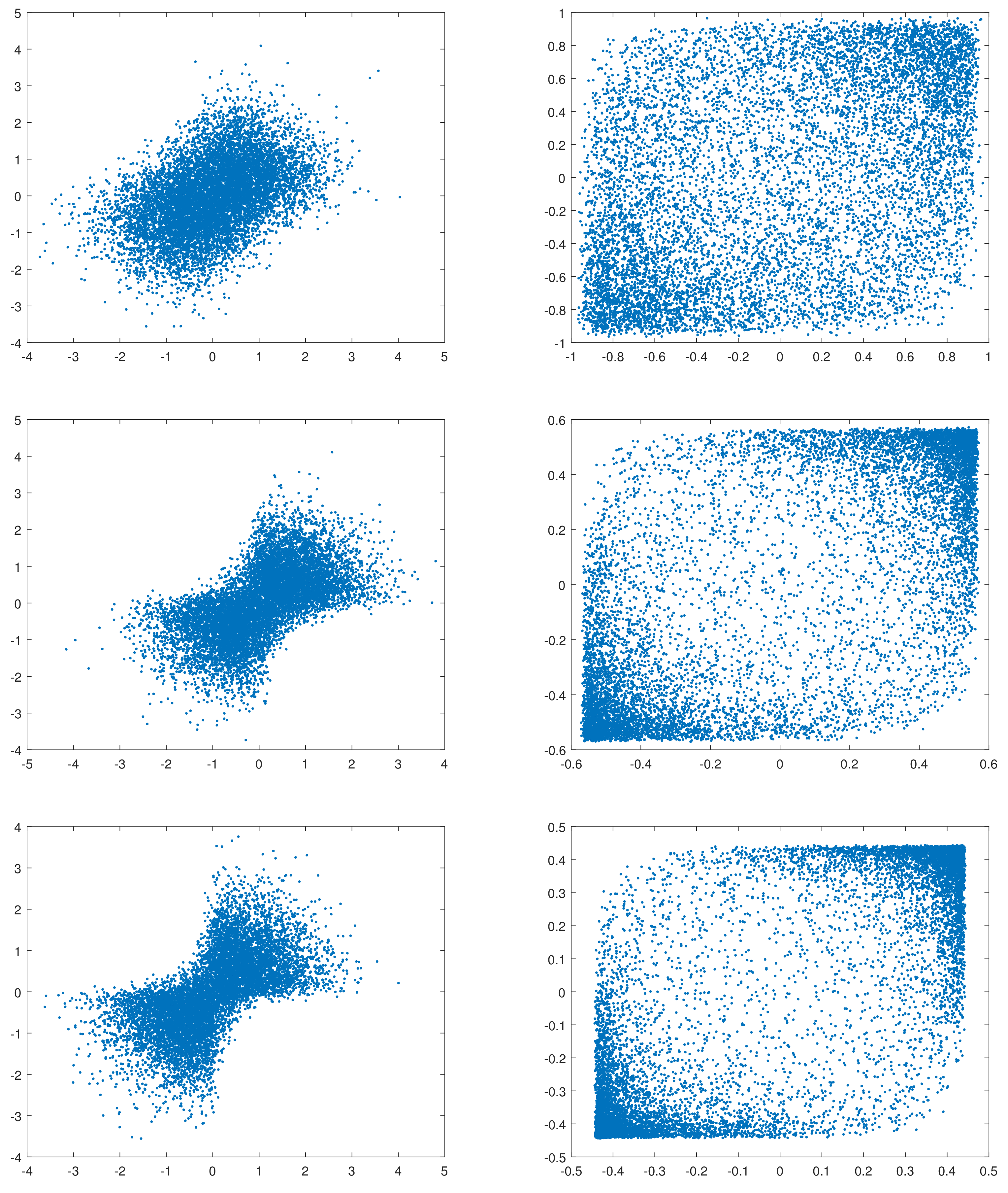
The above theorem does not guarantee that $E\left(Y\right|X)$ is the nonlinear transformation of one component that is maximally correlated with Y, nor that such correlation is smaller than the correlation between $E\left(X\right|Y)$ and $E\left(Y\right|X)$. We empirically address this point by simulating n = 10,000 bivariate data from $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$, where $\lambda \in \left\{1,2,3,4,5,6\right\}$. The left-hand scatterplots in Figure 1 clearly hint at positive dependence: more points lie in the first and in the third quadrants as the association parameter increases, despite the absence of the ellipsoidal shapes associated with bivariate normality. For each simulated sample, we computed Kendall’s tau, Spearman’s rho and Pearson’s correlation and report their values in

Table 1. Mean values of Pearson’s correlation, Kendall’s tau and Spearman’s rho for $100,00$ outcomes from $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$, where $\lambda \in \left\{1,2,3,4,5,6\right\}$. The column “Transformed” contains Pearson’s correlations between the transformed components.

Lambda	Kendall	Pearson	Spearman	Transformed
1	$0.311$	$0.439$	$0.468$	$0.469$
2	$0.412$	$0.552$	$0.619$	$0.642$
3	$0.444$	$0.587$	$0.667$	$0.713$
4	$0.458$	$0.598$	$0.689$	$0.752$
5	$0.471$	$0.612$	$0.709$	$0.791$
6	$0.480$	$0.618$	$0.720$	$0.810$

. The three measures of ordinal association are positive and they increase with the association parameter, consistently with the theoretical results in Section 2. More surprisingly, Spearman’s rho is always greater than Kendall’s tau and Pearson’s correlation, unlike the bivariate normal distribution, where Pearson’s correlation is always greater than Kendall’s tau and Spearman’s rho.

Finally, for each simulated sample $\left(X_1,Y_1\right)$ ,…, $\left(X_n,Y_n\right)$, we computed Pearson’s correlation between $Z_1$, …, $Z_n$ and $W_1$, …, $W_n$, where

$$Z_i=\frac{X_i}{\sqrt{1+{\lambda }^2{X}_i^2}}\mathrm{and}{W}_i=\frac{Y_i}{\sqrt{1+{\lambda }^2{Y}_i^2}}$$

are proportional to the sample counterpart of the expectation of Y given $X=x$ and X given $Y=y$ under the model $2\varphi \left(x\right)\varphi \left(y\right)\Phi \left(\lambda xy\right)$. For each simulated sample, these correlations are always greater than the correlations between the original data, consistently with Theorem 7. Moreover, Pearson’s correlations between $W_1$, …, $W_n$ and $Z_1$, …, $Z_n$ are always greater their Spearman’s correlations. 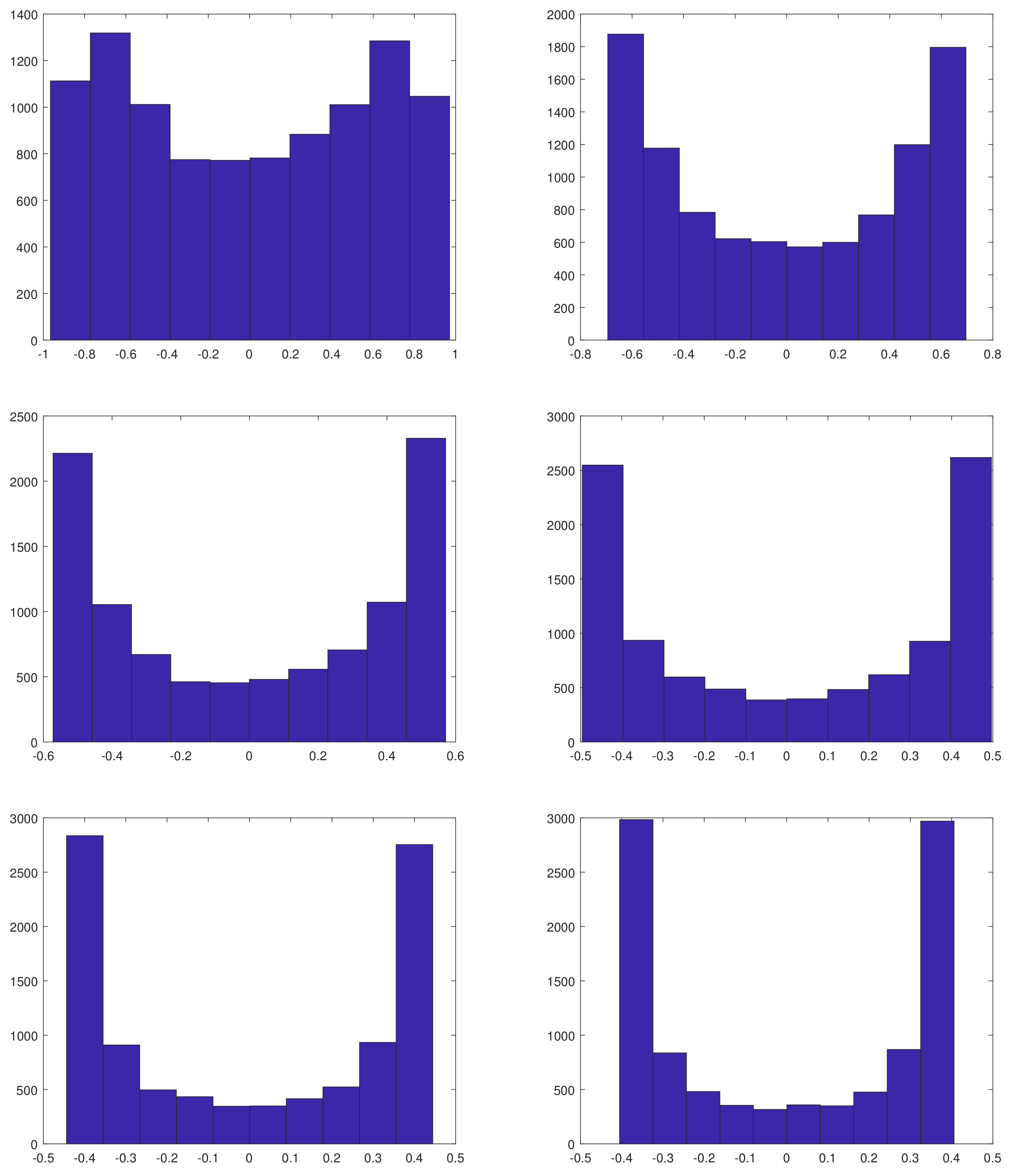As shown in the right-hand scatterplots of Figure 1 and Figure 2, the transformed data lie at the lower left corner and at the upper right corner of a square. This pattern becomes more evident as the association parameter increases. The histograms of $Z_1$, …, $Z_n$ in Figure 2 are symmetric and bimodal, with both modes at the ends of the observed range. Bimodality becomes more evident as the association parameter increases. The behavior of the transformed data $W_1$, …, $W_n$ is virtually identical and therefore is not reported.

We conclude that perturbed independence distributions, by modeling the nonlinear association between random variables, might help in finding the nonlinear transformations that are maximally correlated to each other. A positive Pearson’s correlation much lower than Spearman’s rho and Kendall’s tau hints for the presence of nonlinear association, whose analytical form might be estimated by looking for the maximally correlated nonlinear transformations of the random variables. This approach is particularly appropriate for the single index regression model $Y=g\left(X\right)+\epsilon$, where the response variable Y is the sum of a smooth function $g\left(·\right)$ of the predictor X and the error term $\epsilon$. When $g\left(·\right)$ is monotone, its analytical form might be estimated by looking for the transformation $g\left(X\right)$ that is maximally correlated with Y.

As remarked in the Introduction, kernel canonical correlation analysis (KCCA) and distance canonical correlation analysis (DCCA) are the two most popular generalizations of CCA aimed at dealing with nonlinear dependencies. A formal description of KCCA, based on Hilbert spaces and their inner products, might be found in the seminal papers by [32,33]. For most practical purposes, KCCA might be defined as the statistical method searching for linear projections of nonlinear functions of a random vector that are maximally correlated with linear projections of nonlinear functions of another random vector. Let $\mathbb{F}$ be a class of p-dimensional random vectors whose i-th components are nonlinear fuctions of the p-dimensional random vector $\mathbf{x}$. Similarly, let $\mathbb{G}$ be a class of q-dimensional random vectors whose i-th components are nonlinear fuctions of the q-dimensional random vector $\mathbf{y}$. Then KCCA looks for the random vectors $\mathbf{f}\in \mathbb{F}$, $\mathbf{g}\in \mathbb{G}$ and for the real vectors $\mathbf{a}\in {\mathbb{R}}^p$, $\mathbf{b}\in {\mathbb{R}}^q$ such that ${\mathbf{a}}^{\top }\mathbf{f}$ and ${\mathbf{b}}^{\top }\mathbf{g}$ are maximally correlated with each other.

In a nonparametric framework, the choice of the nonlinear functions may not be straightforward. On the other hand, in the perturbed independence framework, the theoretical and empirical results in this section suggest to set them equal to the conditional expectations: $\mathbf{f}=\mathrm{E}\left(\mathbf{x}|\mathbf{y}\right)$ and $\mathbf{g}=\mathrm{E}\left(\mathbf{y}|\mathbf{x}\right)$. In particular, for the perturbed independence model

$$2{\varphi }_p\left(\mathbf{x};\mathbf{\mu },\mathsf{\Omega }\right){\varphi }_q\left(\mathbf{y};\mathbf{\nu },\mathsf{\Gamma }\right)\mathsf{\Phi }\left\{{\left(\mathbf{y}-\mathbf{\nu }\right)}^{\top }\mathsf{\Psi }\left(\mathbf{x}-\mathbf{\mu }\right)\right\}$$

the suggested nonlinear functions of $\mathbf{x}$ and $\mathbf{y}$ are

$$\mathbf{f}=\mathbf{\mu }+\sqrt{\frac{2}{\pi }}{\displaystyle \frac{\mathsf{\Omega }{\mathsf{\Psi }}^{\top }\left(\mathbf{y}-\mathbf{\nu }\right)}{\sqrt{1+\left(\mathbf{y}-\mathbf{\nu }\right){}^{\top }\mathsf{\Psi }\mathsf{\Omega }{\mathsf{\Psi }}^{\top }\left(\mathbf{y}-\mathbf{\nu }\right)}}}\mathrm{and}\mathbf{g}=\mathbf{\nu }+\sqrt{\frac{2}{\pi }}{\displaystyle \frac{\mathsf{\Gamma }\mathsf{\Psi }\left(\mathbf{x}-\mathbf{\mu }\right)}{\sqrt{1+{\left(\mathbf{x}-\mathbf{\mu }\right)}^{\top }{\mathsf{\Psi }}^{\top }\mathsf{\Gamma }\mathsf{\Psi }\left(\mathbf{x}-\mathbf{\mu }\right)}}}.$$

DCCA looks for two projections whose joint distribution differs the most from the product of their marginal distributions, where difference is measured by distance correlation. The distance correlation between the random variables X and Y with respect to the weight function w is

$$\mathcal{R}\left(X,Y,w\right)=\frac{\mathcal{V}\left(X,Y,w\right)}{\sqrt{\mathcal{V}\left(X,X,w\right)\mathcal{V}\left(Y,Y,w\right)}},$$

where ${\mathcal{V}}^2\left(X,Y,w\right)$ is the distance covariance between X and Y with respect to w, as defined in the previous section. Hence the first canonical correlation between the p-dimensional random vector $\mathbf{x}$ and the q-dimensional random vector $\mathbf{y}$ is

$$\underset{\mathbf{a}\in {\mathbb{R}}^p}{max}\underset{\mathbf{b}\in {\mathbb{R}}^q}{max}\mathcal{R}\left({\mathbf{a}}^{\top }\mathbf{x},{\mathbf{b}}^{\top }\mathbf{y},w\right).$$

For other distance canonical correlations, the distance canonical pairs and the distance canonical transformations are defined similarly to their CCA analogues.

A natural question to ask is whether CCA and DCCA lead to identical projections, under the assumption of perturbed independence. At present, we are unable to either prove or disprove this statement, which we conjecture to be true, under the assumptions of Theorem 6: increasing perturbing functions that increase more steeply are more likely to imply both higher Pearson and distance correlations. We plan to investigate this conjecture by means of both theoretical arguments and simulation studies.