Cumulants of Multivariate Symmetric and Skew Symmetric Distributions
Abstract
1. Introduction
2. Spherical and Elliptically Symmetric Distributions
2.1. Marginal Moments and Cumulants
2.1.1. Moment and Cumulant Parameters
2.1.2. Using the Representation RU
2.2. Multivariate Moments and Cumulants
3. Multivariate t and Skew-t Distributions
3.1. Multivariate t-Distribution
3.2. Multivariate Skew-t Distribution
Cumulants of the Skew-t Distribution
4. Applications and Examples
4.1. Cumulant-Based Measures of Skewness and Kurtosis
4.2. Covariance Matrices
4.3. Illustrative Numerical Examples
5. Proofs
5.1. Commutator and Symmetrizer Matrices
Author Contributions
Funding
Conflicts of Interest
References
- Kollo, T.; von Rosen, D. Advanced Multivariate Statistics with Matrices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 579. [Google Scholar]
- McCullagh, P. Tensor Methods in Statistics; Courier Dover Publications: New York, NY, USA, 2018. [Google Scholar]
- Ould-Baba, H.; Robin, V.; Antoni, J. Concise formulae for the cumulant matrices of a random vector. Linear Algebra Appl. 2015, 485, 392–416. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Qi, L. Rank and eigenvalues of a supersymmetric tensor, the multivariate homogeneous polynomial and the algebraic hypersurface it defines. J. Symb. Comput. 2006, 41, 1309–1327. [Google Scholar] [CrossRef]
- Berkane, M.; Bentler, P.M. Moments of elliptically distributed random variates. Stat. Probab. Lett. 1986, 4, 333–335. [Google Scholar] [CrossRef]
- Mardia, K.V. Measures of Multivariate Skewness and Kurtosis with Applications. Biometrika 1970, 57, 519–530. [Google Scholar] [CrossRef]
- Malkovich, J.F.; Afifi, A.A. On tests for multivariate normality. J. Am. Stat. Assoc. 1973, 68, 176–179. [Google Scholar] [CrossRef]
- Srivastava, M.S. A measure of skewness and kurtosis and a graphical method for assessing multivariate normality. Stat. Probab. Lett. 1984, 2, 263–267. [Google Scholar] [CrossRef]
- Koziol, J.A. A Note on Measures of Multivariate Kurtosis. Biom. J. 1989, 31, 619–624. [Google Scholar] [CrossRef]
- Móri, T.F.; Rohatgi, V.K.; Székely, G.J. On multivariate skewness and kurtosis. Theory Probab. Appl. 1994, 38, 547–551. [Google Scholar] [CrossRef]
- Shoukat Choudhury, M.; Shah, S.; Thornhill, N. Diagnosis of poor control-loop performance using higher-order statistics. Automatica 2004, 40, 1719–1728. [Google Scholar] [CrossRef]
- Oja, H.; Sirkiä, S.; Eriksson, J. Scatter matrices and independent component analysis. Austrian J. Stat. 2006, 35, 175–189. [Google Scholar]
- Balakrishnan, N.; Brito, M.R.; Quiroz, A.J. A vectorial notion of skewness and its use in testing for multivariate symmetry. Commun. Stat. Theory Methods 2007, 36, 1757–1767. [Google Scholar] [CrossRef]
- Kollo, T. Multivariate skewness and kurtosis measures with an application in ICA. J. Multivar. Anal. 2008, 99, 2328–2338. [Google Scholar] [CrossRef]
- Tyler, D.E.; Critchley, F.; Dümbgen, L.; Oja, H. Invariant co-ordinate selection. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009, 71, 549–592. [Google Scholar] [CrossRef]
- Ilmonen, P.; Nevalainen, J.; Oja, H. Characteristics of multivariate distributions and the invariant coordinate system. Stat. Probab. Lett. 2010, 80, 1844–1853. [Google Scholar] [CrossRef]
- Peña, D.; Prieto, F.J.; Viladomat, J. Eigenvectors of a kurtosis matrix as interesting directions to reveal cluster structure. J. Multivar. Anal. 2010, 101, 1995–2007. [Google Scholar] [CrossRef]
- Tanaka, K.; Yamada, T.; Watanabe, T. Applications of Gram–Charlier expansion and bond moments for pricing of interest rates and credit risk. Quant. Financ. 2010, 10, 645–662. [Google Scholar] [CrossRef]
- Huang, H.H.; Lin, S.H.; Wang, C.P.; Chiu, C.Y. Adjusting MV-efficient portfolio frontier bias for skewed and non-mesokurtic returns. N. Am. J. Econ. Financ. 2014, 29, 59–83. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, J.; Yao, Y. Online monitoring of multivariate processes using higher-order cumulants analysis. Ind. Eng. Chem. Res. 2014, 53, 4328–4338. [Google Scholar] [CrossRef]
- Lin, S.H.; Huang, H.H.; Li, S.H. Option pricing under truncated Gram–Charlier expansion. N. Am. J. Econ. Financ. 2015, 32, 77–97. [Google Scholar] [CrossRef]
- Loperfido, N. Singular value decomposition of the third multivariate moment. Linear Algebra Appl. 2015, 473, 202–216. [Google Scholar] [CrossRef]
- De Luca, G.; Loperfido, N. Modelling multivariate skewness in financial returns: A SGARCH approach. Eur. J. Financ. 2015, 21, 1113–1131. [Google Scholar] [CrossRef]
- Fiorentini, G.; Planas, C.; Rossi, A. Skewness and kurtosis of multivariate Markov-switching processes. Comput. Stat. Data Anal. 2016, 100, 153–159. [Google Scholar] [CrossRef]
- León, A.; Moreno, M. One-sided performance measures under Gram-Charlier distributions. J. Bank. Financ. 2017, 74, 38–50. [Google Scholar] [CrossRef]
- Nordhausen, K.; Oja, H.; Tyler, D.E.; Virta, J. Asymptotic and bootstrap tests for the dimension of the non-Gaussian subspace. IEEE Signal Process. Lett. 2017, 24, 887–891. [Google Scholar] [CrossRef]
- Loperfido, N. Skewness-based projection pursuit: A computational approach. Comput. Stat. Data Anal. 2018, 120, 42–57. [Google Scholar] [CrossRef]
- Jammalamadaka, S.; Taufer, E.; Terdik, G.H. On Multivariate Skewness and Kurtosis. Sankhya A 2021, 83-A, 607–644. [Google Scholar] [CrossRef]
- Jammalamadaka, S.; Taufer, E.; Terdik, G.H. Asymptotic theory for statistics based on cumulant vectors with applications. Scand. J. Stat. 2021, 48, 708–728. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2003, 65, 367–389. [Google Scholar] [CrossRef]
- Azzalini, A.; Regoli, G. Some properties of skew-symmetric distributions. Ann. Inst. Stat. Math. 2011, 64, 857–879. [Google Scholar] [CrossRef]
- Sahu, S.K.; Dey, D.K.; Branco, M.D. A new class of multivariate skew distributions with applications to Bayesian regression models. Can. J. Stat. 2003, 31, 129–150. [Google Scholar] [CrossRef]
- Jones, M.C.; Faddy, M. A skew extension of the t-distribution, with applications. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2003, 65, 159–174. [Google Scholar] [CrossRef]
- Adcock, C.; Azzalini, A. A Selective Overview of Skew-Elliptical and Related Distributions and of Their Applications. Symmetry 2020, 12, 118. [Google Scholar] [CrossRef]
- Rao Jammalamadaka, S.; Subba Rao, T.; Terdik, G. Higher Order Cumulants of Random Vectors and Applications to Statistical Inference and Time Series. Sankhya Ser. A Methodol. 2006, 68, 326–356. [Google Scholar]
- NIST Digital Library of Mathematical Functions. Release 1.0.17 of 2017-12-22. 2020. Available online: http://dlmf.nist.gov/ (accessed on 23 June 2021).
- Fang, K.W.; Kotz, S.; Ng, K.W. Symmetric Multivariate and Related Distributions; Chapman and Hall: London, UK; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Muirhead, R.J. Aspects of Multivariate Statistical Theory; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 197. [Google Scholar]
- Anderson, T.W. An Introduction to Multivariate Statistical Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Steyn, H. On the problem of more than one kurtosis parameter in multivariate analysis. J. Multivar. Anal. 1993, 44, 1–22. [Google Scholar] [CrossRef][Green Version]
- Azzalini, A.; Dalla Valle, A. The Multivariate Skew-Normal Distribution. Biometrika 1996, 83, 715–726. [Google Scholar] [CrossRef]
- Azzalini, A.; Capitanio, A. Statistical applications of the multivariate skew normal distribution. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1999, 61, 579–602. [Google Scholar] [CrossRef]
- Genton, M.G.; He, L.; Liu, X. Moments of skew-normal random vectors and their quadratic forms. Stat. Probab. Lett. 2001, 51, 319–325. [Google Scholar] [CrossRef]
- Azzalini, A. The Skew-normal Distribution and Related Multivariate Families. Scand. J. Stat. 2005, 32, 159–188. [Google Scholar] [CrossRef]
- Branco, M.D.; Dey, D.K. A General Class of Multivariate Skew-Elliptical Distributions. J. Multivar. Anal. 2001, 79, 99–113. [Google Scholar] [CrossRef]
- Kim, H.J.; Mallick, B.K. Moments of random vectors with skew t distribution and their quadratic forms. Stat. Probab. Lett. 2003, 63, 417–423. [Google Scholar] [CrossRef]
- Sutradhar, B.C. On the characteristic function of multivariate Student t-distribution. Can. J. Stat. 1986, 14, 329–337. [Google Scholar] [CrossRef]
- Holmquist, B. The D-Variate Vector Hermite Polynomial of Order. Linear Algebra Appl. 1996, 237/238, 155–190. [Google Scholar] [CrossRef]
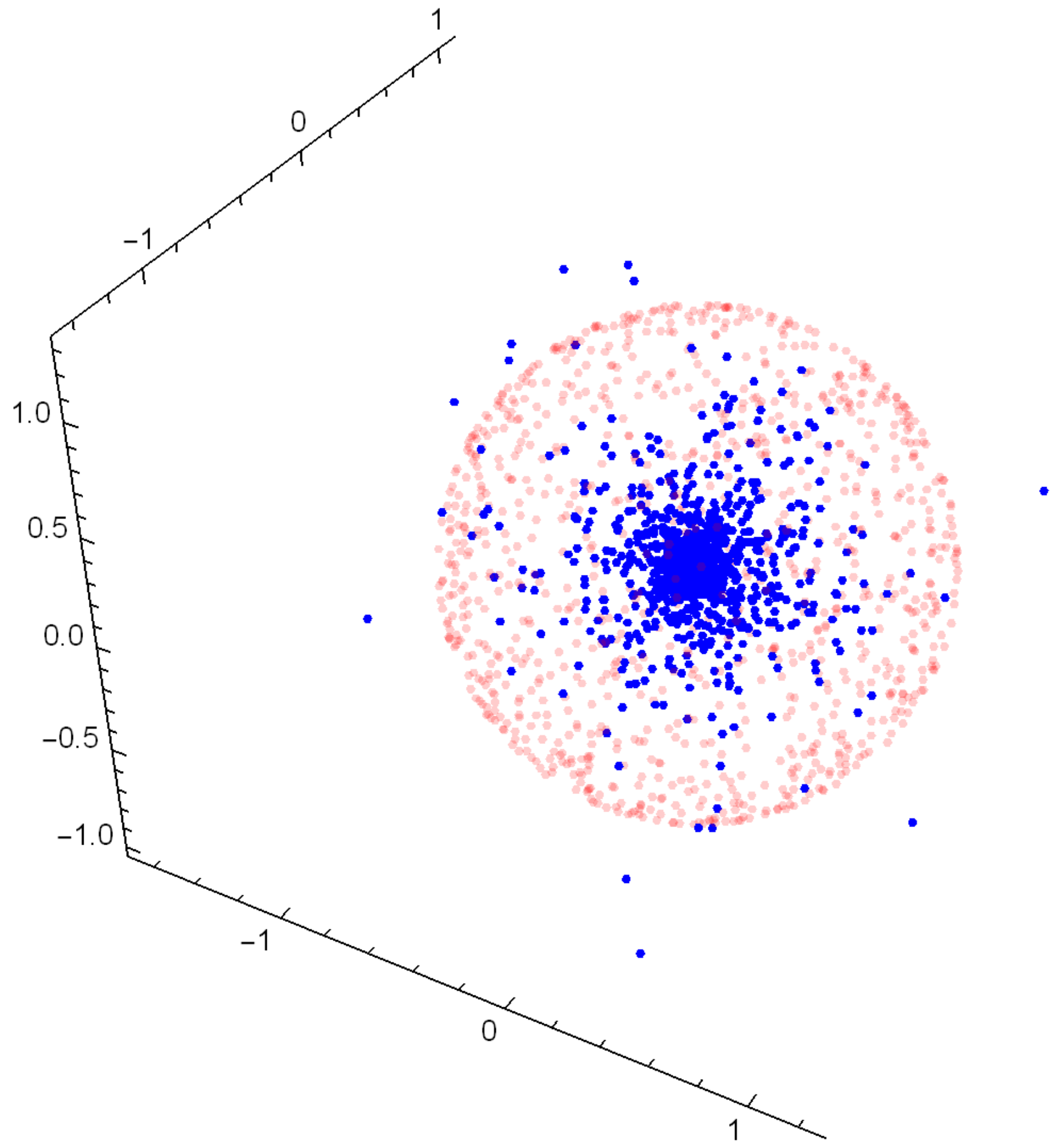
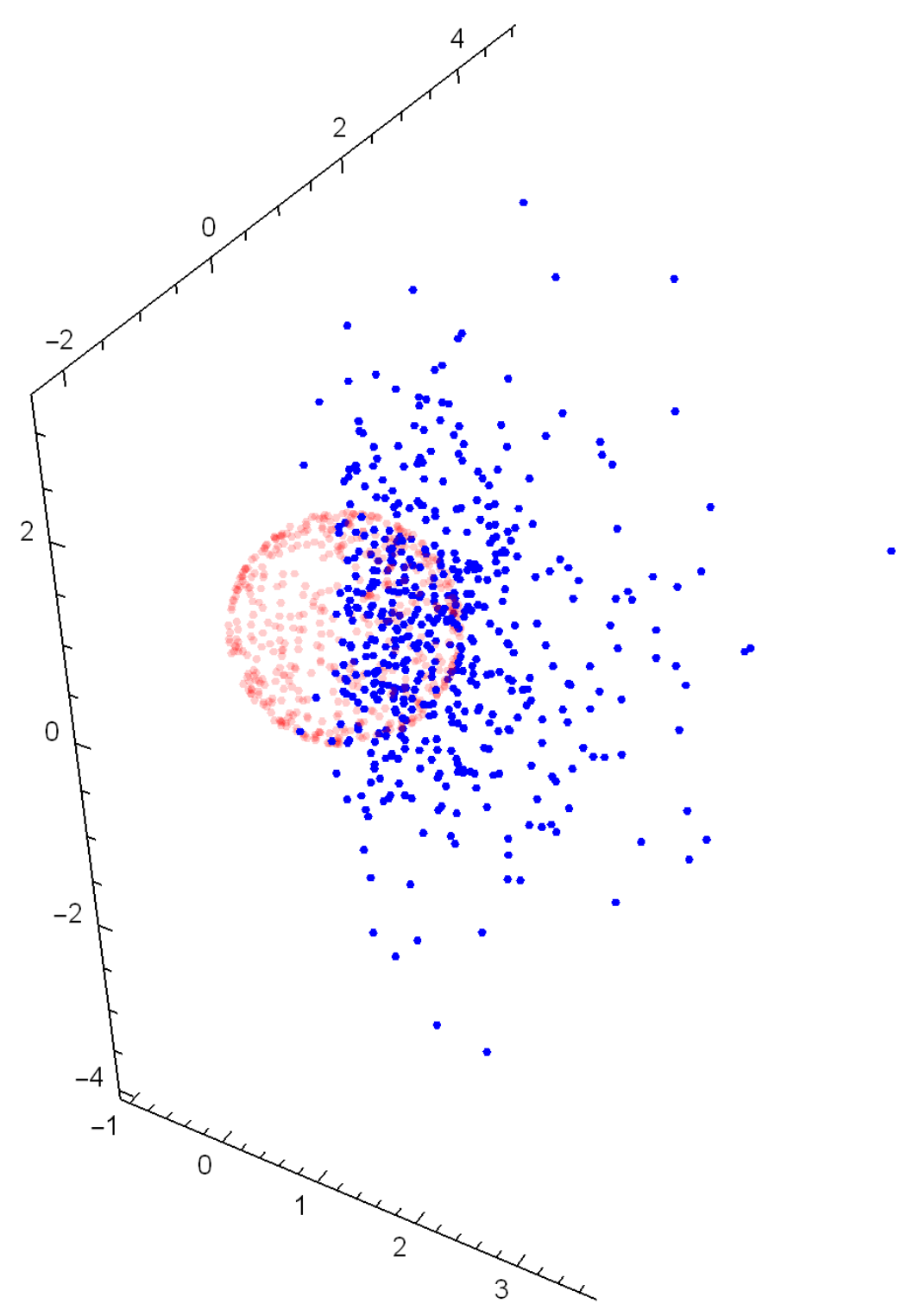
| 2m | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|
| True | 0.0600 | 0.0388 | 0.0750 | 0.2939 | 1.9480 |
| Sample | 0.0597 | 0.0331 | 0.0412 | 0.0718 | 0.1438 |
| Sample | 0.0597 | 0.0371 | 0.0606 | 0.1612 | 0.5439 |
| Sample | 0.0602 | 0.0394 | 0.0734 | 0.2401 | 1.0682 |
| Sample | 0.0601 | 0.0391 | 0.0740 | 0.2614 | 1.3682 |
| m | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| True | 0.0300 | 0.00324 | 0.00062 | 0.00017 | 2.60 |
| Sample | 0.0334 | 0.00477 | 0.00132 | 0.00040 | 3.28 |
| Sample | 0.0313 | 0.00331 | 0.00052 | 0.00009 | 2.38 |
| Sample | 0.0303 | 0.00333 | 0.00067 | 0.00019 | 2.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jammalamadaka, S.R.; Taufer, E.; Terdik, G.H. Cumulants of Multivariate Symmetric and Skew Symmetric Distributions. Symmetry 2021, 13, 1383. https://doi.org/10.3390/sym13081383
Jammalamadaka SR, Taufer E, Terdik GH. Cumulants of Multivariate Symmetric and Skew Symmetric Distributions. Symmetry. 2021; 13(8):1383. https://doi.org/10.3390/sym13081383
Chicago/Turabian StyleJammalamadaka, Sreenivasa Rao, Emanuele Taufer, and Gyorgy H. Terdik. 2021. "Cumulants of Multivariate Symmetric and Skew Symmetric Distributions" Symmetry 13, no. 8: 1383. https://doi.org/10.3390/sym13081383
APA StyleJammalamadaka, S. R., Taufer, E., & Terdik, G. H. (2021). Cumulants of Multivariate Symmetric and Skew Symmetric Distributions. Symmetry, 13(8), 1383. https://doi.org/10.3390/sym13081383






