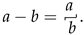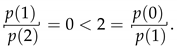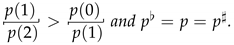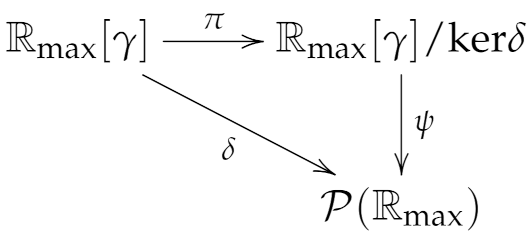Ordered Structures of Polynomials over Max-Plus Algebra

Abstract

The ordered structures of polynomial idempotent algebras over max-plus algebra are investigated in this paper. Based on the antisymmetry, the partial orders on the sets of formal polynomials and polynomial functions are introduced to generate two partially ordered idempotent algebras (POIAs). Based on the symmetry, the quotient POIA of formal polynomials is then obtained. The order structure relationships among these three POIAs are described: the POIA of polynomial functions and the POIA of formal polynomials are orderly homomorphic; the POIA of polynomial functions and the quotient POIA of formal polynomials are orderly isomorphic. By using the partial order on formal polynomials, an algebraic method is provided to determine the upper and lower bounds of an equivalence class in the quotient POIA of formal polynomials. The criterion for a formal polynomial to be the minimal element of an equivalence class is derived. Furthermore, it is proven that any equivalence class is either an uncountable set with cardinality of the continuum or a finite set with a single element.

1. Introduction

Max-plus algebra [1,2,3,4] has a nice algebraic structure and is effectively used to model, analyze, control and optimize some nonlinear time-evolution systems with synchronization but no concurrency (see, e.g., [5,6,7,8,9,10,11]). These nonlinear systems can be described by a max-plus linear time-invariant model, which is called the max-plus linear system. The matrix theory in max-plus algebra has been developed, including the computation for eigenvalues and eigenvectors [12,13,14,15,16,17], The Cayley–Hamilton theorem [18,19], QR decomposition [20] and solvability of linear equations [21,22,23]. Meanwhile, the polynomial theory in max-plus algebra has also been studied. For example, Cuninghame-Green and Meijer [24,25] investigated the factorization of maxpolynomials and found out that the polynomials over max-plus algebra have algebraic properties closely similar to the conventional algebra, especially the fundamental theorem of algebra, which also exists in max-plus algebra. Baccelli et al. [2] introduced the idempotent algebras of formal polynomials and polynomial functions and explored the evaluation homomorphism between them. De Schutter and De Moor [26] have given all solutions of a system of multivariate polynomial equalities and inequalities. Burkard and Butkovič [27,28] established an algorithm with polynomial complexity to compute all essential terms of a characteristic maxpolynomial. Izhakian et al. [29,30] showed that systems of tropical polynomials formed from univariate monomials define subsemigroups with respect to tropical addition (maximum). Rosenmann et al. [31] created an exact and simple description of all roots of convolutions in terms of the roots of involved maxpolynomials. Wang and Tao [32] introduced the matrix representation of formal polynomials over max-plus algebra to factorize polynomial functions. The polynomials over max-plus algebra have important applications in modeling and analysis of max-plus linear systems. For example, both the state transition function and characteristic polynomial of a max-plus linear system are maxpolynomials. The former describes state evolution and the latter determines cycle time of the system (see, e.g., [7,19,27]).

Ordered structures are everywhere in mathematics and computer sciences, and they provide a formal framework for describing the idea of being greater or less than another element. There are many examples of ordered structures appearing in different algebraic systems, for instance, ordered groups, ordered rings, ordered vector spaces, and so on (see, e.g., [33,34,35]). This paper will consider the ordered structures of polynomial idempotent algebras over max-plus algebra. Based on the symmetry and antisymmetry of binary relations, the partial orders on the idempotent algebras of formal polynomials and polynomial functions, and the quotient idempotent algebra of formal polynomials relative to the kernel of evaluation homomorphism, are introduced to derive three partially ordered idempotent algebras (POIAs). The orderly structural relationships among these three POIAs are then studied. It is proven that the POIA of polynomial functions and the POIA of formal polynomials are orderly homomorphic; the POIA of polynomial functions and the quotient POIA of formal polynomials are orderly isomorphic. By using the partial order on formal polynomials, the boundary and cardinality of an equivalence class in the quotient POIA of formal polynomials will be also considered. Baccelli et al. [2] used a graphic approach to prove that the concavified polynomial and skeleton are the maximum and minimum elements in an equivalence class, respectively. This paper will provide an algebraic proof for it. Such an investigation leads to an interesting observation, that is, any equivalence class is either an uncountable set with cardinality of the continuum or a finite set with cardinality of 1. In [2], a criterion for the maximal element of an equivalence class was given. In this paper, a criterion for the minimal element is derived. The ordered structures of polynomials over max-plus algebra will help to solve polynomial programming and linear assignment problems (see, e.g., [6,28]).

The remaining sections are as follows. Section 2 recalls some concepts about binary relations, idempotent algebras and maxpolynomials. Section 3 introduces three POIAs of maxpolynomials and discusses the orderly homomorphisms among them. The boundary and cardinality of an equivalence class in the quotient POIA of formal polynomials are provided in Section 4 and Section 5, respectively. Section 6 draws the conclusion.

2. Preliminaries

2.1. Binary Relation

A binary relation R is defined on a set A if, for $a,b\in A$, one can determine whether or not a is in R to b. If a is in R to b, one writes $aRb$. For $a,b,c\in A$, R is reflexive if $aRa$; R is symmetric if $aRb$ $\Rightarrow bRa$; R is antisymmetric if $aRb\mathrm{and}bRa\Rightarrow a=b$; R is transitive if $aRb\mathrm{and}bRc\Rightarrow aRc$.

A binary relation ∼ is called an equivalence relation if it is reflexive, symmetric and transitive. The equivalence class (relative to ∼) of an element a is the subset of all elements of A which are equivalent to a, i.e., $\left[a\right]=\{x\in A|x\sim a\}.$ A set A can be partitioned in equivalence classes given by an equivalence relation ∼, which is called a quotient set of A relative to ∼, i.e., $A/\sim =\left\{\right[a\left]\right|a\in A\}.$

A binary relation ⪯ is called a partial order if it is reflexive, antisymmetric and transitive. A partially ordered set $(A,⪯)$ is a set A with a partial order ⪯. For $a,b\in A$, $a\prec b$ means that $a⪯b$ and $a\ne b$. An element a of $(A,⪯)$ is said to be maximal (resp. minimal) if there exists no $b\in A$ such that $a\prec b$ (resp. $b\prec a$).

2.2. Partially Ordered Idempotent Algebra

Definition 1

([2]). Let $(\mathcal{M},{\oplus }_1)$ be an abelian group with zero element ${\epsilon }_1$ and $(\mathcal{K},{\oplus }_2,{\otimes }_2)$ be an idem-potent semifield with zero and identity elements ${\epsilon }_2$ and e, respectively. $\mathcal{M}$ is called a moduloid over $\mathcal{K}$ if there exists

$$\begin{array}{cc}\hfill \phi :\mathcal{K}\times \mathcal{M}& \to \mathcal{M},\hfill \\ \hfill (k,a)& \mapsto ka,\hfill \end{array}$$

satisfying properties:

• $\phi (k,a{\oplus }_{1}b)=\phi (k,a){\oplus }_1\phi (k,b)$;
• $\phi (k{\oplus }_{2}l,a)=\phi (k,a){\oplus }_1\phi (l,a)$;
• $\phi (k,\phi (l,a))=\phi (k{\otimes }_{2}l,a)$;
• $\phi (e,a)=a$;
• $\phi ({\epsilon }_2,a)={\epsilon }_1$.

where $a,b\in \mathcal{M}$ and $k,l\in \mathcal{K}$.

Definition 2

([2]). Let $(\mathcal{M},{\oplus }_1)$ be a moduloid over the idempotent semifield $(\mathcal{K},{\oplus }_2,{\otimes }_2)$. $(\mathcal{M},{\oplus }_1)$ together with an internal operation ${\otimes }_1$ is called an idempotent algebra if ${\otimes }_1$ is associative and distributive with respect to ${\oplus }_1$, and has an identity element.

For simplicity, subscripts 1 and 2 of operation notations ⊕ and ⊗ are sometimes omitted or ⊗ is omitted altogether, if these do not lead to confusion.

There are various kinds of ordered structures in different algebraic systems (see, e.g., [33,34,35,36,37]). Let us introduce the concept of partial order to the idempotent algebra.

Definition 3.

Let $(\mathcal{M},\oplus ,\otimes )$ be an idempotent algebra over the semifield $\mathcal{K}$. $(\mathcal{M},\oplus ,\otimes )$ endowed with a partial order ⪯ is called a partially ordered idempotent algebra (POIA) if

$$\left\{\begin{array}{ccc}{a}_1\hfill & ⪯\hfill & b_1\hfill \\ a_2\hfill & ⪯\hfill & b_2\hfill \end{array}\right.⟹\left\{\begin{array}{ccc}\hfill a_1\oplus a_2& ⪯& b_1\oplus b_2\hfill \\ \hfill a_1\otimes a_2& ⪯& b_1\otimes b_2\hfill \\ \hfill k{a}_1& ⪯& k{b}_1\hfill \end{array}\right.,$$

where $a_1,a_2,b_1,b_2\in \mathcal{M}$ and $k\in \mathcal{K}$.

Definition 4.

Let $({\mathcal{M}}_1,{\oplus }_1,{\otimes }_1)$ and $({\mathcal{M}}_2,{\oplus }_2,{\otimes }_2)$ be two idempotent algebras over the semifield $\mathcal{K}$. A map $\xi :{\mathcal{M}}_1\to {\mathcal{M}}_2$ is said to be homomorphic if

$$\begin{array}{cc}\hfill \xi \left(a{\oplus }_{1}b\right)& =\xi \left(a\right){\oplus }_2\xi \left(b\right),\hfill \\ \hfill \xi \left(a{\otimes }_{1}b\right)& =\xi \left(a\right){\otimes }_{2}f\left(b\right),\hfill \\ \hfill \xi \left(ka\right)& =k\xi \left(a\right),\hfill \end{array}$$

where $a,b\in {\mathcal{M}}_1$ and $k\in \mathcal{K}$. The kernel of a homomorphic map ξ is defined by

$$\ker \xi =\left\{(a,b)\right|\xi \left(a\right)=\xi \left(b\right),a,b\in {\mathcal{M}}_1\}.$$

The ordered homomorphism of ordered semigroups has been introduced in [36]. The following is an extension of such an ordered homomorphism to POIAs.

Definition 5.

Two POIAs, $({\mathcal{M}}_1,{⪯}_1)$ and $({\mathcal{M}}_2,{⪯}_2)$, are said to be orderly homomorphic if there exists a homomorphism ξ from ${\mathcal{M}}_1$ to ${\mathcal{M}}_2$ such that the following propositions hold:

• for $a,b\in {\mathcal{M}}_1$, if $a{⪯}_{1}b$, then $\xi \left(a\right){⪯}_2\xi \left(b\right)$;
• for $u,v\in {\mathcal{M}}_2$, if $u{⪯}_{2}v$, then there exist $a,b\in {\mathcal{M}}_1$ such that $\xi \left(a\right)=u,\xi \left(b\right)=v\mathrm{and}a{⪯}_{1}b.$

POIAs ${\mathcal{M}}_1$ and ${\mathcal{M}}_2$ are said to be orderly isomorphic if ξ is also isomorphic, i.e.,

• for $a,b\in {\mathcal{M}}_1$, $a{⪯}_{1}b⟺\xi \left(a\right){⪯}_2\xi \left(b\right)$.

2.3. Polynomial Idempotent Algebras over ${\mathbb{R}}_{max}$

Let $\mathbb{R}$ and $\mathbb{N}$ be the sets of real numbers and natural numbers, respectively. For $a,b\in \mathbb{R}\cup \{-\infty \}$,

$$a\oplus b=max\{a,b\},a\otimes b=a+b,$$

where $max\{a,-\infty \}=a$ and $a+(-\infty )=-\infty$. Then, $\{\mathbb{R}\cup \{-\infty \},\oplus ,\otimes \}$ is a commutative idempotent semifield, which is called max-plus algebra and simply denoted by ${\mathbb{R}}_{max}$ (see [1,2,3]). In ${\mathbb{R}}_{max}$, the zero and identity elements are $-\infty$ and 0, which are denoted by $\epsilon$ and e, respectively. The conventional subtraction − is denoted by a two-dimensional display notation in ${\mathbb{R}}_{max}$, i.e.,

                      

For $a,b\in {\mathbb{R}}_{max}$, $a⩽b$ if $a\oplus b=b$.

A formal polynomial over ${\mathbb{R}}_{max}$ is a set of finite sequences

$$p=\left(p\right(k),p(k+1),\cdots ,p(n\left)\right),$$

(1)

where $p(·)\in {\mathbb{R}}_{max}$, $p\left(k\right)\ne \epsilon$ and $p\left(n\right)\ne \epsilon$. The extreme values k and n are called the valuation and degree of p, which are denoted by $\mathrm{val}\left(p\right)$ and $\mathrm{deg}\left(p\right)$, respectively. For the convenience of expression, $N\left(p\right)$ denotes the set $\{k,k+1,\cdots ,$$n\}$, where $k=\mathrm{val}\left(p\right)$ and $n=\mathrm{deg}\left(p\right)$. The support of p is defined by $\mathrm{supp}\left(p\right)=\{l\in \mathbb{N}|p\left(l\right)\ne \epsilon \}.$ A formal polynomial p has full support if $p\left(l\right)\ne \epsilon$ for any $l\in N\left(p\right).$

Define a formal polynomial $\gamma$ as

$$\gamma \left(l\right)=\left\{\begin{array}{cc}e,\hfill & l=1;\hfill \\ \epsilon ,\hfill & else.\hfill \end{array}\right.$$

Then, (1) can be represented as

$$p=\underset{l=k}{\overset{n}{⨁}}p\left(l\right)\otimes {\gamma }^{\otimes l}.$$

(2)

${\mathbb{R}}_{max}\left[\gamma \right]$ denotes the set of formal polynomials over ${\mathbb{R}}_{max}$. For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$, $d\in {\mathbb{R}}_{max}$ and $l\in \mathbb{N}$, the internal and external operations of ${\mathbb{R}}_{max}\left[\gamma \right]$ are defined as below:

• Internal operations:
  addition: $(p\oplus q)\left(l\right)=p\left(l\right)\oplus q\left(l\right)$;
  multiplication: $(p\otimes q)\left(l\right)={⨁}_{i+j=l}p\left(i\right)\otimes q\left(j\right).$
• External operation: $\left(dp\right)\left(l\right)=d\otimes p\left(l\right)$.

Then, $({\mathbb{R}}_{max}\left[\gamma \right],\oplus ,\otimes )$ is an idempotent algebra over ${\mathbb{R}}_{max}$ (see [2] (Theorem 3.31)).

Formal polynomial (2) is associated with a polynomial function as below:

$$\begin{array}{cc}\hfill \widehat{p}:{\mathbb{R}}_{max}& \to {\mathbb{R}}_{max},\hfill \\ \hfill c& \mapsto \widehat{p}\left(c\right)=\underset{l=k}{\overset{n}{⨁}}p\left(l\right)\otimes c^{\otimes l}.\hfill \end{array}$$

$\mathcal{P}\left({\mathbb{R}}_{max}\right)$ denotes the set of polynomial functions over ${\mathbb{R}}_{max}$. For $\widehat{p},\widehat{q}\in \mathcal{P}\left({\mathbb{R}}_{max}\right)$ and $d,c$ $\in {\mathbb{R}}_{max}$, the internal and external operations of $\mathcal{P}\left({\mathbb{R}}_{max}\right)$ are defined as below:

• Internal operations:
  addition: $(\widehat{p}\oplus \widehat{q})\left(c\right)=\widehat{p}\left(c\right)\oplus \widehat{q}\left(c\right)$,
  multiplication: $(\widehat{p}\otimes \widehat{q})\left(c\right)=\widehat{p}\left(c\right)\otimes \widehat{q}\left(c\right)$;
• External operation: $\left(d\widehat{p}\right)\left(c\right)=d\otimes \widehat{p}\left(c\right)$.

Then, $(\mathcal{P}\left({\mathbb{R}}_{max}\right),\oplus ,\otimes )$ is an idempotent algebra over ${\mathbb{R}}_{max}$ (see [2] (Theorem 3.33)).

By setting $p\left(l\right)=\epsilon$ for $l\notin N\left(p\right)$, the domain of p can be extended from $N\left(p\right)$ to $\mathbb{N}$. Then, a formal polynomial p can be viewed as a function from $\mathbb{N}$ to ${\mathbb{R}}_{max}$, i.e.,

$$\begin{array}{cc}\hfill p:\mathbb{N}& \to {\mathbb{R}}_{max},\hfill \\ \hfill l& \mapsto p\left(l\right).\hfill \end{array}$$

It is pointed out in [2] (Remark 3.36) that

$$\widehat{p}\left(c\right)=\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+p\left(l\right)).$$

(3)

The hypograph of p is defined by $\mathrm{hypo}\left(p\right)=\left\{(x,y)\right|y⩽p\left(x\right),x\in \mathbb{N},y\in {\mathbb{R}}_{max}\}.$

For the idempotent algebras ${\mathbb{R}}_{max}\left[\gamma \right]$ and $\mathcal{P}\left({\mathbb{R}}_{max}\right)$, let

$$\begin{array}{cc}\hfill \delta :{\mathbb{R}}_{max}\left[\gamma \right]& \to \mathcal{P}\left({\mathbb{R}}_{max}\right),\hfill \\ \hfill p& \mapsto \widehat{p}.\hfill \end{array}$$

Then, $\delta$ is a homomorphism from ${\mathbb{R}}_{max}\left[\gamma \right]$ to $\mathcal{P}\left({\mathbb{R}}_{max}\right)$, which is called the evaluation homomorphism. The kernel of $\delta$ is

$$\ker \delta =\left\{(p,q)\right|\delta \left(p\right)=\delta \left(q\right)\}=\left\{(p,q)\right|\widehat{p}=\widehat{q}\}.$$

Obviously, $\ker \delta$ is an equivalence relation on ${\mathbb{R}}_{max}\left[\gamma \right]$. The quotient set of ${\mathbb{R}}_{max}\left[\gamma \right]$ relative to $\ker \delta$ is

$${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta =\left\{\left[p\right]\right|p\in {\mathbb{R}}_{max}\left[\gamma \right]\},\mathrm{where}\left[p\right]=\left\{q\right|(p,q)\in \ker \delta \}=\left\{q\right|\widehat{p}=\widehat{q}\}.$$

The following lemma will show that the equivalence relation $\ker \delta$ is also a congruence relation on ${\mathbb{R}}_{max}\left[\gamma \right]$.

Lemma 1.

For $p_1,p_2,q_1,q_2\in {\mathbb{R}}_{max}\left[\gamma \right]$, if $\left[p_1\right]=\left[p_2\right]$ and $\left[q_1\right]=\left[q_2\right]$, then

$$\begin{array}{cc}\hfill [p_1\oplus q_1]& =[p_2\oplus q_2],[p_1\otimes q_1]=[p_2\otimes q_2]\mathit{and}\left[d{p}_1\right]=\left[d{p}_2\right],\hfill \end{array}$$

(4)

where $d\in {\mathbb{R}}_{max}$.

Proof. 

If $\left[p_1\right]=\left[p_2\right]$, then ${\widehat{p}}_1={\widehat{p}}_2$. If $\left[q_1\right]=\left[q_2\right]$, then ${\widehat{q}}_1={\widehat{q}}_2$. Hence,

$$\begin{array}{cc}\hfill & \widehat{p_1\oplus q_1}={\widehat{p}}_1\oplus {\widehat{q}}_1={\widehat{p}}_2\oplus {\widehat{q}}_2=\widehat{p_2\oplus q_2},\hfill \\ \hfill & \widehat{p_1\otimes q_1}={\widehat{p}}_1\otimes {\widehat{q}}_1={\widehat{p}}_2\otimes {\widehat{q}}_2=\widehat{p_2\otimes q_2},\hfill \\ \hfill & \widehat{d{p}_1}=\widehat{d\otimes p_1}=\widehat{d}\otimes {\widehat{p}}_1=\widehat{d}\otimes {\widehat{p}}_2=\widehat{d{p}_2},\hfill \end{array}$$

and so the equations in (4) hold. □

Based on the lemma above, the internal and external operations of the quotient set ${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta$ can be defined as follows: For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$ and $d\in {\mathbb{R}}_{max}$,

• Internal operations:
  addition: $\left[p\right]\oplus \left[q\right]=[p\oplus q]$;
  multiplication: $\left[p\right]\otimes \left[q\right]=[p\otimes q]$.
• External operation: $d\left[p\right]=\left[dp\right]$.

The quotient idempotent algebra of ${\mathbb{R}}_{max}\left[\gamma \right]$ relative to $\ker \delta$ can be then obtained.

Lemma 2.

$({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,\oplus ,\otimes )$ is an idempotent algebra over ${\mathbb{R}}_{max}$.

Proof. 

It can be seen that $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,\oplus )$ is a moduloid over ${\mathbb{R}}_{max}$. Since ${\mathbb{R}}_{max}\left[\gamma \right]$ is an idempotent algebra, for $p,q,r\in {\mathbb{R}}_{max}\left[\gamma \right]$,

$$\begin{array}{cc}\hfill \left(\right[p\left]\right[q\left]\right)\left[r\right]& =\left[pq\right]\left[r\right]=\left[\right(pq\left)r\right]=\left[p\right(qr\left)\right]=\left[p\right]\left[qr\right]=\left[p\right]\left(\right[q\left]\right[r\left]\right),\hfill \end{array}$$

i.e., ⊗ is associative. In addition,

$$\begin{array}{cc}\hfill \left[p\right]\left(\right[q]\oplus [r\left]\right)& =\left[p\right][q\oplus r]=\left[p\right(q\oplus r\left)\right]=[pq\oplus pr]=\left[pq\right]\oplus \left[pr\right]=\left[p\right]\left[q\right]\oplus \left[p\right]\left[r\right],\hfill \end{array}$$

i.e., ⊗ is distributive with respect to ⊕. Since $\left[e\right]\left[p\right]=\left[ep\right]=\left[p\right],$ one has that $\left[e\right]$ is the identity element of ${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta$. Hence, $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,$$\oplus ,\otimes )$ is an idempotent algebra. □

3. Ordered Structures of Polynomial Idempotent Algebras over ${\mathbb{R}}_{max}$

Define the binary relation ${⪯}_1$ on ${\mathbb{R}}_{max}\left[\gamma \right]$ as below: for $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$,

$$p{⪯}_{1}q⟺p\left(l\right)⩽q\left(l\right),l\in \mathbb{N}.$$

The POIA of formal polynomials can be then obtained.

Lemma 3.

${⪯}_1$ is a partial order on ${\mathbb{R}}_{max}\left[\gamma \right]$.

Proof. 

$p{⪯}_{1}p$, ${⪯}_1$ is reflexive. If $p{⪯}_{1}q$, then $p\left(l\right)⩽q\left(l\right)$. If $q{⪯}_{1}p$, then $q\left(l\right)⩽p\left(l\right)$. Hence, $p\left(l\right)=q\left(l\right)$ for $l\in \mathbb{N}$, i.e., $p=q$, and so ${⪯}_1$ is antisymmetric. If $p{⪯}_{1}q$, then $p\left(l\right)⩽q\left(l\right)$. If $q{⪯}_{1}r$, then $q\left(l\right)⩽r\left(l\right)$. Hence, $p\left(l\right)⩽r\left(l\right)$ for $l\in \mathbb{N}$, i.e., $p{⪯}_{1}r$, and so ${⪯}_1$ is transitive. Therefore, ${⪯}_1$ is a partial order. □

The partial order of formal polynomials over the max-plus algebra has the same form as that over the conventional algebra. According to the partial order ${⪯}_1$, two formal polynomials can be compared with each other. Note that, ${⪯}_1$ is not a total order. For example, formal polynomials $p={\gamma }^2\oplus 2\gamma \oplus 1$ and $q={\gamma }^2\oplus 1\gamma \oplus 2$ are not comparable.

Theorem 1.

$({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ is a POIA.

Proof. 

For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$, it can be seen that $p{⪯}_{1}q$ if and only if $p\oplus q=q$. For $p_1,p_2,q_1,$$q_2\in {\mathbb{R}}_{max}\left[\gamma \right]$, if $p_1{⪯}_1{q}_1$ and $p_2{⪯}_1{q}_2$, then $p_1\oplus q_1=q_1\mathrm{and}{p}_2\oplus q_2=q_2.$ It follows that

$$(p_1\oplus p_2)\oplus (q_1\oplus q_2)=(p_1\oplus q_1)\oplus (p_2\oplus q_2)=q_1\oplus q_2,$$

i.e., $p_1\oplus p_2{⪯}_1{q}_1\oplus q_2$. In addition, for $i,j\in \mathbb{N}$,

$$\begin{array}{cc}\hfill q_1\left(i\right)q_2\left(j\right)& =(p_1\oplus q_1)\left(i\right)(p_2\oplus q_2)\left(j\right)\hfill \\ \hfill & =(p_1\left(i\right)\oplus q_1\left(i\right))(p_2\left(j\right)\oplus q_2\left(j\right))\hfill \\ \hfill & =p_1\left(i\right)p_2\left(j\right)\oplus p_1\left(i\right)q_2\left(j\right)\oplus q_1\left(i\right)(p_2\left(j\right)\oplus q_2\left(j\right))\hfill \\ \hfill & =p_1\left(i\right)p_2\left(j\right)\oplus p_1\left(i\right)q_2\left(j\right)\oplus q_1\left(i\right)q_2\left(j\right)\hfill \\ \hfill & =p_1\left(i\right)p_2\left(j\right)\oplus (p_1\left(i\right)\oplus q_1\left(i\right))q_2\left(j\right)\hfill \\ \hfill & =p_1\left(i\right)p_2\left(j\right)\oplus q_1\left(i\right)q_2\left(j\right).\hfill \end{array}$$

Then, for $l\in \mathbb{N}$,

$$\begin{array}{cc}\hfill (p_1{p}_2\oplus q_1{q}_2)\left(l\right)& =\left(p_1{p}_2\right)\left(l\right)\oplus \left(q_1{q}_2\right)\left(l\right)=\underset{i+j=l}{⨁}(p_1\left(i\right)p_2\left(j\right)\oplus q_1\left(i\right)q_2\left(j\right))\hfill \\ \hfill & =\underset{i+j=l}{⨁}{q}_1\left(i\right)q_2\left(j\right)=\left(q_1{q}_2\right)\left(l\right),\hfill \end{array}$$

i.e., $p_1{p}_2{⪯}_1{q}_1{q}_2$. Moreover, for $d\in {\mathbb{R}}_{max}$,

$$\begin{array}{cc}\hfill (d{p}_1\oplus d{q}_1)\left(l\right)& =d{p}_1\left(l\right)\oplus d{q}_1\left(l\right)=d(p_1\left(l\right)\oplus q_1\left(l\right))=d{q}_1\left(l\right),\hfill \end{array}$$

i.e., $d{p}_1{⪯}_{1}d{q}_1$. Hence, $({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ is a POIA. □

Define the binary relation ${⪯}_2$ on $\mathcal{P}\left({\mathbb{R}}_{max}\right)$ as below: for $\widehat{p},\widehat{q}\in \mathcal{P}\left({\mathbb{R}}_{max}\right)$,

$$\widehat{p}{⪯}_2\widehat{q}⟺\widehat{p}\left(c\right)⩽\widehat{q}\left(c\right),c\in {\mathbb{R}}_{max}.$$

The POIA of polynomial functions can be then obtained.

Lemma 4.

${⪯}_2$ is a partial order on $\mathcal{P}\left({\mathbb{R}}_{max}\right)$.

Proof. 

$\widehat{p}{⪯}_2\widehat{p}$, ${⪯}_2$ is reflexive. If $\widehat{p}{⪯}_2\widehat{q}$, then $\widehat{p}\left(c\right)⩽\widehat{q}\left(c\right)$. If $\widehat{q}{⪯}_2\widehat{p}$, then $\widehat{q}\left(c\right)⩽\widehat{p}\left(c\right)$. It follows that $\widehat{p}\left(c\right)=\widehat{q}\left(c\right)$ for $c\in {\mathbb{R}}_{max}$, i.e., $\widehat{p}=\widehat{q}$. Hence, ${⪯}_2$ is antisymmetric. If $\widehat{p}{⪯}_2\widehat{q}$, then $\widehat{p}\left(c\right)⩽\widehat{q}\left(c\right)$. If $\widehat{q}{⪯}_2\widehat{r}$, then $\widehat{q}\left(c\right)⩽\widehat{r}\left(c\right)$. It follows that $\widehat{p}\left(c\right)⩽\widehat{r}\left(c\right)$ for $c\in {\mathbb{R}}_{max}$, i.e., $\widehat{p}{⪯}_2\widehat{r}$. Hence, ${⪯}_2$ is transitive. Therefore, ${⪯}_2$ is a partial order. □

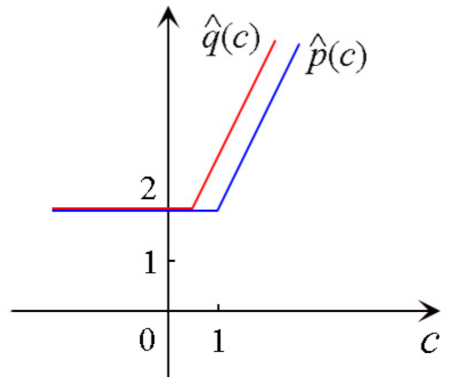
The partial order of polynomial functions over the max-plus algebra has the same form as that over the conventional algebra. Note that ${⪯}_2$ is not a total order. For example, for $\widehat{p}\left(c\right)=c^2\oplus 2c\oplus 1$ and $\widehat{q}\left(c\right)=c^2\oplus$$1c\oplus 2$, the graphs of $\widehat{p}$ and $\widehat{q}$ are depicted in Figure 1. It can be seen that $\widehat{p}$ and $\widehat{q}$ are not comparable.

Theorem 2.

$(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ is a POIA.

Proof. 

For $\widehat{p},\widehat{q}\in \mathcal{P}\left({\mathbb{R}}_{max}\right)$, it can be seen that $\widehat{p}{⪯}_2\widehat{q}$ if and only if $\widehat{p}\oplus \widehat{q}=\widehat{q}$. For ${\widehat{p}}_1,{\widehat{p}}_2,{\widehat{q}}_1,$${\widehat{q}}_2\in \mathcal{P}\left({\mathbb{R}}_{max}\right)$, if ${\widehat{p}}_1{⪯}_2{\widehat{q}}_1$ and ${\widehat{p}}_2{⪯}_2{\widehat{q}}_2$, then ${\widehat{p}}_1\oplus {\widehat{q}}_1={\widehat{q}}_1\mathrm{and}{\widehat{p}}_2\oplus {\widehat{q}}_2={\widehat{q}}_2.$ It follows that

$$({\widehat{p}}_1\oplus {\widehat{p}}_2)\oplus ({\widehat{q}}_1\oplus {\widehat{q}}_2)=({\widehat{p}}_1\oplus {\widehat{q}}_1)\oplus ({\widehat{p}}_2\oplus {\widehat{q}}_2)={\widehat{q}}_1\oplus {\widehat{q}}_2,$$

i.e., ${\widehat{p}}_1\oplus {\widehat{p}}_2{⪯}_2{\widehat{q}}_1\oplus {\widehat{q}}_2$. In addition,

$$\begin{array}{cc}\hfill {\widehat{p}}_1{\widehat{p}}_2\oplus {\widehat{q}}_1{\widehat{q}}_2& ={\widehat{p}}_1{\widehat{p}}_2\oplus ({\widehat{p}}_1\oplus {\widehat{q}}_1)({\widehat{p}}_2\oplus {\widehat{q}}_2)={\widehat{p}}_1{\widehat{p}}_2\oplus {\widehat{p}}_1{\widehat{p}}_2\oplus {\widehat{p}}_1{\widehat{q}}_2\oplus {\widehat{q}}_1{\widehat{p}}_2\oplus {\widehat{q}}_1{\widehat{q}}_2\hfill \\ \hfill & ={\widehat{p}}_1({\widehat{p}}_2\oplus {\widehat{q}}_2)\oplus {\widehat{q}}_1({\widehat{p}}_2\oplus {\widehat{q}}_2)={\widehat{p}}_1{\widehat{q}}_2\oplus {\widehat{q}}_1{\widehat{q}}_2=({\widehat{p}}_1\oplus {\widehat{q}}_1){\widehat{q}}_2={\widehat{q}}_1{\widehat{q}}_2,\hfill \end{array}$$

i.e., ${\widehat{p}}_1{\widehat{p}}_2{⪯}_2{\widehat{q}}_1{\widehat{q}}_2$. Moreover, for $d\in {\mathbb{R}}_{max}$, $d{\widehat{p}}_1\oplus d{\widehat{q}}_1=d({\widehat{p}}_1\oplus {\widehat{q}}_1)=d{\widehat{q}}_1,$ i.e., $d{\widehat{p}}_1{⪯}_{2}d{\widehat{q}}_1$. Hence, $(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ is a POIA. □

Define the binary relation ${⪯}_3$ on ${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta$ as below: for $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$,

$$\left[p\right]{⪯}_3\left[q\right]⟺\mathrm{there} \mathrm{exist} u\in \left[p\right],v\in \left[q\right]\mathrm{such} \mathrm{that} u{⪯}_{1}v.$$

The quotient POIA of formal polynomials can be then obtained.

Lemma 5.

${⪯}_3$ is a partial order on ${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta$.

Proof. 

It follows from $p{⪯}_{1}p$ that $\left[p\right]{⪯}_3\left[p\right]$. Hence, ${⪯}_3$ is reflexive. If $\left[p\right]{⪯}_3\left[q\right]$, then there exist $u_1\in \left[p\right]$ and $v_1\in \left[q\right]$, such that $u_1{⪯}_1{v}_1$, i.e., $u_1\oplus v_1=v_1$. If $\left[q\right]{⪯}_3\left[p\right]$, then there exist $u_2\in \left[p\right]$ and $v_2$ $\in \left[q\right]$, such that $v_2{⪯}_1{u}_2$, i.e., $u_2\oplus v_2=u_2$. It follows that

$$\widehat{p}={\widehat{u}}_2=\widehat{u_2\oplus v_2}={\widehat{u}}_2\oplus {\widehat{v}}_2={\widehat{u}}_1\oplus {\widehat{v}}_1=\widehat{u_1\oplus v_1}={\widehat{v}}_1=\widehat{q},$$

i.e., $\left[p\right]=\left[q\right]$. Hence, ${⪯}_3$ is antisymmetric. If $\left[p\right]{⪯}_3\left[q\right]$, then there exist $u_1\in \left[p\right]$ and $v_1\in \left[q\right]$, such that $u_1{⪯}_1{v}_1$, i.e., $u_1\oplus v_1=v_1$. If $\left[q\right]{⪯}_3\left[r\right]$, then there exist $v_2\in \left[q\right]$ and $w_1\in \left[r\right]$, such that $v_2{⪯}_1{w}_1$, i.e., $v_2\oplus w_1=w_1$. It follows that

$$\begin{array}{cc}\hfill \widehat{u_1\oplus v_1\oplus w_1}& =\widehat{u_1\oplus v_1}\oplus {\widehat{w}}_1={\widehat{v}}_1\oplus {\widehat{w}}_1={\widehat{v}}_2\oplus {\widehat{w}}_1=\widehat{v_2\oplus w_1}={\widehat{w}}_1=\widehat{r}.\hfill \end{array}$$

Let $w_2=u_1\oplus v_1\oplus w_1$. Then, there exist $u_1\in \left[p\right]$ and $w_2\in$$\left[r\right]$, such that $u_1{⪯}_1{w}_2$, i.e., $\left[p\right]{⪯}_3\left[r\right]$. Hence, ${⪯}_3$ is transitive. Therefore, ${⪯}_3$ is a partial order. □

The special properties of the semifiled lead to the different forms of the partial order on the quotient set of formal polynomials over the max-plus algebra from that over a linear space. Note that ${⪯}_3$ is not a total order. For example, for $p={\gamma }^2\oplus 2\gamma \oplus 1$ and $q={\gamma }^2\oplus 1\gamma \oplus 2$, any formal polynomial in $\left[p\right]$ is not comparable with any one in $\left[q\right]$. Obviously, for $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$, if $p{⪯}_{1}q$, then $\left[p\right]{⪯}_3\left[q\right]$. However, $\left[p\right]{⪯}_3\left[q\right]$ does not mean that any formal polynomial in $\left[p\right]$ is not greater than any one in $\left[q\right]$. This fact can be illustrated by the following example.

Example 1.

For $p={\gamma }^2\oplus 1\gamma \oplus 2$ and $q=1{\gamma }^2\oplus 2$, it can be seen that p and q are not comparable. Let $u=p\in \left[p\right]$ and $v=1{\gamma }^2\oplus 1\gamma \oplus 2\in \left[q\right]$. Then, $u{⪯}_{1}v$. This implies that $\left[p\right]{⪯}_3\left[q\right]$.

Theorem 3.

$({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$ is a POIA.

Proof. 

Let $p_1,q_1,p_2,q_2\in {\mathbb{R}}_{max}\left[\gamma \right]$. If $\left[p_1\right]{⪯}_3\left[q_1\right]$, then there exist $u_1\in \left[p_1\right]$ and $v_1$$\in \left[q_1\right]$, such that $u_1{⪯}_1{v}_1$, i.e., $u_1$$\oplus v_1=v_1$. If $\left[p_2\right]{⪯}_3\left[q_2\right]$, then there exist $u_2\in \left[p_2\right]$ and $v_2\in \left[q_2\right]$, such that $u_2{⪯}_1{v}_2$, i.e., $u_2\oplus v_2=v_2$. Since $({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ is a POIA, one has $u_1\oplus u_2{⪯}_1{v}_1\oplus v_2$ and $u_1\otimes u_2{⪯}_1$$v_1\otimes v_2$. In addition,

$$\widehat{u_1\oplus u_2}={\widehat{u}}_1\oplus {\widehat{u}}_2={\widehat{p}}_1\oplus {\widehat{p}}_2=\widehat{p_1\oplus p_2}.$$

Then, $u_1\oplus u_2\in [p_1\oplus p_2]$. Similarly, $v_1\oplus v_2\in [q_1\oplus q_2]$. This implies that there exist $u_1\oplus u_2\in [p_1\oplus p_2]$ and $v_1\oplus v_2\in [q_1\oplus q_2]$, such that $u_1\oplus u_2{⪯}_1{v}_1\oplus v_2$. Hence, $[p_1\oplus p_2]{⪯}_3[q_1\oplus q_2]$, and so $\left[p_1\right]\oplus \left[p_2\right]{⪯}_3\left[q_1\right]\oplus \left[q_2\right]$. Similarly, $\left[p_1\right]\otimes \left[p_2\right]{⪯}_3\left[q_1\right]\otimes \left[q_2\right]$. Moreover, for $d\in {\mathbb{R}}_{max}$, there exist $d{u}_1\in \left[d{p}_1\right]$ and $d{v}_1\in \left[d{q}_1\right]$ such that $d{u}_1{⪯}_{1}d{v}_1$. Hence, $\left[d{p}_1\right]{⪯}_3\left[d{q}_1\right]$, and so $d\left[p_1\right]{⪯}_{3}d\left[q_1\right]$. Therefore, $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$ is a POIA. □

There exists a natural homomorphism from idempotent algebra ${\mathbb{R}}_{max}\left[\gamma \right]$ to quotient idempotent algebra ${\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta$, i.e.,

$$\begin{array}{cc}\hfill \pi :{\mathbb{R}}_{max}\left[\gamma \right]& \to {\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,\hfill \\ \hfill p& \mapsto \left[p\right].\hfill \end{array}$$

The following theorem gives the relationship between POIAs $({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$.

Theorem 4.

$({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$ are orderly homomorphic.

Proof. 

For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$ and $d\in {\mathbb{R}}_{max}$, it is easy to verify that

$$\begin{array}{cc}\hfill \pi (p\oplus q)& =[p\oplus q]=\left[p\right]\oplus \left[q\right]=\pi \left(p\right)\oplus \pi \left(q\right),\hfill \\ \hfill \pi (p\otimes q)& =[p\otimes q]=\left[p\right]\otimes \left[q\right]=\pi \left(p\right)\otimes \pi \left(q\right),\hfill \\ \hfill \pi \left(dp\right)& =\left[dp\right]=d\left[p\right]=d\pi \left(p\right).\hfill \end{array}$$

Then, $\pi$ is homomorphic. In addition, if $p{⪯}_{1}q$, then there exist $p\in \left[p\right]$ and $q\in \left[q\right]$, such that $p{⪯}_{1}q$. Hence, $\left[p\right]$${⪯}_3\left[q\right]$, i.e., $\pi \left(p\right){⪯}_3\pi \left(q\right)$. If $\left[p\right]{⪯}_3\left[q\right]$, then there exist $u\in$ $\left[p\right]$ and $v\in \left[q\right]$ such that $u{⪯}_{1}v$, where $\pi \left(u\right)=\left[u\right]=\left[p\right]$ and $\pi \left(v\right)=\left[v\right]=\left[q\right]$. Hence, $({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,$${⪯}_3)$ are orderly homomorphic. □

Let us discuss the relationship between POIAs $(\mathcal{P}\left({\mathbb{R}}_{max}\right),$${⪯}_2)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$. Let

$$\begin{array}{cc}\hfill \psi :{\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta & \to \mathcal{P}\left({\mathbb{R}}_{max}\right),\hfill \\ & \mapsto \widehat{p}.\hfill \end{array}$$

The following structural relationship can be then obtained.

Theorem 5.

$(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$ are orderly isomorphic.

Proof. 

For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$ and $d\in {\mathbb{R}}_{max}$, it is easy to verify that

$$\begin{array}{cc}\hfill \psi \left(\right[p]\oplus [q\left]\right)& =\psi \left([p\oplus q]\right)=\widehat{p\oplus q}=\widehat{p}\oplus \widehat{q}=\psi \left(\left[p\right]\right)\oplus \psi \left(\left[q\right]\right),\hfill \\ \hfill \psi \left(\right[p]\otimes [q\left]\right)& =\psi \left([p\otimes q]\right)=\widehat{p\otimes q}=\widehat{p}\otimes \widehat{q}=\psi \left(\left[p\right]\right)\otimes \psi \left(\left[q\right]\right),\hfill \\ \hfill \psi \left(d\right[p\left]\right)& =\psi \left(\left[dp\right]\right)=\widehat{dp}=d\widehat{p}=d\psi \left(\left[p\right]\right).\hfill \end{array}$$

Then, $\psi$ is homomorphic. In addition,

$$\begin{array}{cc}\hfill \widehat{p}{⪯}_2\widehat{q}& ⟺\widehat{p}\oplus \widehat{q}=\widehat{q}⟺\widehat{p\oplus q}=\widehat{q}⟺[p\oplus q]=\left[q\right]⟺\left[p\right]\oplus \left[q\right]=\left[q\right].\hfill \end{array}$$

Next, let us prove that $\left[p\right]{⪯}_3\left[q\right]$ is equivalent to $\left[p\right]\oplus \left[q\right]=\left[q\right]$. On the one hand, if $\left[p\right]{⪯}_3\left[q\right]$, then there exist $u\in \left[p\right]$ and $v\in \left[q\right]$, such that $u{⪯}_{1}v$, i.e., $u\oplus v=v$. Hence,

$$\left[p\right]\oplus \left[q\right]=\left[u\right]\oplus \left[v\right]=[u\oplus v]=\left[v\right]=\left[q\right].$$

On the other hand, if $\left[p\right]\oplus \left[q\right]=\left[q\right]$, then $[p\oplus q]=\left[q\right]$, i.e., $p\oplus q\in \left[q\right]$. Let $v=p\in \left[p\right]$ and $u=$ $p\oplus q\in \left[q\right]$. Then, $v{⪯}_{1}u$, and so $\left[p\right]{⪯}_3\left[q\right]$. Hence, $(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,{⪯}_3)$ are orderly isomorphic. □

Example 2.

For $p={\gamma }^2\oplus 1\gamma \oplus 2$ and $q=1{\gamma }^2\oplus 2$, the graphs of $\widehat{p}$ and $\widehat{q}$ are depicted in Figure 2. It can be seen that $\widehat{p}{⪯}_2\widehat{q}$. In addition, it has been stated in Example 1 that $\left[p\right]{⪯}_3\left[q\right]$.

From Theorems 4 and 5, the relationship between POIAs $({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ and $(\mathcal{P}\left({\mathbb{R}}_{max}\right),$${⪯}_2)$ can naturally be obtained as below.

Corollary 1.

$({\mathbb{R}}_{max}\left[\gamma \right],{⪯}_1)$ and $(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ are orderly homomorphic.

It then follows that $\delta =\psi \pi$, which is equivalent to the commutativity of the diagram depicted in Figure 3.

The general algebra theorems above are straightforward since they use algebraic properties that are common to linear spaces and the max-plus algebra. In particular, Lemmas 1–4 have the same forms as the relative results in the conventional algebra, while other results only exist in the max-plus algebra. Furthermore, the results in the following two sections only exist in POIAs of polynomials over the max-plus algebra, rather than the conventional algebra.

4. Boundary of $(\left[\mathbf{p}\right],{⪯}_{\mathbf{1}})$

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, let

$$\begin{array}{cc}\hfill p_1^{♯}\left(l\right)& =\underset{\begin{array}{c}0⩽\mu ⩽1\\ i\ne j,i,j\in \mathbb{N}\end{array}}{max}(\mu p\left(i\right)+(1-\mu )p\left(j\right)),\mathrm{subject}\mathrm{to}l=\mu i+(1-\mu )j,\hfill \\ \hfill p_2^{♯}\left(l\right)& =\underset{c\in {\mathbb{R}}_{max}}{min}(\widehat{p}\left(c\right)-lc).\hfill \end{array}$$

(5)

By [2] (Theorem 3.38), $p_1^{♯}=p_2^{♯}$, which can be genrally denoted by $p^{♯}$ and called the concavified polynomial of p. The skeleton of p, denoted by $p^{♭}$, can be obtained from p by canceling the monomials of p which do not correspond to the extremal points of $\mathrm{hypo}\left(p^{♯}\right)$. The concavified polynomial $p^{♯}$ and the skeleton $p^{♭}$ are exactly the maximal and minimal elements of $(\left[p\right],{⪯}_1)$, respectively. Let us now confirm these two results.

Theorem 6.

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, $p^{♯}$ is the maximal element of $(\left[p\right],{⪯}_1)$.

Proof. 

By ([2], Theorem 3.38) $\widehat{p^{♯}}=\widehat{p}$, i.e., $p^{♯}\in \left[p\right]$. Suppose that there exists $q\in \left[p\right]$, such that $p^{♯}\prec q$, i.e., $p^{♯}\left(l\right)<q\left(l\right)$ for some $l\in \mathbb{N}$. By (3),

$$\widehat{q}\left(c\right)=\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+q\left(l\right))>\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+p^{♯}\left(l\right))=\widehat{p^{♯}}\left(c\right)=\widehat{p}\left(c\right),$$

which is in conflict with $q\in \left[p\right]$. Hence, $q{⪯}_1{p}^{♯}$ for any $q\in \left[p\right]$, and so $p^{♯}$ is the maximal element of $(\left[p\right],{⪯}_1)$. □

The following result has been proven in [2] (Theorem 3.38) using a graphic method. Let us now provide an algebraic proof for it.

Lemma 6.

For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$, if $\left[p\right]=\left[q\right]$, then

(i) 

$\mathrm{val}\left(p\right)=\mathrm{val}\left(q\right)$, $\mathrm{deg}\left(p\right)=\mathrm{deg}\left(q\right)$;

(ii) 

$p^{♯}=q^{♯}$, $p^{♭}=q^{♭}$.

Proof. 

(i) Let $p={⨁}_{l=k_1}^{n_1}p\left(l\right){\gamma }^l,q={⨁}_{l=k_2}^{n_2}q\left(l\right){\gamma }^l,$ and $\left[p\right]=\left[q\right]$. For $c\in {\mathbb{R}}_{max}$,

$$\begin{array}{cc}\hfill \widehat{p}\left(c\right)=\widehat{q}\left(c\right)& ⟺\underset{l=k_1}{\overset{n_1}{⨁}}p\left(l\right)c^l=\underset{l=k_2}{\overset{n_2}{⨁}}q\left(l\right)c^l\hfill \\ \hfill & ⟺\underset{l\in N\left(p\right)}{max}\{lc+p\left(l\right)\}=\underset{l\in N\left(q\right)}{max}\{lc+q\left(l\right)\}.\hfill \end{array}$$

(6)

For the convenience of expression, let

$$\begin{array}{cc}\hfill {\overline{c}}_1& =\underset{l\in N\left(p\right)\backslash \left\{n_1\right\}}{max}\left\{{\displaystyle \frac{p\left(l\right)-p\left(n_1\right)}{n_1-l}}\right\},{\overline{c}}_2=\underset{l\in N\left(q\right)\backslash \left\{n_2\right\}}{max}\left\{{\displaystyle \frac{q\left(l\right)-q\left(n_2\right)}{n_2-l}}\right\},\hfill \\ \hfill {\underline{c}}_1& =\underset{l\in N\left(p\right)\backslash \left\{k_1\right\}}{min}\left\{{\displaystyle \frac{p\left(l\right)-p\left(k_1\right)}{k_1-l}}\right\},{\underline{c}}_2=\underset{l\in N\left(q\right)\backslash \left\{k_2\right\}}{min}\left\{{\displaystyle \frac{q\left(l\right)-q\left(k_2\right)}{k_2-l}}\right\}.\hfill \end{array}$$

If $c>{\overline{c}}_1$, then for any $l\in N\left(p\right)\backslash \left\{n_1\right\}$, ${\displaystyle c>\frac{p\left(l\right)-p\left(n_1\right)}{n_1-l},}$ i.e., $n_{1}c+p\left(n_1\right)>lc+p\left(l\right)$. Hence, the left of (6) equals $n_{1}c+p\left(n_1\right)$ for $c>{\overline{c}}_1$. Similarly, if $c>{\overline{c}}_2$, then

$$n_{2}c+q\left(n_2\right)>lc+q\left(l\right) \mathrm{for} \mathrm{any} l\in N\left(q\right)\backslash \left\{n_2\right\}.$$

Hence, the right of (6) equals $n_{2}c+q\left(n_2\right)$ for $c>{\overline{c}}_2$. Let $\overline{c}=max\{{\overline{c}}_1,{\overline{c}}_2\}$. Then,

$$n_{1}c+p\left(n_1\right) = n_{2}c+q\left(n_2\right) \mathrm{for}c>\overline{c},$$

i.e., $(n_1-n_2)c+(p\left(n_1\right)-q\left(n_2\right))\equiv 0$ for $c>c_3$. This implies that $n_1=n_2$ and $p\left(n_1\right)=q\left(n_2\right)$. Similarly, the left of (6) equals $k_{1}c+p\left(k_1\right)$ for $c<{\underline{c}}_1$, and the right of (6) equals $k_{2}c+q\left(k_2\right)$ for $c<{\underline{c}}_2$. Let $\underline{c}=min\{{\underline{c}}_1,{\underline{c}}_2\}$. Then,

$$k_{1}c+p\left(k_1\right)=k_{2}c+q\left(k_2\right)\mathrm{for} c<\underline{c}.$$

Hence, $k_1=k_2$ and $p\left(k_1\right)=q\left(k_2\right)$.

(ii) Since $\left[p\right]=\left[q\right]$, one has $\widehat{p}\left(c\right)=\widehat{q}\left(c\right)$ for any $c\in {\mathbb{R}}_{max}$. By (5), $p^{♯}=q^{♯}$. Obviously, the monomials of $p^{♭}$ and $q^{♭}$ correspond to the extremal points of $\mathrm{hypo}\left(p^{♯}\right)$ and $\mathrm{hypo}\left(q^{♯}\right)$, respectively. Hence, $p^{♭}=q^{♭}$. □

Combining Theorem 6 with Lemma 6, the following corollary can immediately be obtained.

Corollary 2.

${\left(p^{♯}\right)}^{♯}=p^{♯}$, ${\left(p^{♯}\right)}^{♭}=p^{♭}$.

Proof. 

Since $p^{♯}\in \left[p\right]$, it follows from Lemma 6 that ${\left(p^{♯}\right)}^{♯}=p^{♯}$ and ${\left(p^{♯}\right)}^{♭}=p^{♭}$. □

Theorem 7.

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, $p^{♭}$ is the minimal element of $(\left[p\right],{⪯}_1)$.

Proof. 

Firstly, let us prove $p^{♭}\in \left[p\right]$ (as has been proven in [2] (Theorem 3.38) using a graphic method; here is an algebraic proof). Let $p^{♯}={⨁}_{l=k}^n{p}^{♯}\left(l\right){\gamma }^l.$ Since $p^{♯}$ has full support, $p^{♯}\left(l\right)\ne \epsilon$ for any $l\in N\left(p^{♯}\right).$ It follows from Corollary 2 that $p^{♭}={\left(p^{♯}\right)}^{♭}$. Then, $p^{♭}$ can be obtained from $p^{♯}$ by canceling the monomials which do not correspond to the extremal points of $\mathrm{hypo}\left(p^{♯}\right)$. Assume that

$$p^{♭}=\underset{l\ne i}{⨁}{p}^{♯}\left(l\right){\gamma }^l,k<i<n,$$

which can be taken without loss of generality. Then, $(i,p^{♯}\left(i\right))$ is not an extremal point of $\mathrm{hypo}\left(p^{♯}\right)$. Hence, there exists $a,b\in N\left(p^{♯}\right)\backslash \left\{i\right\}$ such that $(i,p^{♯}\left(i\right))$ is a convex combination of $(a,p^{♯}\left(a\right))$ and $(b,p^{♯}\left(b\right))$—that is, there exists $\mu \in [0,1]$ such that

$$p^{♯}\left(i\right)=\mu p^{♯}\left(a\right)+(1-\mu )p^{♯}\left(b\right),\mathrm{subject}\mathrm{to}i=\mu a+(1-\mu )b.$$

Then,

$$\begin{array}{cc}\hfill & p^{♯}\left(a\right)c^a\oplus p^{♯}\left(i\right)c^i\oplus p^{♯}\left(b\right)c^b=max\left\{ac+p^{♯}\left(a\right),ic+p^{♯}\left(i\right),bc+p^{♯}\left(b\right)\right\}\hfill \\ \hfill & =max\{ac+p^{♯}\left(a\right),bc+p^{♯}\left(b\right),\mu ac+(1-\mu )bc+\mu p^{♯}\left(a\right)+(1-\mu )p^{♯}\left(b\right),\}\hfill \\ \hfill & =max\{ac+p^{♯}\left(a\right),bc+p^{♯}\left(b\right),\mu (ac+p^{♯}\left(a\right))+(1-\mu )(bc+p^{♯}\left(b\right))\}\hfill \\ \hfill & =max\left\{ac+p^{♯}\left(a\right),bc+p^{♯}\left(b\right)\right\}=p^{♯}\left(a\right)c^a\oplus p^{♯}\left(b\right)c^b.\hfill \end{array}$$

Hence, $\widehat{p^{♭}}=\widehat{p^{♯}}=\widehat{p}$, and so $p^{♭}\in \left[p\right]$.

It remains to be proved that $p^{♭}$ is the minimal element of $(\left[p\right],{⪯}_1)$. Assume that there exists $q\in \left[p\right]$ such that $q\prec p^{♭}$, i.e., $q\left(l\right)<p^{♭}\left(l\right)$ for some $l\in \mathbb{N}$. By (3),

$$\widehat{q}\left(c\right)=\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+q\left(l\right))<\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+p^{♭}\left(l\right))=\widehat{p^{♭}}\left(c\right)=\widehat{p}\left(c\right),$$

which is in conflict with $q\in \left[p\right]$. Hence, $p^{♭}{⪯}_{1}q$ for $q\in \left[p\right]$, and so $p^{♭}$ is the minimal element of $(\left[p\right],{⪯}_1)$. □

Combining Theorem 7 with Lemma 6, the following corollary can immediately be obtained.

Corollary 3.

${\left(p^{♭}\right)}^{♯}=p^{♯}$, ${\left(p^{♭}\right)}^{♭}=p^{♭}$.

Proof. 

Since $p^{♭}\in \left[p\right]$, it follows from Lemma 6 that ${\left(p^{♭}\right)}^{♯}=p^{♯}$ and ${\left(p^{♭}\right)}^{♭}=p^{♭}$. □

There are some equivalent statements for two formal polynomials belonging to the same class.

Corollary 4.

For $p,q\in {\mathbb{R}}_{max}\left[\gamma \right]$, the following statements are equivalent:

(i) 

$\left[p\right]=\left[q\right]$;

(ii) 

$p^{♯}=q^{♯}$;

(iii) 

$p^{♭}=q^{♭}$.

Proof. 

According to Lemma 6, (i) implies (ii). By Corollary 2, $p^{♭}={\left(p^{♯}\right)}^{♭}$ and $q^{♭}={\left(q^{♯}\right)}^{♭}$. If $p^{♯}=q^{♯}$, then ${\left(p^{♯}\right)}^{♭}=$${\left(q^{♯}\right)}^{♭}$, i.e., $p^{♭}=q^{♭}$. Hence, (ii) implies (iii). If $p^{♭}=q^{♭}$, then $\widehat{p^{♭}}=\widehat{q^{♭}}$. Since $\widehat{p^{♭}}=\widehat{p}$ and $\widehat{q^{♭}}=\widehat{q}$, $\widehat{p}=\widehat{q}$, i.e., $\left[p\right]=\left[q\right]$. Hence, (iii) implies (i). □

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, $p^{♯}$ and $p^{♭}$ can be viewed as the upper and lower bounds of $(\left[p\right],{⪯}_1)$, respectively, and any formal polynomial in $\left[p\right]$ has to be in between.

Theorem 8.

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, $\left[p\right]=\left\{q\in {\mathbb{R}}_{max}\left[\gamma \right]\right|p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}\}.$

Proof. 

For any $q\in \left[p\right]$, it follows from Lemma 6 that $p^{♯}=q^{♯}$ and $p^{♭}=q^{♭}$. By Theorems 6 and 7, $q^{♭}{⪯}_{1}q{⪯}_1{q}^{♯}$. Then, $p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}$, and so $\left[p\right]\subseteq \left\{q\right|p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}\}.$ For $p^{♭}{⪯}_{1}q$, $p^{♭}\left(l\right)⩽q\left(l\right)$ for any $l\in \mathbb{N}$. Then,

$$\widehat{q}\left(c\right)=\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+q\left(l\right))⩾\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+p^{♭}\left(l\right))=\widehat{p^{♭}}\left(c\right)=\widehat{p}\left(c\right).$$

For $q{⪯}_1{p}^{♯}$, $q\left(l\right)⩽p^{♯}\left(l\right)$ for any $l\in \mathbb{N}$. Then,

$$\widehat{q}\left(c\right)=\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+q\left(l\right))⩽\underset{\begin{array}{c}l\in \mathbb{N}\end{array}}{max}(lc+p^{♯}\left(l\right))=\widehat{p^{♯}}\left(c\right)=\widehat{p}\left(c\right).$$

Hence, $\widehat{p}=\widehat{q}$, i.e., $q\in \left[p\right]$, and so $\left\{q\right|p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}\}\subseteq \left[p\right]$. Therefore, $\left[p\right]=\left\{q\right|p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}\}$. □

Thanks to the order isomorphism between $(\mathcal{P}\left({\mathbb{R}}_{max}\right),{⪯}_2)$ and $({\mathbb{R}}_{max}\left[\gamma \right]/\ker \delta ,$${⪯}_3)$, one can determine whether two formal polynomials lead to a same function using the above theorem. Let us give an example.

Example 3.

For $p={\gamma }^2\oplus \gamma \oplus 2$, it can be calculated that $p^{♯}={\gamma }^2\oplus 1\gamma \oplus 2$ and $p^{♭}={\gamma }^2\oplus 2$. Let $q={\gamma }^2\oplus -1\gamma \oplus 2$. Then, $p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}$. By Theorem 8, $q\in \left[p\right]$. Indeed,

$$\widehat{p}\left(c\right)=\widehat{q}\left(c\right)=\left\{\begin{array}{cc}2,\hfill & c⩽1;\hfill \\ 2c,\hfill & c>1,\hfill \end{array}\right.$$

i.e., $q\in \left[p\right]$.

5. Cardinality of $(\left[\mathit{p}\right],{⪯}_{\mathbf{1}})$

By using the upper and lower bounds, the cardinality of $(\left[p\right],{⪯}_1)$ can be obtained. Before that, it is necessary to make some preparations.

Lemma 7.

Ref. [2] (Lemma 3.41): Let p be a formal polynomial with full support. Then, $p=p^{♯}$ if and only if

              

where $k=\mathrm{val}\left(p\right)$ and $n=\mathrm{deg}\left(p\right)$.

Let us provide a criterion for a formal polynomial p to be the minimal element of the equivalence class $\left[p\right]$.

Theorem 9.

Let p be a formal polynomial with full support. Then, $p=p^{♭}$ if and only if

              

where $k=\mathrm{val}\left(p\right)$ and $n=\mathrm{deg}\left(p\right)$.

Proof. 

Necessity: Since p has full support and $p=p^{♭}$, $p^{♭}$ has full support. This implies that each monomial of p corresponds to an extremal point of $\mathrm{hypo}\left(p^{♯}\right)$. Since $\mathrm{hypo}\left(p^{♯}\right)$ is convex, $\mathrm{hypo}\left(p\right)$ is convex. Let p be of the form (2) and

$$S=\left\{\right(k,p\left(k\right)),(k+1,p(k+1)),\cdots ,(n,p\left(n\right)\left)\right\}$$

(9)

be the set of extremal points of $\mathrm{hypo}\left(p\right)$. According to the property of convex set, one obtains

$$\begin{array}{cc}\hfill \frac{p\left(k\right)-p(k+1)}{k-(k+1)}& ⩾\frac{p(k+1)-p(k+2)}{(k+1)-(k+2)}⩾\cdots ⩾\frac{p(n-1)-p\left(n\right)}{(n-1)-n}.\hfill \end{array}$$

By simplifying the inequation above, one obtains

$$p\left(k\right)-p(k+1)⩽p(k+1)-p(k+2)⩽\cdots ⩽p(n-1)-p\left(n\right).$$

Then, (7) holds. Assume that there exists an integer $l\in N\left(p\right)$ such that

              

i.e., $p(l-1)-p\left(l\right)=p\left(l\right)-p(l+1).$ Then, there exists $\mu =1/2$ such that

$$p\left(l\right)=\mu p(l-1)+(1-\mu )p(l+1), \mathrm{subject}\mathrm{to} l=\mu (l-1)+(1-\mu )(l+1).$$

Hence, $p\left(l\right){\gamma }^l$ does not correspond to any extremal point of $\mathrm{hypo}\left(p^{♯}\right)$. This contradiction implies (8) holds.

Sufficiency: Since p has full support, all points in (9) are well defined. Since (8) holds, one has $p=p^{♯}$ from Lemma 7. Then, (8) can be rewritten as

$$\begin{array}{cc}\hfill \frac{p(n-1)-p\left(n\right)}{(n-1)-n}& <\frac{p(n-2)-p(n-1)}{(n-2)-(n-1)}<\cdots <\frac{p\left(k\right)-p(k+1)}{k-(k+1)}.\hfill \end{array}$$

This implies the slope of the lines connecting with the successive pairs of points $(l-1,p(l-1\left)\right)$ and $(l,p(l\left)\right)$ are strictly decreasing with l, i.e., $\mathrm{hypo}\left(p\right)$ is strictly convex. Then, each point in S is an extremal point of $\mathrm{hypo}\left(p\right)$. Since $p=p^{♯}$, each point in S is also an extremal point of $\mathrm{hypo}\left(p^{♯}\right)$. Hence, each monomial of p corresponds to an extremal point of $\mathrm{hypo}\left(p^{♯}\right)$, and so $p=p^{♭}$. □

Example 4.

(i) Let $p={\gamma }^2\oplus \gamma \oplus 2$. By a direct calculation,

              

By Theorem 9, $p\ne p^{♭}$. Indeed, $p^{♭}={\gamma }^2\oplus 2\ne p$.

(ii) Let $p={\gamma }^2\oplus 2\gamma \oplus 2$. By a direct calculation,

              

By Theorem 9, $p=p^{♭}$. Indeed, $p^{♭}={\gamma }^2\oplus 2\gamma \oplus 2=p$.

To ensure that (8) is well defined even when p has no full support, let

$$\frac{\epsilon }{p\left(i\right)}=-\infty ,\frac{p\left(i\right)}{\epsilon }=+\infty ,\frac{\epsilon }{\epsilon }=-\infty ,$$

where $-\infty (\mathrm{resp}.+\infty )$ is less (resp. greater) than any real number. Then, Theorem 9 can be also used to formal polynomial that has no full support.

Corollary 5.

For $p\in {\mathbb{R}}_{max}\left[\gamma \right]$, $p^{♭}$ has full support if and only if (8) holds.

Proof. 

Necessity: Since $p^{♭}$ has full support, p has the full support and each monomial of p corresponds to an extremal point of $\mathrm{hypo}\left(p^{♯}\right)$. Then, $p=p^{♭}$. By Theorem 9, (8) holds.

Sufficiency: It follows from $p\left(n\right)\ne \epsilon$ and $p\left(k\right)\ne \epsilon$ that $p(n-1)\ne \epsilon$. Otherwise, $\epsilon -p\left(n\right)=-\infty$, which is not greater than any element in ${\mathbb{R}}_{max}$. Similarly, $p\left(l\right)\ne \epsilon$ for any $l\in N\left(p\right)$, i.e., p has full support. By Theorem 9, $p=$$p^{♭}$. Hence, $p^{♭}$ has full support. □

From the above discussion, the cardinality of $(\left[p\right],{⪯}_1)$ can be then obtained.

Theorem 10.

If (8) holds, then $\left|\right[p\left]\right|=1$. Otherwise, $\left|\right[p\left]\right|=\left|\mathbb{R}\right|$, where $|·|$ is the cardinality of a set.

Proof. 

If (8) holds, then $p^{♭}$ has full support by Corollary 5. Hence, p has full support. Combining (8) with Lemma 7, one obtains $p=p^{♯}$. Combining (8) with Theorem 9, one obtains $p=p^{♭}$. Then, $p^{♭}=p=p^{♯}$. By Theorem 8, $\left[p\right]=$$\left\{p\right\}$. If (8) is not true, then it follows from Corollary 5 that there exists an integer $i\in N\left(p\right)$ such that $p^{♭}\left(i\right)=\epsilon$. Let

$$q\left(l\right)=\left\{\begin{array}{cc}{m}_i,\hfill & l=i,\hfill \\ p\left(l\right),\hfill & l\ne i,\hfill \end{array}\right.$$

(10)

where $m_i\in (-\infty ,p^{♯}\left(l\right)]$. It is clear that $p^{♭}{⪯}_{1}q{⪯}_1{p}^{♯}$. By Theorem 8, $q\in \left[p\right]$. It is known that the interval $(-\infty ,p^{♯}\left(l\right)]$ is equinumerous with $\mathbb{R}$, which is also true for r-dimensional Euclidean space ${\mathbb{R}}^r$. Hence, $\left|\left[p\right]\right|=|{(-\infty ,p^{♯}\left(l\right)]}^r|=|{\mathbb{R}}^r|=|\mathbb{R}|,$ where $r=\mathrm{deg}\left(p\right)-\mathrm{val}\left(p\right)-$ $\left|\mathrm{supp}\right(p^{♭}\left)\right|+1.$ □

The theorem above tells us that any equivalence class $(\left[p\right],{⪯}_1)$ is either an uncountable set with cardinality of the continuum or a finite set with cardinality of 1, which is determined by inequation (8). The proof of Theorem 10 is constructive, and (10) provides a formula to compute all formal polynomials that correspond to the same polynomial function with the given one. Let us illustrate it with an example.

Example 5.

(i) Let $p={\gamma }^2\oplus 2\gamma \oplus 2$. It has been shown in Example 4 that

              

Then, $\left[p\right]=\{{\gamma }^2\oplus 2\gamma \oplus 2\}$ and $\left|\right[p\left]\right|=1$.

(ii) Let $p={\gamma }^2\oplus \gamma \oplus 2$. It has been shown in Example 4 that

            

Then, $\left[p\right]=\{{\gamma }^2\oplus q\left(1\right)\gamma$$\oplus 2\left|q\right(1)⩽1\}$ and $\left|\right[p\left]\right|=\left|\right(-\infty ,1\left]\right|=\left|\mathbb{R}\right|$.

6. Conclusions

This paper presents three POIAs of polynomials over ${\mathbb{R}}_{max}$ based on the symmetry and antisymmetry of binary relations and analyzes the orderly structural relationships among them. It is proven that the POIA of polynomial functions and the POIA of formal polynomials are orderly homomorphic; the POIA of polynomial functions and the quotient POIA of formal polynomials are orderly isomorphic. By using the partial order on formal polynomials, the boundary and cardinality of an equivalence class in the quotient POIA of formal polynomials are determined. The concavified polynomial and the skeleton are proven to be the upper and lower bounds of an equivalence class, respectively. Then, it is shown that the cardinality of an equivalence class is either ℵ or 1. The approaches proposed in this paper are analytic and constructive.