Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations
Abstract
:1. Introduction
2. Preliminaries
3. The EDM Method, Applied to Two Equations
3.1. EDM for Fractional-Order One-Dimensional Dispersive Equation
3.2. EDM for Fractional Multi-Dimensional Dispersive Equation
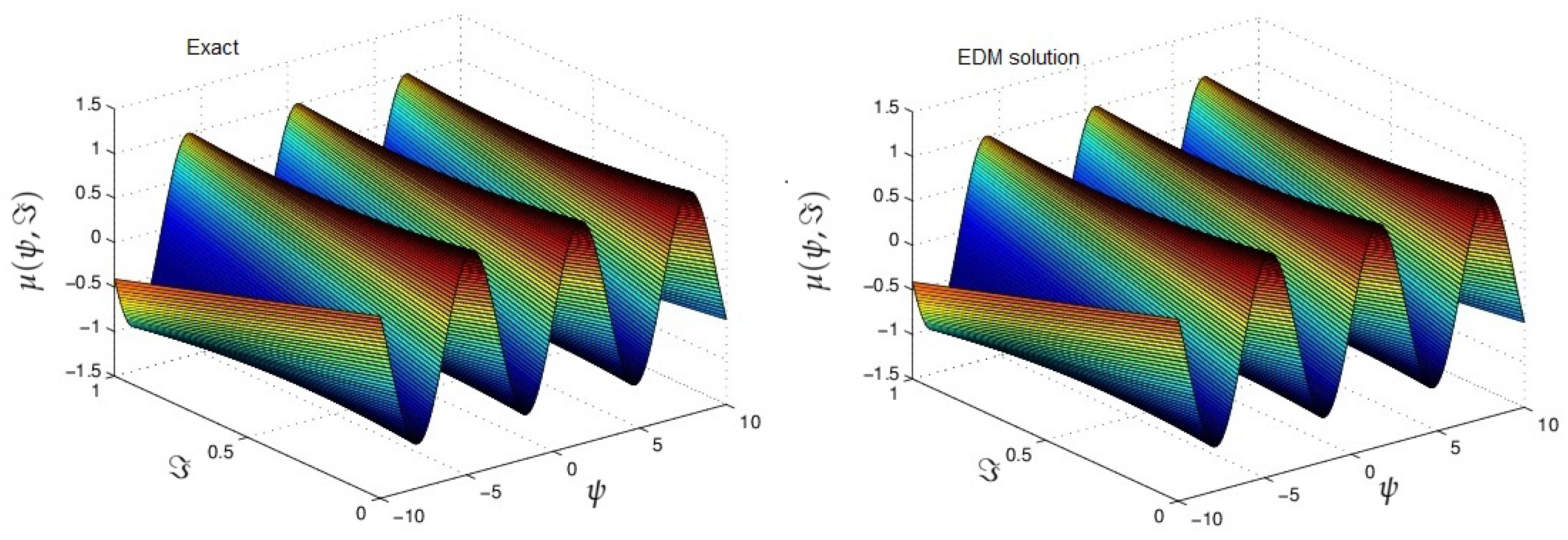
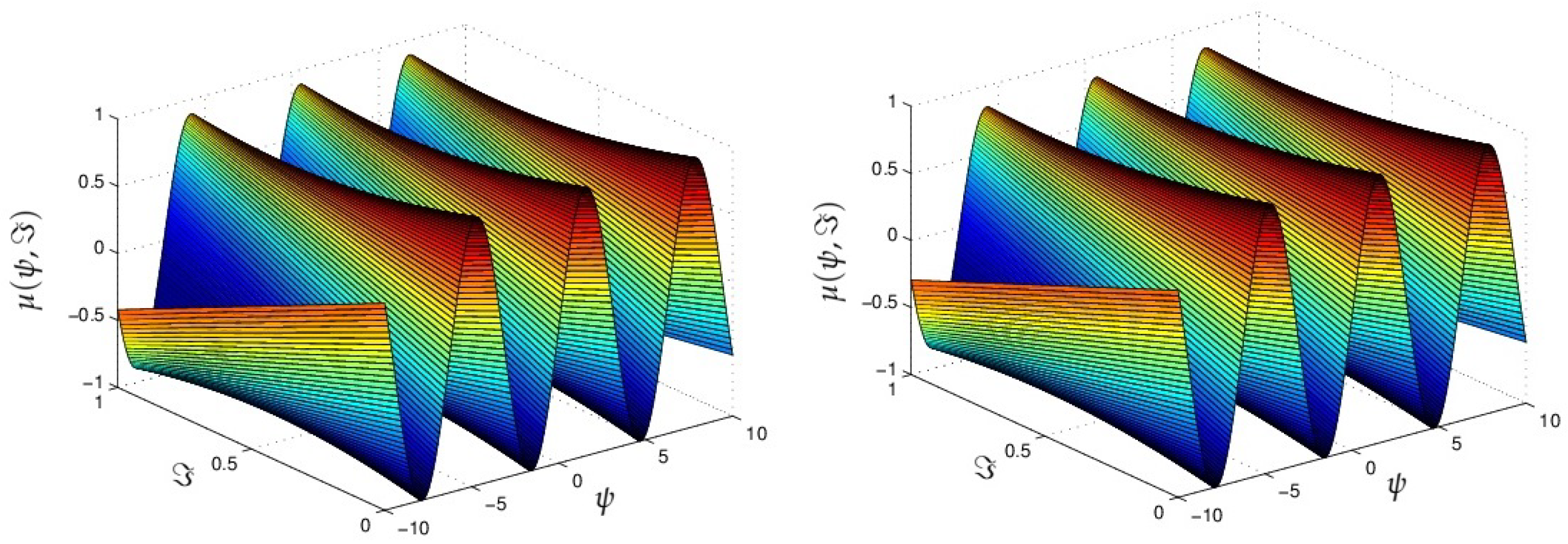
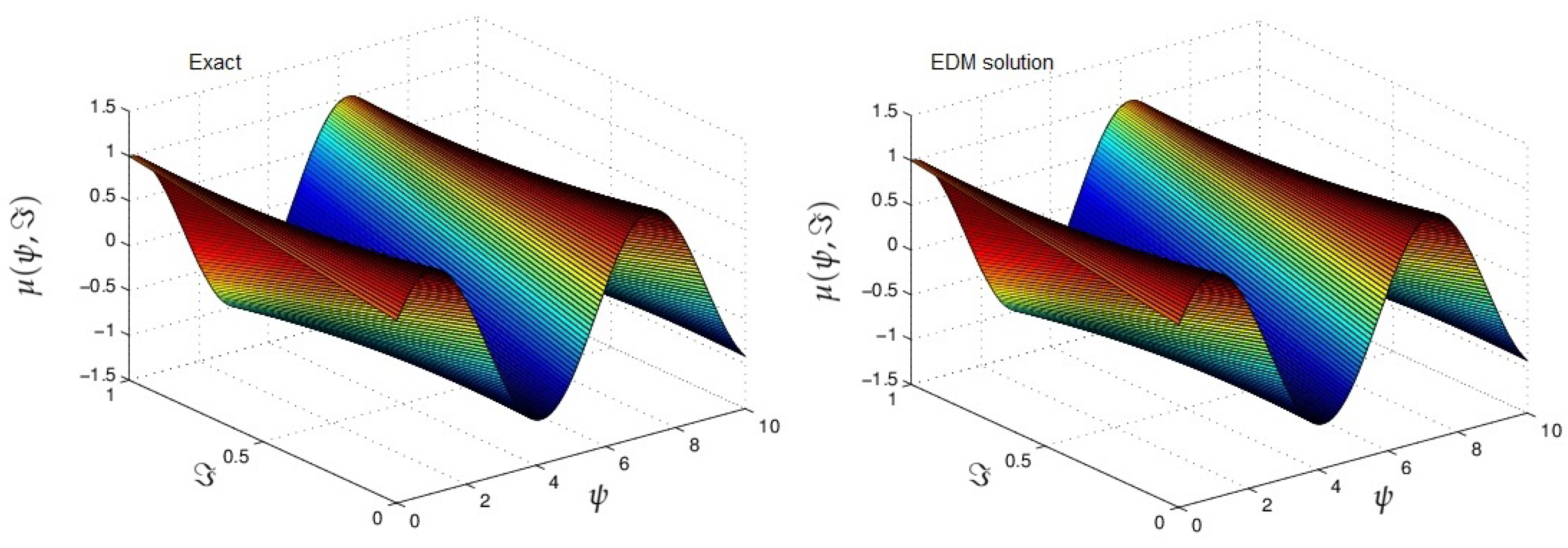
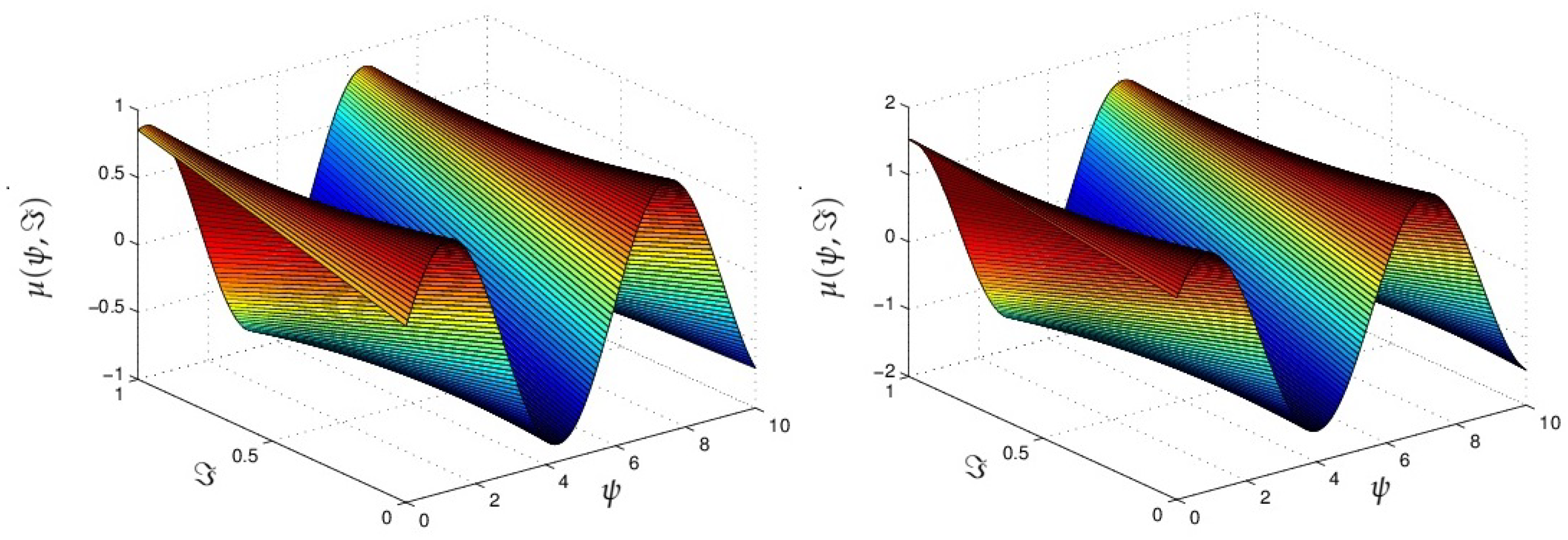
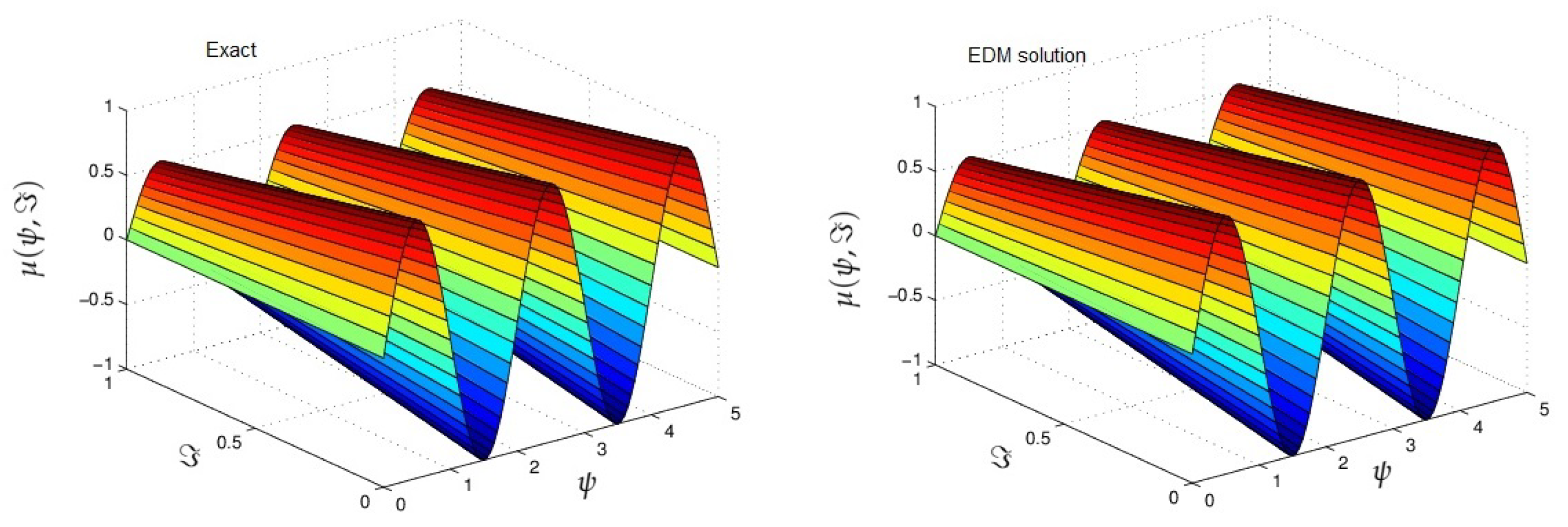
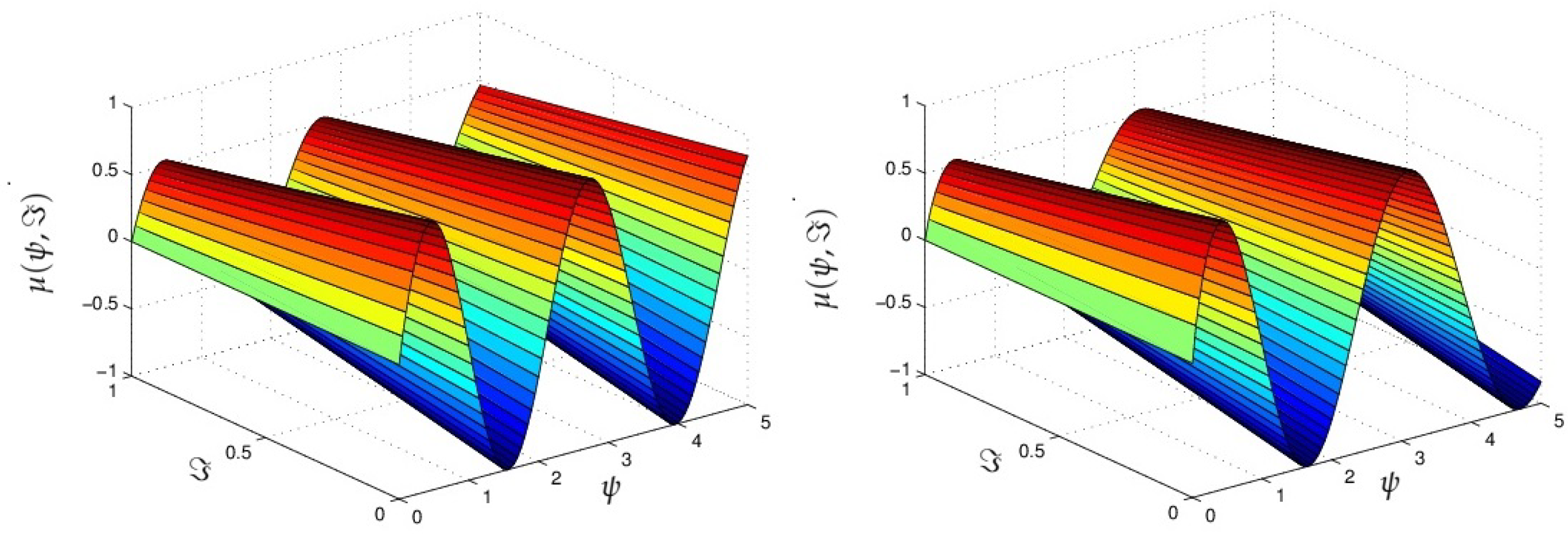
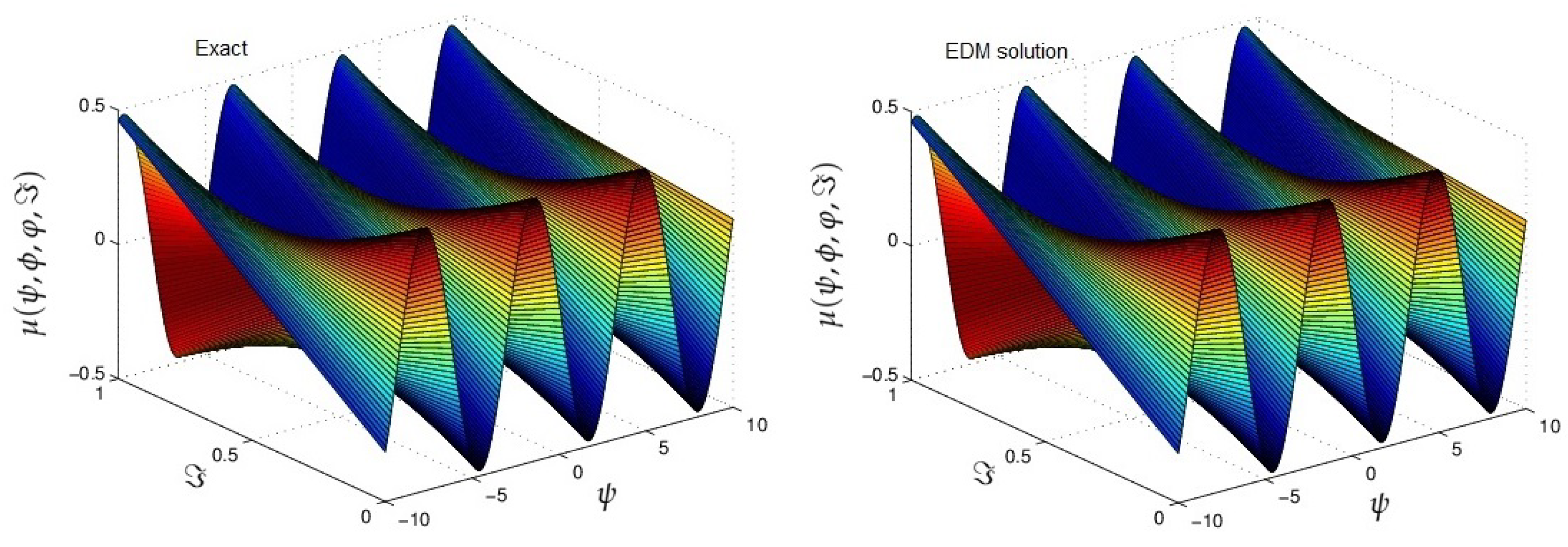
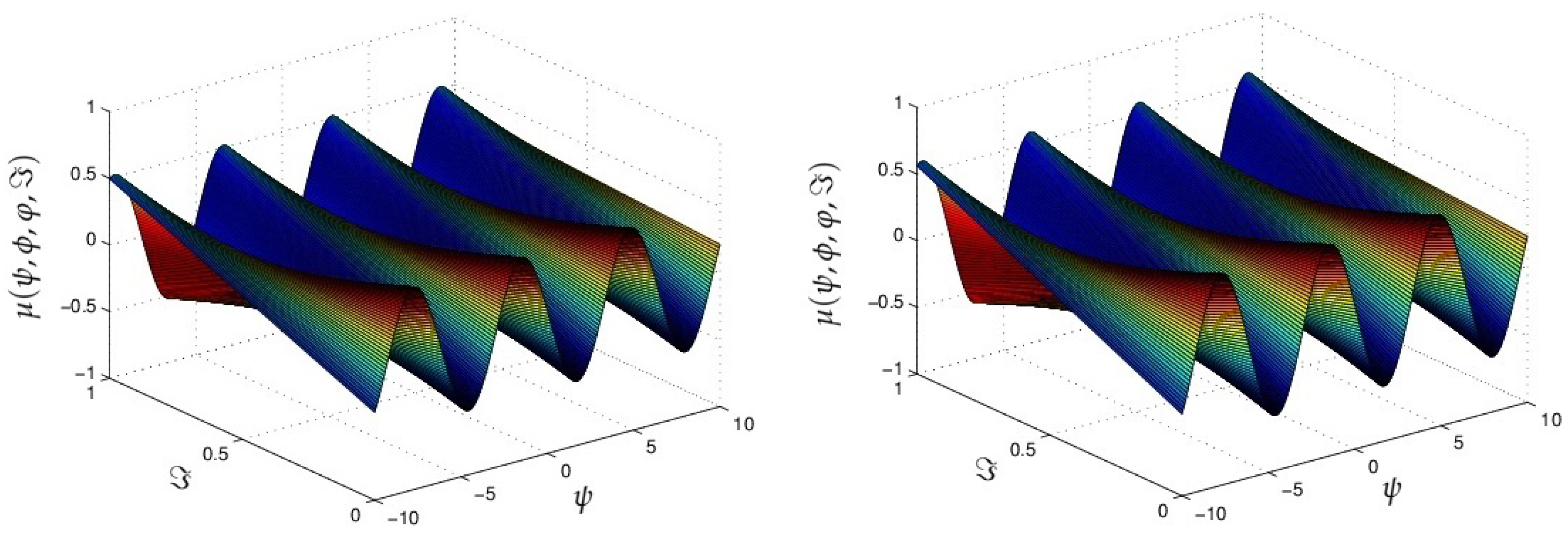
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Drapaca, C.S.; Sivaloganathan, S. A fractional model of continuum mechanics. J. Elast. 2012, 107, 105–123. [Google Scholar] [CrossRef]
- Deshpande, A.; Daftardar-Gejji, V. Chaos in discrete fractional difference equations. Pramana 2016, 87, 1–10. [Google Scholar] [CrossRef]
- Fang, L.; Liu, J.; Ju, S.; Zheng, F.; Dong, W.; Shen, M. Experimental and theoretical evidence of enhanced ferromagnetism in sonochemical synthesized BiFeO3 nanoparticles. Appl. Phys. Lett. 2010, 97, 242501. [Google Scholar] [CrossRef]
- Shah, N.A.; Dassios, I.; Chung, J.D. Numerical Investigation of Time-Fractional Equivalent Width Equations that Describe Hydromagnetic Waves. Symmetry 2021, 13, 418. [Google Scholar] [CrossRef]
- Goswami, A.; Singh, J.; Kumar, D. Numerical simulation of fifth order Kdv equations occurring in magneto-acoustic waves. Ain Shams Eng. J. 2017, 9, 2265–2273. [Google Scholar] [CrossRef]
- Steudel, H.; Drazin, P.G.; Johnson, R.S. Solitons: An Introduction, 2nd ed.; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Djidjeli, K.; Price, W.G.; Twizell, E.H.; Wang, Y. Numerical methods for the solution of the third-and fifth-order dispersive Korteweg-de Vries equations. J. Comput. Appl. Math. 1995, 58, 307–336. [Google Scholar] [CrossRef] [Green Version]
- Zahran, M.A.; El-Shewy, E.K. Contribution of Higher-Order Dispersion to Nonlinear Electron-Acoustic Solitary Waves in a Relativistic Electron Beam Plasma System. Phys. Scr. 2007, 6, 803. [Google Scholar] [CrossRef]
- Seadawy, A.R. New exact solutions for the KdV equation with higher order nonlinearity by using the variational method. Comput. Math. Appl. 2011, 62, 3741–3755. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Xu, B.; Guo, Y. Numerical solution of Korteweg-de Vries-Burgers equation by the compact-type CIP method. Adv. Differ. Equ. 2015, 2015, 353. [Google Scholar] [CrossRef] [Green Version]
- Yavuz, M.; Ãzdemir, N. European vanilla option pricing model of fractional order without singular kernel. Fractal Fract. 2018, 2, 3. [Google Scholar] [CrossRef] [Green Version]
- Thabet, H.; Kendre, S.; Chalishajar, D. New analytical technique for solving a system of nonlinear fractional partial differential equations. Mathematics 2017, 5, 47. [Google Scholar] [CrossRef] [Green Version]
- Yepez-Martinez, H.; Gomez-Aguilar, F.; Sosa, I.O.; Reyes, J.M.; Torres-Jimenez, J. The Feng’s first integral method applied to the nonlinear mKdV space-time fractional partial differential equation. Rev. Mex. Fis. 2016, 62, 310–316. [Google Scholar]
- Prakash, A.; Kumar, M. Numerical method for fractional dispersive partial differential equations. Commun. Numer. Anal. 2017, 1, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Kocak, H.; Pinar, Z. On solutions of the fifth-order dispersive equations with porous medium type non-linearity. Waves Random Complex Media 2018, 28, 516–522. [Google Scholar] [CrossRef]
- Kanth, A.R.; Aruna, K. Solution of fractional third-order dispersive partial differential equations. Egypt. J. Basic Appl. Sci. 2015, 2, 190–199. [Google Scholar]
- Sultana, T.; Khan, A.; Khandelwal, P. A new non-polynomial spline method for solution of linear and non-linear third order dispersive equations. Adv. Differ. Equ. 2018, 2018, 316. [Google Scholar] [CrossRef]
- Pandey, R.K.; Mishra, H.K. Homotopy analysis Sumudu transform method for time-fractional third order dispersive partial differential equation. Adv. Comput. Math. 2017, 43, 365–383. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; With a Preface by Yves Cherruault; Fundamental Theories of Physicss; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1994; Volume 60. [Google Scholar]
- Elzaki, T.M. The new integral transform Elzaki transform. Glob. J. Pure Appl. Math. 2011, 7, 57–64. [Google Scholar]
- Elzaki, T.M. On the connections between Laplace and Elzaki transforms. Adv. Theor. Appl. Math. 2011, 6, 1–11. [Google Scholar]
- Elzaki, T.M. On The New Integral Transform “Elzaki Transform” Fundamental Properties Investigations and Applications. Glob. J. Math. Sci. Theory Pract. 2012, 4, 1–13. [Google Scholar]
- Jena, R.M.; Chakraverty, S. Solving time-fractional Navier-Stokes equations using homotopy perturbation Elzaki transform. SN Appl. Sci. 2019, 1, 16. [Google Scholar] [CrossRef] [Green Version]
- Sedeeg, A.K.H. A coupling Elzaki transform and homotopy perturbation method for solving nonlinear fractional heat-like equations. Am. J. Math. Comput. Model. 2016, 1, 15–20. [Google Scholar]
- Neamaty, A.; Agheli, B.; Darzi, R. Applications of homotopy perturbation method and Elzaki transform for solving nonlinear partial differential equations of fractional order. J. Nonlinear Evol. Equ. Appl. 2016, 6, 91–104. [Google Scholar]
- Wazwaz, A.M. An analytic study on the third-order dispersive partial differential equations. Appl. Math. Comput. 2003, 142, 511–520. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.-S.; Areshi, M.; Agarwal, P.; Shah, N.A.; Chung, J.D.; Nonlaopon, K. Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations. Symmetry 2021, 13, 939. https://doi.org/10.3390/sym13060939
Zhou S-S, Areshi M, Agarwal P, Shah NA, Chung JD, Nonlaopon K. Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations. Symmetry. 2021; 13(6):939. https://doi.org/10.3390/sym13060939
Chicago/Turabian StyleZhou, Shuang-Shuang, Mounirah Areshi, Praveen Agarwal, Nehad Ali Shah, Jae Dong Chung, and Kamsing Nonlaopon. 2021. "Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations" Symmetry 13, no. 6: 939. https://doi.org/10.3390/sym13060939
APA StyleZhou, S.-S., Areshi, M., Agarwal, P., Shah, N. A., Chung, J. D., & Nonlaopon, K. (2021). Analytical Analysis of Fractional-Order Multi-Dimensional Dispersive Partial Differential Equations. Symmetry, 13(6), 939. https://doi.org/10.3390/sym13060939








