Optimal Sample Size for the Birnbaum–Saunders Distribution under Decision Theory with Symmetric and Asymmetric Loss Functions
Abstract
1. Introduction
2. The Birnbaum–Saunders Model
2.1. Properties
- P1:
- If , then , that is, the BS distribution is a homogeneous family;
- P2:
- If , then , that is, the BS distribution is invariant under the reciprocal transformation. This property can be important in financial applications.
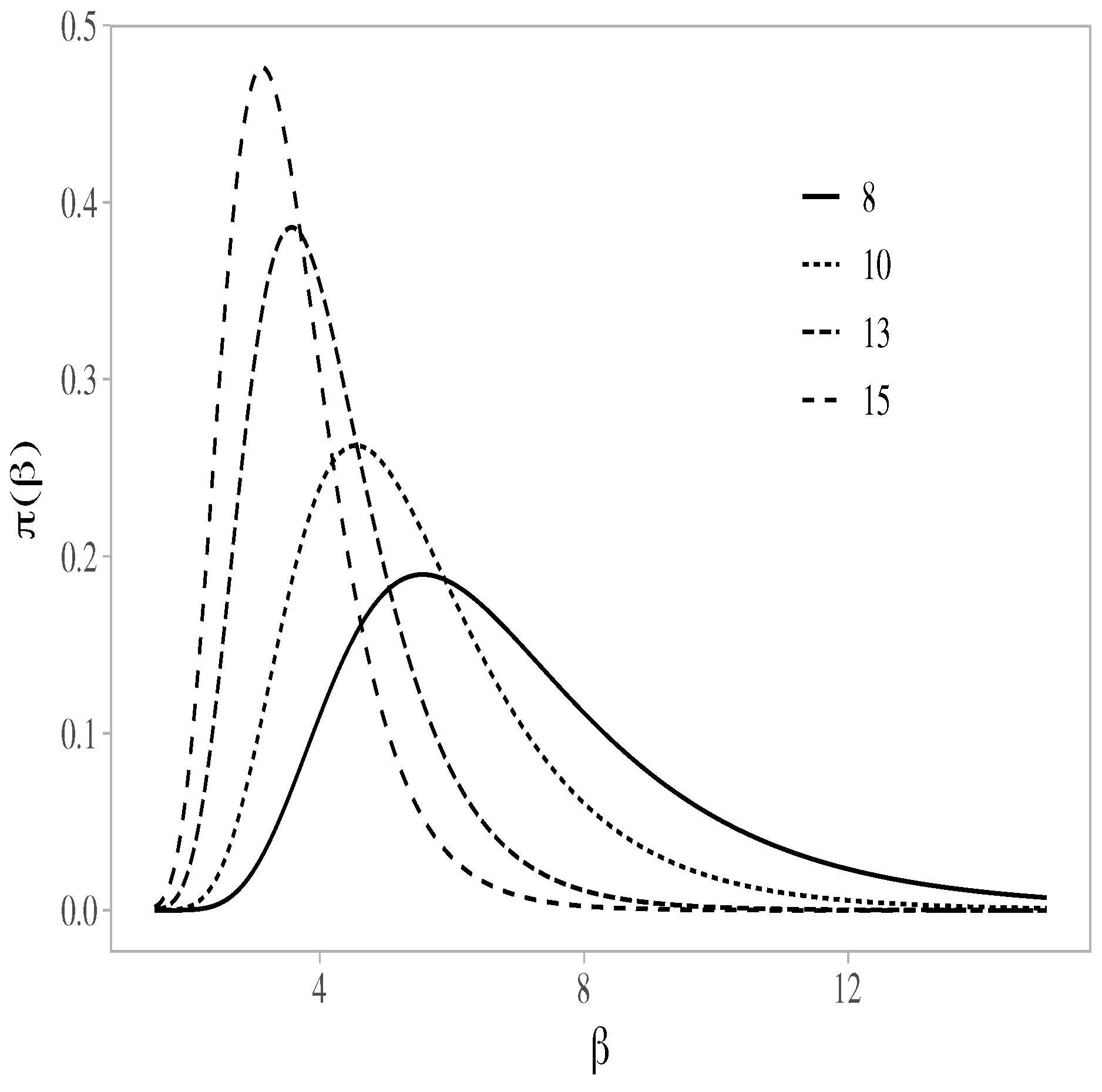
2.2. Inference
3. Optimal Sample Size
3.1. Determining the Optimal Sample Size
| Algorithm 1: Estimation of the minimized Bayes risk. |
|
3.2. Loss Functions
- L1: Loss Function 1. The first loss function is defined as:which is known as the absolute loss function. For this loss function, the Bayes rule is the median of the posterior distribution of . Given a sample , for , of the posterior distribution of , an estimate of may be obtained from , where is the median of the sample , for .
- L2: Loss Function 2. Second, we consider the well-known quadratic loss function stated as:
- L3: Loss Function 3. The loss functions L1 and L2 suffer from two disadvantages in practical applications: both are symmetric and unbounded. In the list of bounded loss functions that might be considered, we may include those suggested in [29,30]. However, in our case, these loss functions are not simple to deal with. Nevertheless, there is a simple well-know asymmetric loss function that we may consider. This is the linear exponential (known as LINEX) loss function given by:where . As ℓ increases positively, the overestimation is more costly than the underestimation. As ℓ increases negatively, the situation is reversed [31]. From p. 447 in [31], the Bayes rule for this loss function is established as:
- L4: Loss Function 4. The fourth function is defined as:where is a weight, is the half-length of the desired interval, and the function is equal to x if and equal to zero, otherwise. Note that as decreases, the interval is narrower. The terms and are included to penalized intervals that do not contain the parameter of interest . These terms are equal to zero if and increase as moves away from the interval. Note that the loss function given in (7) is a weighted sum of two terms, and , where the weights are and one, respectively. The Bayes rule corresponds to taking a and b as the 100th and 100th quantiles of the posterior distribution of [8,32]. If we consider this loss function applied to the Bayes rule, we have that:where , , and are the corresponding bounds of the Bayes rule , whereas is the indicator function. Given a sample , for , of the posterior distribution of , an estimate of may be obtained from:
- L5: Loss Function 5. The fifth and last loss function considered here is expressed as:where is a fixed constant and is the center of the credible interval. The first term defined in (8) involves the half-width of the interval, and the second term is the square of the distance between the parameter of interest and the center of the interval, which is divided by the half-width to maintain the same measurement unit of the first term. The weights attributed to each term stated in (8) are and one, respectively. If , we attribute the largest weight to the second term; if , the situation is reversed; and if , the two terms have the same weight. For this loss function, the Bayes rule corresponds to the quantities that define the interval , where and , that is, the corresponding standard deviation [4,8,32]. In this case, we have that:
4. Computational Aspects and Empirical Applications
4.1. Computer Characteristics
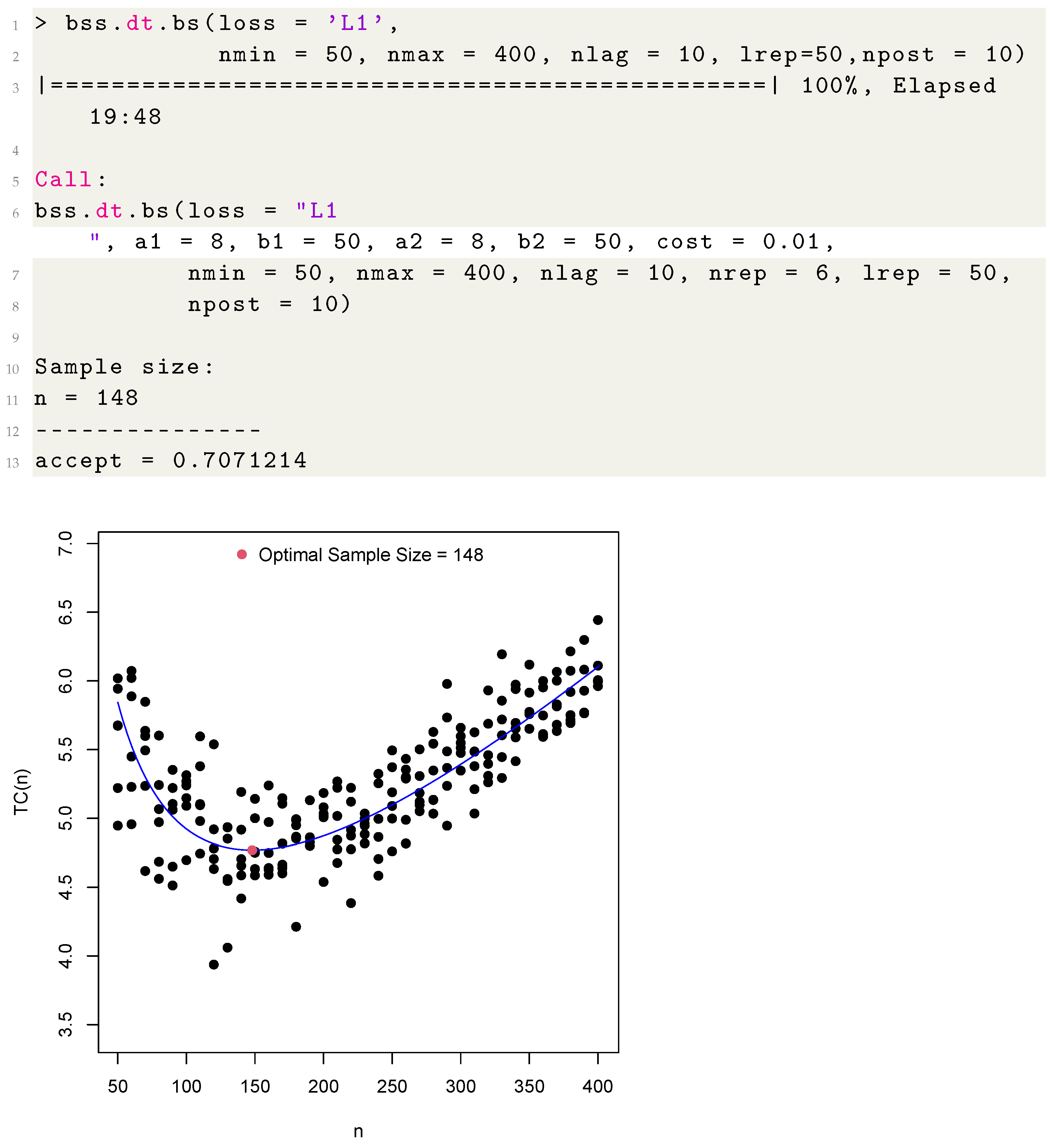
4.2. The samplesizeBS Functions
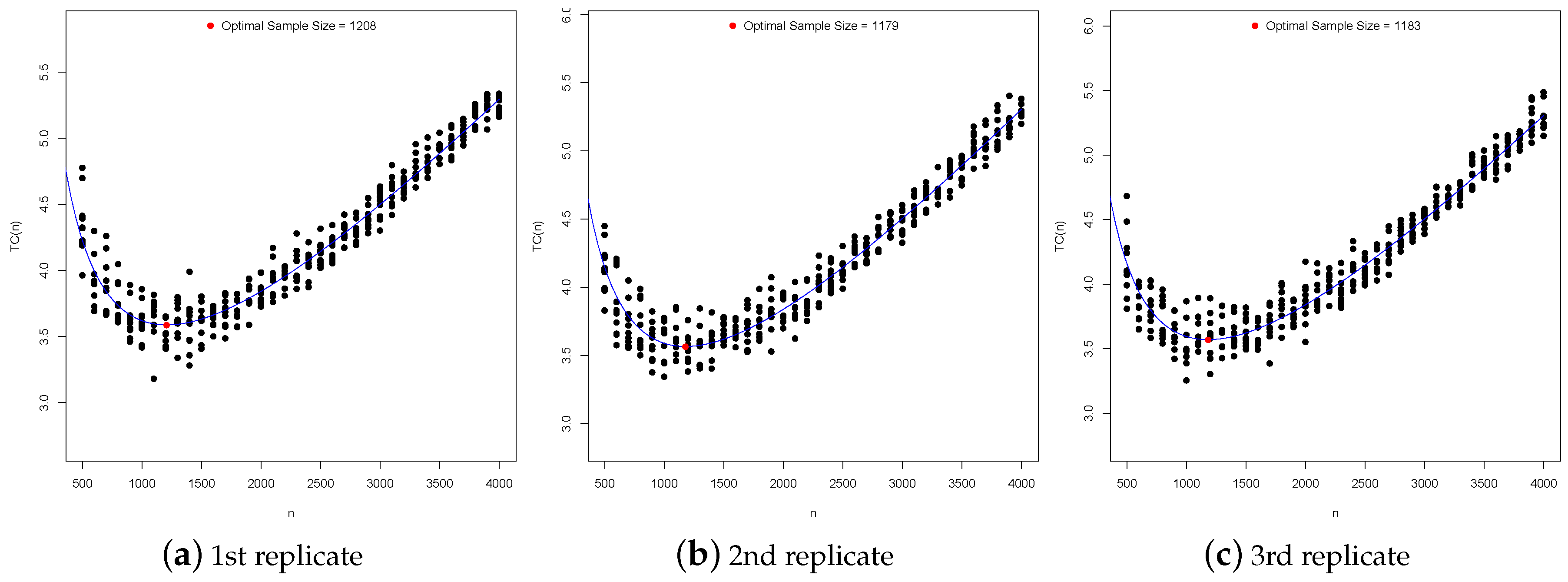
4.3. Optimal Sample Sizes
4.4. Illustrative Example
5. Discussion, Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spiegelhalter, D.J.; Abrams, K.R.; Myles, J.P. Bayesian Approaches to Clinical Trials and Health-Care Evaluation; Wiley: Chichester, UK, 2004. [Google Scholar]
- Etzioni, R.; Kadane, J.B. Optimal experimental design for another’s analysis. J. Am. Stat. Assoc. 1993, 88, 1404–1411. [Google Scholar] [CrossRef]
- Sahu, S.K.; Smith, T.M.F. A Bayesian method of sample size determination with practical applications. J. R. Stat. Soc. A 2006, 169, 235–253. [Google Scholar] [CrossRef]
- Parmigiani, G.; Inoue, L. Decision Theory: Principles and Approaches; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Islam, A.F.M.S.; Pettit, L.I. Bayesian sample size determination using LINEX loss and linear cost. Commun. Stat. Theory Methods 2012, 41, 223–240. [Google Scholar] [CrossRef]
- Islam, A.F.M.S.; Pettit, L.I. Bayesian sample size determination for the bounded LINEX loss function. J. Stat. Comput. Simul. 2014, 84, 1644–1653. [Google Scholar] [CrossRef]
- Santis, F.D.; Gubbiotti, S. A decision-theoretic approach to sample size determination under several priors. Appl. Stoch. Model. Bus. Ind. 2017, 33, 282–295. [Google Scholar] [CrossRef]
- Costa, E.G. Sample Size for Estimating the Organism Concentration in Ballast Water: A Bayesian Approach. Ph.D. Thesis, Department of Statistics, Universidade de São Paulo, São Paulo, Brazil, 2017. (In Portuguese). [Google Scholar]
- Birnbaum, Z.W.; Saunders, S.C. A new family of life distributions. J. Appl. Probab. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Bourguignon, M.; Leao, J.; Leiva, V.; Santos-Neto, M. The transmuted Birnbaum–Saunders distribution. REVSTAT Stat. J. 2017, 15, 601–628. [Google Scholar]
- Mazucheli, M.; Leiva, V.; Alves, B.; Menezes, A.F.B. A new quantile regression for modeling bounded data under a unit Birnbaum–Saunders distribution with applications in medicine and politics. Symmetry 2021, 13, 682. [Google Scholar] [CrossRef]
- Santos-Neto, M.; Cysneiros, F.J.A.; Leiva, V.; Barros, M. Reparameterized Birnbaum–Saunders regression models with varying precision. Electron. J. Stat. 2016, 10, 2825–2855. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gomez, H.W. Generalized modified slash Birnbaum—Saunders distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Gomez-Deniz, E.; Gomez, L. The Rayleigh Birnbaum Saunders distribution: A general fading model. Symmetry 2020, 12, 389. [Google Scholar] [CrossRef]
- Desousa, M.; Saulo, H.; Leiva, V.; Santos-Neto, M. On a new mixture-based regression model: Simulation and application to data with high censoring. J. Stat. Comput. Simul. 2020, 90, 2861–2877. [Google Scholar] [CrossRef]
- Sanchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum–Saunders quantile regression and its diagnostics with application to economic data. Appl. Stoch. Models Bus. Ind. 2021, 37, 53–73. [Google Scholar] [CrossRef]
- Villegas, C.; Paula, G.A.; Leiva, V. Birnbaum–Saunders mixed models for censored reliability data analysis. IEEE Trans. Reliab. 2011, 60, 748–758. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F.J.A. A multivariate log-linear model for Birnbaum–Saunders distributions. IEEE Trans. Reliab. 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Arrue, J.; Arellano, R.; Gomez, H.W.; Leiva, V. On a new type of Birnbaum–Saunders models and its inference and application to fatigue data. J. Appl. Stat. 2020, 47, 2690–2710. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kundu, D. Birnbaum–Saunders distribution: A review of models, analysis, and applications. Appl. Stoch. Model. Bus. Ind. 2019, 35, 4–49. [Google Scholar] [CrossRef]
- Bourguignon, M.; Ho, L.L.; Fernandes, F.H. Control charts for monitoring the median parameter of Birnbaum–Saunders distribution. Qual. Reliab. Eng. Int. 2020, 36, 1333–1363. [Google Scholar] [CrossRef]
- Costa, E.G.; Santos-Neto, M.; Leiva, V. samplesizeBS: Bayesian Sample Size in a Decision-Theoretic Approach for the Birnbaum–Saunders, R Package Version 1.1-1; 2020. Available online: www.github.com/santosneto/samplesizeBS (accessed on 21 May 2021).
- Aykroyd, R.G.; Leiva, V.; Marchant, C. Multivariate Birnbaum–Saunders distributions: Modelling and applications. Risks 2018, 6, 21. [Google Scholar] [CrossRef]
- Leiva, V. The Birnbaum–Saunders Distribution; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Ng, H.; Kundu, D.; Balakrishnan, N. Modified moment estimation for the two-parameter Birnbaum–Saunders distribution. Comput. Stat. Data Anal. 2003, 43, 283–298. [Google Scholar] [CrossRef]
- Wang, M.; Sun, X.; Park, C. Bayesian analysis of Birnbaum–Saunders distribution via the generalized ratio-of-uniforms method. Comput. Stat. 2016, 31, 207–225. [Google Scholar] [CrossRef]
- Leiva, V.; Ruggeri, F.; Saulo, H.; Vivanco, J.F. A methodology based on the Birnbaum–Saunders distribution for reliability analysis applied to nano-materials. Reliab. Eng. Syst. Saf. 2017, 157, 192–201. [Google Scholar] [CrossRef]
- Raiffa, H.; Schlaifer, R. Applied Statistical Decision Theory; Harvard University Press: Boston, MA, USA, 1961. [Google Scholar]
- Spiring, F.A. The reflected normal loss function. Can. J. Stat. 1993, 21, 321–330. [Google Scholar] [CrossRef]
- Leung, B.P.K.; Spiring, F.A. The inverted beta loss function: Properties and applications. IEE Trans. 2002, 34, 1101–1109. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian estimation and prediction using asymmetric loss functions. J. Am. Stat. Assoc. 1986, 81, 446–451. [Google Scholar] [CrossRef]
- Rice, K.M.; Lumley, T.; Szpiro, A.A. Trading Bias for Precision: Decision Theory for Intervals and Sets. Working Paper 336, UW Biostatistics. 2008. Available online: https://biostats.bepress.com/uwbiostat/paper336/ (accessed on 21 May 2021).
- Hsieh, H.K. Estimating the critical time of the inverse Gaussian hazard rate. IEEE Trans. Reliab. 1990, 39, 342–345. [Google Scholar] [CrossRef]
- Puentes, R.; Marchant, C.; Leiva, V.; Figueroa, J.I.; Ruggeri, F. Predicting PM2.5 and PM10 levels during critical episodes management in Santiago, Chile, with a bivariate Birnbaum–Saunders log-linear model. Mathematics 2021, 9, 645. [Google Scholar] [CrossRef]
- Leiva, V.; Saulo, H.; Souza, R.; Aykroyd, R.G.; Vila, R. A new BISARMA time series model for forecasting mortality using weather and particulate matter data. J. Forecast. 2021, 40, 346–364. [Google Scholar] [CrossRef]
- Martinez, S.; Giraldo, R.; Leiva, V. Birnbaum–Saunders functional regression models for spatial data. Stoch. Environ. Res. Risk Assess. 2019, 33, 1765–1780. [Google Scholar] [CrossRef]
- Huerta, M.; Leiva, V.; Liu, S.; Rodriguez, M.; Villegas, D. On a partial least squares regression model for asymmetric data with a chemical application in mining. Chemom. Intell. Lab. Syst. 2019, 190, 55–68. [Google Scholar] [CrossRef]
- Carrasco, J.M.F.; Finiga, J.I.; Leiva, V.; Riquelme, M.; Aykroyd, R.G. An errors-in-variables model based on the Birnbaum–Saunders and its diagnostics with an application to earthquake data. Stoch. Environ. Res. Risk Assess. 2020, 34, 369–380. [Google Scholar] [CrossRef]
| Function | Output |
|---|---|
| rbs() | A sample of size n from the BS distribution |
| logp.beta() | The logarithm of the marginal posterior distribution of |
| rbeta.post() | A random sample from the marginal posterior distribution of using the random walk Metropolis–Hastings algorithm |
| bss.dt.bs() | An integer representing the optimal sample size for estimating of the BS distribution and the acceptance rate for the random walk Metropolis–Hastings algorithm |
| Loss function L1 | ||||||||||||
| 651 | 117 | 23 | 436 | 80 | 13 | 267 | 47 | 9 | 210 | 36 | 6 | |
| 641 | 121 | 22 | 429 | 77 | 14 | 267 | 47 | 8 | 209 | 36 | 6 | |
| 627 | 140 | 21 | 429 | 77 | 13 | 268 | 47 | 8 | 209 | 37 | 6 | |
| Loss function L2 | ||||||||||||
| 2096 | 641 | 176 | 1130 | 317 | 108 | 542 | 144 | 33 | 381 | 88 | 21 | |
| 2129 | 697 | 200 | 1198 | 326 | 97 | 558 | 138 | 42 | 380 | 89 | 23 | |
| 2075 | 622 | 218 | 1182 | 292 | 81 | 530 | 139 | 32 | 360 | 89 | 21 | |
| Loss function L3 | ||||||||||||
| 1787 | 354 | 61 | 1111 | 229 | 41 | 631 | 138 | 24 | 467 | 101 | 18 | |
| 1826 | 363 | 62 | 1115 | 235 | 40 | 640 | 135 | 25 | 468 | 101 | 18 | |
| 1820 | 352 | 61 | 1112 | 229 | 41 | 616 | 134 | 25 | 454 | 97 | 19 | |
| 929 | 190 | 34 | 553 | 122 | 22 | 310 | 69 | 13 | 226 | 51 | 9 | |
| 924 | 197 | 34 | 556 | 122 | 22 | 311 | 69 | 13 | 227 | 51 | 9 | |
| 925 | 190 | 34 | 552 | 116 | 22 | 308 | 67 | 13 | 222 | 49 | 9 | |
| 465 | 101 | 19 | 281 | 63 | 12 | 153 | 35 | 7 | 111 | 25 | 5 | |
| 463 | 101 | 19 | 275 | 63 | 12 | 155 | 35 | 7 | 111 | 25 | 4 | |
| 471 | 99 | 18 | 275 | 59 | 12 | 146 | 33 | 6 | 105 | 23 | 4 | |
| Loss function L4 | ||||||||||||
| 279 | 53 | 9 | 175 | 31 | 7 | 103 | 18 | 3 | 79 | 14 | 2 | |
| 271 | 54 | 10 | 171 | 31 | 6 | 106 | 18 | 3 | 79 | 14 | 2 | |
| 284 | 53 | 10 | 168 | 33 | 5 | 103 | 18 | 3 | 80 | 14 | 2 | |
| 187 | 37 | 8 | 118 | 22 | 4 | 70 | 13 | 2 | 54 | 9 | 0 | |
| 197 | 37 | 8 | 121 | 22 | 4 | 71 | 12 | 2 | 55 | 9 | 0 | |
| 184 | 40 | 7 | 121 | 22 | 4 | 71 | 13 | 2 | 55 | 9 | 0 | |
| 82 | 18 | 3 | 54 | 9 | 0 | 30 | 5 | 0 | 22 | 4 | 0 | |
| 85 | 19 | 3 | 52 | 9 | 0 | 29 | 5 | 0 | 22 | 4 | 0 | |
| 83 | 18 | 3 | 49 | 9 | 0 | 30 | 5 | 0 | 22 | 4 | 0 | |
| Loss function L5 | ||||||||||||
| 1461 | 271 | 51 | 899 | 171 | 30 | 556 | 103 | 18 | 441 | 78 | 13 | |
| 1472 | 292 | 55 | 942 | 162 | 31 | 561 | 99 | 18 | 438 | 78 | 13 | |
| 1460 | 282 | 56 | 883 | 162 | 30 | 554 | 101 | 18 | 433 | 78 | 13 | |
| 1208 | 203 | 39 | 684 | 132 | 23 | 427 | 78 | 14 | 337 | 59 | 10 | |
| 1179 | 201 | 38 | 690 | 130 | 23 | 434 | 78 | 14 | 335 | 59 | 10 | |
| 1183 | 213 | 42 | 693 | 134 | 24 | 436 | 80 | 14 | 338 | 60 | 10 | |
| 796 | 166 | 32 | 538 | 106 | 18 | 333 | 59 | 10 | 259 | 46 | 8 | |
| 859 | 171 | 30 | 540 | 99 | 19 | 331 | 62 | 11 | 260 | 47 | 8 | |
| 894 | 167 | 32 | 531 | 101 | 18 | 333 | 60 | 10 | 260 | 46 | 8 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, E.; Santos-Neto, M.; Leiva, V. Optimal Sample Size for the Birnbaum–Saunders Distribution under Decision Theory with Symmetric and Asymmetric Loss Functions. Symmetry 2021, 13, 926. https://doi.org/10.3390/sym13060926
Costa E, Santos-Neto M, Leiva V. Optimal Sample Size for the Birnbaum–Saunders Distribution under Decision Theory with Symmetric and Asymmetric Loss Functions. Symmetry. 2021; 13(6):926. https://doi.org/10.3390/sym13060926
Chicago/Turabian StyleCosta, Eliardo, Manoel Santos-Neto, and Víctor Leiva. 2021. "Optimal Sample Size for the Birnbaum–Saunders Distribution under Decision Theory with Symmetric and Asymmetric Loss Functions" Symmetry 13, no. 6: 926. https://doi.org/10.3390/sym13060926
APA StyleCosta, E., Santos-Neto, M., & Leiva, V. (2021). Optimal Sample Size for the Birnbaum–Saunders Distribution under Decision Theory with Symmetric and Asymmetric Loss Functions. Symmetry, 13(6), 926. https://doi.org/10.3390/sym13060926







