Abstract
The fatigue-life or Birnbaum–Saunders distribution is an asymmetrical model that has been widely applied in several areas of science and mainly in reliability. Although diverse methodologies related to this distribution have been proposed, the problem of determining the optimal sample size when estimating its mean has not yet been studied. In this paper, we derive a methodology to determine the optimal sample size under a decision-theoretic approach. In this approach, we consider symmetric and asymmetric loss functions for point and interval inference. Computational tools in the R language were implemented to use this methodology in practice. An illustrative example with real data is also provided to show potential applications.
1. Introduction
The determination of the sample size is a relevant topic in all studies when statistical methods are applied. For example, in clinical trials, this determination was adequately discussed in ch. 6 of [1] and the references therein, giving an overview on this topic. The optimal sample size in the classical statistical setting depends crucially on the alternative hypothesis. However, this is not the case in a Bayesian framework where there is no need to state a specific alternative hypothesis.
In order to determine the sample size in any knowledge area, prior information must be available. Introducing uncertainty into this information is essentially a Bayesian approach. Then, the use of Bayesian methods for determining an optimal sample size should be explored within the distributional framework that is relevant according to the problem under study. In general, there are empirical limitations that require sample sizes to be determined in advance. Therefore, we can determine an optimal sample size that satisfies a criterion based on the Bayes risk. Given specific loss and sampling cost functions, a full Bayesian analysis may be performed for determining an optimal sample size. In the absence of precise information on costs and losses, the loss functions can be approximate, and a Bayesian approach might be employed to provide reasonable estimates of the optimal sample size. For more details about this methodology, see [2,3,4,5,6,7,8] and the references therein.
Birnbaum and Saunders [9] introduced a family of distributions to model failure times for metals subject to periodic stress. The authors provided a natural physical justification for this family, which is known as the fatigue-life or Birnbaum–Saunders (BS) distribution. In the last few decades, this distribution has received considerable attention in the literature, and many methodologies have been proposed for parameter inference. Such attention is justified by its wide applicability, and its variations have been applied in several areas [10,11,12,13,14,15,16], but mainly in reliability [17,18,19]. A detailed review of the BS distribution including methodologies under the classical and Bayesian approaches was presented in [20]. Recently, guidelines about the minimum sample size for monitoring the BS median in quality control under a classical statistical approach were presented in [21]. Although diverse methodologies related to the BS distribution have been proposed, the problem of determining an optimal sample size when estimating the BS mean has not yet been studied.
The main objective of this paper is to derive a methodology for determining the optimal sample size when estimating the mean of the BS distribution under decision theory. We develop a methodology via a Bayesian decision-theoretic approach based on a criterion that minimizes the Bayes risk and sampling cost. The proposed approach depends on ad-hoc loss functions (symmetric or asymmetric) defined to accommodate the implications of a decision. We consider three loss functions for point inference and two for interval inference. Computational tools in the R language were developed to use this methodology in practice.
The paper unfolds as follows. In Section 2, we provide background on the BS distribution, the inference of its parameters, and the Bayesian approach. Section 3 presents the methodology to obtain the optimal sample size under a decision-theoretic approach. In Section 4, we show the use of the main functions and methods of an R package implemented by the authors for the present work [22]. An illustrative example is also provided in this section. Finally, we conclude with a discussion of the results in Section 5, including ideas for future research.
2. The Birnbaum–Saunders Model
In this section, we present the properties of the BS distribution, the inference of its parameters, and discuss the Bayesian approach. Much of the background information about the BS distribution presented in this section has been gathered from other works [9,20,23,24].
2.1. Properties
Let X be a BS distributed random variable with a shape parameter and a scale parameter , which we denote by . Then, the probability density function of X is given by:
where .
Besides being a scale parameter, is also the median of the BS distribution. Furthermore, the mean and variance of the BS distribution are stated as:
Moreover, if X is BS distributed, then:
where Z follows a standard normal distribution, which is useful to generate random values from the distribution. It is possible to show that:
Some useful properties of the BS distribution are:
- P1:
- If , then , that is, the BS distribution is a homogeneous family;
- P2:
- If , then , that is, the BS distribution is invariant under the reciprocal transformation. This property can be important in financial applications.
2.2. Inference
Given a sample and their observed values , modified moment estimates [25] for and are expressed, respectively, as:
where is the sample arithmetic mean and is the sample harmonic mean, that is,
In addition, the estimates and are well defined because , that is, these estimates are always positive and mathematically well determined or unique. We may use and as initial values in a sampling algorithm. Furthermore, the likelihood function obtained from the probability density function satisfies:
For the parameters and of the model, we consider proper prior distributions because the use of non-informative prior distributions yields an improper posterior distribution and continuous conjugate priors do not exist [26]. A possible choice of a prior distribution for is the inverse gamma (IG) distribution whose probability density function satisfies:
where and are positive and known constants (hyperparameters) of the IG distribution. We denote this as , that is, the IG distribution of parameters and . We also assume an IG prior distribution for with hyperparameters and . Thus, the model can be written hierarchically as:
where “IID” stands for independent and identically distributed. In this context, the conditional posterior distribution of given and is stated as:
whereas the marginal posterior distribution of given can be obtained from:
which is not a known distribution [26]. In this way, we use the random walk Metropolis–Hastings algorithm [27] to generate samples from the marginal posterior distribution of given . Using this sampling algorithm and the posterior distribution defined in (4), we may generate values from the joint posterior distribution of and . For a given , first, we generate values of from (5), and with them, we draw values of using (4). Note that the parameter of interest is the mean of the BS distribution, which is a function of and . In order to obtain a random sample of the posterior distribution of given , we may draw values from the joint posterior of and . Then, we apply the expression defined in (1) for each sampled pair of values.
3. Optimal Sample Size
In this section, we introduce the methodology to obtain the optimal sample size for estimating of the BS distribution under a decision-theoretic approach. Furthermore, we define the different loss functions to be considered.
3.1. Determining the Optimal Sample Size
We may approach the problem of determining the optimal sample size as a decision problem [4,28]. Given that is the parameter of interest, we specify a loss function based on a sample and a decision function . For a given n and depending on the adopted loss function, the action consists of specifying a quantity (point inference case) representing an estimate for or two quantities (interval inference case) representing the lower and upper limits of a credible interval for .
Let be associated with a prior distribution for the unknown parameter and be a decision function. Then, the Bayes risk [4] is defined as:
where g is related to the sampling distribution for given , M is the parameter space, and is the sample space. The decision that minimizes among all the possible decisions is called the Bayes rule. In this context, we define the optimal sample size as the one that minimizes the total cost (TC) stated as:
where is a function representing the cost of sampling n observations. Here, we take , where c is the per-unit cost for observing a unit in the population. Since it is not possible to compute analytically, we use Monte Carlo simulations as an alternative to estimate for each n.
Suppose that the order of the integration may be reversed in (6). Note that this reversal is possible whenever the conditions for the Fubini theorem are satisfied. In this case, as is known, minimizing the Bayes risk is equivalent to minimizing the posterior expected loss. Then, we have:
so that we may estimate the minimized Bayes risk through the posterior expected value of the loss function applied to the Bayes rule . This may be done as summarized in Algorithm 1.
After obtaining an estimate of , we added the respective sampling cost , which provided us an estimate of for a given n. We apply this procedure for a grid of plausible values of n. For example, if we set this grid of values as , then we estimate , respectively. The choice of the grid values is arbitrary, but as the distance between its consecutive elements is shorter, a better visualization is reached of the behavior of the TC. However, as this distance decreases, the required computer processing power also increases, as well as the time to compute all these estimates. Thus, the choice of this grid must consider all these settings.
| Algorithm 1: Estimation of the minimized Bayes risk. |
|
In Step 4 of Algorithm 1, when sampling from the marginal posterior distribution stated in (5), we consider a burn-in of 500 iterations and a thinning of 20 with a final number of iterations of 500. We use these 500 iterations to estimate the Bayes risk. A trace and autocorrelation plot for a lower value of the grid used for n is inspected. We expect the same or better behavior as n increased in the grid. All the trace plots showed a random behavior around a value, and in all the autocorrelation plots, the autocorrelations for almost all lags were zero. In each value of n in the grid, we estimate the Bayes risk ten times. We inspect the trace plots, autocorrelations plots, and the acceptance rate to set the burn-in, thinning, and final number of iterations as 500. All these inspection tools showed that such settings provide good results. If we increase these values, we may have the same or better behavior. However, we must consider the computational cost, which increases notoriously as these values increase. Then, taking all this into account, we decide to set 500 iterations. Due to the computational burden, other values were not tested, but we use triplicate values to show the stability of our results.
Consider the fitting proposed by [8] of the total cost curve established as:
to the grid of values of n and the respective estimates of , denoted by , where E and G are parameters to be estimated. This curve may be linearized by means of:
whereas the estimates of E and G can be computed by the least-squares method. In this setting, the optimal sample size () is the integer closest to:
where and are, respectively, the least-squares estimates of E and G.
3.2. Loss Functions
We consider five loss functions to determine the optimal sample size. The loss functions 1 and 2 may be used for point inference and are symmetric. The loss function 3 also may be used for point inference, but this loss function is asymmetric. The loss functions 4 and 5 may be used for interval inference. Such loss functions are defined below.
- L1: Loss Function 1. The first loss function is defined as:which is known as the absolute loss function. For this loss function, the Bayes rule is the median of the posterior distribution of . Given a sample , for , of the posterior distribution of , an estimate of may be obtained from , where is the median of the sample , for .
- L2: Loss Function 2. Second, we consider the well-known quadratic loss function stated as:
For this loss function, the Bayes rule corresponds to the posterior expected value of , and in this case, . Given a sample , for , of the posterior distribution of , an estimate of may be obtained from the respective sample variance.
- L3: Loss Function 3. The loss functions L1 and L2 suffer from two disadvantages in practical applications: both are symmetric and unbounded. In the list of bounded loss functions that might be considered, we may include those suggested in [29,30]. However, in our case, these loss functions are not simple to deal with. Nevertheless, there is a simple well-know asymmetric loss function that we may consider. This is the linear exponential (known as LINEX) loss function given by:where . As ℓ increases positively, the overestimation is more costly than the underestimation. As ℓ increases negatively, the situation is reversed [31]. From p. 447 in [31], the Bayes rule for this loss function is established as:
Given a sample , for , of the posterior distribution of , we may compute an estimate of through:
For the LINEX function, we have that [5]:
An estimate of may be obtained from:
- L4: Loss Function 4. The fourth function is defined as:where is a weight, is the half-length of the desired interval, and the function is equal to x if and equal to zero, otherwise. Note that as decreases, the interval is narrower. The terms and are included to penalized intervals that do not contain the parameter of interest . These terms are equal to zero if and increase as moves away from the interval. Note that the loss function given in (7) is a weighted sum of two terms, and , where the weights are and one, respectively. The Bayes rule corresponds to taking a and b as the 100th and 100th quantiles of the posterior distribution of [8,32]. If we consider this loss function applied to the Bayes rule, we have that:where , , and are the corresponding bounds of the Bayes rule , whereas is the indicator function. Given a sample , for , of the posterior distribution of , an estimate of may be obtained from:
- L5: Loss Function 5. The fifth and last loss function considered here is expressed as:where is a fixed constant and is the center of the credible interval. The first term defined in (8) involves the half-width of the interval, and the second term is the square of the distance between the parameter of interest and the center of the interval, which is divided by the half-width to maintain the same measurement unit of the first term. The weights attributed to each term stated in (8) are and one, respectively. If , we attribute the largest weight to the second term; if , the situation is reversed; and if , the two terms have the same weight. For this loss function, the Bayes rule corresponds to the quantities that define the interval , where and , that is, the corresponding standard deviation [4,8,32]. In this case, we have that:
Given a sample , for , of the posterior distribution of , an estimate of may be obtained from the sample variance and the expression (9).
4. Computational Aspects and Empirical Applications
In this section, we provide the characteristics of the computer that was used in our study. Also, we show the capabilities and features of a new R package which is named samplesizeBS [22] and is available from GitHub at https://github.com/santosneto/samplesizeBS (accessed on 21 May 2021). The capabilities of the samplesizeBS package allow us to calculate an optimal sample size when estimating the BS mean and generate random numbers of the joint posterior BS/IG distribution. This section finishes with an empirical application based on real data.
4.1. Computer Characteristics
The characteristics of the Cluster Euler, used when calculating the optimal sample size in Section 4.3, are available at http://www.cemeai.icmc.usp.br/Euler/index.html (accessed on 22 May 2021). The other numerical results presented in the simple example of Section 4.2, and the illustrative example with real data of Section 4.4, were obtained by a computer with the following characteristics: (i) OS: Linux Mint 19.3 Cinnamon; (ii) RAM: 7.7 GiB; and (iii) processor: Intel Core i5-7200U CPU@2.50GHz x 2. In addition, the following tools and programming languages were used: (i) development tool –IDE–: RStudio Version (1.3.1093); and (ii) statistical software: R. Note that, in the simple example regarding the use of the function bss.dt.bs(), the elapsed time was: 19 m 48 s.
4.2. The samplesizeBS Functions
In Table 1, we present the details of the functions contained in the samplesizeBS package.

Table 1.
Functions and the respective outputs of the samplesizeBS package.
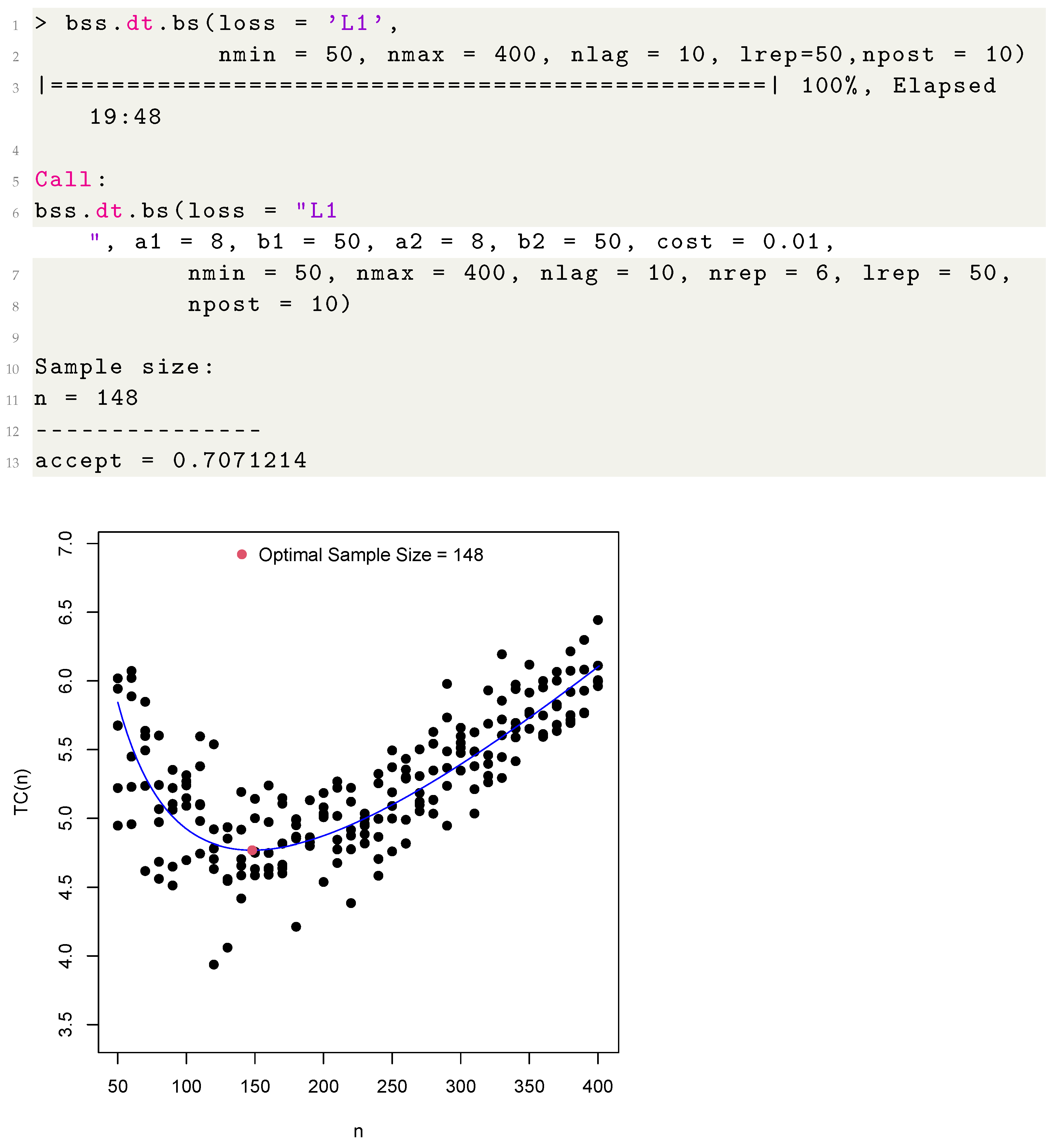
In order to determinate the BS optimal sample size, we use the function bss.dt.bs(). In the example below, we calculate the optimal sample size considering the loss function L1, with , , and . The function also returns the graph with the sample size (n) versus the of sampling, that is, takes into account both the cost of sampling n observations and the cost of inference through the loss function. In this way, the optimal sample size is the value that minimizes the total cost (see Figure 1).
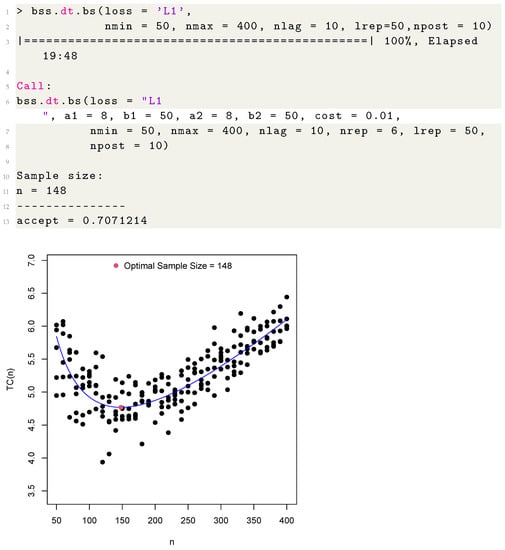
Figure 1.
Fitted curve with the respective optimal sample size obtained using the loss function L1.
4.3. Optimal Sample Sizes
Next, we calculate the optimal sample size assuming different scenarios. For the hyperparameters of the prior distribution of , we take and . With these values, we have different degrees of prior information (see Figure 2). For the prior distribution of , we set and . We consider for the per-unit cost. For the loss function L3, we take , for L4, , and for L5, . For each combination of these values, we compute the optimal sample size for estimating . The average acceptance rate for the Metropolis–Hastings algorithm in all these combinations was . Since the proposed methodology is based on simulation methods, we obtain in triplicate and observe the difference for the three values. Table 2 reports the optimal sample sizes computed with these settings. In addition, may be reached via the following link, which also presents a graph with the fitted curve:
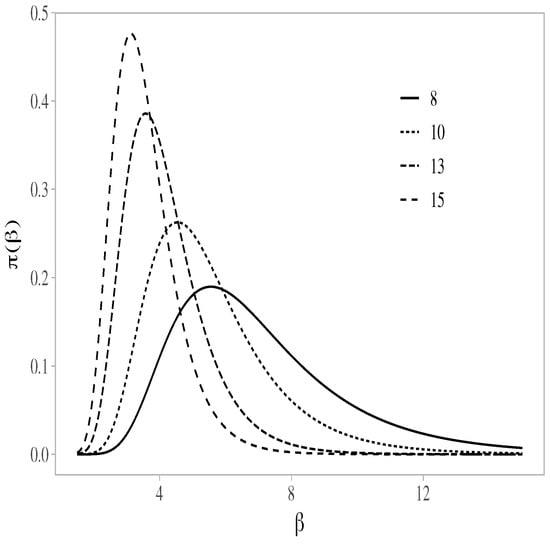
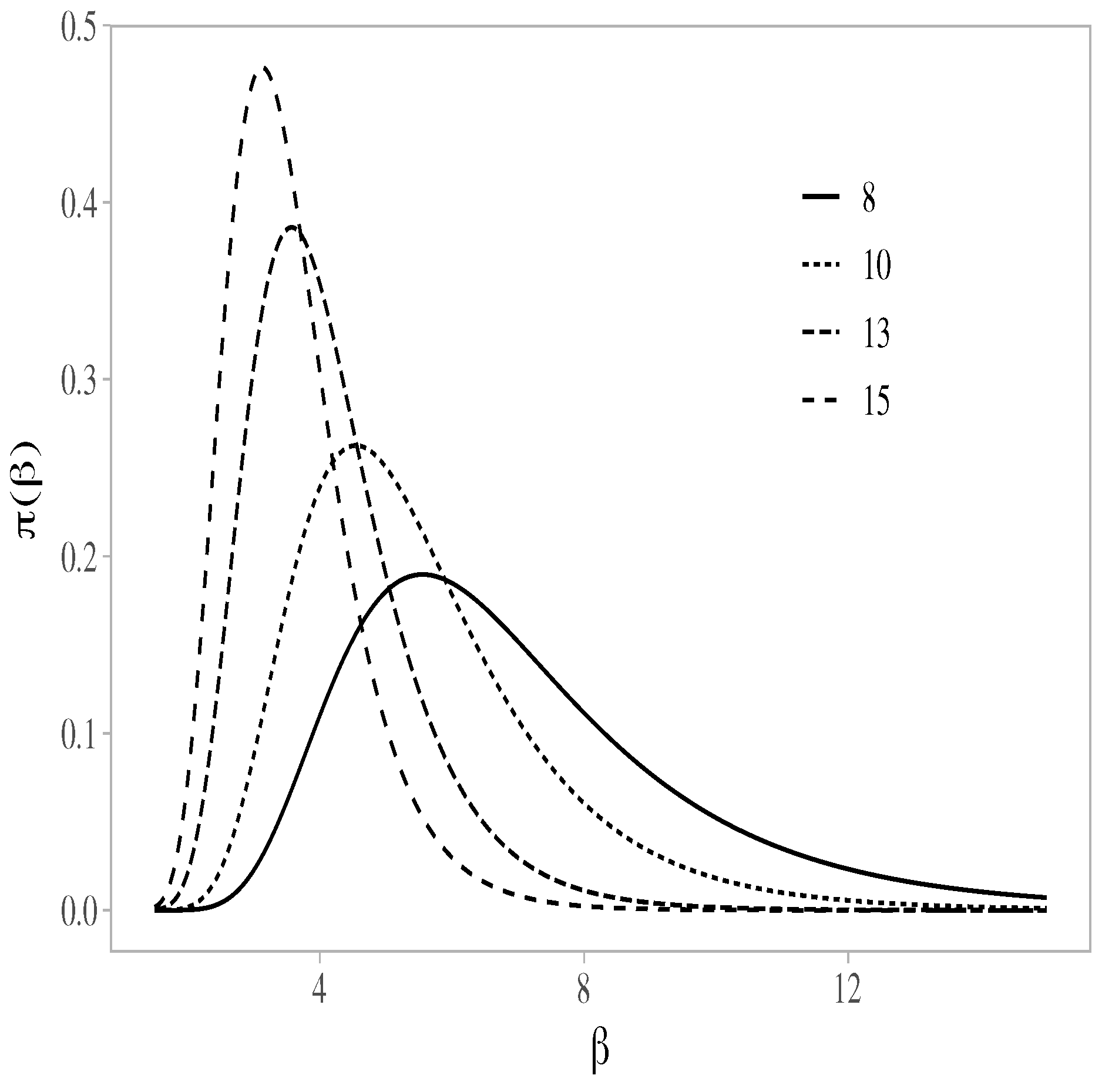
Figure 2.
Probability density functions for different values of the hyperparameter () of the IG prior distribution for .

Table 2.
Optimal sample sizes (in triplicate) when estimating the mean of the BS distribution via five different loss functions.
https://santosneto.shinyapps.io/samplesizeBSapp (accessed on 21 May 2021).
Note that values of the hyperparameters are fixed according to the practitioner’s knowledge for the parameters and (see Step 1 of Algorithm 1). For example, if we set the hyperparameters as and , it means that our prior knowledge indicates the most likely values for in the interval between the numbers 3 and 5 (see Figure 2) and similarly for the parameter . Thus, for instance, if the practitioner’s prior knowledge is that the possible values for (and/or ) are in the interval between the numbers 6 and 9, the practitioner must set the values of the hyperparameters (parameters of the IG distribution) such that the greatest mass of probability of the IG distribution is in the interval between the numbers 6 and 9.
4.4. Illustrative Example
A practical application of the methodology to compute the optimal sample size when estimating the mean of the BS distribution is illustrated here with one example. In this example, we consider a data set composed by 46 observations given in [33] and available in the samplesizeBS package [22]. These observations correspond to maintenance data on active repair times (in hours) for an airborne communications transceiver. Let be the observation i of this data set associated with the random variable .
First, we estimate and using the modified moment method defined in (3), which result in and , respectively. In this way, we can set IG prior distributions for and with and (see Figure 2). Hence, if our interest is in obtaining a credible interval for considering the loss function L5, with and , the optimal sample size may be obtained from Table 2, which is .
Now, we generate 1000 observations from the posterior distribution of and estimate the mean and variance of the respective posterior distribution through the sample mean and variance, respectively. With these estimates, we obtain a credible interval for given by [2.108; 3.939].
5. Discussion, Conclusions and Future Research
We proposed a methodology to compute the optimal sample size for estimating the mean of the Birnbaum–Saunders distribution, a widely applied and studied distribution in several areas of science. We considered five different loss functions, which allowed us to perform both point and interval inference for the parameter of interest.
An advantage of the proposed methodology is that the per-unit cost, represented by c, is explicitly taken into account. When the cost c is fixed and , the optimal sample size decreases as increases (or as the prior variance decreases), as expected, since in such a case, the prior knowledge increases as increases. This occurred with all loss functions considered in our study. For and fixed, also decreases as c increases, but the sampling total cost increases. For example, if we take the loss function L1, and , the corresponding is 651 (see Table 2), which generates a sampling cost of , whereas if we take , the corresponding is 23 (see Table 2), which produces a sampling cost of . For the loss function L3, increases as ℓ increases, if we consider and c fixed, which makes sense since overestimation is more costly as ℓ increases. For the loss function L4, when increases, also increases, if we consider and c fixed. This makes sense because is the weight attributed to the term in L4, a term related to the length of the credible interval. In addition, when increases, we expect longer credible intervals, and consequently, the probability of the respective interval decreases. The same is valid for in the loss function L5, but in this case, the decreasing of the corresponding credible interval is easily noted by the presence of the term in the expression of the respective Bayes rule. When increases, this term shrinks the length of the interval.
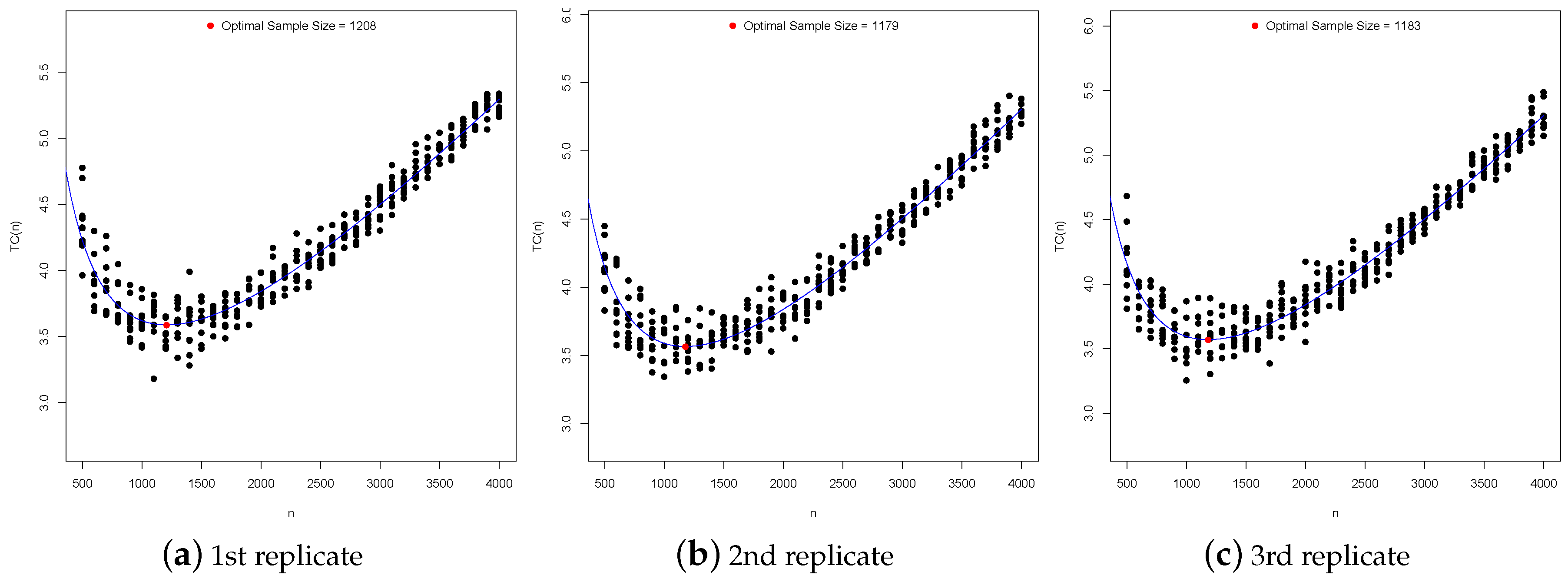
Since the proposed methodology was based on simulations, we obtained the value of in triplicate for each scenario of values of , c, ℓ, , and . We observed that the largest discrepancies in the scenarios occurred for . However, these discrepancies decreased as increased, or when the prior variance decreased. This also occurred when and/or when we considered the loss function L2. In general, the discrepancy was close to zero, but if a large discrepancy occurs, we suggest visually inspecting the graph of the fitted curves and taking the value of that corresponds to the best fit. Nevertheless, if all the curves fit visually well, we suggest using the median of the values obtained for . In our case, we obtained the values of in triplicate, as mentioned. For example, in Figure 3, under the loss function L5 with , , and , the values of were 1208, 1179, and 1183. Since there was a discrepancy between these values and the fittings of the curves were visually suitable, in this case, we suggest using . Note that we have optimal sample sizes equal to zero in Table 2 in some scenarios, which means that it is not worth sampling in these cases because the sampling cost outweighs the decreasing of the minimized Bayes risk. This was also observed in [2,6].
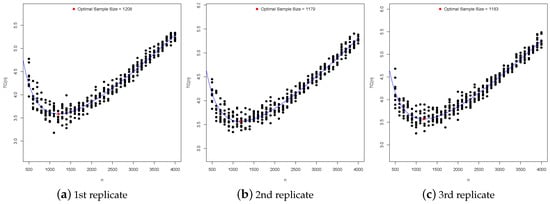
Figure 3.
Fitted curves with the respective optimal sample sizes obtained via the loss function L5 with , , and .
We recall that the objective of the present investigation was to calculate the optimal sample size when estimating the mean of the Birnbaum–Saunders distribution. Simulation experiments should be performed to study the relative bias of the estimator of the mean (or the width of the corresponding interval estimate). A sensitivity analysis considering such simulation experiments would also be helpful. However, as mentioned, our methodology uses very intensive computational resources, which limits the implementation of such experiments. In addition, we plan to consider different priors for the parameters and to examine the robustness and the sensitivity of the results. Moreover, we are interested in studying the possibility of using bounded loss functions and other sampling algorithms.
The relevance of calculating sample sizes in statistics is undeniable. Another important challenge to be implemented is related to calculating the sample size when estimating the Birnbaum–Saunders mean (or other parameters) under more complex modeling structures, such as regression, temporal, spatial, functional, PLS, and errors-in-variables settings [34,35,36,37,38]. We hope to report findings associated with these open aspects in future research.
Author Contributions
Data curation, E.C., and M.S.-N.; formal analysis, E.C., M.S.-N., and V.L.; investigation, E.C. and M.S.-N.; methodology, E.C., M.S.-N., and V.L.; writing—original draft, E.C. and M.S.-N.; writing—review and editing, V.L. All authors read and agreed to the published version of the manuscript.
Funding
This research was carried out using the computational resources of the Center for Mathematical Sciences Applied to Industry (CeMEAI) supported by FAPESP (Grant 2013/07375-0) from the São Paulo Research Foundation, a public foundation located in São Paulo, Brazil. The research of V. Leiva was partially supported by FONDECYT (Grant 1200525) from the National Agency for Research and Development (ANID) of the Chilean government under the Ministry of Science.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The real-world data set used in this work is available in the samplesizeBS package. To access the data, use the R command data(repair).
Acknowledgments
The authors would also like to thank the Editor and three Reviewers for their constructive comments, which led to the improvement of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Spiegelhalter, D.J.; Abrams, K.R.; Myles, J.P. Bayesian Approaches to Clinical Trials and Health-Care Evaluation; Wiley: Chichester, UK, 2004. [Google Scholar]
- Etzioni, R.; Kadane, J.B. Optimal experimental design for another’s analysis. J. Am. Stat. Assoc. 1993, 88, 1404–1411. [Google Scholar] [CrossRef]
- Sahu, S.K.; Smith, T.M.F. A Bayesian method of sample size determination with practical applications. J. R. Stat. Soc. A 2006, 169, 235–253. [Google Scholar] [CrossRef]
- Parmigiani, G.; Inoue, L. Decision Theory: Principles and Approaches; Wiley: New York, NY, USA, 2009. [Google Scholar]
- Islam, A.F.M.S.; Pettit, L.I. Bayesian sample size determination using LINEX loss and linear cost. Commun. Stat. Theory Methods 2012, 41, 223–240. [Google Scholar] [CrossRef]
- Islam, A.F.M.S.; Pettit, L.I. Bayesian sample size determination for the bounded LINEX loss function. J. Stat. Comput. Simul. 2014, 84, 1644–1653. [Google Scholar] [CrossRef]
- Santis, F.D.; Gubbiotti, S. A decision-theoretic approach to sample size determination under several priors. Appl. Stoch. Model. Bus. Ind. 2017, 33, 282–295. [Google Scholar] [CrossRef]
- Costa, E.G. Sample Size for Estimating the Organism Concentration in Ballast Water: A Bayesian Approach. Ph.D. Thesis, Department of Statistics, Universidade de São Paulo, São Paulo, Brazil, 2017. (In Portuguese). [Google Scholar]
- Birnbaum, Z.W.; Saunders, S.C. A new family of life distributions. J. Appl. Probab. 1969, 6, 319–327. [Google Scholar] [CrossRef]
- Bourguignon, M.; Leao, J.; Leiva, V.; Santos-Neto, M. The transmuted Birnbaum–Saunders distribution. REVSTAT Stat. J. 2017, 15, 601–628. [Google Scholar]
- Mazucheli, M.; Leiva, V.; Alves, B.; Menezes, A.F.B. A new quantile regression for modeling bounded data under a unit Birnbaum–Saunders distribution with applications in medicine and politics. Symmetry 2021, 13, 682. [Google Scholar] [CrossRef]
- Santos-Neto, M.; Cysneiros, F.J.A.; Leiva, V.; Barros, M. Reparameterized Birnbaum–Saunders regression models with varying precision. Electron. J. Stat. 2016, 10, 2825–2855. [Google Scholar] [CrossRef]
- Reyes, J.; Barranco-Chamorro, I.; Gallardo, D.I.; Gomez, H.W. Generalized modified slash Birnbaum—Saunders distribution. Symmetry 2018, 10, 724. [Google Scholar] [CrossRef]
- Gomez-Deniz, E.; Gomez, L. The Rayleigh Birnbaum Saunders distribution: A general fading model. Symmetry 2020, 12, 389. [Google Scholar] [CrossRef]
- Desousa, M.; Saulo, H.; Leiva, V.; Santos-Neto, M. On a new mixture-based regression model: Simulation and application to data with high censoring. J. Stat. Comput. Simul. 2020, 90, 2861–2877. [Google Scholar] [CrossRef]
- Sanchez, L.; Leiva, V.; Galea, M.; Saulo, H. Birnbaum–Saunders quantile regression and its diagnostics with application to economic data. Appl. Stoch. Models Bus. Ind. 2021, 37, 53–73. [Google Scholar] [CrossRef]
- Villegas, C.; Paula, G.A.; Leiva, V. Birnbaum–Saunders mixed models for censored reliability data analysis. IEEE Trans. Reliab. 2011, 60, 748–758. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Cysneiros, F.J.A. A multivariate log-linear model for Birnbaum–Saunders distributions. IEEE Trans. Reliab. 2016, 65, 816–827. [Google Scholar] [CrossRef]
- Arrue, J.; Arellano, R.; Gomez, H.W.; Leiva, V. On a new type of Birnbaum–Saunders models and its inference and application to fatigue data. J. Appl. Stat. 2020, 47, 2690–2710. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Kundu, D. Birnbaum–Saunders distribution: A review of models, analysis, and applications. Appl. Stoch. Model. Bus. Ind. 2019, 35, 4–49. [Google Scholar] [CrossRef]
- Bourguignon, M.; Ho, L.L.; Fernandes, F.H. Control charts for monitoring the median parameter of Birnbaum–Saunders distribution. Qual. Reliab. Eng. Int. 2020, 36, 1333–1363. [Google Scholar] [CrossRef]
- Costa, E.G.; Santos-Neto, M.; Leiva, V. samplesizeBS: Bayesian Sample Size in a Decision-Theoretic Approach for the Birnbaum–Saunders, R Package Version 1.1-1; 2020. Available online: www.github.com/santosneto/samplesizeBS (accessed on 21 May 2021).
- Aykroyd, R.G.; Leiva, V.; Marchant, C. Multivariate Birnbaum–Saunders distributions: Modelling and applications. Risks 2018, 6, 21. [Google Scholar] [CrossRef]
- Leiva, V. The Birnbaum–Saunders Distribution; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Ng, H.; Kundu, D.; Balakrishnan, N. Modified moment estimation for the two-parameter Birnbaum–Saunders distribution. Comput. Stat. Data Anal. 2003, 43, 283–298. [Google Scholar] [CrossRef]
- Wang, M.; Sun, X.; Park, C. Bayesian analysis of Birnbaum–Saunders distribution via the generalized ratio-of-uniforms method. Comput. Stat. 2016, 31, 207–225. [Google Scholar] [CrossRef]
- Leiva, V.; Ruggeri, F.; Saulo, H.; Vivanco, J.F. A methodology based on the Birnbaum–Saunders distribution for reliability analysis applied to nano-materials. Reliab. Eng. Syst. Saf. 2017, 157, 192–201. [Google Scholar] [CrossRef]
- Raiffa, H.; Schlaifer, R. Applied Statistical Decision Theory; Harvard University Press: Boston, MA, USA, 1961. [Google Scholar]
- Spiring, F.A. The reflected normal loss function. Can. J. Stat. 1993, 21, 321–330. [Google Scholar] [CrossRef]
- Leung, B.P.K.; Spiring, F.A. The inverted beta loss function: Properties and applications. IEE Trans. 2002, 34, 1101–1109. [Google Scholar] [CrossRef]
- Zellner, A. Bayesian estimation and prediction using asymmetric loss functions. J. Am. Stat. Assoc. 1986, 81, 446–451. [Google Scholar] [CrossRef]
- Rice, K.M.; Lumley, T.; Szpiro, A.A. Trading Bias for Precision: Decision Theory for Intervals and Sets. Working Paper 336, UW Biostatistics. 2008. Available online: https://biostats.bepress.com/uwbiostat/paper336/ (accessed on 21 May 2021).
- Hsieh, H.K. Estimating the critical time of the inverse Gaussian hazard rate. IEEE Trans. Reliab. 1990, 39, 342–345. [Google Scholar] [CrossRef]
- Puentes, R.; Marchant, C.; Leiva, V.; Figueroa, J.I.; Ruggeri, F. Predicting PM2.5 and PM10 levels during critical episodes management in Santiago, Chile, with a bivariate Birnbaum–Saunders log-linear model. Mathematics 2021, 9, 645. [Google Scholar] [CrossRef]
- Leiva, V.; Saulo, H.; Souza, R.; Aykroyd, R.G.; Vila, R. A new BISARMA time series model for forecasting mortality using weather and particulate matter data. J. Forecast. 2021, 40, 346–364. [Google Scholar] [CrossRef]
- Martinez, S.; Giraldo, R.; Leiva, V. Birnbaum–Saunders functional regression models for spatial data. Stoch. Environ. Res. Risk Assess. 2019, 33, 1765–1780. [Google Scholar] [CrossRef]
- Huerta, M.; Leiva, V.; Liu, S.; Rodriguez, M.; Villegas, D. On a partial least squares regression model for asymmetric data with a chemical application in mining. Chemom. Intell. Lab. Syst. 2019, 190, 55–68. [Google Scholar] [CrossRef]
- Carrasco, J.M.F.; Finiga, J.I.; Leiva, V.; Riquelme, M.; Aykroyd, R.G. An errors-in-variables model based on the Birnbaum–Saunders and its diagnostics with an application to earthquake data. Stoch. Environ. Res. Risk Assess. 2020, 34, 369–380. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).