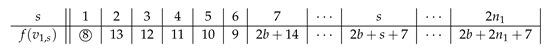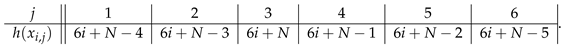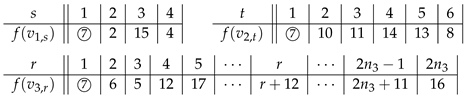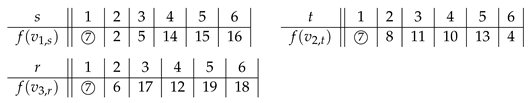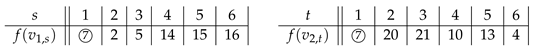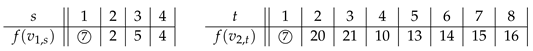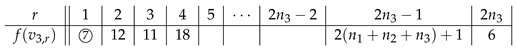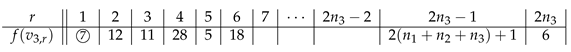1. Introduction
Let
(or simply
for short, if there is no ambiguity) be a simple, finite and undirected graph of order
and size
. For convenience, we shall use
to denote the set of integers from
a to
b, where
. All notation not defined in this paper can be found in [
1].
Since the introduction of the concept of graph labeling by Rosa in 1967 [
2], thousands of papers on various graph labeling problems have been published. It is interesting to note that the field of graph labelings is becoming more significant with more applications in other topics of graph theory being found. For example, the friendly index of a graph is related to eigenvalues, bipartition width, max-cut problem and isoperimetric problem of a graph [
3].
One of the graph labeling problems that attracts great interest of researchers is the concept of prime graphs introduced in 1982 [
4].
Definition 1. A bijection induces an edge labeling such that for an edge in G, if , and otherwise. Such a labeling is called a prime labeling if for all . We say G is a prime graph if it admits a prime labeling.
Since then, many papers that attempt to determine the primality of graphs are published (for example, [
5,
6,
7,
8,
9,
10,
11]). Although a wheel graph of order
is prime if and only if
n is even [
12], it was proved that the one point union of cycles and that of wheels at the center vertex are all prime graphs [
13]. However, we are unaware of any vertex labelings in which the induced edge labels are associated to the sum and difference of the incident end-vertex labels.
In view of this, Lau and Shiu [
14] introduced a variant of prime graph labeling, known as SD-prime labeling, as defined below.
Given a bijection , and every edge in E, one can associate two integers and .
Definition 2. A bijection induces an edge labeling such that for an edge in G, if , and otherwise. Such a labeling is called an SD-prime labeling if for all . We say G is SD-prime if it admits an SD-prime labeling.
In [
15], Lau et al. provided more discussion on SD-prime labelings. This new concept leads to new research direction and possible future applications. In [
16], one may find that the one point union of various families of standard graphs have been investigated under various labeling problems (see, for example, [
17,
18,
19]). However, we are not aware of the study on one point union of gear graphs under any graph labeling problems. Thus, in this paper, we aim to determine the SD-primality of the various families of one point union of gear graphs. The following results follow directly from the definitions.
Corollary 1. Every spanning subgraph of an SD-prime graph is also an SD-prime graph.
Corollary 2. Suppose G admits an SD-prime labeling, then G also admits a prime labeling.
The following results are obtained in [
14].
Theorem 1 ([
14], Theorem 1).
Let f be an SD-prime labeling of G, then and have different parity for each edge . Theorem 2 ([
14], Theorem 3).
Let G be an SD-prime graph of order greater than 1, then G is a spanning subgraph of either or for some . Theorem 3 ([
14], Theorem 2.2).
A graph G of order n is SD-prime if and only if G is bipartite and that there exists a bijection such that for each edge of G, and are of different parity and . 2. Preliminary
For
, let
be the graph obtained from a wheel graph
of order
by deleting
n spokes where no two of the spokes are consecutive. Such a graph is called a gear graph (or gear, for short). The core (center vertex) of the wheel is also called the core of the gear. From ([
14], Theorem 2.13) we know that
is SD-prime for all
. In the paper, we want to study the SD-primality of some one point unions of gears.
Let be a graph and be fixed, . A one point union of , , is a graph obtained from the disjoint union of by merging all into a single vertex which is called the merged vertex. So, there will be many different one point unions of ’s.
There are three types of vertices in a gear. We shall say that a noncore vertex of degree 2 is of Type 1; a noncore vertex of degree 3 is of Type 2; a core vertex is of Type 3.
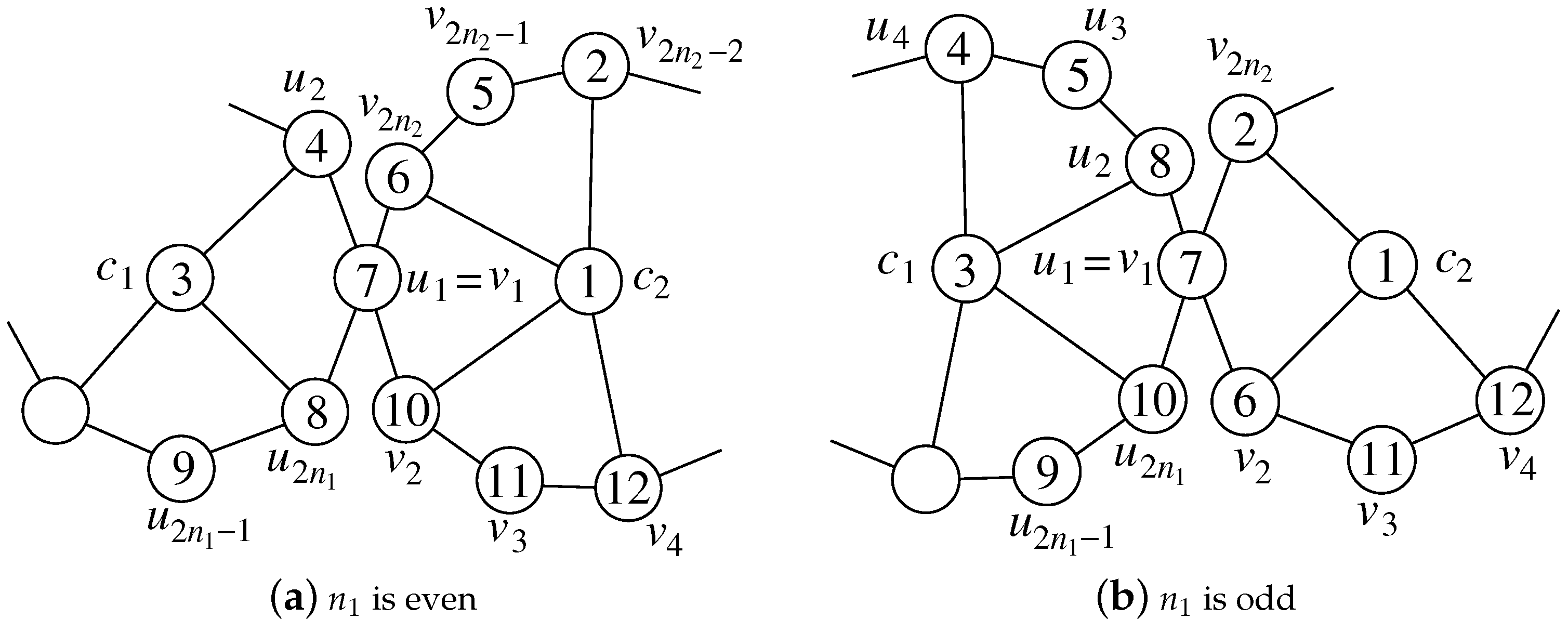
Let be a gear, and . Suppose . Let be a Type 1 vertex in for (this case does not occur if ), a Type 2 vertex for (this case does not occur if ) and a Type 3 vertex for (this case does not occur if ). The graph is a one point union of the gear ’s by merging all into a vertex, say v. When one of the sequences ; or is empty, we will denote it by ⌀. We shall also denote by and by , for short.
Theorem 4. If is SD-prime, then or k.
Proof. Clearly, G is bipartite. We color each vertex of G by white or by black so that no two adjacent vertices receive the same color. Suppose the merged vertex is white.
Consider the subgraphs for . All the Type 1 and Type 3 vertices are colored by white. So, there are white vertices and black vertices.
Consider the subgraphs for . All the Type 1 and Type 3 vertices are colored by black. So, there are white vertices and black vertices.
Consider the subgraphs for . All the Type 1 and Type 3 vertices are colored by white. So, there are white vertices and black vertices.
To obtain
G, we identify
t white vertices as the merged vertex. Thus, there are
By Theorem 2 we have . It is equivalent to . Thus, we have Theorem 4. □
Corollary 3. If is SD-prime, then all the Type 1 and Type 3 vertices are labeled by odd numbers.
Proof. From the proof of Theorem 4, we know that all the Type 1 and Type 3 vertices are colored white. Since the number of white vertices is one more than that of black vertices, white vertices are labeled by odd numbers. □
Corollary 4. If is SD-prime, then the merged vertex is labeled by even numbers.
Proof. For this case, from the proof of Theorem 4, the number of white vertices is one less than that of black vertices. Hence, the merged vertex is labeled by even number. □
The above theorem implies that at most one Type 2 vertex can be merged to obtain an SD-prime one point union of gears. In the following sections, we shall consider some simple cases. For the gear
, denote its vertex set by
where
.
3. Merging of Type 1 Vertices
In this section, we only consider , when . Before the discussion, we define two sequences first.
For
, we define a sequence
of 4 elements by
We also define an order pair
by
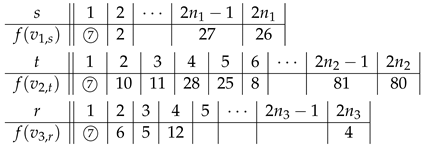
Let and .
Lemma 1. Let sequences S and T be defined above. Then,
- (1)
each pair of consecutive terms in S is of different parity and coprime,
- (2)
each pair of consecutive terms in T is of different parity and coprime.
- (1)
Clearly, (1) is true when the two numbers come from the same subsequence for some l.
Suppose . The last term of is and the first term of is . Now, .
Suppose . The last term of is and the first term of is . Clearly, .
Suppose . The last term of is and the first term of is . Now, . Since , .
- (2)
Clearly, (2) is true when the two numbers come from the same subsequence for some l.
Suppose . The last term of is and first term of is . Clearly, .
Suppose . The last term of is and first term of is . Clearly, .
□
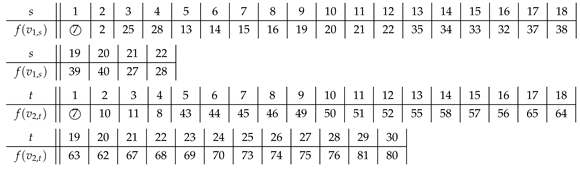
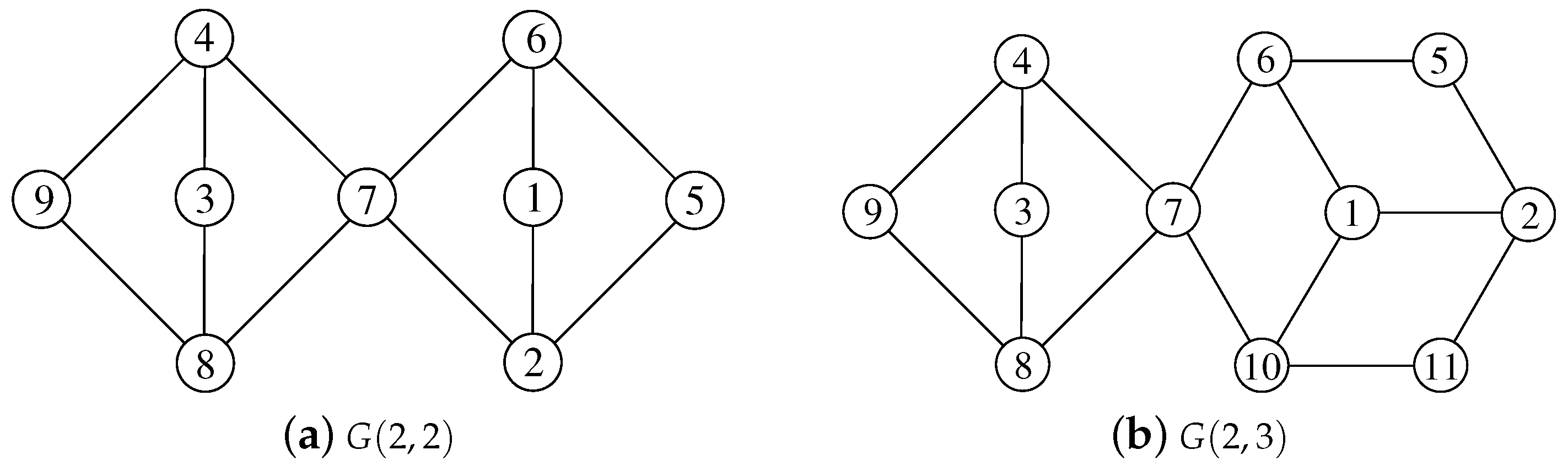
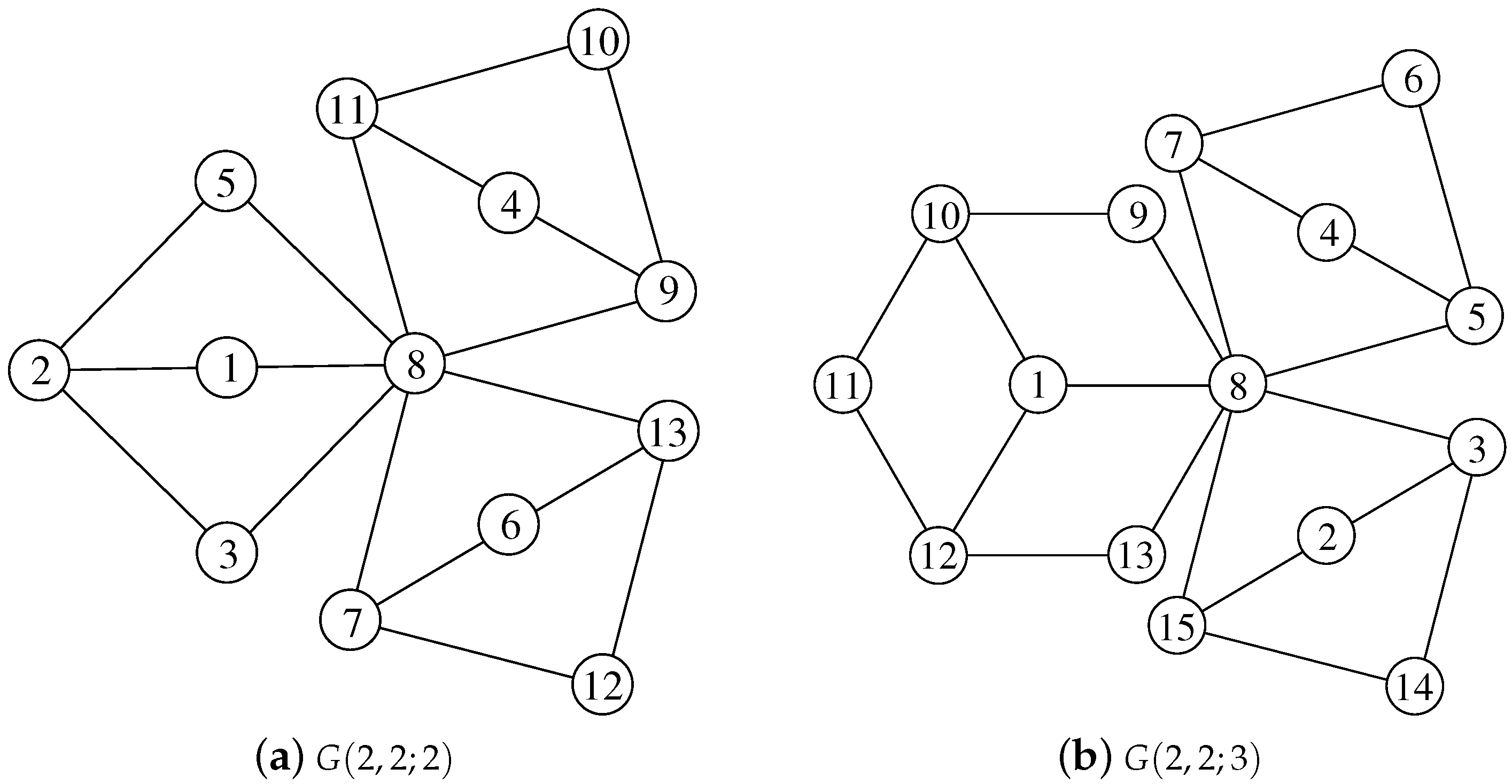
Theorem 5. is SD-prime for any .
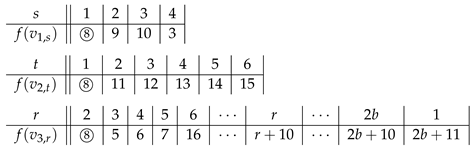
Proof. For simplicity, we replace by , and by , where and . Let f be a labeling of G.
When
and
, we let
,
,
,
,
,
,
,
and
. When
, we have
Figure 1a. When
, labels in
need to be assigned. For this case, we simply label the vertices from
to
by 10 to
consecutively. By Theorem 3, we see that
f is an SD-prime labeling.
Figure 1b shows the SD-prime labeling for
according to the construction above.
Now, we assume that .
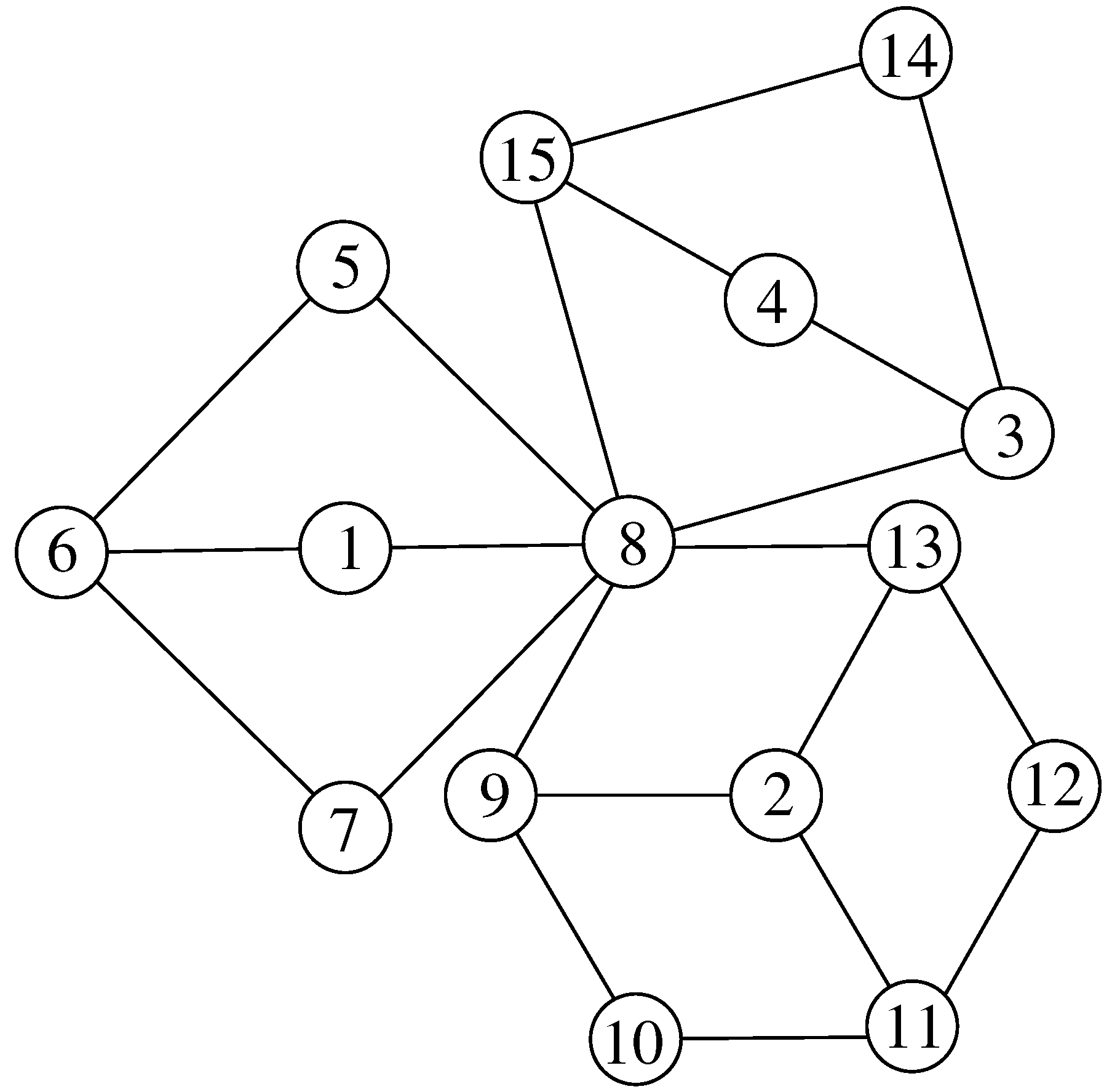
- Case 1:
Suppose
for some
. We let
,
,
,
,
,
,
,
,
,
,
and
(see
Figure 2a).
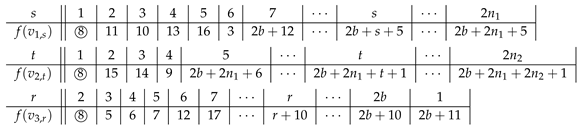
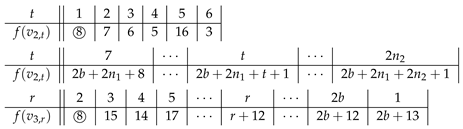
Now, there are and uncolored vertices in and , respectively. We label consecutively the vertices from to by the first terms of S and from to by the first terms of T, respectively, where S and T are the sequences in Lemma 1.
Note that or , and the vertex labeled by is not adjacent to the core for every l. So, f satisfies the requirement of SD-prime labeling for . Up to now, we have used labels from 1 to . Finally, we label the unlabeled vertices from to by to consecutively, if . Note that, . By Theorem 3, we see that f is an SD-prime labeling of G.
For the remaining case, i.e., . Since , . Only is a case. For this case, we have the labeling:
- Case 2:
Suppose
for some
. We let
,
,
,
,
,
,
,
,
,
,
and
(see
Figure 2b). When
, the graph
is labeled completely. For this case, we simply label the vertices from
to
by 13 to
consecutively.
So, we assume that . Similar to Case 1, we may label the vertices from to and from to using the labels in .
Following that, we consider , where . We always merge vertices , and as v and let , , and , where f is an expected SD-prime labeling of G.
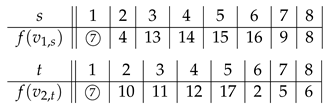
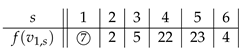
Theorem 6. is SD-prime for any .
Proof. The following are SD-prime labelings for and .
For , the labeling f for is listed in the following table.
The labeling
f for the two
’s are same as the two
’s in
(see
Figure 3b).
It is easy to check that f is an SD-prime labeling. □
Theorem 7. is SD-prime for any , and .
Proof. Similar to the proof of Theorem 5, we let be the sequence obtained from S by removing subsequences and , where S is defined in Lemma 1. Observe that the subsequences and have adjacent terms that are coprime. Hence, each pair of consecutive terms in is of different parity and coprime.
- Case 1:
Suppose and for some and . The initial labeling for some vertices are listed as follows:
When , then and are already labeled. For this case, the set of unassigned labels is . Here, we may simply label the remaining vertices of consecutively.
Suppose . We label consecutively the vertices from to and then to by the first terms of and from to by the first terms of T, respectively, where T is the sequence defined in Lemma 1. Note that, when , no vertices of are labeled at this step.
After this step, let
R be the set of remaining labels arranged in natural order. Namely,
By part (2) of Lemma 1, we see that each pair of consecutive terms in R is of different parity and coprime.
So, we may label the vertices from to .
Hence, we obtain an SD-prime labeling for this case.
- Case 2:
Suppose and for some and .
If , then and . The labeling is defined as follows:
Suppose . The initial labeling for some vertices are listed as follows:
Similar to Case 1, we label consecutively the vertices from to and then to by the first terms of and from to by the first terms of T, respectively. The rest is similar to Case 1.
- Case 3:
Suppose and for some and . The initial labeling for some vertices are listed as follows:
This case is similar to Case 2.
- Case 4:
Suppose and for some and . The initial labeling for some vertices are listed as follows:
Similar to Case 1, we label consecutively the vertices from to and then to by the first terms of and from to by the first terms of T, respectively. The rest is similar to Case 1.
□
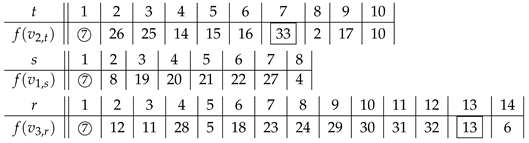
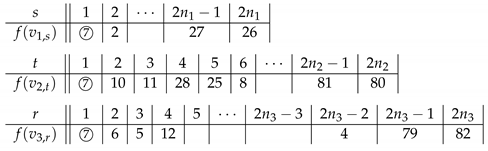
Example 1. Below is the SD-prime labeling of following the construction in Case 1 of the proof of Theorem 7.
Example 2. Below is the SD-prime labeling of following the construction in Case 4 of the proof of Theorem 7.
The labeling for is the same as in Example 1.
Corollary 5. is SD-prime for any , and .
Proof. Basically, the proof is the same as that of Theorem 7. The difference is that 82 is not an available label. So, we have to change the initial labeling of each case in the proof of Theorem 7.
Here, we only show the first case below. Other cases are similar.
Suppose and for some and . The initial labeling for some vertices are listed as follows:
The rest assignment is same as that in the proof of Theorem 7.
Note that, in all cases, 79 is the largest unassigned label. Follow the labeling shown in the proof of Theorem 7, 79 is labeled at . □
From Case 2 of the proof of Theorem 7 we have
Corollary 6. is SD-prime for any .
For the remaining cases, we may assume . Hence, .
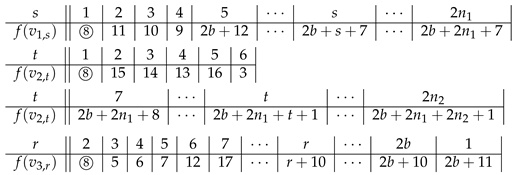
Theorem 8. Suppose , then is SD-prime for .
Proof. We label and as follows:
- Case 1:
. We have .
When . This implies that . For this case, following is an SD-prime labeling for :
Now, we assume that .
When . We label and as follows:
When . We label and as follows:
The initial labeling for some vertices of are as follows:
The unassigned labels in , if any, can be labeled from to consecutively.
- Case 2:
.
When .
The labeling for is as in Case 1.
When . We label as in Case 1 and label as
The initial labeling for is as in Case 1. The unassigned labels in can be labeled from to consecutively.
- Case 3:
.
Suppose . If , we label as in Case 1.
The labeling for and are as follows:
If , the labeling for is as follows:
The labeling for is as in Case 1.
When . We label as
The labeling for is as in Case 2.
When . We label as in Case 1 and label as
The initial labeling for is as follows:
The unassigned labels in , if any, can be labeled from to consecutively.
It is easy to see that all above labelings are SD-prime labelings. □
Now, the remaining case is and . This implies that and .
Theorem 9. Suppose and . is SD-prime for .
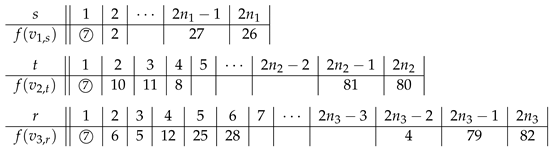
Proof. Let be the subsequence of S by removing and , and be the subsequence of T by removing , where S and T are defined in Lemma 1. That is, and . Clearly, each pair of consecutive terms in or is of different parity and coprime.
Note that and
- Case 1:
Suppose and for some and . In this case, . The initial labeling for some vertices in and are listed as follows:
We label consecutively the vertices from to and then to , if any, by the first terms of . It is easy to see that the last term of is not a multiple of 17 for . The maximum used label is at most . So, we may label initially as follows:
We label consecutively the vertices from to by the first terms of . The rest is similar to Case 1 of the proof of Theorem 7. Since , . The above labeling is SD-prime if .
If , then . We swap the labels of and . One may check that the resulting labeling is SD-prime.
- Case 2:
Suppose and for some and . In this case, . The initial labeling for some vertices in and are listed as follows:
We label consecutively the vertices from to and then to , if any, by the first terms of . Note that . The maximum used label is at most when . So, we may label initially as follows:
We label consecutively the vertices from to by the first terms of . The rest is similar to Case 1. Since , , the above labeling is SD-prime if .
When . We swap the labels of and . Similar to Case 1, one may check that the resulting labeling is SD-prime.
When , there are only two cases: .
Suppose . After labeling and , the maximum used labels is 35. Since , , we have so that . Hence, the labeling method is as the case when .
Suppose . After labeling and , the maximum used labels is 65. In this case, we have . When , the labeling method is as the case when . We now deal with . It implies that . Actually, it is not a case according to the previous construction so we list a required labeling as follows:
- Case 3:
Suppose and for some and . In this case, . The initial labeling for some vertices in and are listed as follows:
We label consecutively the vertices from to and then to , if any, by the first terms of . Note that . The rest is as Case 2.
- Case 4:
Suppose and for some and . In this case, . The initial labeling for some vertices in and are listed as follows:
We label consecutively the vertices from to and then to , if any, by the first terms of . The maximum used label is at most . So, we may label initially as follows:
The rest is similar to Case 1.
□
Example 3. Following is an SD-prime labeling of according to the construction in the proof of Theorem 9:
Conjecture 1. is SD-prime for .
4. Merging of Type 1 and Exactly One Type 2 Vertices
In this section, we assume that . For convenience, we use to denote a sequence of length n whose terms are a.
Theorem 10. For , is SD-prime.
Proof. Without loss of generality, we assume that
is merged with
,
. Now, we define a labeling
f (see
Figure 4) for
G by
It is easy to check that f is an SD-prime labeling. □
Theorem 11. For , is SD-prime.
Proof. Same as the proof of Theorem 5, we use to replace and to replace , where and . Suppose is merged with . Let f be a labeling of G. We always set , and . We assign the labels to other vertices as follows.
- Case 1:
Suppose
. Let
Here, since .
- Case 2:
- Case 3:
Suppose
and
,
. Let
- Case 4:
Suppose
and
. Let
- Case 5:
Suppose
and
. Let
Now, .
It is easy to check the coprimality of other adjacent vertices. By Theorem 3, f is an SD-prime labeling of G. □
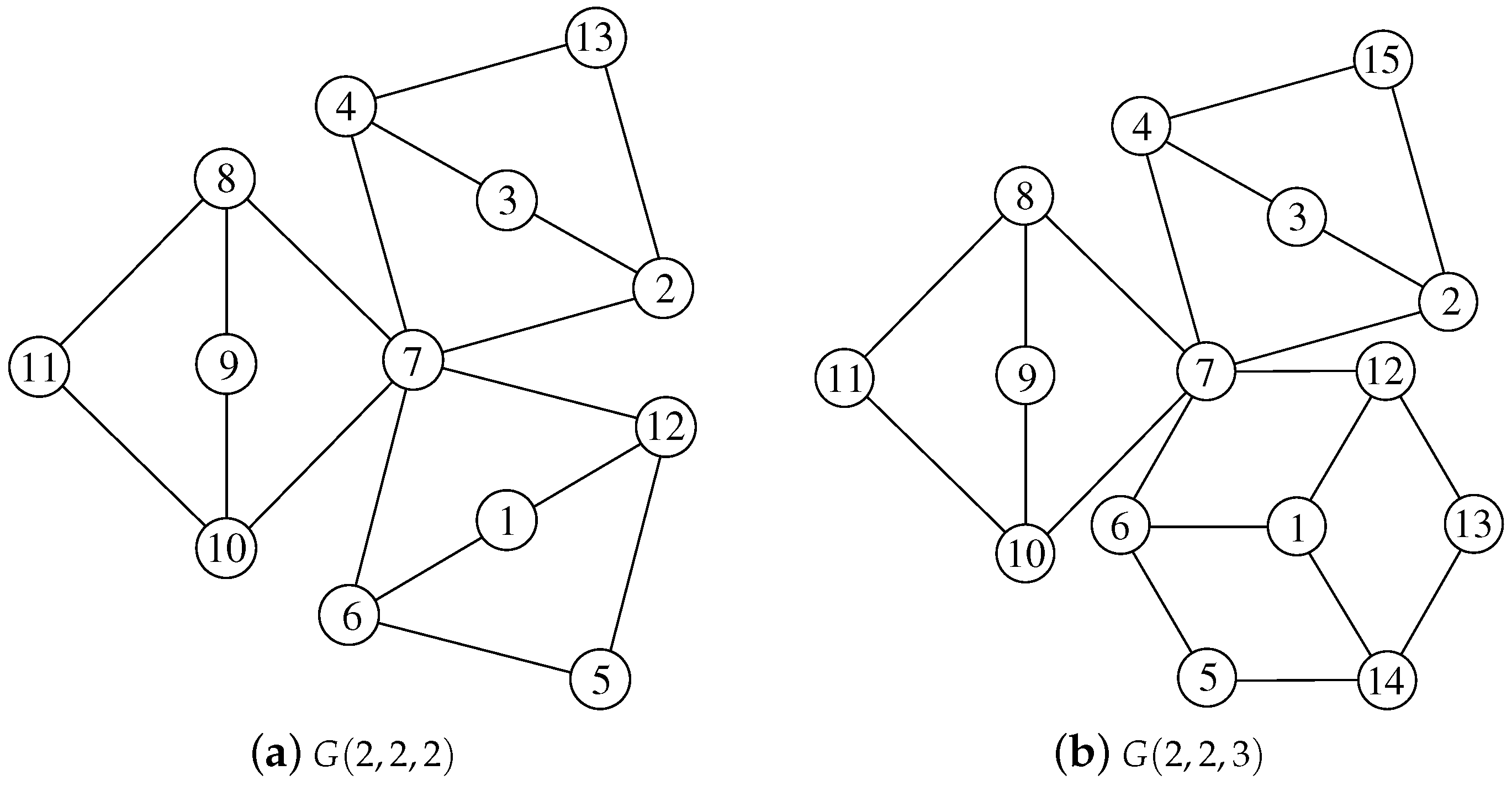
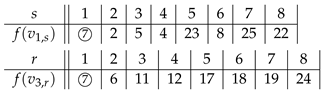
Theorem 12. For , is SD-prime.
Proof. When , we have the following SD-prime labelings:
For , we merge vertices , and and let , , and .
We define the labeling f by the following table.
The labeling of the two
’s are same as shown in
Figure 5b.
Clearly, f is an SD-prime labeling of . □
Theorem 13. For , is SD-prime.
Proof. When . We have proved in Theorem 12. So, we assume that . We merge vertices , and and let , , and .
- Case 1:
Suppose . We define the labeling f by the following table.
Since , we have . So, and when .
- Case 2:
Suppose . We list the labeling as in the following table.
Clearly, .
By Theorem 3, f is an SD-prime labeling of G for each case. □
Example 4. By the construction from the proof of Case 1 above, we have an SD-prime labeling of (Figure 6): Theorem 14. For , and , is SD-prime.
Proof. We always merge vertices , and and let , , and .
Case 1: Suppose and . This implies that . We define the labeling f by the following table.
Clearly, f satisfies the last two conditions of Theorem 3 for all vertices in . Since , . Thus, . Since , .
Suppose and . This implies that and . We define the labeling f by the following table.
Same as the Case 1, f satisfies the last two conditions of Theorem 3 for all vertices in and . Since , .
Suppose and . This implies that . We define the labeling f by the following table.
Since , . Thus, . Since , . Others are similar to the previous cases, we omit the arguments.
Case 2:Suppose and . If , then . We have the following labeling.
We define the labeling f by the following table for .
Since , . If others are similar to the previous cases, we omit the arguments.
By Theorem 3, f is an SD-prime labeling of G for each case. □
Conjecture 2. is SD-prime, where and .
5. Merging of Type 3 Vertices
We study the case first. We shall obtain some ad hoc results.
Theorem 15. For , is SD-prime.
Proof. Let f be a labeling of G defined by and
for . Now, and . Hence, by Theorem 3, f is an SD-prime labeling of G. □
Theorem 16. For , is SD-prime.
Proof. Let f be a labeling of G defined by
and
for
,
. In this case,
So, we have the theorem. □
Remark 1. If we extend the labeling f in the proof of Theorem 16 to , then . Here, . For this case, we may swap the labels of and . Then, f is an SD-prime labeling of . Now, by the same way, we may extend f up to . For the 13-th , we may use the same f and swap the labels of and a suitable labeled vertex. So, that we believe that f can be extended to and then to , and so on. So, we make the following conjecture.
Conjecture 3. is SD-prime for .
Theorem 17. Let v be the merged vertex of with the following conditions, where ,
- (1)
,
- (2)
there is an SD-prime labeling h of H such that for some .
Then, is SD-prime, for .
Proof. Let . By the assumption, all cores of ’s are merged to v. Now, we want to extend h to G by assigning labels in . Let the vertices of the i-th be , , . For , let
Then, and . Hence, h is extended to be an SD-prime labeling of for . □
Theorem 18. For and , is SD-prime.
Proof. From Remark 1, we label first, . Note that the merged vertex is labeled by 1. Then, shift the original labeling f defined in the proof of Theorem 15 by . By the same argument in the proof of Theorem 15, we have the theorem. □
To illustrate the proof of the above theorem, we provide the following example.
Example 5. Consider , where . We use the labeling defined in the proof of Theorem 16 to label the three ’s. Here, labels in are occupied.
Let be vertex of the i-th , . We let
Now, and . Hence, by Theorem 3, f is an SD-prime labeling of G.