q-Generalized Tangent Based Hybrid Polynomials
Abstract
1. Introduction
2. Preliminaries
3. q-Generalized Tangent-Apostol Type Frobenius–Euler Polynomials and Their Related Formulas
4. Explicit Representations
5. q-Derivative and q-Integral Formulas
6. Graphical Representations and Locations of Zeros
7. Concluding Remarks, Further Observations, and Posing Questions
Observations and Questions
- (i)
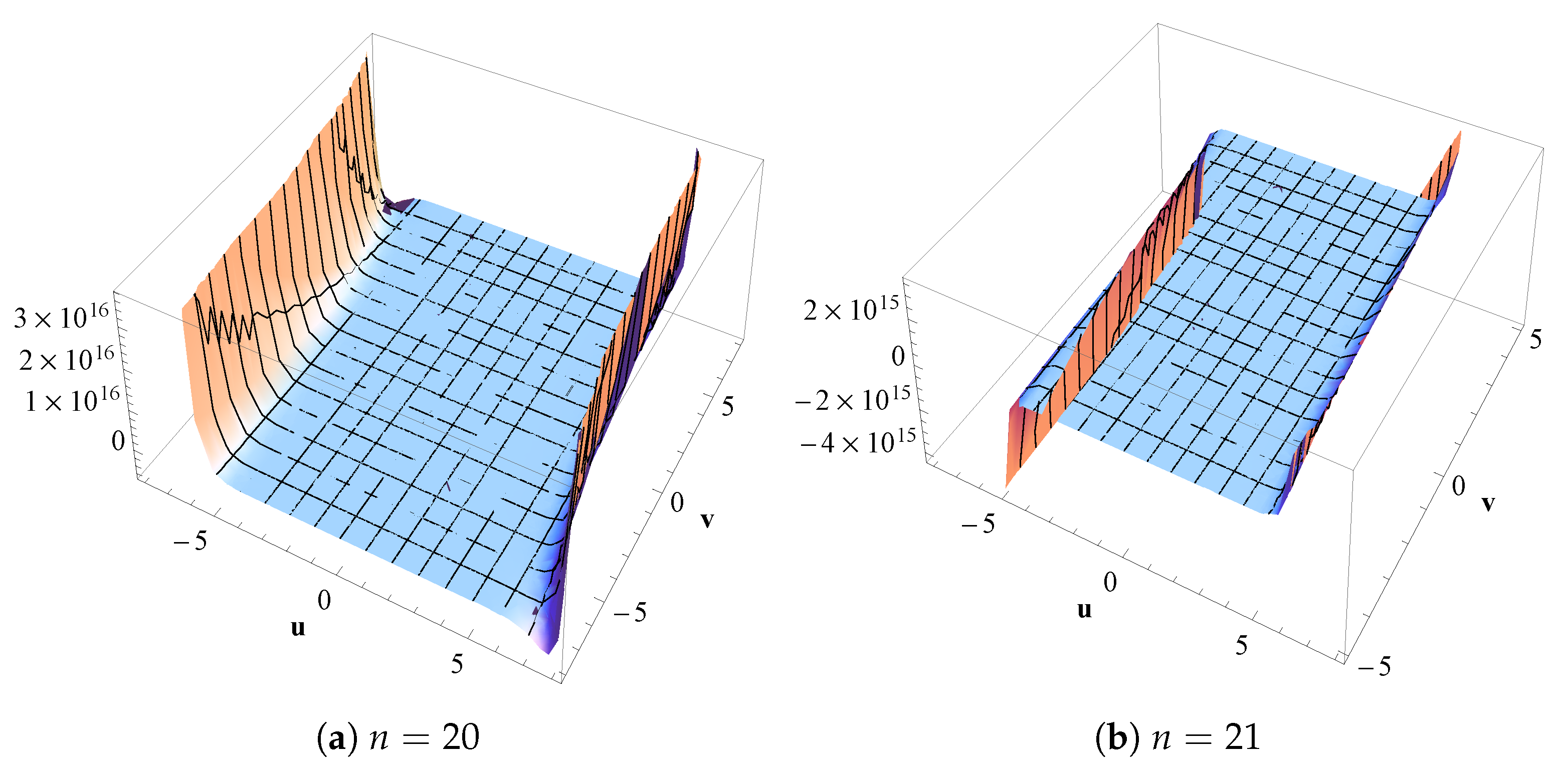
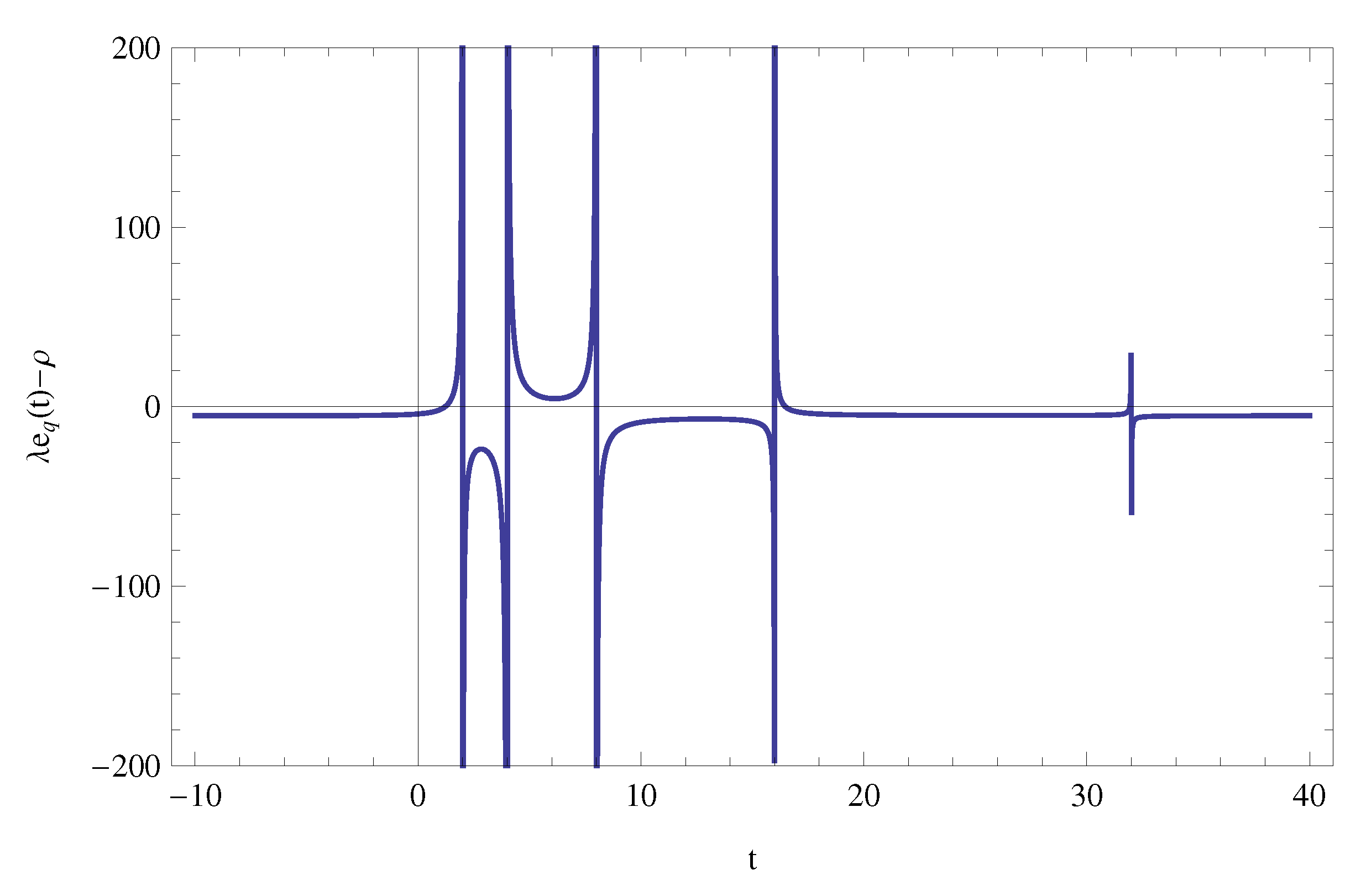
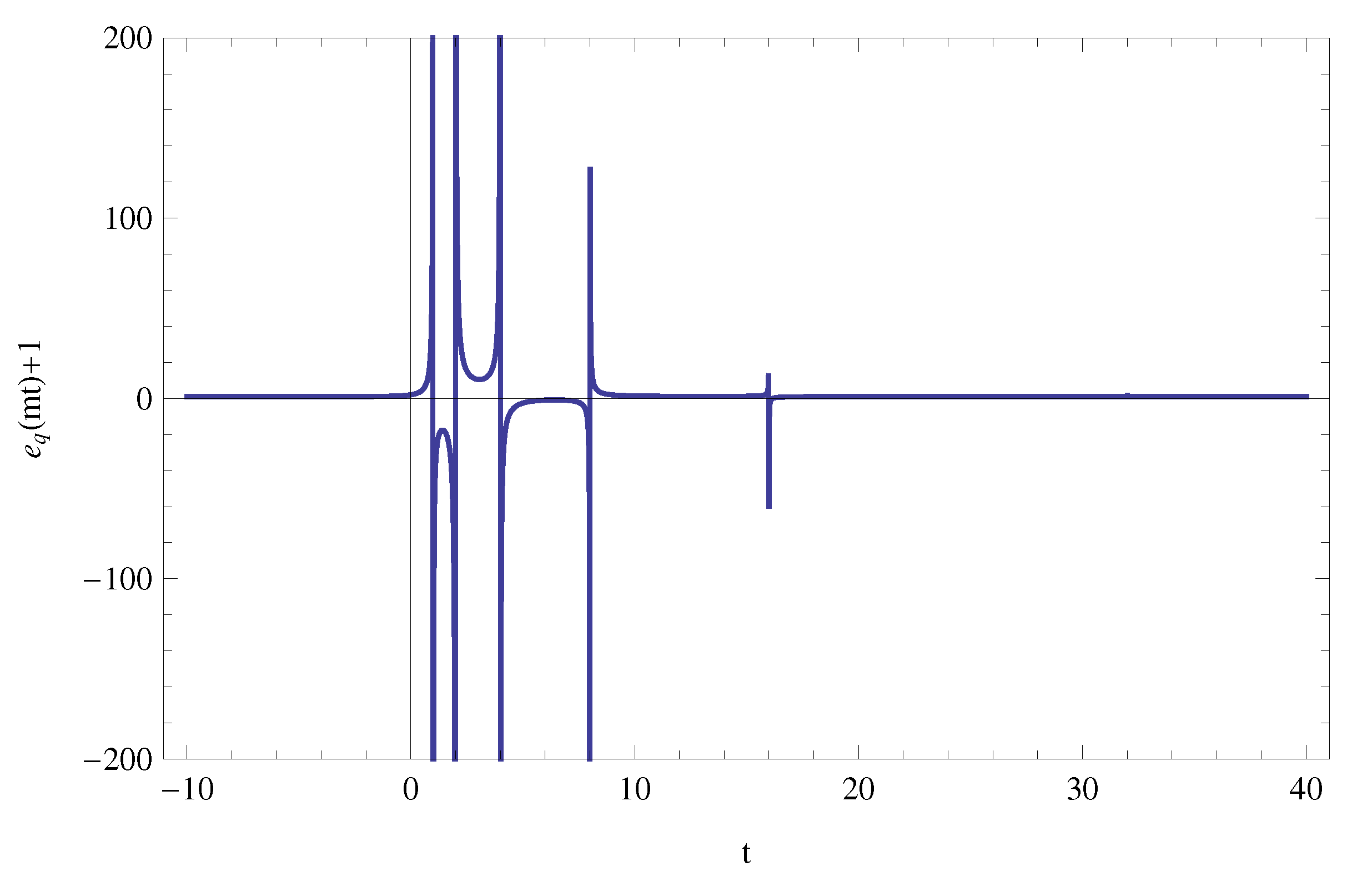
- It may be important to find complex zeros of the following equationsfrom Definitions 1 and 6 (see also generating functions in Definitions 2, 3, and 5), in particular, in order to determine the and there exactly. When , the zeros of two equations in (63) are easily given, respectively, bywhere is an argument of .Question 1: Find or approximate the zeros of two equations in (63).Graph of (for and ) as follows:Certain approximate real and complex zeros ofare given, respectively, asand
- (ii)
- (iii)
- (iv)
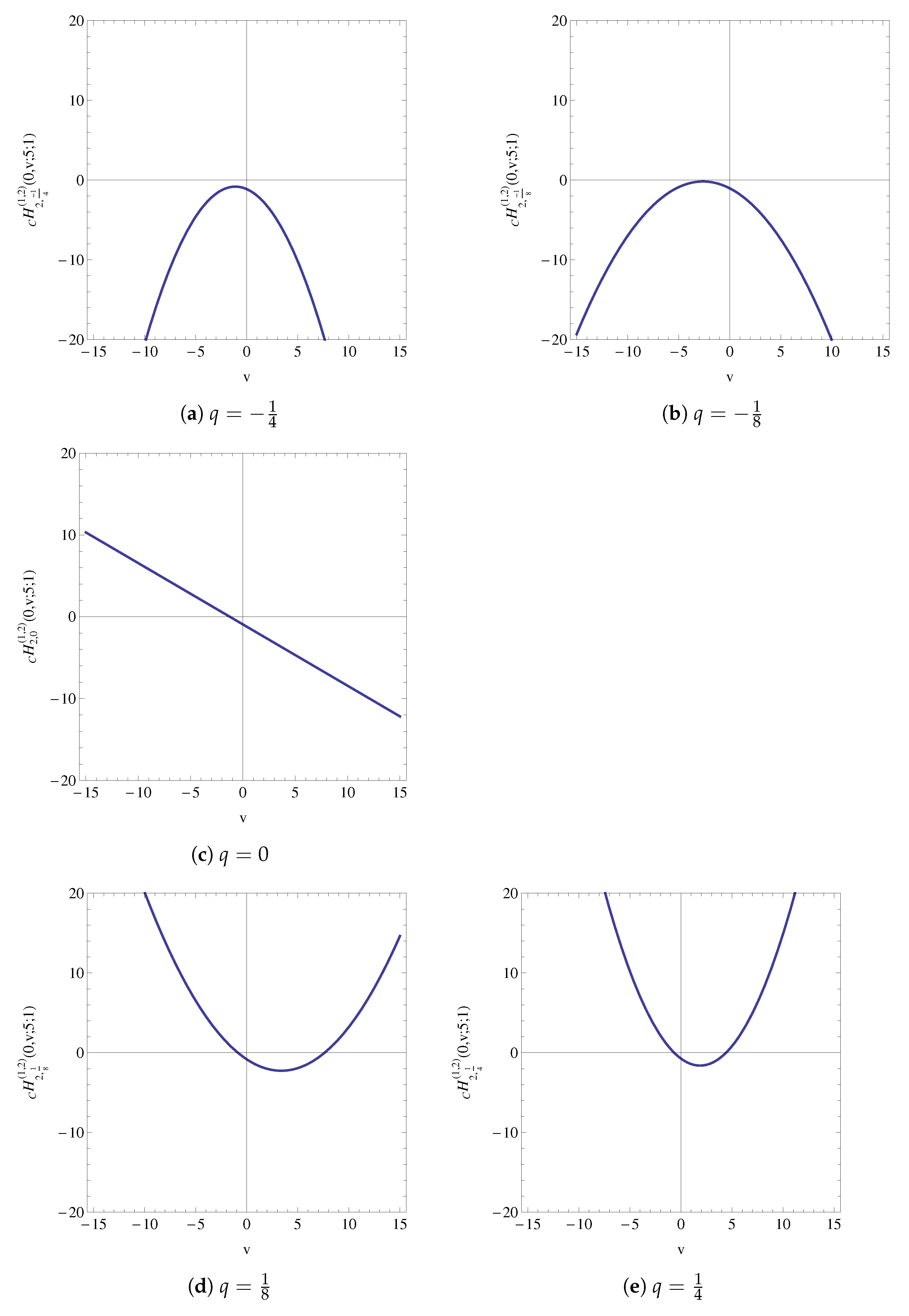
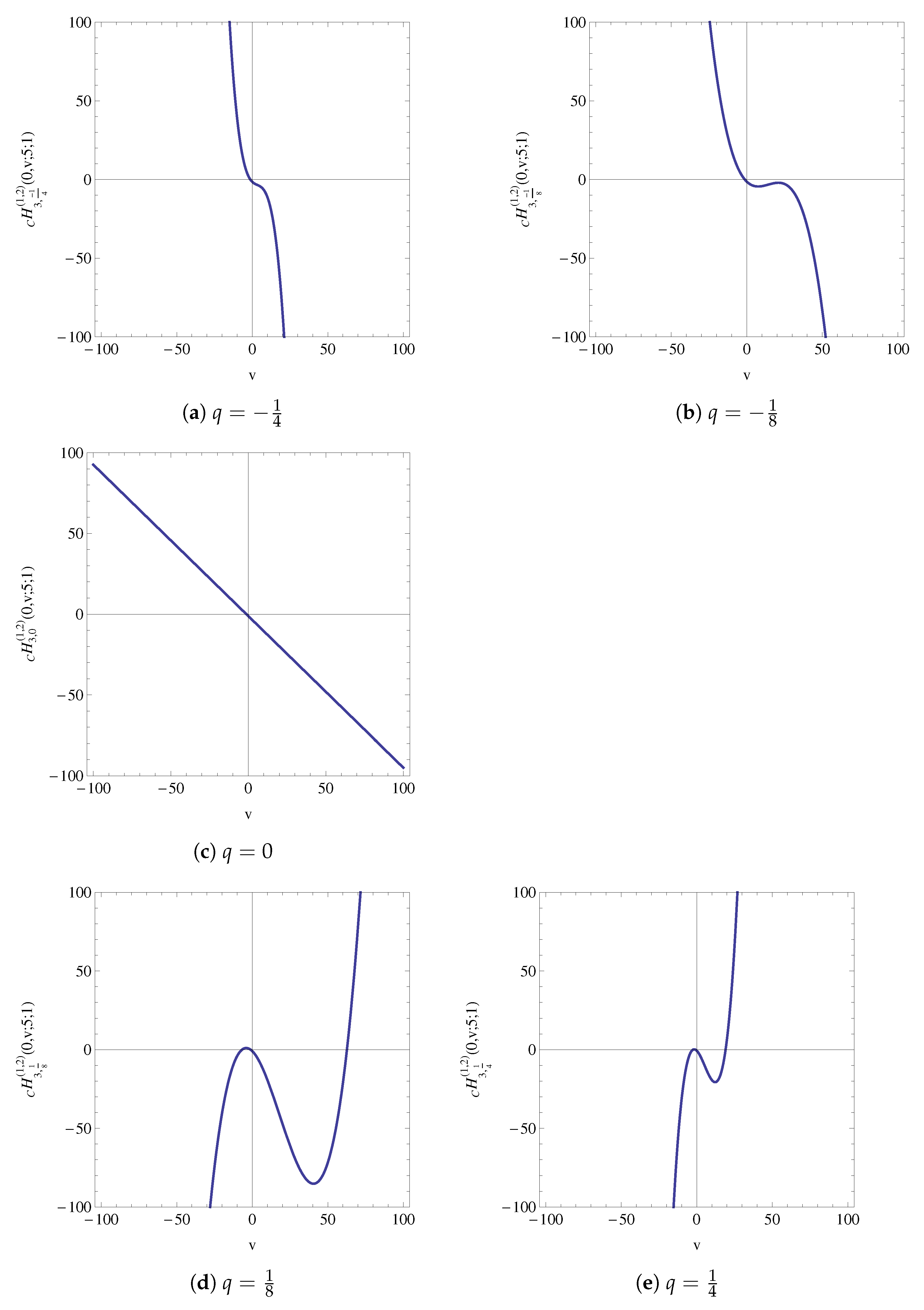
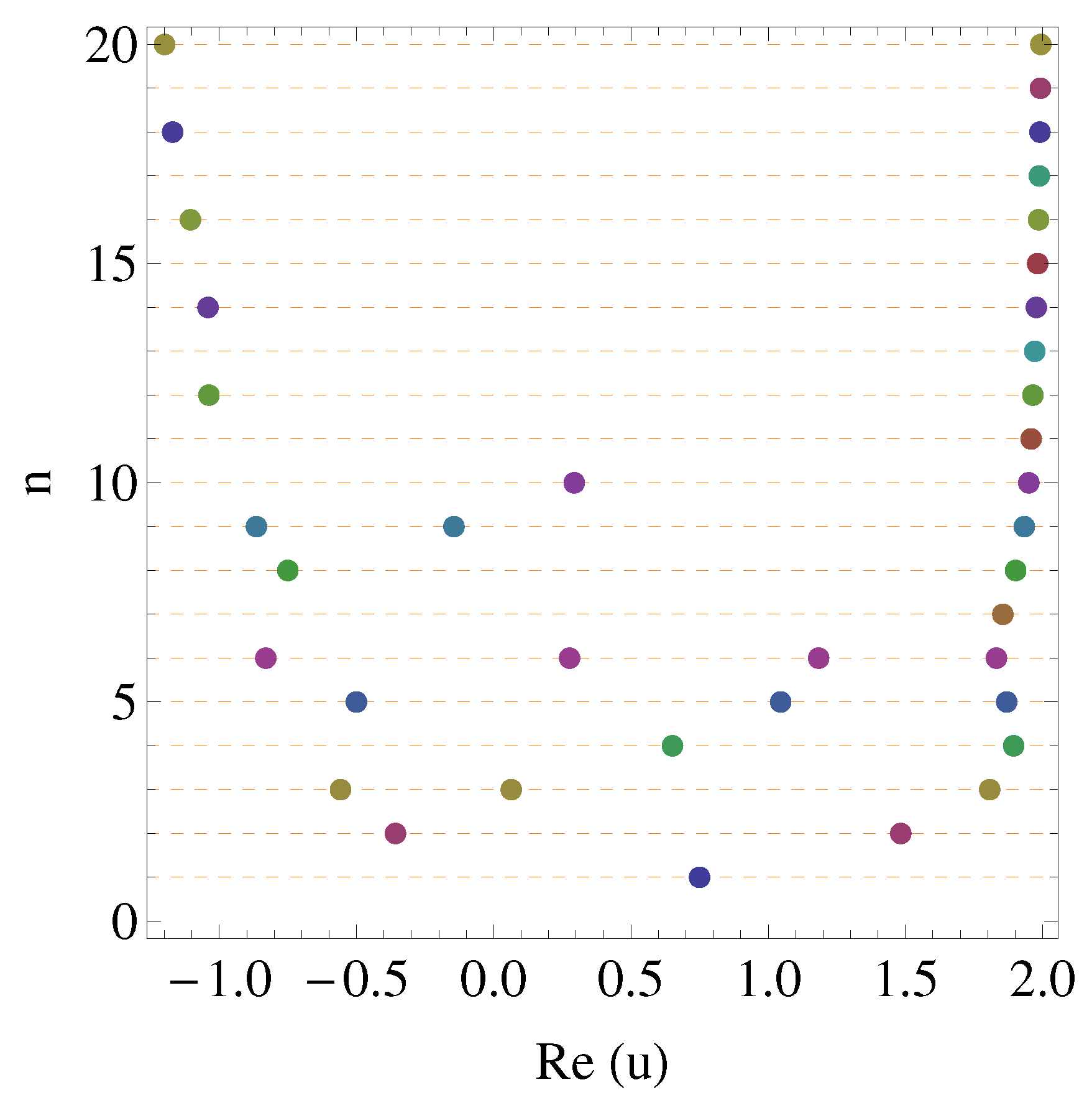
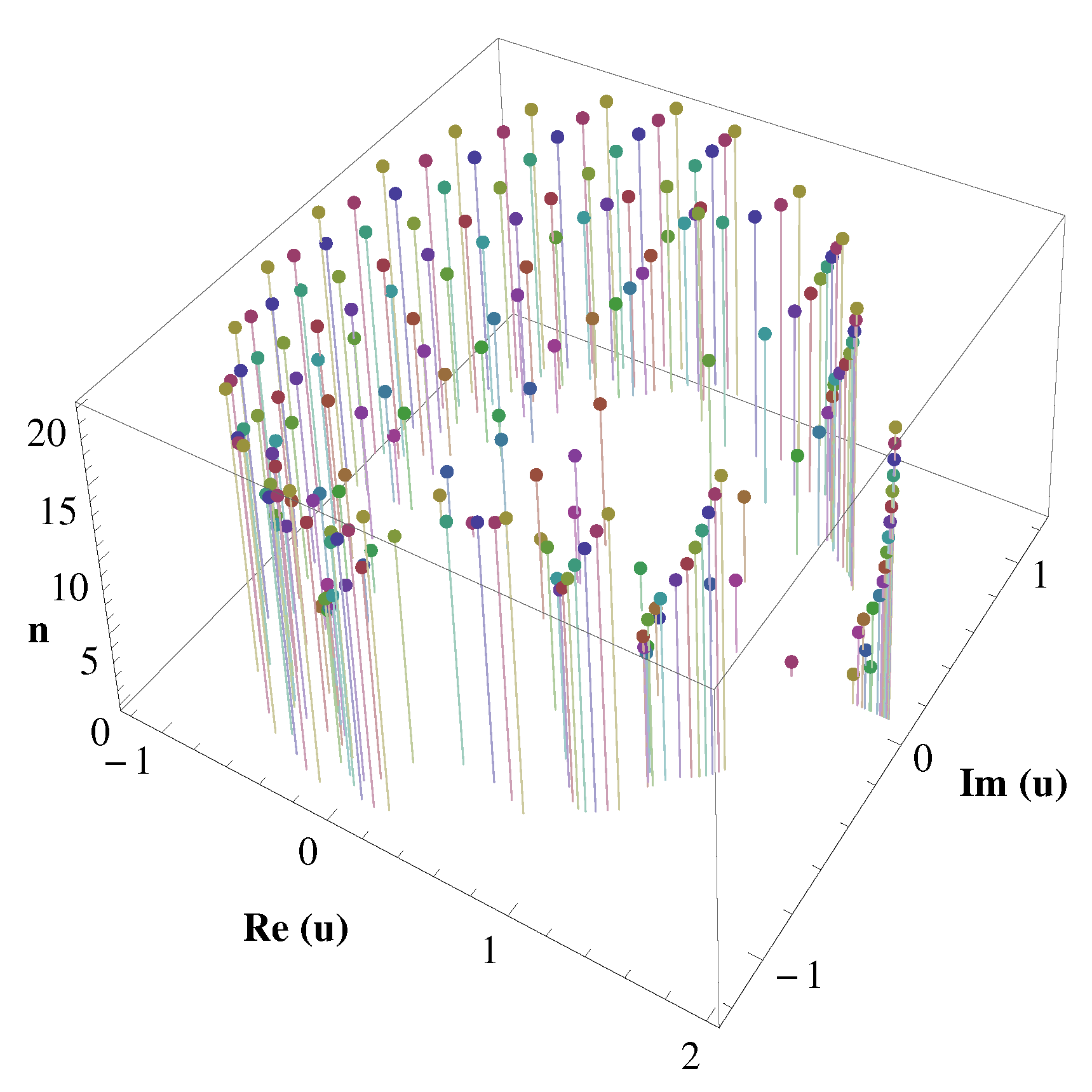
- As shown in Figure 5, all zeros of the polynomials with the other parameters being real are found to be symmetrically located with respect to the real axis of u (that is, ). Indeed, if is among its zeros, then, in view of (47), we havewhich implies that the complex conjugate of is also zero.One may also recall the reflection principle (see, e.g., [35] (p. 57)).
- (v)
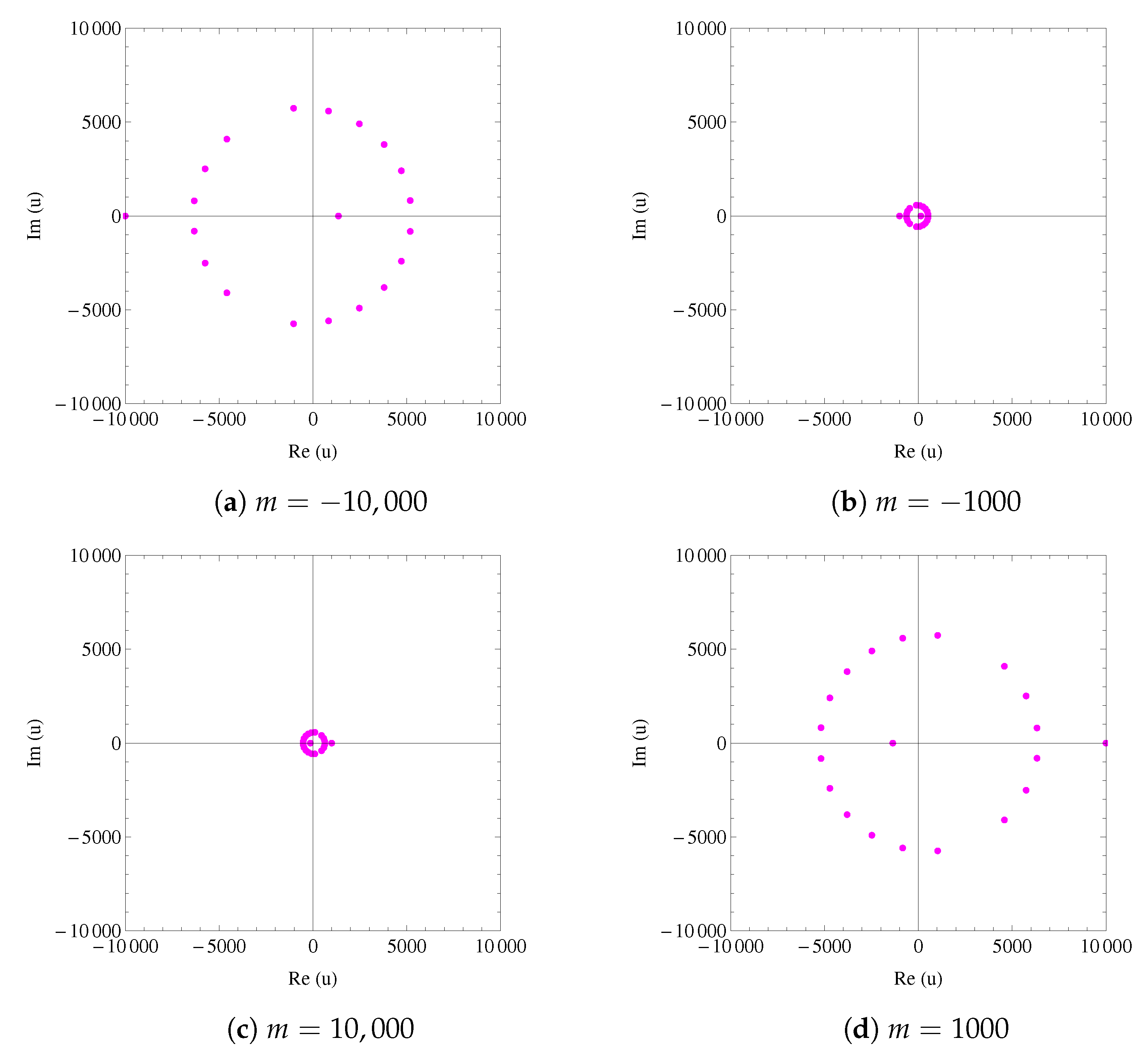
- In Figure 5, as m becomes larger, the corresponding absolute values (distances from the origin) of zeros of are getting greater (become more distant from the origin).Question 2: Prove or disprove that this observation is true as .Question 3: Prove or disprove truth of this observation for where becomes larger and .This can be observed graphically. For several different values of m (−10,000, −1000, 1000, 10,000), graphs of zeros of are demonstrated in Figure 10.
- (vi)
- From Figure 6, the number of real zeros of is observed to range from 1 to 4.Question 4: Prove or disprove that this observation is true for general .Question 5: Prove or disprove truth of this observation for where varies and .For , it is observed experimentally (Mathematica) for n up to 200 that for even values of , number of real zeros are 2 and for odd values of , number of real zero is 1. For , number of zeros are mentioned in Table 3.
- (vii)
- In each of Definitions 1–5 and Definition 6, the ordinary Taylor (Maclaurin) series expansion is employed, even though each generating function is involved in q-analogues.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Abdalla, M.; Akel, M.; Choi, J. Certain matrix Riemann–Liouville fractional integrals associated with functions involving generalized Bessel matrix polynomials. Symmetry 2021, 13, 622. [Google Scholar] [CrossRef]
- Bayad, A.; Kim, T. Identities for Apostol-type Frobenius–Euler polynomials resulting from the study of a nonlinear operator. Russ. J. Math. Phys. 2016, 23, 164–171. [Google Scholar] [CrossRef]
- Bildirici, C.; Acikgoz, M.; Araci, S. A note on analogues of tangent polynomials. J. Algebra Number Theor. Acad. 2014, 4, 21–29. [Google Scholar]
- Jain, S.; Nieto, J.J.; Singh, G.; Choi, J. Certain generating relations involving the generalized multi-index Bessel-Maitland function. Math. Prob. Eng. 2020, 2020, 8596736. [Google Scholar] [CrossRef]
- Khammash, G.S.; Agarwal, P.; Choi, J. Extended k-Gamma and k-Beta functions of matrix arguments. Mathematics 2020, 8, 1715. [Google Scholar] [CrossRef]
- Khan, N.U.; Usman, T.; Choi, J. A new class of generalized polynomials involving Laguerre and Euler polynomials. Hacet. J. Math. Stat. 2021, 50, 1–13. [Google Scholar] [CrossRef]
- Kurt, B. A note on the Apostol type q-Frobenius–Euler polynomials and generalizations of the Srivastava-Pinter addition theorems. Filomat 2016, 30, 65–72. [Google Scholar] [CrossRef][Green Version]
- Mahmudov, N.I. On a class of q-Bernoulli and q-Euler polynomials. Adv. Differ. Equ. 2013, 2013, 108. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Keleshteri, M.E. q-extensions for the Apostol type polynomials. J. Appl. Math. 2014, 2014, 868167. [Google Scholar] [CrossRef]
- Mahmudov, N.I.; Momenzadeh, M. On a class of q-Bernoulli, q-Euler, and q-Genocchi polynomials. Abs. Appl. Anal. 2014, 2014, 696454. [Google Scholar] [CrossRef]
- Nahid, T.; Alam, P.; Choi, J. Truncated-exponential-based Appell-type Changhee polynomials. Symmetry 2020, 12, 1588. [Google Scholar] [CrossRef]
- Ryoo, C.S. A note on the tangent numbers and polynomials. Adv. Stud. Theor. Phys. 2013, 7, 447–454. [Google Scholar] [CrossRef]
- Ryoo, C.S. Generalized tangent numbers and polynomials associated with p-adic integral on Zp. Appl. Math. Sci. 2013, 7, 4929–4934. [Google Scholar] [CrossRef]
- Satoh, J. A construction of q-analogue of Dedekind sums. Nagoya Math. J. 1992, 127, 129–143. Available online: https://projecteuclid.org/euclid.nmj/1118783238 (accessed on 15 March 2021). [CrossRef]
- Simsek, Y. q-analogue of twisted l-series and q-twisted Euler numbers. J. Number Theory 2005, 110, 267–278. [Google Scholar] [CrossRef]
- Simsek, Y. Generating functions for q-Apostol type Frobenius–Euler numbers and polynomials. Axioms 2012, 1, 395–403. [Google Scholar] [CrossRef]
- Usman, T.; Saif, M.; Choi, J. Certain identities associated with (p,q)-binomial coefficients and (p,q)-Stirling Polynomials of the second kind. Symmetry 2020, 12, 1436. [Google Scholar] [CrossRef]
- Yasmin, G.; Muhyi, A. Certain results of 2-variable q-generalized tangent-Apostol type polynomials. J. Math. Comput. Sci. 2020, 22, 238–251. [Google Scholar] [CrossRef]
- Yasmin, G.; Ryoo, C.S.; Islahi, H. A numerical computation of zeros of q-generalized tangent-Appell polynomials. Mathematics 2020, 8, 383. [Google Scholar] [CrossRef]
- Aral, A.; Gupta, V.; Agarwal, R.P. Applications of q-Calculus in Operator Theory; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Dalir, M.; Bashour, M. Applications of fractional calculus. Appl. Math. Sci. 2010, 4, 1021–1032. [Google Scholar]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Andrews, G.E.; Askey, R.; Roy, R. Special Functions; Encyclopedia of Mathematics and Its Applications 71; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ernst, T. A newew method for q-calculus. J. Nonlinear Math. Phys. 2003, 10, 487–525. [Google Scholar] [CrossRef]
- Ernst, T. The different tongues of q-calculus. Proc. Est. Acad. Sci. 2008, 57, 81–99. [Google Scholar] [CrossRef]
- Kac, V.G.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Nalli, P. Sopra un procedimento di calcolo analogo all’integrazione. Palermo Rend. 1923, 47, 337–374. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Choi, J. Zeta and q-Zeta Functions and Associated Series and Integrals; Elsevier Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2012. [Google Scholar]
- Jackson, F.H. On q-definite integrals. Quart. J. Pure Appl. Math. 1910, 41, 193–203. [Google Scholar]
- Choi, J. Notes on formal manipulations of double series. Commun. Korean Math. Soc. 2003, 18, 781–789. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; NIST and Cambridge University Press: Cambridge, UK; New York, NY, USA; Melbourne, Australia; Madrid, Spain; Cape Town, South Africa; Singapore; São Paulo, Brazil; Delhi, India; Dubai, United Arab Emirates; Tokyo, Japan, 2010. [Google Scholar]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Abdelsalam, S.I. Editorial: Recent Trends in Computational Fluid Dynamics. Front. Phys. 2020, 8, 593111. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Marin, M.; Zeeshan, A.; Ellahi, R.; Abdelsalam, S.I. Swimming of motile gyrotactic microorganisms and nanoparticles in blood flow through anisotropically tapered arteries. Front. Phys. 2020, 8, 95. [Google Scholar] [CrossRef]
- Wade, W.R. An Introduction to Analysis, 4th ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Brown, J.W.; Churchill, R.V. Complex Variables and Applications, 6th ed.; McGraw-Hill International Editions: New York, NY, USA, 1996. [Google Scholar]

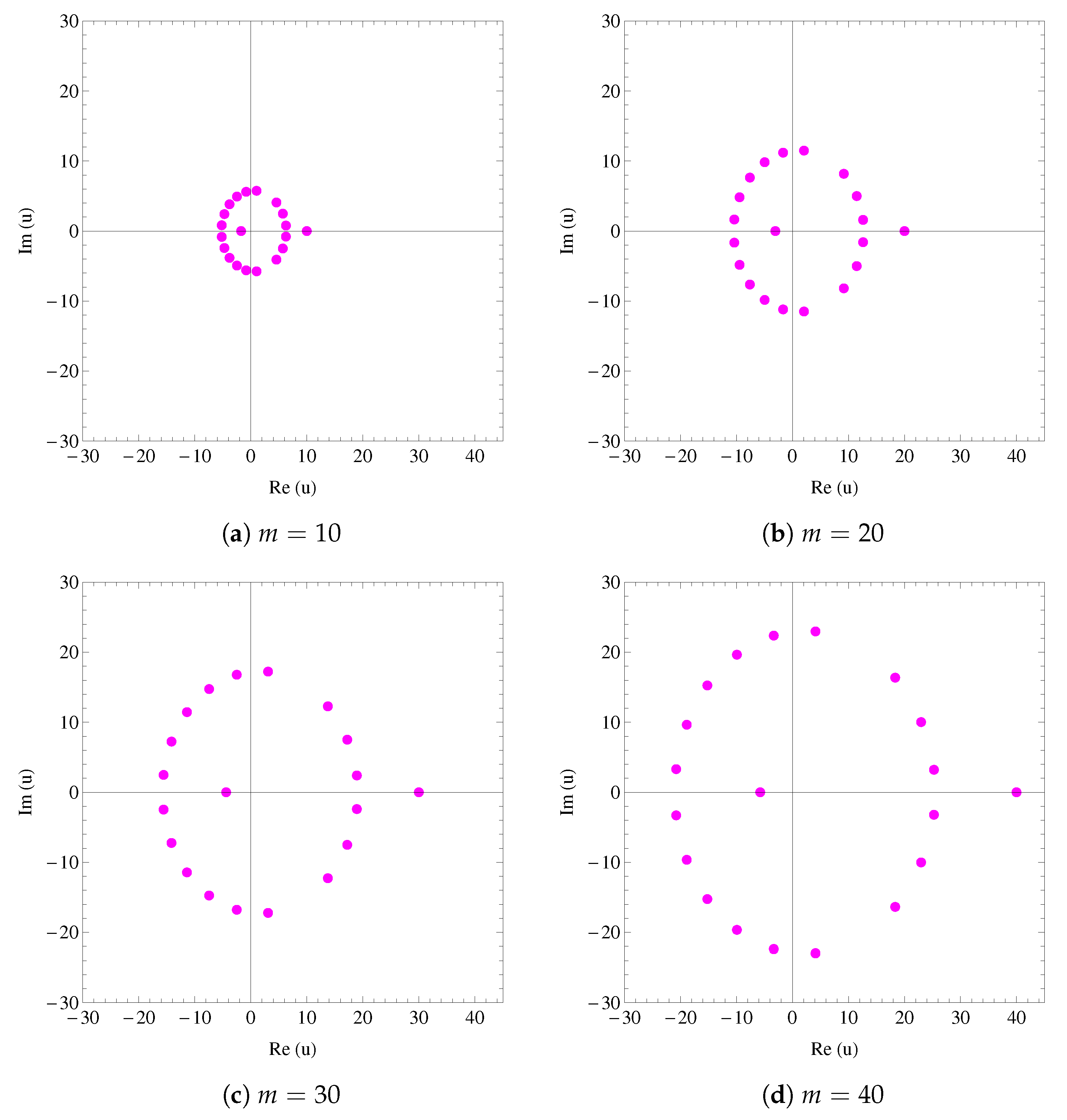
| S. No. | Relations between the and Its Particular Cases | Names of the Resultant q-Special Polynomials | Generating Functions of the Resultant q-Special Polynomials |
|---|---|---|---|
| I. | q-generalized tangent-Apostol | ||
| Euler polynomials (qGTAEP) | |||
| II. | q-generalized tangent-Frobenius | ||
| -Euler polynomials (qGTFEP) | |||
| III. | q-generalized tangent | ||
| -Euler polynomials (qGTEP) | |||
| IV. | q-tangent-Apostol Frobenius | ||
| -Euler polynomials (qTAFEP) | |||
| V. | q-tangent-Apostol | ||
| Euler polynomials (qTAEP) | |||
| VI. | q-tangent-Frobenius | ||
| -Euler polynomials (qTFEP) | |||
| VII. | q-tangent-Euler | ||
| polynomials (qTEP) | |||
| VIII. | q-Euler-Apostol Frobenius | ||
| -Euler polynomials (qEAFEP) | |||
| IX. | q-Euler-Apostol | ||
| Euler polynomials (qEAEP) | |||
| X. | q-Euler-Frobenius | ||
| -Euler polynomials (qEFEP) | |||
| XI. | 2-iterated q-Euler | ||
| polynomials (2IqEP) |
| Results | |||
|---|---|---|---|
| I. Series | |||
| expansions | |||
| II. Summation | |||
| Formulae | |||
| n | Number of Real Zeros | Real Zeros | Number of Complex Zeros | Complex Zeros |
|---|---|---|---|---|
| 1 | 1 | 0 | – | |
| 2 | 2 | 0 | – | |
| 3 | 3 | 0 | – | |
| 4 | 2 | 2 | , | |
| 5 | 3 | 2 | ||
| 6 | 4 | 2 | ||
| 7 | 1 | 6 | ||
| 8 | 2 | 6 | ||
| 9 | 3 | 6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasmin, G.; Islahi, H.; Choi, J. q-Generalized Tangent Based Hybrid Polynomials. Symmetry 2021, 13, 791. https://doi.org/10.3390/sym13050791
Yasmin G, Islahi H, Choi J. q-Generalized Tangent Based Hybrid Polynomials. Symmetry. 2021; 13(5):791. https://doi.org/10.3390/sym13050791
Chicago/Turabian StyleYasmin, Ghazala, Hibah Islahi, and Junesang Choi. 2021. "q-Generalized Tangent Based Hybrid Polynomials" Symmetry 13, no. 5: 791. https://doi.org/10.3390/sym13050791
APA StyleYasmin, G., Islahi, H., & Choi, J. (2021). q-Generalized Tangent Based Hybrid Polynomials. Symmetry, 13(5), 791. https://doi.org/10.3390/sym13050791







