Machine-Learning Based Memory Prediction Model for Data Parallel Workloads in Apache Spark
Abstract
1. Introduction
- This paper proposes a memory usage model of data-parallel workloads that considers the characteristics of data, workloads, and system environments in the general-purpose distributed-processing Spark platform.
- Based on the memory usage model, we propose the memory prediction model for estimating efficient amounts of memory of data-parallel workloads using machine learning techniques.
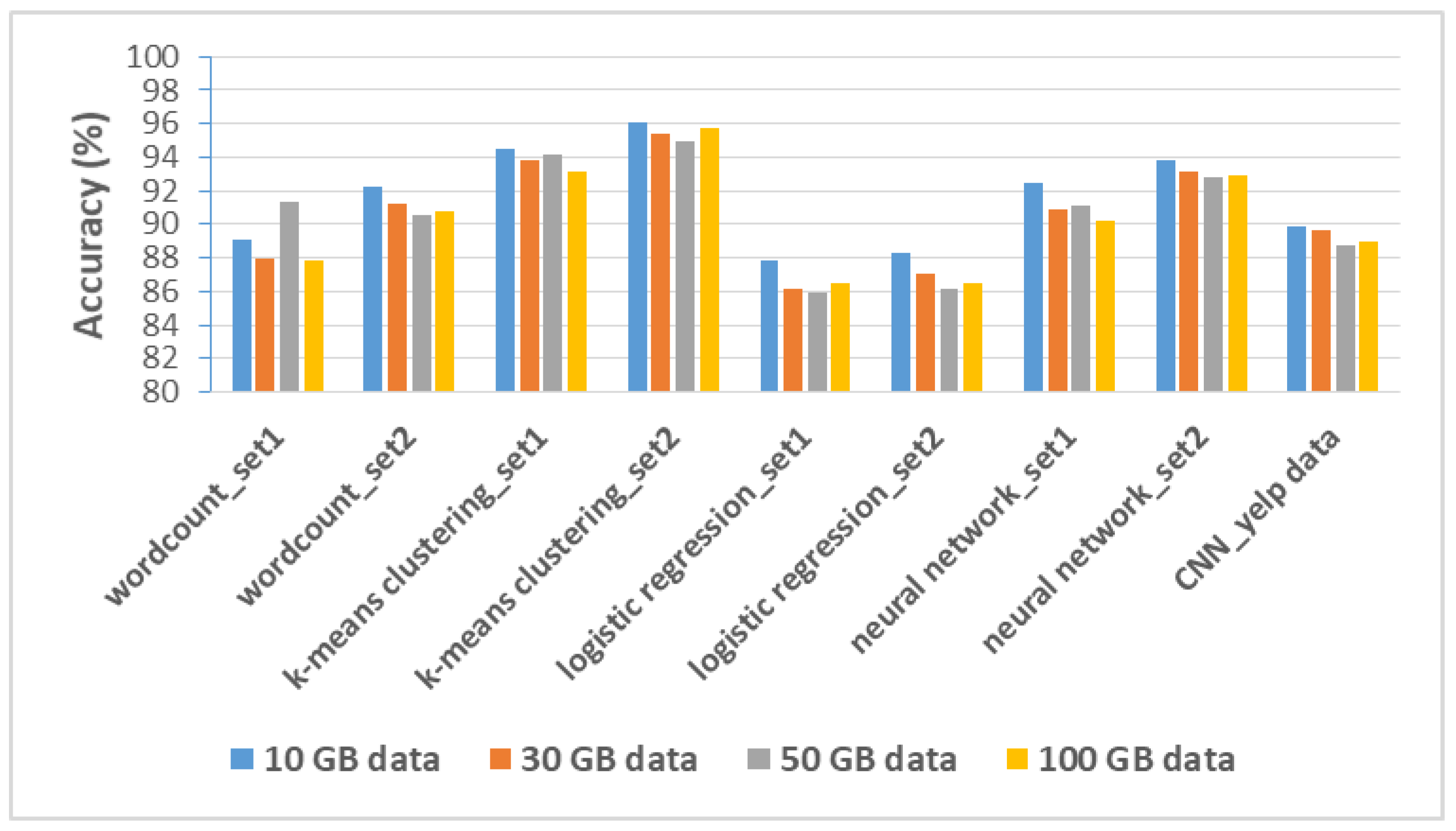
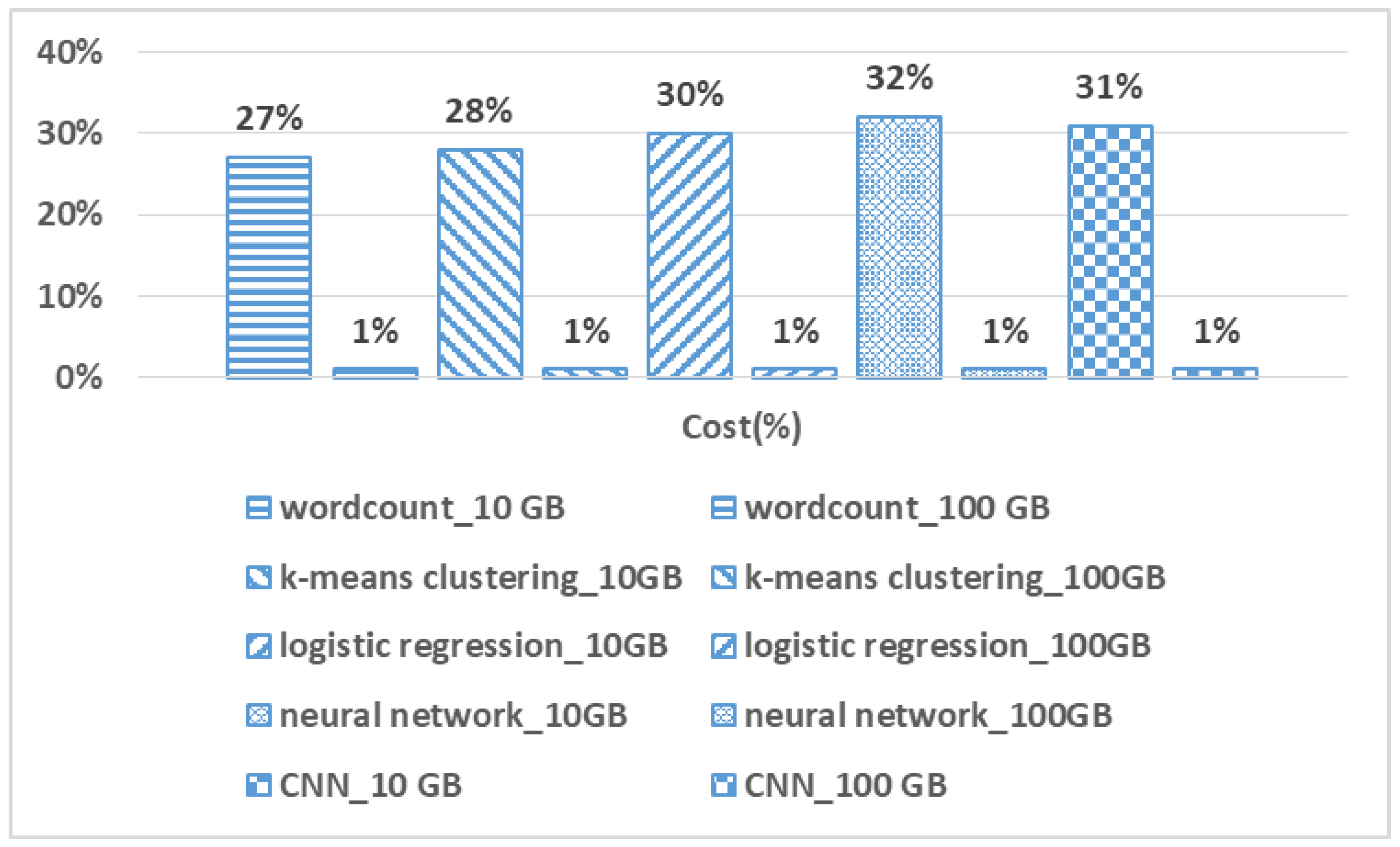
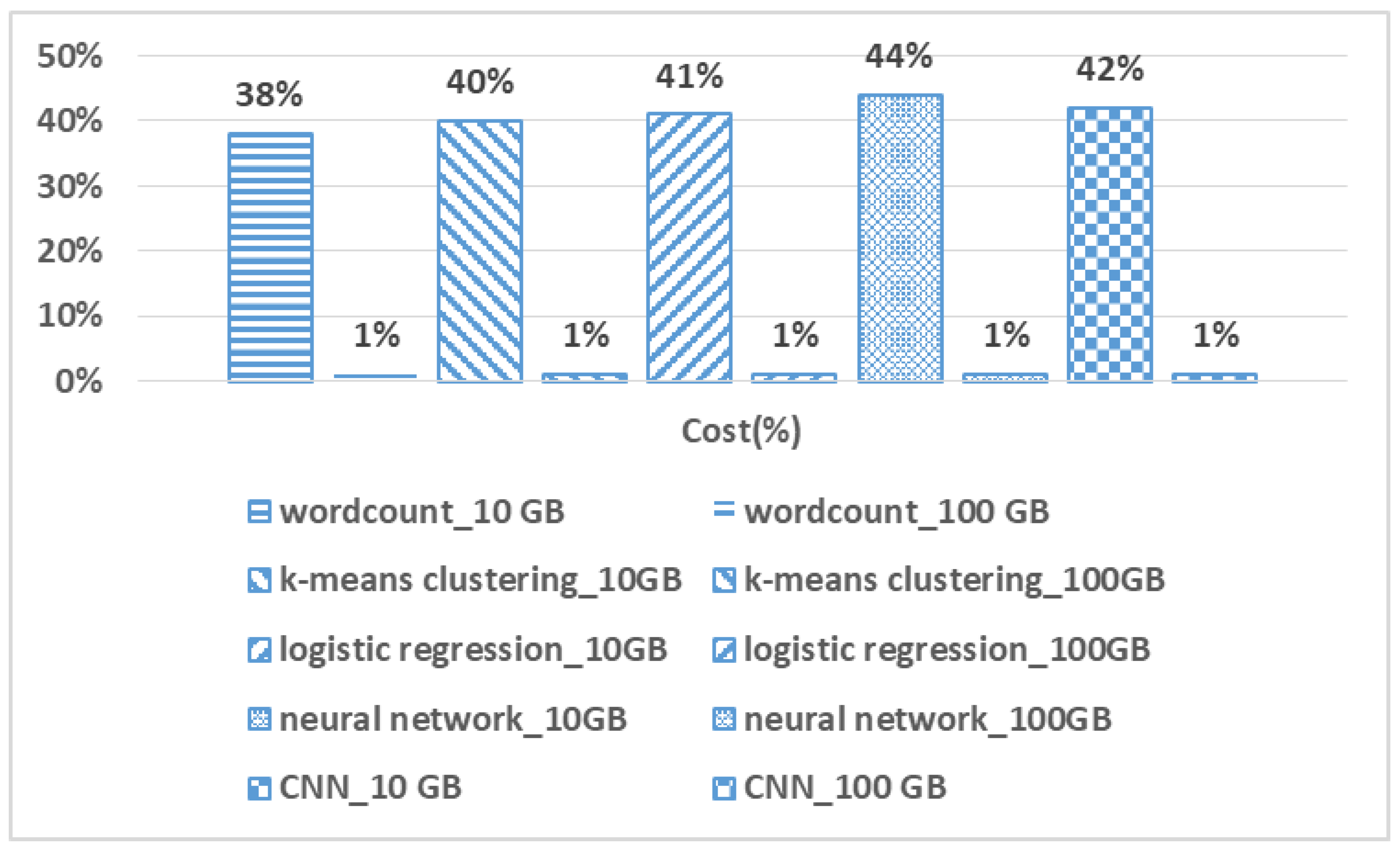
- When the memory prediction model is applied to data-parallel workloads in the Spark environment, it estimates the appropriate amount of memory at a maximum of 99% accuracy of the actual efficient memory requirements. In terms of cost, efficient memory can be estimated in less than 44% of the workloads’ actual processing time.
2. Related Work
3. Background
3.1. Data-Parallel Workloads
3.2. Memory Management Model of the Java Runtime Environment
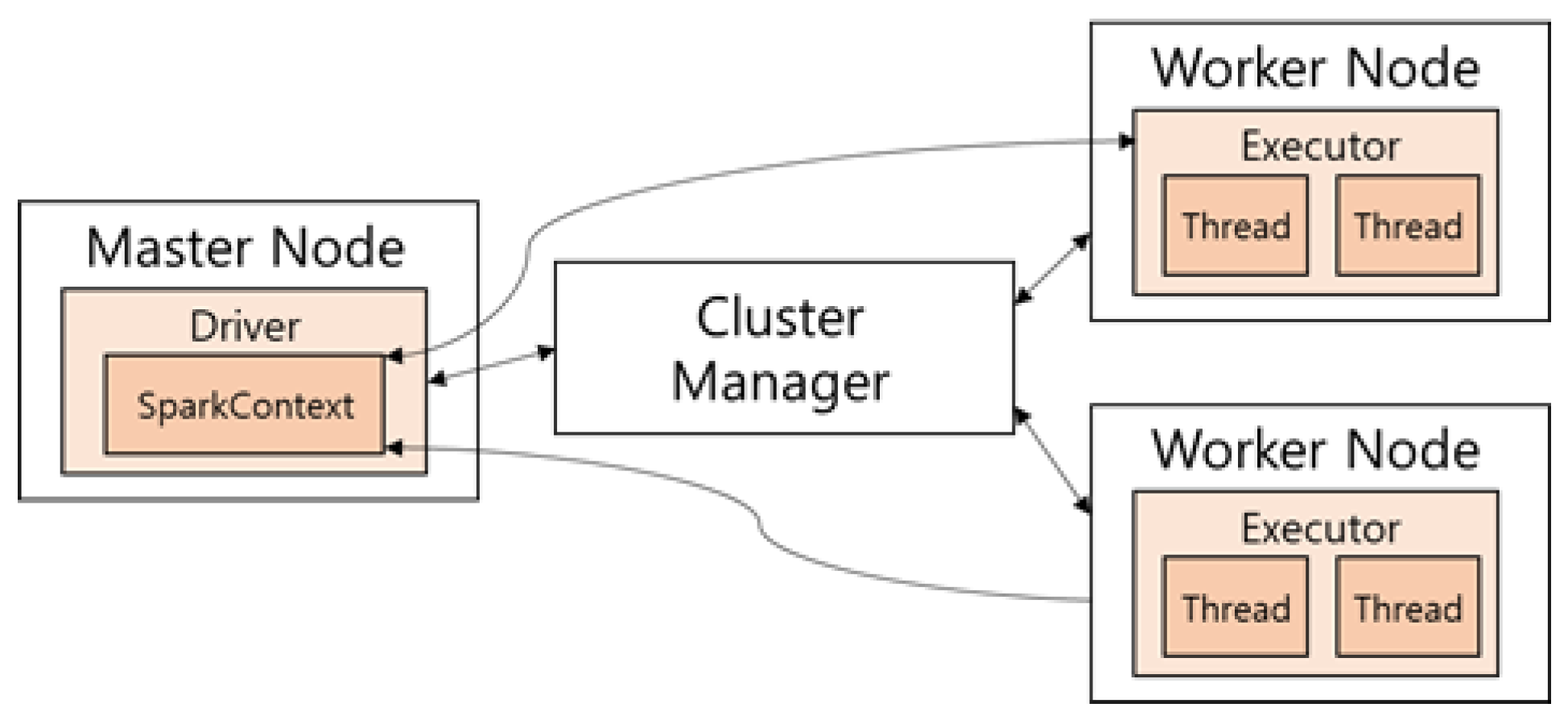
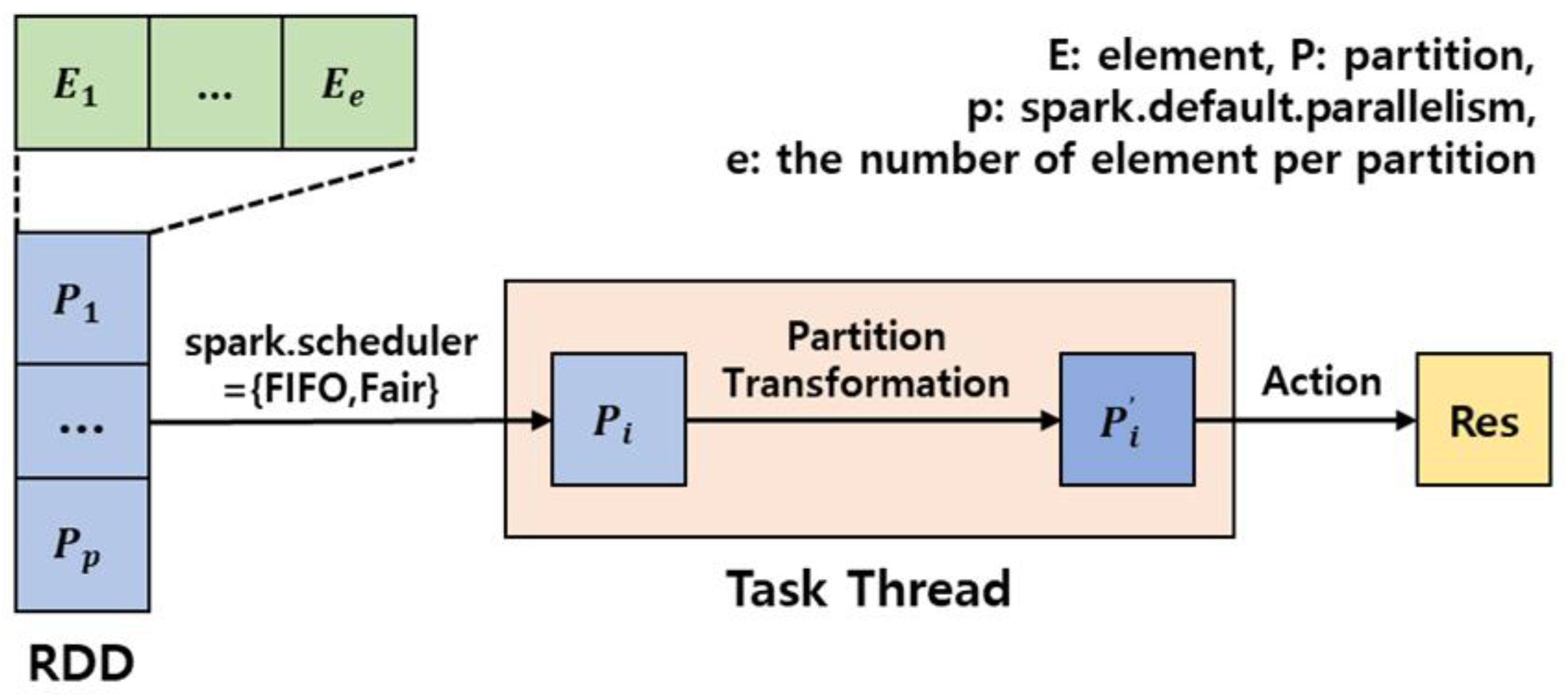
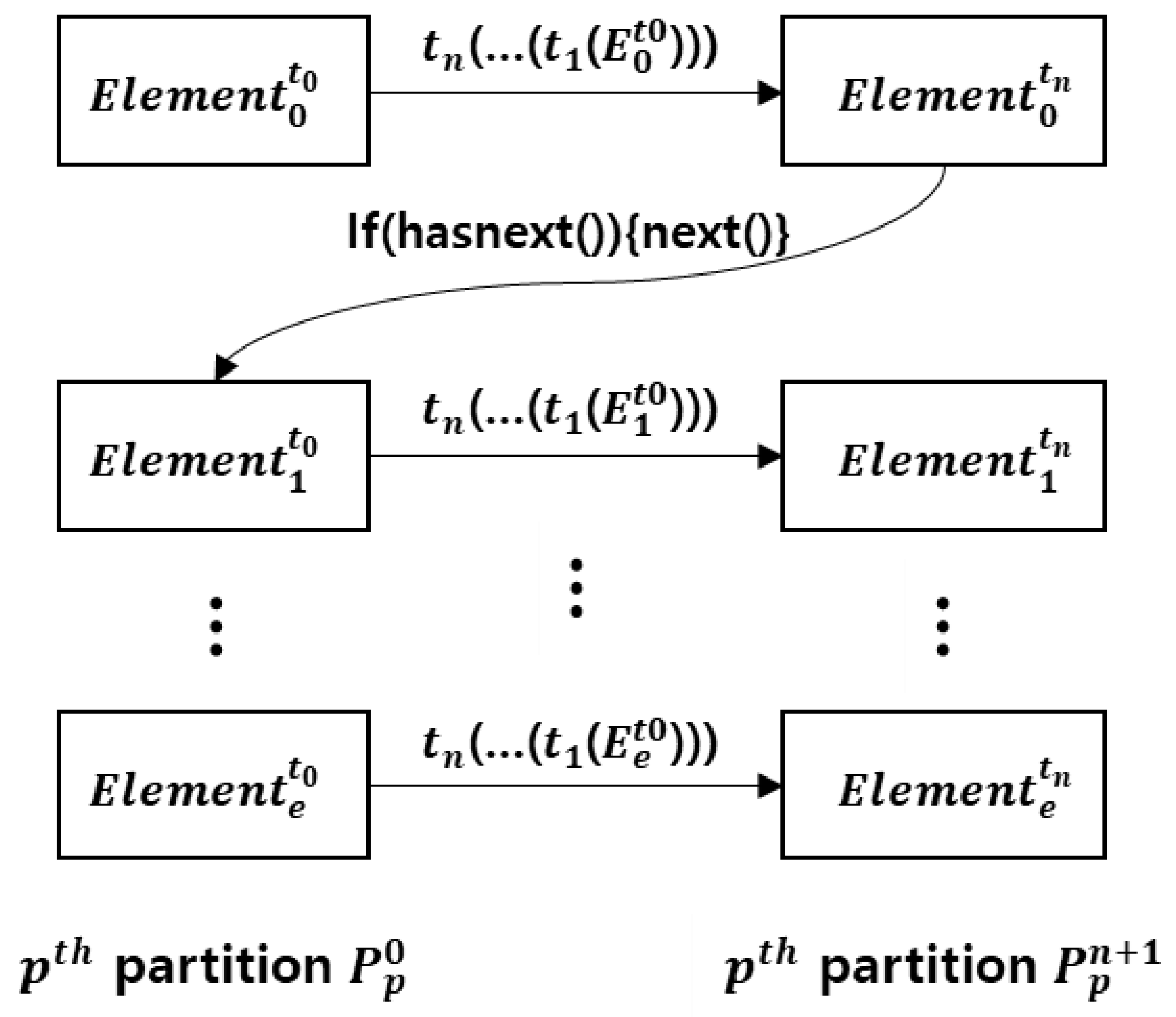
3.3. Data-Parallel Model in Spark
4. Spark Memory Model
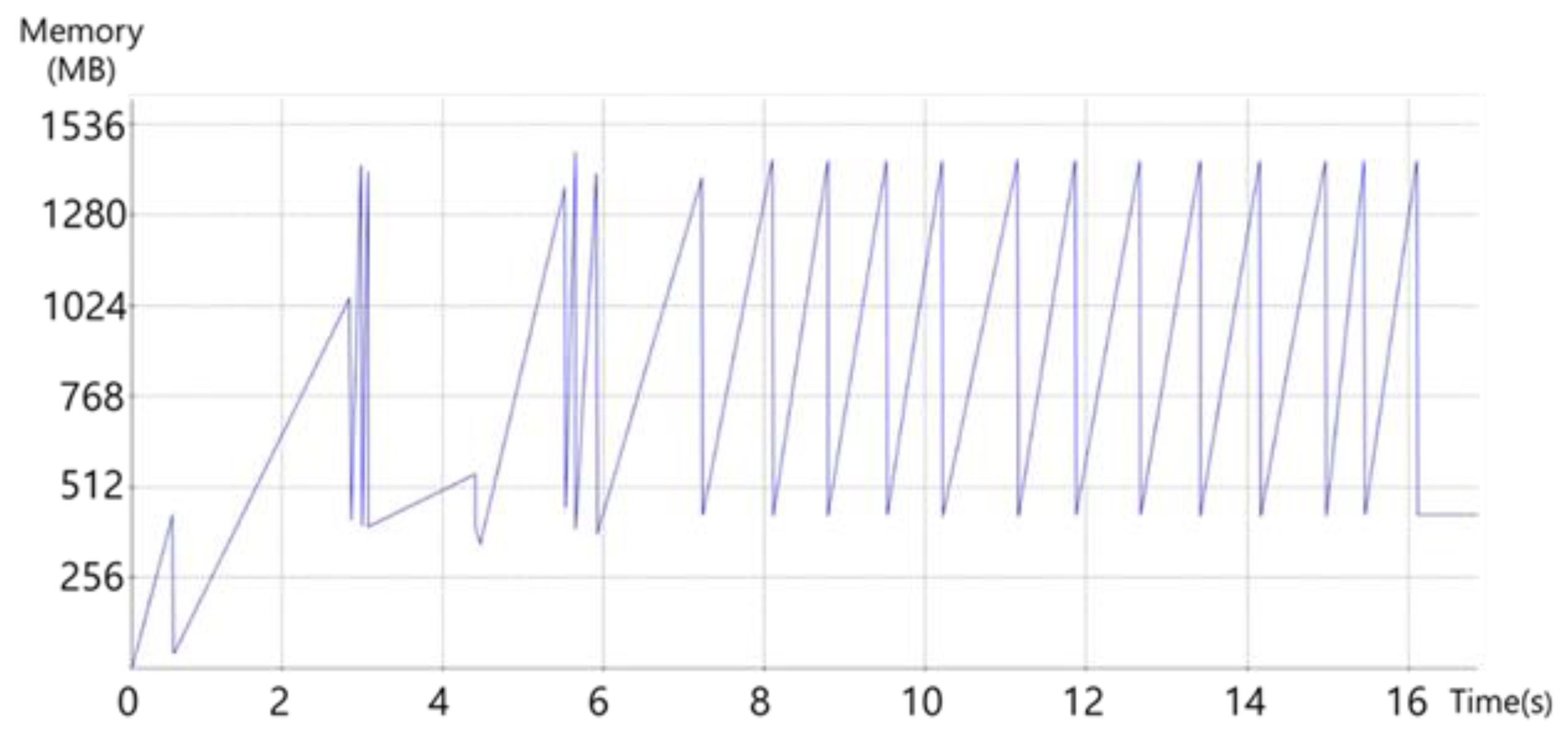
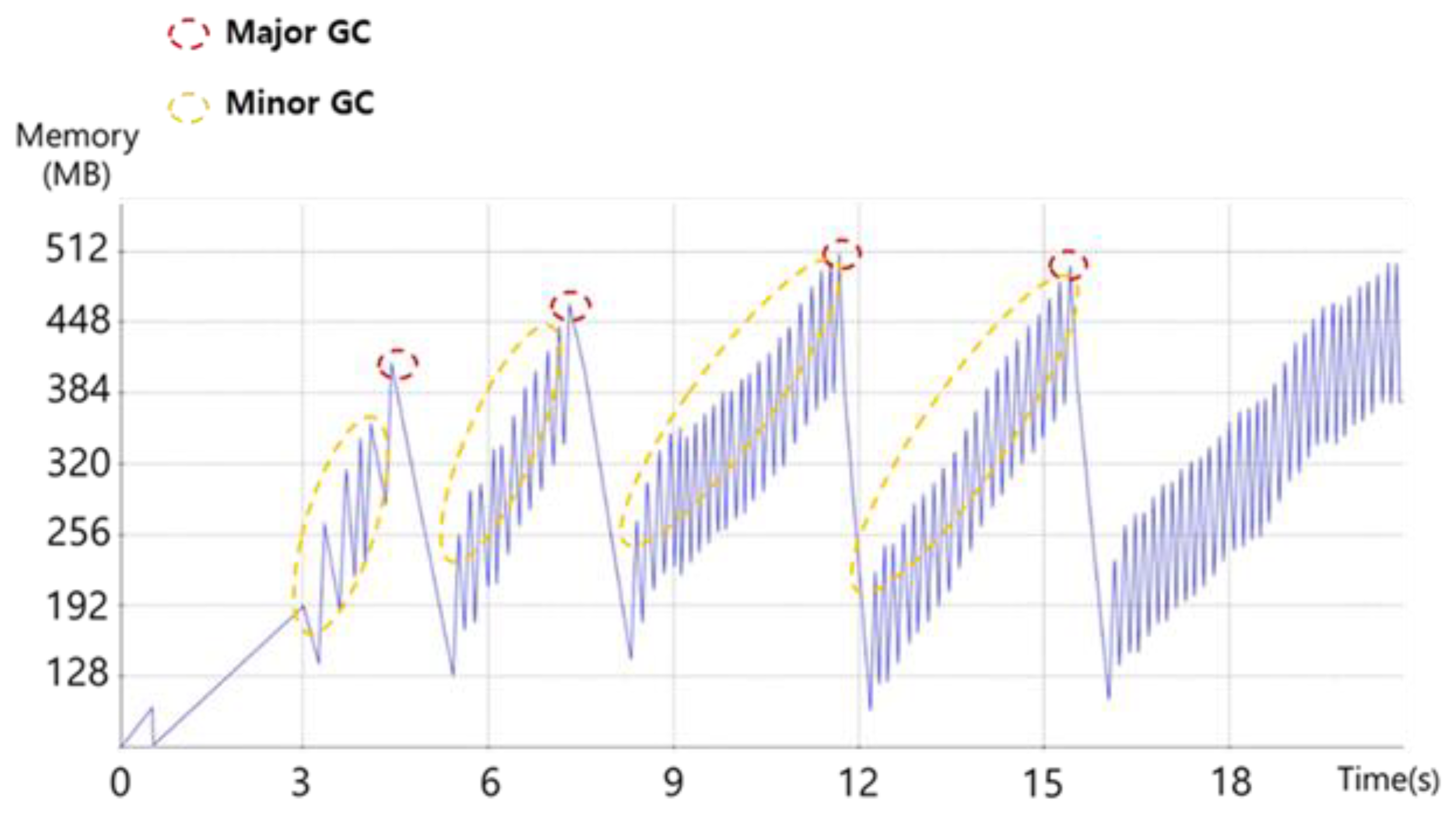
4.1. Memory Usage Pattern
4.2. Memory Undersupply
4.3. Memory Oversupply
5. Runtime Memory Profiling
5.1. Data-Parallel Characteristics in Spark
5.2. Data Characteristics
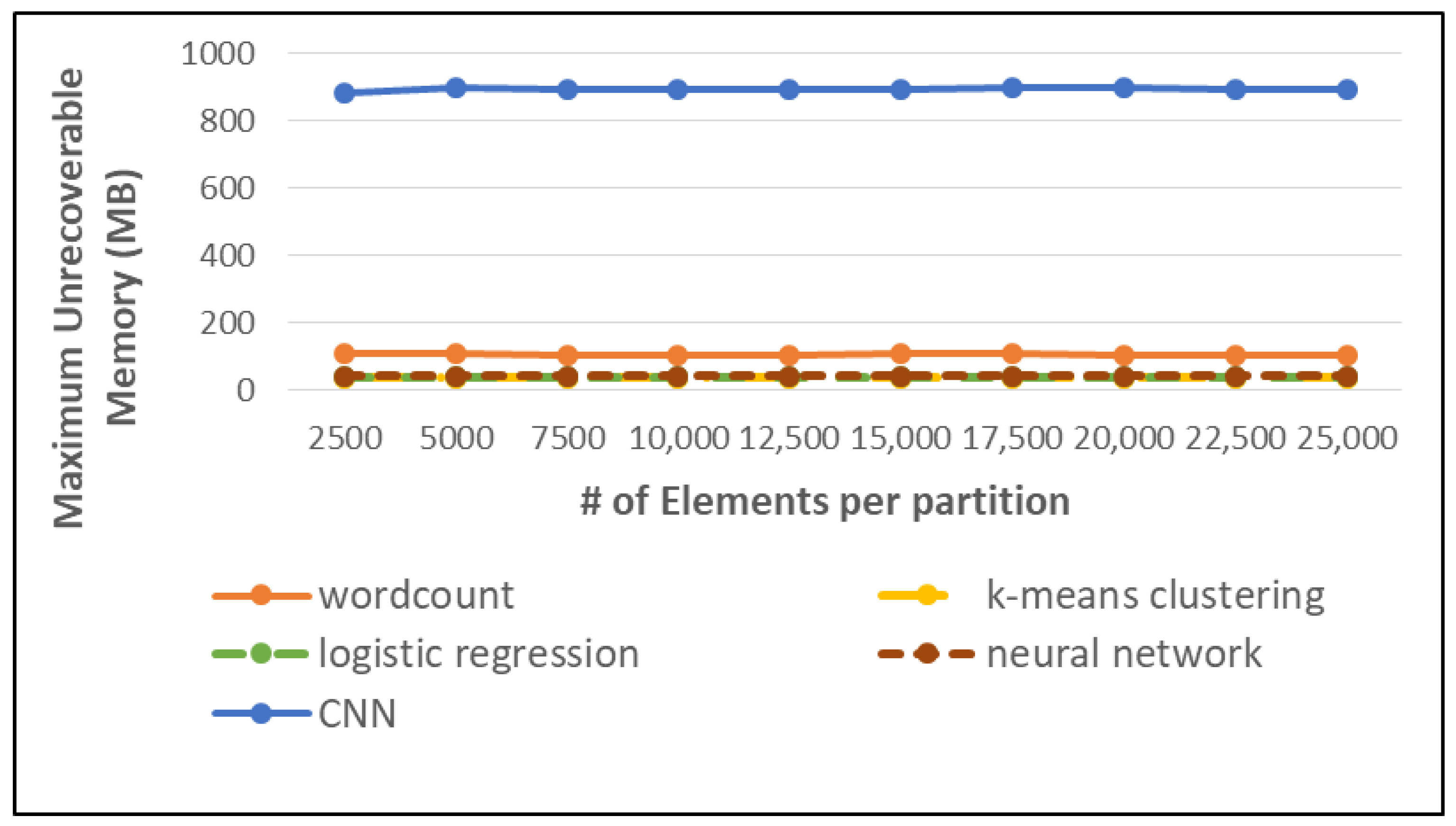
6. Maximum Unrecoverable Memory Estimation
6.1. Estimation Model
- T is a finite set of transformation t.
- a is an action called right after the last transformation.
- For n trials of W, MUM(W) is the maximum value of all runtime memory usages after GC.
- The first term is bias;
- The second term is product of SoE multiplied and;
- The third term is product of square root of SoE multiplied and;
- The fourth term is product of logarithm of SoE multiplied and;
- The fifth term is product of square root of SoE and logarithm of SoE and;
- The sixth term is product of logarithm of SoE and SoE and.
6.2. Model Building Methods
7. Experiment
7.1. Experiment Environment
7.2. Performance Metrics
7.3. Workload
7.3.1. Wordcount
7.3.2. K-Means Clustering
7.3.3. Logistic Regression and Neural Network
7.3.4. Convolutional Neural Network (CNN)
7.4. Workload Input Data Description
7.5. Performance Evaluation
7.5.1. Prediction Accuracy
7.5.2. Prediction Cost
7.5.3. Memory Efficiency
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hu, H.; Wen, Y.; Chua, T.S.; Li, X. Toward scalable systems for big data analytics: A technology tutorial. IEEE Access 2014, 2, 652–687. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: Simplified data processing on large clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Zaharia, M.; Xin, R.S.; Wendell, P.; Das, T.; Armbrust, M.; Dave, A.; Meng, X.; Rosen, J.; Venkataraman, S.; Franklin, M.J.; et al. Apache Spark: A unified engine for big data processing. Commun. ACM 2016, 59, 56–65. [Google Scholar] [CrossRef]
- Meng, X.; Bradley, J.; Yavuz, B.; Sparks, E.; Venkataraman, S.; Liu, D.; Freeman, J.; Tsai, D.B.; Amde, M.; Owen, S.; et al. Mllib: Machine learning in apache Spark. J. Mach. Learn. Res. 2016, 17, 1235–1241. [Google Scholar]
- Zaharia, M.; Das, T.; Li, H.; Hunter, T.; Shenker, S.; Stoica, I. Discretized streams: Fault-tolerant streaming computation at scale. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles; ACM Association for Computing Machinery: New York, NY, USA, 2013; pp. 423–438. [Google Scholar]
- Xin, R.S.; Gonzalez, J.E.; Franklin, M.J.; Stoica, I. Graphx: A resilient distributed graph system on Spark. In First International Workshop on Graph Data Management Experiences and Systems; ACM Association for Computing Machinery: New York, NY, USA, 2013; p. 2. [Google Scholar]
- Zaharia, M.; Chowdhury, M.; Das, T.; Dave, A.; Ma, J.; McCauly, M.; Franklin, M.J.; Shenker, S.; Stoica, I. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In Proceedings of the 9th USENIX Conference on Networked Systems Design and Implementation, San Jose, CA, USA, 25–27 April 2012; USENIX Association: Berkeley, CA, USA, 2012; p. 2. [Google Scholar]
- Apache Spark, Preparing for the Next Wave of Reactive Big Data. Available online: http://goo.gl/FqEh94 (accessed on 31 March 2021).
- Yuan, H.; Bi, J.; Tan, W.; Zhou, M.; Li, B.H.; Li, J. TTSA: An effective scheduling approach for delay bounded tasks in hybrid clouds. IEEE Trans. Cybern. 2016, 47, 3658–3668. [Google Scholar] [CrossRef] [PubMed]
- Bi, J.; Yuan, H.; Tan, W.; Zhou, M.; Fan, Y.; Zhang, J.; Li, J. Application-aware dynamic fine-grained resource provisioning in a virtualized cloud data center. IEEE Trans. Autom. Sci. Eng. 2015, 14, 1172–1184. [Google Scholar] [CrossRef]
- Ousterhout, K.; Rasti, R.; Ratnasamy, S.; Shenker, S.; Chun, B.G. Making sense of performance in data analytics frameworks. In Proceedings of the 12th USENIX Symposium on Networked Systems Design and Implementation (NSDI 15), Oakland, CA, USA, 4–6 May 2015; USENIX Association: Berkeley, CA, USA, 2015; pp. 293–307. [Google Scholar]
- Bollella, G.; Gosling, J. The real-time specification for Java. Computer 2000, 33, 47–54. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Z.; Wang, L. Tuning performance of Spark programs. In 2018 IEEE International Conference on Cloud Engineering (IC2E); IEEE: New York, NY, USA, 2018; pp. 282–285. [Google Scholar]
- Venkataraman, S.; Yang, Z.; Franklin, M.; Recht, B.; Stoica, I. Ernest: Efficient performance prediction for large-scale advanced analytics. In 13th Symposium on Networked Systems Design and Implementation (NSDI); USENIX Association: Berkeley, CA, USA, 2016; pp. 363–378. [Google Scholar]
- Yadwadkar, N.J.; Ananthanarayanan, G.; Katz, R. Wrangler: Predictable and faster jobs using fewer resources. In Proceedings of the ACM Symposium on Cloud Computing, Seattle, WA, USA, 3–5 November 2014; ACM Association for Computing Machinery: New York, NY, USA, 2014; pp. 1–14. [Google Scholar]
- Paul, A.K.; Zhuang, W.; Xu, L.; Li, M.; Rafique, M.M.; Butt, A.R. Chopper: Optimizing data partitioning for in-memory data analytics frameworks. In Proceedings of the 2016 IEEE International Conference on Cluster Computing (CLUSTER), Taipei, Taiwan, 12–16 September 2016; IEEE: New York, NY, USA, 2016; pp. 110–119. [Google Scholar]
- Tsai, L.; Franke, H.; Li, C.S.; Liao, W. Learning-Based Memory Allocation Optimization for Delay-Sensitive Big Data Processing. IEEE Trans. Parallel Distrib. Syst. 2018, 29, 1332–1341. [Google Scholar] [CrossRef]
- Maros, A.; Murai, F.; da Silva, A.P.; Almeida, J.M.; Lattuada, M.; Gianniti, E.; Hosseini, M.; Ardagna, D. Machine learning for performance prediction of spark cloud applications. In Proceedings of the 2019 IEEE 12th International Conference on Cloud Computing (CLOUD), Milan, Italy, 8–13 July 2019; IEEE: New York, NY, USA, 2019; pp. 99–106. [Google Scholar]
- Ha, H.; Zhang, H. Deepperf: Performance prediction for configurable software with deep sparse neural network. In Proceedings of the 2019 IEEE/ACM 41st International Conference on Software Engineering (ICSE), Montreal, QC, Canada, 25–31 May 2019; IEEE: New York, NY, USA, 2019; pp. 1095–1106. [Google Scholar]
- Abdullah, M.; Iqbal, W.; Bukhari, F.; Erradi, A. Diminishing Returns and Deep Learning for Adaptive CPU Resource Allocation of Containers. IEEE Trans. Netw. Serv. Manag. 2020, 17, 2052–2063. [Google Scholar] [CrossRef]
- Chen, C.O.; Zhuo, Y.Q.; Yeh, C.C.; Lin, C.M.; Liao, S.W. Machine learning-based configuration parameter tuning on hadoop system. In Proceedings of the 2015 IEEE International Congress on Big Data, New York, NY, USA, 27 June–2 July 2015; IEEE: New York, NY, USA, 2015; pp. 386–392. [Google Scholar]
- Shvachko, K.; Kuang, H.; Radia, S.; Chansler, R. The hadoop distributed file system. In Proceedings of the 2010 IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST), Incline Village, NV, UAS, 3–7 May 2010; IEEE: New York, NY, USA, 2010; pp. 1–10. [Google Scholar]
- Jeong, J.S.; Lee, W.Y.; Lee, Y.; Yang, Y.; Cho, B.; Chun, B.G. Elastic memory: Bring elasticity back to in-memory big data analytics. In 15th Workshop on Hot Topics in Operating Systems (HotOS {XV}); USENIX Association: Berkeley, CA, USA, 2015. [Google Scholar]
- Spinner, S.; Herbst, N.; Kounev, S.; Zhu, X.; Lu, L.; Uysal, M.; Griffith, R. Proactive memory scaling of virtualized applications. In Proceedings of the 2015 IEEE 8th International Conference on Cloud Computing, New York, NY, USA, 27 June–2 July 2015; IEEE: New York, NY, USA, 2015; pp. 277–284. [Google Scholar]
- Shanmuganathan, G.; Gulati, A.; Holler, A.; Kalyanaraman, S.; Padala, P.; Zhu, X.; Griffith, R. Towards Proactive Resource Management in Virtualized Datacenters; VMware Labs: Palo Alto, CA, USA, 2013. [Google Scholar]
- Li, M.; Zeng, L.; Meng, S.; Tan, J.; Zhang, L.; Butt, A.R.; Fuller, N. Mronline: Mapreduce online performance tuning. In Proceedings of the 23rd International Symposium on High-Performance Parallel and Distributed Computing, Vancouver, BC, Canada, 23–27 June 2014; ACM Association for Computing Machinery: New York, NY, USA, 2014; pp. 165–176. [Google Scholar]
- Mao, F.; Zhang, E.Z.; Shen, X. Influence of program inputs on the selection of garbage collectors. In Proceedings of the 2009 ACM SIGPLAN/SIGOPS International Conference on Virtual Execution Environments, Washington, DC, USA, 11–13 March 2009; ACM Association for Computing Machinery: New York, NY, USA, 2009; pp. 91–100. [Google Scholar]
- Hines, M.R.; Gordon, A.; Silva, M.; Da Silva, D.; Ryu, K.; Ben-Yehuda, M. Applications know best: Performance-driven memory overcommit with ginkgo. In Proceedings of the 2011 IEEE Third International Conference on Cloud Computing Technology and Science, Athens, Greece, 29 November–1 December 2011; IEEE: New York, NY, USA, 2011; pp. 130–137. [Google Scholar]
- Hertz, M.; Berger, E.D. Quantifying the performance of garbage collection vs. explicit memory management. In ACM SIGPLAN Notices; ACM Association for Computing Machinery: New York, NY, USA, 2005; Volume 50, pp. 313–326. [Google Scholar]
- Alsheikh, M.A.; Niyato, D.; Lin, S.; Tan, H.P.; Han, Z. Mobile big data analytics using deep learning and apache spark. IEEE Netw. 2016, 30, 22–29. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16)), Savannah, GA, USA, 2–4 November 2016; USENIX Association: Berkeley, CA, USA, 2016; pp. 265–283. [Google Scholar]
- Dean, J.; Corrado, G.S.; Monga, R.; Chen, K.; Devin, M.; Le, Q.V.; Mao, M.Z.; Ranzato, M.A.; Senior, A.; Tucker, P.; et al. Large scale distributed deep networks. In Advances in Neural Information Processing Systems; Curran Associates Inc.: New York, NY, USA, 2012; pp. 1223–1231. [Google Scholar]
- Java Virtual Machine Technology. Available online: https://docs.oracle.com/javase/8/docs/technotes/guides/vm/index.html (accessed on 16 April 2021).
- Flood, C.H.; Detlefs, D.; Shavit, N.; Zhang, X. Parallel Garbage Collection for Shared Memory Multiprocessors. In Java Virtual Machine Research and Technology Symposium; USENIX Association: Berkeley, CA, USA, 2001. [Google Scholar]
- Guller, M. Cluster Managers. In Big Data Analytics with Spark; Apress: Berkeley, CA, USA, 2015; pp. 231–242. [Google Scholar]
- Vavilapalli, V.K.; Murthy, A.C.; Douglas, C.; Agarwal, S.; Konar, M.; Evans, R.; Graves, T.; Lowe, J.; Shah, H.; Seth, S.; et al. Apache hadoop yarn: Yet another resource negotiator. In Proceedings of the 4th annual Symposium on Cloud Computing, Santa Clara, CA, USA, 1–3 October 2013; pp. 1–16. [Google Scholar]
- Kakadia, D. Apache Mesos Essentials; Packt Publishing Ltd.: Birmingham, UK, 2015. [Google Scholar]
- Reiss, C.A. Understanding Memory Configurations for In-Memory Analytics. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2016. [Google Scholar]
- Zhao, W.; Ma, H.; He, Q. Parallel k-means clustering based on mapreduce. In Proceedings of the IEEE International Conference on Cloud Computing, Bangalore, India, 21–25 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 674–679. [Google Scholar]
- Lin, C.Y.; Tsai, C.H.; Lee, C.P.; Lin, C.J. Large-scale logistic regression and linear support vector machines using spark. In Proceedings of the 2014 IEEE International Conference on Big Data, Washington, DC, USA, 27–30 October 2014; IEEE: New York, NY, USA, 2014; pp. 519–528. [Google Scholar]
- Zhang, H.J.; Xiao, N.F. Parallel implementation of multilayered neural networks based on Map-Reduce on cloud computing clusters. Soft Comput. 2016, 20, 1471–1483. [Google Scholar] [CrossRef]
- YelpOpenData. Available online: http://www.yelp.com/academic_dataset (accessed on 5 August 2020).
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the 31st AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Myung, R.; Yu, H. Performance prediction for convolutional neural network on spark cluster. Electronics 2020, 9, 1340. [Google Scholar] [CrossRef]
- Merkel, D. Docker: Lightweight linux containers for consistent development and deployment. Linux J. 2014, 2014, 2. [Google Scholar]
- Fan, G.F.; Qing, S.; Wang, H.; Hong, W.C.; Li, H.J. Support vector regression model based on empirical mode decomposition and auto regression for electric load forecasting. Energies 2013, 6, 1887–1901. [Google Scholar] [CrossRef]
- Li, M.W.; Wang, Y.T.; Geng, J.; Hong, W.C. Chaos cloud quantum bat hybrid optimization algorithm. Nonlinear Dyn. 2021, 103, 1167–1193. [Google Scholar] [CrossRef]








| (a) | ||||||||||
| workload\memsize | 1 GB | 1.1 GB | 1.2 GB | 1.3 GB | 1.4 GB | 1.5 GB | 1.6 GB | 1.7 GB | 1.8 GB | 1.9 GB |
| wordcount | OOME | OOME | OOME | OOME | OOME | OOME | 1010.70% | 659.10% | 238.70% | 100% |
| K-Means | OOME | OOME | OOME | OOME | OOME | OOME | 1123.40% | 791.00% | 325.20% | 100% |
| logistic regression | OOME | OOME | OOME | OOME | 1338.70% | 832.10% | 583.90% | 343.80% | 172.90% | 100% |
| neural network | OOME | OOME | OOME | OOME | OOME | 1265.20% | 884.50% | 522.60% | 281.90% | 100% |
| (b) | ||||||||||
| workload\memsize | 2 GB | 3 GB | 4 GB | 5 GB | 6 GB | 7 GB | 8 GB | 9 GB | 10 GB | 11 GB |
| Wordcount | 100% | 101.70% | 101.00% | 102.40% | 100.70% | 100.90% | 101.60% | 101.10% | 100.70% | 101.70% |
| K-Means | 100.20% | 100% | 100.50% | 102.80% | 100.90% | 101.60% | 100.40% | 101.00% | 100.20% | 102.50% |
| logistic regression | 100.30% | 102.90% | 101.40% | 100% | 100.70% | 101.10% | 100.90% | 100.80% | 102.00% | 101.40% |
| neural network | 103% | 102.80% | 103% | 101.20% | 101.80% | 100% | 100.50% | 102.70% | 101.40% | 100.70% |
| CNN | OOME | OOME | OOME | OOME | OOME | OOME | 101.90% | 100.70% | 100% | 101.20% |
| Notation | Description |
|---|---|
| i-th Transformation among series of transformation which is applied to partition(s). | |
| (i.e., ) | i-th partition in a RDD that j-th transformation has been applied. If j is 0, no transformation has been applied to the partition. |
| (i.e., ) | i-th element in a partition that j-th transformation has been applied. If j is 0, no transformation has been applied to the element. |
| hasnext() | A function that checks whether there is the next element. |
| next() | A function that point the next element. |
| Lasso and Ridge | |
|---|---|
| Hyperparameter | Values |
| Penalty alpha | 1 × 10−10, 1 × 10−5, 0.1, 1, 5, 10, 20 |
| RF | |
|---|---|
| Hyper-Parameter | Values |
| # of estimators | 50, 100, 150 |
| Max features | auto, sqrt, log2 |
| Max depth | 50, 100, 150 |
| Lasso and Ridge | |
|---|---|
| Hyperparameter | Values |
| Solver | Lbfgs, adam, sgd |
| Activation functions | Sigmoid, ReLU |
| Max iteration | 1000, 5000, 10,000 |
| Learning rate alpha | 0.01, 0.05 |
| Hidden layer size | 50, 100, 150 |
| Workload | Element Format | Element Size |
|---|---|---|
| wordcount | Set of randomly chosen characters that fulfill element size (e.g., if element size is 4byte, “abcd”) | Element size set1 = {1 KB, 150 KB, 300 KB, 450 KB, 600 KB, 750 KB, 1 MB} Element size set2 = {1 KB, 100 KB, 200 KB, 300 KB, 500 KB, 600 KB, 700 KB, 800 KB, 900 KB} |
| k-means clustering | Set of randomly chosen double type numbers that fulfill element size (e.g., if element size is 32byte, (1,2,3,4)) | |
| logistic regression | ||
| neural network | ||
| CNN | image | Open image dataset [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Myung, R.; Choi, S. Machine-Learning Based Memory Prediction Model for Data Parallel Workloads in Apache Spark. Symmetry 2021, 13, 697. https://doi.org/10.3390/sym13040697
Myung R, Choi S. Machine-Learning Based Memory Prediction Model for Data Parallel Workloads in Apache Spark. Symmetry. 2021; 13(4):697. https://doi.org/10.3390/sym13040697
Chicago/Turabian StyleMyung, Rohyoung, and Sukyong Choi. 2021. "Machine-Learning Based Memory Prediction Model for Data Parallel Workloads in Apache Spark" Symmetry 13, no. 4: 697. https://doi.org/10.3390/sym13040697
APA StyleMyung, R., & Choi, S. (2021). Machine-Learning Based Memory Prediction Model for Data Parallel Workloads in Apache Spark. Symmetry, 13(4), 697. https://doi.org/10.3390/sym13040697






