Abstract
The collision effects on the low-frequency ion-acoustic Trivelpiece–Gould wave are investigated in weakly and completely ionized plasma waveguides by using the normal mode analysis. In weakly ionized plasma waveguides, it is found that the dependence of the harmonic mode on the absolute value of the scaled damping rate shows the opposite tendency for large and small radii of the cylindrical waveguide. It is also is found that the scaled damping rates for both weakly and completely ionized plasma waveguides decrease with an increase of the electron temperature. It is interesting to note that the scaled damping rate for weakly ionized plasma waveguides shows anti-symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction. However, it is found that the scaled damping rate for completely ionized plasma waveguides shows the symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction.
PACS:
52.20-j; 52.35.Fp
1. Introduction
The stability analysis of the propagation of linear and nonlinear waves in various physical systems has received considerable attention since the conditions for the stable or unstable modes can provide useful information on the geometrical configuration and the physical characteristics [1]. In plasma environments, it has been shown that the influence of wave–particle and wave–wave interactions plays an important role in the stability of the propagation of linear and nonlinear plasma waves [2]. The condition for the stability of plasma waves in a confined configuration of the bounded plasma has been extensively investigated owing to the wide application of the surface plasma wave [3,4,5,6,7]. It has been shown that the condition for the propagation of surface waves in bounded and semi-bounded plasmas can be explored from the dispersion relation obtained by the surface impedance on the interface between the two different media. Hence, it is obvious that the appropriate boundary conditions at the interface are essential to legitimate the physical properties of surface waves. It is also shown that the cylindrical plasma waveguide has received considerable attention since the space-change wave on the interface of the plasma column would support various harmonic modes owing to the multi-existence of harmonized cylindrical Bessel solutions [8]. The stability of cylindrical plasma with sharp boundaries has been extensively investigated since the non-zero azimuthal component related to a flutelike perturbation is related to the kink instability [9]. In collisional plasmas, it is well known that the influence of collision frequencies causes complex imaginary terms in plasma susceptibilities [10]. Even though there are many investigations on Trivelpiece–Gould waves [11,12,13], we do not have enough information on the effect of collisional damping on the propagation and stability of Trivelpiece–Gould waves in a plasma waveguide containing noble electrons and ions. In addition, the influences of the ion-neutral and ion–ion collisions in weakly and completely ionized plasma waveguides on the Trivelpiece–Gould have not been investigated yet. Hence, this work is motivated to present general descriptions of Trivelpiece–Gould waves propagating in weakly and completely ionized plasma waveguides, including ion-neutral and ion–ion collisions, which seem to affect the dispersive properties. It would be expected that the damping and instability modes could exist in collisional plasma waveguides. Then, in this work, the influence of ion collisions on the low-frequency ion-acoustic space-change wave known as the Trivelpiece–Gould wave are investigated in weakly and completely ionized plasma waveguides. This investigation was conducted to understand the theoretical aspects of the collision effects on the propagation of the low-frequency ion-acoustic Trivelpiece–Gould wave by using the method of normal modes and the separation of variables. Hence, the dispersion relations of the low-frequency ion-acoustic Trivelpiece–Gould waves are derived for weakly ionized plasma waveguides as well as for completely ionized plasma waveguides. The variations of the damping rates owing to ion collisions in weakly and completely ionized plasma waveguides are also discussed.
2. Strum–Liouville Equations for Weakly and Completely Ionized Plasmas
The continuity equation and the momentum equation for the species j of plasma particles are given by, respectively,
where , , , , , and are density, velocity, mass, pressure, charge, and electrostatic potential. Here, Poisson’s equation is given by , where and . In the frequency range, , the plasma dielectric function for weakly ionized plasmas (W) and the plasma dielectric function for completely ionized plasmas (C) can be, respectively, expressed as follows [14]:
where is the frequency, k is the wave number, is the thermal velocity, is the plasma frequency of the species j, is the ion-neutral collision frequency, and is the ion-ion collision frequency. Based on the perturbation theory, the small perturbations from the equilibrium values for the density, velocity, and electrostatic potential would be given as , , and , where the subscript 1 stands for the small perturbing quantity and the subscript 0 for the equilibrium quantity. Here, the time-dependent parts of the perturbed density, perturbed velocity, and perturbed electrostatic potential are given by , , and . In cylindrical coordinates, these perturbed quantities can be represented by the wave-like forms [15,16,17]: , , and , where , , and are the perturbed quantities in the transverse plane, is the wave number along the axial z-direction, is the transverse wave number, and is the azimuthal wave number. From Equations (1)–(4), the differential equation for the perturbed electrostatic potential would be written as the following self-adjoint form of the Strum–Liouville eigenvalue problem [18]:
In Equation (5), the operator is a self-adjoint operator and , where for weakly ionized plasma waveguides (WIP) and for completely ionized plasma waveguides (CIP), respectively,
Hence, the Strum–Liouville equations for weakly and completely ionized plasma waveguides are, respectfully, found to be
3. Dispersion Relations for Weakly and Completely Ionized Plasmas
The general eigenvalue solutions of the Strum–Liouville equations (Equations (8) and (9)) for weakly and completely ionized plasma waveguides can be represented by , where the constants A and B are functions of the separation constants and , and is the -th order cylindrical Bessel function, and is the -th order Neumann function. Hence, a general solution for is found to be . If the plasma waveguide is assumed to be the azimuthally symmetric cylindrical system, we can set so that the r-dependence of for the azimuthally symmetric plasma waveguide is put by . Since the singular behavior of the zeroth-order Neumann function for , this constraint implies . In addition, the r-dependence of must be null on the surface of the cylindrical waveguide at , i.e., . Since has the oscillatory behavior with many zeros, such as where is the q-th zero of the Bessel function of zeroth order (for example, , , ), the parameter is then obtained by , where for weakly ionized plasma waveguides (WIP) and for completely ionized plasma waveguides (CIP), respectively. Hence, we can obtain the following equations for weakly and completely ionized plasmas such as
Hence, the dispersion relation for weakly ionized plasma waveguides yields
where and denote the real and the imaginary parts of the dispersion function , respectively. The dispersion relation for completely ionized plasma waveguides is then obtained as
where and are the real and the imaginary parts of the dispersion function , respectively. As shown in Equations (12) and (13), the dispersion relations for weakly and completely ionized plasma waveguides are complex functions so that the corresponding frequencies should be complex forms, such as , where the real part of the frequency and the damping rate are holding the following constraint condition: . From Equations (12) and (13), we have found that
with . The real part of the frequency for weakly and completely ionized plasma waveguides is obtained as
From Equations (12), (14) and (15) with , the small damping rate for weakly ionized plasma waveguides becomes
Hence, the absolute scaled damping rate in the unit of the ion plasma frequency for weakly ionized plasma waveguides is found to be
where , , is the scaled axial wave number, is the scaled radius of the cylindrical plasma waveguide, and is the electron Debye length. From Equations (13)–(15) with , the small damping rate for completely ionized plasma waveguides is found to be
The absolute scaled damping rate in units of the ion plasma frequency for completely ionized plasma waveguides is then obtained as
where and is the ion Debye length. Recently, the properties of quantum plasmas including the quantum-diffraction and electron-exchange effects have been extensively explored in various laboratory and natural plasma systems, such as astrophysical compact objects, laser-induced plasmas, nano-wires, quantum dots, and semiconductor plasmas [19,20,21]. Therefore, the study on the collision effects on quantum Trivelpiece–Gould wave in plasma waveguides composed of degenerate electrons and ions, including the electron-exchange phenomena, will be treated elsewhere.
4. Discussion
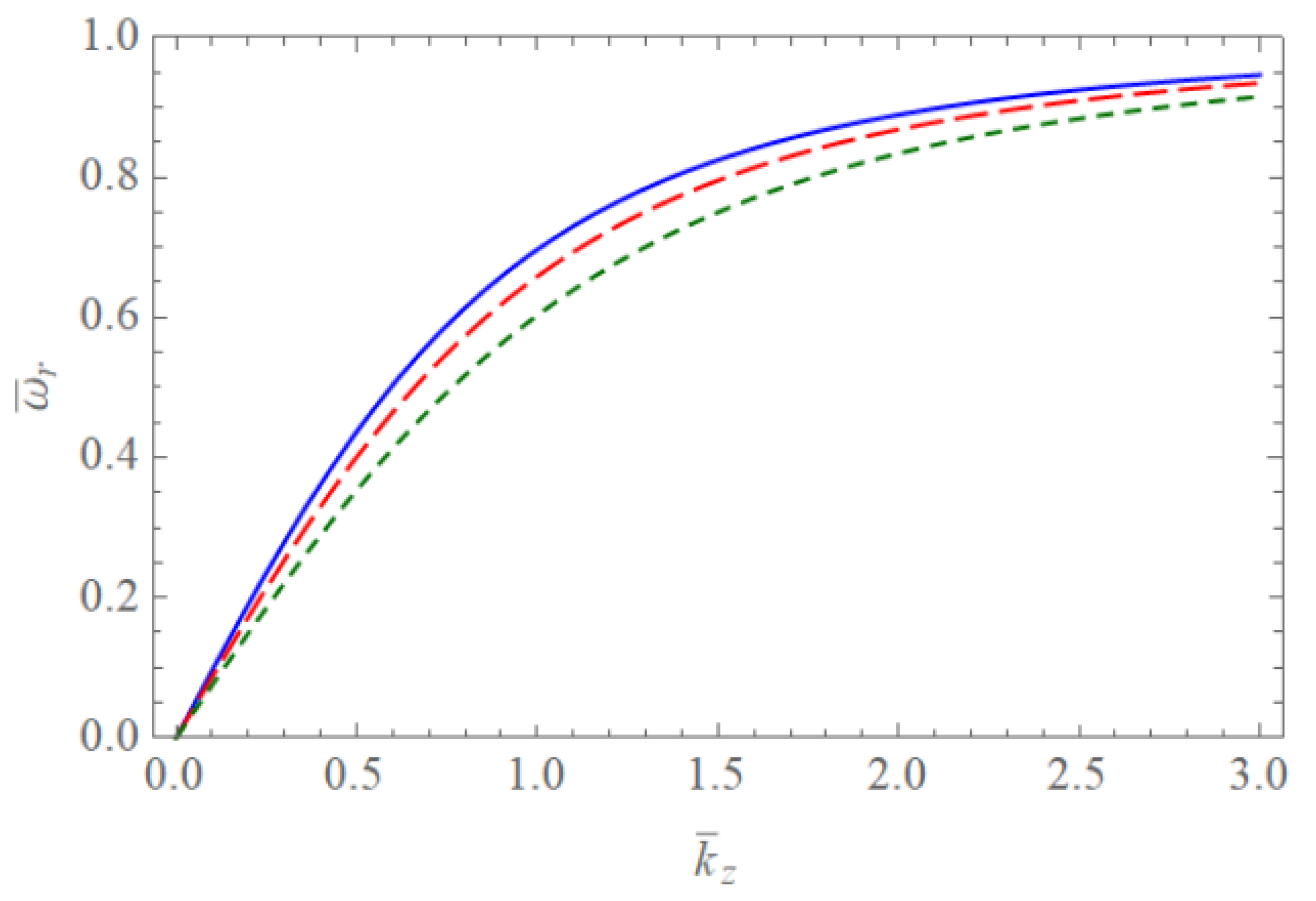
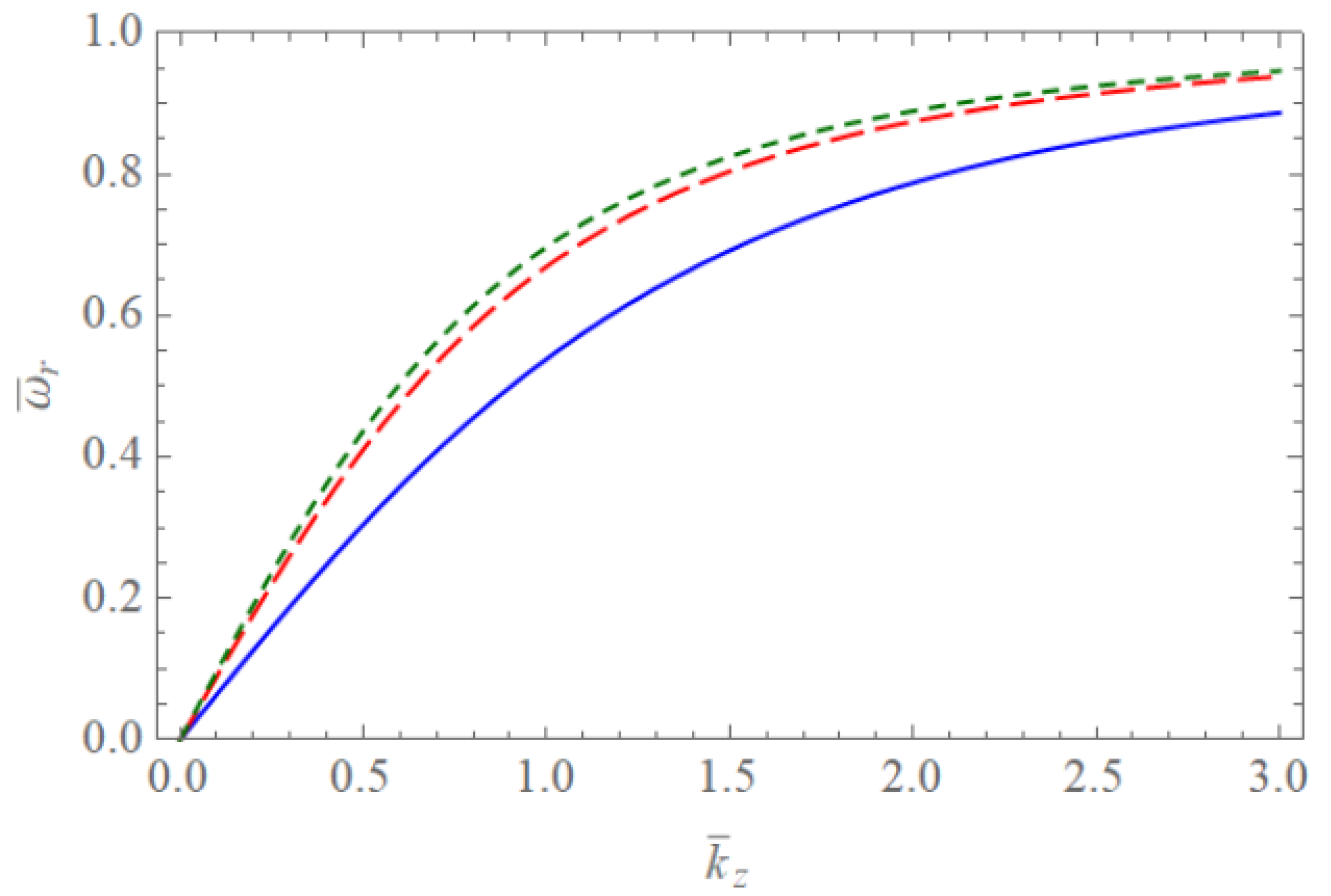
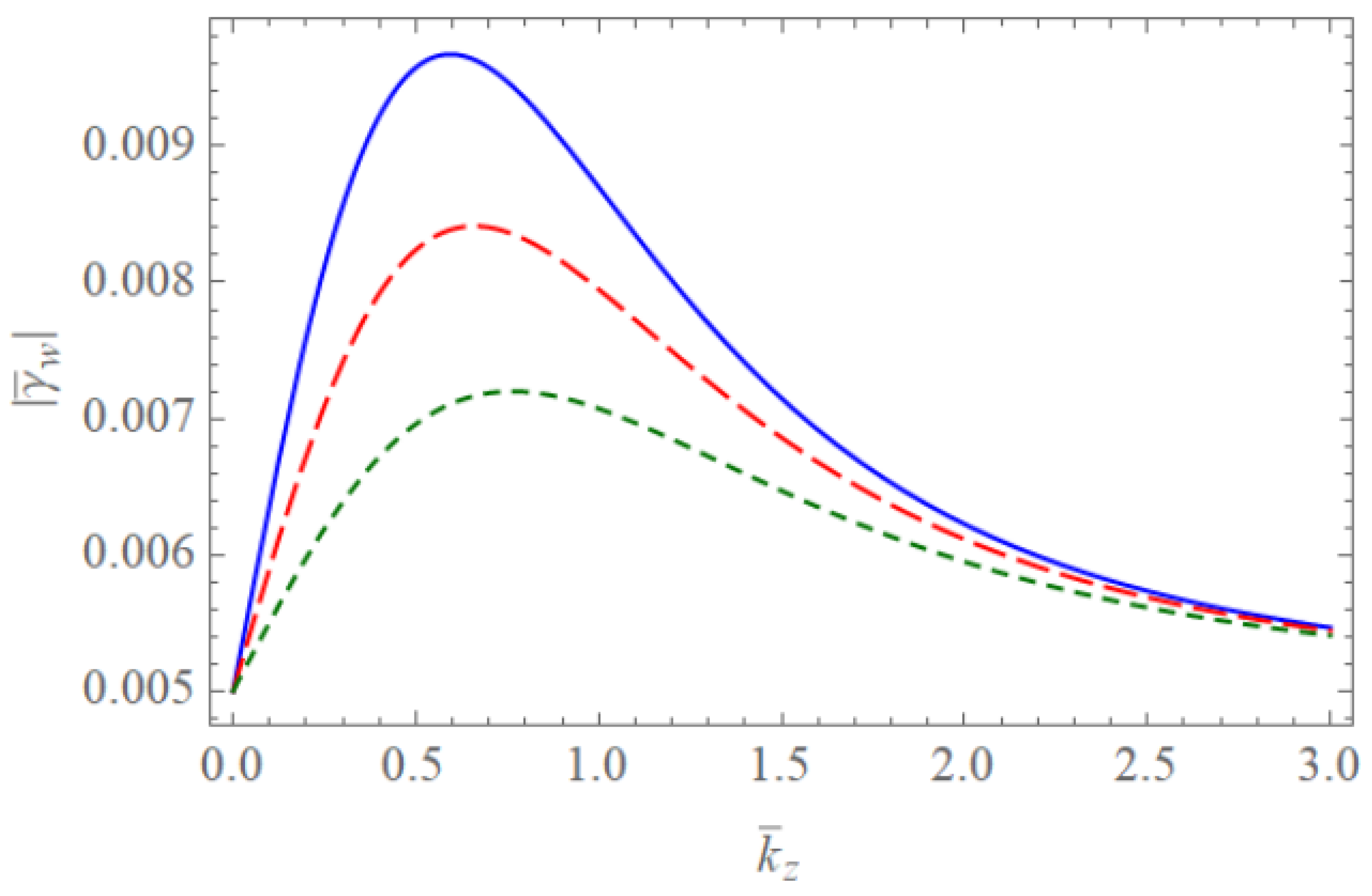
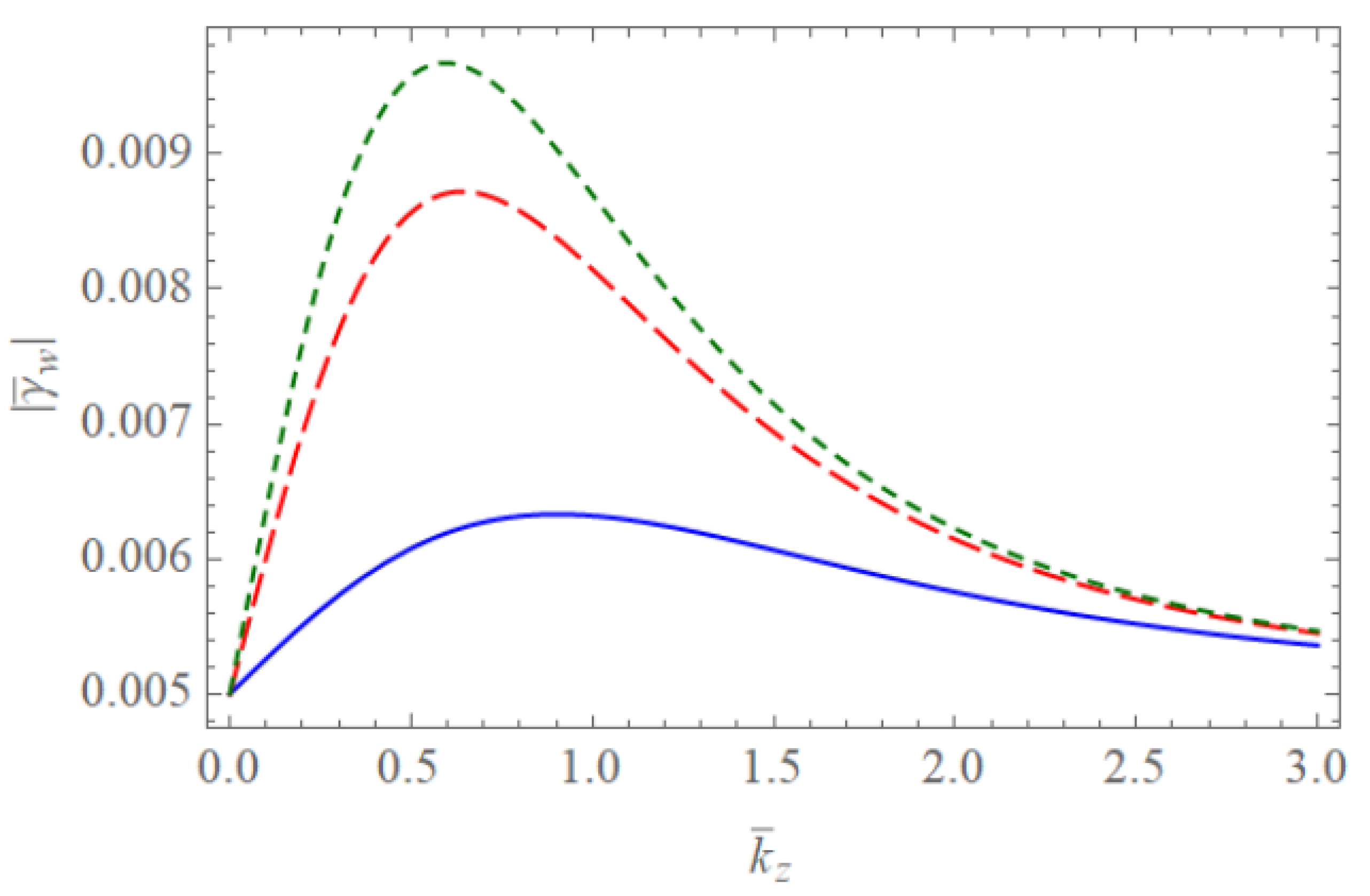
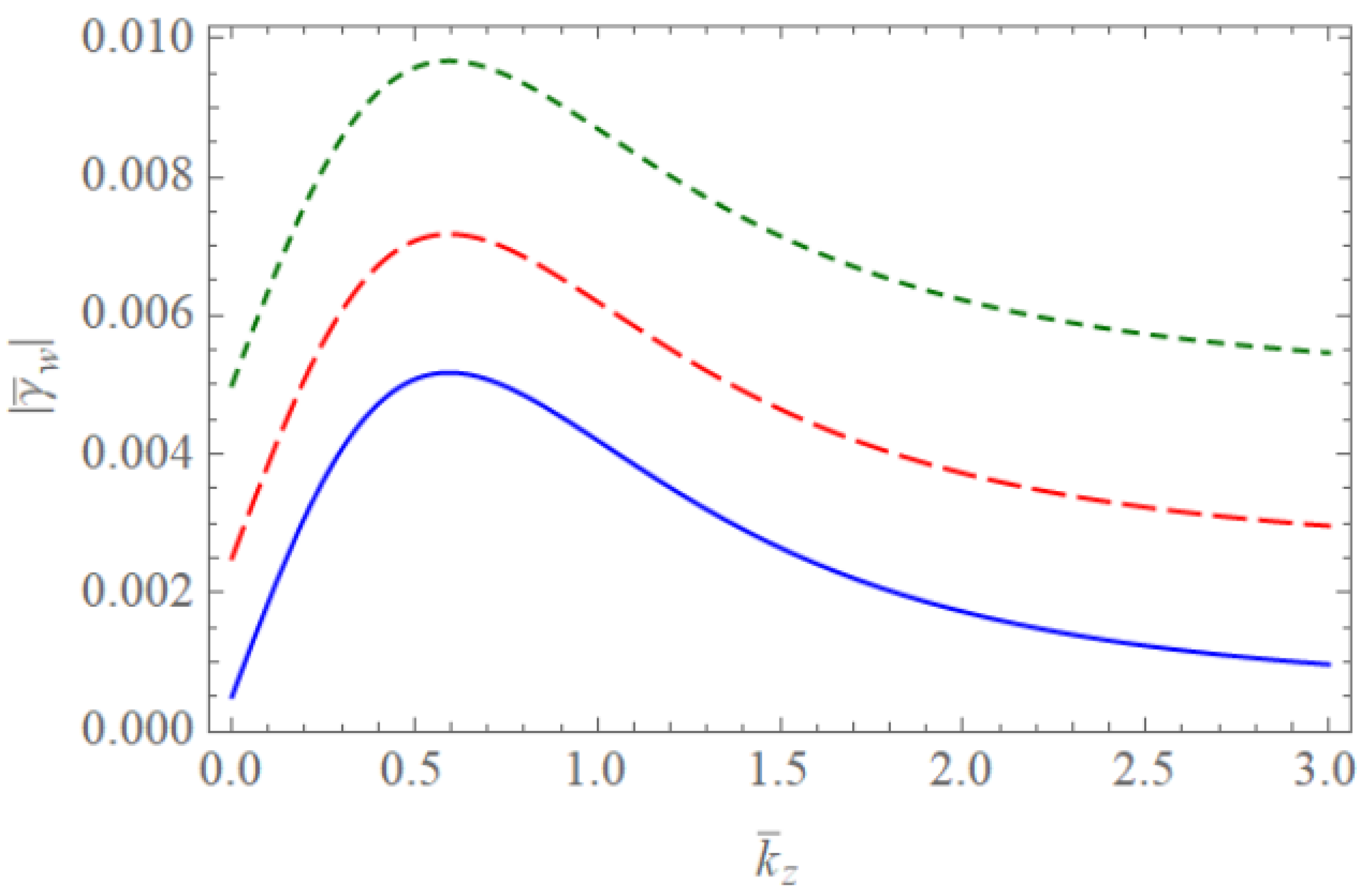
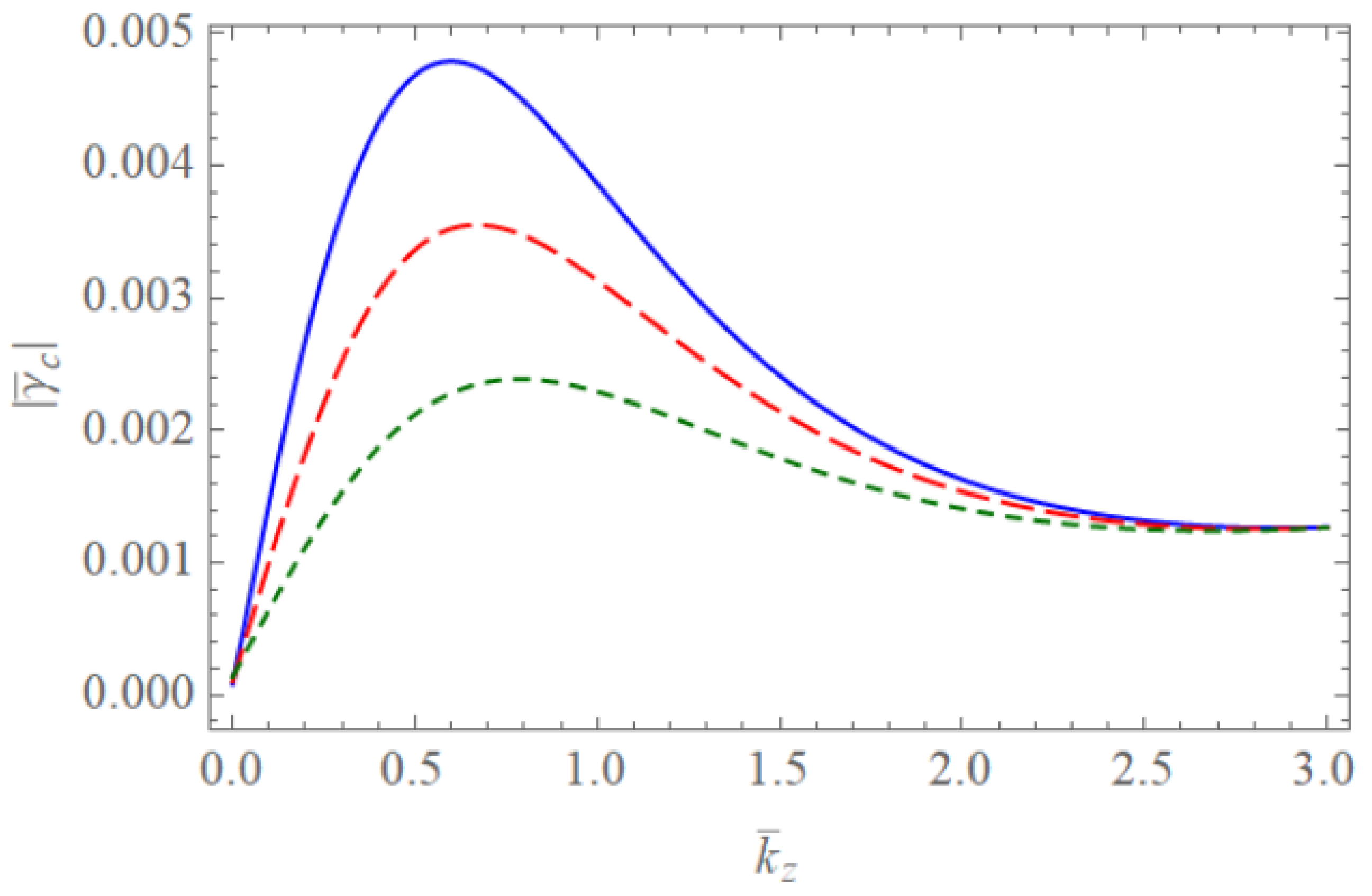
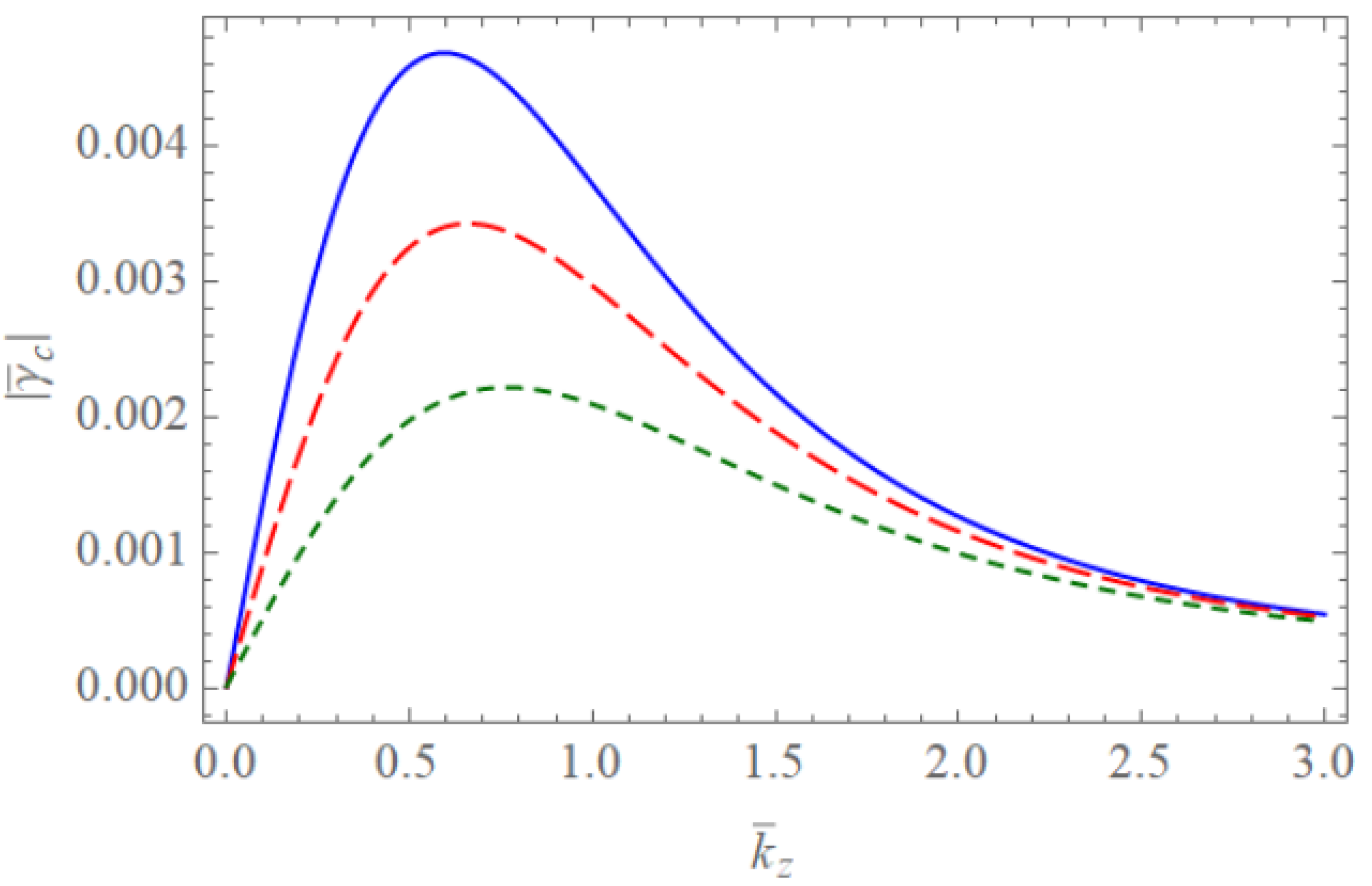
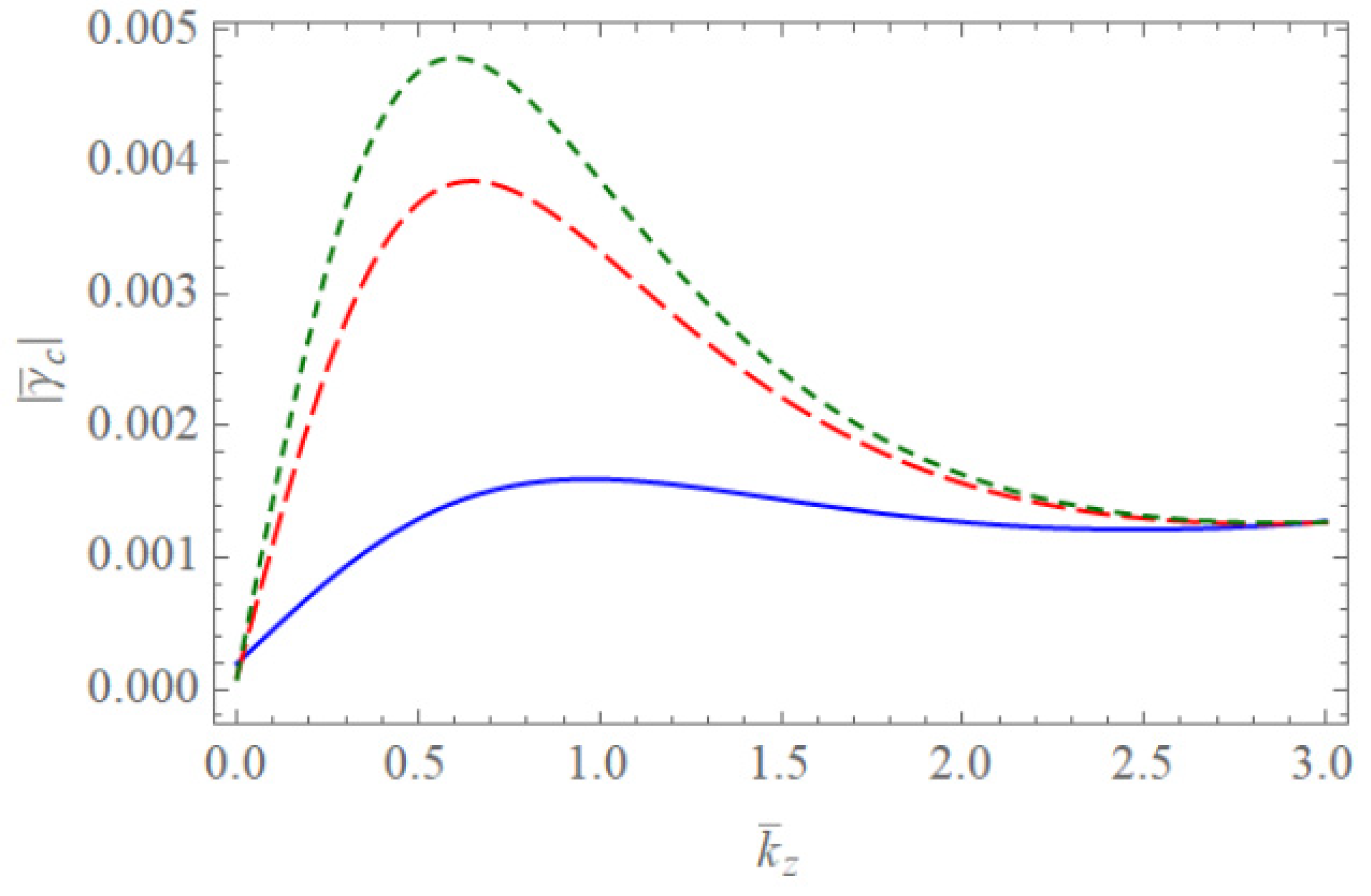
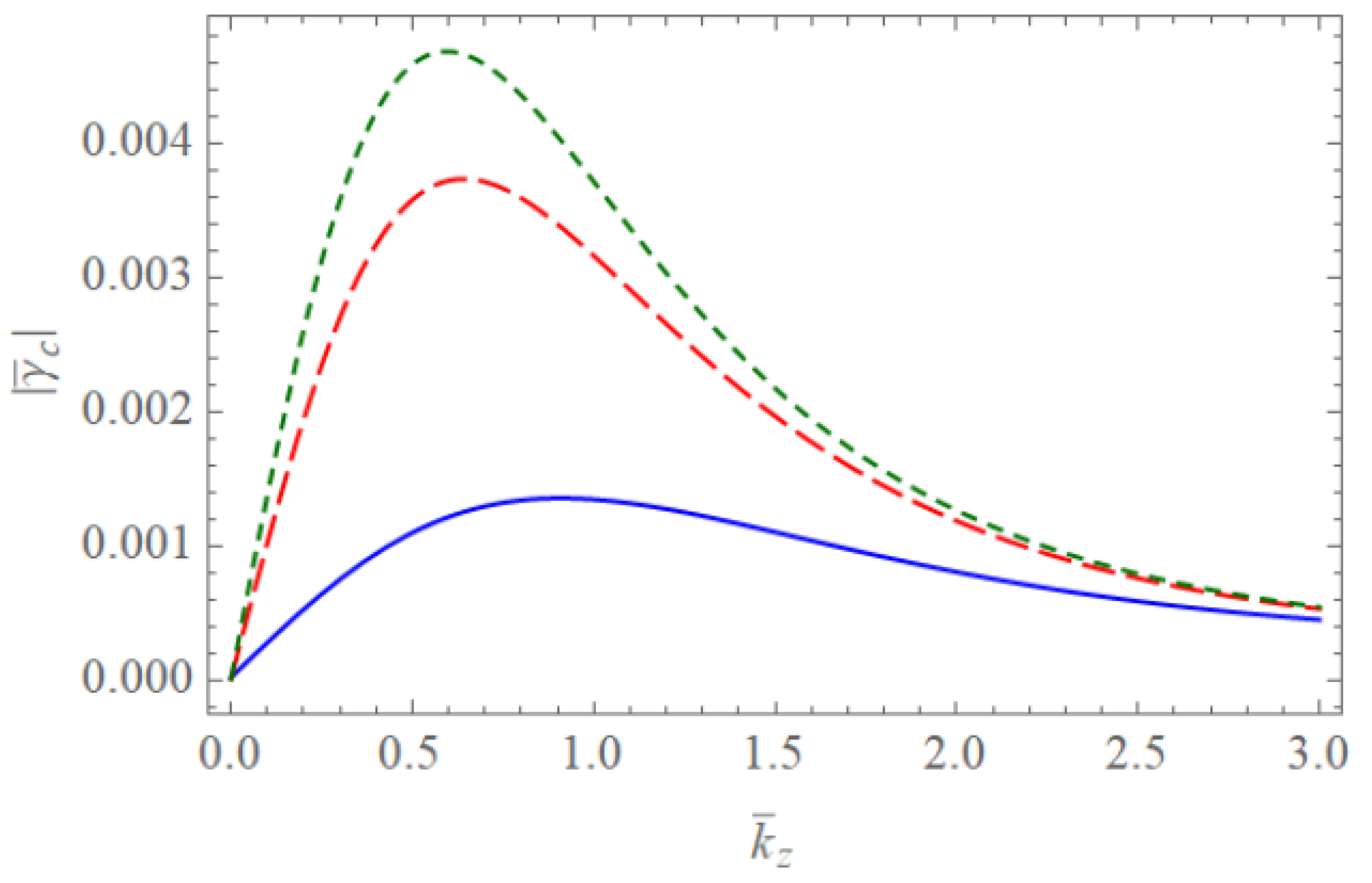
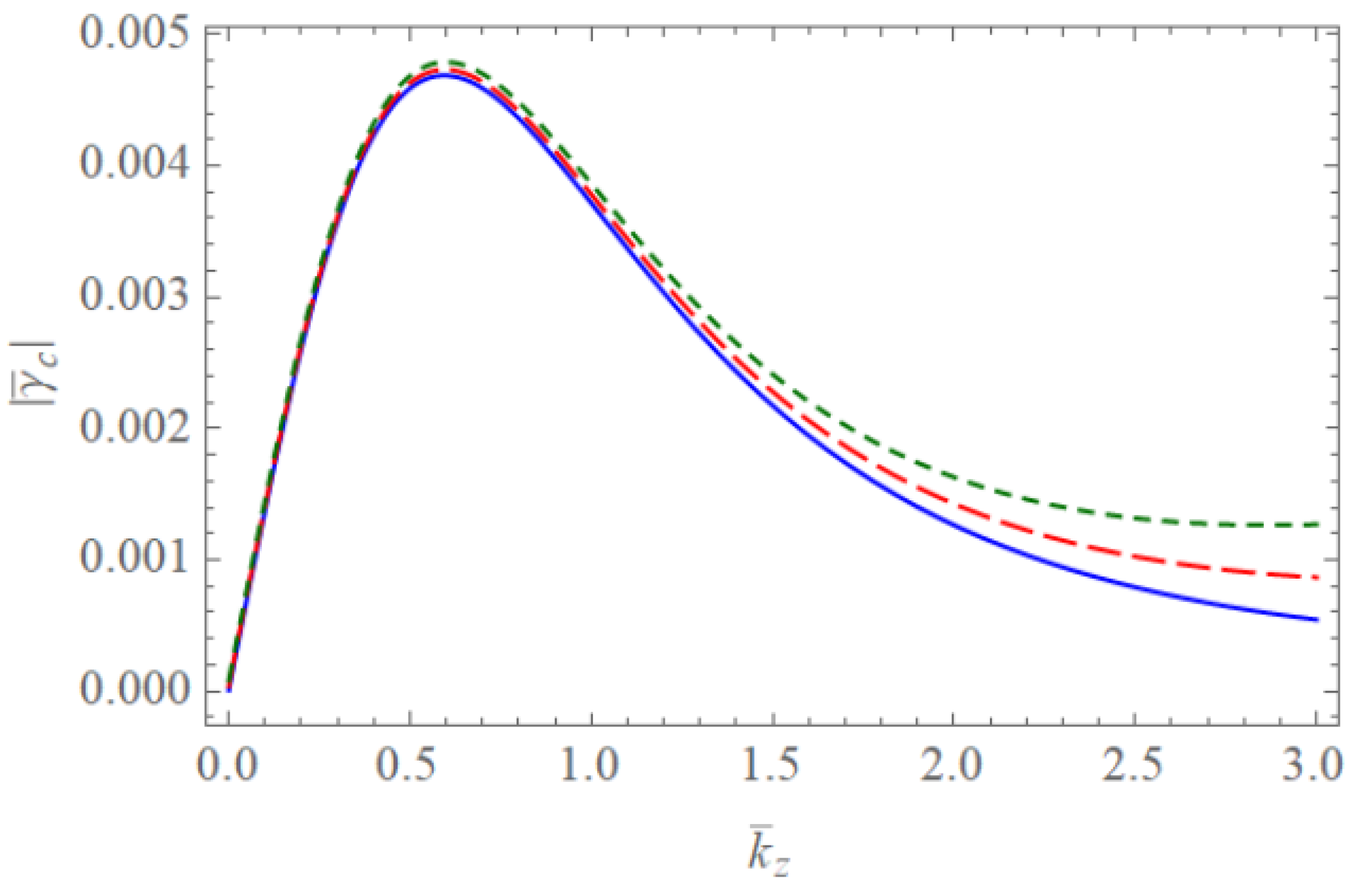
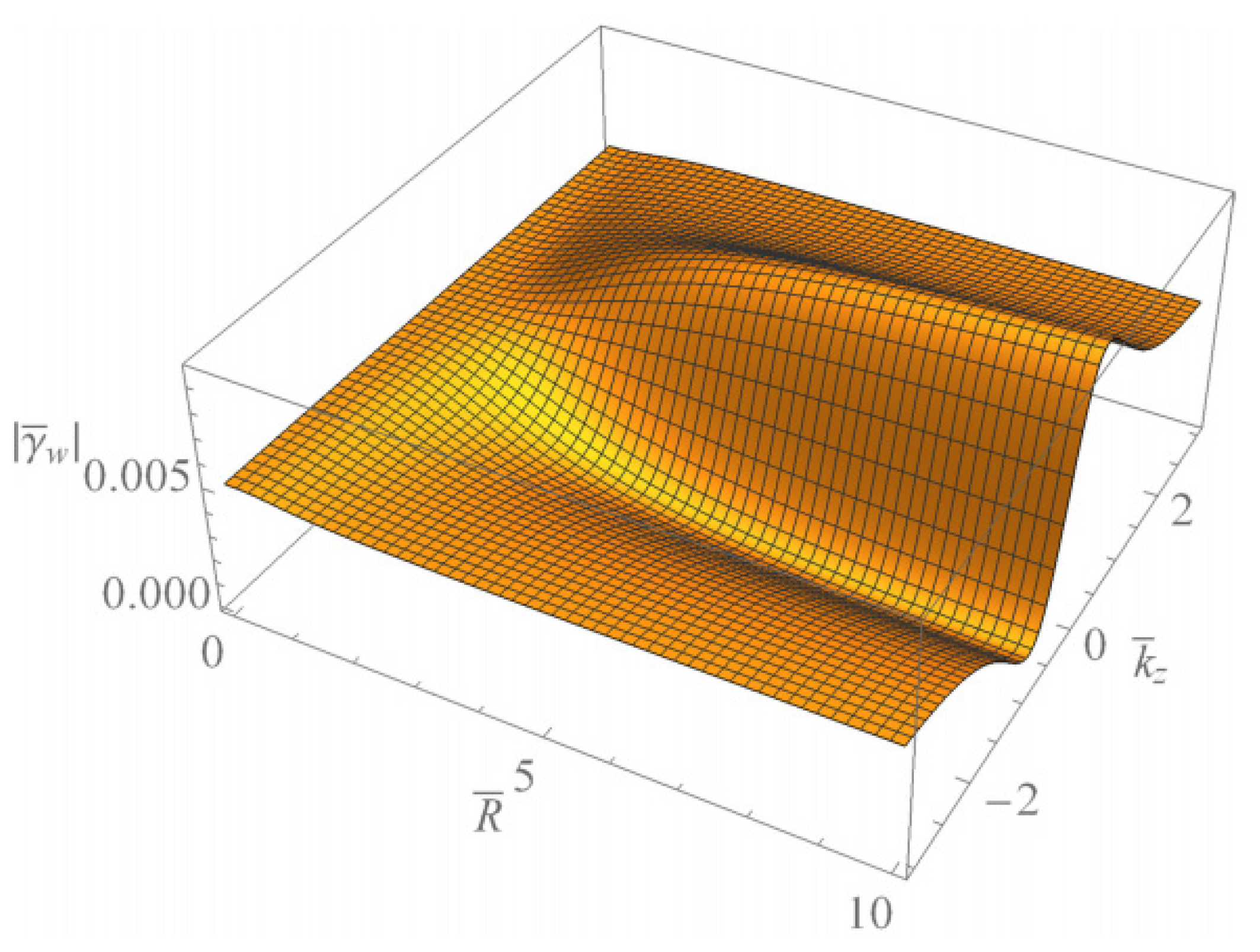
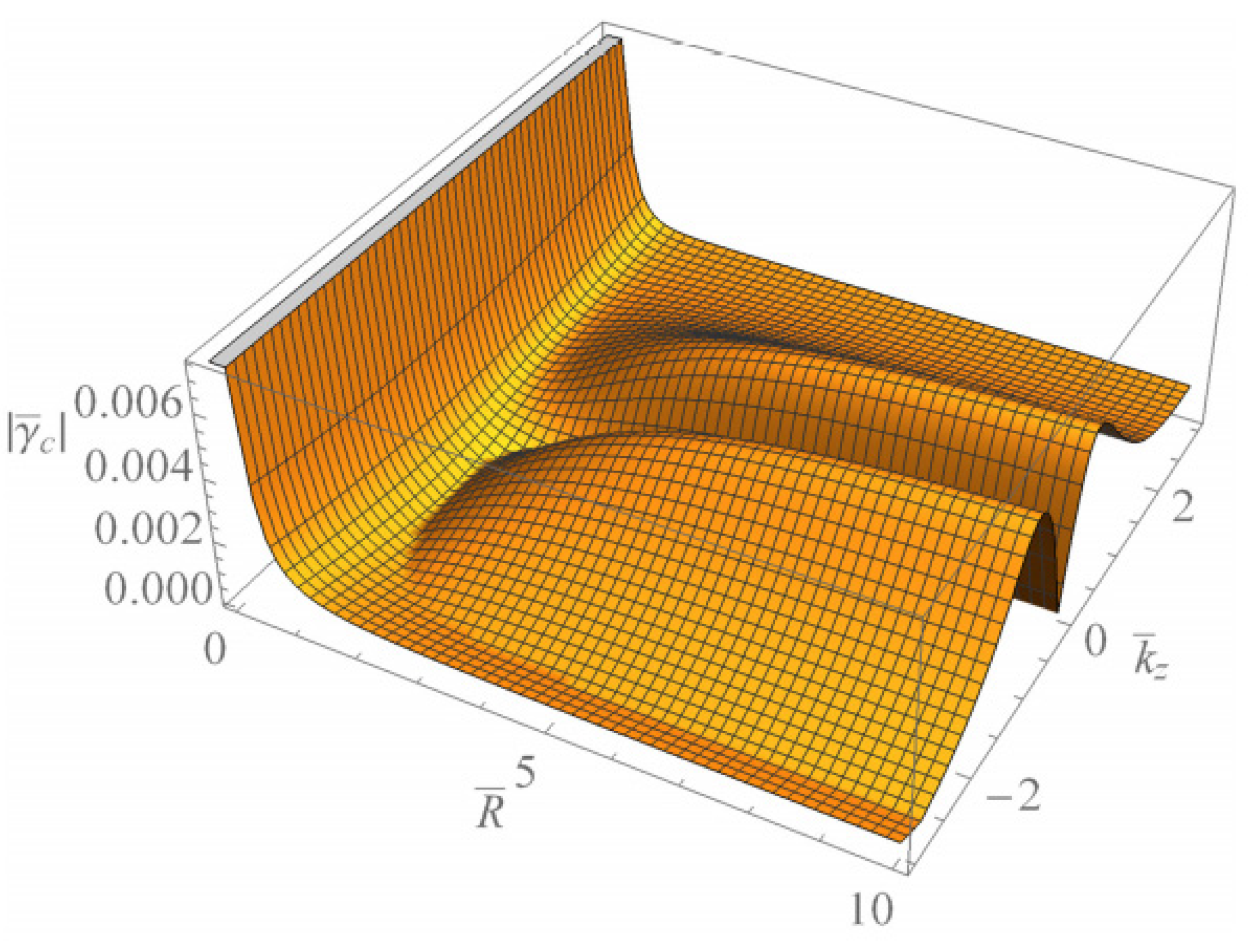
Figure 1 and Figure 2 show the scaled real frequencies for weakly and completely ionized plasma waveguides as a function of for various values of the harmonic modes when and , respectively. As we see in Figure 1 and Figure 2, the scaled real frequency decreases with the harmonic number p for the Bessel eigenvalue when . However, it is interesting to note that the scaled real frequency increases with the harmonic number p for the Bessel eigenvalue when . Hence, we have found that the dependence of the harmonic mode on the scaled real frequency shows the opposite tendency for large and small radii of the cylindrical waveguide. Figure 3 and Figure 4 show the absolute values of the scaled damping rate for weakly ionized plasma waveguides as a function of for various values of the harmonic modes when and , respectively. As shown in Figure 3 and Figure 4, the scaled damping rate decreases with the harmonic number p for the Bessel solution when . However, it is interesting to note the scaled damping rate increases with the harmonic number p for the Bessel solution when . Hence, it is found that the dependence of the harmonic mode on the scaled damping rate shows the opposite tendency for large and small radii of the cylindrical waveguide. Figure 5 represents the absolute value of the scaled damping rate for weakly ionized plasma waveguides as a function of for various values of the ion-neutral collision frequency . As we can see from this figure, the scaled damping rate increases with an increase of the collision frequency . Figure 6 and Figure 7 show the absolute values of the scaled damping rate for the weakly ionized plasma waveguides as a function of for various values of the harmonic modes when and the temperature ratio are and , respectively. As shown in Figure 6 and Figure 7, the scaled damping rate decreases with a decrease of the temperature ratio . Hence, it is found that the scaled damping rate for weakly ionized plasma waveguides decreases with an increase of the electron temperature. Figure 8 and Figure 9 show the absolute values of the scaled damping rate for completely ionized plasma waveguides as a function of for various values of the harmonic modes when and the temperature ratio are and , respectively. As shown in Figure 8 and Figure 9, the scaled damping rate decreases with a decrease of the temperature ratio . Hence, the scaled damping rate is found to decrease with an increase of the electron temperature. Figure 10 represents the absolute value of the scaled damping rate for completely ionized plasma waveguides as a function of for various values of the ion-ion collision frequency . As we can see from this figure, the scaled damping rate increases with an increase of the collision frequency . In addition, it is shown that the influence of the collision frequency is found to be more significant when . Figure 11 represents the surface profile of the absolute value of the scaled damping rate for weakly ionized plasma waveguides as a function of and . As we can see from this figure, the dependence of the wave number on the scaled damping rate is getting more significant as an increase of the scaled radius of the waveguide. It is interesting to note that the scaled damping rate for weakly ionized plasmas shows the anti-symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction. Figure 12 represents the surface plot of the absolute value of the scaled damping rate for completely ionized plasma waveguides as a function of and . As we can see from this figure, the dependence of the wave number on is getting more significant as the scaled radius increases. We should note that for completely ionized plasmas shows symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction. Hence, it is quite important to note that the mirror-reflection behavior of the scaled damping rate shows the opposite tendency for weakly and completely ionized plasmas.
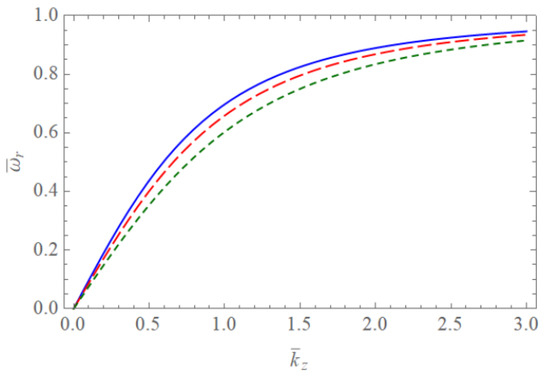
Figure 1.
The scaled real frequency of the Trivelpiece–Gould wave for weakly and completely ionized plasma waveguides as a function of when . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
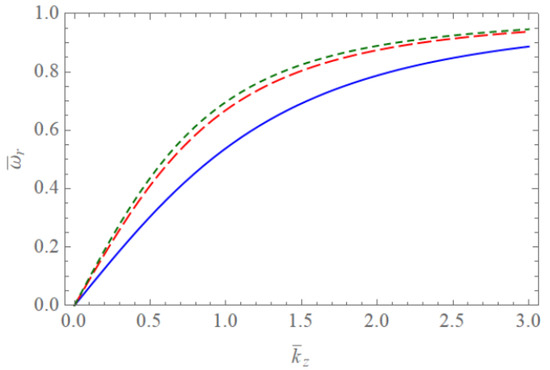
Figure 2.
The scaled real frequency of the Trivelpiece–Gould wave for weakly and completely ionized plasma waveguides as a function of when . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
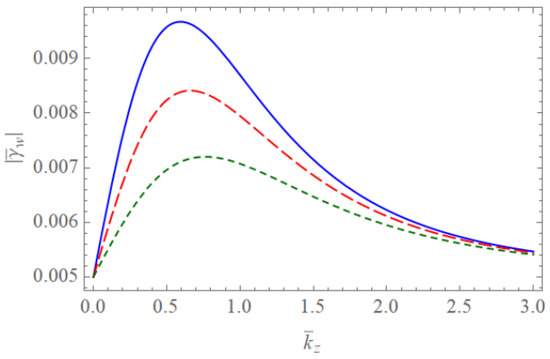
Figure 3.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for weakly ionized plasma waveguides as a function of when and . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
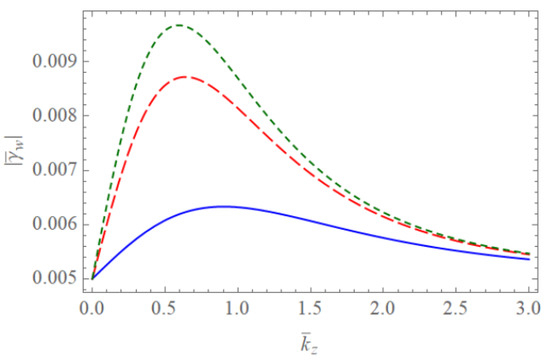
Figure 4.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for weakly ionized plasma waveguides as a function of when and . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
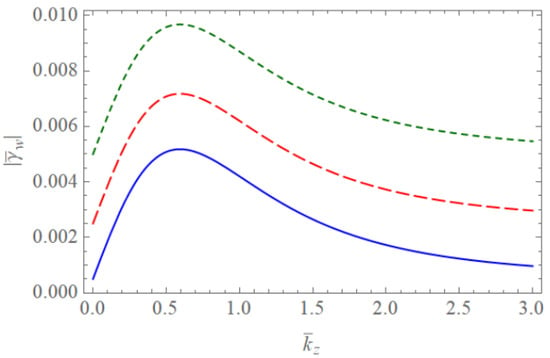
Figure 5.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for weakly ionized plasma waveguides as a function of when . with . The blue dashed line is the case of . The red dotted line is the case of . The green dotted line is the case of .
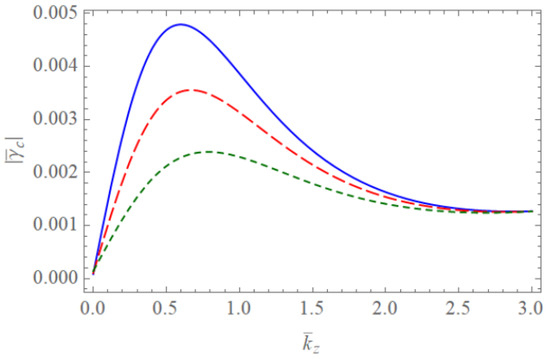
Figure 6.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of when , , and . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
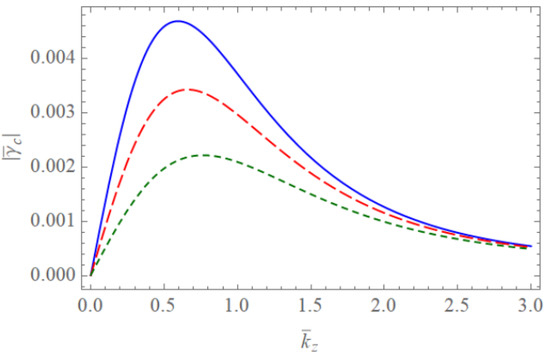
Figure 7.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of when , , and . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
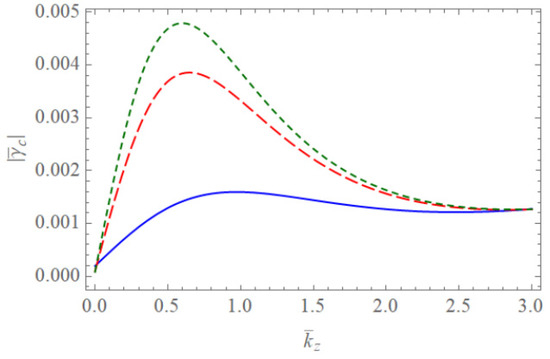
Figure 8.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of when and with . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
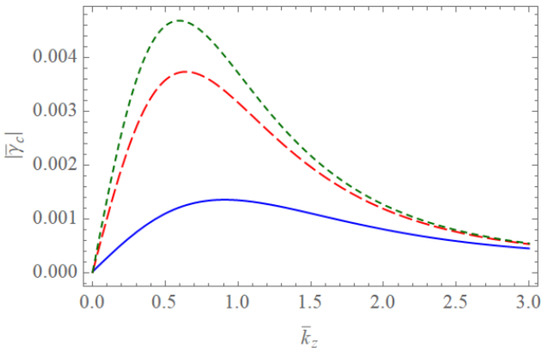
Figure 9.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of when and with . The blue solid line is the case of . The red dashed line is the case of . The green dotted line is the case of .
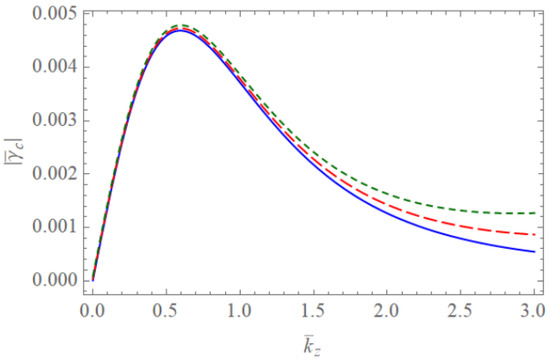
Figure 10.
The absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of when with . The blue solid line is the case of . The red dashed line is the case of . The green solid line is the case of .
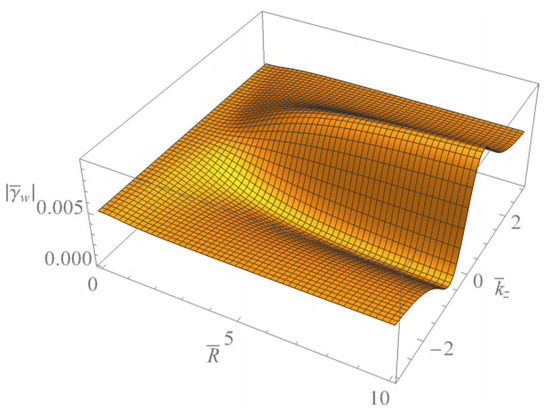
Figure 11.
The surface plot of the absolute value of the scaled damping rate of the Trivelpiece–Gould wave for weakly ionized plasma waveguides as a function of and when with .
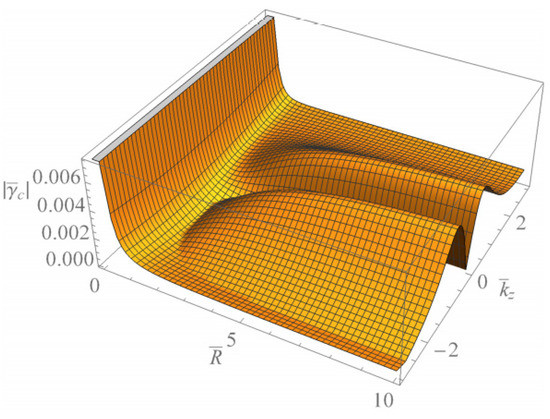
Figure 12.
The surface plot of the absolute value of the scaled damping rate of the Trivelpiece–Gould wave for completely ionized plasma waveguides as a function of and when and with .
5. Summary
In this work, we investigated the influence of ion collisions on the low-frequency ion-acoustic Trivelpiece–Gould wave in weakly and completely ionized plasma waveguides by using the method of normal modes and the separation of variables. Trivelpiece–Gould waves contain many advantages over bulk waves since they can produce plasmas with more spatially confined uniform density profiles, resulting in a wide range of applications. Since the collision frequency is not often small under experimental conditions for plasma research, we should take into account the collision frequency for the dielectric permittivity of the plasma when the deviation of the experimental results from the theoretical prediction is evident. In weakly ionized plasma waveguides, the dependence of the harmonic modes on the absolute value of the scaled damping rate shows the opposite tendency for large and small radii of the cylindrical waveguide. The scaled damping rates for both weakly and completely ionized plasma waveguides also decrease with an increase of the electron temperature. It is interesting to find that the scaled damping rate for weakly ionized plasma waveguides shows the anti-symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction. However, it is found that the scaled damping rate for completely ionized plasma waveguides shows symmetric behavior when the Trivelpiece–Gould wave propagates in the negative-z direction. Hence, it is quite interesting to note that the mirror-reflection behavior of the scaled damping rate shows the opposite tendency for weakly and completely ionized plasma waveguides. From this work, we have found that the collision effects on the damping rates of the Trivelpiece–Gould waves play significant roles in weakly and completely ionized plasma waveguides. These results would provide useful information on the stability of the Trivelpiece–Gould waves in collisional plasma waveguides.
Author Contributions
Conceptualization, M.-J.L. and Y.-D.J.; Formal analysis, M.-J.L. and Y.-D.J.; Funding acquisition, M.-J.L.; Investigation, M.-J.L. and Y.-D.J.; Methodology, M.-J.L. and Y.-D.J.; Project administration, M.-J.L.; Resources, M.-J.L. and Y.-D.J.; Software, M.-J.L. and Y.-D.J.; Writing—original draft, M.-J.L. and Y.-D.J.; Writing—review & editing, M.-J.L. and Y.-D.J. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (NRF-2019R1A2C1003363).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request from the authors.
Acknowledgments
The authors gratefully acknowledge N. Ashikawa for warm hospitality and useful discussions while visiting National Institute for Fusion Science (NIFS), Japan. This research was initiated while the authors were visiting NIFS as visiting professors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kaw, P.K. Surface Waves on a Plasma Half-Space. Phys. Fluids 1970, 13, 1784–1790. [Google Scholar] [CrossRef]
- Gradov, O.; Stenflo, L. Linear theory of a cold bounded plasma. Phys. Rep. 1983, 94, 111–137. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Nonlinear Waves; Wiley: New York, NY, USA, 1999; pp. 209–262. [Google Scholar]
- Davidson, R.C. Methods in Nonlinear Plasma Theory; Academic Press: New York, NY, USA, 1972; pp. 54–129. [Google Scholar]
- Alexandrov, A.F.; Bogdankevich, L.S.; Rukhadze, A.A. Principles of Plasma Electrodynamics; Springer: Berlin/Heidelberg, Germany, 1984; pp. 308–309. [Google Scholar]
- Lee, M.-J.; Jung, Y.-D. Ion-driven instabilities of surface dust ion-acoustic waves in bounded plasma devices. Plasma Sources Sci. Technol. 2018, 27, 025010. [Google Scholar] [CrossRef]
- Lee, M.-J.; Takahashi, K.; Jung, Y.-D. Unstable electrostatic surface waves in a turbulent plasma containing streaming ions: Transverse truncation approach. Plasma Sources Sci. Technol. 2019, 29, 015007. [Google Scholar] [CrossRef]
- Aliev, Y.M.; Schlüter, H.; Shivarova, A. Guided-Wave-Produced Plasmas; Springer: Berlin/Heidelberg, Germany, 2000; pp. 49–50. [Google Scholar]
- Miyamoto, K. Plasma Physics for Controlled Fusion; Springer: Berlin/Heidelberg, Germany, 2016; pp. 110–115. [Google Scholar]
- Hasegawa, A. Plasma Instabilities and Nonlinear Effects; Springer: Berlin/Heidelberg, Germany, 1975; pp. 99–106. [Google Scholar]
- Semenov, V.E.; Zharova, N.A.; Anderson, D.; Lisak, M.; Puech, J. Simulations of multipactor in circular waveguides. Phys. Plasmas 2010, 17, 123503. [Google Scholar] [CrossRef]
- Khalil, S.M.; Mousa, N.M. Dispersion characteristics of plasma-filled cylindrical waveguide. J. Theor. Appl. Phys. 2014, 8, 111. [Google Scholar] [CrossRef]
- Girka, I.O.; Girka, O.I.; Thumm, M. Azimuthal surface waves in cylindrical metal waveguides partially filled by magnetoactive plasma: Analysis of energy transfer. Phys. Plasmas 2020, 27, 062108. [Google Scholar] [CrossRef]
- Shokri, B.; Rukhadze, A.A. Electrodynamics of Conducting Dispersive Media; Springer: Cham, Switzerland, 2019; pp. 227–339. [Google Scholar]
- Krall, N.A.; Trivelpiece, A.W. Principles of Plasma Physics; McGraw-Hill: New York, NY, USA, 1973; pp. 173–175. [Google Scholar]
- Zhang, K.-Z.; Xue, J.-K. Streaming instability in bounded three-component quantum plasmas. Phys. Plasmas 2010, 17, 32113. [Google Scholar] [CrossRef]
- Lee, M.-J.; Jung, Y.-D. Characteristics of Nonthermal Dupree Diffusion on Space-Charge Wave in a Kappa Distribution Plasma Column with Turbulent Diffusion. Entropy 2020, 22, 257. [Google Scholar] [CrossRef] [PubMed]
- Wyld, H.W. Mathematical Methods for Physics; Perseus Books: Reading, UK, 1999; pp. 139–141. [Google Scholar]
- Ramazanov, T.S.; Dzhumagulova, K.N.; Gabdullin, M.T. Effective potentials for ion-ion and charge-atom interactions of dense semiclassical plasma. Phys. Plasmas 2010, 17, 42703. [Google Scholar] [CrossRef]
- Akbari-Moghanjoughi, M. Quantized plasmon excitations of electron gas in potential well. Phys. Plasmas 2019, 26, 012104. [Google Scholar] [CrossRef]
- Akbari-Moghanjoughi, M.; Eliasson, B.E. Quantum Faraday excitations in degenerate electron-ion plasma. Phys. Scr. 2019, 95, 045604. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).