Periodic Solutions of Nonlinear Relative Motion Satellites

Abstract

The relative motion of an outline of the rendezvous problem has been studied by assuming that the chief satellite is in circular symmetric orbits. The legitimacy of perturbation techniques and nonlinear relative motion are investigated. The deputy satellite equations of motion with respect to the fixed references at the center of the chief satellite are nonlinear in the general case. We found the periodic solutions of the linear relative motion satellite and for the nonlinear relative motion satellite using the Lindstedt–Poincaré technique. Comparisons among the analytical solutions of linear and nonlinear motions and the obtained solution by the numerical integration of the explicit Euler method for both motions are investigated. We demonstrate that both analytical and numerical solutions of linear motion are symmetric periodic. However, the solutions of nonlinear motion obtained by the Lindstedt–Poincaré technique are periodic and the numerical solutions obtained by integration by using explicit Euler method are non-periodic. Thus, the Lindstedt–Poincaré technique is recommended for designing the periodic solutions. Furthermore, a comparison between linear and nonlinear analytical solutions of relative motion is investigated graphically.

1. Introduction

1.1. Importance of Relative Motion Satellites

Relative motion is considered one of the fundamental problems in orbital mechanics, it has different applications that arise in the literature of astrodynamics for rendezvous and formation of flying satellites. The first idea concerning this problem was explained by the author of [1] in the late 19th century, who proposed analyzing the Moon’s motion. His objective was to establish a more mathematically sound method for developing tables of lunar motion, this was at the time based on “practical astronomy rather than of mathematics” in his talk.

The first practical space of relative motion was in the field of intercept and space rendezvous throughout the late 1950s and extends up to the current time. In the intercept model, a chase satellite is compelled to move in such a way that its orbit intersects the trajectory of the chief satellite at a certain time. In the rendezvous problem the relative velocities of both vehicles must be pushed to zero at the intersection instant; thereby, a docking or berthing procedure or other activities may be carried out.

The authors in [2] analyzed the relative motion within the frame of developing a guidance algorithm for a rendezvous task with an assumption that the chief satellite moves in a circular orbit, and acts as a control center. It sends messages with relative location and velocity data to slave satellites. Based on that data, the satellites perform a docking maneuver and rendezvous by using an on-board propulsion system.

The comprehension of relative motion satellites is substantial for two significant applications of orbital mechanics:

• The space rendezvous problem.
• The formation flight problem.

The first problem investigates the designing of centralization and decentralization algorithms to dock a satellite successfully, for instance, the space shuttle with the International Space Station. These algorithms demand the modeling of relative motion satellites, without needing permanent communication with ground-based stations. Rendezvous orbital dynamics and control is one of the key elements of space flight technology for operating space rendezvous and docking missions. Rendezvous demands a specific congruent of the orbital velocities and position vectors of the two vehicles, permitting them to stay at a constant separation during orbital station-keeping. It may or may not be followed by docking or berthing, procedures which bring the spacecraft into physical connection and generate a link between them. The same rendezvous method could be used for a spacecraft “landing” on a natural celestial body with a weak gravitational field, for example, landing on one of the Martian moons will demand the same conveniency of orbital velocities, followed by a “descent” that shares some similarities with docking.

The second problem is related to the formation of a satellite system, where the dynamics of the system are exploited to place a number of satellites in space. Formation of satellites is a novel concept that distributes a large spacecraft function among several small satellites, which are less expensive and cooperative. Most applications to relative motion are in the formation satellites, which have a considerable significance, because the use of a large number of satellites with low impact satellites running, in a concrete style, could introduce a better outcome than a single high implementation satellite. Furthermore, these formations do not require a big cost, which means a great opportunity for space mission success with more resiliency. Satellite formations have good benefits for Earth observation of space missions, where the group distribution of low resolution devices, operating in conjunction with each other, may provide a higher overall information quality than a single high resolution device.

1.2. Mathematical Models of Relative Motion Satellites

The relative motion between two satellites is described by several mathematical models [3,4,5,6]. The “Hill–Clohessy–Wiltshire model (HCW)” is as a classical approach described by a set of linearized, time-invariant ordinary differential equations. However, this model assumes a circular chief orbit and it is valid only for small initial separations between the satellites.

An assumption of an elliptical shape of the chief satellite orbit results in time-varying differential equations. In this work such a model is represented by the Tschauner–Hempel (TH) equations. However, since the applicability of this model is also limited to small initial separations between the satellites, this investigation deploys it only for comparative purposes.

In cases where a chief satellite (target or passive vehicle) is moving in a circular orbit, the orbital relative motion can be described using HCW equations [2]. A principal assumption for the application of HCW equations is a distance of separation between chief and deputy (chase or active vehicle) satellites of less than 1 km.

The authors of [7] were the first to find a closed-form solution for linearized relative motion within the frame of elliptic orbits. The authors of [8] found a singularity in Lawden’s solution and then constructed a state-transition matrix that depends explicitly on the true and the eccentric anomaly, overcoming the singularity. We find a closed-form solution for a linearized relative motion within the frame of elliptic orbits in [7] for the first time. The author of [8] found a singularity in Lawden’s solution. Afterwards, they proposed a new state-transition matrix without a singularity by explicitly using the true and the eccentric anomaly data. They derived the state transition matrix (STM) of the (TH) equations for orbits with small eccentricity, based mainly on the solutions of the HCW equations using a perturbation theory. In the framework of improving the obtained solution, approximation solutions of the second–order relative motion equations set in spherical coordinates are constructed [9].

Several versions of the relative motion dynamics have been developed to involve the perturbations effect [10,11,12,13]. The inhomogeneous gravitational field generated by the presence of the non-sphericity of objects, such as the Earth’s oblateness, is based on an assumption that the gravitational field is a sum of zonal harmonics coefficients; the authors of [10] derived a set of relative dynamics time-variant equations under the effect of the zonal harmonic parameter. An analytical solution of relative motion subject to Lorentz-force perturbations is constructed in [14]. Within the frame of developing the analysis of relative motion using state transition, matrices for the elliptical case are found, by the authors in [15,16], to be under the perturbation effect.

Furthermore, an outstanding piece of work studied the reformulation of relative motion based on non-linear system dynamics; see [17]. Another excellent piece of work proposed to analyze relative motion dynamics, control techniques and specific applications for formation flying, deployment, station keeping, and reconfiguration; see [18,19,20,21,22].

The aim of the proposed paper is to find the Periodic solutions of nonlinear relative motion using the perturbation technique of the Lindstedt–Poincaré method, which enable us to remove the secular terms, which will be growth with increasing time and will go to infinity with increasing time to infinity. However, there are some numerical methods, which can be used to estimate such solutions; for example: The Verrlet method, the step size control algorithm and the explicit Runge–Kutta method; for details, comparisons and effective methods, see [23,24]. However, we emphasize that the numerical methods are not used to verify the analytical solutions in most cases, and vice versa. In addition, there is no full warranty for convergence of numerical solutions in most cases. Thus, we are interested to find the periodic solution of non-linear relative motion, which is more realistic in practical applications by using the perturbation technique of Lindstedt–Poincaré.

2. Formulation of Motion Model

We consider a set of two satellites model, the first is called target satellite (or chief or passive vehicle) and the second is called chaser (or deputy or active vehicle). In general, this model is implemented to accomplish some space mission such as space rendezvous. The mission between two space crafts or satellites is successful when the two satellites have the same velocity and position vectors at a certain time. In the initiates of rendezvous time the two parts in a rendezvous sequence are:

• Phasing of maneuvers to accomplish a rendezvous in the timing sequence, which will bring the two satellites into close proximity.
• Maneuvers of finalizing rendezvous that involve the relative motion between the two satellites for rendezvous and docking.

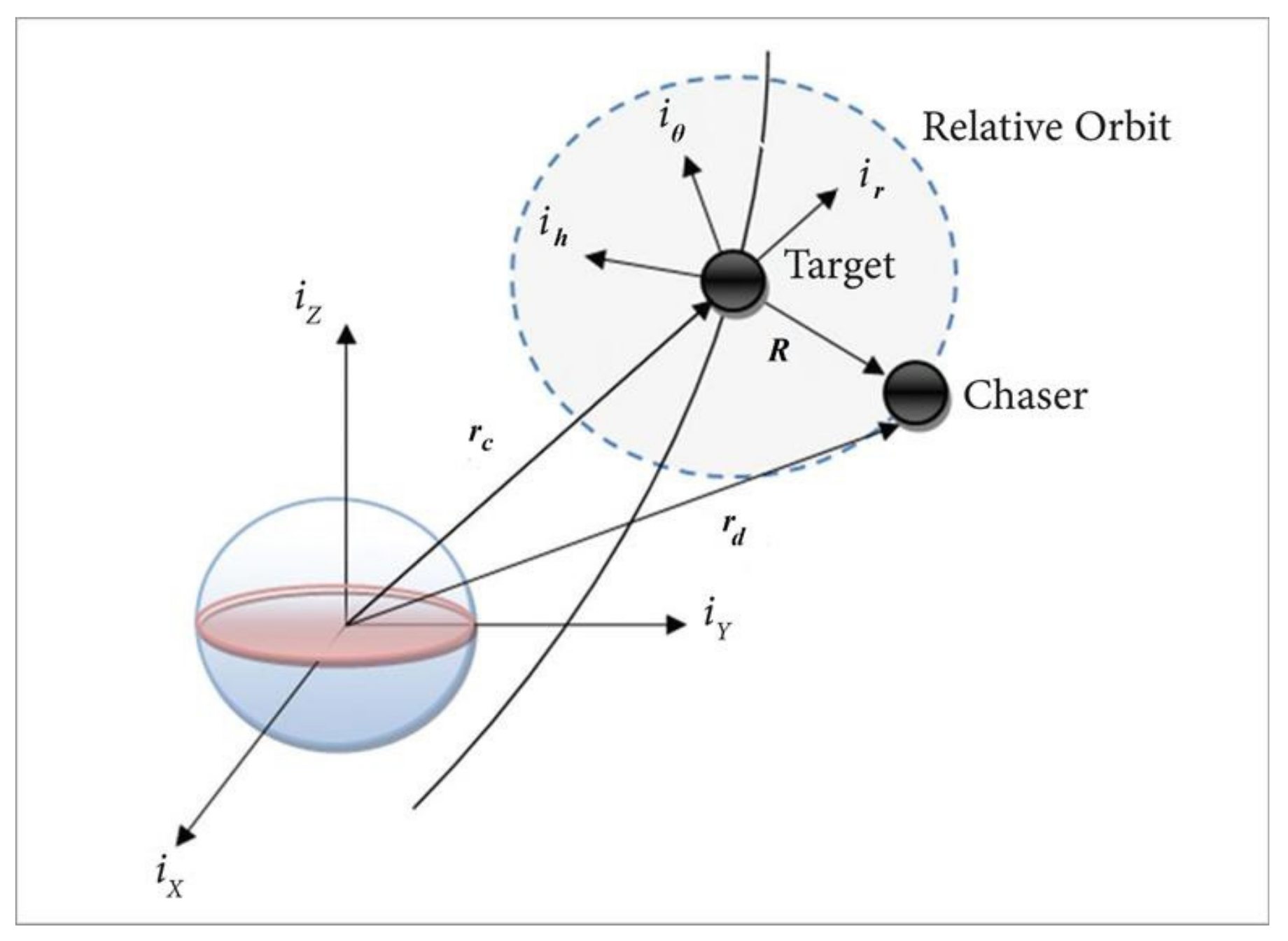
Now we will assume that the inertial references frame with origin, which coincides with the center of the main body, say Earth’s center; the orthogonal unit vector is denoted by $\{i_x,i_y,i_z\}$. The vector $i_x$ in the direction of the equinoxes and the vectors $i_y$ is perpendicular to it, while $i_z$ passes through the North Pole. To describe a relative motion satellite in Local-Vertical-Local-Horizontal (LVLH) coordinates, we proposed that the orientation of these frame by the unit vector triad $\{i_r,i_{\theta },i_h\}$, where the vector $i_r$ lies in the chief radial direction, $i_h$ lies in the direction of the chief angular momentum, and $i_{\theta }$ completes the right-handed orthogonal triad, such that $i_{\theta }=i_h\wedge i_r$; see Figure 1.

According to Figure 1, the deputy satellite relative position vector in LVLH coordinates can be written as:

$$\mathit{R}=\xi i_r+\vartheta i_{\theta }+\zeta i_h,$$

(1)

where $\xi$, $\zeta$, and $\vartheta$ are the components of the relative position vector along the radial, long track, and out of plane, respectively.

Since ${\mathit{r}}_d={\mathit{r}}_c+\mathit{r}$, then

$${\mathit{r}}_d=(r+\xi )i_r+\vartheta i_{\theta }+\zeta i_h,$$

where ${\mathit{r}}_c=r{i}_r$ represents the current radius of the chief’s satellite orbit. The LVLH frame rotation with angular velocity $\mathit{\omega }$ is given by

$$\mathit{\omega }={\omega }_r{i}_r+{\omega }_{\theta }{i}_{\theta }+{\omega }_h{i}_h,$$

where ${\omega }_r={\omega }_{\theta }=0$ and $\mathit{\omega }={\omega }_h{i}_h$, while the attached frame rotates with the angular velocity ${\omega }_h=\dot{\theta }=\dot{f}$. We have to note that $\theta =\Omega +f$ in which $\Omega$ and f are the argument of perigee and the true anomaly, respectively, within the frame of two-body motion. The angular momentum magnitude of the chief satellite is expressed by

$$\begin{array}{cc}\hfill h=& r^2\dot{\theta },\hfill \\ \hfill \ddot{\theta }=& -2{\displaystyle \frac{\dot{r}\dot{\theta }}{r}},\hfill \end{array}$$

where r is the trajectory of the chief (target) satellite, which may be circular or elliptical. On the other hand, the expression of the chief’s true anomaly rate $\dot{\theta }$ can be written in terms of a semi-latus rectum as

$$\dot{\theta }=\sqrt{{\displaystyle \frac{\mu p}{r^4}}},$$

wherein the elliptical case $p=a(1-e^2)$, a are the semi-major axes and e is the eccentricity, $\mu$ is the gravitational constant and $r=p/(1+ecosf)$. The angular velocity and the acceleration of the the LVLH reference frame are given by

$$\begin{array}{cc}\hfill \mathit{\omega }=& \dot{\theta }{i}_h={\displaystyle \frac{h}{r^2}}{i}_h,\hfill \\ \hfill \dot{\mathit{\omega }}=& \ddot{\theta }{i}_h=-2{\displaystyle \frac{\dot{r}\dot{\theta }}{r}}{i}_h.\hfill \end{array}$$

(2)

Now, the general vectorial equations that model the relative motion in the LVLH reference frame are

$$\begin{array}{c}\hfill \ddot{\mathit{R}}+2\mathit{\omega }\times \dot{\mathit{R}}+\dot{\mathit{\omega }}\times \mathit{R}+\mathit{\omega }\times (\mathit{\omega }\times \mathit{R})=\mathit{T},\end{array}$$

(3)

where $\mathit{T}$ is the sum of total external forces acting on the deputy and chief, respectively; $(.)$ and $(..)$ denote the first and second derivative with respect to time.

Substituting Equations (1) and (2) into Equation (3), we obtain

$$\left(\ddot{\xi }-2\ddot{\theta }\vartheta -\dot{\theta }\dot{\vartheta }-{\dot{\theta }}^2\xi \right)i_r+\left(\ddot{\vartheta }+\ddot{\theta }\xi +2\dot{\theta }\dot{\xi }-{\dot{\theta }}^2\vartheta \right)i_{\theta }+\ddot{\zeta }{i}_h=\mathit{T},$$

(4)

Now we can write the right-hand side of Equation (4) in the form

$$\mathit{T}={\mathit{T}}_d-{\mathit{T}}_c,$$

where ${\mathit{T}}_d$ is the external forces acting on the deputy and ${\mathit{T}}_c$ is the external forces acting on the chief satellite, which can be written in the case of the gravitational field being generated by a spherical object, such as

$$\begin{array}{c}\hfill {\mathit{T}}_d=-\mu \frac{{\mathit{R}}_d}{r_d^3},\\ \hfill {\mathit{T}}_c=-\mu \frac{{\mathit{R}}_c}{r_c^3},\end{array}$$

Hence,

$$\mathit{T}=-\mu {\displaystyle \frac{(r+\xi )i_r+\vartheta i_{\theta }+\zeta i_h}{{\left[{(r+\xi )}^2+{\vartheta }^2+{\zeta }^2\right]}^{3/2}}}+\mu {\displaystyle \frac{1}{r^2}}{i}_r,$$

(5)

Substitution Equation (5) into Equation (4); then, the vector form or relative motion equations will be controlled by

$$\begin{array}{cc}\hfill \left(\ddot{\xi }-2\ddot{\theta }\vartheta -\dot{\theta }\dot{\vartheta }-{\dot{\theta }}^2\xi \right)i_r& +\left(\ddot{\vartheta }+\ddot{\theta }\xi +2\dot{\theta }\dot{\xi }-{\dot{\theta }}^2\vartheta \right)i_{\theta }\hfill \\ \hfill & +\ddot{\zeta }{i}_h=-\mu \frac{(r+\xi )i_r+\vartheta i_{\theta }+\zeta i_h}{{\left[{(r+\xi )}^2+{\vartheta }^2+{\zeta }^2\right]}^{3/2}}+\mu {\displaystyle \frac{1}{r^2}}{i}_r,\hfill \end{array}$$

(6)

The vector Equation (6) can be degraded to

$$\begin{array}{cc}\hfill \ddot{\xi }-2\dot{\theta }\dot{\vartheta }-{\dot{\theta }}^2\xi -\ddot{\theta }\vartheta =& -{\displaystyle \frac{\mu (r+\xi )}{{\left[{(r+\xi )}^2+{\vartheta }^2+{\zeta }^2\right]}^{3/2}}}+{\displaystyle \frac{\mu }{r^2}},\hfill \\ \hfill \ddot{\vartheta }+2\dot{\theta }\dot{\xi }-{\dot{\theta }}^2\vartheta +\ddot{\theta }\xi =& -{\displaystyle \frac{\mu \vartheta }{{\left[{(r+\xi )}^2+{\vartheta }^2+{\zeta }^2\right]}^{3/2}}},\hfill \\ \hfill \ddot{\zeta }=& -{\displaystyle \frac{\mu \zeta }{{\left[{(r+\xi )}^2+{\vartheta }^2+{\zeta }^2\right]}^{3/2}}}.\hfill \end{array}$$

(7)

Equation (7) represents the general equations of the satellite relative motion in LVLH coordinates.

2.1. General Circular Relative Motion Satellites

Now, we denote $v_c$ and $v_d$ as the potential functions for gravitational forces ${\mathit{T}}_c$ and ${\mathit{T}}_d$, acting on the chief and deputy satellite, respectively; hence,

$$\begin{array}{ccc}\hfill v_c& =& -{\displaystyle \frac{\mu }{r}},\hfill \\ \hfill v_d& =& -{\displaystyle \frac{\mu }{r}}{\left(1+{\displaystyle \frac{R^2}{r^2}}+2{\displaystyle \frac{\xi }{r}}\right)}^{-1/2},\hfill \end{array}$$

(8)

Note that $(\xi /r)=(\xi /R).(R/r)$; Equation (8) is a generating function for Legendre polynomials with argument $-(\xi /R)$; consequently,

$$\begin{array}{c}\hfill v_d=-{\displaystyle \frac{\mu }{r}}\sum _{n=0}^{\infty }{(-1)}^n{\left({\displaystyle \frac{R}{r}}\right)}^n{P}_n\left(\xi /R\right),\end{array}$$

where $P_n$ is the Legendre polynomial with degree n, where

$$\begin{array}{ccc}& & P_0\left(\xi /R\right)=1,\hfill \\ & & P_1\left(\xi /R\right)=\frac{\xi }{R},\hfill \\ & & P_2\left(\xi /R\right)=\frac{1}{2}\left({\left(\frac{\xi }{R}\right)}^2-1\right),\hfill \end{array}$$

Then,

$$\begin{array}{c}\hfill v_d=-\frac{\mu }{R}\left[1-\frac{\xi }{r}+\frac{(2{\xi }^2-{\vartheta }^2-{\zeta }^2)}{2r^2}\right]+v_h,\end{array}$$

where $v_h$ is the higher-order of a Legendre polynomial given by

$$\begin{array}{c}\hfill v_h=-\frac{\mu }{r}\sum _{n=3}^{\infty }{(-1)}^n{\left({\displaystyle \frac{R}{r}}\right)}^n{P}_n\left(\xi /R\right).\end{array}$$

Then the total external forces can be rewritten as

$$\begin{array}{c}\hfill \mathit{T}=-\Delta v,\end{array}$$

where

$$\begin{array}{c}\hfill \Delta v=-\left(\Delta v_d-\Delta v_c\right).\end{array}$$

Since $\Delta v_d$ is the gravitational acceleration acting on the deputy and $\Delta v_c$ is the gravitational acceleration acting on the chief’s satellite, while $\Delta v$ is the total relative gravitational acceleration, then

$$\Delta v=\left(-{\displaystyle \frac{2\mu \xi }{r^3}}+{\displaystyle \frac{\partial v_h}{\partial \xi }}\right)i_r+\left({\displaystyle \frac{\mu \vartheta }{r^3}}+{\displaystyle \frac{\partial v_h}{\partial \vartheta }}\right)i_{\theta }+\left({\displaystyle \frac{\mu \zeta }{r^3}}+{\displaystyle \frac{\partial v_h}{\partial \zeta }}\right)i_h,$$

(9)

and

$$\mathit{T}=\left(\frac{2\mu \xi }{r^3}-{\displaystyle \frac{\partial v_h}{\partial \xi }}\right)i_r-\left({\displaystyle \frac{\mu \vartheta }{r^3}}+{\displaystyle \frac{\partial v_h}{\partial \vartheta }}\right)i_{\theta }-\left({\displaystyle \frac{\mu \zeta }{r^3}}+{\displaystyle \frac{\partial v_h}{\partial \zeta }}\right)i_h,$$

(10)

Utilizing Equations (9) and (10) with Equation (4), the vector equation of relative motion can be rewritten as

$$\begin{array}{cc}\hfill & \left(\ddot{\xi }-2\ddot{\theta }\vartheta -\dot{\theta }\dot{\vartheta }-{\dot{\theta }}^2\xi \right)i_r+\left(\ddot{\vartheta }+\ddot{\theta }\xi +2\dot{\theta }\dot{\xi }-{\dot{\theta }}^2\vartheta \right)i_{\theta }+\ddot{\zeta }{i}_h\hfill \\ \hfill & =\left({\displaystyle \frac{2\mu \xi }{r^3}}-{\displaystyle \frac{\partial v_h}{\partial \xi }}\right)i_r+\left(-\frac{\mu \vartheta }{r^3}-\frac{\partial v_h}{\partial \vartheta }\right)i_{\theta }+\left(-{\displaystyle \frac{\mu \zeta }{r^3}}-{\displaystyle \frac{\partial v_h}{\partial \zeta }}\right)i_h,\hfill \end{array}$$

(11)

Hence, Equation (11) can be written as three differential equations of second order

$$\begin{array}{cc}\hfill \ddot{\xi }-2\dot{\theta }\dot{\vartheta }-\left({\dot{\theta }}^2+\frac{2\mu }{r^3}\right)\xi -\ddot{\theta }\vartheta =& -{\displaystyle \frac{\partial v_h}{\partial \xi }},\hfill \\ \hfill \ddot{\vartheta }+2\dot{\theta }\dot{\xi }-\left({\dot{\theta }}^2-\frac{\mu }{r^3}\right)\vartheta +\ddot{\theta }\xi =& -{\displaystyle \frac{\partial v_h}{\partial \vartheta }},\hfill \\ \hfill \ddot{\zeta }+\frac{\mu \zeta }{r^3}=& -{\displaystyle \frac{\partial v_h}{\partial \zeta }}.\hfill \end{array}$$

(12)

Equation (12) represents the general dynamical system of the relative motion satellite. However, we have to observe that the quantities in the right-hand sides, $\partial v_h/\partial \xi ,\partial v_h/\partial \vartheta ,\partial v_h/\partial \zeta$, represent the components of perturbing gravitational accelerations, which are considered the main contribution for higher order of nonlinearity to a dynamical system of relative motion.

2.2. Linear Circular Relative Motion Satellites

In the case where the chief’s orbit is moving in circular orbits, then $r=a$ and $\dot{\theta }=n$ are constants. Thereby, the rotation frame with these properties is referred to as Hill’s frame and rotates with angular velocity $n=\sqrt{\mu /a^3}$, and the resulting equations are referred to as HCW equations, as in [2]. In addition, if the perturbing acceleration or the higher order on nonlinearity terms ($v_h=0$) are neglected. Then the linearized relative motion equations will be governed by

$$\begin{array}{c}\hfill \ddot{\xi }-2n\dot{\vartheta }-3n^2\xi =0,\\ \hfill \ddot{\vartheta }+2n\dot{\xi }=0,\\ \hfill \ddot{\zeta }+n^2\zeta =0.\end{array}$$

Let $\xi =x$, $\vartheta =y$, $\zeta =z$; thereby, the above equations can be written as

$$\begin{array}{cc}\hfill \ddot{x}-2n\dot{y}-3n^{2}x& =0,\hfill \\ \hfill \ddot{y}+2n\dot{x}& =0,\hfill \\ \hfill \ddot{z}+n^{2}z& =0.\hfill \end{array}$$

(13)

The above dynamical system is famous and is called the Hill–Clohessy–Wiltshire equations, and represents the linearity of relative satellite motion. Furthermore, the dynamical system of relative motion (HCW) is invariant under the symmetry $(x,y,z)\to (-x,-y,-z)$.

3. Solutions of HCW Equations

In order to construct the solutions of the dynamical system which represent the linear relative motion satellite, we will assume that the deputy satellite starts its motion under the following set of the initial conditions

$$\begin{array}{c}\hfill x(0)=x_0^0,\dot{x}(0)={\dot{x}}_0^0,\\ \hfill y(0)=y_0^0,\dot{y}(0)={\dot{y}}_0^0,\\ \hfill z(0)=z_0^0,\dot{z}(0)={\dot{z}}_0^0,\end{array}$$

(14)

Thereby, after integration of the second equation in System (13), we obtain

$$\begin{array}{c}\hfill \dot{y}+2nx=X_0,\end{array}$$

(15)

where $X_0$ is a constant which can be determined from the initial conditions, so one obtains

$$\begin{array}{c}\hfill X_0={\dot{y}}_0^0+2n{x}_0^0,\end{array}$$

and Equation (15) will take the following form

$$\begin{array}{c}\hfill \dot{y}=X_0-2nx.\end{array}$$

(16)

Substituting $\dot{y}$ into the first equation in System (13), we get

$$\begin{array}{c}\hfill \ddot{x}+n^2\left(x-{\displaystyle \frac{2X_0}{n}}\right)=0.\end{array}$$

(17)

Let $\psi =x-2X_0/n$, then $d\psi /dt=dX/dt$ and $d^2\psi /d{t}^2=d^{2}X/d{t}^2$ and, the Equation (17) becomes

$$\begin{array}{c}\hfill {\displaystyle \frac{d^2\psi }{d{t}^2}}+n^2\psi =0,\end{array}$$

(18)

Hence, Equation (18) has the solution

$$\begin{array}{c}\hfill \psi =Xsin[nt+{\theta }_0].\end{array}$$

Then the final form solution is

$$\begin{array}{c}\hfill x=Xsin[nt+{\theta }_0]+\frac{2}{n}\left({\dot{y}}_0^0+2n{x}_0^0\right).\end{array}$$

(19)

Substituting Equation (19) into Equation (16) and integrating it, we get

$$\begin{array}{c}\hfill y=2Xcos[nt+{\theta }_0]-3\left({\dot{y}}_0^0+2n{x}_0^0\right)t+Y_0,\end{array}$$

(20)

where $Y_0$ the constant of the integration.

To complete our steps, we have to integrate the third equation in System (13), which represents the out-plane motion; hence, we get

$$\begin{array}{c}\hfill z=Zsin(nt+{\phi }_0).\end{array}$$

(21)

Using the obtained solutions of Equations (19)–(21), the solutions of System (13) are summarized in the following formulas

$$\begin{array}{c}x=Xsin[nt+{\theta }_0]+{\displaystyle \frac{2}{n}}\left({\dot{y}}_0^0+2n{x}_0^0\right),\hfill \\ y=2Xcos[nt+{\theta }_0]-3\left({\dot{y}}_0^0+2n{x}_0^0\right)t+Y_0,\hfill \\ z=Zsin(nt+{\phi }_0),\hfill \end{array}$$

(22)

where $X,Y,Z,{\theta }_0,$ and ${\phi }_0$ are arbitrary constants that must match the initial conditions.

Here, we observe that the second formula in Solutions (22) contains an unbounded term, which will grow to infinity with increasing time. To get bounded solutions, in particular, periodic solutions, the coefficient of the unbounded term must equal zero; these will give an additional condition to get periodic and bounded solutions; thereby, we will obtain the new conditions on the initial conditions as

$$\begin{array}{c}\hfill {\dot{y}}_0^0+2n{x}_0^0=0.\end{array}$$

(23)

So we rewrite the periodic solutions of System (13) in the following formulas

$$\begin{array}{ccc}& & x=Xsin[nt+{\theta }_0],\hfill \\ & & y=Y_0+2Xcos[nt+{\theta }_0],\hfill \\ & & z=Zsin(nt+{\phi }_0).\hfill \end{array}$$

(24)

Applying the first derivative to Equations (24), we obtain the relative velocities in the form

$$\begin{array}{ccc}& & \dot{x}=nXcos[nt+{\theta }_0],\hfill \\ & & \dot{y}=-2nXsin[nt+{\theta }_0],\hfill \\ & & \dot{z}=nZcos(nt+{\phi }_0),\hfill \end{array}$$

(25)

If we apply the initial conditions on Equation (24) and the condition in Equation (23), then the constants of integration can be determined by

$$\begin{array}{ccc}& & Y_0=y_0^0-\frac{2}{n}{\dot{x}}_0^0,\hfill \\ & & X^2={\left(x_0^0\right)}^2+{\displaystyle \frac{1}{n^2}}{\left({\dot{x}}_0^0\right)}^2,\hfill \\ & & Z^2={\left(z_0^0\right)}^2+{\displaystyle \frac{1}{n^2}}{\left({\dot{z}}_0^0\right)}^2,\hfill \end{array}$$

(26)

and

$$\begin{array}{cc}\hfill & tan{\theta }_0={\displaystyle \frac{n{x}_0^0}{{\dot{x}}_0^0}},\hfill \\ \hfill & tan{\phi }_0={\displaystyle \frac{n{z}_0^0}{{\dot{z}}_0^0}}.\hfill \end{array}$$

(27)

Equations (24) and (25) represent the relative positions and velocities of the chaser satellite for space rendezvous within the framework of linearized motion.

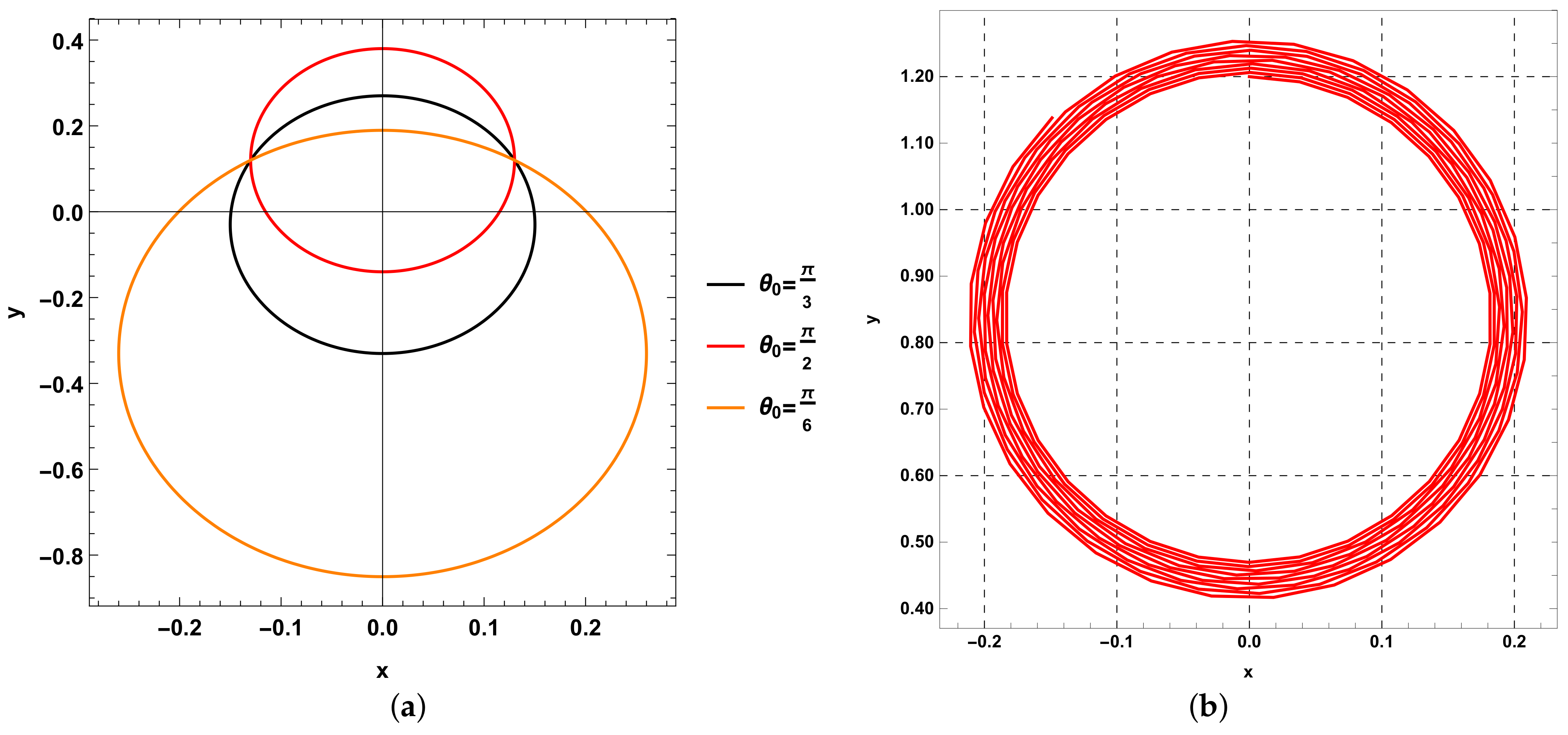
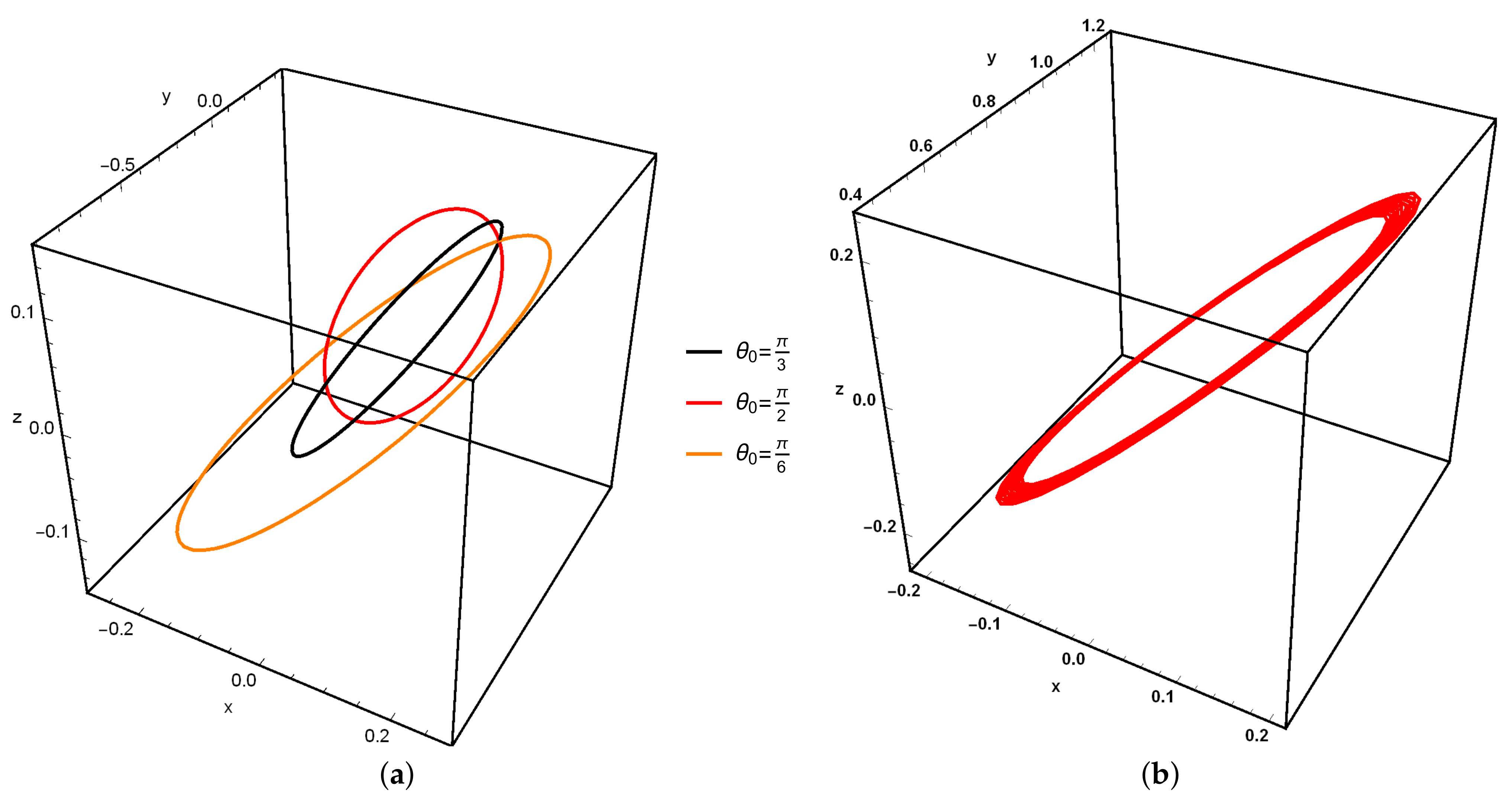
With the help of Equations (24)–(27), the initial amplitude of the chaser satellite for space rendezvous, i.e., $(x_0^0,y_0^0,z_0^0)$ is taken as $(0.13,0.12,0.10)$, with different values of phase angle. The projection of the periodic solution in the xy-plane is shown in Figure 2, whereas the orbit in three dimensions is shown in Figure 3 at different values of the phase angle.

It is clear from Figure 2a that the analytical solution of linear relative motion in two dimensions is periodic, and the obtained solution by a numerical integration of the explicit Euler method using step size ${10}^{-3}$ at a set of initial condition $\left(x_0^0,y_0^0,{\dot{x}}_0^0,{\dot{y}}_0^0\right)$ as $\left(0,1.2,1.0,0\right)$ is also periodic; this solution is shown in Figure 2b. In addition, the two solutions are symmetric due to the y-axis $(x=0)$.

The linear motion in three dimensions is also periodic due two both solutions. We remark that both analytical and numerical solutions of linear relative motion in three dimensions are also periodic. The analytical solution is given in Figure 3a, while the solution by a numerical integration of the explicit Euler method using step size ${10}^{-3}$ at a set of initial condition $\left(x_0^0,y_0^0,{\dot{x}}_0^0,{\dot{y}}_0^0\right)$ as $\left(0,1.2,1.0,0\right)$ is given in Figure 3b.

Nonlinear Circular Relative Motion Satellites

In the case of considering the perturbed potential $v_h\ne 0$, and keeping the nonlinearity up to second order terms, the relative motion satellite equations of System (12) are approximated to the following equations

$$\begin{array}{cc}\hfill \ddot{\xi }-2n\dot{\vartheta }-3n^2\xi =& {\displaystyle \frac{3n^2}{2r}}\left({\vartheta }^2+{\zeta }^2-2{\xi }^2\right),\hfill \\ \hfill \ddot{\vartheta }+2n^2\dot{\xi }=& {\displaystyle \frac{3n^2\xi \vartheta }{r}},\hfill \\ \hfill \ddot{\zeta }+n^2\zeta =& {\displaystyle \frac{3n^2\xi \zeta }{r}}.\hfill \end{array}$$

(28)

The above dynamical system consists of the three second-order differential equations with second degree, which represent the relative motion of the deputy satellite.

Now we intend to find the periodic solutions of these equations to find the relative position and velocity of the deputy satellite to accomplish space rendezvous. The solutions of these equations will be generalized or extended for the linear solutions; then, we have to find the solutions under the previous conditions of linear relative motion. Unfortunately, there are no exact analytical solutions for these equations, and the exact solutions are not possible. Thereby, we must introduce techniques or perturbation methods, which can be used to evaluate approximate or semi-analytical solutions; in particular, we must construct periodic solutions. So, the next section will be devoted to analysis of a perturbation technique, which enables us to find an appropriate approximated analytical solution to perform a space rendezvous mission.

4. Periodic Solution of Nonlinear Relative Motion Satellites

This section is devoted to constructing the periodic solutions of the nonlinear relative motion satellite. From physical point of view, it is sufficient to find the solutions of the dynamical system within the frame of second degree or third in maximum. This view can be applied for the model of relative motion satellite, because the relative distance (distance between chief and deputy satellites) is very small compared to the initial position of the target satellite.

4.1. Legitimacy of Perturbation Techniques

The classical perturbation theory, which is called the straightforward expansion technique, the Lindstedt–poincaré method, and the multiple scales method are used when the dynamical systems are either weakly nonlinear or weakly non-autonomous; this means that the effects of either nonlinearity or non-autonomy are very small. Alternatively, the dynamical systems with these properties can be considered either linear or quasi-linear. In most cases, the systems of differential equations have linear expressions and small nonlinear or non-autonomous expressions in such a way that they are separated from each other.

In the context of either weak nonlinearity or weak non-autonomy, more approximations may still be required by finding a parameter in the dynamical system, which can be used as a very small perturbation effect, but its value will be replaced by one at the end. This technique is reasonable and accepted when the terms of the dynamical system are quasi-linear or small in themselves. The obtained parameters in this case are called “place keeping parameters”.

4.2. Legitimacy of Relative Motion Equations

In line with the reasons outlined in the previous subsection, we can neither apply the multiple scales technique nor the Lindstedt–Poincaré method to System (28). Thereby, we will use the place keeping parameters method, after carrying out the relative equations of motion in dimensionless variables.

In order to set the equations in dimensionless variables, we assume that $(\xi ,\vartheta ,\zeta )=r(x,y,z)$; then, System (28) can be written as

$$\begin{array}{cc}\hfill \ddot{x}-2n\dot{y}-3n^{2}x=& {\displaystyle \frac{3}{2}}{n}^2(y^2+z^2-2x^2),\hfill \\ \hfill \ddot{y}+2n\dot{x}=& 3n^{2}xy,\hfill \\ \hfill \ddot{z}+n^{2}z=& 3n^{2}xz.\hfill \end{array}$$

(29)

Since $R_0<<r$, we can write $ϵ=\frac{R_0}{r}<<1$, where $R_0$ is the measure of relative orbit size. Regarding this idea, we can use the place keeping parameters method, and replace the coordinate $(x,y,z)$ by $(ϵx,ϵy,ϵz)$. Then System (29) can be written as

$$\begin{array}{cc}\hfill \ddot{x}-2n\dot{y}-3n^{2}x=& {\displaystyle \frac{3}{2}}{n}^2ϵ(y^2+z^2-2x^2),\hfill \\ \hfill \ddot{y}+2n\dot{x}=& 3ϵn^{2}xy,\hfill \\ \hfill \ddot{z}+n^{2}z=& 3ϵn^{2}xz.\hfill \end{array}$$

(30)

The above equations represent the nonlinear relative motion satellite in dimensionless variables, which are convenient for applying some perturbation techniques, such as multiple scales technique [25,26,27] and KBM methods or Lindstedt–Poincaré [28,29,30,31]. However, we will examine the provided solution by the latter method with the initial conditions of the linear relative motion satellite; these conditions are describe in Equation (14).

5. Periodic Solutions by the Lindstedt–Poincar é Technique

Now we will apply the Lindstedt–Poincaré technique on the relative satellite motion to find the periodic solution of the equations of motion of the second degree, say System (30). For simplicity, we suppose that $\theta =nt$; then, System (30) can be written in the form

$$\begin{array}{cc}\hfill {\displaystyle \frac{d^{2}x}{d{\theta }^2}}-2{\displaystyle \frac{dy}{d\theta }}-3x=& {\displaystyle \frac{3}{2}}ϵ(y^2+z^2-2x^2),\hfill \\ \hfill {\displaystyle \frac{d^{2}y}{d{\theta }^2}}+2{\displaystyle \frac{dx}{d\theta }}=& 3ϵxy,\hfill \\ \hfill {\displaystyle \frac{d^{2}z}{d{\theta }^2}}+z=& 3ϵxz.\hfill \end{array}$$

(31)

To account for the nonlinear dependence of the frequency, we will introduce the stretch variable, $\tau =\omega \theta$; we denote $d\Gamma /d\tau ={\Gamma }^{″}$ and $d^2\Gamma /d{\tau }^2={\Gamma }^{″}$; then, System (31) can be written in the form

$$\begin{array}{cc}\hfill {\omega }^2{x}^{″}-2\omega y^{\prime }-3x=& {\displaystyle \frac{3}{2}}ϵ(y^2+z^2-2x^2),\hfill \\ \hfill {\omega }^2{y}^{″}+2\omega x^{\prime }=& 3ϵxy,\hfill \\ \hfill {\omega }^2{z}^{″}+z=& 3ϵxz.\hfill \end{array}$$

(32)

Now we look for approximated solutions in the form of a power series as

$$\begin{array}{cc}\hfill & x(\tau ,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{x}_n(\tau ),\hfill \\ \hfill & y(\tau ,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{y}_n(\tau ),\hfill \\ \hfill & z(\tau ,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{z}_n(\tau ),\hfill \end{array}$$

(33)

and

$$\begin{array}{c}\hfill \omega (ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{\omega }_n,{\omega }_0=1,\end{array}$$

(34)

The initial conditions of position components can be rewritten in the form

$$\begin{array}{cc}\hfill & x(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{x}_n(0)=x_0^0,\hfill \\ \hfill & y(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{y}_n(0)=y_0^0,\hfill \\ \hfill & z(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{z}_n(0)=z_0^0,\hfill \end{array}$$

(35)

while the initial conditions of velocity components can also be rewritten in the form

$$\begin{array}{cc}\hfill & x^{\prime }(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{x}_n^{\prime }(0)=x_0^{\prime 0},\hfill \\ \hfill & y^{\prime }(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{y}_n^{\prime }(0)=y_0^{\prime 0},\hfill \\ \hfill & z^{\prime }(0,ϵ)=\sum _{n=0}^{\infty }{ϵ}^n{z}_n^{\prime }(0)=z_0^{\prime 0}.\hfill \end{array}$$

(36)

Substituting Equation (33) into Equation (32) with the help of Equation (34) and keeping the terms up to first order in $ϵ$, we obtain

$$\begin{array}{cc}\hfill x_0^{″}-2y_0^{\prime }-3x_0+ϵ\left[x_1^{\prime \prime }-2y_1^{\prime }-3x_1+2{\omega }_1{x}_0^{\prime \prime }\left(-2{\omega }_1{y}_0^{\prime }-\frac{3}{2}(y_0^2+z_0^2-2x_0^2)\right)\right]=& 0,\hfill \\ \hfill y_0^{″}+2x_0^{\prime }+ϵ\left[y_1^{\prime \prime }+2x_1^{\prime }+2{\omega }_1{y}_0^{\prime \prime }+2{\omega }_1{x}_0^{\prime }-3x_0{y}_0\right]=& 0,\hfill \\ \hfill z_0^{″}+z_0+ϵ\left[z_1^{\prime \prime }+z_1+2ϵ{\omega }_1{Z}_0^{\prime \prime }-3x_0{z}_0\right]=& 0\hfill \end{array}$$

(37)

where the frequency is

$$\begin{array}{c}\hfill \omega (ϵ)=1+ϵ{\omega }_1,\end{array}$$

The set of initial conditions in Equations (35) and (36) may be rewritten as

$$\begin{array}{cc}\hfill & x(0,ϵ)=x_0(0)+ϵx_1(0)=x_0^0,\hfill \\ \hfill & y(0,ϵ)=y_0(0)+ϵy_1(0)=y_0^0,\hfill \\ \hfill & z(0,ϵ)=z_0(0)+ϵz_1(0)=z_0^0,\hfill \end{array}$$

(38)

and

$$\begin{array}{cc}\hfill & x^{\prime }(0,ϵ)=x_0^{\prime }(0)+ϵx_1^{\prime }(0)=x_0^0,\hfill \\ \hfill & y^{\prime }(0,ϵ)=y_0^{\prime }(0)+ϵy_1^{\prime }(0)=y_0^0,\hfill \\ \hfill & z^{\prime }(0,ϵ)=z_0^{\prime }(0)+ϵz_1^{\prime }(0)=z_0^0,\hfill \end{array}$$

(39)

Equating each of the coefficients of $ϵ$ that have the same power in System (37), using Conditions (38) and (39), we get the unperturbed equations system in the form

$$\begin{array}{cc}\hfill x_0^{″}-2y_0^{\prime }-3x_0=& 0,\hfill \\ \hfill y_0^{″}+2x_0^{\prime }=& 0,\hfill \\ \hfill z_0^{″}+z_0=& 0,\hfill \end{array}$$

(40)

and the set of initial conditions is

$$\begin{array}{cc}\hfill & x_0(0)=x_0^0,x_0^{\prime }(0)={\dot{x}}_0^0,\hfill \\ \hfill & y_0(0)=y_0^0,y_0^{\prime }(0)={\dot{y}}_0^0,\hfill \\ \hfill & z_0(0)=z_0^0,z_0^{\prime }(0)={\dot{z}}_0^0,\hfill \end{array}$$

(41)

while the equations which represent the first corrections are

$$\begin{array}{cc}\hfill x_1^{″}-2y_1^{\prime }-3x_1=& {\displaystyle \frac{3}{2}}\left(y_0^2+z_0^2-2x_0^2\right)-2{\omega }_1{x}_0^{″}+2{\omega }_1{y}_0^{\prime },\hfill \\ \hfill y_1^{″}+2x_1^{\prime }=& 3x_0{y}_0-2{\omega }_1{y}_0^{″}-2{\omega }_1{x}_0^{\prime },\hfill \\ \hfill z_1^{″}+z_1=& 3x_0{z}_0-2{\omega }_1{z}_0^{″},\hfill \end{array}$$

(42)

with the initial conditions

$$\begin{array}{cc}\hfill & x_1(0)=0,x_1^{\prime }(0)=0,\hfill \\ \hfill & y_1(0)=0,y_1^{\prime }(0)=0,\hfill \\ \hfill & z_1(0)=0,z_1^{\prime }(0)=0,\hfill \end{array}$$

(43)

To accomplish our procedure and find the approximated periodic solutions, we have to find solutions for both the dynamical systems in Equations (40) and (42)

Zero order solutions

According to the solutions of linear motion, the general periodic solutions of the unperturbed relative motion will be controlled by

$$\begin{array}{cc}\hfill & x_0=Xsin[\tau +{\theta }_0],\hfill \\ \hfill & y_0=Y_0+2Xcos[\tau +{\theta }_0],\hfill \\ \hfill & z_0=Zsin[\tau +{\phi }_0],\hfill \end{array}$$

(44)

With a help of Conditions (41), the constants of integration are given by

$$\begin{array}{cc}\hfill & Y_0=y_0^0-2{\dot{x}}_0^0,\hfill \\ \hfill & X^2={\left(x_0^0\right)}^2+{\left({\dot{x}}_0^0\right)}^2,\hfill \\ \hfill & Z^2={\left(z_0^0\right)}^2+{\left({\dot{z}}_0^0\right)}^2,\hfill \end{array}$$

and

$$\begin{array}{c}\hfill tan{\theta }_0={\displaystyle \frac{x_0^0}{{\dot{x}}_0^0}},tan{\phi }_0=\frac{z_0^0}{{\dot{z}}_0^0}.\end{array}$$

First order solutions

Substituting Equation (44) into Equation (42), we obtain

$$\begin{array}{cc}\hfill x_1^{″}-2y_1^{\prime }-3x_1=& X_{11}+X_{12}cos(\tau +{\theta }_0)+X_{13}sin(\tau +{\theta }_0)+X_{14}sin(\tau +{\phi }_0)\hfill \\ \hfill & +X_{15}cos2(\tau +{\theta }_0)+X_{16}cos2(\tau +{\phi }_0),\hfill \\ \hfill y_1^{″}+2x_1^{\prime }=& Y_{11}sin(\tau +{\theta }_0)+Y_{12}cos(\tau +{\theta }_0)+Y_{13}sin2(\tau +{\theta }_0),\hfill \\ \hfill z_1^{″}+z_1=& Z_{11}+Z_{12}sin(\tau +{\phi }_0)+Z_{13}cos(2\tau +{\theta }_0+{\phi }_0),\hfill \end{array}$$

(45)

where $X_{1i}$, $i=1,2,3,\cdots 6$, $Y_{ij}$ and $Z_{1j},j=1,2,3$ are constants, which are calculated by the following relations

$$\begin{array}{cc}\hfill & X_{11}={\displaystyle \frac{3}{4}}\left(2X^2+2Y_0^2+Z^2\right),X_{12}=6X{Y}_0,\hfill \\ \hfill & X_{13}=-4{\omega }_{1}X,X_{14}=4{\omega }_{1}Z,X_{15}={\displaystyle \frac{9}{2}}{X}^2,\hfill \\ \hfill & X_{16}=-{\displaystyle \frac{3}{4}}{Z}^2,Y_{11}=3X{Y}_0,Y_{12}=2{\omega }_{1}X,\hfill \\ \hfill & Y_{13}=3X^2,Z_{11}={\displaystyle \frac{3}{2}}XZcos({\theta }_0-{\phi }_0),\hfill \\ \hfill & Z_{12}=-2{\omega }_{1}Z,Z_{13}=-{\displaystyle \frac{3}{2}}XZ.\hfill \end{array}$$

Equation (45) consists of a dynamical system of second-order non-homogeneous differential equations. After integrating this system with the help of Conditions (43), we observe that the terms with coefficients $X_{1i}=1,2,3,4$, $Y_{11},Y_{12}$, and $Z_{12}$ represent secular terms, as well as the extra term with coefficient $S=2X^2+Z^2+3X^{2}cos2{\theta }_0$. Therefore, if these coefficients are nonzero, then the correction solutions will involve secular terms in the scale $\tau$. However, that is exactly what we need to avoid. Hence we will remove these terms by equating their coefficients by zeros. These procedures ensure that the solutions will not include secular terms and at least no secularities appear in the first two terms in the perturbation series. Furthermore, the terms with coefficients $X_{1i}=1,2,3,4$, $Y_{11},Y_{12}$, and $Z_{12}$ represent solutions for the associated homogeneity of Equation (45); hence, we set the coefficients to zeros before integration.

In this context, the removal of the secular terms yields

$$\begin{array}{c}\hfill {\omega }_1=0,Y_0=0,S=0.\end{array}$$

Then the first correction will be controlled by

$$\begin{array}{cc}\hfill x_1(\tau )=& {\displaystyle \frac{1}{2}}\left[\begin{array}{cc}& 3\left(2X^2+Z^2\right)\hfill \\ \hfill & +2X^2\left[7cos2{\theta }_0+2cos(2\theta +\tau )\right]\hfill \\ \hfill & -Z^2\left(cos2{\varphi }_0+2cos(\tau +{\varphi }_0)\right)\hfill \end{array}\right]{sin}^2{\displaystyle \frac{1}{2}}\tau ,\hfill \\ \hfill y_1(\tau )=& {\displaystyle \frac{1}{4}}\left[\begin{array}{cc}& 9X^{2}sin2{\theta }_0-14X^{2}sin(2{\theta }_0-\tau )\hfill \\ & +Z^2\left(8cos{\displaystyle \frac{1}{2}}(\tau +4{\varphi }_0){sin}^3{\displaystyle \frac{1}{2}}\tau +6sin\tau \right)\hfill \\ & +X^2\left(12sin\tau -sin2({\theta }_0+\tau )+6sin(2{\theta }_0+\tau )\right)\hfill \end{array}\right],\hfill \\ \hfill z_1(\tau )=& XZ\left[3cos({\theta }_0-{\varphi }_0)-cos({\theta }_0+{\varphi }_0)-2cos(\tau +{\theta }_0-{\varphi }_0)\right]{sin}^2{\displaystyle \frac{1}{2}}\tau .\hfill \end{array}$$

(46)

Therefore, the periodic solutions of the nonlinear relative motion satellite can be written in the form

$$\begin{array}{cc}\hfill & x(\tau ,ϵ)=x_0(\tau )+ϵx_1(\tau ),\hfill \\ \hfill & y(\tau ,ϵ)=y_0(\tau )+ϵy_1(\tau ),\hfill \\ \hfill & z(\tau ,ϵ)=z_0(\tau )+ϵz_1(\tau ),\hfill \end{array}$$

(47)

where $\tau =n\omega t$.

Since we use the method of place keeping parameters, we have to take $ϵ=1$; then, Solutions (47) will be rewritten as

$$\begin{array}{cc}\hfill & x(\tau ,ϵ)=x_0(\tau )+x_1(\tau ),\hfill \\ \hfill & y(\tau ,ϵ)=y_0(\tau )+y_1(\tau ),\hfill \\ \hfill & z(\tau ,ϵ)=z_0(\tau )+z_1(\tau ).\hfill \end{array}$$

(48)

Substituting Equations (44) and (46) into Equation (48), the periodic solutions of the nonlinear relative motion satellite, with the first corrections, can be estimated approximately by using the Lindstedt–Poincaré technique.

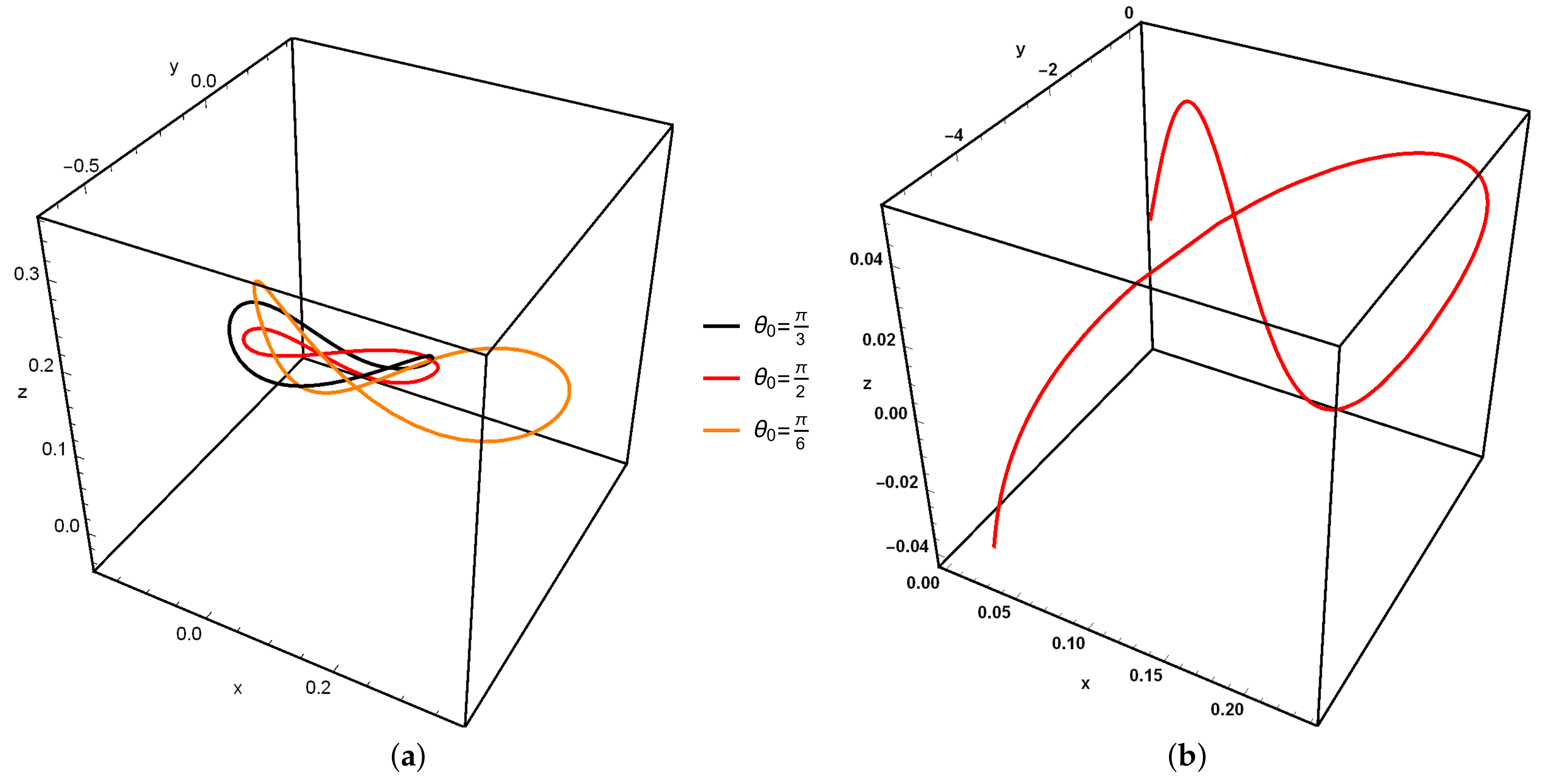
With the help of Equation (48), the initial amplitude of the chaser satellite for space rendezvous, i.e., $(x_0^0,y_0^0,z_0^0)$, works similar to in the previous section $(0.13,0.12,0.10)$ with different values for the phase angle. The projection of the periodic solution in the xy-plane is shown in Figure 4, whereas the orbit in three dimensions is shown in Figure 5 with different values of phase angle.

A comparison between the nonlinear relative motion solutions of the Lindstedt–Poincaré technique obtained by the numerical integration of the explicit Euler method are shown in Figure 4, in two dimensions, and in Figure 5, in three-dimensional motion. While numerical solutions for linear motion are periodic, the numericality of nonlinear motion is not periodic; this can be observed in Figure 4b and Figure 5b.

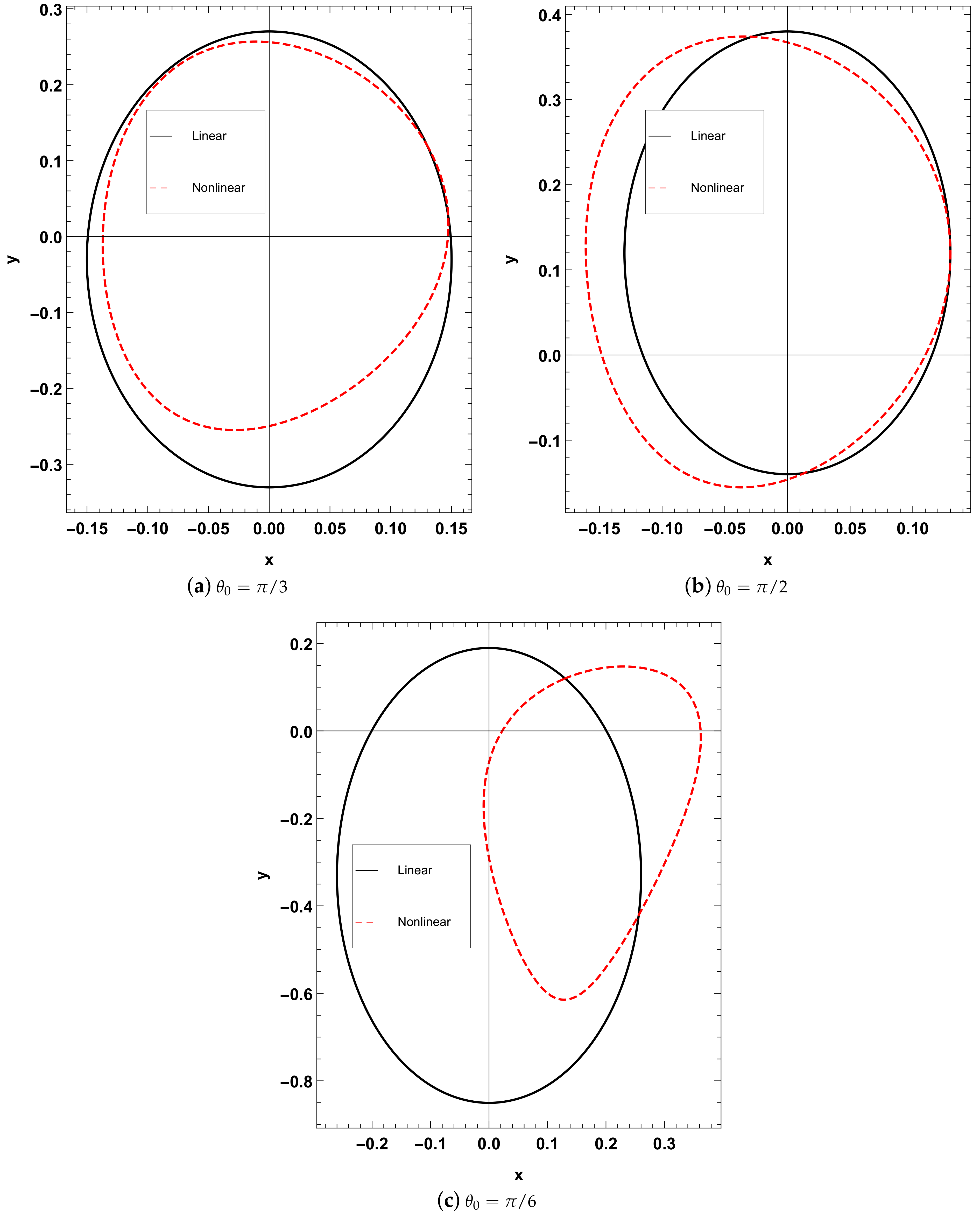
The projections in the xy-plane of the periodic solution of linear and nonlinear motion are shown in Figure 6 at different phases, whereas the differences between orbits in three dimensions of the linear and nonlinear motion at the same different phases angle with ${\phi }_0=\pi /4$ are shown in Figure 7.

The graphical investigations in both Figure 6 and Figure 7 show that the analytical solutions of linear and nonlinear motions are periodic; however, there are differences between the style of the two motions. The periodicity of the nonlinear relative motion solutions gives a considerable verification due to the solution obtained with the Lindstedt–Poincaré technique.

6. Conclusions

In this paper, we studied the relative motion of an outline of the space rendezvous problem, assuming that the chief satellite was in circular symmetric orbits. It was found that the equations that describe the motion of the deputy satellite with respect to the references fixed at the center of the chief satellite is nonlinear in the general case. Then the periodic solutions first for linear relative motion satellite were evaluated. Here a key role is the symmetry of the periodic solution joined with the fact that the system HCW is invariant under negative symmetry.

The Lindstedt–Poincaré technique was used to get the approximated periodic solutions for nonlinear differential equations of the second degree. This method is referred to by many sources as a method of successive approximations. In our study, we use it to find the first corrections of a relative motion satellite. In this context, the obtained solutions are more general compared to the linear solutions. The analysis of a linear relative motion satellite and its periodic solutions are constructed. The approximate periodic solutions of the nonlinear relative motion satellite are constructed using the Lindstedt–Poincaré technique.

Comparisons among the analytical solution of linear motion and the obtained solution by the numerical integration of the explicit Euler method are investigated, and we show that bth solutions are periodic in two and three dimensions. Moreover, comparisons among the obtained solutions of nonlinear relative motion using the Lindstedt–Poincaré technique and the numerical solution by integration of the explicit Euler method were studied. However, the numerical solutions are not periodic in both motions in two and three dimensions. Thus, the Lindstedt–Poincaré technique is recommended for designing the periodic solutions.