On the Dressed Photon Constant and Its Implication for a Novel Perspective on Cosmology

Abstract

As an important follow-up report on the latest study of the first author (H.S.) on an off-shell quantum field causing a dressed photon and dark energy, we further discuss a couple of intriguing subjects based on the new notion of simultaneous conformal symmetry breaking. One is the dressed photon constant. If we use it, in addition to $\overline{h}$ and c, as the third component of natural units, it is defined as the geometric mean of the smallest and the largest lengths: Planck length and that relating to the cosmological constant. Interestingly, this length (≈50 nanometers) seems to give a rough measure of the Heisenberg cut for electromagnetic phenomena. The other is a new perspective on cosmology that combines two original notions, i.e., twin universes and conformal cyclic cosmology, proposed, respectively, by Petit and Penrose, into one novel picture where universes expand self-similarly. We show the possibility that twin universes having a dual structure of (matter with (dark energy and matter)) vs. corresponding anti-entities, separated by an event horizon embedded in the geometric structure of de Sitter space, undergo endless cyclic processes of birth and death, as in the case of the pair creation and annihilation of elementary particles through the intervention of a conformal light field.

1. Introduction

Application studies of quantum theory in nanosciences have continued to accomplish a variety of spectacular modern technological achievements. The technology involving the dressed photon (DP) phenomena is one such achievement that makes the impossible possible. While a reliable theory has not yet been established to explain the characteristic behaviors of DPs, a comprehensive review of DP studies, including the impossibility of understanding DP phenomena within the conventional framework of Maxwell’s equation, was given by Ohtsu [1], together with a series of associated intriguing technologies and the status of theoretical attempts to understand DPs up to 2017. The research on the DP phenomena is now being pursued more actively than ever before both experimentally and theoretically. The most important point on the DP, clarified through decades-long investigations, is that the DP field is not a simple variant of the light field such as evanescent light, which is essentially a free mode, but involves largely transmuted and locally condensed (within an area smaller than several tens of nanometers) electromagnetic field energy achieved through light–matter field interactions involving point-like singularities, which seem to be a key factor for DP generation. The peculiarity of the DP field compared with the free light field is concisely summarized in Section 1 of the latest paper on DPs by Sakuma et al. [2] (S3O hereafter), where a new theory is proposed, focusing on the aspects of quantum field interactions thus far neglected.

The real reason for the unsuccessful attempts at a full-fledged theory of DPs seems to be related to the fact that a DP is not a free mode, but is the outcome of light–matter field interactions, the complexity of which makes constructing a simple mathematical model difficult. In fact, contrary to the above-mentioned remarkable technological successes of quantum theory, the current stage of development of quantum field theory (QFT) is far from a firmly established one, such as the theory of Newtonian mechanics. From this viewpoint, a major stumbling block might be the lack of mathematical support for interacting quantum field models satisfying the covariance under the Poincaré group $\mathcal{P}$ in 4-dimensional Minkowski spacetime (defined as the crossed product $\mathcal{P}:={\mathbb{R}}^4⋊\mathcal{L}$ of the Lorentz group $\mathcal{L}$ acting on the 4-dimensional Minkowski spacetime ${\mathbb{R}}^4$). While the main subject here is the DP system, to be described as a subsystem of relativistic 4-dimensional QFT, a survey of the basic structure of the 4-dimensional QFT itself would be useful for our purpose of discussing the various aspects of the DP system.

First, the physical interpretations of QFT described by the interacting Heisenberg fields ${\phi }_H$ are realized by the notion of on-shell particles contained in ${\phi }_H$ with the 4-mometum $p_{\mu }$ given by Equation (1):

$$p^2:={\eta }_{\mu \nu }{p}^{\mu }{p}^{\nu }:=p_{\nu }{p}^{\nu }={(m_{0}c)}^2\ge 0,\mu ,\nu =0,1,2,3,$$

(1)

where we adopt the sign convention $(+1,-1,-1,-1)$ for the Minkowski metric $\eta$ given by

$$\begin{array}{c}\hfill {\eta }_{\mu \nu }=\left(\begin{array}{cccc}+1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right).\end{array}$$

The physical meaning of the asymptotic fields ${\varphi }^{as}$ ($as=in$ or $out$) can be seen in their role in a scattering process formed by the in-fields ${\varphi }_1^{in}(p_1),···,{\varphi }_m^{in}(p_m)$ with momenta $p_1,···,p_m$ converging from the remote past to the scattering center and by the out-fields ${\varphi }_1^{out}(q_1),···,{\varphi }_m^{out}(q_n)$ with momenta $q_1,···,q_n$ diverging from the scattering center to the remote future. In contrast with the interacting Heisenberg field ${\phi }_H$, which causes and controls the above scattering process behind the scenes, the asymptotic field ${\varphi }^{as}$ carrying the above momentum spectrum as an observable quantity can be easily realized as a free field obtained by the so-called second quantization, as shown below. Owing to its linearity, the asymptotic field ${\varphi }^{as}$ is governed by the well-known Klein–Gordon (KG) Equation (2).

In the simplest case of a scalar field ${\varphi }^{as}$, the first quantization $p_{\mu }\to i\overline{h}{\mathrm{\partial }}_{\mu }$ applied to (1) realizes the KG equation:

$$[{\overline{h}}^2{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }+{(m_{0}c)}^2]{\varphi }^{as}=0,$$

(2)

where the operand ${\varphi }^{as}$ determined by the second quantization becomes a quantum field ${\varphi }^{as}$ describing a multi-particle system given by

$${\varphi }^{as}(x^0,\tilde{x})=\int \frac{d^3\tilde{k}}{\sqrt{{(2\pi )}^{3}2E_k}}[a(\tilde{k})exp(-i{k}_{\nu }{x}^{\nu })+a^{†}(\tilde{k})exp(i{k}_{\nu }{x}^{\nu })].$$

(3)

Here, ($a^{†}(\tilde{k})$, $a(\tilde{l})$) and ($\tilde{x}$ and $\tilde{k}$), respectively, denote a pair of creation-annihilation operators and of 3-vectors consisting of spatial components of $x^{\mu }$ and $k_{\nu }$, with $E_k$ defined by $E_k:=\sqrt{{(\tilde{k})}^2+{(m_0)}^2}$. A familiar Fock space is constructed on the basis of (3) and of the vacuum state vector $|0\rangle$ satisfying $a|0\rangle =0$, according to which a positive energy spectrum is selected in the state vector space. While the field ${\varphi }^{as}$ thus constructed embodies the wave–particle duality of a quantum system, it still lives in the realm of linearity due to the linear KG Equation (2). With the restriction due to this linearity (or the on-shell property (1)) overlooked, however, essential features of Fock spaces such as the positive energy spectra in the state vector space generated by repeated applications of the creation operators on the Fock vacuum $|0\rangle$ (under the cyclicity assumption) are misinterpreted as the universal structure to be found in interacting multiparticle systems. Accordingly, $|0\rangle$ becomes as mysterious as the creation of everything from emptiness. We return to this point in Section 4 on cosmology.

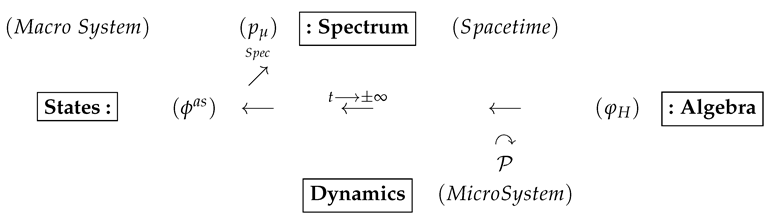
The mutual relations among the Poincaré group $\mathcal{P}$, Heisenberg field ${\phi }_H$, asymptotic field ${\varphi }^{as}$, and momentum spectrum $(p_{\mu })$ can be clearly visualized by means of the quadrality scheme to describe the duality relation between Micro and Macro (Micro-Macro duality based on the quadrality scheme [3]):

Remark 1.

In the specific example of scattering process with asymptotic completeness, the original quadrality scheme of micro–macro duality can be seen in the above relations among the dynamics $\mathcal{P}$ acting on the algebras of interacting Heisenberg fields ${\phi }_H$ and of their asymptotic fields ${\varphi }^{as}$ and the spectrum of energy-momentum $p_{\mu }$. It gives a unified categorical description of the system of interacting quantum fields in terms of quantum and classical systems, both of which are characterized dynamically by their non-commutative and commutative algebras. As our new ideas on quantum field theory of the dressed photons depends heavily on this quadrality scheme, it will be convenient to explain here its minimal essential points to those who are familiar only with quantum mechanics with finite degrees of freedom.

The scheme is a theoretical framework consisting of a couple of different dualities that are interweaved to describe the theoretically phenomena under consideration: among the four basic ingredients in the scheme, Dynamics and the Algebra $\mathcal{X}$ of physical quantities belong to the micro side of the quantum system, while the remaining two elements—States (and their representations) and Spectrum—belong to the macro side. To visualize the invisible quantum micro system, we need to exert certain action $E:\mathcal{A}\to \mathcal{X}$ on the microscopic quantum system $\mathcal{X}$ from the macro side $\mathcal{A}$. The response of the acted micro side to the acting macro side is to be given by $F:\mathcal{A}\leftarrow \mathcal{X}$, according to which we have an adjoint pair of functors $\mathcal{A}{}^{F(x)}{\leftrightarrows }_{E(a)}\mathcal{X}$; ($x\in \mathcal{X}$ and $a\in \mathcal{A}$). In this way, we see that the basic structure of the quantum theory is mathematically formulated by the so-called “adjunction” in category theory, which can be understood as the precise mathematical form of “duality”$\mathcal{A}\simeq \mathcal{X}$ (one of the weaker forms of equivalence), where $\mathcal{X}$ and $\mathcal{A}$, respectively, denote unknown mathematical object belonging to micro system and known object (as the familiar vocabulary) in the classical macro system and symbol ≃ denotes natural equivalence.

As we see in the above diagram, the abscissa axis represents the duality between the algebra$\mathcal{X}$of quantum variables and its states with Gel’fand–Naimark–Segal (GNS) representations realized in a Hilbert space. Central problematic issues we have in considering quantum systems with infinite degrees of freedom would be those on unitary nonequivalence and the uniqueness of irreducible decomposition, which are usually regarded as a pathological aspect of systems with infinite degrees of freedom. However, omitting the details of extensive researches so far done on the generalized sector problem, we can briefly summarize the main conclusions of them as follows. A system with infinite degrees of freedom can be represented with multiple sectors where a sector is defined by a factor representation with trivial center containing only scalar multiples of the identity, which generalizes the notion of irreducible representations with trivial commutants. Here, disjointness means the absence of intertwiners, as the refined notion of unitary nonequivalence adapted to the situations with infinite degrees of freedom. By this kind of generalization, we also have the change in the classification of representation, that is to say, an irreducible representation is to be replaced by a factorial representation which has a self-evident center playing the role of a commutative (classical) order parameter.Thus, we show that macroscopic order parameters emerge naturally from the disjoint representations appearing in the micro systems and the spectrum of those order parameters gives the classification space for describing a variety of configurations the micro system would take. The duality relation illustrated in the ordinate axis, that is, $[Dyn\leftrightarrows Spec]$ expresses the duality between invariability and variability of coupled micro and macro systems.

The asymptotic fields ${\varphi }^{as}$ given by (3) are placed in this scheme in duality relation with the interacting Heisenberg fields ${\phi }_H$, where ${\varphi }^{as}$ itself consist only of linear free modes without anything to do with nonlinear field interactions having the off-shell property. Because the clear-cut mathematical criterion to distinguish nonlinear field interactions from the free time evolution of noninteracting modes, known as the Greenberg–Robinson theorem [4,5], states that if the Fourier transform$\phi (p)$of a given quantum field${\varphi }^{as}(x)$does not contain an off-shell spacelike momentum$p_{\mu }$with$p_{\nu }{p}^{\nu }<0$(cf. Equation (1)), then${\varphi }^{as}(x)$ is a generalized free field. A caveat to be made here is that a spacelike momentum field does not necessarily mean the presence of a tachyonic field representing particle-like localized energy field moving with superluminous velocity, which violates the Einstein causality. This localized field is known to be unstable such that the existing spacelike momentum fields take naturally simple wavy forms. Another crucial piece of knowledge necessary to understand the enigmatic DP phenomena is the important property of quantum fields with infinite degrees of freedom, referred to in the above remark. As is well known, we have only one sector in the familiar case of quantum mechanical systems with finite degrees of freedom which are governed by unitary time evolution (the Stone–von Neumann theorem [6]). In sharp contrast to this situation, quantum fields with infinite degrees of freedom have multiple sectors [3,7], which are mutually disjoint (i.e., separated by the absence of intertwiners), stronger than unitary inequivalence. Regarding the unitary equivalence, Haag’s theorem [8] states that any quantum field satisfying Poincaré covariance is a free field if it is connected to a free field by a unitary transformation. According to this no-go theorem, it is meaningless to consider that an interacting Heisenberg field can be realized through a unitary transformation of a free field by means of the well-known Dyson S-matrix involving the interaction term. In this way, the essential part of our common knowledge cultivated in quantum mechanical systems with finite degrees of freedom is invalidated in relativistic QFT.

The notions of spacelike momentum field and the existence of multiple sectors must be quite foreign for many who are unfamiliar with quantum systems with infinite degrees of freedom, so that it is worthwhile to give a simple heuristic example. Let us consider a simple wave propagation, $\psi =expi(k_0{x}^0-k_1{x}^1)$, in a certain background field. One may regard it as a wave, say, in the atmosphere. When the wave exists in a uniform background, it propagates such that it satisfies $({\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }+k^2)\psi =0$, with $k^2:={(k_0)}^2-{(k_1)}^2$, which may be compared to a “unitary” time evolution of a free mode in the timelike sector. If the background field becomes nonuniform but its degree of nonuniformity is rather smooth, then though its way of propagation is deformed to some extent, we can describe the deformed propagation pattern by employing perturbative methods, and the solution still remains in the timelike sector mentioned above. As an extreme case of severe interactions with the environmental field for which the perturbative method is break down, we can consider a frontal instability of the atmosphere in which the front is defined as a line of discontinuity of the temperature and velocity fields. A wavelike perturbation with small amplitude put into this frontal zone, due to hydrodynamic shear instability, can no longer keep its wavy form, and its amplitude starts to either (i) grow or to (ii) damp exponentially in a region that is narrow in the traverse direction. In view of such situations that QFT is basically a theory involving complex numbers and that the frequency and wave number of a given wavelike field represent the energy and momentum, the abrupt change in the energy and momentum brought about by a certain kind of discontinuity of the field can be represented in the simplest crude model by a discrete jump of $(k_0,k_1)$ into $(\pm i{l}_0,-i{l}_1)$ with $l^2:={(l_0)}^2-{(l_1)}^2>0$. Note that with this abrupt change, $({\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }+k^2)\psi =0$ becomes $({\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }-l^2)\psi =0$, namely, the wave dynamics shifts abruptly from a timelike sector to a spacelike one with the properties $exp(\mp l_0{x}^0)$ and $exp(-l_1{x}^1)$ (valid in the domain $x^1\ge 0$), respectively, corresponding to the above-mentioned properties of (i) and (ii). Needless to say, this example, due to the atmospheric dynamics, could be transferred to situations involving interactions among elementary particles, where a “severe interaction” would evoke these changes on the interacting Heisenberg fields to which on-shell field theory cannot be applied. We believe that this simple toy model gives an intuitive explanation of the essential features of severe field interactions involving a certain kind of discontinuity and why spacelike momentum modes are necessary to describe these field interactions. We will further discuss this problem in Section 2.2 on DP model.

Now, going back to the general argument on QFT, notice that the above two theorems in axiomatic QFT for relativistic quantum fields, especially the first one, justify our investigation into the existence of a spacelike momentum domain, in the sense of a different sector, with which the conventional Maxwell’s equation is to be augmented for a complete description of electromagnetic field interactions. A helpful hint regarding an appropriate form of the spacelike momentum can be found in the longitudinal Coulomb mode or the virtual photon, which behaves as a carrier of electromagnetic force. In their series of papers, Sakuma et al. (and the latest S3O [9,10,11,12]) derived an extended field covering the spacelike momentum domain by applying a mathematical technique called Clebsch parameterization to electromagnetic 4-vector potential $A_{\mu }$. The extension of the field was accomplished in two steps: (I) semi-spacelike and (II) spacelike extensions. To avoid confusion, here we replace the common notation $A_{\mu }$ for a 4-vector potential with $U_{\mu }$. In step (I), $U_{\mu }$ satisfies

$$[{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }-{({\kappa }_0)}^2]U_{\mu }=0,U_{\nu }{U}^{\nu }=0,$$

(4)

where ${\kappa }_0$ is an important constant, to be identified as the DP constant. At first glance, one may consider this to be the wrong equation, as a null (massless) condition $U_{\nu }{U}^{\nu }=0$ seems to be incompatible with the first equation in (4). As shown in the next section, however, it is indeed correct. The reason why it looks bizarre is because it corresponds to a longitudinally propagating electromagnetic wave of which the quantum version is eliminated as unphysical in the conventional interpretation. We believe that this bizarre mode, massless in the sense of $U_{\nu }{U}^{\nu }=0$, corresponds qualitatively to an invisible virtual photon, i.e., a $U(1)$gauge boson, and in step (II), this field is extended further to the case of a genuine spacelike field satisfying $U_{\nu }{U}^{\nu }<0$. As we will touch upon in Section 2.2, the formulation of steps (I) and (II) is generalized to cover the case of a curved spacetime. As the first equation in (4) can be considered a dual form of the timelike Proca equation, i.e., $[{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }+{(m_0)}^2]A_{\mu }=0$, we call it the Clebsch dual (CD) field and denote its skew-symmetric field strength by $S_{\mu \nu }:={\mathrm{\partial }}_{\mu }{U}_{\nu }-{\mathrm{\partial }}_{\nu }{U}_{\mu }$.

As the source-free Maxwell’s equation is conformally invariant, the derivation of an augmented Maxwell field can be viewed mathematically as a conformal extension of the electromagnetic field $F_{\mu \nu }$. From this viewpoint, note that the derivation of the CD field is conceptually similar to the notion of a twistor introduced by Penrose [13], and in this sense, the essence of our new proposal on cosmology has a closer connection to the conformal cyclic cosmology (CCC) proposed by Penrose [14] than the antipodal twin universe model of Petit [15]. To see this, let us consider the rotation group $SO(3)$ acting on three-dimensional vectors. For $SO(3)$, the universal covering group $SU(2)$ exists, which is locally isomorphic to $SO(3)$ and in relation to which a spinor is defined as its irreducible representation. Extending this context to the Lorentz group $SO(1,3)$ in four-dimensional spacetime, $SL(2,C)$ arises as the universal covering group corresponding to $SU(2)$. If we further extend $SO(1,3)$ to a four-dimensional conformal group, then $SO(1,3)$ and $SL(2,C)$ are extended, respectively, to $SO(2,4)$ and $SU(2,2)$, and Penrose’s twistor appears as an element of the complex four-dimensional space on which $SU(2,2)$ acts. As a parallel argument, we can consider the case of a conformal extension of the electromagnetic field $F_{\mu \nu }$ that acts on the spinor as a $U(1)$ gauge field. CD field $S_{\mu \nu }$, introduced as the spacelike extension of $F_{\mu \nu }$, is thus also regarded as a conformal extension of $F_{\mu \nu }$. As has been shown in S3O, we believe that this fact explains why the CD field plays an important role in the dark energy dynamics of the self-similarly (conformally) expanding universe described as a de Sitter space, in sharp contrast to the simple-minded intuition that the mutual relations between the DP and cosmological phenomena are irrelevant owing to their extremely large scale difference.

This paper is organized as follows. To discuss the theme addressed in the title, we first need prior knowledge on the CD field, which is a very new concept, and on several important conclusions on cosmology reported in S3O. We reserve Section 2 and Section 3 for the purpose of recapitulating the minimal required knowledge in a simple way. Then, in Section 4, we discuss the main topics of this paper, namely, the dressed photon constant and a perspective on the possible relation between our novel cosmology and the CCC.

2. Augmented Maxwell’s Theory

2.1. Clebsch Dual Field

As mentioned above, the CD field can be regarded as a field of longitudinal electromagnetic waves. To understand this, we first note that a serious misunderstanding regarding the longitudinally propagating wave modes has persisted. In the physical science communities, this misunderstanding has been prevailing and left untouched, but it cannot be overlooked in the present context. As a matter of fact, one frequently encounters this statement in standard textbooks on electromagnetism, which asserts that electromagnetic waves are not longitudinal but transversal. This concept seems, however, to be a superfluous reaction to the assertion in “advanced” quantum electrodynamics (QED), where longitudinal modes are eliminated as unphysical. In the classical theory of electromagnetism, however, the longitudinally propagating modes have been proved unmistakably to exist in a light beam with finite width, both theoretically in [16] and experimentally in [17]. In these papers, the existence of longitudinal modes is shown without using the electromagnetic 4-vector potential $A_{\mu }$. Here, the significance of introducing the CD field can be seen in the following two aspects:

(i)

in the above classical theory, the longitudinally propagating electric field can be reinterpreted as the null current vector ${\mathrm{\partial }}_{\mu }\varphi$$(\varphi :={\mathrm{\partial }}_{\nu }{A}^{\nu })$, and

(ii)

through a process similar to the analytic continuation in complex analysis, the electromagnetic field $A_{\mu }$ is extended to a CD field $U_{\mu }$. Via the Clebsch parameterization of $U_{\mu }$, $A_{\mu }$ is extended to the semi-spacelike momentum domain, which is regarded as the classical version of the $U(1)$ gauge boson as the mediator of the electromagnetic force. Thus, we can obtain a consistent picture of the classical electromagnetic longitudinal modes: the non-virtual one reported in [16,17] and the “virtual” one of the CD field.

To confirm what is stated above, let us consider Maxwell’s Equation (5) and the associated energy-momentum tensor (7), together with its divergence (8):

$$\begin{array}{ccc}\hfill {\mathrm{\partial }}^{\nu }{F}_{\mu \nu }& =& {\mathrm{\partial }}^{\nu }({\mathrm{\partial }}_{\mu }{A}_{\nu }-{\mathrm{\partial }}_{\nu }{A}_{\mu })=[-{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{A}_{\mu }+{\mathrm{\partial }}_{\mu }({\mathrm{\partial }}^{\nu }{A}_{\nu })]=j_{\mu },\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill A_{\mu }& =& {\alpha }_{\mu }+{\mathrm{\partial }}_{\mu }\chi ,({\mathrm{\partial }}_{\nu }{\alpha }^{\nu }=0,\varphi :={\mathrm{\partial }}_{\nu }{A}^{\nu }={\mathrm{\partial }}_{\nu }{\mathrm{\partial }}^{\nu }\chi ).\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill T_{\mu }^{\nu }& =& -F_{\mu \sigma }{F}^{\nu \sigma }+\frac{1}{4}{\eta }_{\mu }^{\nu }{F}_{\sigma \tau }{F}^{\sigma \tau },(F_{\sigma \tau }{F}^{\sigma \tau }=0\mathrm{for}\mathrm{free}\mathrm{wave}\mathrm{modes}),\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\mathrm{\partial }}_{\nu }{T}_{\mu }^{\nu }& =& {\mathrm{\partial }}_{\nu }(-F_{\mu \sigma }{F}^{\nu \sigma })=F_{\mu \nu }{\mathrm{\partial }}_{\sigma }{F}^{\nu \sigma }=F_{\mu \nu }{j}^{\nu }.\hfill \end{array}$$

(8)

If the Lorentz gauge condition ${\mathrm{\partial }}^{\nu }{A}_{\nu }=0$ is imposed, additionally or formally, to the above Maxwell’s equation, then Equation (5) reduces to ${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{A}_{\mu }=0$, according to which the free Maxwell’s equation can be identified in the sense of $j_{\mu }=0$. Apart from this conventional method, however, another possibility to find the free equation begins with

$${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{A}_{\mu }=0,$$

(9)

without assuming ${\mathrm{\partial }}^{\nu }{A}_{\nu }=0$. In this case, (5) tells us that we have a nontrivial (${\mathrm{\partial }}_{\mu }\varphi \ne 0$) balance equation

$${\mathrm{\partial }}^{\nu }{F}_{\mu \nu }={\mathrm{\partial }}_{\mu }\varphi ,\to {\mathrm{\partial }}^{\mu }{\mathrm{\partial }}_{\mu }\varphi ={\mathrm{\partial }}^{\mu }{\mathrm{\partial }}^{\nu }{F}_{\mu \nu }=0.$$

(10)

The first equation in (10) can be justified in two steps: First, from (5) and (8), we see that the conservation law of ${\mathrm{\partial }}_{\nu }{T}_{\mu }^{\nu }=0$ is satisfied when $j^{\nu }=0$ in the usual free case (8). In the case of (10), however, we use the expression ${\mathrm{\partial }}_{\nu }{T}_{\mu }^{\nu }=F_{\mu \nu }{\mathrm{\partial }}_{\sigma }{F}^{\nu \sigma }$ in (8) and ${\mathrm{\partial }}^{\nu }{F}_{\mu \nu }={\mathrm{\partial }}_{\mu }{\mathrm{\partial }}^{\nu }{A}_{\nu }$ in (5), which leads to

$${\mathrm{\partial }}_{\nu }{T}_{\mu }^{\nu }=F_{\mu \nu }{\mathrm{\partial }}^{\nu }\varphi =0,$$

(11)

if $F_{\mu \nu }\perp {\mathrm{\partial }}^{\nu }\varphi$ with ${\mathrm{\partial }}^{\mu }{\mathrm{\partial }}_{\mu }\varphi =0$. This expression indicates that the longitudinally propagating vector ${\mathrm{\partial }}^{\nu }\varphi$ is physical in the sense that it satisfies the energy-momentum conservation.

In the second step of the physical justification of (10), we consider (9) in terms of ${\alpha }_{\mu }$ and $\chi$ given in (6), which becomes

$${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{\alpha }_{\mu }^{(h)}=0,{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{\alpha }_{\mu }^{(i)}+{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }({\mathrm{\partial }}_{\mu }\chi )=0,$$

(12)

with homogeneous and inhomogeneous solutions, i.e., ${\alpha }_{\mu }^{(h)}$ and ${\alpha }_{\mu }^{(i)}$, respectively, for a given $\chi$ satisfying the second equation in (10). ${\alpha }_{\mu }^{(h)}$ obviously represents a transverse mode, and the second equation gives a balance between the rotational and irrotational modes. The existence of this balance is well documented in the hydrodynamic literature explaining the mathematical description of the irrotational motion of a two-dimensional incompressible fluid. Due to the irrotationality of the motion, the velocity vector ($v_1,v_2$) is expressed in terms of the gradient of the vector potential $\widehat{\varphi }$, namely, ($v_1={\mathrm{\partial }}_1\widehat{\varphi },v_2={\mathrm{\partial }}_2\widehat{\varphi }$); on the other hand, the incompressibility of the fluid makes its motion nondivergent such that ($v_1,v_2$) is alternatively expressed as ($v_1=-{\mathrm{\partial }}_2\widehat{\psi },v_2={\mathrm{\partial }}_1\widehat{\psi }$), where $\widehat{\psi }$ denotes a stream function. Equating these two, we obtain ${\mathrm{\partial }}_1\widehat{\varphi }=-{\mathrm{\partial }}_2\widehat{\psi },{\mathrm{\partial }}_2\widehat{\varphi }={\mathrm{\partial }}_1\widehat{\psi }$, showing that $\widehat{\varphi }$ and $\widehat{\psi }$ satisfy the Cauchy–Riemann relation in complex analysis. This heuristic example serves as a helpful reference in proving that a null vector current${\mathrm{\partial }}_{\mu }\varphi$ propagating along the $x^1$ axis perpendicular to $F_{\mu \nu }$ can be reinterpreted as the current of the longitudinal ($x^1$-directed) electric field, of which a detailed explanation is given in [10]. As referred to at the beginning of this subsection, the existence of this longitudinally propagating electric field was actually reported in [16,17]. Thus, we can say that the vector field ${\mathrm{\partial }}_{\mu }\varphi$ is the physical mode that represents a longitudinally propagating electric field.

The orthogonality condition (11) is mathematically equivalent to the relativistic hydrodynamic equation of motion of a barotropic (isentropic) fluid [18]: ${\omega }_{\mu \nu }(w{u}^{\nu })=0$, where ${\omega }_{\mu \nu }:={\mathrm{\partial }}_{\mu }(w{u}_{\nu })-{\mathrm{\partial }}_{\nu }(w{u}_{\mu })$, $u^{\nu }$, and w are the vorticity tensor, 4-velocity, and proper enthalpy density of the fluid, respectively. This observation suggests that the unknown form of the 4-vector potential $U_{\mu }$ can be clarified through the Clebsch parameterization [19] because the Clebsch parameterization is used to study the Hamiltonian structure of the above-mentioned barotropic fluid motion in terms of a couple of canonically conjugate scalar parameters $(\lambda ,\varphi )$ whose two degrees of freedom are equal to those of $(\overrightarrow{E},\overrightarrow{M})$ in electromagnetic waves. Thus, in case (I) of the semi-spacelike CD field, the electromagnetic vector potential $U_{\mu }$ is parameterized as

$$\begin{array}{ccc}\hfill U_{\mu }& =& \lambda {\mathrm{\partial }}_{\mu }\varphi ,(\varphi ={\mathrm{\partial }}_{\nu }{A}^{\nu },\mathrm{which} \mathrm{satisfies}{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\varphi =0),\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill {\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\lambda -{({\kappa }_0)}^2\lambda & =& 0,\hfill \end{array}$$

(14)

where ${\kappa }_0$ is a constant determined by DP experiments. If we introduce two gradient vectors—$L_{\mu }:={\mathrm{\partial }}_{\mu }\lambda$ and $C_{\mu }:={\mathrm{\partial }}_{\mu }\varphi$, then the skew-symmetric field strength $S_{\mu \nu }$ can be represented by a simple bivector of the form

$$S_{\mu \nu }=L_{\mu }{C}_{\nu }-L_{\nu }{C}_{\mu },\to Pf(S):=S_{01}{S}_{23}+S_{02}{S}_{31}+S_{03}{S}_{12}=0,$$

(15)

which shows that, as in the case of $\overrightarrow{E}$ and $\overrightarrow{H}$ of an electromagnetic wave, the “electric” and “magnetic” fields of the CD field also satisfy the above orthogonality condition. $Pf(S)$ in (15) is the Pfaffian of the skew-symmetric matrix $S_{\mu \nu }:{(Pf(S))}^2=Det(S_{\mu \nu })$ and the barotropic fluid motions governed by the equation of motion ${\omega }_{\mu \nu }(w{u}^{\nu })=0$ are characterized by the condition that the Pfaffian vanishes. Another important property of an electromagnetic wave is that $\overrightarrow{E}$ and $\overrightarrow{H}$ are advected along a null Poynting vector. In the CD model now under consideration, a null vector $C^{\mu }$ would naturally be expected to satisfy

$$C^{\nu }{\mathrm{\partial }}_{\nu }{L}_{\mu }=0,$$

(16)

from which we obtain

$$\begin{array}{ccc}\hfill L^{\mu }(C^{\nu }{\mathrm{\partial }}_{\nu }{L}_{\mu })& =& 0,\to C^{\nu }{\mathrm{\partial }}_{\nu }(L^{\mu }{L}_{\mu })=0,\hfill \end{array}$$

(17)

$$\begin{array}{ccc}\hfill C^{\mu }(C^{\nu }{\mathrm{\partial }}_{\nu }{L}_{\mu })& =& 0,\to C^{\nu }{\mathrm{\partial }}_{\nu }(C^{\mu }{L}_{\mu })=0.\hfill \end{array}$$

(18)

In deriving (18), we utilized the fact that $C^{\nu }{\mathrm{\partial }}_{\nu }{C}^{\mu }=0$. For (18), the following orthogonality condition in the CD field

$$L_{\nu }{C}^{\nu }=0$$

(19)

can be imposed as an additional condition, which turns out later to be an important equation.

To see in what sense (19) is consistent with (15), we consider a null geodesic field ($U_{\nu }{U}^{\nu }=0$):

$$U^{\nu }{\mathrm{\partial }}_{\nu }{U}_{\mu }=U^{\nu }({\mathrm{\partial }}_{\nu }{U}_{\mu }-{\mathrm{\partial }}_{\mu }{U}_{\nu })=0,$$

(20)

which is expected to satisfy an extended light field. Using (13) and (15), we readily obtain

$$U^{\nu }{\mathrm{\partial }}_{\nu }{U}_{\mu }=-S_{\mu \nu }(\lambda C^{\nu })=(C_{\mu }{L}_{\nu }-L_{\mu }{C}_{\nu })(\lambda C^{\nu })=(L_{\nu }{C}^{\nu })\lambda C_{\mu },$$

(21)

which vanishes by the orthogonality condition (19). The importance of (19) in the CD field formulation is that $L_{\mu }$ must be a spacelike vector, because $L_{\mu }$ satisfying (19) is either $C_{\mu }$ or a spacelike vector, which explains why the $\lambda$ field introduced in the CD formulation satisfies the spacelike KG equation given in (14). Using the relations derived above between $C_{\mu }$ and $L_{\mu }$, we can show the form of the extended Maxwell’s equation:

$${\mathrm{\partial }}^{\nu }{S}_{\nu \mu }={({\kappa }_0)}^2{U}_{\mu }⟺[{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }-{({\kappa }_0)}^2]U_{\mu }=0,(\mathrm{with}{\mathrm{\partial }}_{\nu }{U}^{\nu }=0).$$

(22)

The energy-momentum tensor ${\widehat{T}}_{\mu }^{\nu }$ of the lightlike CD field can be derived easily from the conventional one with the following form: $T_{\mu }^{\nu }=-F_{\mu \sigma }{F}^{\nu \sigma }$. Considering the sign change of the energy at the boundary between the timelike and spacelike domains, we define the tensor as

$$\begin{array}{ccc}\hfill {\widehat{T}}_{\mu \nu }^{}& :& =S_{\mu \sigma }{S}_{\nu }^{\sigma }=(L_{\mu }{C}_{\sigma }-C_{\mu }{L}_{\sigma })(L_{\nu }{C}^{\sigma }-C_{\nu }{L}^{\sigma })\hfill \\ & =& (L_{\sigma }{L}^{\sigma })C_{\mu }{C}_{\nu }=\rho C_{\mu }{C}_{\nu },\rho :=L_{\sigma }{L}^{\sigma }<0.\hfill \end{array}$$

(23)

The negative density $\rho$ corresponds to the negative norm of the longitudinal modes in the QED, which makes this mode unphysical in the conventional interpretation. However, we believe that the usage of the term “unphysical” in this context is inappropriate, because if we regard the CD field as virtual photons, then the former is physical in the sense that the latter, as the mediator of the electromagnetic force, is physical though it is invisible. As the argument regarding the reference point of the gravitational potential energy shows, the decision regarding whether a given quantity under consideration is physical depends essentially on the physical setting of our problem; therefore, the Clebsch duality relation between $F_{\mu \nu }$ and $S_{\mu \nu }$ should not be viewed as the duality between physical and unphysical aspects but instead as the duality between the positive and negative sides of the light-cone $p^2=0$, the latter of which is, as we will see in Section 3 on cosmology, often closely related to the invisibility of a given quantity. Actually, the “state-dependent” physicality of the longitudinal photons was already pointed out by Ojima [20], who stated that while the longitudinal photons or unphysical Goldstone bosons in the Higgs mechanism are eliminated from the physical space of states in the usual formulation, this statement applies to the above modes only in their particle forms. In their non-particle forms, the former appear physically as infrared Coulomb tails, and the latter, as the so-called “macroscopic wave functions” arising from the Cooper pairs, both of which play essential physical roles. The CD formulation based on the Greenberg–Robinson theorem has revealed that the momenta of the non-particle forms in the above statement are invisible non-localized spacelike ones. Thus, regarding the negativity of $\rho$, we point out that it can be likened to the simple fact that the complexified time coordinate $ict$ in Minkowski space is invisible, though it is an important element without which we cannot describe a given dynamical system in a satisfactory way.

In step (II) of the CD field formulation, we relax the condition ${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\varphi =0$ given by the second equation in (10) to allow the following extended vector potential $U_{\mu }$, which is advected by itself along a geodesic:

$$\begin{array}{ccc}\hfill U_{\mu }:=\frac{1}{2}(\lambda C_{\mu }-\varphi L_{\mu }),⟹U^{\nu }{\mathrm{\partial }}_{\nu }{U}_{\mu }& =& -S_{\mu \nu }{U}^{\nu }+\frac{1}{2}{\mathrm{\partial }}_{\mu }(U^{\nu }{U}_{\nu })=0,\hfill \end{array}$$

$$\begin{array}{ccc}\hfill U_{\nu }{U}^{\nu }& <& 0,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\lambda -{({\kappa }_0)}^2\lambda =0,{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\varphi -{({\kappa }_0)}^2\varphi & =& 0,C^{\nu }{L}_{\nu }=0.\hfill \end{array}$$

(25)

The form of $S_{\mu \nu }$, given by the first equation in (15), remains unchanged in (24). Note that the condition ${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\varphi =0(\varphi ={\mathrm{\partial }}_{\nu }{A}^{\nu })$ can certainly be considered a gauge fixing condition, but at the same time, the second equation in (10) can be interpreted as a special gauge condition where gauge invariance is represented by the charge conservation due to ${\mathrm{\partial }}^{\mu }{\mathrm{\partial }}^{\nu }{F}_{\mu \nu }=0$, while ${\mathrm{\partial }}_{\mu }\varphi$ is not a usual timelike electric current.

In the extended Maxwell’s equation given in (22), an electrically neutral current ${({\kappa }_0)}^2{U}_{\mu }={({\kappa }_0)}^2(\lambda {\mathrm{\partial }}_{\mu }\varphi )$ behaves exactly like $j_{\mu }$ in the original Maxwell’s equation, which shows that the constant ${\kappa }_0$ serves as a fundamental unit, such as the electric charge. Therefore, violation of condition (10) causes gauge symmetry breaking, according to which the CD field extended in step (II) suffers from breakdown of both the gauge symmetry and conformal symmetry in the sense of $U_{\nu }{U}^{\nu }=0$.

Corresponding to the above extension, the energy-momentum tensor satisfying the conservation law of ${\mathrm{\partial }}_{\nu }{\widehat{T}}_{\mu }^{\nu }=0$ is redefined as

$$\begin{array}{ccc}\hfill {\widehat{T}}_{\mu \nu }& =& {\widehat{S}}_{\mu \sigma \nu }^{\sigma }-\frac{1}{2}{\widehat{S}}_{\alpha \beta }^{\alpha \beta }{\eta }_{\mu \nu },{\widehat{S}}_{\alpha \beta \gamma \delta }:=S_{\alpha \beta }{S}_{\gamma \delta },\hfill \\ & ⟺& G_{\mu \nu }:=R_{\mu \nu }-R{g}_{\mu \nu }/2.\hfill \end{array}$$

(26)

Note that ${\widehat{S}}_{\alpha \beta \gamma \delta }$ defined above has the same skew-symmetric properties as those of the Riemann tensor $R_{\alpha \beta \gamma \delta }$, including the first Bianchi identity, $S_{\alpha \left[\beta \gamma \delta \right]}=0$ (equivalent to the second equation in (15)), which is valid as $S_{\mu \nu }$ is a bivector field given by the first equation in (15). Thus, ${\widehat{T}}_{\mu \nu }$ given in (26) becomes isomorphic to the Einstein tensor $G_{\mu \nu }:=R_{\mu \nu }-R{g}_{\mu \nu }/2$, where the Ricci tensor $R_{\mu \nu }:=R_{\mu \nu \sigma }^{\sigma }$.

2.2. Quantization of the CD Field and DP Model

Going back to (23), we note that it is isomorphic to the energy-momentum tensor of freely moving fluid particles. The $\rho$ field for an actual fluid will be discretized if the kinetic theory of molecules is taken into account. When the light field is quantized, this form will obey Planck’s quantization of light energy $E=h\nu$. As the CD field variable $L^{\mu }$ has the dimension of length, we introduce a certain quantized elemental length $l_{dp}$ whose inverse is ${\kappa }_0$, namely, the discretization of $\rho$ leads to

$${\kappa }_0:={(l_{dp})}^{-1},$$

(27)

which can be considered an energy quantization of the CD field. Recall that the Dirac equation of the form

$$(i{\gamma }^{\nu }{\mathrm{\partial }}_{\nu }+m)\Psi =0$$

(28)

can be regarded as the “square root” of the timelike KG equation $({\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }+m^2)\Psi =0$. Therefore, the Dirac equation for the spacelike KG equation $({\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }-{({\kappa }_0)}^2)\Psi =0$ must be

$$i({\gamma }^{\nu }{\mathrm{\partial }}_{\nu }+{\kappa }_0)\Psi =0.$$

(29)

On the other hand, an electrically neutral Majorana representation exists for (28), in which all the $\gamma$ matrices become purely imaginary such that these matrices have the form $({\gamma }_{(M)}^{\nu }{\mathrm{\partial }}_{\nu }+m)\Psi =0$, which is identical to (29). The Majorana field is fermionic with a half-integer spin 1/2; thus, the same (momentum) state cannot be occupied by two fields according to Pauli’s exclusion principle. Note that by using the Pauli–Lubanski vector $W_{\mu }$ to describe the spin polarization of moving particles, we can find a specific orthogonal momentum configuration of a pair of Majorana fields whose resultant spin becomes 1, namely,

$$M_{\mu \nu }{p}^{\nu }=N_{\mu \nu }{q}^{\nu }=W_{\mu },$$

(30)

where $M_{\mu \nu }$ and $p^{\nu }$ denote the angular and linear momenta of a given Majorana field, respectively, while $N_{\mu \nu }$ and $q^{\nu }$ are the corresponding momenta of the other, of which the linear momentum $q^{\nu }$ is perpendicular to $p^{\nu }$. We believe that this configuration (30) gives a quantum mechanical justification for the orthogonality condition (19) and (25) of the CD field.

For a plane wave solution ($\lambda ={\widehat{\lambda }}_{c}exp\left[i(k_{\nu }{x}^{\nu })\right]$) to the spacelike KG equation (14), $L_{\nu }={\mathrm{\partial }}_{\nu }\lambda$ satisfies

$$L^{\nu }{L}_{\nu }^{*}=-{({\kappa }_0)}^2({\widehat{\lambda }}_c{\widehat{\lambda }}_c^{*})=const.<0,$$

(31)

which shows that the momentum vector $L^{\mu }$ lies in a submanifold of the Lorentzian manifold, called de Sitter space in cosmology, which is a pseudo-hypersphere with a certain constant radius embedded in $R^5$. Quite independent of the cosmological arguments on de Sitter space, Snyder [21] discussed the unique role of this space in spacetime quantization. He showed that with the introduction of the hypothetical momentum 5-vector ${\eta }^{\mu }(0\le \mu \le 4)$ in $R^5$ constrained to lie on the de Sitter space, i.e., ${\eta }^{\nu }{\eta }_{\nu }^{*}=-{({\eta }_c)}^2=const.$, the following commutation relations are derived. For the definitions of $p_{\mu }$, ${\widehat{p}}_{\mu }$, and ${\widehat{x}}^{\mu }$, we have

$$\begin{array}{ccc}\hfill p_{\mu }& :& =\frac{\overline{h}}{l_p}\frac{{\eta }_{\mu }}{{\eta }_4},{\widehat{p}}_{\mu }:=-\frac{i\overline{h}}{l_p{\eta }_4}\frac{\mathrm{\partial }}{\mathrm{\partial }{\eta }_{\mu }},{\widehat{x}}^{\mu }:=i{l}_p\left({\eta }_4\frac{\mathrm{\partial }}{\mathrm{\partial }{\eta }_{\mu }}-{\xi }_{\mu }{\eta }_{\mu }\frac{\mathrm{\partial }}{\mathrm{\partial }{\eta }_4}\right);\hfill \\ \hfill (0& \le & \mu \le 3),\hfill \end{array}$$

(32)

where $l_p$ denotes the Planck length, and ${\xi }_{\mu }$ takes a value of $-1$ when $\mu =0$ and 1 when $\mu \ne 0$, from which we obtain

$$\begin{array}{ccc}\hfill \left[{\widehat{x}}^{\mu },{\widehat{p}}_{\mu }\right]& =& i\overline{h}\left[1+{\xi }_{\mu }{\left(\frac{l_p}{\overline{h}}\right)}^2{(p_{\mu })}^2\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill \left[{\widehat{x}}^{\mu },{\widehat{p}}_{\nu }\right]& =& \left[{\widehat{x}}^{\nu },{\widehat{p}}_{\mu }\right]=i\overline{h}{\left(\frac{l_p}{\overline{h}}\right)}^2{p}_{\mu }{p}_{\nu }0\le (\mu ,\nu )\le 3,\hfill \end{array}$$

(33)

$$\begin{array}{ccc}\hfill \left[{\widehat{x}}^i,{\widehat{x}}^j\right]& =& \frac{i{(l_p)}^2}{\overline{h}}{ϵ}_{ijk}{L}_k,\left[{\widehat{x}}^0,{\widehat{x}}^i\right]=\frac{i{(l_p)}^2}{\overline{h}}{M}_i;1\le (i,j,k)\le 3,\hfill \end{array}$$

(34)

where ${ϵ}_{ijk}$ is Eddington’s epsilon, and $L_i$ and $M_i$ are angular momentum vectors generated, respectively, by (spatial-spatial) and (spatial-temporal) rotations. Snyder further showed that the “Lorentz transformation” in his spacelike momentum space$\left\{{\eta }^{\mu }\right\},(0\le \mu \le 3)$ naturally induces the Lorentz transformation in the usual spacetime $\left\{x^{\mu }\right\}$. Thus, the energy-momentum tensor${\widehat{T}}_{\mu \nu }$of the CD field given in (26) can be regarded as the one constructed on this Snyder’s momentum “spacetime”${\eta }^{\mu }$with Lorentz invariance as in the case of$R_{\mu \nu }$, also constructed on the spacetime$x^{\mu }$with Lorentz invariance, which becomes a very important property in the discussion of dark energy in the next section. In [12] and S3O, we showed that, by virtue of the bivector property of $S_{\mu \nu }$ given in (15), the form of ${\widehat{T}}_{\mu \nu }$ can be extended to a curved spacetime. Thus, the intriguing isomorphism between ${\widehat{T}}_{\mu \nu }$ and $G_{\mu \nu }$ in (26) seems to suggest an important consequence: the quantization of the CD field attained by the above commutation relations may also be applied to the quantization of the gravitational field. The research pursuing this goal can be found, for instance, Girelli [22] and Glikman [23].

Now, we move on to a new DP model. Although the constant ${\kappa }_0$ plays a crucial role in formulating the CD field, its value clearly cannot be determined solely by theoretical arguments. We already explained in S3O how the value of the DP constant ${\kappa }_0$ was estimated by the extensive DP experiments by Ohtsu, who utilized the photochemical vapor deposition and autonomous etching techniques [24]. Through those experiments, the maximum size of the DP that can be considered as $l_{dp}$ introduced in (27) was estimated to be

$$50nanometer<l_{dp}={({\kappa }_0)}^{-1}<70nanometer.$$

(35)

As emphasized in the introduction, we do not yet know a reliable QFT that can deal with the off-shell properties of the field playing an important role in the DP generating mechanism. Thus, we need to resort to a certain kind of simplified argument to bring in the experimental outcome to CD field theory. In the following, we give such a simplified argument. In the first paragraph of the introduction, we mentioned that the existence of point-like singularities, similar to the pointed end of a fiber probe or impurities with extremely tiny size scattered across a given background material, is the crucial element for generating DPs. We can safely say that field interactions in which these singularities come into play should be so serious that the involvement of the spacelike momenta predicted by the Greenberg–Robinson theorem will be crucial in these cases compared with those without singularities.

Remember that, in the introductory Section 1, we have touched upon a heuristic toy model with which we show the intervention of spacelike momentum in the field interactions. Aharonov et al. [25] conducted an advanced analysis of the response behavior of the spacelike KG equation perturbed by a point-like delta function $\delta (x^0)\delta (x^1)$, in which the above essential aspect was incorporated. They showed that the solutions excited by this point-like disturbance consist of two different types: the stable spacelike mode and the unstable timelike mode. The unstable timelike mode excited from the spacelike KG Equation (14) with spherical symmetry has the form $\lambda (x^0,r)=exp(\pm k_0{x}^0)R(r)$, where $R(r)$ satisfies

$$R^{\prime \prime }+\frac{2}{r}{R}^{\prime }-{({\widehat{\kappa }}_r)}^{2}R=0,{({\widehat{\kappa }}_r)}^2:={(k_0)}^2-{({\kappa }_0)}^2>0,$$

(36)

according to which $R(r)$ is the Yukawa potential of $R(r)=exp(-{\widehat{\kappa }}_{r}r)/r$. For a Majorana field, as with the quantum version of the $\lambda$ field, the energy in terms of $k_0$ is discretized by ${\kappa }_0$, as shown in (27). Thus, the nonzero minimum $Min\left[{\widehat{\kappa }}_r\right]$ in the Yukawa potential is ${\kappa }_0$, which gives the maximum size of the localized DP to be compared with the experimental result (35). Although the CD field consists of a pair of Majorana fields satisfying the orthogonality conditions (19) and (25), the orthogonal configuration must be broken down by the perturbation, and the timelike pair will turn, respectively, into $\lambda (x^0,r)=exp(\pm k_0{x}^0)R(r)$, namely, particle and antiparticle pairs, as an electrically neutral antiparticle can be considered a particle traveling backward in time. The excited field is non-propagating in nature; thus, a pair of particle and antiparticle fields will be combined into either an “electric” field with spin 0 or a “magnetic” field with spin 1 [26]. We believe that the DP is generated through this pair annihilation of the Majorana field. As the DP field is basically electromagnetic, once it is generated, its behavior in a uniform environment can be described by the Proca equation of the form ${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }{A}_{\mu }+{({\kappa }_0)}^2{A}_{\mu }=0$. From the viewpoint of nanophotonical engineering, however, what really matters is the control of the DP energy flows driven by the existence of point-like sources and sinks. In the above argument, we showed that the energy of incident photons working as the triggering cause of $\delta (x^0)$ at the singular point eventually turns into the energy of the DP. At the present stage, we do not have clear knowledge of the sink mechanisms, but the research on DP energy flow with source–sink-type driving forces is pursued actively by employing a certain class of quantum walk models [27,28,29]. Intuitively, however, we can expect that some kind of $\zeta$-function enters here as the carrier to convey the above singularity waves, which explains the observation of $\zeta$-function singularities in the quantum walks. Moreover, the parallelism between $\zeta$-functions and partition functions (the latter appearing in statistical mechanics) explains the relevance of Tomita–Takesaki modular duality [30] to the basis of the conformal symmetry discussed below.

3. On Dark Energy and Dark Matter

In our discussion so far, we have developed a new concept of a CD field carrying spacelike momentum modes, which are required for electromagnetic field interactions. In comparison to the conventional QFT, the CD field can be compared with invisible virtual photons that can be excited from the vacuum ($|0\rangle =0$), regarded as the ground state of a one-sided energy spectrum within the bound of the uncertainty principle. Apparently, simply employing this excitation scenario is problematic because the concept of the CD field contradicts the vacuum state mentioned above. We believe that the orthogonal relation between a pair of momentum vectors $p^{\nu }$ and $q^{\nu }$ given in (30) gives us a hint to solve this problem concerning the ground state. For spacetime with three spatial dimensions, as shown below, the maximum number of Majorana fermion fields as the limited capacity of spacetime is also three, of which the configuration is shown by

$$M_{\mu \nu }{p}^{\nu }=N_{\mu \nu }{q}^{\nu }=L_{\mu \nu }{r}^{\nu }=W_{\mu }.$$

(37)

This compound state with a resultant spin $3/2$ is called a Rarita–Schwinger state, which we denote by ${|M3\rangle }_g$. The role of the vector ${|M3\rangle }_g$ is to give the GNS cyclic vector of a mixed state which is disjoint from the vacuum state whose cyclic vector is given by $|0\rangle$ [31]. The important characteristic of ${|M3\rangle }_g$ is that the CD vector boson field can be excited from any of the three different pairs, which propagates along one of the ($x^1$, $x^2$, $x^3$) directions. In view of the universality of electromagnetic interactions, the incessant occurrence of excitation–de-excitation cycles between ${|M3\rangle }_g$ and non-ground states makes ${|M3\rangle }_g$ a fully occupied state in the macroscopic time scale. Therefore, we can say that ${|M3\rangle }_g$ exists not as a momentary virtual state, but also as a stable invisible off-shell state. In the following, we show that ${|M3\rangle }_g$ exerts on the universe a cosmological effect identified as dark energy.

To investigate the property of ${|M3\rangle }_g$, let us consider plane wave solutions $\lambda$ and $\varphi$ for the spacelike case of $U_{\nu }{U}^{\nu }<0$, in which $\lambda =N_{\lambda }{\widehat{\lambda }}_{c}exp(i{k}_{\nu }{x}^{\nu })$ and $\varphi =N_{\varphi }{\widehat{\varphi }}_{c}exp(i{k}_{\nu }{x}^{\nu })$, with $k_{\nu }{k}^{\nu }=-{({\kappa }_0)}^2$, where ${\widehat{\lambda }}_c$ and ${\widehat{\varphi }}_c$ denote elemental amplitudes of the respective fields, and $N_{\lambda }$ and $N_{\varphi }$ are the numbers of the respective modes. As Equation (15) shows, $\lambda$ and $\varphi$ always appear in the form of a product; thus, we may rewrite these two expressions as

$$\lambda =N{({\kappa }_0)}^{-2}exp(i{k}_{\nu }{x}^{\nu }),\varphi ={\widehat{\varphi }}_{c}exp(i{k}_{\nu }{x}^{\nu }),$$

(38)

where N is a combined number $N:=N_{\lambda }{N}_{\varphi }$, and we can identify ${\widehat{\lambda }}_c$ as ${\widehat{\lambda }}_c={({\kappa }_0)}^{-2}$, as ${\widehat{\lambda }}_c$ has the dimension of ${(length)}^2$. By substituting these into the first equation in (26) and setting $N=1$, we obtain the absolute value of ${\widehat{T}}_{\nu }^{\nu }(1)$, denoted as $|{\widehat{T}}_{\nu }^{\nu }(1)|$:

$$|{\widehat{T}}_{\nu }^{\nu }(1)|=-2\left[{\widehat{\varphi }}_c{({\widehat{\varphi }}_c)}^{*}\right]<0,$$

(39)

where ${(•)}^{*}$ denotes the complex conjugate of $(•)$. The right-hand side of (39) can be evaluated by the light-like case of the CD field (23), in which we have ${\widehat{T}}_{\mu \nu }^{}=\rho C_{\mu }{C}_{\nu }$. For the light-like case, we have $\varphi ={\widehat{\varphi }}_{c}exp(i{k}_{\nu }{x}^{\nu }),k_{\nu }{k}^{\nu }=0$ and $\lambda =N{({\kappa }_0)}^{-2}exp(i{l}_{\nu }{x}^{\nu }),l_{\nu }{l}^{\nu }=-{({\kappa }_0)}^2$, from which we have

$${(C_{\mu })}^{*}{C}^{\nu }=k_{\mu }{k}^{\nu }{\widehat{\varphi }}_c{({\widehat{\varphi }}_c)}^{*},\rho =-N^2{({\kappa }_0)}^{-2}.$$

(40)

Next, we consider a case in which the $k^{\mu }$ vector of $\varphi$ is parallel to the $x^1$ direction and consider a rectangular parallelepiped V spanned by the vectors $(1/k_1,1,1)$. For $k_0={\nu }_0/c$, where c and ${\nu }_0$ denote the light velocity and the frequency of the $\varphi$ field, the volume integral of ${\widehat{T}}_0^0/(-N^2)$ over V as the energy per quantum is

$$\frac{1}{(-N^2)}{\int }_V{\widehat{T}}_0^{0}d{x}^{1}d{x}^{2}d{x}^3={({\kappa }_0)}^{-2}ϵ\left[{\widehat{\varphi }}_c{({\widehat{\varphi }}_c)}^{*}\right]\frac{{\nu }_0}{c},$$

(41)

where $ϵ$ denotes the unit length squared. Equating (41) with $E=h{\nu }_0$, we obtain

$$hc{({\kappa }_0)}^2=ϵ\left[{\widehat{\varphi }}_c{({\widehat{\varphi }}_c)}^{*}\right],ϵ=1{(meter)}^2.$$

(42)

As stated after (37), we need three fields propagating along the $x^1$, $x^2$, and $x^3$ directions to achieve isotropic radiation of the CD field. These three fields are given by $(S_{23},S_{02})$, $(S_{31},S_{03})$, and $(S_{12},S_{01})$. The energy-momentum tensor ${\widehat{T}}_{\mu }^{\nu }(3)$ derived by the superposition of these fields becomes

$${\widehat{T}}_{\mu }^{\nu }(3)=\left(\begin{array}{cccc}-3{\sigma }^2& -\tau \sigma & -\tau \sigma & -\tau \sigma \\ \tau \sigma & 2{\tau }^2-{\sigma }^2& 0& 0\\ \tau \sigma & 0& 2{\tau }^2-{\sigma }^2& 0\\ \tau \sigma & 0& 0& 2{\tau }^2-{\sigma }^2,\end{array}\right).$$

(43)

In deriving (43), we set $S_{23}=S_{31}=S_{12}=\sigma$ and $S_{01}=S_{02}=S_{03}=\tau$. We note that ${\widehat{T}}_{\mu }^{\nu }(3)$ can be regarded as the energy-momentum tensor of the anti-dark energy (dark energy with a negative energy density, that is, ${\widehat{T}}_0^0(3)=-3{\sigma }^2<0$). Dark energy (with positive energy density) ${}^{*}{\widehat{T}}_{\mu }^{\nu }(3)$ having exactly the same trace as that of the anti-dark energy ${\widehat{T}}_{\mu }^{\nu }(3)$ can be introduced by the Hodge dual exchange between $(\sigma ,\tau )$ and $(i\tau ,i\sigma )$ in (43), which becomes

$${}^{*}{\widehat{T}}_{\mu }^{\nu }(3)=\left(\begin{array}{cccc}3{\tau }^2& \tau \sigma & \tau \sigma & \tau \sigma \\ -\tau \sigma & -2{\sigma }^2+{\tau }^2& 0& 0\\ -\tau \sigma & 0& -2{\sigma }^2+{\tau }^2& 0\\ -\tau \sigma & 0& 0& -2{\sigma }^2+{\tau }^2,\end{array}\right).$$

(44)

At this point, we recall the important remark on the validity of extending our discussion, which started from Minkowski space, to the case of a curved spacetime. As already pointed out in the explanation of Snyder space written in italics below in Equation (34), the isomorphism between ${\widehat{T}}_{\mu \nu }$ and $G_{\mu \nu }$ given in (26) can be extended to a curved spacetime by virtue of the bivector property of (15). If the dark energy is modeled by a cosmological term of $\Lambda g_{\mu \nu }$, then the Einstein field equation with the sign convention of $R_{\mu \nu }=R_{\mu \nu \sigma }^{\sigma }$ together with the metric convention of $(+1,-1,-1,-1)$ becomes

$$R_{\mu }^{\nu }-\frac{R}{2}{g}_{\mu }^{\nu }+\Lambda g_{\mu }^{\nu }=-\frac{8\pi G}{c^4}{T}_{\mu }^{\nu },$$

(45)

where $\Lambda$ becomes negative for an expanding universe. Before proceeding further, we note that ${}^{*}{\widehat{T}}_{\mu }^{\nu }(3)$ is not a quantity that directly fits into the conventional cosmological analysis utilizing the isotropic spacetime structure assumed by Weyl’s hypothesis on the cosmological principle. First, as ${}^{*}{\widehat{T}}_{\mu }^{\nu }(3)$ is spacelike in nature, it cannot be reduced to a diagonalized matrix form. Second, it is the energy-momentum tensor of fermionic ${|M3\rangle }_g$ with spin $3/2$. The crucial problem in our analysis therefore is whether we can find observable quantities in ${}^{*}{\widehat{T}}_{\mu }^{\nu }(3)$. Because the relevant criterion for singling out an observable quantity may depend on the situation, we have no choice but to make a good guess. The fact that seems to work as “the guiding principle” is that within the framework of relativistic QFT, any observable without exception associated with a given internal symmetry is invariant under the action of a transformation group materializing the symmetry under consideration. By extending this knowledge on the internal symmetry to the external (spacetime) one, we assume that the trace ${\Lambda }_{de}{g}_{\nu }^{\nu }$ defined by

$${\Lambda }_{de}{g}_{\nu }^{\nu }:=-\frac{8\pi G}{c^4}{}^{*}{\widehat{T}}_{\nu }^{\nu }(3)>0,\to {\Lambda }_{de}=\frac{12\pi Gh}{c^3ϵ}{({\kappa }_0)}^2$$

(46)

is observable as the invariant of the general coordinate transformation, which is consistent with the built-in Lorentz invariance of Snyder’s momentum space on which the CD field is constructed. Thus, the validity of our new model on dark energy can be checked by comparing the following two models:

$$\begin{array}{ccc}\hfill R_{\mu }^{\nu }-\frac{R}{2}{g}_{\mu }^{\nu }-{\Lambda }_{obs}{g}_{\mu }^{\nu }& =& -\frac{8\pi G}{c^4}{T}_{\mu }^{\nu },\hfill \\ \hfill R_{\mu }^{\nu }-\frac{R}{2}{g}_{\mu }^{\nu }& =& -\frac{8\pi G}{c^4}{T}_{\mu }^{\nu }+{\Lambda }_{de}{g}_{\mu }^{\nu },\hfill \end{array}$$

(47)

where ${\Lambda }_{obs}$ denotes the value obtained by Planck satellite observations. (In S3O, ${\Lambda }_{obs}$ in the above Equation (47) appeared with the wrong sign in the corresponding Equation (25), which should be corrected.) Using (39), ${}^{*}{\widehat{T}}_{\nu }^{\nu }(3)=3{\widehat{T}}_{\nu }^{\nu }(1)$, and (42), we obtain ${\Lambda }_{de}\approx 2.47\times {10}^{-53}{\mathrm{m}}^{-2}$ and ${\Lambda }_{obs}\approx 3.7\times {10}^{-53}{\mathrm{m}}^{-2}$ [32]. Thus, ${|M3\rangle }_g$ seems to be a promising candidate model for dark energy.

In the above arguments on the dark energy model, the physical meaning of the “real” cosmological term $\Lambda g_{\mu \nu }$ should be revised, because it does not correspond in our model to dark energy. We believe that one of the intriguing possibilities is that ${\Lambda }_{dm}{g}_{\mu \nu }$ with ${\Lambda }_{dm}>0$ (valid in our sign convention) represents dark matter. The main reason for this is due to a simple fact that we can represent the metric tensor $g_{\mu \nu }$ in terms of the Weyl (conformal) curvature tensor $W_{\alpha \beta \gamma \delta }$ as long as its magnitude does not vanish, namely,

$$g_{\mu \nu }=\frac{4}{W^2}{W}_{\mu \alpha \beta \gamma }{W}_{\nu }^{\alpha \beta \gamma },W^2:=W_{\alpha \beta \gamma \delta }{W}^{\alpha \beta \gamma \delta }\ne 0,$$

(48)

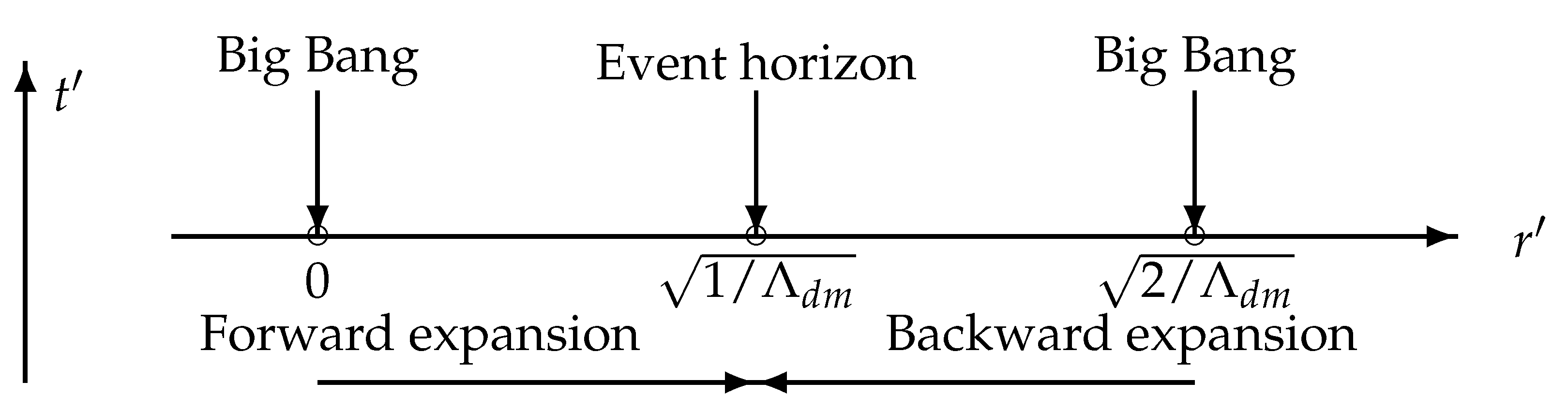
as shown by straightforward calculations [33]. Recall that Weyl curvature represents the deviation of spacetime from the conformally flat Friedmann–Robertson–Walker (FRW) metric for an isotropic universe. In addition, the monotonic decrease in $W^2$ along the radial direction in the field of $W_{\alpha \beta \gamma \delta }$ in the well-known spherically symmetric Schwarzschild outer solution of a given star suggests that the local maxima of $W^2$ would behave as “particles” or that its existence tends to correlate with the created matter field. Therefore, ${\tilde{T}}_{\mu \nu }$, defined as

$${\tilde{T}}_{\mu \nu }:={\Lambda }_{dm}{g}_{\mu \nu },{\Lambda }_{dm}>0,g_{00}>0,$$

(49)

to be put on the left-hand side of (45), gives an energy-momentum tensor of this pseudomatter field as a candidate for dark matter. The existence of ${\tilde{T}}_{\mu \nu }$ will further accelerate the deviation of spacetime from the FRW metric and thus serve as the fostering mechanism of galaxy formation. (In Equation (30) of S3O, the above ${\tilde{T}}_{\mu \nu }$ was defined with negative ${\Lambda }_{dm}$, which is a second error related to the first error of $+{\Lambda }_{obs}$ in (47)). In determining the magnitude of ${\Lambda }_{dm}$, we first refer to the observational fact that the estimated abundance ratio of dark energy to dark matter is $3:1$. AS ${\Lambda }_{de}={-}^{*}{\widehat{T}}_{\nu }^{\nu }(3)=-3{\widehat{T}}_{\nu }^{\nu }(1)$, we have

$${\Lambda }_{dm}=-{\widehat{T}}_{\nu }^{\nu }(1)=\frac{{\Lambda }_{de}}{3},$$

(50)

the theoretical justification of which is given in the next section. Notice that the constant ${\widehat{T}}_{\nu }^{\nu }(1)$ appearing first in (39) is a quantity belonging to the off-shell electromagnetic field discussed in Section 2.1 in which spacelike CD field is introduced by the conformal symmetry breaking (CSB) of light-like CD field. Although we already alluded to the importance of CSB in our previous paper (S3O), our discussion on it in the context of cosmological dynamics remains quite vague. In the subsequent section covering the main theme of this paper, we will show that the new notion of CSB which applies simultaneously to electromagnetic as well as gravitational fields will play an important role in connecting our novel cosmological model to the preceding intriguing CCC proposed by Penrose [14,34].

4. Dressed Photon Constant and a New Version of CCC

4.1. Dressed Photon Constant

Using (39), (42), and (50), we have

$${\Lambda }_{dm}=\frac{4\pi Gh{({\kappa }_0)}^2}{c^3ϵ},$$

(51)

which is rewritten as follows in terms of the Planck length $l_p$, length scales of the universe $l_{dm}$, and DP:

$$\begin{array}{c}\hfill l_p:=\sqrt{hG/c^3},l_{dm}:=\sqrt{{({\Lambda }_{dm})}^{-1}},l_{dp}={({\kappa }_0)}^{-1},\end{array}$$

(52)

$$\begin{array}{c}\hfill l_p{l}_{dm}=\frac{\sqrt{ϵ}}{2\sqrt{\pi }}{l}_{dp}\to \left[l_p{l}_{dm}={({\widehat{l}}_{dp})}^2\right].\end{array}$$

(53)

Equation (53) reveals that if we choose ${\widehat{l}}_{dp}:=l_{dp}/2\sqrt{\pi }$ as the third component of a natural unit in which we set ${\widehat{l}}_{dp}=1$, then ${\widehat{l}}_{dp}$ gives the geometric mean of the smallest scale $l_p$ and the largest one of $l_{dm}$ in that natural unit system. By rewriting the second equation in (46) as

$$l_{dp}=\sqrt{\frac{12\pi Gh}{c^3ϵ}}{({\Lambda }_{de})}^{-1/2},\to l_{dp}^{†}=\sqrt{\frac{12\pi Gh}{c^3ϵ}}{({\Lambda }_{obs})}^{-1/2},$$

(54)

we can use this equation to estimate the DP constant $l_{dp}^{†}$ solely by the fundamental physical constants G, h, and c together with the observed cosmological constant ${\Lambda }_{obs}$ in place of the above ${\Lambda }_{de}$. Directly from the second equation in (54), we obtain

$$l_{dp}^{†}\approx 40.0\mathrm{nm},\left[\mathrm{Experiments}:50\mathrm{nm}<l_{dp}<70\mathrm{nm}\right].$$

(55)

4.2. New Version of CCC

The main aim of this subsection is to explain a new factor we would like to add to the CCC which has more than a decade of research history. At the present moment, we are not sure whether our new factor will fit consistently into the basic schemes of the CCC so far investigated. However, we hope that our proposal presented here could be a somewhat useful contribution to the CCC which is related, for instance, to a particular study by Lübbe [35] who discussed the inclusion problem of a cosmological constant. As our dark energy model introduced in (47) is related to de Sitter space, we start from the run-through of the well-known characteristics of it by looking into the Einstein field equation

$$R_{\mu }^{\nu }-\frac{R}{2}{g}_{\mu }^{\nu }-{\Lambda }_{de}{g}_{\mu }^{\nu }=0,$$

(56)

which yields a familiar solution given by

$$d{s}^2={(cdt)}^2-{(R_0)}^{2}exp\left[2\sqrt{\frac{{\Lambda }_{de}}{3}}ct\right][d{r}^2+r^2(d{\theta }^2+{sin}^2\theta )d{\phi }^2],$$

(57)

where the constant $R_0$ serves as the coefficient of the time-dependent scale factor. In the use of (50), this solution can be simplified by taking $R_0=l_p$ into

$$d{s}^2={(cdt)}^2-{(l_p)}^{2}exp\left[2\sqrt{{\Lambda }_{dm}}ct\right][d{r}^2+r^2(d{\theta }^2+{sin}^2\theta )d{\phi }^2].$$

(58)

At the end of Section 3, the simultaneous CSB in electromagnetic and gravitational fields was mentioned. We now explain what this exactly means. Recall that the energy-momentum tensor ${\widehat{T}}_{\mu }^{\nu }$ of the spacelike ($U_{\nu }{U}^{\nu }<0$) CD field is given in Section 2.1 by (26), which is isomorphic to the Einstein tensor $G_{\mu }^{\nu }$. The same quantity ${\widehat{T}}_{\mu }^{\nu }$ also emerges from the light-like case of $U_{\nu }{U}^{\nu }=0$ by replacing ${\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }\varphi =0$ with $[{\mathrm{\partial }}^{\nu }{\mathrm{\partial }}_{\nu }-{({\kappa }_0)}^2]\varphi =0$, which can be regarded as the breaking of both symmetries, i.e., conformal and gauge (cf. (10)). Therefore, this CSB from the light-like to the spacelike CD field can be seen as responsible simultaneously for the breaking from $d{s}^2=0$ to nonzero $d{s}^2$ in (58) through (53), which corresponds to the CSB of gravitational field with the scale parameter ${\Lambda }_{dm}$.

A well-known remarkable characteristic of the solution (58) is that it is transformed into a stationary solution

$$d{s}^2=\left(1-{\Lambda }_{dm}{(r^{\prime })}^2\right){(cd{t}^{\prime })}^2-\frac{{(d{r}^{\prime })}^2}{\left(1-{\Lambda }_{dm}{(r^{\prime })}^2\right)}-{(r^{\prime })}^2(d{\theta }^2+{sin}^2\theta d{\phi }^2)$$

(59)

by the following variable changes:

$$l_{p}r=\frac{r^{\prime }}{\sqrt{D}}exp[-\sqrt{{\Lambda }_{dm}}c{t}^{\prime }],t=t^{\prime }+\frac{1}{2c}\sqrt{\frac{1}{{\Lambda }_{dm}}}lnD,$$

(60)

where D is defined either by $1>D:=1-{\Lambda }_{dm}{(r^{\prime })}^2>0$ (case I) or by $1>D:={\Lambda }_{dm}{(r^{\prime })}^2-1>0$ (case II). Note that the metric (59) is similar in form to the Schwarzschild metric given below, for which an event horizon exists at $r^{\prime }=\alpha$, while that in (59) exists at $r^{\prime }=\sqrt{1/{\Lambda }_{dm}}$. (See Figure 1)

$$d{s}^2=\left(1-\frac{\alpha }{r^{\prime }}\right){(cd{t}^{\prime })}^2-\frac{{(d{r}^{\prime })}^2}{\left(1-\frac{\alpha }{r^{\prime }}\right)}-{(r^{\prime })}^2(d{\theta }^2+{sin}^2\theta d{\phi }^2).$$

(61)

In case I of the stationary metric (59), we have $r^{\prime }=0$ by the synchronization $t=t^{\prime }$ of t and $t^{\prime }$ owing to (60). If $t^{\prime }$ is adjusted as $t^{\prime }=\Theta t,(\Theta >1)$, then we see that $r^{\prime }$ moves from 0 to $1/\sqrt{({\Lambda }_{dm})}$ as t moves from 0 to $+\infty$. Similarly, in case II, we see that $r^{\prime }$ moves from $\sqrt{2/({\Lambda }_{dm})}$ to $1/\sqrt{({\Lambda }_{dm})}$ as t moves from 0 to $+\infty$. This dual structure, illustrated in Figure 1, clearly shows that by taking $t=0$ as the origin of time from which twin Big Bang universes evolve, they will meet at the event horizon in (59) an eon later ($t=\infty$). To the best of our knowledge, the concept of twin universes with matter vs. antimatter duality was first discussed by Petit [15]. We believe that his cosmological model fits exactly into the configuration illustrated in Figure 1, which tells us that $\sqrt{{({\Lambda }_{dm})}^{-1}}$ is a genuine characteristic length scale of our universe. This justifies the fact that ${\Lambda }_{dm}$ defined in (50) is the cosmological constant that appears in the form of (49). The forward and backward time evolutions of twin universes correspond, respectively, to positive and negative field operators of the 4-momentum, while the existence of twin universes naturally explains the reason why one-sided energy spectra at the level of state vector space works for many practical situations in each universe. If the birth of these twin universes was brought about by conformal symmetry breaking of certain light fields in which the duality between “matter (with positive energy) and antimatter (with negative energy)” works as the separation rule of the twin structure, then the twin pair will return to the original light fields when they meet at the event horizon. The next Big Bangs of the twin pair will occur at certain locations on this event horizon distant from each other by $\sqrt{2/{\Lambda }_{dm}}$.

According to the arguments developed thus far, we can say that the original conformal light field is composed of light fields with the following duality structures:

$$\begin{array}{ccc}& & \left[T_{\mu }^{\nu }=-F_{\mu \sigma }{F}^{\nu \sigma },{}^{*}{\widehat{T}}_{\mu }^{\nu }{=}^{*}(S_{\mu \sigma }{S}^{\nu \sigma }),T_0^0>0,{}^{*}{\widehat{T}}_0^0>0\right],\hfill \end{array}$$

(62)

$$\begin{array}{ccc}& & \left[{}^{*}{T}_{\mu }^{\nu }={-}^{*}(F_{\mu \sigma }{F}^{\nu \sigma }),{\widehat{T}}_{\mu }^{\nu }=S_{\mu \sigma }{S}^{\nu \sigma },{}^{*}{T}_0^0<0,{\widehat{T}}_0^0<0\right],\hfill \end{array}$$

(63)

where the symbol ${}^{*}$ denotes the Hodge duality explained in the derivation of (44). Although (62) and (63) can be considered as light and anti-light (light with positive energy moving backward in time) fields, respectively, they can coexist as free modes without interacting with each other, unlike the case of matter and antimatter interactions. As all of these fields are trace free, the associated Ricci scalar curvature is zero. Equation (26) tells us that the Riemann curvature associated with these light fields takes the form $R_{\lambda \rho \mu \nu }=F_{\lambda \rho }{F}_{\mu \nu }(=S_{\lambda \rho }{S}_{\mu \nu })$. In addition to $R_{\nu }^{\nu }=0$, we can readily show $R_{\mu \nu }{R}^{\mu \nu }=0$ using (23). Under the former condition $R_{\nu }^{\nu }=0$, the Weyl tensor $W_{\lambda \rho \mu \nu }$ assumes the form

$$W_{\lambda \rho \mu \nu }=R_{\lambda \rho \mu \nu }+\frac{1}{2}(R_{\lambda \mu }{g}_{\rho \nu }-R_{\lambda \nu }{g}_{\rho \mu }-R_{\rho \mu }{g}_{\lambda \nu }+R_{\rho \nu }{g}_{\lambda \mu });$$

(64)

thus, by direct calculations using the latter condition of $R_{\mu \nu }{R}^{\mu \nu }=0$, we obtain $W^2=0$. Therefore, for light fields (62) and (63), we have

$$R_{\nu }^{\nu }=0,W^2=W_{\nu \alpha \beta \gamma }{W}^{\nu \alpha \beta \gamma }=0.$$

(65)

The second equation in (65) is related to Penrose’s Weyl curvature hypothesis [14].

In modern cosmology, cosmic inflation theory was introduced to explain the observed highly tuned initial condition of the Big Bang, in which the notion of “false vacua” plays a key role in explaining the tremendous exponential expansion of space. In the introduction, however, we pointed out that the notion of the vacuum state in conventional QFT is highly biased by the one in Fock space, which may be called “Fock vacuum prejudice” if adhering to the idea of creation from emptiness. One of the aims of our present paper is to overcome this prejudice in the spirit of Occam’s razor as follows: in view of the present circumstances showing that inflation theory seems to be “lost in a maze” in achieving the above-mentioned original goal, the basic premise of our working hypothesis in cosmology can be shifted from the Fock vacuum to the phase transition of the extended light field arising from its CSB, according to which a simpler alternative view emerges such that the initial condition of the Big Bang and the dynamics of both dark energy and matter can be naturally explained.

For light fields, $d{s}^2=0$, the amplitude of the smallest perturbations of CSB in the length scale would be $l_p$ in (58), but its magnitude in the converted energy scale is tremendously large because energy is inversely proportional to length. By virtue of the Weyl curvature hypothesis of (65), and especially of the peculiar form of (49) through which the Weyl tensor contributes to part of the energy-momentum field, we see that the Weyl contribution to the energy field is a very low value of ${\Lambda }_{dm}$. Therefore, the energy field with extremely high density thus created must have a distribution in spacetime very close to the FRW metric on which small amplitude perturbations of $W^2$ exist. The emergence of the FRW metric is the result of unfolding the “blueprint” (14) encoded in the lightlike CD field. Note that in the limit of $W^2\to 0$, the energy-momentum field (49) approaches the anti-de Sitter (AdS) space; thus, the weak gravitational field and high energy conformal field share a common AdS spacetime, which is an essential part of the Maldacena duality [36]. In our new revised version of the CCC of twin universes, the beginning and end of the cycle are, respectively, compared to the pair creation and annihilation of elementary particles through the intervention of conformal light fields. Within the cycle in each universe, a couple of different classes of entities exist, i.e., both visible matter and invisible dark energy and dark matter exist. In S3O, we already discussed an extended thermodynamical viewpoint on the dynamics at cosmological scales.

When we take into account the remarkable abundance ratios of invisible dark energy and dark matter in comparison to the negligible one of ordinary visible matter, the time evolution of visible material subsystems in the universe, for instance, galaxy cluster formations, may be compared to the “heat engines” working between invisible “heat reservoirs” with higher and lower temperature, which, respectively, correspond to dark matter with positive energy and negative dark energy. If we denote the space averaged $W^2$ by $W^2{|}_{ave.}$, then due to the property of universal gravitation, it will increase with the passage of time and thus may be related to the gravitational entropy of the visible subsystem in the universe. From this viewpoint, the effect of the gravitational field, including that of dark matter, modeled as ${\Lambda }_{dm}{g}_{\mu \nu }$ in our theory, can be interpreted by a certain model of thermodynamics. Actually, attempts at this have already been made, for instance, in [37,38].

As the final remarks on CCC, first, we note that the conformal symmetry of source-free Maxwell’s equation holds well only in four dimensions, which may explain why the dimensions of spacetime in which we live are four. Second, the first author would appreciate if his philosophical preference of helical evolution to cyclic motion is reflected in CCC. His speculative “Book of Genesis” on CCC is as follows:

In the beginning, God, as a mathematician, created the primordial light with conformal symmetry, and God said: “Let there be conformal symmetry breaking, and there were twin universes, beginning their long journey towards a brighter future of a light world one stage higher in eternal evolution.”