New Variational Problems with an Action Depending on Generalized Fractional Derivatives, the Free Endpoint Conditions, and a Real Parameter

Abstract

This work presents optimality conditions for several fractional variational problems where the Lagrange function depends on fractional order operators, the initial and final state values, and a free parameter. The fractional derivatives considered in this paper are the Riemann–Liouville and the Caputo derivatives with respect to an arbitrary kernel. The new variational problems studied here are generalizations of several types of variational problems, and therefore, our results generalize well-known results from the fractional calculus of variations. Namely, we prove conditions useful to determine the optimal orders of the fractional derivatives and necessary optimality conditions involving time delays and arbitrary real positive fractional orders. Sufficient conditions for such problems are also studied. Illustrative examples are provided.

1. Introduction

Fractional calculus refers to the integration and differentiation of a non-integer order and is as old as the classical (integer order) calculus [1]. It is a subject that has gained much popularity and importance in the last few decades and has been applied in several fields of knowledge, such as mechanics [2,3], bioengineering [4], signal and image processing [5], physics [6,7], viscoelasticity [8], electrical engineering [9], economics [10], epidemiology [11,12], control theory [13,14], energy supply-demand systems [15], and fuzzy problems [16].

One of the specificities of fractional calculus is that there are many definitions of fractional derivatives that allow the researcher to choose the one that best corresponds to a given problem. Some of the most commonly used fractional derivatives are the Riemann–Liouville, the Erdélyi–Kober, the Caputo, the Hadamard, and the Grünwald–Letnikov derivatives. For a detailed study on this subject, see [1,17]. In this present work, we consider fractional operators with respect to an arbitrary kernel (see [17] for the Riemann–Liouville sense and [18] for the Caputo sense).

Fractional calculus of variations is a recent field that consists of minimizing or maximizing functionals that depend on fractional operators. The first works in this scientific area are due to Riewe [3,19]. Since then, many papers were published on different topics of the fractional calculus of variations for different types of fractional operators (see [2,20,21,22,23,24,25,26,27,28,29] and the references therein). For more details, we recommend the works [30,31,32].

By considering a more general form of the fractional derivative, like the Caputo fractional derivative with respect to an arbitrary kernel (see [18]), we can generalize different fractional variational problems. In [23,33], necessary and sufficient optimality conditions were proven for different variational problems depending on the Caputo fractional derivative with respect to an arbitrary kernel.

In [33], the following problem was studied: determine $x\in C^1([a,b],\mathbb{R})$ and $\zeta \in \mathbb{R}$ that extremize:

$$\mathcal{J}(x,\zeta ):={\int }_a^{b}L\left(t,x\left(t\right),\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{\delta ,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right)dt,$$

(1)

where $L\in C^1([a,b]\times {\mathbb{R}}^6,\mathbb{R})$ and ${}^C{D}_{a^{+}}^{\gamma ,g}x$ and ${}^C{D}_{b^{-}}^{\delta ,g}x$ denote, respectively, the left and right g-Caputo fractional derivatives of x of order $\gamma$ and $\delta$, with $\gamma ,\delta \in ]0,1[$ (see Definition 3). The main results of [33] are optimality conditions for variational problems with or without isoperimetric and holonomic constraints. The aim of this paper is to generalize these previous results. It is important to mention that this type of generalized fractional variational problem cannot be solved using the classical theory. Moreover, since the g-Caputo fractional derivatives are generalizations of several fractional derivatives and the variational problem (1) is a generalization of several kinds of the calculus of variation problems, the results obtained in [33] not only generalize some known results, but also give new contributions to the theory of the fractional calculus of variations.

In this paper, we prove optimality conditions for different fractional variational problems that are generalizations of the one introduced in [33]. Namely, we prove the generalized fractional variational principle for problems with optimal orders, with time delay and with arbitrary real order fractional derivatives. In addition, we prove sufficient optimality conditions for all of the problems considered in the paper.

This main structure of this paper is as follows. In Section 2, we present some preliminaries on fractional calculus. In Section 3, we exhibit the main results. We finish the paper with two examples and some conclusions.

2. Preliminaries

We begin with a brief review of some important concepts and results that will be used in this paper. In what follows, $\mathrm{\Gamma }$ represents the well-known Gamma function, and the integer part of $\gamma \in \mathbb{R}$ is denoted by $\left[\gamma \right]$.

Definition 1.

[17] Let γ be a positive real, $g:[a,b]\to \mathbb{R}$ a $C^1$ function with positive derivative, and $x\in L^1([a,b],\mathbb{R})$. The left Riemann–Liouville fractional integral of x of order γ, with respect to the kernel g, is defined as:

$$\left(I_{a^{+}}^{\gamma ,g}x\right)\left(t\right):=\frac{1}{\mathrm{\Gamma }\left(\gamma \right)}{\int }_a^t{g}^{\prime }\left(\tau \right){(g\left(t\right)-g\left(\tau \right))}^{\gamma -1}x\left(\tau \right)d\tau ,t>a,$$

and the right derivative is given by:

$$\left(I_{b^{-}}^{\gamma ,g}x\right)\left(t\right):=\frac{1}{\mathrm{\Gamma }\left(\gamma \right)}{\int }_t^b{g}^{\prime }\left(\tau \right){(g\left(\tau \right)-g\left(t\right))}^{\gamma -1}x\left(\tau \right)d\tau ,t<b.$$

Next, we present the definitions of the g-Riemann–Liouville fractional derivatives of a function x of order $\gamma$.

Definition 2.

[17] Let γ be a positive real, $g:[a,b]\to \mathbb{R}$ a $C^n$ function with positive derivative, and $x\in L^1([a,b],\mathbb{R})$. The left Riemann–Liouville fractional derivative of x of order γ, with respect to the kernel g, is given by:

$$\left(D_{a^{+}}^{\gamma ,g}x\right)\left(t\right):={\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n\left(I_{a^{+}}^{n-\gamma ,g}x\right)\left(t\right),t>a,$$

and the right derivative by:

$$\left(D_{b^{-}}^{\gamma ,g}x\right)\left(t\right):={\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^n\left(I_{b^{-}}^{n-\gamma ,g}x\right)\left(t\right),t<b,$$

where $n=\left[\gamma \right]+1$.

Remark 1.

It is easily seen that:

1. 

for certain choices of the kernel g, we recover well-known fractional derivatives, such as Riemann–Liouville ($g\left(t\right)=t$), Hadamard ($g\left(t\right)=ln\left(t\right)$, $a>0$), and Erdélyi–Kober fractional derivatives ($g\left(t\right)=t^{\sigma }$, $\sigma >0$);

2. 

if $\gamma =m\in \mathbb{N}$, then:

$$\left(D_{a^{+}}^{\gamma ,g}x\right)\left(t\right)={\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{m}x\left(t\right)and\left(D_{b^{-}}^{\gamma ,g}x\right)\left(t\right)={\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{m}x\left(t\right).$$

Next, the concept of g-Caputo fractional derivatives of x of order $\gamma$ is presented, which is fundamental for the formulation of our problem.

Definition 3.

[18] Let γ be a positive real and:

$$n=\left\{\begin{array}{cc}\left[\gamma \right]+1\hfill & if\gamma \notin \mathbb{N}\hfill \\ \gamma \hfill & if\gamma \in \mathbb{N}\hfill \end{array}\right.$$

Let $x,g$ be two real $C^n$ functions defined on $[a,b]$, where g satisfies $g^{\prime }\left(t\right)>0$. The left Caputo fractional derivative of x of order γ, with respect to the kernel g, is defined as:

$$\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right):=\left(I_{a^{+}}^{n-\gamma ,g}{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n}x\right)\left(t\right),t>a,$$

and the right derivative as:

$$\left({}^C{D}_{b^{-}}^{\gamma ,g}x\right)\left(t\right):=\left(I_{b^{-}}^{n-\gamma ,g}{\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n}x\right)\left(t\right),t<b.$$

Remark 2.

It is clear that if g is the identity, then ${}^C{D}_{a^{+}}^{\gamma ,g}x$ and ${}^C{D}_{b^{-}}^{\gamma ,g}x$ are the usual Caputo fractional derivatives of x. Notice that if $\gamma =m\in \mathbb{N}$, then:

$$\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right)={\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{m}x\left(t\right)and\left({}^C{D}_{b^{-}}^{\gamma ,g}x\right)\left(t\right)={\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{m}x\left(t\right).$$

Otherwise,

$$\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\gamma )}{\int }_a^t{g}^{\prime }\left(\tau \right){(g\left(t\right)-g\left(\tau \right))}^{n-\gamma -1}{\left(\frac{1}{g^{\prime }\left(\tau \right)}\frac{d}{d\tau }\right)}^{n}x\left(\tau \right)d\tau$$

and:

$$\left({}^C{D}_{b^{-}}^{\gamma ,g}x\right)\left(t\right)=\frac{1}{\mathrm{\Gamma }(n-\gamma )}{\int }_t^b{g}^{\prime }\left(\tau \right){(g\left(\tau \right)-g\left(t\right))}^{n-\gamma -1}{\left(-\frac{1}{g^{\prime }\left(\tau \right)}\frac{d}{d\tau }\right)}^{n}x\left(\tau \right)d\tau .$$

Since the integration by parts formula is of great importance in the calculus of variations, we state here this basic result.

Theorem 1.

[18] Let x be a continuous function and $y,g$ two $C^n$ functions, with domain $[a,b]$. Then,

$$\begin{array}{cc}\hfill {\int }_a^b& x\left(t\right)·\left({}^C{D}_{a^{+}}^{\gamma ,g}y\right)\left(t\right)dt={\int }_a^{b}y\left(t\right)·\left(D_{b^{-}}^{\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)dt\hfill \\ \hfill & +{\left[\sum _{k=0}^{n-1}{\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^k\left(I_{b^{-}}^{n-\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)·{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n-k-1}y\left(t\right)\right]}_{t=a}^{t=b}\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill {\int }_a^b& x\left(t\right)·\left({}^C{D}_{b^{-}}^{\gamma ,g}y\right)\left(t\right)dt={\int }_a^{b}y\left(t\right)·\left(D_{a^{+}}^{\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)dt\hfill \\ \hfill & +{\left[\sum _{k=0}^{n-1}{(-1)}^{n-k}{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^k\left(I_{a^{+}}^{n-\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)·{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{n-k-1}y\left(t\right)\right]}_{t=a}^{t=b}.\hfill \end{array}$$

Remark 3.

In particular, if $0<\gamma <1$, Theorem 1 reduces to:

$${\int }_a^{b}x\left(t\right)·\left({}^C{D}_{a^{+}}^{\gamma ,g}y\right)\left(t\right)dt={\int }_a^{b}y\left(t\right)·\left(D_{b^{-}}^{\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)dt+{\left[\left(I_{b^{-}}^{1-\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)·y\left(t\right)\right]}_{t=a}^{t=b}$$

and:

$${\int }_a^{b}x\left(t\right)·\left({}^C{D}_{b^{-}}^{\gamma ,g}y\right)\left(t\right)dt={\int }_a^{b}y\left(t\right)·\left(D_{a^{+}}^{\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)dt-{\left[\left(I_{a^{+}}^{1-\gamma ,g}\frac{x}{g^{\prime }}\right)\left(t\right)·y\left(t\right)\right]}_{t=a}^{t=b}.$$

Next, we present the following result, which is useful in applications. For a more detailed study of the g-Caputo fractional derivatives, we refer to [18].

Lemma 1.

[18] If $n<\sigma \in \mathbb{R}$, then:

$${}^C{D}_{a^{+}}^{\gamma ,g}{(g\left(t\right)-g\left(a\right))}^{\sigma -1}=\frac{\mathrm{\Gamma }\left(\sigma \right)}{\mathrm{\Gamma }(\sigma -\gamma )}{(g\left(t\right)-g\left(a\right))}^{\sigma -\gamma -1}$$

and:

$${}^C{D}_{b^{-}}^{\gamma ,g}{(g\left(b\right)-g\left(t\right))}^{\sigma -1}=\frac{\mathrm{\Gamma }\left(\sigma \right)}{\mathrm{\Gamma }(\sigma -\gamma )}{(g\left(b\right)-g\left(t\right))}^{\sigma -\gamma -1}.$$

Throughout the text, the partial derivative of L with respect to its i-th argument is denoted by ${\partial }_{i}L$.

3. Main Results

Now, we are ready to present the main contributions of this work, by proving some generalizations of the fractional variational problem studied in [33]. The results of the paper are trivially generalized for the case of vector functions x.

3.1. Generalized Fractional Variational Principle with Optimal Orders

One of the advantages of fractional derivatives is that, in many real problems, they better describe the dynamics of the problems compared to the classical derivative. With this in mind, a natural issue is to include the order of the fractional derivatives in the optimization process, that is, the variational problem under study consists of finding a curve x, a parameter $\zeta$, and the order of the fractional derivatives $\gamma$ and $\delta$ that extremize the variational functional.

Consider the following problem:

Problem 1.

Determine the functions $x:[a,b]\to \mathbb{R}$ of class $C^1$, the parameters $\zeta \in \mathbb{R}$, and fractional orders $\gamma ,\delta \in ]0,1[$ that minimize or maximize:

$${\mathcal{J}}_1(x,\zeta ,\gamma ,\delta ):={\int }_a^{b}L\left(t,x\left(t\right),\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{\delta ,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right)dt,$$

(2)

where $L\in C^1([a,b]\times {\mathbb{R}}^6,\mathbb{R})$ and $x\left(a\right)$ and $x\left(b\right)$ can be fixed or free.

For simplification, we use the notation:

$$[x,\zeta ,\gamma ,\delta ]\left(t\right):=\left(t,x\left(t\right),\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{\delta ,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right).$$

The next result is the optimal fractional order variational principle for Problem 1.

Theorem 2.

If $(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})$ is an extremizer of functional ${\mathcal{J}}_1$ defined by (2) and if the maps:

$$t\mapsto \left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)andt\mapsto \left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)$$

are continuous, then, for all t,

$$\begin{array}{c}{\partial }_{2}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)+\left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)\hfill \\ \hfill +\left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)=0.\end{array}$$

(3)

Furthermore, the following conditions hold:

$${\displaystyle {\int }_a^b{\partial }_{7}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt=0,}$$

(4)

$${\displaystyle {\int }_a^b{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt=0,}$$

(5)

$${\displaystyle {\int }_a^b{g}_t^{\prime }\left({\delta }^{★}\right)·{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt=0,}$$

(6)

where, for each $t\in [a,b]$, $f_t:]0,1[\to \mathbb{R}$ and $g_t:]0,1[\to \mathbb{R}$ are the functions defined as follows:

$$f_t\left(\gamma \right)={(}^C{D}_{a^{+}}^{\gamma ,g}{x}^{★})\left(t\right)and{g}_t\left(\delta \right)={(}^C{D}_{b^{-}}^{\delta ,g}{x}^{★})\left(t\right).$$

If $x\left(a\right)$ is not fixed, the following is verified:

$$\begin{array}{c}{\int }_a^b{\partial }_{5}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt\hfill \\ \hfill =\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(a\right)-\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(a\right);\end{array}$$

(7)

Furthermore, if $x\left(b\right)$ is not fixed,

$$\begin{array}{c}{\int }_a^b{\partial }_{6}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt\hfill \\ \hfill =\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(b\right)-\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(b\right).\end{array}$$

(8)

Proof. 

Suppose that $(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})$ is an extremizer for functional ${\mathcal{J}}_1$. Hence, for any (fixed) $\eta \in C^1([a,b],\mathbb{R})$, $\mathrm{\Delta }\zeta ,\mathrm{\Delta }\gamma ,\mathrm{\Delta }\delta \in \mathbb{R}$ such that $0<{\gamma }^{★}+ϵ\mathrm{\Delta }\gamma <1$ and $0<{\delta }^{★}+ϵ\mathrm{\Delta }\delta <1$, with $ϵ$ in a neighborhood of zero, we conclude that:

$$\frac{d}{dϵ}{\mathcal{J}}_1(x^{★}+ϵ\eta ,{\zeta }^{★}+ϵ\mathrm{\Delta }\zeta ,{\gamma }^{★}+ϵ\mathrm{\Delta }\gamma ,{\delta }^{★}+ϵ\mathrm{\Delta }\delta ){|}_{ϵ=0}=0.$$

Therefore, the following condition holds:

$$\begin{array}{c}{\displaystyle {\int }_a^b({\partial }_{2}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\eta \left(t\right)+{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\left(f_t^{\prime }\left({\gamma }^{★}\right)\mathrm{\Delta }\gamma +{(}^C{D}_{a^{+}}^{{\gamma }^{★},g}\eta )\left(t\right)\right)}\hfill \\ {\displaystyle +{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\left(g_t^{\prime }\left({\delta }^{★}\right)\mathrm{\Delta }\delta +{(}^C{D}_{b^{-}}^{{\delta }^{★},g}\eta )\left(t\right)\right)}\\ \hfill {\displaystyle +{\partial }_{5}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\eta \left(a\right)+{\partial }_{6}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\eta \left(b\right)+{\partial }_{7}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\mathrm{\Delta }\zeta )dt=0.}\end{array}$$

Integration by parts gives (see Remark 3):

$$\begin{array}{c}{\displaystyle {\int }_a^b({\partial }_{2}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)+\left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)}\hfill \\ {\displaystyle +\left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right))·\eta \left(t\right)dt+{\left[\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}}\\ {\displaystyle -{\left[\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}}\\ {\displaystyle +\mathrm{\Delta }\gamma {\int }_a^b{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt+\mathrm{\Delta }\delta {\int }_a^b{g}_t^{\prime }\left({\delta }^{★}\right)·{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt}\\ {\displaystyle +{\int }_a^b({\partial }_{5}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\eta \left(a\right)+{\partial }_{6}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\eta \left(b\right)}\\ \hfill +{\partial }_{7}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)·\mathrm{\Delta }\zeta )dt=0.\end{array}$$

(9)

We first consider functions $\eta$ such that $\eta \left(a\right)=\eta \left(b\right)=0$. In this case, Equation (9) becomes:

$$\begin{array}{c}{\displaystyle {\int }_a^b({\partial }_{2}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)+\left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)}\hfill \\ {\displaystyle +\left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right))·\eta \left(t\right)dt+\mathrm{\Delta }\gamma {\int }_a^b{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt}\\ \hfill {\displaystyle +\mathrm{\Delta }\delta {\int }_a^b{g}_t^{\prime }\left({\delta }^{★}\right)·{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt+\mathrm{\Delta }\zeta {\int }_a^b{\partial }_{7}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt=0.}\end{array}$$

(10)

By the arbitrariness of $\mathrm{\Delta }\gamma$, $\mathrm{\Delta }\delta$, and $\mathrm{\Delta }\zeta$, if we consider that all of them are null, using Lemma 2.2.2 in [34], we get:

$$\begin{array}{c}{\partial }_{2}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)+\left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)\hfill \\ & \hfill +\left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)=0,\end{array}$$

for all t, proving the Euler–Lagrange Equation (3). Since $(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})$ satisfies Equality (3) for all $t\in [a,b]$, the first integral in (10) vanishes, and then, it takes the form:

$$\begin{array}{c}{\displaystyle \mathrm{\Delta }\gamma {\int }_a^b{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt+\mathrm{\Delta }\delta {\int }_a^b{g}_t^{\prime }\left({\delta }^{★}\right)·{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt}\hfill \\ \hfill {\displaystyle +\mathrm{\Delta }\zeta {\int }_a^b{\partial }_{7}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt=0.}\end{array}$$

(11)

By the arbitrariness of $\mathrm{\Delta }\gamma$, $\mathrm{\Delta }\delta$, and $\mathrm{\Delta }\zeta$, we deduce from (11) the necessary conditions (4)–(6). We now seek the natural boundary conditions.

1.

If $x\left(a\right)$ is not fixed in the formulation of the problem, then $\eta$ need not to be null at $t=a$. Restricting $\eta$ to be null at $t=b$ and substituting the necessary conditions (3)–(6) into (9), it follows that:

$$\begin{array}{c}\hfill (\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(a\right)-\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]}{g^{\prime }}\right)\left(a\right)\\ \hfill +{\int }_a^b{\partial }_{5}L[x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★}]\left(t\right)dt)·\eta \left(a\right)=0.\end{array}$$

Since $\eta \left(a\right)$ is an arbitrary real, we prove (7).

2.

Suppose now that $x\left(b\right)$ is not fixed. Restricting $\eta$ to be null at $t=a$ and using similar arguments as previously, we get Equation (8).

 □

Remark 4.

We note that if L does not depend on ${(}^C{D}_{b^{-}}^{\delta ,g}x)\left(t\right)$, $x\left(a\right)$, $x\left(b\right)$, and ζ, then Theorem 2 reduces to Theorem 2.9 from [23] if the final time is fixed.

3.2. Generalized Variational Problems with Time Delay

It is known that a delay is inherent in many problems, such as in control theory, bioengineering, electrochemistry, and social sciences. Differential equations with time delays have been used to model complex systems and have led to an intense topic of research for many years. Although fractional derivatives are not local in nature and are capable of modeling memory effects, delays are also very important because they take into account the system’s history from a previous state. For these reasons, many real-world problems can be modeled more precisely, including fractional derivatives and time delays. In recent years, delayed fractional differential equations have started to attract the attention of many researchers [35,36,37]. Few works are yet devoted to fractional variational problems with time delay so far [38,39,40].

Encouraged by the importance of considering a delay in many real-world problems, we study here the following fractional problem with a time delay $\tau$, where $\tau \in \mathbb{R}$ satisfies $0\le \tau <b-a$.

Problem 2.

Determine a $C^1$ function $x:[a-\tau ,b]\to \mathbb{R}$, subject to $x\left(t\right)=X\left(t\right)$, for all $t\in [a-\tau ,a]$, where X is a given initial function of class $C^1$ and $\zeta \in \mathbb{R}$ that minimize or maximize:

$${\mathcal{J}}_2(x,\zeta ):={\int }_a^{b}L\left(t,x\left(t\right),x(t-\tau ),\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{\delta ,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right)dt,$$

(12)

where $L\in C^1([a,b]\times {\mathbb{R}}^7,\mathbb{R})$.

Define:

$${[x,\zeta ]}_{\tau }\left(t\right):=\left(t,x\left(t\right),x(t-\tau ),\left({}^C{D}_{a^{+}}^{\gamma ,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{\delta ,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right).$$

Theorem 3.

Suppose that $(x^{★},{\zeta }^{★})$ is an extremizer of ${\mathcal{J}}_2$ defined by (12) and that the functions exist and are continuous:

$$t\mapsto \left(D_{{(b-\tau )}^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)andt\mapsto \left(D_{a^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)on[a,b-\tau ]$$

and:

$$t\mapsto \left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)andt\mapsto \left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)on[b-\tau ,b].$$

Then, for all $t\in [a,b-\tau ]$,

$$\begin{array}{c}{\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)+{\partial }_{3}L{[x^{★},{\zeta }^{★}]}_{\tau }(t+\tau )+\left(D_{{(b-\tau )}^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\hfill \\ \hfill +\left(D_{a^{+}}^{{\delta }^{,}g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)-\frac{1}{\mathrm{\Gamma }(1-\gamma )}\frac{d}{dt}{\int }_{b-\tau }^b{(g\left(s\right)-g\left(t\right))}^{-\gamma }{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds=0,\end{array}$$

(13)

and for all $t\in [b-\tau ,b]$,

$$\begin{array}{c}{\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)+\left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)+\left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\hfill \\ \hfill +\frac{1}{\mathrm{\Gamma }(1-\delta )}\frac{d}{dt}{\int }_a^{b-\tau }{(g\left(t\right)-g\left(s\right))}^{-\delta }{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds=0.\end{array}$$

(14)

Moreover,

$${\displaystyle {\int }_a^b{\partial }_{8}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)dt=0}$$

(15)

and if $x\left(b\right)$ is not fixed, then:

$${\int }_a^b{\partial }_{7}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)dt=\left(I_{a^{+}}^{1-\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(b\right)-\left(I_{b^{-}}^{1-\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(b\right).$$

(16)

Proof. 

Let $\eta :[a-\tau ,b]\to \mathbb{R}$ be a $C^1$ function vanishing on $[a-\tau ,a]$, and let $\mathrm{\Delta }\zeta$ be a real. Consider:

$$\varpi \left(ϵ\right)={\mathcal{J}}_2(x^{★}+ϵ\eta ,{\zeta }^{★}+ϵ\mathrm{\Delta }\zeta )$$

defined on an open interval containing zero. Since $(x^{★},{\zeta }^{★})$ is an extremizer of ${\mathcal{J}}_2$, then ${\varpi }^{\prime }\left(0\right)=0$, and therefore:

$$\begin{array}{c}{\displaystyle {\int }_a^b({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta \left(t\right)+{\partial }_{3}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta (t-\tau )+{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·{(}^C{D}_{a^{+}}^{\gamma ,g}\eta )\left(t\right)}\hfill \\ {\displaystyle +{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·{(}^C{D}_{b^{-}}^{\delta ,g}\eta )\left(t\right)+{\partial }_{6}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta \left(a\right)+{\partial }_{7}L[x,\zeta ]\left(t\right)·\eta \left(b\right)}\\ \hfill {\displaystyle +{\partial }_{8}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\mathrm{\Delta }\zeta )dt=0.}\end{array}$$

(17)

Considering $t=u+\tau$, we obtain:

$${\int }_a^b{\partial }_{3}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta (t-\tau )dt={\int }_a^{b-\tau }{\partial }_{3}L{[x^{★},{\zeta }^{★}]}_{\tau }(t+\tau )·\eta \left(t\right)dt.$$

(18)

Observe that, for $a\le t\le b-\tau$,

$$\begin{array}{cc}\left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)\hfill & =\left(D_{{(b-\tau )}^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)\hfill \\ & \hfill -\frac{1}{\mathrm{\Gamma }(1-\gamma )}\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right){\int }_{b-\tau }^b{(g\left(s\right)-g\left(t\right))}^{-\gamma }{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds\end{array}$$

(19)

and for $b-\tau \le t\le b$,

$$\begin{array}{cc}\left(D_{a^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)\hfill & =\left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)\hfill \\ & \hfill +\frac{1}{\mathrm{\Gamma }(1-\delta )}\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right){\int }_a^{b-\tau }{(g\left(t\right)-g\left(s\right))}^{-\delta }{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds.\end{array}$$

(20)

By Theorem 1 and (19), we obtain:

$$\begin{array}{c}{\int }_a^b{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·{(}^C{D}_{a^{+}}^{\gamma ,g}\eta )\left(t\right)dt={\int }_a^{b-\tau }(\left(D_{{(b-\tau )}^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\hfill \\ -\frac{1}{\mathrm{\Gamma }(1-\gamma )}\frac{d}{dt}{\int }_{b-\tau }^b{(g\left(s\right)-g\left(t\right))}^{-\gamma }{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds)·\eta \left(t\right)dt\\ \hfill +{\int }_{b-\tau }^b\left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)·\eta \left(t\right)dt+{\left[\left(I_{b^{-}}^{1-\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}.\end{array}$$

(21)

Again, by Theorem 1 and (20), we obtain:

$$\begin{array}{c}{\int }_a^b{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·{(}^C{D}_{b^{-}}^{\delta ,g}\eta )\left(t\right)dt={\int }_a^{b-\tau }\left(D_{a^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)·\eta \left(t\right)dt\hfill \\ -{\left[\left(I_{a^{+}}^{1-\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}+{\int }_{b-\tau }^b(\left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\\ \hfill +\frac{1}{\mathrm{\Gamma }(1-\delta )}\frac{d}{dt}{\int }_a^{b-\tau }{(g\left(t\right)-g\left(s\right))}^{-\delta }{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds)·\eta \left(t\right)dt.\end{array}$$

(22)

Introducing (18), (21), and (22) into Equation (17), we can conclude that:

$$\begin{array}{c}{\displaystyle {\int }_a^{b-\tau }({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)+{\partial }_{3}L{[x^{★},{\zeta }^{★}]}_{\tau }(t+\tau )+\left(D_{{(b-\tau )}^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)}\hfill \\ -\frac{1}{\mathrm{\Gamma }(1-\gamma )}\frac{d}{dt}{\int }_{b-\tau }^b{(g\left(s\right)-g\left(t\right))}^{-\gamma }{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds+\left(D_{a^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right))·\eta \left(t\right)dt\\ {\displaystyle +{\int }_{b-\tau }^b({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)+\left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)+\left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)}\\ +\frac{1}{\mathrm{\Gamma }(1-\delta )}\frac{d}{dt}{\int }_a^{b-\tau }{(g\left(t\right)-g\left(s\right))}^{-\delta }{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds)·\eta \left(t\right)dt\\ {\displaystyle +{\left[\left(I_{b^{-}}^{1-\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}-{\left[\left(I_{a^{+}}^{1-\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}}\\ \hfill +{\int }_a^b({\partial }_{6}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta \left(a\right)+{\partial }_{7}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta \left(b\right)+{\partial }_{8}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\mathrm{\Delta }\zeta )dt=0.\end{array}$$

(23)

Since Equation (23) is valid for any variations $\eta$ and all $\mathrm{\Delta }\zeta$, assuming that $\eta$ vanishes on the interval $[b-\tau ,b]$ and taking $\Delta \zeta =0$, from Lemma 2.2.2 in [34], we prove that Condition (13) holds on $[a,b-\tau ]$. Restricting the variations $\eta$ to those functions that satisfy $\eta \left(b\right)=0$ and introducing Condition (13) into (23), we obtain:

$$\begin{array}{c}{\displaystyle {\int }_{b-\tau }^b({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)+\left(D_{b^{-}}^{\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)+\left(D_{{(b-\tau )}^{+}}^{\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)}\hfill \\ +\frac{1}{\mathrm{\Gamma }(1-\delta )}\frac{d}{dt}{\int }_a^{b-\tau }{(g\left(t\right)-g\left(s\right))}^{-\delta }{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(s\right)ds)·\eta \left(t\right)dt\\ \hfill +{\int }_a^b{\partial }_{8}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\mathrm{\Delta }\zeta dt=0.\end{array}$$

(24)

Since the last equality holds for all $\mathrm{\Delta }\zeta$, then, in particular, it holds for $\mathrm{\Delta }\zeta =0$; hence, from Lemma 2.2.2 in [34], Condition (14) holds on the interval $[b-\mathrm{\tau },b]$. Introducing (14) into (24), we conclude, from the arbitrariness of $\Delta \zeta$, that ${\displaystyle {\int }_a^b{\partial }_{8}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)dt=0,}$ proving the necessary condition (15). If $x\left(b\right)$ is free, $\eta \left(b\right)$ need not to be null; in this case, we get from (23) that:

$$\begin{array}{c}{\int }_a^b{\partial }_{7}L{[x^{★},{\zeta }^{★}]}_{\tau }\left(t\right)·\eta \left(b\right)dt+\left(I_{b^{-}}^{1-\gamma ,g}\frac{{\partial }_{4}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(b\right)·\eta \left(b\right)\hfill \\ \hfill -\left(I_{a^{+}}^{1-\delta ,g}\frac{{\partial }_{5}L{[x^{★},{\zeta }^{★}]}_{\tau }}{g^{\prime }}\right)\left(b\right)·\eta \left(b\right)=0.\end{array}$$

From the arbitrariness of $\eta \left(b\right)$, we prove Condition (16), as desired. □

Remark 5.

We remark that:

1. 

if the delay is removed ($\tau =0$), then Problem 2 coincides with the problem given by (1) if we consider $x\left(a\right)$ fixed, and therefore, the fractional variational principle given by Theorem 3 in [33] can be obtained from Theorem 3;

2. 

when the final time is fixed, Theorem 2.7 in [23] can be obtained from Theorem 3.

3.3. Generalized Higher Order Fractional Variational Principle

In this subsection, we consider an extension of the generalized variational problem given by (1), by including in the Lagrangian function arbitrary real fractional orders $\gamma ,\delta >0$. With this, we obtain what is known as a fractional variational problem with arbitrary higher order fractional derivatives. The problem formulation is the following.

Problem 3.

Find functions $x:[a,b]\to \mathbb{R}$ of class $C^n$ and $\zeta \in \mathbb{R}$ that minimize or maximize the functional:

$$\begin{array}{c}{\mathcal{J}}_3(x,\zeta ):={\int }_a^{b}L\left(t,x\left(t\right),\left({}^C{D}_{a^{+}}^{{\gamma }_1,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{{\delta }_1,g}x\right)\left(t\right),\dots ,\left({}^C{D}_{a^{+}}^{{\gamma }_n,g}x\right)\left(t\right),\right.\hfill \\ \hfill \left.\left({}^C{D}_{b^{-}}^{{\delta }_n,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right)dt,\end{array}$$

(25)

where $L\in C^1([a,b]\times {\mathbb{R}}^{2n+4},\mathbb{R})$, and $k-1<{\gamma }_k,{\delta }_k<k$, for $k=1,\dots ,n$. Furthermore, the boundary conditions:

$$x^{\left(k\right)}\left(a\right)=x_a^{k}and{x}^{\left(k\right)}\left(b\right)=x_b^k,k=1,\dots ,n-1,$$

(26)

are assumed to hold, where $x_a^k,x_b^k\in \mathbb{R}$ are fixed, for all k.

To abbreviate, define:

$${[x,\zeta ]}_n\left(t\right):=\left(t,x\left(t\right),\left({}^C{D}_{a^{+}}^{{\gamma }_1,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{{\delta }_1,g}x\right)\left(t\right),\dots ,\left({}^C{D}_{a^{+}}^{{\gamma }_n,g}x\right)\left(t\right),\left({}^C{D}_{b^{-}}^{{\delta }_n,g}x\right)\left(t\right),x\left(a\right),x\left(b\right),\zeta \right).$$

Theorem 4.

If $(x^{★},{\zeta }^{★})$ is an extremizer of functional ${\mathcal{J}}_3$ defined by (25) and the functions exist and are continuous:

$$t\mapsto \left(D_{b^{-}}^{{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)andt\mapsto \left(D_{a^{+}}^{{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right),$$

for all $i=1,\dots ,n$, then:

$$\begin{array}{c}{\partial }_{2}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)+\sum _{i=1}^n\left[\left(D_{b^{-}}^{{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\right.\hfill \\ \hfill \left.+\left(D_{a^{+}}^{{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)·g^{\prime }\left(t\right)\right]=0\end{array}$$

(27)

and:

$${\displaystyle {\int }_a^b{\partial }_{2n+5}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)dt=0.}$$

(28)

If $x\left(a\right)$ is not fixed, then:

$$\begin{array}{cc}\hfill {\int }_a^b{\partial }_{2n+3}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)dt=[\sum _{i=1}^n& ({\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{b^{-}}^{i-{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)\hfill \\ \hfill & -{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{a^{+}}^{i-{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)){]}_{t=a},\hfill \end{array}$$

(29)

and if $x\left(b\right)$ is not fixed, then:

$$\begin{array}{cc}\hfill {\int }_a^b{\partial }_{2n+4}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)dt=[\sum _{i=1}^n& ({\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{a^{+}}^{i-{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)\hfill \\ \hfill & -{\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{b^{-}}^{i-{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)){]}_{t=b}.\hfill \end{array}$$

(30)

Proof. 

Consider the pair given by $(x^{★}+ϵ\eta ,{\zeta }^{★}+ϵ\mathrm{\Delta }\zeta )$, where $\eta \in C^n([a,b],\mathbb{R})$ satisfies ${\eta }^{\left(i\right)}\left(a\right)=0$ and ${\eta }^{\left(i\right)}\left(b\right)=0$, for all $i\in \{1,\dots ,n-1\}$, and $\mathrm{\Delta }\zeta ,ϵ$ are two arbitrary real numbers. Observe that:

$${\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^i\eta \left(t\right)=0\mathrm{a}\mathrm{t}t\in \{a,b\},\forall i\in \{1,\dots ,n-1\}.$$

Defining:

$$\nu \left(ϵ\right)={\mathcal{J}}_3(x^{★}+ϵ\eta ,{\zeta }^{★}+ϵ\mathrm{\Delta }\zeta ),$$

the condition ${\nu }^{\prime }\left(0\right)=0$ implies that:

$$\begin{array}{c}{\int }_a^b({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\eta \left(t\right)+\sum _{i=1}^n\left[{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\left({}^C{D}_{a^{+}}^{{\gamma }_i,g}\eta \right)\left(t\right)\right.\hfill \\ \left.+{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\left({}^C{D}_{b^{-}}^{{\delta }_i,g}\eta \right)\left(t\right)\right]+{\partial }_{2n+3}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\eta \left(a\right)\\ \hfill +{\partial }_{2n+4}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\eta \left(b\right)+{\partial }_{2n+5}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\mathrm{\Delta }\zeta )dt=0.\end{array}$$

Applying Theorem 1, we get, for each $i\in \{1,\dots ,n\}$,

$$\begin{array}{cc}\hfill {\int }_a^b{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·& \left({}^C{D}_{a^{+}}^{{\gamma }_i,g}\eta \right)\left(t\right)dt={\int }_a^b\left(D_{b^{-}}^{{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)·\eta \left(t\right)dt\hfill \\ \hfill & +{\left[{\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{b^{-}}^{i-{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}\hfill \end{array}$$

and:

$$\begin{array}{cc}\hfill {\int }_a^b{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·& \left({}^C{D}_{b^{-}}^{{\delta }_i,g}\eta \right)\left(t\right)dt={\int }_a^b\left(D_{a^{+}}^{{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)·\eta \left(t\right)dt\hfill \\ \hfill & -{\left[{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{a^{+}}^{i-{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)·\eta \left(t\right)\right]}_{t=a}^{t=b}.\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill {\int }_a^b({\partial }_{2}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)+\sum _{i=1}^n[& \left(D_{b^{-}}^{{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)\hfill \\ \hfill & +\left(D_{a^{+}}^{{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)\left]\right)·\eta \left(t\right)dt\hfill \\ \hfill +\sum _{i=1}^n\left[\right(& {\left(-\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{b^{-}}^{i-{\gamma }_i,g}\frac{{\partial }_{2i+1}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right)\hfill \\ \hfill & -{\left(\frac{1}{g^{\prime }\left(t\right)}\frac{d}{dt}\right)}^{i-1}\left(I_{a^{+}}^{i-{\delta }_i,g}\frac{{\partial }_{2i+2}L{[x^{★},{\zeta }^{★}]}_n}{g^{\prime }}\right)\left(t\right))·\eta \left(t\right){]}_{t=a}^{t=b}\hfill \\ \hfill +{\int }_a^b({\partial }_{2n+3}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\eta \left(a\right)& +{\partial }_{2n+4}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\eta \left(b\right)+{\partial }_{2n+5}L{[x^{★},{\zeta }^{★}]}_n\left(t\right)·\mathrm{\Delta }\zeta )dt=0.\hfill \end{array}$$

Since $\eta$ and $\mathrm{\Delta }\zeta$ are arbitrary, we prove Equations (27)–(30). □

Remark 6.

We remark that:

1. 

we considered the constraints (26) for the simplicity of presentation; of course, we could consider the case when $x^{\left(k\right)}\left(a\right)$ and $x^{\left(k\right)}\left(b\right)$, $k=1,\dots ,n-1$, are free, and at the end deduce the respective natural boundary conditions;

2. 

Theorem 2.8 in [23] with the final time fixed is a corollary of Theorem 4.

3.4. Sufficient Optimality Conditions

In this subsection, we give sufficient conditions of optimization for all the problems considered previously, first for Problem 1.

Theorem 5.

Suppose that L satisfies the inequality:

$$\begin{array}{c}L\left(t,x_1+\mathrm{\Delta }{x}_1{,}^C{D}_{a^{+}}^{\gamma +\mathrm{\Delta }\gamma ,g}(x_1+\Delta x_1){,}^C{D}_{b^{-}}^{\delta +\mathrm{\Delta }\delta ,g}(x_1+\mathrm{\Delta }{x}_1),x_4+\mathrm{\Delta }{x}_4,x_5+\mathrm{\Delta }{x}_5,x_6+\mathrm{\Delta }{x}_6\right)\hfill \\ -L\left(t,x_1{,}^C{D}_{a^{+}}^{\gamma ,g}{x}_1{,}^C{D}_{b^{-}}^{\delta ,g}{x}_1,x_4,x_5,x_6\right)\ge (resp.\le ){\partial }_{2}L[•]\mathrm{\Delta }{x}_1+\sum _{i=4}^6{\partial }_{i+1}L[•]\mathrm{\Delta }{x}_i\\ \hfill +{\partial }_{3}L[•]\left(f_t^{\prime }\left(\gamma \right).\mathrm{\Delta }\gamma {+}^C{D}_{a^{+}}^{\gamma ,g}\mathrm{\Delta }{x}_1\right)+{\partial }_{4}L[•]\left(g_t^{\prime }\left(\delta \right).\mathrm{\Delta }\delta {+}^C{D}_{b^{-}}^{\delta ,g}\mathrm{\Delta }{x}_1\right)\end{array}$$

(31)

for all $x_1,\mathrm{\Delta }{x}_1\in C^1([a,b],\mathbb{R})$, $x_4,x_5,x_6,\mathrm{\Delta }{x}_4,\mathrm{\Delta }{x}_5,\mathrm{\Delta }{x}_6\in \mathbb{R}$, and $\mathrm{\Delta }\gamma ,\mathrm{\Delta }\delta \in \mathbb{R}$ such that $0<\gamma +\mathrm{\Delta }\gamma <1$ and $0<\delta +\mathrm{\Delta }\delta <1$, where $[•]:=(t,x_1{,}^C{D}_{a^{+}}^{\gamma ,g}{x}_1{,}^C{D}_{b^{-}}^{\delta ,g}{x}_1,x_4,x_5,x_6)$ and $f_t,g_t$ as defined in Theorem 2. If $(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})$ satisfies the necessary conditions (3)–(8), then $(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})$ is a minimizer (resp. maximizer) of functional ${\mathcal{J}}_1$.

Proof. 

We present the proof only when the inequality (31) holds for ≥; the other case is similar. Let $\eta \in C^1([a,b],\mathbb{R})$, $\mathrm{\Delta }\zeta \in \mathbb{R}$, and $\mathrm{\Delta }\gamma ,\mathrm{\Delta }\delta \in \mathbb{R}$ such that $0<{\gamma }^{★}+\mathrm{\Delta }\gamma <1$ and $0<{\delta }^{★}+\mathrm{\Delta }\delta <1$. In what follows, we denote:

$$[★]\left(t\right):=\left(t,x^{★}\left(t\right),{(}^C{D}_{a^{+}}^{{\gamma }^{★},g}{x}^{★})\left(t\right),{(}^C{D}_{b^{-}}^{{\delta }^{★},g}{x}^{★})\left(t\right),x^{★}\left(a\right),x^{★}\left(b\right),{\zeta }^{★}\right).$$

Observe that:

$$\begin{array}{cc}\hfill & {\mathcal{J}}_1(x^{★}+\eta ,{\zeta }^{★}+\mathrm{\Delta }\zeta ,{\gamma }^{★}+\mathrm{\Delta }\gamma ,{\delta }^{★}+\mathrm{\Delta }\delta )-{\mathcal{J}}_1(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})\hfill \\ \hfill & ={\int }_a^b\left(L\right(t,x^{★}\left(t\right)+\eta \left(t\right),{(}^C{D}_{a^{+}}^{{\gamma }^{★}+\mathrm{\Delta }\gamma ,g}(x^{★}+\eta ))\left(t\right),{(}^C{D}_{b^{-}}^{{\delta }^{★}+\mathrm{\Delta }\delta ,g}(x^{★}+\eta ))\left(t\right),x^{★}\left(a\right)+\eta \left(a\right),\hfill \\ \hfill & x^{★}\left(b\right)+\eta \left(b\right),{\zeta }^{★}+\mathrm{\Delta }\zeta )-L\left(t,x^{★}\left(t\right),{(}^C{D}_{a^{+}}^{{\gamma }^{★},g}{x}^{★})\left(t\right),{(}^C{D}_{b^{-}}^{{\delta }^{★},g}{x}^{★})\left(t\right),x^{★}\left(a\right),x^{★}\left(b\right),{\zeta }^{★}\right))dt\hfill \\ \hfill & \ge {\int }_a^b({\partial }_{2}L[★]\left(t\right)·\eta \left(t\right)+{\partial }_{3}L[★]\left(t\right)\left(f_t^{\prime }\left({\gamma }^{★}\right).\mathrm{\Delta }\gamma +{(}^C{D}_{a^{+}}^{{\gamma }^{★},g}\eta )\left(t\right)\right)\hfill \\ \hfill & +{\partial }_{4}L[★]\left(t\right)\left(g_t^{\prime }\left({\delta }^{★}\right).\mathrm{\Delta }\delta +{(}^C{D}_{b^{-}}^{{\delta }^{★},g}\eta )\left(t\right)\right)+{\partial }_{5}L[★]\left(t\right)·\eta \left(a\right)\hfill \\ \hfill & +{\partial }_{6}L[★]\left(t\right)·\eta \left(b\right)+{\partial }_{7}L[★]\left(t\right)·\mathrm{\Delta }\zeta )dt\hfill \\ \hfill & ={\int }_a^b({\partial }_{2}L[★]\left(t\right)+\left(D_{b^{-}}^{{\gamma }^{★},g}\frac{{\partial }_{3}L[★]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right)+\left(D_{a^{+}}^{{\delta }^{★},g}\frac{{\partial }_{4}L[★]}{g^{\prime }}\right)\left(t\right)g^{\prime }\left(t\right))·\eta \left(t\right)dt\hfill \\ \hfill & {\displaystyle +\mathrm{\Delta }\gamma {\int }_a^b{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[★]\left(t\right)dt+\mathrm{\Delta }\delta {\int }_a^b{g}_t^{\prime }\left({\delta }^{★}\right)·{\partial }_{4}L[★]\left(t\right)dt}\hfill \\ \hfill & +\eta \left(a\right)({\int }_a^b{\partial }_{5}L[★]\left(t\right)dt+\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[★]}{g^{\prime }}\right)\left(a\right)-\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[★]}{g^{\prime }}\right)\left(a\right))\hfill \\ \hfill & +\eta \left(b\right)({\int }_a^b{\partial }_{6}L[★]\left(t\right)dt+\left(I_{b^{-}}^{1-{\gamma }^{★},g}\frac{{\partial }_{3}L[★]}{g^{\prime }}\right)\left(b\right)-\left(I_{a^{+}}^{1-{\delta }^{★},g}\frac{{\partial }_{4}L[★]}{g^{\prime }}\right)\left(b\right))+\mathrm{\Delta }\zeta {\int }_a^b{\partial }_{7}L[★]\left(t\right)dt.\hfill \end{array}$$

Using Conditions (3)–(8), we conclude that:

$${\mathcal{J}}_1(x^{★}+\eta ,{\zeta }^{★}+\mathrm{\Delta }\zeta ,{\gamma }^{★}+\mathrm{\Delta }\gamma ,{\delta }^{★}+\mathrm{\Delta }\delta )-{\mathcal{J}}_1(x^{★},{\zeta }^{★},{\gamma }^{★},{\delta }^{★})\ge 0$$

proving the desired result. □

Definition 4.

Let $m\in \mathbb{N}$ and $c,d\in \mathbb{R}$ such that $c<d$. Function $L(t,x_1,\dots ,x_m)$ is said to be jointly convex in $S\subseteq [c,d]\times {\mathbb{R}}^m$ if, for all $i=2,3,\dots ,m+1$, ${\partial }_{i}L$ are continuous and satisfy:

$$L(t,x_1+\mathrm{\Delta }{x}_1,\dots ,x_m+\mathrm{\Delta }{x}_m)-L(t,x_1,\dots ,x_m)\ge \sum _{i=1}^m{\partial }_{i+1}L(t,x_1,\dots ,x_m)\mathrm{\Delta }{x}_i,$$

for all $(t,x+\mathrm{\Delta }{x}_1,\dots ,x_m+\mathrm{\Delta }{x}_m),(t,x_1,\dots ,x_m)\in S$. We say that L is jointly concave in $S\subseteq [c,d]\times {\mathbb{R}}^m$ if the previous inequality holds, replacing ≥ by ≤.

Next, we present a sufficient optimality condition for the problem considered in Section 3.2.

Theorem 6.

Let L be jointly convex (respectively jointly concave) in $[a-\tau ,b]\times {\mathbb{R}}^7$. If $(x^{★},{\zeta }^{★})$ satisfies the necessary conditions (13)–(16), then $(x^{★},{\zeta }^{★})$ is a minimizer (respectively maximizer) of functional ${\mathcal{J}}_2$.

Proof. 

Consider a function $\eta :[a-\tau ,b]\to \mathbb{R}$, of class $C^1$, vanishing at $[a-\tau ,a]$, and let $\mathrm{\Delta }\zeta$ be an arbitrary real number. Using the same ideas used to prove Theorem 3, one gets:

$${\mathcal{J}}_2(x^{★}+\eta ,{\zeta }^{★}+\mathrm{\Delta }\zeta )-{\mathcal{J}}_2(x^{★},{\zeta }^{★})\ge H(x^{★},{\zeta }^{★}),$$

where $H(x^{★},{\zeta }^{★})$ denotes the left-hand side of Equation (23). Introducing (13)–(16) into the last expression, we get that ${\mathcal{J}}_2(x^{★}+\eta ,{\zeta }^{★}+\mathrm{\Delta }\zeta )-{\mathcal{J}}_2(x^{★},{\zeta }^{★})\ge 0$, as desired. □

The following result can be proven using the same methods as before.

Theorem 7.

Suppose that L is jointly convex (respectively jointly concave) in $[a,b]\times {\mathbb{R}}^{2n+4}$. If $(x^{★},{\zeta }^{★})$ satisfies the necessary conditions (27)–(30), then $(x^{★},{\zeta }^{★})$ is a minimizer (respectively maximizer) of functional ${\mathcal{J}}_3$.

4. Illustrative Examples

In this section, we provide two examples that show the applicability of some of our results.

Example 1.

Suppose we want to find a minimizer of the following functional:

$$\begin{array}{c}\mathcal{J}(x,\zeta ,\gamma )={\int }_0^1\left({\left({}^C{D}_{0^{+}}^{\gamma ,g}x\right)}^2\left(t\right)\frac{{(g\left(t\right)-g\left(0\right))}^{\gamma }}{\mathrm{\Gamma }(\gamma +1)}-2\left({}^C{D}_{0^{+}}^{\gamma ,g}x\right)\left(t\right){(g\left(t\right)-g\left(0\right))}^{\gamma }\right.\hfill \\ \hfill {\left.+\frac{{\left(x\left(0\right)\right)}^2}{2}+\frac{{(\zeta -1)}^4}{2}\right)}^{2}dt,\end{array}$$

subject to the boundary condition $x\left(1\right)={(g\left(1\right)-g\left(0\right))}^{\gamma }$, for the case $0<\gamma <1$. Let $x^{★}\left(t\right)={(g\left(t\right)-g\left(0\right))}^{\gamma }$, ${\zeta }^{★}=1$, and ${\gamma }^{★}$ be given later. Using Lemma 1, we get:

$${(}^C{D}_{0^{+}}^{\gamma ,g}{x}^{★})\left(t\right)=\mathrm{\Gamma }(\gamma +1),$$

and therefore,

$$\begin{array}{c}{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★}]=2\left({\left({}^C{D}_{0^{+}}^{{\gamma }^{★},g}{x}^{★}\right)}^2\left(t\right)\frac{{(g\left(t\right)-g\left(0\right))}^{{\gamma }^{★}}}{\mathrm{\Gamma }({\gamma }^{★}+1)}-2\left({}^C{D}_{0^{+}}^{{\gamma }^{★},g}x\right)\left(t\right){(g\left(t\right)-g\left(0\right))}^{{\gamma }^{★}}\right.\hfill \\ \hfill \left.+\frac{{\left(x^{★}\left(0\right)\right)}^2}{2}+\frac{{({\zeta }^{★}-1)}^4}{2}\right)\left(2\left({}^C{D}_{0^{+}}^{{\gamma }^{★},g}{x}^{★}\right)\left(t\right)\frac{{(g\left(t\right)-g\left(0\right))}^{{\gamma }^{★}}}{\Gamma ({\gamma }^{★}+1)}-2{(g\left(t\right)-g\left(0\right))}^{{\gamma }^{★}}\right)=0.\end{array}$$

Following Theorem 2, we observe that $x^{★}$ and ${\zeta }^{★}$ solve Equation (3), Equation (4), and the natural boundary condition (7). Moreover,

$${\displaystyle {\int }_0^1{f}_t^{\prime }\left({\gamma }^{★}\right)·{\partial }_{3}L[x^{★},{\zeta }^{★},{\gamma }^{★}]\left(t\right)dt=0,}$$

where $f_t\left(\gamma \right)=\mathrm{\Gamma }(\gamma +1)$, and so, $f_t^{\prime }\left(\gamma \right)=g_0(\gamma +1)\mathrm{\Gamma }(\gamma +1)$, where $g_0$ denotes the Digamma function, proving that Equation (5) holds. Let:

$$\mathrm{\Psi }\left(\gamma \right):=\mathcal{J}(x^{★},{\zeta }^{★},\gamma )={\int }_0^1(\mathrm{\Gamma }(\gamma +1){(g\left(t\right)-g\left(0\right))}^{\gamma }{)}^{2}dt.$$

In Figure 1, we present the graphs of function Ψ, with respect to three different kernels $g\left(t\right)=t$ (Figure 1a), $g\left(t\right)=2sin\left(t\right)$ (Figure 1b), and $g\left(t\right)={(t+1)}^{3/2}$ (Figure 1c). The optimal values are ${\gamma }^{★}\approx 0.9010$, ${\gamma }^{★}\approx 0.4139$, and ${\gamma }^{★}\approx 0.4335$, respectively.

As we can observe, the value of the functional depends on the value of the fractional order when we evaluated it at the optimal solution $(x^{★},{\zeta }^{★})$. Thus, it is also an important question to determine the optimal value ${\gamma }^{★}$ in these types of variational problems.

Figure 1. Plots of function Ψ.

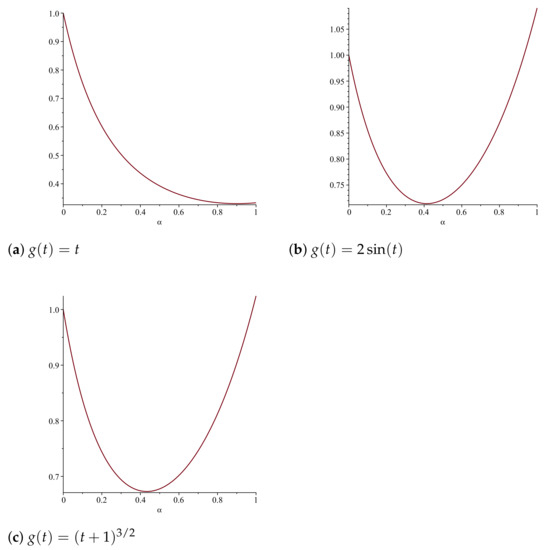
Figure 1. Plots of function Ψ.

Example 2.

We now consider an example containing higher order derivatives. Let $\gamma \in [1,2]$ and $\delta \in [0,1]$. Suppose we want to find a minimizer of:

$$\begin{array}{c}\mathcal{J}(x,\zeta )={\int }_0^1({\left(\left({}^C{D}_{0^{+}}^{\gamma ,g}x\right)\left(t\right)-\frac{2{(g\left(t\right)-g\left(0\right))}^{2-\gamma }}{\mathrm{\Gamma }(3-\gamma )}\right)}^2\hfill \\ +{\left(\left({}^C{D}_{1^{-}}^{\delta ,g}x\right)\left(t\right)-\frac{2{(g\left(1\right)-g\left(t\right))}^{2-\delta }}{\mathrm{\Gamma }(3-\delta )}-\frac{2(g\left(0\right)-g\left(1\right)){(g\left(1\right)-g\left(t\right))}^{1-\delta }}{\mathrm{\Gamma }(2-\delta )}\right)}^2\\ \hfill +{(x\left(1\right)-{(g\left(1\right)-g\left(0\right))}^2)}^2+{\zeta }^2)dt,\end{array}$$

under the constraints $x\left(0\right)=x^{\prime }\left(0\right)=0$ and $x^{\prime }\left(1\right)=2(g\left(1\right)-g\left(0\right))$. Let $x^{★}\left(t\right)={(g\left(t\right)-g\left(0\right))}^2$ and ${\zeta }^{★}=0$. Using Lemma 1, we get:

$$\left({}^C{D}_{0^{+}}^{\gamma ,g}{x}^{★}\right)\left(t\right)=\frac{2{(g\left(t\right)-g\left(0\right))}^{2-\gamma }}{\mathrm{\Gamma }(3-\gamma )},$$

and:

$$\begin{array}{cc}\hfill \left({}^C{D}_{1^{-}}^{\delta ,g}{x}^{★}\right)\left(t\right)& =\left({}^C{D}_{1^{-}}^{\delta ,g}{((g\left(1\right)-g)+(g\left(0\right)-g\left(1\right)))}^2\right)\left(t\right)\hfill \\ \hfill & =\left({}^C{D}_{1^{-}}^{\delta ,g}{(g\left(1\right)-g)}^2\right)\left(t\right)+2(g\left(0\right)-g\left(1\right))\left({}^C{D}_{1^{-}}^{\delta ,g}(g\left(1\right)-g)\right)\left(t\right)\hfill \\ \hfill & =\frac{2{(g\left(1\right)-g\left(t\right))}^{2-\delta }}{\mathrm{\Gamma }(3-\delta )}+\frac{2(g\left(0\right)-g\left(1\right)){(g\left(1\right)-g\left(t\right))}^{1-\delta }}{\mathrm{\Gamma }(2-\delta )}.\hfill \end{array}$$

Clearly, $(x^{★},{\zeta }^{★})$ satisfies (27), (28), and (30), proving that the pair $(x^{★},{\zeta }^{★})$ is a candidate to be a solution of the problem. Since L is jointly convex, we can conclude by Theorem 7 that $(x^{★},{\zeta }^{★})$ is a solution of the proposed problem.

5. Concluding Remarks

Optimization problems are an important issue in several fields of research. In particular, variational problems are useful in Newton’s laws of motion, geometric optics, mathematical economics, hydrodynamics, minimal surfaces, Noether’s theorems, etc. For centuries, the considered problems involved integer order derivatives only, but in the last few years, generalizations of such a rich theory were considered, by including fractional derivatives in the formulation of the variational problems. However, due to the large number of choices for such fractional derivatives, we considered here a general form of the fractional derivative. We continued our study initiated in [33], by considering three new questions: first, how to find the best order of the fractional derivatives that extremizes the functional, secondly to determine the necessary conditions of optimization with time delay, and finally, when the Lagrangian function contains higher order derivatives. To end, sufficient conditions were proven and some examples were given.

For the future, one important problem is to develop numerical methods to deal directly with the variational problems of these types, without the use of necessary conditions, for example: using discretizations of the fractional derivatives and of the integral, reduce each problem to a finite dimensional one or, using appropriate approximations of the derivatives, depending only on the first order derivative, convert the fractional variational system as an ordinary optimal control problem. Other possibilities can be studied to enrich this theory.