Abstract
To address the problem that traditional stream ciphers are not sensitive to changes in the plaintext, a novel plaintext-related color image encryption scheme is proposed in this paper, which combines the 6-dimensional cellular neural network (CNN) and Chen’s chaotic system. This encryption scheme belongs to symmetric cryptography. In the proposed scheme, the initial key and switching function generated by the plaintext image are first utilized to control the CNN to complete the scrambling process. Then, Chen’s chaotic system is used to diffuse the scrambled image for realizing higher security. Finally, extensive performance evaluation is undertaken to validate the proposed scheme’s ability to offer the necessary security. Furthermore, the scheme is compared alongside state-of-the-art algorithms to establish its efficiency.
1. Introduction
The Internet’s impact on society is increasing due to the explosive development of information technology. A large amount of information is transmitted on the network by short messages, videos, images, audio, etc. Especially, the continuous update of electronic equipment makes the transmission of images on the network increasingly more convenient. Nevertheless, some of the images spreading across networks that are widely used in various communication systems such as telemedicine, military imaging, and video conferencing are secret, and the owner does not want others to access them without authorization. Thus, it is extremely important to protect the contents of these secret images.
The chaotic signal is suitable for secure communication technology because of its long-term unpredictability, initial value sensitivity, and noise-like [1,2]. Moreover, the chaos-based algorithms show outstanding characteristics in terms of security, complexity, speed, and computing power [3,4]. In recent years, the research of chaotic cryptography on image encryption has received a lot of attention from scholars [5,6,7,8,9]. For instance, on the basis of the permutation-substitution, an image encryption algorithm is presented in [10]. Meanwhile, Wang et al. [11] presented an encryption algorithm of images that uses the 1-dimensional and 2-dimensional logistic map to generate the chaotic matrix. Moreover, the 1-dimensional and 2-dimensional chaotic maps are repeatedly replaced in sequence. The results of the experiment demonstrate the reliability and applicability of the algorithm. Further, in [12] a pseudorandom number generator (PRNG) is generated using the 2-dimensional Logistic map to control the confusion and diffusion of pixels by XOR operation. Broumandnia [13] generates an incoherent cryptographic image by harnessing modular chaotic maps, which hides the information of original images. Then, Chai et al. [14] proposed a dynamic DNA and chaos-based encryption scheme for images and calculated initial values by using the hash function and extrinsic parameters. Moreover, Sundari and Karthika [15] presented an image encryption method associated with the concept of Logistic map. However, the encryption scheme of a single chaotic system can no longer meet the security and real-time requirements of modern life rhythm for image communication. Researchers have discovered that when CNN theory is applied to the chaotic encryption algorithm, hyperchaotic systems provide more complex dynamic behaviors, with strong randomness, unpredictability, and higher security performance [16].
CNN is a nonlinear analog processor with locally interconnected, double-valued output signals [17]. It is an artificial neural network formed by the improvement of Hopfield neural network and cellular automata [18], which adopts the local connection of cellular automata and at the same time resolves the difficulty of Hopfield neural network on hardware. As a flexible and efficient local interconnection network, CNN not only has complex chaotic dynamics characteristics but also can be easily integrated on the very large scale integration (VLSI) [19]. Compared with traditional chaotic systems, CNN has more extensive keyspace and outstanding permutation and diffusion properties. Therefore, CNN is widely utilized in encryption systems [20], and has achieved good encryption effects on digital watermark technology [21], voice encryption [22], and image encryption [23]. For example, Wang et al. [24] proposed the use of cellular automata (CA) to deal with the problems that match parallel computing. Furthermore, Qing et al. [25] analyzed the chaotic phenomenon of CNN model, then Peng et al. [26] conceived an encryption scheme for the image based on the theoretical model in [25]. Further, on the basis of the “scrambling-diffusion” mechanism, Kadir et al. [16] applied the CNN hyperchaotic system to construct the diffusion sequence to encrypt images. Meanwhile, a color image cryptography system based on hyperchaotic CNN and chaotic control parameter was proposed in [27], which adopted the compound “scrambling-diffusion” framework to encrypt the color image.
To overcome the shortcoming of traditional stream ciphers that is insensitive to the changes in the plaintext and further improve the security of the image encryption algorithm, obtain a larger key space, and better unpredictability, this paper proposes a new plaintext-related color image encryption scheme based on a 6-dimensional CNN and Chen’s chaotic system. First, the plaintext image is utilized to generate the initial key that is used as initial values of CNN, and the switching key is then utilized to select the chaotic sequences. Finally, the selected chaotic sequences are used in the two stages of scrambling and diffusion, respectively, to complete the image encryption. Consequently, the proposed scheme can not only change the histogram of the image, but also break the high correlation between adjacent pixels. Meanwhile, associating the initial parameters of the CNN with the plaintext image contributes to obtaining unique keystreams for each image, which ensures that the encryption scheme proposed in this paper is sufficiently sensitive to plaintext and has the advantages of resisting the known-plaintext attacks and chosen-plaintext attacks effectively. Additionally, the proposed scheme adopts a 6-dimensional CNN hyperchaotic system, which greatly expands the key space and makes it sufficient to resist the brute force attack. Extensive experimental results including histogram, correlation of adjacent pixels, entropy, sensitivity, keyspace, robustness, randomness, and known- and chosen-plaintext attacks show that the presented scheme meets the security requirements of the encryption algorithm and has a satisfactory encryption effect.
Based on the aforementioned, the main contributions of this study are threefold: (i) the proposed scheme that combines CNN with a high-dimensional chaotic system manifests higher security than the traditional encryption scheme based on a single chaotic system. (ii) We exploit the original image to generate one-time-key streams, which could be equated to signatures reflecting the respective pixel states of each input image. This enhances the sensitivity of both the input images and secret keys to small alterations to their respective contents, which helps to disable known or chosen plaintext attacks and overcomes the shortcomings of traditional stream ciphers that are not sensitive to changes in the plaintext. (iii) We utilize the 6-dimensional CNN hyperchaotic system, which increases the key space greatly and makes the scheme sufficient to resist various brute force attacks.
The rest of the paper is organized as follows. Section 2 briefly introduces the preliminaries related to the proposed encryption scheme, including the mathematical model and chaotic characteristics of the CNN and Chen’s chaotic system. Section 3 explains the design of the cryptosystem and the application of the proposed encryption scheme on the color image. The experimental results and security analysis are presented in Section 4. Finally, the conclusions are drawn in Section 5.
2. Preliminaries
2.1. Cellular Neural Network
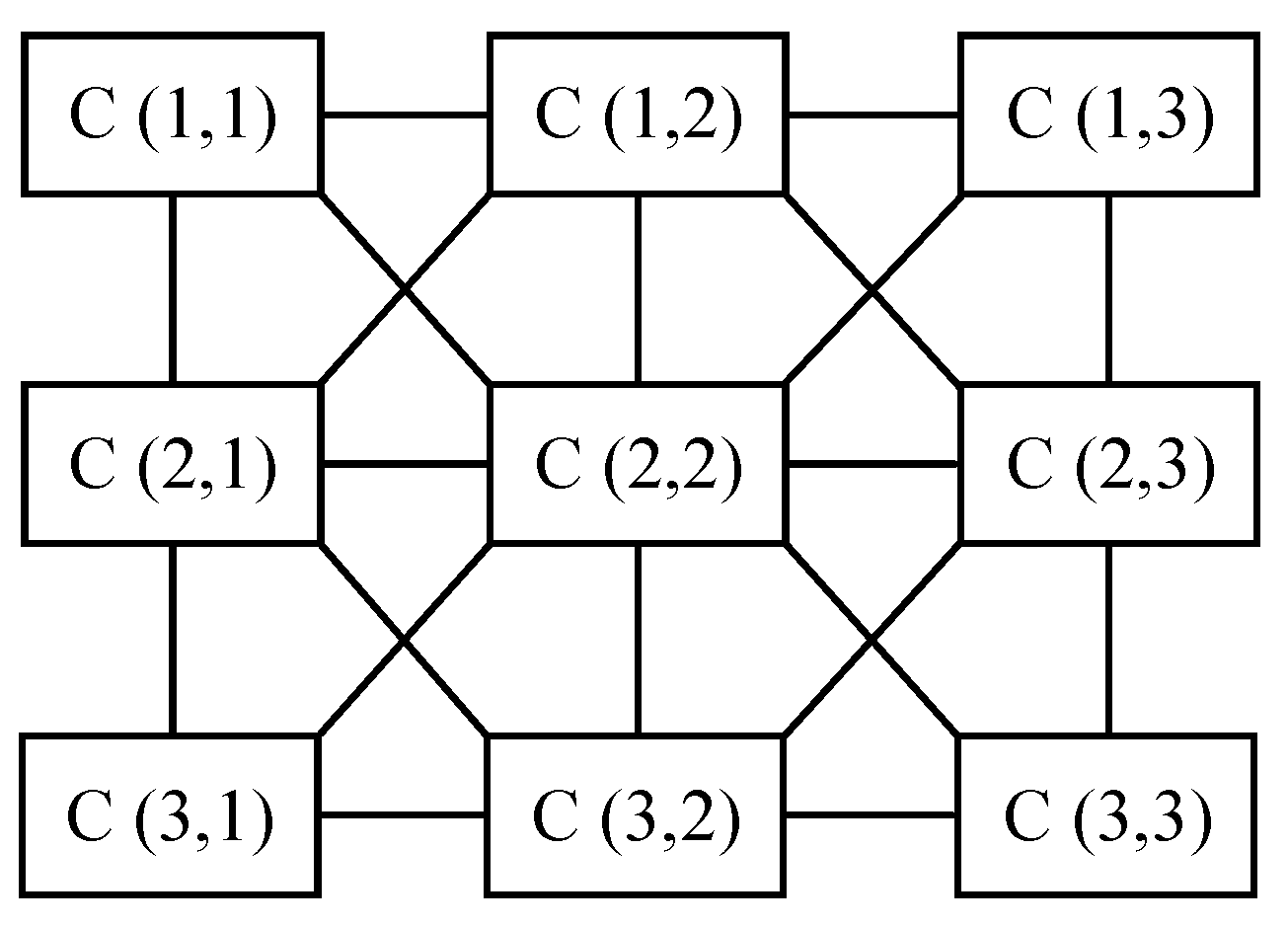
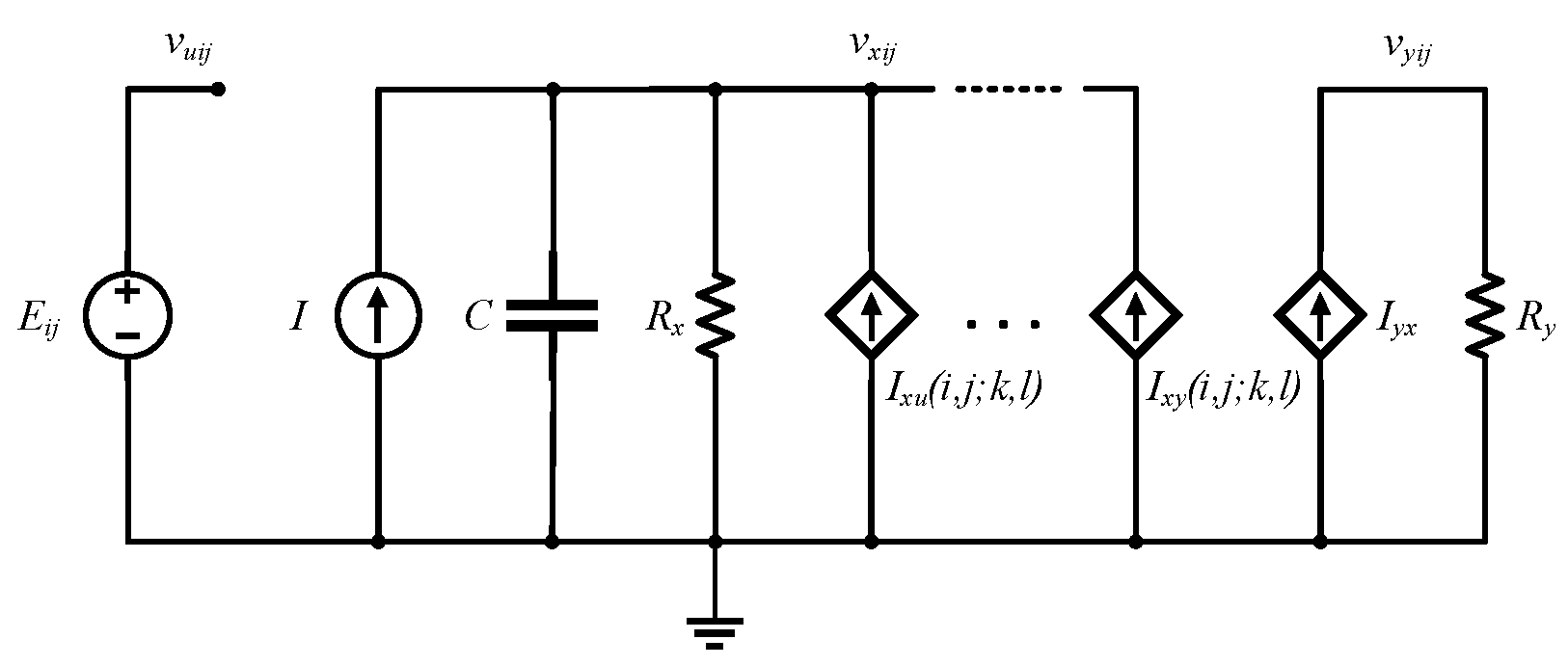
The cell is the basic component unit of CNN. Besides, each cell can be equivalent to a nonlinear 1-order circuit as shown in Figure 1. CNN is formed by the regular arrangement and connection of the same cell neurons in space. Each neuron is only connected with the adjacent eight neurons and the cells that are not directly connected influence each other through continuous and dynamic propagation effect [28]. Each neuron has the input and output states. A CNN is constructed in Figure 2, where represents the cells in the i-th row and j-th column in the cellular neural network. The chaotic phenomenon of the 6-dimensional CNN hyperchaotic system is described in [29]. The state equation of the 6-order fully interconnected CNN is shown in Equation (1):
where j = 1, 2, …, 6.
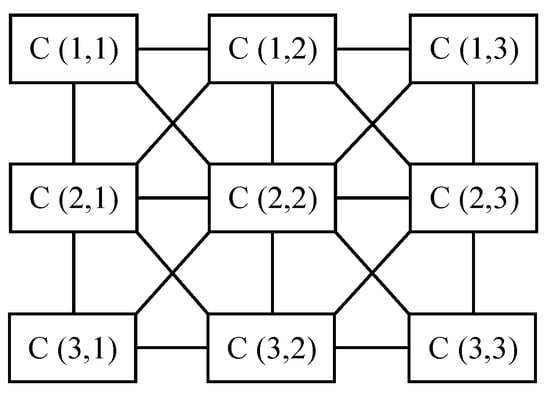
Figure 1.
Cellular neural network structure of .
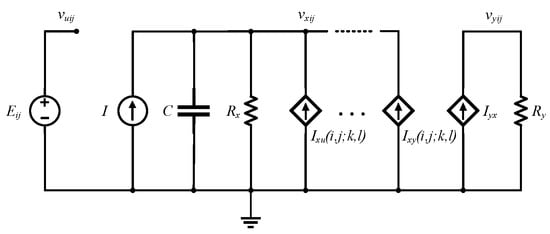
Figure 2.
Equivalent circuit diagram of each cell.
The system is in a chaotic state when the parameters are set as follows [30]: , ; ; , , , , , , , , . The mathematical model of 6-order CNN is shown in Equation (2), which can be obtained by substituting the parameters into Equation (1).
where .
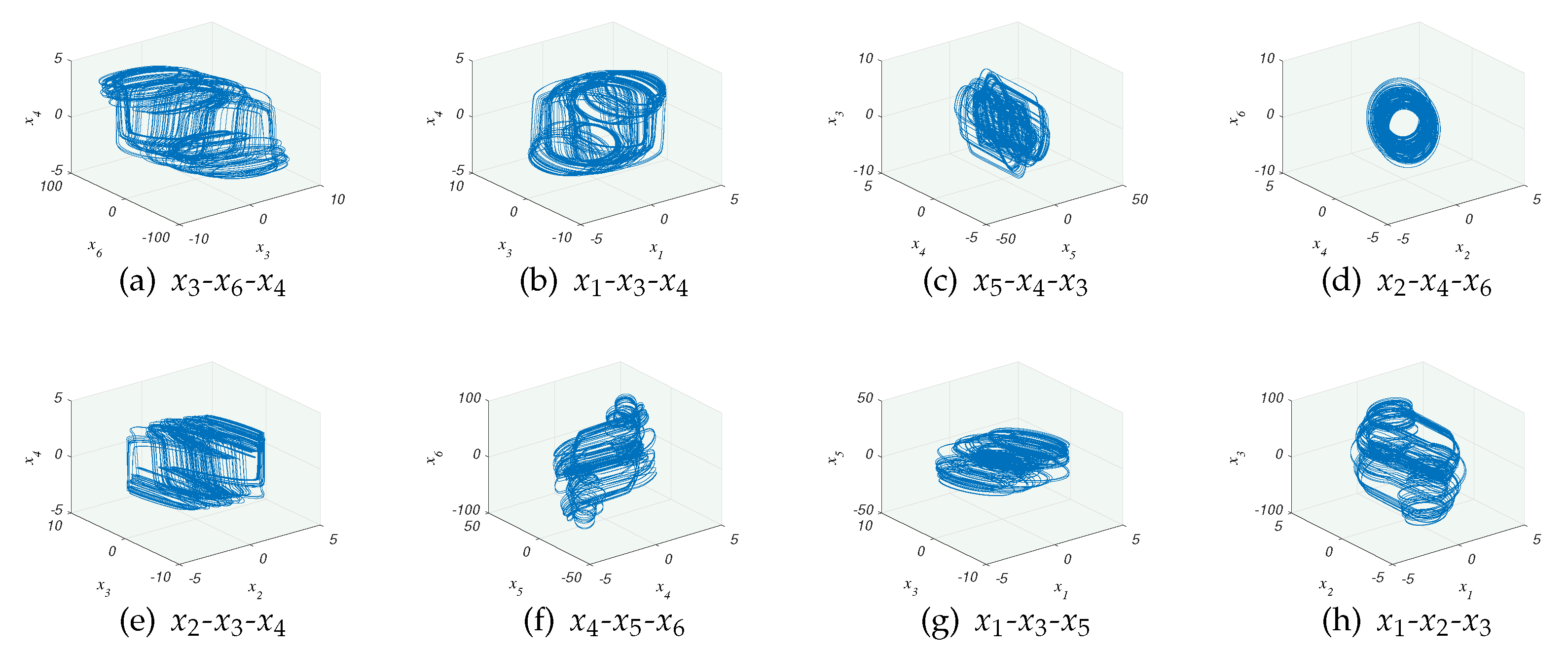
The Lyapunov exponent of the 6-order CNN can be calculated, , , , , , when . Two of them are positive, which indicates that the system is hyperchaotic [31]. As the initial values can be arbitrary values of any length, this greatly increases the key space and security. The iteration step size h is set to , and the initial values are set as follows: . The phase diagram of partial corresponding 6-order CNN hyperchaotic attractor obtained by Runge–Kutta method is plotyed in Figure 3.
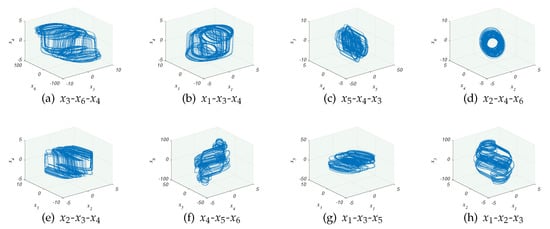
Figure 3.
Partial 6-order CNN hyperchaotic attractor distribution: (a) Distribution in the direction of --. (b) Distribution in the direction of --. (c) Distribution in the direction of --. (d) Distribution in the direction of --. (e) Distribution in the direction of --. (f) Distribution in the direction of -- . (g) Distribution in the direction of --. (h) Distribution in the direction of --.
2.2. Chen’s Chaotic System
In 1999, the authors of [32] discovered a system with more complex dynamic behaviors than Lorenz system when studying chaotic feedback control. The chaotic attractors of Chen’s system had more complex and abundant dynamic characteristics than that of Lorenz system. The mathematical model of Chen’s chaotic system is expressed as
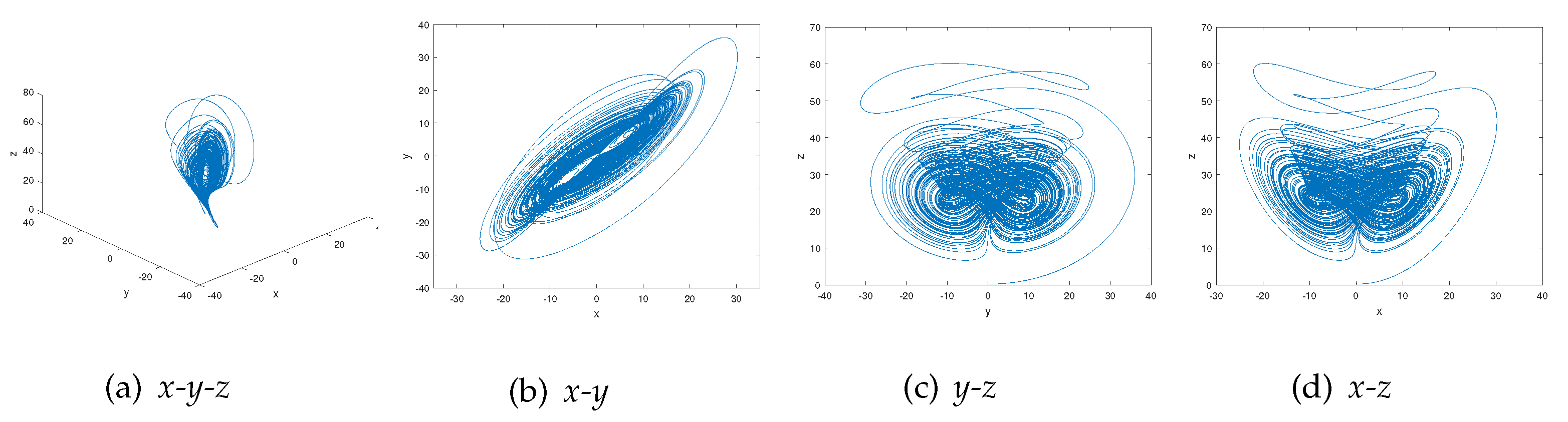
where a, b, and c are system parameters, when , , and , the system is in a chaotic state [33]. The 4-order Runge–Kutta algorithm is used to calculate Equation (3). The initial parameters are set as , , , and step length , and 100,000 iterations are performed. The chaotic attractors of this system are obtained as shown in Figure 4.
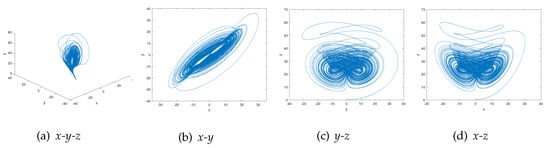
Figure 4.
Chaotic attractors of Chen’s system: (a) Distribution in the direction of x-y-z. (b) Distribution in the direction of x-y. (c) Distribution in the direction of y-z. (d) Distribution in the direction of x-z.
3. Encryption and Decryption on Color Images
Having outlined CNN and Chen’s chaotic system and established their superior properties, in this part, we outline the design process of the proposed plaintext-related color image encryption scheme, which is based on the classical “Scrambling-Diffusion” framework. For the sake of generality, it is assumed that the plaintext image with the size of . In addition, the ciphertext image is with the size of . The specific encryption steps and corresponding decryption steps are shown below.
3.1. Key Generation
Key generation is defined as the process of generating keys used in cryptography. In this study, key generation includes two parts: the initial key and the switching key. Outcomes of them depend on the plaintext, which leads to a unique key for each different output.
3.1.1. Initial Key
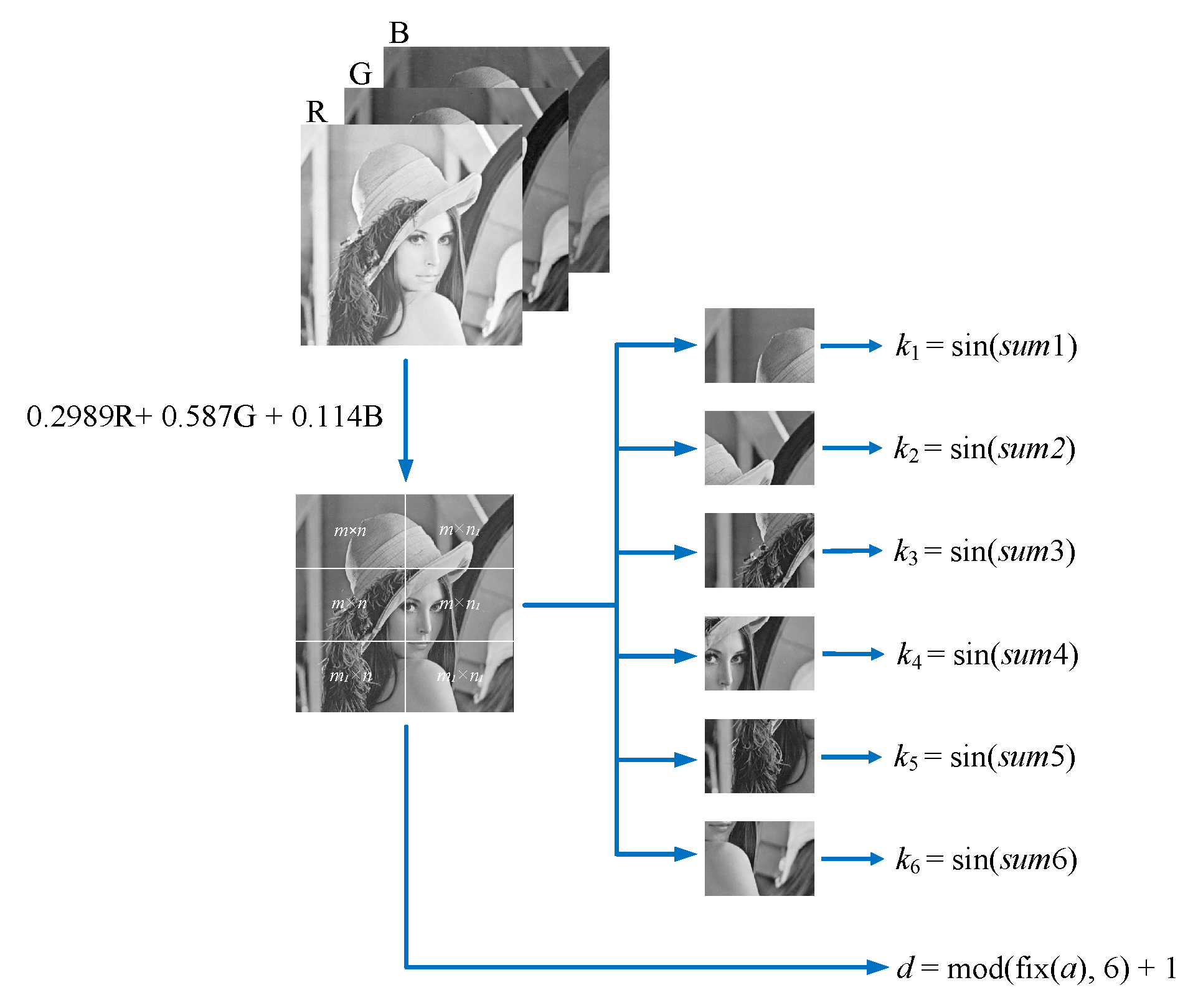
Initial key is inputted into the CNN hyperchaotic system as initial values, which is an integral part of the initial conditions for generating chaotic sequences. As shown in Figure 5, a three-channel color plaintext image with the size of is converted into a single-channel grayscale image, it is then divided into six non-overlapping cells, and the size of each cell is , , , , , and , where mod, mod, , and . We calculate the sum of gray values of each cell, respectively, and record them as , , …, , then let , , …, denote their sine values. That is, the initial key is dynamically updated by means of the sine values of the sum of the pixels of an image. Thus, one-time chaotic sequences are produced for the image, which results in high sensitivity to the slightest alternations in the corresponding input image. This is a veritable property for good immunity against chosen or known-plaintext attacks.
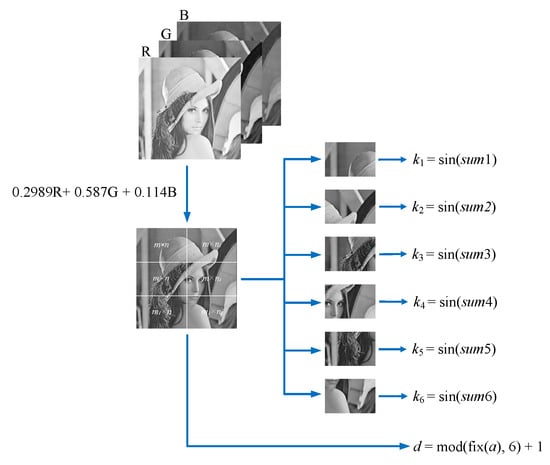
Figure 5.
Key generation.
3.1.2. Switching Key
The function of switching key d in Figure 5 is to control the selection of dimensions. In the process of confusion, to facilitate the implementation, we choose one dimension in the 6-dimensional chaotic sequences generated by CNN to construct a matrix for image confusion. As shown in Figure 6, when the extracted eigenvalue d is 1, the switch is closed, that is, the first dimensional chaotic sequence is selected. Moreover, when the value of d is 2, the switch is closed, that is, the second dimensional chaotic sequence is selected, and so on. We take the gray average value a of the image and transcode it to an integer within the range of 1 to 6 according to Equation (4).
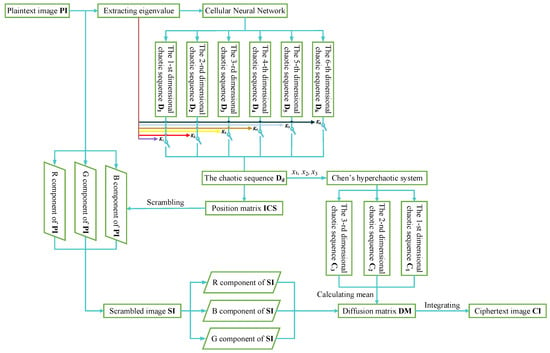
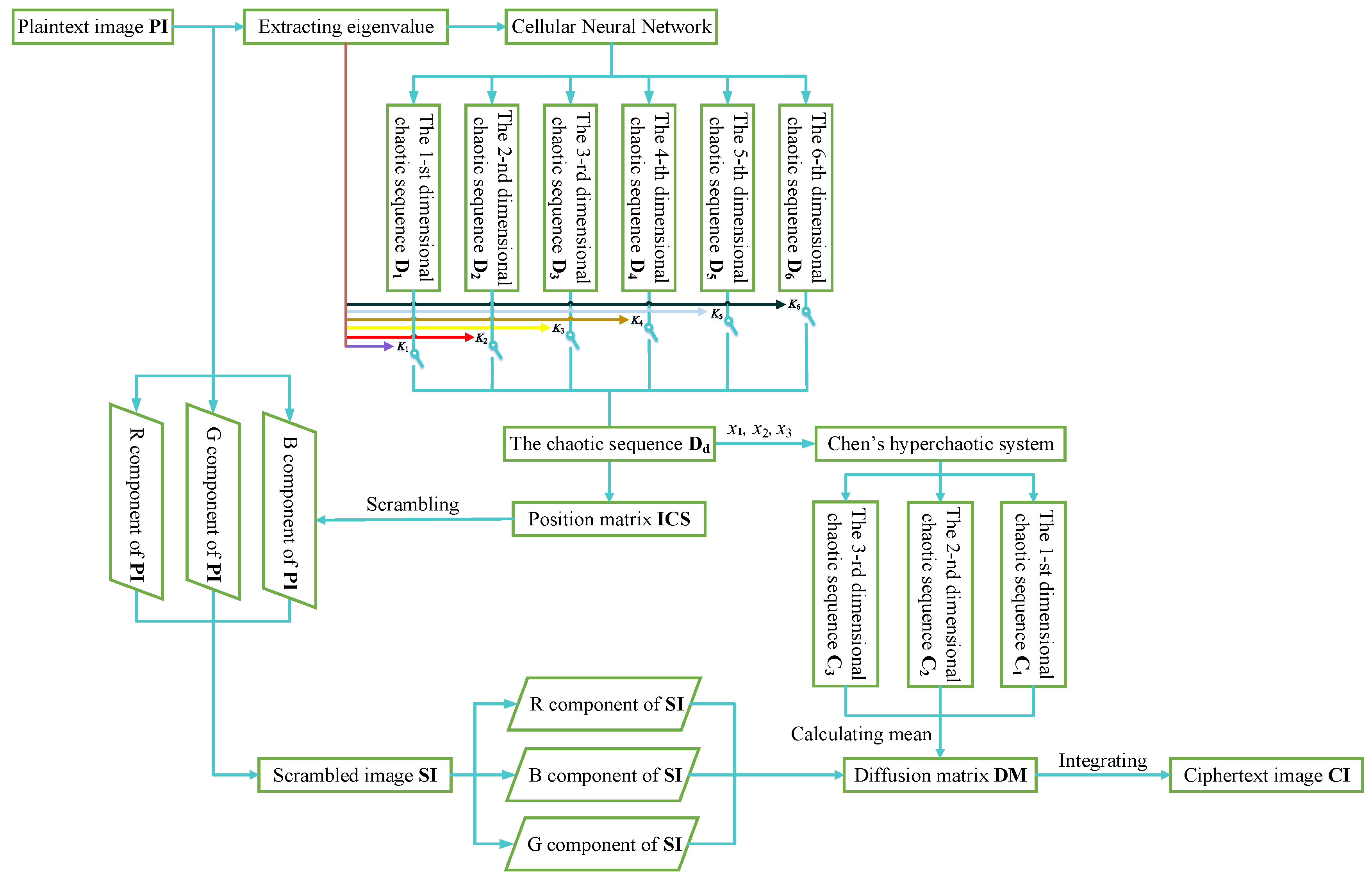
Figure 6.
Flow chart of encryption scheme.
3.2. Encryption Scheme Design
3.2.1. Scrambling
Input the initial key and control parameters into the CNN hyperchaotic system. Meanwhile, enter the switching key d which is used to select a sequence by controlling the switch - on or off. Then, one sequence is selected from the generated 6-dimensional chaotic sequences. Discard the first 1000 elements of the selected sequence to conceal the transient effect and then extract the remaining elements. These elements are quantified according to Equation (5) and denoted as the sequence .
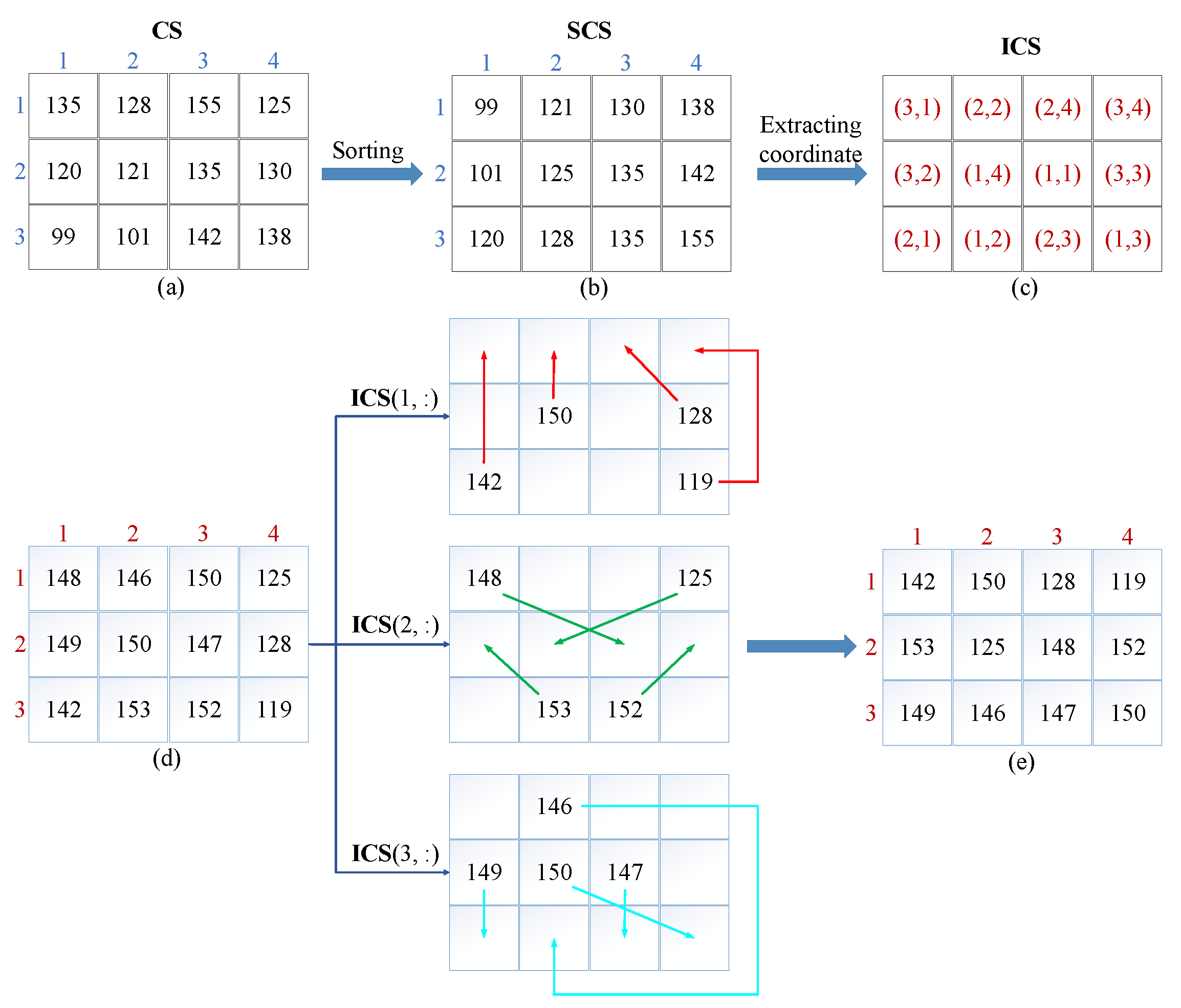
Equation (5) is equivalent to extracting the three digits after the decimal point of the chaotic sequence’s absolute value, and then converting it to a value between [0, 255]. The processed chaotic sequence is transformed into a 2-D matrix, and elements in the 2-D matrix are traversed according to columns. After incremental sorting, the elements are put into a new empty matrix by columns, namely, the sorted chaotic matrix . Additionally, the original position of elements in are recorded in another new empty matrix, namely, the position matrix . If the elements in the increment sorting process are found equal, the element traversed first is placed first. Next, the plaintext pixel matrix is rearranged according to the position matrix and the scrambling transformation is completed. To better understand the proposed scrambling algorithm, an example of the scrambling process is demonstrated in Figure 7, where . Figure 7a,b represents a two-dimensional chaotic matrix and the corresponding sorted two-dimensional scrambling matrix , respectively. Then, the position matrix that represents the original position of elements in sorted chaotic matrix is shown in Figure 7c. The matrix is used to scramble the plaintext matrix in Figure 7d. Ultimately, the resulting scrambled matrix is displayed in Figure 7e.
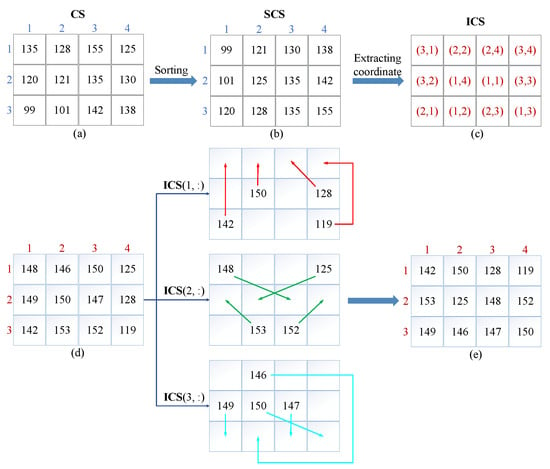
Figure 7.
An example of a scrambling algorithm: (a) The 2D chaotic matrix. (b) The sorted chaotic matrix. (c) The position matrix. (d) The plaintext matrix. (e) The scrambled plaintext matrix.
3.2.2. Diffusion
The 501st to 503rd values of the sequence selected in the scrambling process are taken as the initial values denoted as of Chen’s chaotic system. They are inputted into Chen’s system, and the 4-order Runge–Kutta method was utilized to solve Chen’s system iteratively for times. Then, the generated chaotic sequences are converted according to Equation (6).
where .
That is, the mean of three sequences is calculated and defined as the new sequence . Then, the sequence is quantified according to Equation (5). The quantized data is constructed as a diffusion matrix , whose size is . The XOR operations are performed on it and the three components of the scrambled image , respectively. Moreover, the ciphertext image in the form of RGB will be obtained after integration.
3.3. Decryption Scheme Design
3.3.1. First Decryption
Input the initial key, control parameters, and switching key d into the CNN hyperchaotic system. Following that, extract elements from the resulting chaotic sequence produced by CNN to acquire the position matrix and the initial values , , of Chen’s chaotic system. The initial values , , and are inputted into Chen’s system. Then, the sequence can be generated by averaging the 3-dimensional chaotic sequence acquired from Chen’s system. After processing, the diffusion matrix is obtained, then we respectively XOR the diffusion matrix with the three channels of the ciphertext image . The first stage of the decryption process is completed after integration, and the scrambled image is obtained.
3.3.2. Second Decryption (Reverse Scrambling)
The position matrix obtained in the first stage of decryption process was utilized to reverse scramble the three channels of the scrambled image and integrate results into the RGB form, that is, the second stage of the decryption process was completed.
3.4. Step to Encrypt and Decrypt Color Images
3.4.1. Steps to Encrypt
- Step 1: Initial keys , , …, , switching key d, and control parameters are inputted into the CNN hyperchaotic system, and the position matrix will be obtained. Then, the matrix is utilized to scramble the plaintext image and complete the first encryption.
- Step 2: Input the initial values , , into Chen’s chaotic system. Then, the diffusion matrix can be obtained, which is XORed respectively with the three components matrices of the plaintext image obtained after the first encryption to complete the second encryption.
- Step 3: For higher security, the above steps can be repeated n times.
Figure 6 shows the whole encryption process. Furthermore, as part of our validation, Figure 8a is the original plaintext image, the scrambled image is shown in Figure 8b, and Figure 8c shows the encryption effect. It is obvious that the ciphertext images present a uniform carpet-like distribution, and no valuable information can be distinguished from it. It is indicated that the encryption scheme proposed can cover up the original image successfully.

Figure 8.
The experimental results of encryption and decryption algorithm: (a) The original plaintext image. (b) The scrambled image; (c) The encrypted ciphertext image. (d) The decrypted image.
3.4.2. Steps to Decrypt
- Step 1: Initial keys , , …, ; switching key d; and control parameters are inputted into the CNN hyperchaotic system, the position matrix and the initial values , , of Chen’s system will be obtained.
- Step 2: Input the initial values , , into the Chen’s system, and the diffusion matrix will be obtained. The matrix is XORed respectively with the three components matrices of the ciphertext image . After the integration, the first decryption is completed and the scrambled image is obtained.
- Step 3: The position matrix in step1 is carried out the inverse scrambling on the RGB component of the scrambled image . Integrate it into the RGB form, the second stage of decryption process is completed.
The decryption effect is shown in Figure 8d. As seen throughout that figure, there is almost no visual difference between the decrypted image and the original plaintext image, indicating that the proposed scheme can successfully decrypt color images.
4. Experimental Results and Security Analysis
In this part, we conduct simulation tests to evaluate the quality of the proposed scheme. All simulation tests are carried out in the experimental environment of Matlab R2015b with a 2.90GHz CPU and 8GB memory.
4.1. Histogram Analysis
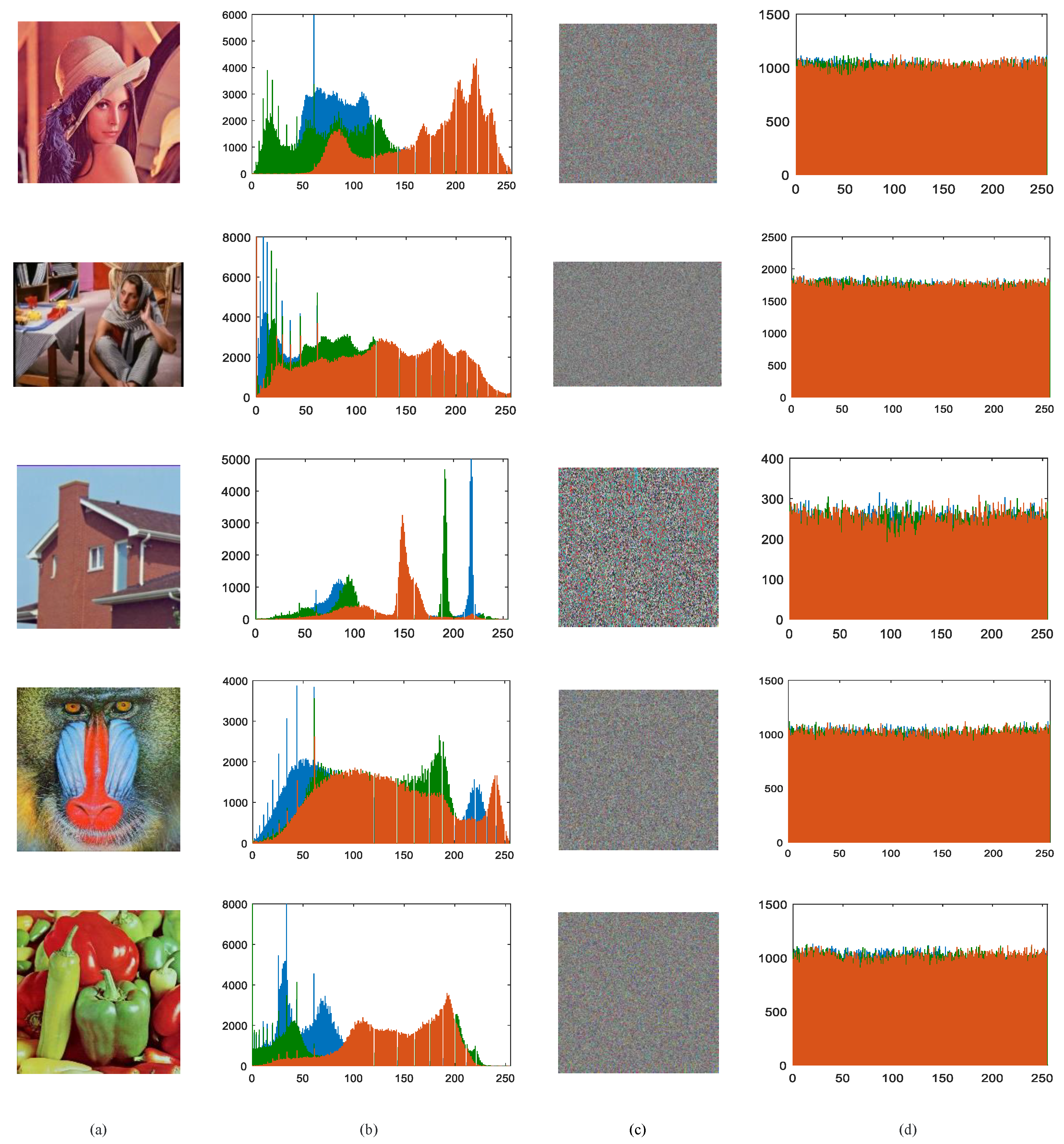
The histogram is one of the indexes to measure the quality of encryption scheme. For encrypted information, if the histogram of the ciphertext information is unevenly distributed, it will be easily cracked by the ciphertext attack. The histogram comparisons of partial test images before and after encryption are shown in Figure 9. It can be intuitively observed that the distributions of original images are uneven before encryption, that is, there is a significant difference in the probability of grayscale. Whereas, the histogram of the cipher image provides a uniform distribution, which enhances the difficulty of decryption. The outcome is evidence of our proposed scheme’s strong resistance against statistical attacks.
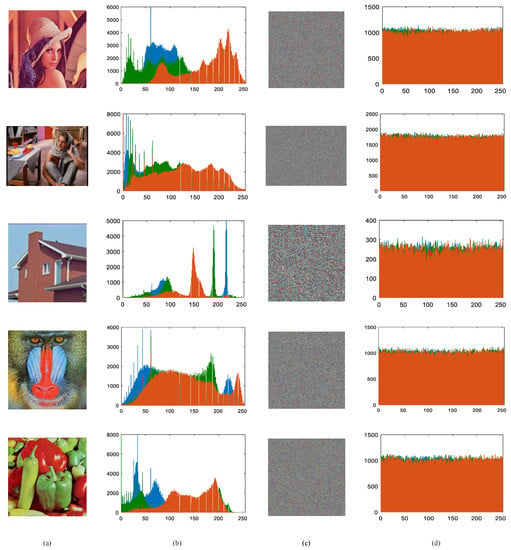
Figure 9.
Histogram tests: (a) The plaintext image. (b) Histogram for RGB components of the plaintext image. (c) The ciphertext image. (d) Histogram for RGB components of ciphertext image.
4.2. Correlation of Adjacent Pixels
The distinct correlation between adjacent pixels is the important features of images. Generally, attackers use it to decipher the ciphertext image. Therefore, making adjacent pixels uncorrelated is important in curtailing such efforts. The correlation should be extremely low (close to 0) in the encrypted image, a property that helps to make it unpredictable and disparate from the corresponding original image. In other words, the encryption scheme is considered to be effective if the information of cipher images cannot be obtained through adjoining pixels. Mathematically, the correlation calculation formula of adjoining pixels is as follows [34].
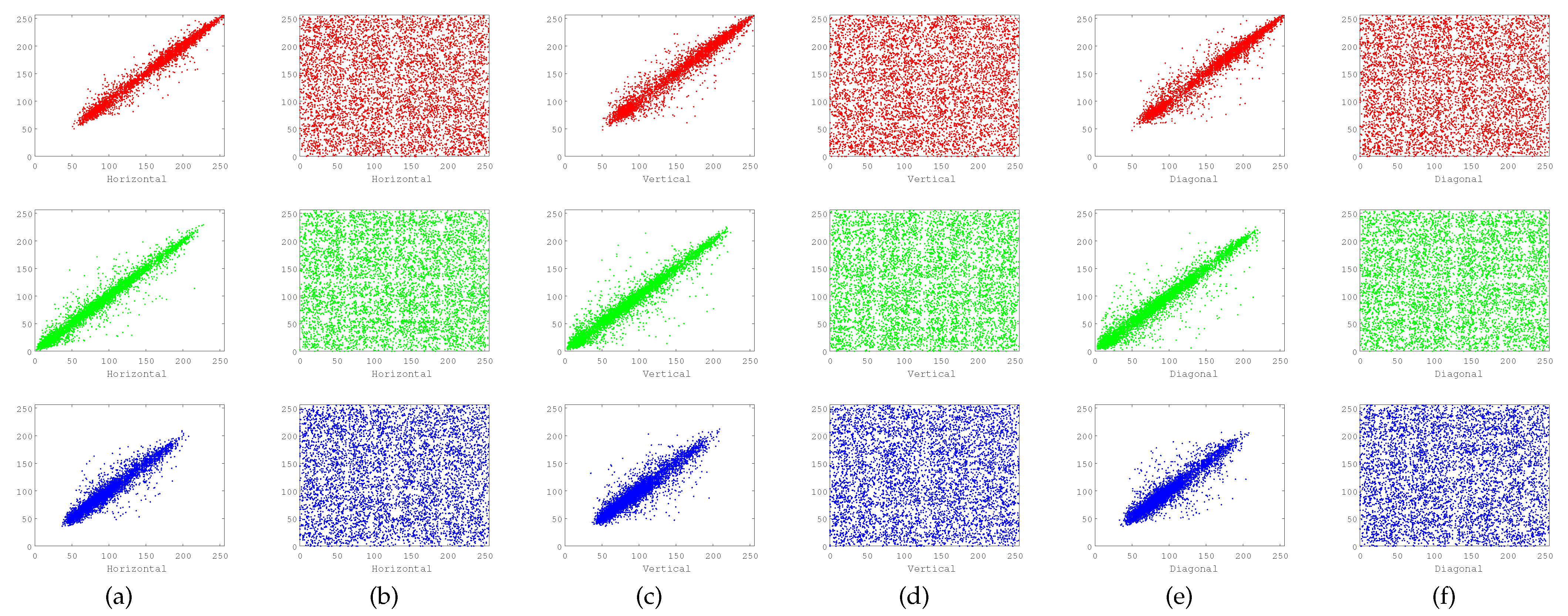
where x and y are the gray values of two adjoining pixels in an image, cov represents the covariance, represents the variance of the variable x, and represents the expectation of variable x. The pixel distribution of plaintext image and cipher image in R, G, and B components of the scheme presented in this paper is shown in Figure 10. As can be observed from the figure, the adjoining pixels of the plaintext image are concentrated in the diagonal region, which is closely related, whereas the encrypted image pixels are distributed in the full region irregularly, which explains why the correlation of the cipher image has been effectively reduced. Table 1 describes the correlation between the three components of the plaintext image and the ciphertext image in the horizontal, vertical, and diagonal directions. These outcomes show that the two adjacent pixels in the plaintext image are highly correlated, whereas the correlation tends to zero in the encrypted image. Table 2 shows the correlation comparison between the scheme proposed in this paper and the scheme proposed in other references. It can be observed that the performance of the scheme proposed in this paper is better. In other words, it is not feasible for attackers to crack ciphertext images by using the correlation of pixels. As a result, it can be concluded that our scheme is security and free from statistical attacks.
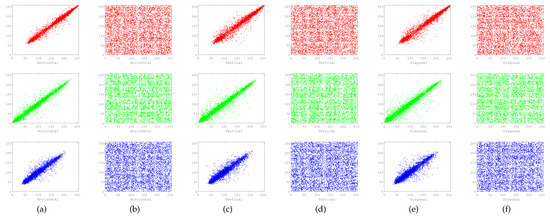
Figure 10.
Distribution of pixels: (a) Original image distribution of horizontal. (b) Cipher image distribution of horizontal. (c) Original image distribution of vertical. (d) Cipher image distribution of vertical. (e) Original image distribution of diagonal. (f) Cipher image distribution of diagonal.

Table 1.
Correlation of adjoining pixels of the original plaintext image and the encrypted ciphertext image.

Table 2.
Comparison of the correlation of the encrypted Lena image with other referenced schemes.
4.3. Information Entropy
Information entropy is utilized to quantitatively evaluate the randomness of random variables, which is defined in Equation (11).
where is the i-th grayscale value of the L-level grayscale image. Information entropy measures the distribution of grayscale values in an image. When the entropy values tend to 8, the pixel values are evenly distributed, and the password is not vulnerable to statistical attacks [26]. Therefore, an effective encryption scheme should introduce enough randomness in the image so that its entropy tends to the theoretical value of 8. The entropy values of original plaintext images and the encrypted ciphertext images in the three components are, respectively, calculated as shown in Table 3, which are very close to the optimum value. Consequently, it can be safely concluded that the information leakage from the proposed algorithm is insignificant.

Table 3.
Information entropy tests of plaintext images and ciphertext images.
4.4. Sensitivity Analysis
4.4.1. Key Sensitivity
Key sensitivity ensures that even a tiny change in the secret key would completely alter the encrypted and the decrypted images. Figure 11 shows the original image, the image encrypted with the correct key, the image encrypted with the wrong key (the key is changed by 1 bit), the difference between the two encrypted images, the image decrypted with the wrong key, and the image decrypted with the correct key. It can be concluded that even if the key is only slightly changed, it will lead to incorrect encrypted images and decrypted images, which suggests that the key sensitivity of the proposed scheme is satisfactory.

Figure 11.
The test results of the key sensitivity: (a) The plaintext image. (b) The correctly encrypted image. (c) The incorrectly encrypted image. (d) The difference between the two encrypted images. (e) The incorrectly decrypted image. (f) The correctly decrypted image.
4.4.2. Plaintext Sensitivity
In the case of altering one or more pixels of the plaintext and encrypting the original plaintext and the slightly altered plaintext, respectively. If the change of position or degree of the obtained two ciphertext pixels is not obvious or shows a regular pattern, then the attacker can use the differential attack to decode the key. Consequently, a satisfactory encryption scheme should be highly sensitive to alterations in the original images, so as to be resistant to differential attacks effectively [38]. The capability of resisting differential attacks is usually measured by the number of pixel of change rate (NPCR) and the unified average changing intensity (UACI).
The NPCR obtains the difference between two images by evaluating the different number of pixels in the two images, which is defined in Equation (12):
where M and N represent the height and width of a image, and is the difference value of the pixels corresponding to the two encrypted images and , which is defined in Equation (13):
The UACI measures the average intensity difference between two different images, which is defined in Equation (14):
When NPCR reaches approximately 99.6% and UACI reaches approximately 33.4%, the algorithm meets the security criteria [8]. Table 4 presents the NPCR and UACI scores for the proposed scheme and its comparison alongside results reported in other references. Outcomes show that NPCR and UACI scores for the proposed scheme are close to the ideal scores. This performance matches those reported in the competing techniques. Consequently, it can be deduced that the proposed scheme is sensitive to plaintext and has sufficient resistance to differential attacks.

Table 4.
The number of pixel of change rate (NPCR) and unified average changing intensity (UACI) of RGB component.
4.5. Key Space
Enough key space is an essential condition for resisting brute force attacks. In the scheme of this paper, the key includes the switching key d ranging from 1 to 6 and the initial values , , …, generated by the plaintext image; it is declared as double-precision type, and the key space of the encryption scheme is . Compared with other references, as shown in Table 5, the key space of the proposed scheme is huge, which is much larger than the theoretical requirement value . Therefore, the proposed scheme has sufficient ability to resist brute force attacks.

Table 5.
Comparison of the key space with other referenced schemes.
4.6. Robustness Analysis
Robustness refers to the ability to decrypt the original image when the encrypted image is polluted or attacked by noise during transmission [41]. We added Pepper & Salt noise and Gaussian noise with different noise densities to the cipher image respectively. The noise-contaminated ciphered images are then decrypted using the same key. The experimental results are shown in Figure 12; it can be seen that the encrypted image with noise can still be decrypted well. Therefore, the scheme is robust to Pepper & Salt noise and Gaussian noise added in ciphertext images.

Figure 12.
Experimental results of adding noise: (a) Cipher House image with Pepper & Salt noise of 0.1. (b) Cipher House image with Pepper & Salt noise of 0.15. (c) Cipher House image with Pepper & Salt noise of 0.5. (d) Decrypted image from cipher with Pepper & Salt noise of 0.1. (e) Decrypted image from cipher with Pepper & Salt noise of 0.15. (f) Decrypted image from cipher with Pepper & Salt noise of 0.5. (g) Cipher House image with Gaussian white noise with variance value 0.01. (h) Cipher House image with Gaussian white noise with variance value 0.1. (i) Cipher House image with Gaussian white noise with variance value 0.15. (j) Decrypted image from cipher with Gaussian white noise with variance value 0.01. (k) Decrypted image from cipher with Gaussian white noise with variance value 0.1. (l) Decrypted image from cipher with Gaussian white noise with variance value 0.15.
Moreover, we conducted a cropped attack test on the scheme proposed in this paper. We cropped and removed parts of the cipher image, and then applied the same key to test its decryption effect. The experimental results are shown in Figure 13. It can be observed that the quality of the reconstructed images is still recognizable and acceptable by cropping a reasonable area, such as 6.25% or 25% of the cipher. Despite a loss rate of 50% in the content of the encrypted image, sufficient visual information is retained in the corresponding decrypted image. Therefore, these outcomes support the conclusion that the scheme proposed has satisfactory robustness.

Figure 13.
Experimental results of decryption from cropped cipher images: (a) Cipher image with 6.25% cropped. (b) Cipher image with 25% cropped. (c) Cipher image with 50% cropped. (d) Decrypted image from 6.25% cropped cipher. (e) Decrypted image from 25% cropped cipher. (f) Decrypted image from 50% cropped cipher.
4.7. Known and Chosen-Plaintext Attacks
Known-plaintext attacks (KPA) are performed when both the original and encrypted images are known to the cryptanalyst. Such foreknowledge equips the attacker to predict some secret information and violate the cipher. In contrast, in the case of a chosen-plaintext attack (CPA), the cryptanalyst encrypts some particular images and examines their encrypted counterparts. Therefore, the attacker tries to recover the secret keys or estimate a process to decrypt the images without access to the keys. In our proposed scheme, the cryptanalyst is unable to acquire any sensitive information regarding the secret key by encrypting some known or particular images because the secret key depends on the input image, i.e., a one-time secret key for each input image. Therefore, the proposed algorithm is capable of withstanding any known and chosen-plaintext attack.
4.8. Randomness Tests Analysis
SP800-22 is a software package containing 16 randomness tests, which is released by the national institute of standards and technology (NIST) [42,43]. The randomness of the data stream is verified by these tests. Therefore, we use SP800-22 to make a qualitative judgment on the randomness of cipher images. The results are shown in Table 6. It can be concluded that the cipher images pass the test successfully through analyzing the data in Table 6. In other words, the cipher images generated by the proposed scheme in this paper have good randomness.

Table 6.
Results of randomness tests.
5. Conclusions
In this paper, a novel plaintext-related color image encryption scheme based on the combination of the 6-dimensional CNN hyperchaotic system and Chen’s system was proposed. Structurally, the proposed scheme is made up of three encryption phases: First, the key generation step that precedes the cryptographic phases is used to provide safeguards needed for the encryption phase. The plaintext image is utilized to extract the initial key. Following that, the initial key is utilized to generate the chaotic sequences. Finally, the selected chaotic sequence is used in the two stages of scrambling and diffusion to complete the image encryption. Here, the key changes with the change of the plaintext image, so that it can resist the known plaintext or ciphertext attacks, and effectively overcome the shortcoming of traditional stream ciphers that are not sensitive to changes in the plaintext. Additionally, the use of the 6-dimensional CNN hyperchaotic system expands the key space greatly and makes the scheme sufficient to resist various brute force attacks. Further, compared with the traditional encryption scheme based on a single chaotic system, combining CNN with a high-dimensional chaotic system can achieve higher security. Extensive experimental analysis including histogram, correlation of adjacent pixels, entropy, sensitivity, key space, robustness, randomness, and known and chosen-plaintext attacks establish the efficacy of the proposed scheme and support the conclusion that the proposed scheme is capable of withstanding targeted attacks aimed at violating its confidentiality and integrity.
Author Contributions
Conceptualization, Q.D.; Data curation, W.D.; Methodology, R.Z. and Q.D.; Software, R.Z. and L.Y.; Validation, L.Y. and D.J.; Writing—original draft, R.Z.; Writing—review and editing, D.J., J.S., and K.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under Grant 61471158.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CNN | Cellular Neural Network |
| UAV | Unmanned Aerial Vehicle |
| VLSI | Very Large Scale Integration |
| NPCR | Number of Pixel of Change Rate |
| PRNG | Pseudorandom Number Generator |
| UACI | Unified Average Changing Intensity |
| NIST | National Institute of Standards and Technology |
| KPA | Known-Plaintext Attack |
| CPA | Chosen-Plaintext Attack |
References
- Jiang, Z. A note on chaotic secure communication systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 92–96. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. Analysing the dynamics of digital chaotic maps via a new period search algorithm. Nonlinear Dyn. 2019, 97, 831–841. [Google Scholar] [CrossRef]
- Li, W.; Yan, W.; Zhang, R.; Wang, C.; Ding, Q. A New 3D Discrete Hyperchaotic System and Its Application in Secure Transmission. Int. J. Bifurc. Chaos 2019, 29, 1950206. [Google Scholar] [CrossRef]
- Kocarev, L. Chaos-based cryptography: A brief overview. IEEE Circ. Syst. Mag. 2001, 1, 6–21. [Google Scholar] [CrossRef]
- Ramli, K.; Suryanto, Y.; Magfirawaty, M.; Hayati, N. Novel Image Encryption Using a Pseudoset Generated by Chaotic Permutation Multicircular Shrinking With a Gradual Deletion of the Input Set. IEEE Access 2020, 8, 110351–110361. [Google Scholar] [CrossRef]
- Özkaynak, F. Brief review on application of nonlinear dynamics in image encryption. Nonlinear Dyn. 2018, 92, 305–313. [Google Scholar] [CrossRef]
- Musanna, F.; Kumar, S. Image encryption using quantum 3-D Baker map and generalized gray code coupled with fractional Chen’s chaotic system. Quantum Inf. Process. 2020, 19, 1–31. [Google Scholar] [CrossRef]
- Xingyuan, W.; Le, F.; Hongyu, Z. Fast Image Encryption Algorithm Based on Parallel Computing System. Inf. Sci. 2019, 486, 340–358. [Google Scholar]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Belazi, A.; El-Latif, A.A.A.; Belghith, S. A novel image encryption scheme based on substitution-permutation network and chaos. Signal Process. 2016, 128, 155–170. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Zhang, H.; Guo, K. A novel color image encryption scheme using alternate chaotic mapping structure. Opt. Lasers Eng. 2016, 82, 79–86. [Google Scholar] [CrossRef]
- Huang, X.; Ye, G. An image encryption algorithm based on irregular wave representation. Multimed. Tools Appl. 2018, 77, 2611–2628. [Google Scholar] [CrossRef]
- Broumandnia, A. The 3D modular chaotic map to digital color image encryption. Future Gener. Comput. Syst. 2019, 99, 489–499. [Google Scholar] [CrossRef]
- Chai, X.; Fu, X.; Gan, Z.; Lu, Y.; Chen, Y. A color image cryptosystem based on dynamic DNA encryption and chaos. Signal Process. 2019, 155, 44–62. [Google Scholar] [CrossRef]
- Sundari, T.J.V.; Karthika, K. Colour Image Encryption Using Chaotic System. Res. J. Eng. Technol. 2017, 8, 301–305. [Google Scholar] [CrossRef]
- Kadir, A.; Hamdulla, A.; Guo, W.Q. Color image encryption using skew tent map and hyper chaotic system of 6th-order CNN. Optik Int. J. Light Electron Opt. 2014, 125, 1671–1675. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, L. Cellular neural networks: Theory. IEEE Trans. Circuits Syst. 1988, 35, 1257–1272. [Google Scholar] [CrossRef]
- Döhler, F.; Mormann, F.; Weber, B.; Elger, C.E.; Lehnertz, K. A cellular neural network based method for classification of magnetic resonance images: Towards an automated detection of hippocampal sclerosis. J. Neurosci. Methods 2008, 170, 324–331. [Google Scholar] [CrossRef]
- Jamshidi, V. A VLSI Majority-Logic Device Based on Spin Transfer Torque Mechanism for Brain-Inspired Computing Architecture. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 1858–1866. [Google Scholar] [CrossRef]
- Ratnavelu, K.; Kalpana, M.; Balasubramaniam, P.; Wong, K.; Raveendran, P. Image Encryption Method based on Chaotic Fuzzy Cellular Neural Networks. Signal Process. 2017, 140, 87–96. [Google Scholar] [CrossRef]
- Jiao, S.; Zhou, C.; Shi, Y.; Zou, W.; Li, X. Review on Optical Image Hiding and Watermarking Techniques. Opt. Laser Technol. 2018, 109, 370–380. [Google Scholar] [CrossRef]
- Huang, Q.; Zhao, X.; Li, G. Research on the Application of Video Encryption Technology Based on 7 Dimensional CNN Hyper Chaos. In Proceedings of the 2018 10th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Changsha, China, 10–11 February 2018; pp. 448–451. [Google Scholar]
- Wang, J.; Long, F.; Ou, W. CNN-based color image encryption algorithm using DNA sequence operations. In Proceedings of the 2017 International Conference on Security, Pattern Analysis, and Cybernetics (SPAC), Shenzhen, China, 15–17 December 2017; pp. 730–736. [Google Scholar]
- Wang, Y.; Zhao, Y.; Zhou, Q.; Lin, Z. Image encryption using partitioned cellular automata. Neurocomputing 2018, 275, 1318–1332. [Google Scholar] [CrossRef]
- Qing, D.; Xiao, S.; Fang, Y. Hyperchaos in a simple CNN. Int. J. Bifurc. Chaos 2006, 16, 2453–2457. [Google Scholar]
- Peng, J.; Zhang, D.; Liao, X. A Digital Image Encryption Algorithm Based on Hyper-chaotic Cellular Neural Network. Fundam. Inform. 2009, 90, 269–282. [Google Scholar] [CrossRef]
- Li, J.; Bai, F.; Di, X. New color image encryption algorithm based on compound chaos mapping and hyperchaotic cellular neural network. J. Electron. Imaging 2013, 22, 3036. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Chua, L.O. n-Double Scroll Hypercubes in 1-D CNNs. Int. J. Bifurc. Chaos 1997, 7, 1873–1885. [Google Scholar] [CrossRef]
- Yen, J.C.; Guo, J.I. A new image encryption algorithm and its VLSI architecture. In Proceedings of the IEEE Workshop on Signal Processing Systems, Taipei, Taiwan, 22 October 1999; pp. 430–437. [Google Scholar]
- Wang, X.; Xu, B.; Zhang, H. A multi-ary number communication system based on hyperchaotic system of 6th-order cellular neural network. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 124–133. [Google Scholar]
- Koçak, H.; Palmer, K. Lyapunov exponents and stability in interval maps. Sema J. 2010, 51, 79–82. [Google Scholar] [CrossRef]
- Chen, G.; Ueta, T. Yet Another Chaotic Attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Zhou, T.; Yun, T.; Chen, G. Complex Dynamical Behaviors of the Chaotic Chen’s System. Int. J. Bifurc. Chaos 2003, 13, 2561–2574. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, D.; An, T.; Guan, Y. A Plaintext-Related Dynamical Image Encryption Algorithm Based on Permutation-Combination-Diffusion Architecture. IEEE Access 2020, 8, 62785–62799. [Google Scholar] [CrossRef]
- Fu, C.; Chen, Z.; Zhao, W.; Jiang, H. A new fast color image encryption scheme using Chen chaotic system. In Proceedings of the 2017 18th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Kanazawa, Japan, 26–28 June 2017; pp. 121–126. [Google Scholar]
- Zhou, R.G.; Sun, Y.J.; Fan, P. Quantum image Gray-code and bit-plane scrambling. Quantum Inf. Process. 2015, 14, 1717–1734. [Google Scholar] [CrossRef]
- Deng, J.; Zhao, S.; Wang, Y.; Wang, L.; Wang, H.; Sha, H. Image compression-encryption scheme combining 2D compressive sensing with discrete fractional random transform. Multimed. Tools Appl. 2017, 76, 1–21. [Google Scholar] [CrossRef]
- Wei, X.; Ling, G.; Qiang, Z.; Zhang, J.; Lian, S. A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system. J. Syst. Softw. 2014, 85, 290–299. [Google Scholar] [CrossRef]
- Wu, X.; Wang, K.; Wang, X.; Kan, H.; Kurths, J. Color image DNA encryption using NCA map-based CML and one-time keys. Signal Process. Off. Publ. Eur. Assoc. Signal Process. (EURASIP) 2018, 148, 272–287. [Google Scholar] [CrossRef]
- Liu, L.; Miao, S. An image encryption algorithm based on Baker map with varying parameter. Multimed. Tools Appl. 2017, 76, 16511–16527. [Google Scholar] [CrossRef]
- Tong, X.; Zhang, M.; Wang, Z.; Liu, Y.; Xu, H.; Ma, J. A fast encryption algorithm of color image based on four-dimensional chaotic system. J. Vis. Commun. Image Represent. 2015, 33, 219–234. [Google Scholar] [CrossRef]
- Nestor, T.; Dieu, N.J.D.; Jacques, K.; Yves, E.J.; El-Latif, A.A.A. A Multidimensional Hyperjerk Oscillator: Dynamics Analysis, Analogue and Embedded Systems Implementation, and Its Application as a Cryptosystem. Sensors 2019, 20, 83. [Google Scholar] [CrossRef] [PubMed]
- Nestor, T.; Kengne, J.; Abd-El-Atty, B.; Iliyasu, A.M.; El-Latif, A.A.A. Design and implementation of a simple dynamical 4-D chaotic circuit with applications in image encryption. Inf. Sci. 2020, 515, 191–217. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).