Abstract
When heavy rain strikes Taiwan, it always results in cracks in road pavement, and damages arising from potholes. Tremendously compromising road safety, road users may have fatal accidents caused by untimely repair actions. The road maintenance department needs to take the responsibilities for road sections in the form of inspections and faces the decision about how to properly allocate available resources to repair pavement damages immediately. When performing pavement repair works, we need to consider the resource consumption behavior and explore the mechanism of replenishing resources and calculating the return time. Therefore, in order to help maintenance units to deal with consumable resource issues, this study proposes a novel approach to offer the mechanism of consumable resource calculation, which is difficult to solve through the traditional vehicle routing problem (VRP) approach. This proposed model treats the pothole repair problem as a resource-constrained project scheduling problem (RCPSP), which is capable of resolving such consumable resource considerations. The proposed model was developed by adopting constraint programming (CP) techniques. Research results showed that the proposed model is capable of providing the optimal decisions of pavement pothole repair tasks and also meets practical requirements to make appropriate adjustment, and helps the maintenance unit to shorten total repair duration and optimize resource assignment decisions of pavement maintenance objectives.
1. Introduction
The changing global climatic causes extreme weather events, such as heavy rainfall, and cyclone events [1]. Those events result in the floods that bring devastating damages to road infrastructure [2] and create new challenges for the goals of efficient maintenance management [3,4]. Due to island geographical conditions, every year Taiwan has a great chance of heavy rains, even typhoons [5]. Whenever heavy rains hit the island, the excessive rainfall accumulation results in pothole damages [6]. Repair delays of those potholes lead to hazards and unsafe conditions for road users [7,8,9]. These pavement potholes threaten the road user’s safety; hence, in the 2010s, the Taiwan government commenced a serious commitment of pavement maintenance projects for repairing road holes promptly to ensure road safety conditions [10].
This study focuses on executing pothole repair actions from the maintenance unit’s perspective after heavy rainfall or typhoon. The maintenance units are defined as the work teams that have to repair potholes with prompt actions. Before the maintenance units execute the repair actions, pavement inspection should be performed to collect the information on the pothole damage severity [11]. This information is used for determining the amount of repair resources required to repair pavement potholes and mark the pavement pothole’s section in terms of the road network map. However, even after pavement inspection, the maintenance unit still faces difficulties to define the proper routing order of delivering the repair resources and repairing all damaged sections. It is obvious that pavement potholes are scattered over the vast road network. Therefore, to avoid a greater risk of traffic accidents caused by pavement potholes, repair actions should be performed as soon as possible, even under vague information.
One of the important concerns when establishing a proper pothole repair schedule is identifying the repair sequence of all existing pothole points according to the relative location distance from the resource points, where all necessary replenishment of repair materials is provided. In addition to work team resources, which are renewable resources in a project environment, asphalt concrete as a major repair material resource has a consumable resource behavior [12]; it can only be utilized once, and needs to be replenished if this resource is still needed. The replenishment activity of consumable resources influences the total transportation time of the loading truck. During the execution phase of the pothole repair process, when the remaining material inside the truck is still enough to satisfy the required quantity of the next damaged section, the truck moves to that section. However, if the rest of the material is not enough to repair the next damaged section, the truck needs to return to the resource point for replenishment. Given the situations where the available resource is often overwhelmed and potholes spread over the vast road network, it is important to optimize the utilization of the limited resources including both renewable and consumable resources when planners prepare the pothole repair schedule. Based on those tough decision problems, this study aims to establish an optimal repair schedule to arrange the delivery and repair activities of the pavement pothole repair problem.
In order to resolve the repair sequence and resource replenishment issues mentioned above, this study attempts to utilize the resource-constraint project scheduling problem (RCPSP) approach to overcome the repair and transport activity scheduling problem. From the perspective of RCPSP, several characteristics of the proposed model are determined as follows: (1) under a resource-constrained environment, resource consumption rules of available repair resources must satisfy the repair material demand for all pavement pothole sections; (2) the responsibility area of each maintenance unit is defined as a pothole repair project, and each pothole inside the responsibility area of maintenance unit is treated as a project activity; (3) the repair duration and the dispatching quantity of material resources vary depending on the damage assessment of each pothole.
Furthermore, based on the RCPSP framework, the maintenance unit is responsible to repair each damaged section inside their responsibility area, and will rely on one or more resource points to supply consumable material resources. One resource point handles several pavement pothole points inside their responsibility area. The proposed model is designed to adapt to different consumable resource requirements based on the pothole severity, through dynamically assigning the transport activities of consumable resources. Subsequently, in order to resolve the difficulties to choose the loading truck’s optimum travel path in serving a lot of scattered potholes points, a constraint programming (CP) technique was adopted in this study. The CP technique is proven as one of the reliable mechanisms to establish optimal scheduling models [13]. Through case analysis, the proposed CP-based model was also proven to solve the pavement pothole repair problems effectively.
The remaining of the paper is structured as follows. In Section 2, the related studies of pavement maintenance and repair strategies for preserving road safety conditions are summarized and discussed. The methodology to develop the optimization model is introduced in Section 3. In Section 4, a case study and discussion of the optimized results are presented. Lastly, a summary of this study and suggestions for future study are given in Section 5.
2. Literature Review
The management strategy of pavement maintenance and repair problems for road networks has been the focus of prior studies over the past few years. Optimization approach has been a prominent method to solve such problems. The literature review is conducted in the following three topics: (1) the types of pavement distress; (2) RCPSP concept and applications; and (3) pavement maintenance and repair strategy.
2.1. Pavement Distress Types
The surface layer of flexible pavement construction uses asphalt mixtures as the major material. The next layer is the sub-base layer that particularly utilizes a hydraulically-bound mixture. The bottom layer, which is generally utilized unbound mixture material, is followed by the sub-grade and road-bed layer [14]. The materials of the asphalt mixture include aggregates and bitumen. Aggregates provide a strong structure to sustain the vehicle loads and give skid resistance, wherein bitumen plays an important role to ensure the joint of the aggregates [12]. Due to the exposure of the environment and traffic load, the pavement will endure distress and slowly lead to changes in the surface shape [15].
Proper assessment on pavement conditions in road sections is essential in the pavement management strategy [16,17]. For the classification of defects found in flexible pavements, discrimination methods of defect types are usually utilized [18]. Based on the distress identification manual from the Federal Highway Administration of the U.S. Department of Transportation, there are several types of asphalt concrete pavement distress, listed as follows [19]:
- Cracking, which is defined as fatigue damage caused by traffic volume exceeding the design standard or improper asphalt mix design and construction. A cracking shape is a line that has a gap, in which gap width is specified as less than 6 mm for low severity and more than 19 mm for high severity. There are six types of damage: fatigue cracking, block cracking, edge cracking, longitudinal cracking, reflection cracking at joints, and transverse cracking.
- Patching and potholes, a portion of pavement surface. The dimensions of a damaged section are usually greater than 0.1 square-meter, and those damages are removed and replaced or additional material applied to the pavement after the original construction. For potholes, the pavement damage shape is bowl-shaped of various sizes in the pavement surface with a minimum dimension of 150 mm. The maximum pothole depth is below pavement surface, which includes high severity levels if the depth is greater than 50 mm.
- Surface deformation is caused by poor material stability, changes in road base materials, or by braking and starting behaviors of vehicles, resulting in sagging or deformation in the horizontal and vertical directions at the place where the wheels are rolled over. This distress type creates a wavy surface with a width size similar to a vehicle wheel. There are two types of damage: rutting and shoving.
- Surface defect is caused by the decomposition of granules, asphalt mud floating out of the surface, or the loss of bonding force between asphalt mud and granules. The physical feature of this distress is reflected in the reduction in pavement surface friction. This type of distress consists of three types: bleeding, polish aggregate, and raveling.
- Miscellaneous distress is pavement damage that does not fall under the above three categories, mainly caused by segmental difference, which generates longitudinal slope irregularities at both ends of the structure. These distress types are included: lane-to-shoulder drop-off, water bleeding and pumping.
Potholes are the most general pavement distress, especially for asphalt concrete (AC) deterioration [20,21]. Before potholes appear, the distress commonly begins with pavement cracks. Pavement cracks occur because aging and environmental exposition chemically degrade the bitumen that binds pavement material [22]. Through the cracks, water then penetrates the pavement and causes the loss of the adhesion between aggregate and binder. [23]. The adhesion loss makes pavements further fragile. Thus, when the pavement experiences thermal exposure, fatigue, and vehicular burden, potholes then appear [12,15,24]. If a small pothole is repaired as soon as possible, it will avoid further pavement deterioration and reduce repair cost. It can be proved that the repair delay after pothole appearance will give great chance for water penetrating the subgrade and cause further severe pavement structural failure [9].
Based on distress classification types, a maintenance unit can perform a pavement distress survey to establish the composite condition index’s weight that reflects the pavement performance [25]. Furthermore, according to the composite condition index’s value, a proper maintenance strategy can be established [26]. The worst severity requires repair material and time to perform the repair activity. Thus, the severity level of pavement distress will influence the method and repair cost [27].
2.2. Resource Constrained Project Scheduling Problem (RCPSP)
In the 21st century, many studies on resource-constrained project scheduling topics have generated numerous variants of optimization models with different considerations in resource constraints, activity assumption, and objective function. Resource project scheduling problem (RCPSP) has proven to be a reliable approach for solving project scheduling problems to minimize makespan with tight renewable resource constraints [28]. The primary objective of RCPSP aims to minimize the total duration of the project schedule, which is composed of a set of activities connected by precedence constraints and restricted by multiple resource limitations [29,30,31,32].
Previous studies have proven that RCPSP can resolve complicated scheduling problems under the circumstances of complex resource allocation and assignment. A mixed-integer linear programming (MILP) optimization model was used in some previous studies to solve RCPSP, such as Pinto et al. [33], who presented an extension of an RCPSP problem in a semiconductor industry multi-mode resource-collaboration and constrained scheduling problem (MRCCSP). Chakrabortty et al. [34] presented a stochastic resource-constrained project scheduling problem (SRCPSP) model to minimize project makespan under stochastic activity durations. Hanzalek and Sucha [35] considered a lacquer production scheduling problem into RCPSP with general temporal and resource constraints (i.e., positive and negative time-lags).
Other studies utilized a genetic algorithm (GA) technique to solve the RCPSP problem, such as Alcaraz and Maroto [36], who presented a single-mode RCPSP environment model to achieve the minimum project duration. Rahman et al. [37] considered three different practical environments—the information technology, the construction industry, and the medical service system—and attempted to examine the effectiveness of the proposed GA-based RCPSP model. Besides MILP and GA techniques, constraint programming (CP) techniques were also applied in previous studies. Wang et al. [38] utilized CP techniques proposed a multimode resource-constrained project scheduling problem (MRCPSP) model combined with a work package-based information model in construction project scheduling. A CP solution model to solve resource-constrained multi-project scheduling problems that considered alternative activity chains and time flexibility (RCMPSP-ACTF) was conducted by Hauder et al. [39].
2.3. Pavement Maintenance and Repair Strategy
Several previous studies attempted to solve the pavement maintenance problem through development of pavement maintenance and repair strategy. For example, a strategy for pavement resurfacing under steady-state conditions was proposed by Li and Madanat [40] to optimize repair action’s frequency and intensity. Ouyang and Madanat [41] introduced a mixed-integer nonlinear programming (MINLP) model to optimize highway pavement rehabilitation planning through minimizing the life-cycle cost in a finite horizon. Chootinan et al. [42] proposed a methodology of multi-year pavement maintenance programming that explicitly accounts for unpredictability in pavement deterioration based on the genetic algorithm (GA) technique. Cohen and Madanat [43] introduced an optimization model to minimize the total expected social cost of maintaining the facilities over a finite planning horizon under facility deterioration uncertainty.
Pamukovic et al. [44] developed a decision support concept for maintaining damaged asphalt pavement by employing the multicriteria preference ranking organization method for enrichment of evaluation (PROMETHEE) method and the analytic hierarchy processing (AHP) method. Alcaraz et al. [45] proposed a procedure to support collection, analysis, processing, and updating of pavement conditions to be implemented in pavement maintenance strategy based on a pavement management system. Mahanpoor et al. [46] considered geometric road configuration and presented three particle swarm optimization (PSO) models to optimize the cost of pavement rehabilitation considering the existing pavement condition and project line elevation, travel time, as well as fuel consumption.
Biancardo et al. considered the infrastructure life cycle perspective and presented a decision support system (DSS) for maintenance operation management of runway pavement [47] and roadway pavement [48]. For the runway pavement, the DSS considered runway friction decay modeling based on aircraft traffic load. This study utilized classification and regression trees (CARTs), chi-squared automatic interaction detector (GCHAID), k-means unsupervised learning algorithms, and Chiu’s subtractive clustering as data mining methods to process the aircraft traffic load data. The results of the data mining process were compared to the standard technical practice to evaluate the measurement value of runway friction decay. The DSS in roadway infrastructure maintenance operations management utilize a building information modeling (BIM) approach. The BIM model in this study used visual programming tools (VPL) that can inform the detailed technical information of pavement condition to the highway agency; thus, the highway agency can conduct proper maintenance actions.
Pavement repair involves machinery to produce, deliver, and spread asphalt concrete, activities which are associated with a large amount of resource consumption and greenhouse gas (GHG) emissions [49]. Therefore, several studies attempted to develop a decision support system (DSS) for pavement maintenance strategy that considers environmental impact. Noland and Hanson [50] examined life-cycle GHG emissions of asphalt concrete for pavements by adopting the green gas assessment spreadsheet for transportation capital project (GASCAP) method in a road maintenance project. A similar study conducted by Ma et al. [51] was to investigate the GHG emissions of pavement maintenance during the life cycle period and compared sixteen different maintenance technologies of asphalt concrete. Yu et al. [52] attempted to find optimal combinations of pavement performance, maintenance cost, and environmental impacts for developing asphalt pavement maintenance plans from the life cycle cost analysis (LCCA) perspective. Veropalumbo et al. [53] compared mechanical and environmental performance of a base layer flexible pavement and considered the life cycle assessment (LCA) of bituminous mixture as an essential material of flexible pavement.
Further studies were focused on the LCA from a road network perspective with maintenance budget limitation. Chu and Huang [54] introduced mixed-integer linear programming (MILP) models for network roads in three different pavement maintenance strategies: optimization-based, worst-first, best-first, and threshold-based from the life-cycle management perspective. Guo et al. [55] proposed a probabilistic treatment path dependence (PTPD) model that considers pavement deterioration uncertainty to obtain the optimum maintenance budget. Mizutani et al. [56] attempted to find an optimal global solution for the repair and work zone policy in the pavement management system at network level. Elhadidy et al. [57] proposed a multi-objective pavement maintenance optimization model based on historical long-term pavement performance (LTTP) data to minimize the maintenance cost and maximize pavement condition.
Most of the above studies aimed to discuss pavement maintenance strategies from the deterioration model’s perspective, or predict the future pavement condition with life cycle analysis. Some of those studies considered establishing sustainable maintenance strategies in the long-term. However, only a few studies have attempted to develop pavement planned-repair strategies, such as Chen et al. [58], who proposed an optimization model for a road network’s daily maintenance operations as a routing problem that considers service time’s uncertainty and operation cost. Lee [59] introduced a scheduling model based on road users’ route-changing behavior to optimize contractor activities when repairing pavements. Huang and Lin [10] proposed an arc routing problem approach to minimize the total cost of the construction machinery routing activity for road resurfacing projects on city road networks. Aarabi and Batta [60] presented an optimization mode for repair worker routes on pothole repair problems in the road network. However, those pavement repair studies that aimed to obtain an optimum repair schedule utilizing the vehicle routing problem (VRP) approach for a problem-solving perspective.
The other approach to solve the pavement repair problem is from the perspective of the emergency repair concept. However, these types of studies have focused on network road repair after a natural hazard. Maya and Sorensen [61] presented a road network repair strategy under scarce resources to maximize society accessibility in an affected disaster area. Based on the previous work, Maya et al. [62] introduced the network repair crew scheduling and routing problem (NRCSRP) framework to minimize the traveling movement of a repair crew to recover an access road from the disaster point to the relief center. Moreover, Aksu and Ozdamar [63] proposed a debris clearance scheduling model (DCSM), employing integer programming to recover blocked road network links in the first three days of emergency response under resource constraints. Inspired by their study, Kim et al. [64] applied the ant colony system (ACS) algorithm as an optimization model for solving NRCSRP in the disaster response phase for short-term disasters; this optimization model was named as network repair crew scheduling for short-term disaster (NRCSSD). Moreover, most of those emergency repair studies also employed the VRP approach similarly to the pavement planned-repair studies above.
This study’s main contribution is to combine the pavement planned-repair strategy with the emergency repair concept to achieve a tangible schedule for immediate pavement pothole repair problems. Prior studies have mostly utilized the VRP approach to resolve the transportation problem and none of those studies have considered consumable resources in their models; this study strives to adopt the advantages of the RCPSP approach in handling consumable resource behavior on the proposed optimization model for pavement pothole repair problems.
3. Methodology
3.1. Model Concept
The routine process to resolve a pothole repair problem starts with compiling the damage data of road pavements through daily inspection operations, then determining the limited number of work teams that are under control by the maintenance unit, and considering whether material resources need to be replenished to assist the maintenance unit’s decision maker in scheduling repair works to assign the repair sequence in the unit’s road area of responsibility.
The proposed model is based on the resource-constrained project scheduling problem (RCPSP) framework, which considers the material consumption behavior at all damaged sections. Under an RCPSP environment, we treat the repair work at each damaged section as “repair activity”, and all repair activities comprise a pothole repair project. In addition to repair activities, the traveling process of material resources through connecting damaged sections is defined as “transport activity”, and the quantity of repair materials required for each repair activity is transported by loading trucks. Therefore, the characteristics of such project environments can be categorized into a dynamic project environment with dynamic activity precedence relationships.
Given the characteristics of pavement pothole repair problems, it can be understood that the project scheduling model proposed in this study should include the resource consumption behavior and the need to return to the resource point for replenishment of materials; the traditional vehicle routing problem (VRP) setting can hardly satisfy such practical considerations. Therefore, from the perspective of RCPSP, both resource consumption behavior and replenishment material requirements should follow consumable resource rules in the project scheduling environment. Comparing the traditional VRP with the proposed model, the specific and common features of both approaches are summarized in Table 1.

Table 1.
Specific and common features of the vehicle routing problem (VRP) and the proposed models.
3.2. Model Assumptions
In the proposed model, based on an RCPSP framework that considers resource consumption behavior, the relevant assumptions for model development are as follows:
- The origin location and number of work teams are assumed to be known.
- The capacity of the trucks for loading repair material is given (e.g., depending on truck type, and typical capacity being 15 cubic meter), and the minimum unit quantity required at all damaged sections set to at least 1 cubic meter, where such potholes are considered relatively big potholes on the pavement surface, thus requiring an immediate response. The repair material resources were asphalt mixes in this study.
- The repair duration and repair material requirements are known for all damaged sections, and only a single work team is allowed to carry out repair work at a specific section at one time.
- The performance of all construction machinery and the quality of materials are in accordance with local safety standards and inspection standards.
- All repair activities can only begin after the work team arrives at each damaged section and are not allowed to be interrupted once starting.
- It is assumed in this study that if the truck is not loaded with enough material to meet the demand of the damaged section, it will first go to the damaged section to unload the material and return to the resource point to fill up the replenished material, and the other construction equipment must wait for the truck to arrive at the site before starting repair works; otherwise, it will continue to the next damaged section for repair.
- For the purpose of immediate repair to reduce the possibility of public hazard, the proposed model does not consider any cost or funding.
- The resource consumption behavior exists only at the damaged section, and no material loss occurs during transportation.
The schematic diagram of the conceptual model development in this study is shown in Figure 1.
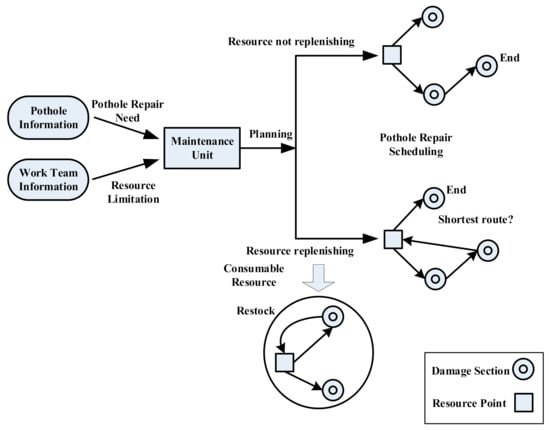
Figure 1.
Conceptual diagram of proposed pavement maintenance scheduling model.
3.3. Model Formulation
To summarize the basic assumptions of the model in the previous subsection, this subsection introduces the mathematical equations of the proposed model, and the definition of model parameters and variables are shown as Table 2. IBM ILOG CPLEX Optimizer software was used for model formulation [65], and the constraint programming (CP) algorithm was adopted.

Table 2.
Parameters and variables of the proposed model.
- Objective function
- Constraints
Total project duration is equal to the finish time of the last repair activity at the last completed damaged section in the pothole repair project, where the last activity will be determined during model solution-seeking runtime, shown as Equation (2).
The finish time of a repair activity at designated damaged section is equal to the sum of the activity start time and corresponding activity duration.
When the quantity of repair material is not enough for the demand of a specific damaged section, the repair work must wait for the loading truck to return to the resource point to replenish. Equation (4) represents the relationship where adjusted repair duration due to resource insufficiency is equal to the original repair duration adding the travel time to the damaged section Lun, which is calculated using Equation (16).
The finish time of transport activity is the sum of activity start time and transport activity duration (e.g., travel time of resource transport path). Transport activities can be divided into two categories: (1) those traveling from the resource point to the damaged section; and the second group (2) those traveling from the preceding damaged section to succeeding damaged section—the restrictions for each category are presented as Equations (5) and (6), respectively.
If a specific resource transport activity is selected for resource dispatching, the amount of equipment resources is greater than zero (i.e., this transport activity is really in execution status), then the duration of this resource transport activity is equal to the corresponding duration tnj/tij; otherwise, it is not executed and its corresponding duration should be equal to zero, where such logical expressions are shown as Equations (7) and (8) for these two categories of transport activities, respectively.
This study investigates the pavement pothole repair issue from a scheduling perspective. The pothole repair work is quite urgent; therefore, this model assumes that all pothole repair works are completed at the damaged section and equipment resources are then immediately transported to the next damaged section through the connecting transport activity, and pothole repair work at the succeeding damaged section starts immediately after the arrival of the resources, which is the FS (finish–start) relationship in scheduling precedence relationships, shown as Equation (9).
The quantity of loading materials required for subsequent damaged section may be transported through several resource transport paths linked with different preceding damaged sections; therefore, it is assumed that for each damaged section, repair activity can start only if the entire quantity of material resources supplied through all paths arrive.
Resource transport can be further divided into two situations: (1) transport from the resource point to the damaged section; and (2) transport from one damaged section to another damaged section; therefore, the relationships between transport activity and repair activity are shown as Equations (10) and (11), respectively.
The repair material requirement for a repair activity may be dispatched from the preceding damaged section or a resource point; therefore, the material capacity accepted by the subsequent damaged section must be the same as the transportation material capacity from the preceding damaged section or resource point dispatch to ensure that the truck loading material actually reaches the damaged section, where such situations are subjected to Equations (12) and (13), respectively.
Given the behavior of material resource consumption, the amount of material left over from the preceding repair activity at the end of repair work is calculated as shown as Equation (14).
When a repair activity consumes the demand of repair materials with insufficient quantity, shown as Equation (15), NEu may be a positive or negative value. If NEu is positive, the truck must return to the resource point to replenish the capacity and the minimum time to return (twice on the same route) to replenish the materials; conversely, if both are zero (Equation (16)):
4. Case Analysis and Discussion
The proposed model treats the damaged sections of the road pavement as repair activities, and the travel times between potholes as transport activities, and the repair materials required for each repair activity are transported by trucks. Two hypothetical cases, including four scenarios, are presented to validate the model applicability and provide research findings in the following subsections.
4.1. Case 1: Single Resource Point
One resource point was assigned in case 1 after the data gathering phase: the damage records of road pavement are compiled through daily inspection operations. The repair material demand and duration of repair activity for each damage point is determined, and the geographical representation of this pavement pothole project is shown in Figure 2. There are six potholes in the responsibility area (with 2, 3, 4, 5, 6, and 7 as the damaged sections) and one resource placement point (1). The shortest route between each pothole node is shown as a node line. If there is no node line, it means that there is no direct connecting route between the nodes.
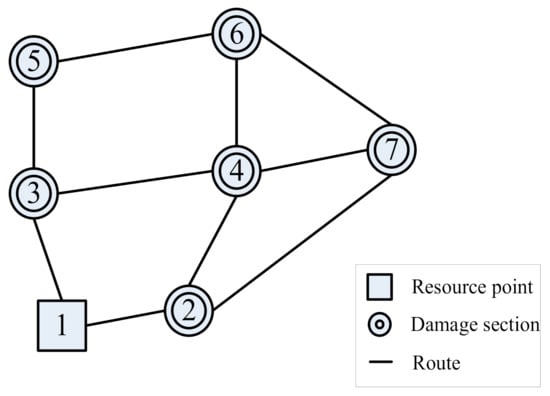
Figure 2.
Diagram of pavement pothole repair project (Case 1).
In this case, two scenarios (scenario A and B) are analyzed. Each work team is equipped with a truck with a loading capacity of 15 units, and the material loaded on the truck will be consumed with repair works for each damaged section. The durations and demands of repair activity at each damaged section are presented in Table 3. The starting points, arrival points, and travel times of each resource transport path are shown in Table 4.

Table 3.
Material quantity required for the repair and corresponding duration (Case 1).

Table 4.
Resource transport information (Case 1).
- Scenario A: Two work teams are available at resource point 1 and can be dispatched to perform repair works; this situation is similar to the application of traditional VRP, and the two work teams should be fully loaded with repair material to meet the repair demands of all damaged sections without returning to the resource point to replenish.
In Scenario A, because the capacity of two truckloads can satisfy the demand of all damaged sections, the whole repair process is shown in Figure 3 and the optimized scheduling results are shown in Table 5. The total duration of the pothole maintenance project is 180 min.
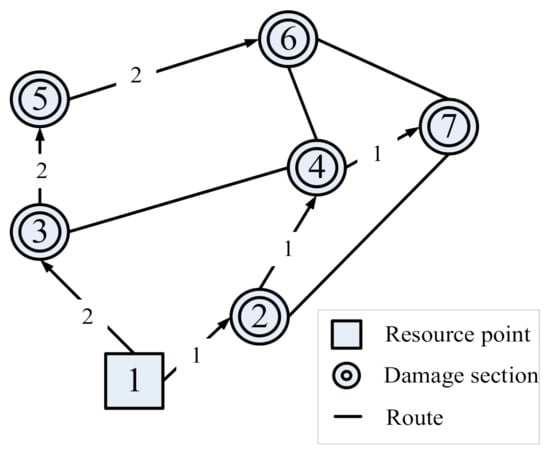
Figure 3.
Diagram of repair process (Scenario A).

Table 5.
Optimized result (Scenario A).
- Scenario B: In this scenario, only one work team is available. Therefore, the travelling behavior of returning to resource points for resource replenishment must be considered in the repair process, which complicates such optimization problems and cannot be solved by the traditional VRP approach. If the remaining material with the loaded truck is not enough to meet the demand of unrepaired damaged sections, because of the time-sensitive nature of pavement material, the remaining material in the truck must be transported to the next damaged section to unload, and then return to the resource point to replenish the capacity and again return to the previous damaged section to continue repair work.
In Scenario B, with the limitation of only one available work team, the maintenance unit often dispatches this work team manually, as shown in Figure 4 and Table 6. The minimum project duration with manual dispatch is 470 min. Such a scheduling strategy examined by expert experience mostly relies on searching for the shortest travel time near the current node while performing neighborhood searches. Comparing manual calculation and optimization solving process, the hand-calculation effort of manual dispatch usually takes couples of minutes depending on the problem scale; the computer solving time of the optimization model takes less than one second. Moreover, manual dispatch often lacks overall planning perspective and cannot guarantee reaching the optimal solution, compared with the proposed optimization-based model which seeks for the global optimum.
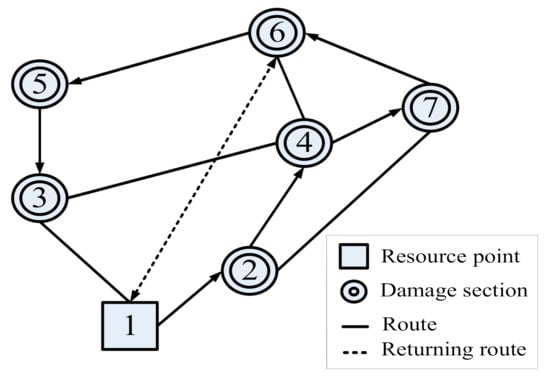
Figure 4.
Diagram of repair process by manual dispatch (Scenario B).

Table 6.
Manual dispatch schedule result (Scenario B)
Based on the optimized result, the repair process is illustrated in Figure 5, and the scheduling results are summarized in Table 6, which shows that the total duration of the pavement pothole maintenance project is 450 min. Comparing Table 6 and Table 7, overall repair schedule is delayed when planning by manual calculation, and the result of proposed model saved 20 min; thus, it is better than the manual dispatch approach in this case. The proposed model can be used to consider the situation of resource replenishment requirements during the solving process, and repair activity can be carried out immediately in accordance with actual situations, and it can help to solve the shortcoming of the VRP approach which cannot judge the successive travel time after the turnaround.
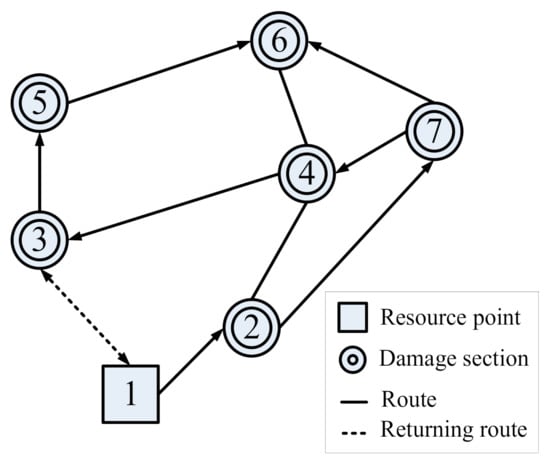
Figure 5.
Diagram of repair process (Scenario B).

Table 7.
Optimized schedule result (Scenario B).
4.2. Case 2: Two Resource Points
In Case 2, the number of the damaged sections increases from six points to ten points, and another resource point (2) is added. The number of damaged sections is extended to 10 for the setup of a pavement pothole repair problem, shown in Figure 6. The relevant information of this pothole repair project is shown in Table 8 and Table 9: points 3, 4, 5, 6, 7, 8, 9, 10, 11, and 12 are marked as damaged section numbers, and the two resource points are 1 and 2. Two new scenarios (C and D) are presented to demonstrate the applicability of the proposed model.
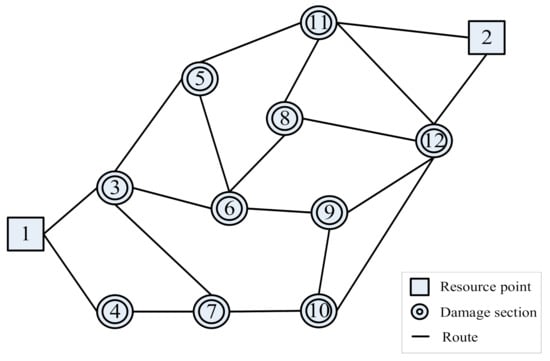
Figure 6.
Diagram of pavement pothole repair project (Case 2).

Table 8.
Material quantity required for repair and corresponding duration (Case 2).

Table 9.
Resource transport information (Case 2).
- Scenario C: The demand of each damage point is known; therefore, two work teams are dispatched from resource points 1 and 2 (total of four teams) to perform maintenance operations. The optimized repair process is shown in Figure 7, and the optimized schedule result is summarized in Table 10. It shows that the total material capacity of the four trucks is sufficient to meet the demand of all damage points, and the optimal repair schedule is achieved when there are four resources. The total duration of the pavement pothole repair project is 150 min.
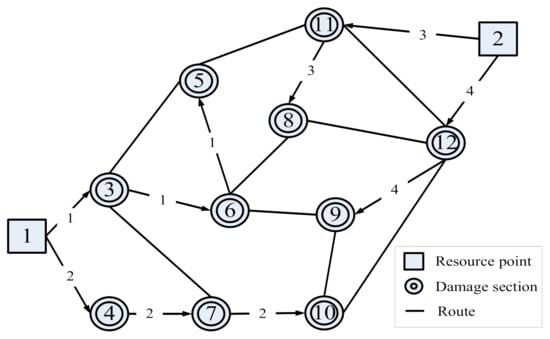 Figure 7. Diagram of repair process (Scenario C).
Figure 7. Diagram of repair process (Scenario C). Table 10. Optimized schedule result (Scenario C).
Table 10. Optimized schedule result (Scenario C). - Scenario D: only one team is available to be dispatched from each resource point to carry out repair works (total two teams); there is a shortage of materials that need to be replenished before finishing all repair works in this pothole repair project. The optimized repair process is shown in Figure 8, and the scheduling results are summarized in Table 11. The total duration of the pavement pothole repair project is 310 min.
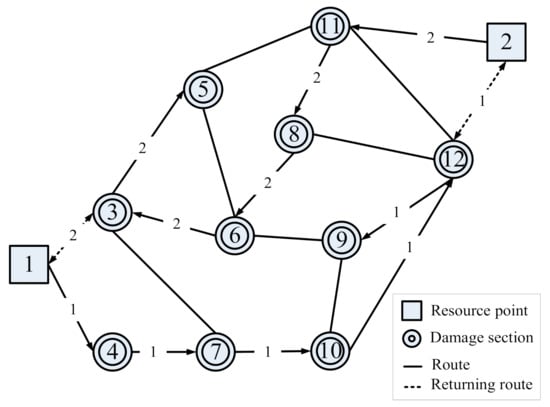 Figure 8. Diagram of repair process (Scenario D).
Figure 8. Diagram of repair process (Scenario D). Table 11. Optimized schedule result (Scenario D).
Table 11. Optimized schedule result (Scenario D).
Based on the above results, this model can handle the situation of whether or not material replenishment is needed. It is easy to plan the pothole repair schedule based on the limitation of the existing work team and consider the material requirement of each damaged section. If there is not enough material at the damaged section, loading trucks have to return to the resource point to replenish the material before continuing the repair operation. Therefore, this model can effectively arrange the optimal repair schedule under a resource-constrained project environment and provide the maintenance unit with the decision suggestions to repair potholes according to the existing resource status.
5. Conclusions and Recommendations
In this study, an optimization model was presented for pavement pothole repair problems to arrange the repair sequence of damaged sections, based on an RCPSP framework. The proposed model considers the material consumption behavior at damage points and the need for replenishing consumable resources, to solve the optimal repair schedule. From the analysis results of the case study, it has been demonstrated that the proposed model is superior to the manual dispatch method in both aspects of calculation effort and schedule optimization, for the sake of time-saving and a better solution. This optimization model can overcome the practical consideration of resource replenishment, which is difficult to solve by the traditional VRP approach. When the decision maker is faced with a practical pothole repair problem, it provides an effective solution to quickly solve the repair scheduling problem.
Future studies could consider financial aspects of the pavement pothole repair problem. Under practical conditions, if this model is capable of dealing with budget limitations, the comparison of various resource statuses such as the time–cost tradeoff can be further explored, so that the decision maker can measure the appropriate assignment of pothole repair works for the amount of available resources to achieve better maintenance management goals. Finally, two hypothetical cases were created for model validation, and the scale of the problem domain could be further expanded by adopting real-world, large-scale cases.
Author Contributions
Conceptualization, S.-S.L., W.T.C., and A.B.; formal analysis, S.-S.L., Y.-H.H., and A.B.; investigation, S.-S.L.; writing—original draft preparation, S.-S.L., A.B., and M.F.A.A.; writing—review and editing, S.-S.L. and M.F.A.A.; supervision, S.-S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data generated or analyzed during the study are available from the corresponding author by request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, J.; Kang, J. Analysis of Flood Damage in the Seoul Metropolitan Government Using Climate Change Scenarios and Mitigation Technologies. Sustainability 2020, 13, 105. [Google Scholar] [CrossRef]
- Mallick, R.B.; Radzicki, M.J.; Daniel, J.S.; Jacobs, J.M. Use of system dynamics to understand long-term impact of climate change on pavement performance and maintenance cost. Transp. Res. Rec. 2014, 2455, 1–9. [Google Scholar] [CrossRef]
- Sultana, M.; Chai, G.; Martin, T.; Chowdhury, S. Modeling the postflood short-term behavior of flexible pavements. J. Transp. Eng. 2016, 142, 1–11. [Google Scholar] [CrossRef]
- Sultana, M.; Chai, G.; Chowdhury, S.; Martin, T.; Anissimov, Y.; Rahman, A. Rutting and Roughness of Flood-Affected Pavements: Literature Review and Deterioration Models. J. Infrastruct. Syst. 2018, 24, 04018006. [Google Scholar] [CrossRef]
- Shih, H.J.; Chen, H.; Liang, T.Y.; Fu, H.S.; Chang, C.H.; Chen, W.B.; Su, W.R.; Lin, L.Y. Generating potential risk maps for typhoon-induced waves along the coast of Taiwan. Ocean. Eng. 2018, 163, 1–14. [Google Scholar] [CrossRef]
- Amin, S.; Tamima, U.; Amador-Jiménez, L.E. Optimal pavement management: Resilient roads in support of emergency response of cyclone affected coastal areas. Transp. Res. Part A Policy Pract. 2019, 119, 45–61. [Google Scholar] [CrossRef]
- Yang, Y.; Qian, Z.; Song, X. A pothole patching material for epoxy asphalt pavement on steel bridges: Fatigue test and numerical analysis. Constr. Build. Mater. 2015, 94, 299–305. [Google Scholar] [CrossRef]
- Montella, A.; Chiaradonna, S.; Criscuolo, G.; De Martino, S. Development and evaluation of a web-based software for crash data collection, processing and analysis. Accid. Anal. Prev. 2019, 130, 108–116. [Google Scholar] [CrossRef] [PubMed]
- Kwon, B.J.; Kim, D.; Rhee, S.K.; Kim, Y.R. Spray injection patching for pothole repair using 100 percent reclaimed asphalt pavement. Constr. Build. Mater. 2018, 166, 445–451. [Google Scholar] [CrossRef]
- Huang, S.H.; Lin, P.C. Multi-treatment capacitated arc routing of construction machinery in Taiwan’s smooth road project. Autom. Constr. 2012, 21, 210–218. [Google Scholar] [CrossRef]
- Cao, M.T.; Tran, Q.V.; Nguyen, N.M.; Chang, K.T. Survey on performance of deep learning models for detecting road damages using multiple dashcam image resources. Adv. Eng. Inform. 2020, 46, 101182. [Google Scholar] [CrossRef]
- Obaidi, H.; Gomez-Meijide, B.; Garcia, A. A fast pothole repair method using asphalt tiles and induction heating. Constr. Build. Mater. 2017, 131, 592–599. [Google Scholar] [CrossRef]
- Liu, S.S.; Wang, C.J. Optimizing linear project scheduling with multi-skilled crews. Autom. Constr. 2012, 24, 16–23. [Google Scholar] [CrossRef]
- Liu, Y.; Su, P.; Li, M.; You, Z.; Zhao, M. Review on evolution and evaluation of asphalt pavement structures and materials. J. Traffic Transp. Eng. 2020, 7, 573–599. [Google Scholar] [CrossRef]
- Jahanbakhsh, H.; Karimi, M.M.; Nejad, F.M. Correlation between asphalt concrete induced healing and rheological properties of asphalt binder. Constr. Build. Mater. 2020, 265, 120577. [Google Scholar] [CrossRef]
- Loprencipe, G.; Pantuso, A.; Di Mascio, P. Sustainable Pavement Management System in Urban Areas Considering the Vehicle Operating Costs. Sustainability 2017, 9, 453. [Google Scholar] [CrossRef]
- Obaidat, M.T.; Al-kheder, S.A. Integration of geographic information systems and computer vision systems for pavement distress classification. Constr. Build. Mater. 2006, 20, 657–672. [Google Scholar] [CrossRef]
- Pinatt, J.M.; Chicati, M.L.; Ildefonso, J.S.; Filetti, C.R.G.D.A. Evaluation of pavement condition index by different methods: Case study of Maringá, Brazil. Transp. Res. Interdiscip. Perspect. 2020, 4, 100100. [Google Scholar] [CrossRef]
- Teng, T.P. Distress Identification Manual, for the Long-Term Pavement Performance Program; US Department of Transportation, Federal Highway Administration: Washington, DC, USA, 2003; pp. 1–169. [Google Scholar]
- Li, J.; Liu, J.; Zhang, W.; Liu, G.; Dai, L. Investigation of thermal asphalt mastic and mixture to repair potholes. Constr. Build. Mater. 2019, 201, 286–294. [Google Scholar] [CrossRef]
- Kamal, K.; Mathavan, S.; Zafar, T.; Moazzam, I.; Ali, S.A.; Ahmad, U.; Rahman, M. Performance assessment of Kinect as a sensor for pothole imaging and metrology. Int. J. Pavement Eng. 2018, 19, 565–576. [Google Scholar] [CrossRef]
- Hunter, R.N.; Self, A.; Read, J. The Shell Bitumen Handbook; Thomas Telford, ICE Publishing: Westminster, London, UK, 2015. [Google Scholar]
- Zheng, C.; Zhao, D.; Chen, C.; Song, Z.; Zheng, S. Quantitative test technology study on the mesoscopic strength parameters of the mineral aggregate contact surface of bituminous-stabilized macadam. Constr. Build. Mater. 2013, 40, 622–631. [Google Scholar] [CrossRef]
- Zborowski, A.; Kaloush, K.E. A fracture energy approach to model the thermal cracking performance of asphalt rubber mixtures. Road Mater. Pavement Des. 2011, 12, 377–395. [Google Scholar] [CrossRef]
- Kuhn, K.D. Pavement Network Maintenance Optimization Considering Multidimensional Condition Data. J. Infrastruct. Syst. 2012, 18, 270–277. [Google Scholar] [CrossRef]
- Mahdev, V.G.; Archana, M.R.; Biligiri, K.P. Development of Pavement Management Strategies for Arterial Roads. Int. J. Res. Eng. Technol. 2013, 02, 174–179. [Google Scholar] [CrossRef][Green Version]
- Weng, X.; Huang, Y.; Wang, W. Segment-based pavement crack quantification. Autom. Constr. 2019, 105, 2018. [Google Scholar] [CrossRef]
- Coelho, J.; Vanhoucke, M. Multi-mode resource-constrained project scheduling using RCPSP and SAT solvers. Eur. J. Oper. Res. 2011, 213, 73–82. [Google Scholar] [CrossRef]
- Baptiste, P.; Le Pape, C. Constraint propagation and decomposition techniques for highly disjunctive and highly cumulative project scheduling problems. Constraints 2000, 5, 119–139. [Google Scholar] [CrossRef]
- Baptiste, P.; Demassey, S. Tight LP bounds for resource constrained project scheduling. OR Spectr. 2004, 26, 251–262. [Google Scholar] [CrossRef]
- Liess, O.; Michelon, P. A constraint programming approach for the resource-constrained project scheduling problem. Ann. Oper. Res. 2008, 157, 25–36. [Google Scholar] [CrossRef]
- Brucker, P.; Knust, S. Linear programming and constraint propagation-based lower bound for the RCPSP. Eur. J. Oper. Res. 2000, 127, 355–362. [Google Scholar] [CrossRef]
- Pinto, G.; Ben-Dov, Y.T.; Rabinowitz, G. Formulating and solving a multi-mode resource-collaboration and constrained scheduling problem (MRCCSP). Ann. Oper. Res. 2013, 206, 311–339. [Google Scholar] [CrossRef]
- Chakrabortty, R.K.; Sarker, R.A.; Essam, D.L. Multi-mode resource constrained project scheduling under resource disruptions. Comput. Chem. Eng. 2016, 88, 13–29. [Google Scholar] [CrossRef]
- Hanzálek, Z.; Šůcha, P. Time symmetry of resource constrained project scheduling with general temporal constraints and take-give resources. Ann. Oper. Res. 2017, 248, 209–237. [Google Scholar] [CrossRef]
- Alcaraz, J.; Maroto, C. A Robust Genetic Algorithm for Resource Allocation in Project Scheduling. Ann. Oper. Res. 2001, 102, 83–109. [Google Scholar] [CrossRef]
- Rahman, H.F.; Chakrabortty, R.K.; Ryan, M.J. Memetic algorithm for solving resource constrained project scheduling problems. Autom. Constr. 2019, 111, 103052. [Google Scholar] [CrossRef]
- Wang, H.W.; Lin, J.R.; Zhang, J.P. Work package-based information modeling for resource-constrained scheduling of construction projects. Autom. Constr. 2020, 109, 102958. [Google Scholar] [CrossRef]
- Hauder, V.A.; Beham, A.; Raggl, S.; Parragh, S.N.; Affenzeller, M. Resource-constrained multi-project scheduling with activity and time flexibility. Comput. Ind. Eng. 2020, 150, 106857. [Google Scholar] [CrossRef]
- Li, Y.; Madanat, S. A steady-state solution for the optimal pavement resurfacing problem. Transp. Res. Part A Policy Pract. 2002, 36, 525–535. [Google Scholar] [CrossRef]
- Ouyang, Y.; Madanat, S. Optimal scheduling of rehabilitation activities for multiple pavement facilities: Exact and approximate solutions. Transp. Res. Part A Policy Pract. 2004, 38, 347–365. [Google Scholar] [CrossRef]
- Chootinan, P.; Chen, A.; Horrocks, M.R.; Bolling, D. A multi-year pavement maintenance program using a stochastic simulation-based genetic algorithm approach. Transp. Res. Part A Policy Pract. 2006, 40, 725–743. [Google Scholar] [CrossRef]
- Durango-Cohen, P.L.; Madanat, S.M. Optimization of inspection and maintenance decisions for infrastructure facilities under performance model uncertainty: A quasi-Bayes approach. Transp. Res. Part A Policy Pract. 2008, 42, 1074–1085. [Google Scholar] [CrossRef]
- Pamuković, J.K.; Rogulj, K.; Dumanić, D.; Jajac, N. A sustainable approach for the maintenance of asphalt pavement construction. Sustainability 2021, 13, 109. [Google Scholar] [CrossRef]
- Montoya-Alcaraz, M.; Mungaray-Moctezuma, A.; García, L. Sustainable road maintenance planning in developing countries based on pavement management systems: Case study in Baja California, México. Sustainability 2020, 12, 36. [Google Scholar] [CrossRef]
- Mahanpoor, M.; Monajjem, S.; Balali, V. Sustainable highway maintenance: Optimization of existing highway vertical alignment considering pavement condition. Sustainability 2019, 11, 1659. [Google Scholar] [CrossRef]
- Biancardo, S.A.; Abbondati, F.; Russo, F.; Veropalumbo, R.; Dell’Acqua, G. A broad-based decision-making procedure for runway friction decay analysis in maintenance operations. Sustainability 2020, 12, 3516. [Google Scholar] [CrossRef]
- Biancardo, S.A.; Viscione, N.; Oreto, C.; Russo, F. BIM Approach for Smart Infrastrcuture Design and Maintenance Operations. In Transportation Systems for Smart, Sustainable, Inclusive and Secure Cities; IntechOpen: London, UK, 2020; Available online: https://www.intechopen.com/online-first/bim-approach-for-smart-infrastructure-design-and-maintenance-operations (accessed on 19 February 2021). [CrossRef]
- Wu, P.; Xia, B.; Zhao, X. The importance of use and end-of-life phases to the life cycle greenhouse gas (GHG) emissions of concrete—A review. Renew. Sustain. Energy Rev. 2014, 37, 360–369. [Google Scholar] [CrossRef]
- Noland, R.B.; Hanson, C.S. Life-cycle greenhouse gas emissions associated with a highway reconstruction: A New Jersey case study. J. Clean. Prod. 2015, 107, 731–740. [Google Scholar] [CrossRef]
- Ma, F.; Dong, W.; Fu, Z.; Wang, R.; Huang, Y.; Liu, J. Life cycle assessment of greenhouse gas emissions from asphalt pavement maintenance: A case study in China. J. Clean. Prod. 2021, 288, 125595. [Google Scholar] [CrossRef]
- Yu, B.; Gu, X.; Ni, F.; Guo, R. Multi-objective optimization for asphalt pavement maintenance plans at project level: Integrating performance, cost and environment. Transp. Res. Part D Transp. Environ. 2015, 41, 64–74. [Google Scholar] [CrossRef]
- Veropalumbo, R.; Russo, F.; Viscione, N. LCA of recycled bituminous mixtures containing jet grouting waste. In Proceedings of the 17th SIIV Summer School 2019, Resilient Road Infrastructures, Climatic Changes and Prespective of Road Infrastructures, San Marino, Republic of San Marino, 16–20 September 2019; Santagata, F.A., Montepara, A., Grili, A., Eds.; Società Italiana Infrastrutture Viarie (SIIV); San Marino University Press, University of the Republic of San Marino Department of Economics, Science and Law Degree Course in Civil Engineering World Trade Center Via Consiglio dei Sessanta. Marche Polytechnic University: Ancona, Italy, 2019; pp. 41–44. Available online: http://creativecommons.org/licenses/by/4.0/ (accessed on 19 February 2021).
- Chu, J.C.; Huang, K.H. Mathematical programming framework for modeling and comparing network-level pavement maintenance strategies. Transp. Res. Part B Methodol. 2018, 109, 1–25. [Google Scholar] [CrossRef]
- Guo, F.; Gregory, J.; Kirchain, R. Incorporating cost uncertainty and path dependence into treatment selection for pavement networks. Transp. Res. Part C Emerg. Technol. 2020, 110, 40–55. [Google Scholar] [CrossRef]
- Mizutani, D.; Nakazato, Y.; Lee, J. Network-level synchronized pavement repair and work zone policies: Optimal solution and rule-based approximation. Transp. Res. Part C Emerg. Technol. 2020, 120, 102797. [Google Scholar] [CrossRef]
- Elhadidy, A.A.; Elbeltagi, E.E.; El-Badawy, S.M. Network-Based Optimization System for Pavement Maintenance Using a Probabilistic Simulation-Based Genetic Algorithm Approach. J. Transp. Eng. Part B Pavements 2020, 146, 04020069. [Google Scholar] [CrossRef]
- Chen, L.; Gendreau, M.; Hà, M.H.; Langevin, A. A robust optimization approach for the road network daily maintenance routing problem with uncertain service time. Transp. Res. Part E Logist. Transp. Rev. 2016, 85, 40–51. [Google Scholar] [CrossRef]
- Lee, H.Y. Optimizing schedule for improving the traffic impact of work zone on roads. Autom. Constr. 2009, 18, 1034–1044. [Google Scholar] [CrossRef]
- Aarabi, F.; Batta, R. Scheduling spatially distributed jobs with degradation: Application to pothole repair. Socioecon. Plann. Sci. 2020, 72, 100904. [Google Scholar] [CrossRef]
- Duque, P.M.; Sörensen, K. A GRASP metaheuristic to improve accessibility after a disaster. OR Spectr. 2011, 33, 525–542. [Google Scholar] [CrossRef]
- Duque, P.A.M.; Dolinskaya, I.S.; Sörensen, K. Network repair crew scheduling and routing for emergency relief distribution problem. Euro. J. Oper. Res. 2016, 248, 272–285. [Google Scholar] [CrossRef]
- Aksu, D.T.; Ozdamar, L. A mathematical model for post-disaster road restoration-Enabling accessibility evacuation. Transp. Res. Part E Logist. Transp. Rev. 2014, 61, 56–67. [Google Scholar] [CrossRef]
- Kim, S.; Shin, Y.; Lee, G.M.; Moon, I. Network repair crew scheduling for short-term disasters. Appl. Math. Model. 2018, 64, 510–523. [Google Scholar] [CrossRef]
- IBM ILOG CPLEX Optimization Studio. Available online: https://www.ibm.com/products/ilog-cplex-optimization-studio/details (accessed on 21 January 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).