Application of Game Theory against Nature in Supporting Bid Pricing in Construction
Abstract
1. Introduction
2. Materials and Methods
2.1. Game against Nature Theory as a Decision-Making Tool
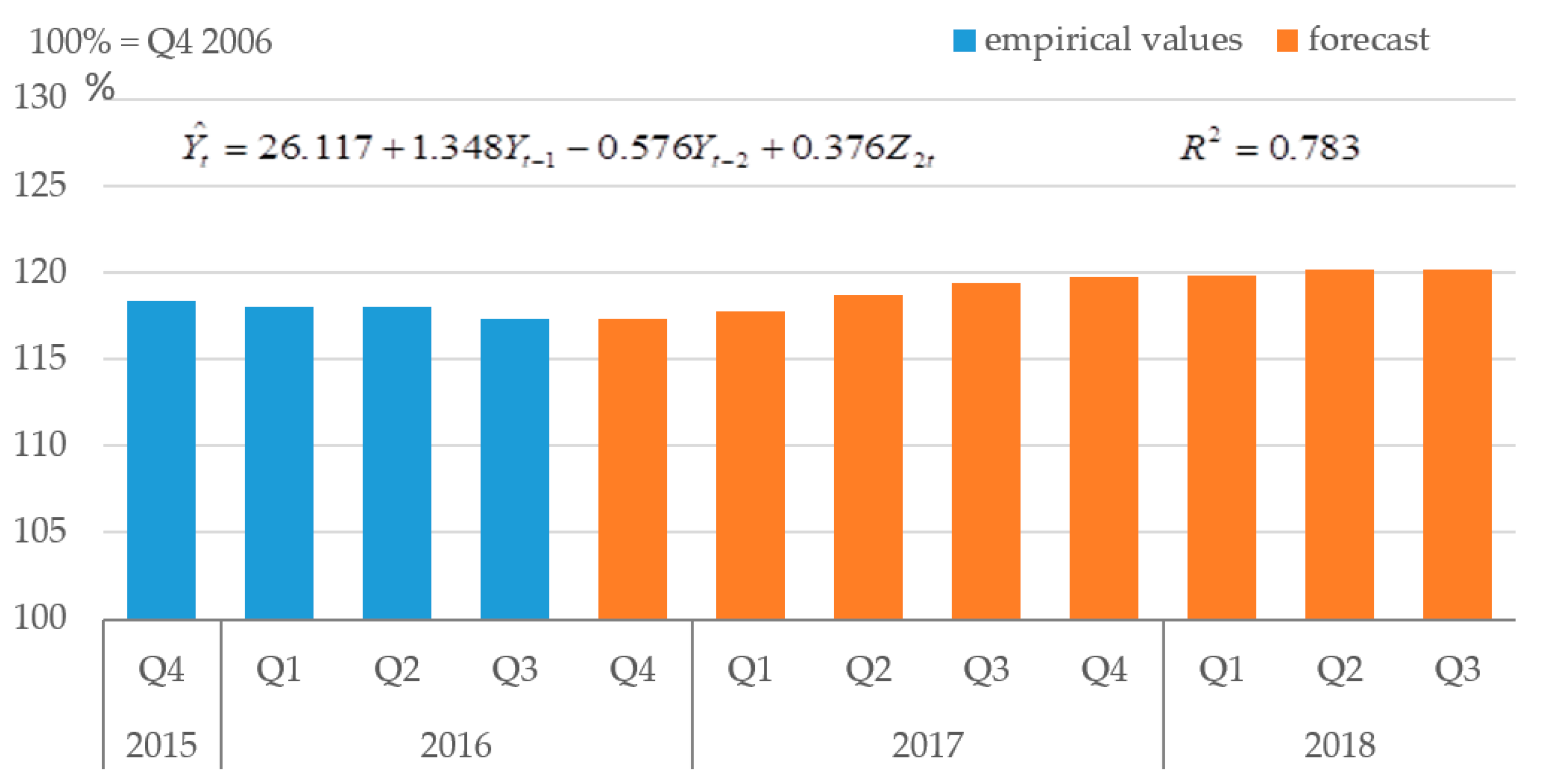
2.2. Forecasting Economic Phenomena
3. Results
- for the value range —the optimal strategy is the strategy a7;
- for the value range —the optimal strategy is the strategy a8.
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Magnussen, O.M.; Olsson, N.O.E. Comparative Analysis of Cost Estimates of Major Public Investment Projects. Int. J. Proj. Manag. 2006, 24, 281–288. [Google Scholar]
- Chou, J.-S. Generalized Linear Model-Based Expert System for Estimating the Cost of Transportation Projects. Expert Syst. Appl. 2009, 36 Pt 1, 4253–4267. [Google Scholar]
- Haile, P.; Hendricks, K.; Porter, R. Recent US offshore oil and gas lease bidding: A progress report. Int. J. Ind. Organ. 2010, 28, 390–396. [Google Scholar]
- Mochtar, K.; Arditi, D. Alternate pricing strategies in construction. Civ. Eng. Dimen. 2000, 2, 56–64. [Google Scholar]
- Simon, H. Theories of Decision-Making in Economics and Behavioral Science. Am. Econ. Rev. 1959, 49, 253–283. [Google Scholar]
- Kapliński, O.; Tamošaitienė, J. Game Theory Applications in Construction Engineering and Management. Technol. Econ. Dev. Econ. 2010, 16, 348–363. [Google Scholar]
- Tomczak, M.; Jaśkowski, P. New Approach to Improve General Contractor Crew’s Work Continuity in Repetitive Construction Projects. J. Constr. Eng. Manag. 2020, 146, 04020043. [Google Scholar]
- Zavadskas, E.K.; Turskis, Z.; Tamošaitienė, J. Contractor Selection of Construction in a Competitive Environment. J. Bus. Econ. Manag. 2008, 9, 181–187. [Google Scholar]
- Tomczak, M.; Jaśkowski, P. Application of Type-2 Interval Fuzzy Sets to Contractor Qualification Process. KSCE J. Civ. Eng. 2018, 22, 2702–2713. [Google Scholar]
- Radziszewska-Zielina, E. The application of multi-criteria analysis in the evaluation of partering relations and the selection of a construction company for the purposes of cooperation. Arch. Civ. Mech. Eng. 2016, 62, 167–182. [Google Scholar]
- Peldschus, F.; Zavadskas, E.K.; Turskis, Z.; Tamosaitiene, J. Sustainable Assessment of Construction Site by Applying Game Theory. Eng. Econ. 2010, 21, 223–237. [Google Scholar]
- Yang, Y.-P.; Wang, M.-J. Analysis on the Interests of Construction Parties in Project Management Model Based on the Game Theory. In Proceedings of the 2009 Chinese Control and Decision Conference, Guilin, China, 17–19 June 2009. [Google Scholar]
- Szafranko, E.; Srokosz, P. Applicability of the theory of similarity in an evaluation of building development variants. Autom. Constr. 2019, 104, 322–330. [Google Scholar] [CrossRef]
- Biruk, S.; Rzepecki, Ł. Simulation Model for Resource-Constrained Construction Project. Open Eng. 2019, 9, 37. [Google Scholar] [CrossRef]
- Tomczak, M.; Rzepecki, L. Evaluation of Supply Chain Management Systems Used in Civil Engineering. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 072005. [Google Scholar] [CrossRef]
- Tomczak, M. Modeling of the Harmonization Method for Executing a Multi-Unit Construction Project. Open Eng. 2019, 9, 282–291. [Google Scholar] [CrossRef]
- Anysz, H.; Buczkowski, B. The association analysis for risk evaluation of significant delay occurrence in the completion date of construction project. Int. J. Environ. Sci. Technol. 2019, 16, 5369–5374. [Google Scholar] [CrossRef]
- Plebankiewicz, E.; Wieczorek, D. Adaptation of a Cost Overrun Risk Prediction Model to the Type of Construction Facility. Symmetry 2020, 12, 1739. [Google Scholar] [CrossRef]
- Kim, D.Y.; Han, S.H.; Kim, H.; Park, H. Structuring the prediction model of project performance for international construction projects: A comparative analysis. Expert Syst. Appl. 2009, 36, 1961–1971. [Google Scholar] [CrossRef]
- Grzyl, B.; Apollo, M.; Kristowski, A. Application of Game Theory to Conflict Management in a Construction Contract. Sustainability 2019, 11, 1983. [Google Scholar] [CrossRef]
- San Cristóbal, J.R. The Use of Game Theory to Solve Conflicts in the Project Management and Construction Industry. Int. J. Inf. Syst. Proj. Manag. 2015, 3, 43–58. [Google Scholar]
- Papadimitriou, C.H. Games against Nature. J. Comput. Syst. Sci. 1985, 31, 288–301. [Google Scholar] [CrossRef]
- Jaworski, K.M. Metodologia Projektowania Realizacji Budowy, 2nd ed.; PWN: Warsaw, Poland, 2009. (In Polish) [Google Scholar]
- Wald, A. Statistical Decision Functions; Wiley: Oxford, UK, 1950; p. 179. [Google Scholar]
- Hurwicz, L. Optimality Criteria for Decision Making Under Ignorance. Statistics 1951, 370. Available online: https://cowles.yale.edu/sites/default/files/files/pub/cdp/s-0370.pdf (accessed on 14 January 2021).
- Savage, L.J. The Theory of Statistical Decision. J. Am. Stat. Assoc. 1951, 46, 55–67. [Google Scholar] [CrossRef]
- Peldschus, F. Experience of the Game Theory Application in Construction Management. Technol. Econ. Dev. Econ. 2008, 14, 531–545. [Google Scholar] [CrossRef]
- Barough, A.S.; Shoubi, M.V.; Skardi, M.J.E. Application of Game Theory Approach in Solving the Construction Project Conflicts. Procedia-Soc. Behav. Sci. 2012, 58, 1586–1593. [Google Scholar] [CrossRef]
- Dong-hong, C.; Xi-yan, Z. Application of Game Theory on Bidding Price Decision. In Proceedings of the 2009 16th International Conference on Industrial Engineering and Engineering Management, Beijing, China, 21–23 October 2009; pp. 58–61. [Google Scholar]
- Ntakaris, A.; Mirone, G.; Kanniainen, J.; Gabbouj, M.; Iosifidis, A. Feature Engineering for Mid-Price Prediction With Deep Learning. IEEE Access 2019, 7, 82390–82412. [Google Scholar] [CrossRef]
- Jaśkowski, P.; Sobotka, A.; Czarnigowska, A. Decision Model for Planning Material Supply Channels in Construction. Autom. Constr. 2018, 90, 235–242. [Google Scholar] [CrossRef]
- Czarnigowska, A.; Sobotka, A. Time–Cost Relationship for Predicting Construction Duration. Arch. Civ. Mech. Eng. 2013, 13, 518–526. [Google Scholar] [CrossRef]
- Leśniak, A.; Juszczyk, M. Prediction of Site Overhead Costs with the Use of Artificial Neural Network Based Model. Arch. Civ. Mech. Eng. 2018, 18, 973–982. [Google Scholar] [CrossRef]
- Tatiya, A.; Zhao, D.; Syal, M.; Berghorn, G.H.; LaMore, R. Cost Prediction Model for Building Deconstruction in Urban Areas. J. Clean. Prod. 2018, 195, 1572–1580. [Google Scholar] [CrossRef]
- Shoar, S.; Banaitis, A. Application of Fuzzy Fault Tree Analysis to identify factors influencing construction labor productivity: A high-rise building cas study. J. Civ. Eng. Manag. 2019, 25, 41–52. [Google Scholar] [CrossRef]
- Gutiérrez-Ruiz, A.M.; Valcarce-Ruiz, L.; Becerra-Vicario, R.; Ruiz-Palomo, D. Identifying Industrial Productivity Factors with Artificial Neural Networks. J. Sci. Ind. Res. 2020, 79, 534–536. [Google Scholar]
- Durdyev, S.; Ismail, S.; Kandymov, N. Structural equation model of the factors affecting construction labor productivity. J. Constr. Eng. M 2018, 144, 1–11. [Google Scholar] [CrossRef]
- Fayek, A. Competitive bidding strategy model and software system for bid preparation. J. Constr. Eng. Manag. 1998, 124, 1–10. [Google Scholar] [CrossRef]
- Ioannou, P.G.; Leu, S.S. Average-bid method—competitive bidding strategy. J. Constr. Eng. Manag. 1993, 119, 131–147. [Google Scholar] [CrossRef]
- Moselhi, O.; Hegazy, T.; Fazio, P. DBID: Analogy-based DSS for bidding in construction. J. Constr. Eng. Manag. 1993, 119, 466–479. [Google Scholar] [CrossRef]
- Friedman, L.A. Competitive-Bidding Strategy. Oper. Res. 1956, 4, 104–112. [Google Scholar] [CrossRef]
- Jaśkowski, P.; Czarnigowska, A. Contractor’s Bid Pricing Strategy: A Model with Correlation among Competitors’ Prices. Open Eng. 2019, 9, 159–166. [Google Scholar] [CrossRef]
- Jaśkowski, P.; Biruk, S.; Czarnigowska, A. Strategy for Mark-up Definition in Competitive Tenders for Construction Work. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471, 112060. [Google Scholar] [CrossRef]

| Forecast (%) | Ex-Post Error (%) | |
|---|---|---|
| Construction materials | 1.7 | 0.834 |
| Plumbing materials | 2.2 | 0.414 |
| Electrical materials | 8.1 | 4.742 |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | |
| s1 | 44,870.77 | 52,044.49 | 59,184.66 | 66,181.30 | 72,668.80 | 77,675.29 | 79,194.56 | 74,241.11 | 60,476.15 | 39,687.65 | 19,247.98 | 6347.56 | 1327.28 |
| s2 | 28,357.40 | 35,533.52 | 42,684.87 | 49,725.96 | 56,363.48 | 61,796.07 | 64,326.55 | 61,355.14 | 50,716.05 | 33,702.61 | 16,523.96 | 5501.32 | 1160.03 |
| s3 | 11,844.02 | 19,022.56 | 26,185.09 | 33,270.62 | 40,058.15 | 45,916.85 | 49,458.55 | 48,469.16 | 40,955.96 | 27,717.58 | 13,799.94 | 4655.08 | 992.78 |
| s4 | 43,664.63 | 50,838.52 | 57,979.52 | 64,979.40 | 71,477.86 | 76,515.47 | 78,108.59 | 73,299.92 | 59,763.27 | 39,250.50 | 19,049.01 | 6285.75 | 1315.07 |
| s5 | 27,151.26 | 34,327.56 | 41,479.73 | 48,524.06 | 55,172.53 | 60,636.25 | 63,240.59 | 60,413.94 | 50,003.17 | 33,265.46 | 16,325.00 | 5439.51 | 1147.81 |
| s6 | 10,637.88 | 17,816.59 | 24,979.94 | 32,068.72 | 38,867.21 | 44,757.02 | 48,372.59 | 47,527.97 | 40,243.08 | 27,280.43 | 13,600.98 | 4593.27 | 980.56 |
| s7 | 42,458.49 | 49,632.56 | 56,774.37 | 63,777.50 | 70,286.92 | 75,355.65 | 77,022.63 | 72,358.73 | 59,050.39 | 38,813.35 | 18,850.05 | 6223.94 | 1302.85 |
| s8 | 25,945.12 | 33,121.59 | 40,274.58 | 47,322.16 | 53,981.59 | 59,476.42 | 62,154.63 | 59,472.75 | 49,290.30 | 32,828.32 | 16,126.03 | 5377.70 | 1135.60 |
| s9 | 9431.74 | 16,610.63 | 23,774.79 | 30,866.82 | 37,676.26 | 43,597.20 | 47,286.63 | 46,586.77 | 39,530.20 | 26,843.28 | 13,402.01 | 4531.46 | 968.34 |
| s10 | 35,196.69 | 42,371.82 | 49,518.55 | 56,541.22 | 63,116.61 | 68,372.72 | 70,484.39 | 66,692.09 | 54,758.37 | 36,181.42 | 17,652.16 | 5851.80 | 1229.30 |
| s11 | 18,683.32 | 25,860.86 | 33,018.76 | 40,085.88 | 46,811.28 | 52,493.50 | 55,616.39 | 53,806.11 | 44,998.27 | 30,196.38 | 14,928.14 | 5005.56 | 1062.05 |
| s12 | 2169.95 | 9349.90 | 16,518.97 | 23,630.54 | 30,505.96 | 36,614.28 | 40,748.39 | 40,920.13 | 35,238.18 | 24,211.34 | 12,204.12 | 4159.32 | 894.79 |
| s13 | 33,990.55 | 41,165.86 | 48,313.40 | 55,339.32 | 61,925.67 | 67,212.90 | 69,398.43 | 65,750.89 | 54,045.49 | 35,744.27 | 17,453.19 | 5789.99 | 1217.08 |
| s14 | 17,477.18 | 24,654.90 | 31,813.61 | 38,883.98 | 45,620.34 | 51,333.68 | 54,530.43 | 52,864.92 | 44,285.39 | 29,759.23 | 14,729.18 | 4943.75 | 1049.83 |
| s15 | 963.81 | 8143.93 | 15,313.82 | 22,428.64 | 29,315.01 | 35,454.46 | 39,662.43 | 39,978.94 | 34,525.30 | 23,774.20 | 12,005.16 | 4097.51 | 882.58 |
| s16 | 32,784.41 | 39,959.90 | 47,108.25 | 54,137.42 | 60,734.72 | 66,053.08 | 68,312.47 | 64,809.70 | 53,332.61 | 35,307.12 | 17,254.23 | 5728.18 | 1204.87 |
| s17 | 16,271.04 | 23,448.93 | 30,608.46 | 37,682.08 | 44,429.40 | 50,173.86 | 53,444.47 | 51,923.72 | 43,572.51 | 29,322.09 | 14,530.21 | 4881.94 | 1037.61 |
| s18 | −242.33 | 6937.97 | 14,108.68 | 21,226.74 | 28,124.07 | 34,294.64 | 38,576.46 | 39,037.74 | 33,812.42 | 23,337.05 | 11,806.20 | 4035.70 | 870.36 |
| s19 | 25,522.62 | 32,699.16 | 39,852.43 | 46,901.15 | 53,564.42 | 59,070.15 | 61,774.23 | 59,143.06 | 49,040.58 | 32,675.19 | 16,056.34 | 5356.05 | 1131.32 |
| s20 | 9009.25 | 16,188.20 | 23,352.64 | 30,445.81 | 37,259.09 | 43,190.93 | 46,906.23 | 46,257.08 | 39,280.49 | 26,690.15 | 13,332.32 | 4509.81 | 964.07 |
| s21 | −7504.13 | −322.77 | 6852.85 | 13,990.47 | 20,953.76 | 27,311.71 | 32,038.22 | 33,371.10 | 29,520.39 | 20,705.11 | 10,608.30 | 3663.57 | 796.81 |
| s22 | 24,316.48 | 31,493.20 | 38,647.28 | 45,699.25 | 52,373.47 | 57,910.33 | 60,688.27 | 58,201.87 | 48,327.70 | 32,238.04 | 15,857.38 | 5294.24 | 1119.10 |
| s23 | 7803.11 | 14,982.23 | 22,147.49 | 29,243.91 | 36,068.14 | 42,031.11 | 45,820.27 | 45,315.89 | 38,567.61 | 26,253.00 | 13,133.36 | 4448.00 | 951.85 |
| s24 | −8710.27 | −1528.73 | 5647.71 | 12,788.57 | 19,762.82 | 26,151.89 | 30,952.26 | 32,429.91 | 28,807.51 | 20,267.97 | 10,409.34 | 3601.76 | 784.60 |
| s25 | 23,110.34 | 30,287.23 | 37,442.14 | 44,497.35 | 51,182.53 | 56,750.51 | 59,602.31 | 57,260.67 | 47,614.82 | 31,800.89 | 15,658.41 | 5232.43 | 1106.89 |
| s26 | 6596.97 | 13,776.27 | 20,942.35 | 28,042.01 | 34,877.20 | 40,871.29 | 44,734.30 | 44,374.69 | 37,854.73 | 25,815.85 | 12,934.39 | 4386.19 | 939.63 |
| s27 | −9916.40 | −2734.69 | 4442.56 | 11,586.67 | 18,571.87 | 24,992.07 | 29,866.30 | 31,488.72 | 28,094.63 | 19,830.82 | 10,210.38 | 3539.95 | 772.38 |
| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | |
| s1 | 34,323.79 | 27,150.07 | 20,009.89 | 13,013.25 | 6525.75 | 1519.27 | 0.00 | 4953.44 | 18,718.41 | 39,506.91 | 59,946.58 | 72,847.00 | 77,867.27 |
| s2 | 35,969.16 | 28,793.03 | 21,641.68 | 14,600.59 | 7963.08 | 2530.49 | 0.00 | 2971.42 | 13,610.50 | 30,623.94 | 47,802.59 | 58,825.24 | 63,166.52 |
| s3 | 37,614.53 | 30,435.99 | 23,273.46 | 16,187.93 | 9400.40 | 3541.70 | 0.00 | 989.39 | 8502.59 | 21,740.98 | 35,658.61 | 44,803.47 | 48,465.77 |
| s4 | 34,443.97 | 27,270.07 | 20,129.08 | 13,129.19 | 6630.73 | 1593.13 | 0.00 | 4808.67 | 18,345.32 | 38,858.09 | 59,059.58 | 71,822.85 | 76,793.53 |
| s5 | 36,089.34 | 28,913.03 | 21,760.86 | 14,716.53 | 8068.06 | 2604.35 | 0.00 | 2826.65 | 13,237.42 | 29,975.13 | 46,915.60 | 57,801.08 | 62,092.78 |
| s6 | 37,734.71 | 30,555.99 | 23,392.65 | 16,303.87 | 9505.38 | 3615.56 | 0.00 | 844.62 | 8129.51 | 21,092.16 | 34,771.61 | 43,779.32 | 47,392.03 |
| s7 | 34,564.14 | 27,390.08 | 20,248.27 | 13,245.13 | 6735.72 | 1666.99 | 0.00 | 4663.91 | 17,972.24 | 38,209.28 | 58,172.58 | 70,798.70 | 75,719.78 |
| s8 | 36,209.51 | 29,033.04 | 21,880.05 | 14,832.47 | 8173.04 | 2678.21 | 0.00 | 2681.88 | 12,864.33 | 29,326.31 | 46,028.60 | 56,776.93 | 61,019.03 |
| s9 | 37,854.88 | 30,676.00 | 23,511.84 | 16,419.81 | 9610.36 | 3689.42 | 0.00 | 699.86 | 7756.43 | 20,443.35 | 33,884.61 | 42,755.17 | 46,318.28 |
| s10 | 35,287.70 | 28,112.57 | 20,965.85 | 13,943.17 | 7367.78 | 2111.67 | 0.00 | 3792.31 | 15,726.03 | 34,302.97 | 52,832.24 | 64,632.59 | 69,255.09 |
| s11 | 36,933.07 | 29,755.53 | 22,597.63 | 15,530.51 | 8805.11 | 3122.89 | 0.00 | 1810.28 | 10,618.12 | 25,420.01 | 40,688.25 | 50,610.83 | 54,554.34 |
| s12 | 38,750.18 | 31,570.24 | 24,401.16 | 17,289.59 | 10,414.18 | 4305.85 | 171.74 | 0.00 | 5681.96 | 16,708.79 | 28,716.01 | 36,760.81 | 40,025.34 |
| s13 | 35,407.88 | 28,232.57 | 21,085.03 | 14,059.11 | 7472.77 | 2185.53 | 0.00 | 3647.54 | 15,352.95 | 33,654.16 | 51,945.24 | 63,608.44 | 68,181.35 |
| s14 | 37,053.25 | 29,875.53 | 22,716.82 | 15,646.45 | 8910.09 | 3196.75 | 0.00 | 1665.51 | 10,245.04 | 24,771.20 | 39,801.25 | 49,586.68 | 53,480.60 |
| s15 | 39,015.13 | 31,835.01 | 24,665.12 | 17,550.29 | 10,663.93 | 4524.48 | 316.51 | 0.00 | 5453.64 | 16,204.74 | 27,973.78 | 35,881.42 | 39,096.36 |
| s16 | 35,528.06 | 28,352.58 | 21,204.22 | 14,175.05 | 7577.75 | 2259.39 | 0.00 | 3502.77 | 14,979.86 | 33,005.35 | 51,058.24 | 62,584.29 | 67,107.60 |
| s17 | 37,173.43 | 29,995.54 | 22,836.00 | 15,762.38 | 9015.07 | 3270.61 | 0.00 | 1520.75 | 9871.95 | 24,122.38 | 38,914.25 | 48,562.52 | 52,406.85 |
| s18 | 39,280.07 | 32,099.78 | 24,929.07 | 17,811.00 | 10,913.68 | 4743.11 | 461.28 | 0.00 | 5225.33 | 15,700.70 | 27,231.55 | 35,002.04 | 38,167.38 |
| s19 | 36,251.61 | 29,075.07 | 21,921.80 | 14,873.08 | 8209.81 | 2704.08 | 0.00 | 2631.17 | 12,733.65 | 29,099.04 | 45,717.89 | 56,418.18 | 60,642.91 |
| s20 | 37,896.98 | 30,718.03 | 23,553.59 | 16,460.42 | 9647.14 | 3715.30 | 0.00 | 649.15 | 7625.74 | 20,216.08 | 33,573.91 | 42,396.42 | 45,942.16 |
| s21 | 40,875.23 | 33,693.87 | 26,518.25 | 19,380.64 | 12,417.34 | 6059.39 | 1332.88 | 0.00 | 3850.71 | 12,665.99 | 22,762.80 | 29,707.54 | 32,574.29 |
| s22 | 36,371.79 | 29,195.07 | 22,040.99 | 14,989.02 | 8314.80 | 2777.94 | 0.00 | 2486.40 | 12,360.57 | 28,450.23 | 44,830.89 | 55,394.03 | 59,569.17 |
| s23 | 38,017.16 | 30,838.03 | 23,672.77 | 16,576.36 | 9752.12 | 3789.16 | 0.00 | 504.38 | 7252.66 | 19,567.26 | 32,686.91 | 41,372.27 | 44,868.42 |
| s24 | 41,140.18 | 33,958.64 | 26,782.20 | 19,641.34 | 12,667.09 | 6278.02 | 1477.65 | 0.00 | 3622.40 | 12,161.95 | 22,020.57 | 28,828.15 | 31,645.31 |
| s25 | 36,491.97 | 29,315.08 | 22,160.17 | 15,104.96 | 8419.78 | 2851.80 | 0.00 | 2341.64 | 11,987.48 | 27,801.42 | 43,943.89 | 54,369.88 | 58,495.42 |
| s26 | 38,137.34 | 30,958.04 | 23,791.96 | 16,692.30 | 9857.10 | 3863.02 | 0.00 | 359.61 | 6879.58 | 18,918.45 | 31,799.91 | 40,348.12 | 43,794.67 |
| s27 | 41,405.12 | 34,223.41 | 27,046.16 | 19,902.05 | 12,916.84 | 6496.65 | 1622.41 | 0.00 | 3394.08 | 11,657.90 | 21,278.34 | 27,948.77 | 30,716.34 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzepecki, Ł.; Jaśkowski, P. Application of Game Theory against Nature in Supporting Bid Pricing in Construction. Symmetry 2021, 13, 132. https://doi.org/10.3390/sym13010132
Rzepecki Ł, Jaśkowski P. Application of Game Theory against Nature in Supporting Bid Pricing in Construction. Symmetry. 2021; 13(1):132. https://doi.org/10.3390/sym13010132
Chicago/Turabian StyleRzepecki, Łukasz, and Piotr Jaśkowski. 2021. "Application of Game Theory against Nature in Supporting Bid Pricing in Construction" Symmetry 13, no. 1: 132. https://doi.org/10.3390/sym13010132
APA StyleRzepecki, Ł., & Jaśkowski, P. (2021). Application of Game Theory against Nature in Supporting Bid Pricing in Construction. Symmetry, 13(1), 132. https://doi.org/10.3390/sym13010132





