1. Introduction
Due to constant technological growth, it is now possible to integrate electronic circuits and computer systems to develop, manage, and monitor a wide variety of devices in many of the structures that surround us [
1,
2,
3]. One of the main advantages of including computational techniques in regular devices is the efficient administration of electrical energy. Researchers have focused their efforts on optimizing these regular devices as well as new research focused on the use of artificial intelligence, neural networks, and fuzzy logic and a study on a new class of optimization problems of constrained interval values [
4,
5]. This paper implements two evolutionary algorithms, a genetic algorithm (GA) and a non-dominated sorting genetic algorithm (NSGA II), to optimize an air conditioning system’s energy consumption. We chose to research air conditioning systems because they consume a large amount of energy regardless of the purpose.
In the literature, it is possible to find some papers focused on ensuring an adequate administration of electrical energy through the so-called home energy management systems which seek to promote renewable energy, lengthen device life, and avoid accidents. In [
1], Collota et al. present an example of this system, where a fuzzy controller is used to improve the home energy management scheme; the results showed the system’s capability to reduce the maximum load demand for electrical energy. Similarly, Attoue et al. [
2] used machine learning techniques, optimization, and data structures to create an energy management system to satisfy the needs of an intelligent building; the results obtained show the proposed mechanisms’ effectiveness to improve the performance.
Even though there is a wide variety of papers aiming to save electricity, air conditioners still consume a significant amount of energy. In [
6], the authors present a fuzzy controller made in Simulink to lower air conditioning energy while dealing with thermal disturbances. The results demonstrate that the fuzzy controller with triangular membership functions gives the desired performance with an error lower than 1% and saving 25% of energy consumption. Chen, Fu, and Liu [
3] proposed a hybrid meta ensemble learning and stacked auto-encoder (SAE), tested with data from the air-conditioning system from a commercial building in Singapore. The proposed meta ensemble learning method showed efficient energy management of the air-conditioning system.
Additionally, Arikiez et al. [
7] proposed a heuristic algorithm based on mixed integer linear programming (MILP) to minimize the cost of electrical energy caused by a set of air conditioners. The result reveals that their algorithm can solve a massive problem in a few seconds and gives reasonable suboptimal solutions. Moreover, Ullah and Kim [
8] proposed two improved optimization algorithms, a particle swarm optimization and a genetic algorithm, to achieve maximum user comfort in the building environment with minimum energy consumption. Results showed that the proposed optimization algorithms produce better results than the baseline scheme in user comfort and consumed energy.
This paper proposes two metaheuristic algorithms to optimize an air conditioning system while considering the users’ preferences, a genetic algorithm (GA) and a non-dominated sorting genetic algorithm (NSGA II). The former intends to replicate the algorithm from [
8], and the latter was selected to analyze the performance of a multi-objective optimization algorithm.
The remainder of the paper is as follows:
Section 2 addresses the design of the optimization algorithms;
Section 3 shows our simulator design;
Section 4 and
Section 5 describe the experimental results and the discussion, respectively. Finally,
Section 6 contains the conclusions and future work.
2. Algorithm Design
2.1. Problem Definition
The proposed algorithms aim to tackle two objectives: energy-saving and user satisfaction. These objectives are directly in conflict because the air conditioner system must be turned on for extended periods of time to increase user satisfaction while increasing energy consumption, which conflicts with energy-saving. Such a task seems relatively simple for NSGA II due to its multi-objective nature. Additionally, the genetic algorithm used a weighted objective function to optimize both objectives simultaneously. In this paper, we use the formulation presented in [
8] by Ullah and Kim. However, we modify Equations (2)–(4) in two different ways. The first modification adds a cost to maintain the current temperature. The second modification nullifies any energy cost when the laboratory’s temperature is lower than the desired temperature. It is important to explain that our climate is warm; therefore, we consider a cooling scheme and turn on the air conditioner system to cool down the room, trying to reach the optimal desired temperature of 22 °C. However, we considered a temperature of 27 °C and below as acceptable yet not no ideal. Furthermore, temperatures below 22 °C are also not desired and would trigger a shutdown of the air conditioner system, nullifying the energy cost and raising the temperature.
For this formulation, expression (1) shows the user-accepted temperature range.
where
and
represent the minimum and maximum temperatures accepted by the user. It is worth noting that for our case,
is the ideal temperature because we are in a tropical environment and a colder climate is desired. Additionally, the current room temperature is
, and the temperature recommended by the optimization algorithms is named
.
With
, it is possible to calculate the optimal energy (
) needed to change or maintain
if it were the same as
; see Equation (2). Additionally, if the current temperature is lower than the optimized temperature (
), the air conditioner system should be turned off; hence the zero in that case. To calculate this parameter, we need to know the power required per unit change in temperature (
).
Similarly, it is possible to calculate the minimum and maximum hypothetical energy consumptions (
) and (
), as shown in expressions (3) and (4), which are used later to calculate the energy-saving gain
. For these equations, there is a similar condition as Equation (2); where if
or
, it would mean that the current temperature is lower than the maximum or minimum temperature and the air conditioner system will not need to be turned on to reach those temperatures, hence requiring 0 energy.
Equations (5) and (6) show the user satisfaction gain (
) and the energy-saving gain (
) where both gains range from 0 to 1, with 0 representing no gain and 1 represents the most gain. Furthermore, both objectives are in direct conflict because increasing user satisfaction entails an increased use of the air conditioner resulting in higher energy cost.
Additionally, the user relevance factor for each objective is determined by
for user satisfaction and
for energy-saving where
. Therefore, the NSGA II would maximize both objectives considering their relevance factor; see Equations (7) and (8).
On the other hand, GA uses the weighted function in Equation (9).
Figure 1 shows an example of the calculation of user satisfaction gain (
) and the energy-saving gain (
) for a given
and
.
2.2. GA and NSGA II
As we said before, we modify the formal definition of [
8], trying to make it more robust by considering new elements; however, we will not be able to compare directly to their results because of the modifications in the definition. Thus, in this paper, we implement their genetic algorithm as explained in [
8], and a multi-objective NSGA II as our proposal (both algorithms are available at
https://github.com/ahgarciar/Air-Conditioner-System-Controllers (accessed on 19 February 2021)).
We use the same population, selection, crossover, and mutation operators for both algorithms with little modifications for the NSGA II, as explained below.
Population. We use a vector of one hundred solutions for both algorithms, where each solution is a possible temperature between 22 and 27 °C.
Selection. The algorithms use a binary tournament between random individuals of the population to select the parents for the crossover operator. The GA uses a binary tournament, comparing the solutions’ objective values, and the winners are selected for crossover. On the other hand, the NSGA II algorithm uses the rank of the Pareto front of each solution to identify the winner, which will be the solution with the lowest level on the Pareto front, meaning that it is less dominated than the other solution. However, suppose both solutions are in the same level of the Pareto front. In that case, we use the crowded comparison operator (), which identifies the solution with the largest crowding distance, which will be explained further in this section.
Crossover. As stated before, our GA and NSGA II have a static population of one hundred solutions; then, another one hundred solutions are produced as offspring, using the Simulated Binary Crossover operator [
9]. This operator requires two parents (
and
) to obtain two new individuals (
and
).
Here, we explain the crossover operator for our specific problem. Thus, we will change some of the original notation of this crossover to match our variables.
First, we identify the two parents’ maximum and minimum temperature values; see Equations (10) and (11).
Then, we calculate Equations (12) and (13) to produce
and
, which also use a random real number (
) and a constant
in Equation (14) to produce
. Finally, we produce
as shown in Equation (15).
Then, we carry out a similar process to produce
. However, the difference is that
is calculated using
instead of
as
, see Equations (16)–(19).
Figure 2 shows an example of the crossover operator.
Mutation. As a mutation operator, we used the polynomial mutation operator [
10], which is applied to fifty percent of the solutions generated in the crossover operator.
Here, we modify the temperature produced by the crossover operation depending on the
value, which ranges from −1 to 1, and also uses a random real number (
) and a constant
; see Equations (20)–(23).
Figure 3 shows an example of the mutation operator.
For this experimentation, we tested several values for constant , resulting in a value of twenty.
The NSGA II requires two additional procedures:
Fast Non-Dominated Sort. This procedure allocates the solutions of the pool of solutions () into Pareto fronts of non-dominated individuals; this allows elitism in selecting the parents for the offspring of NSGA II.
Crowding Distance. A particular solution’s crowding distance value is the average distance of its two neighboring solutions [
11].
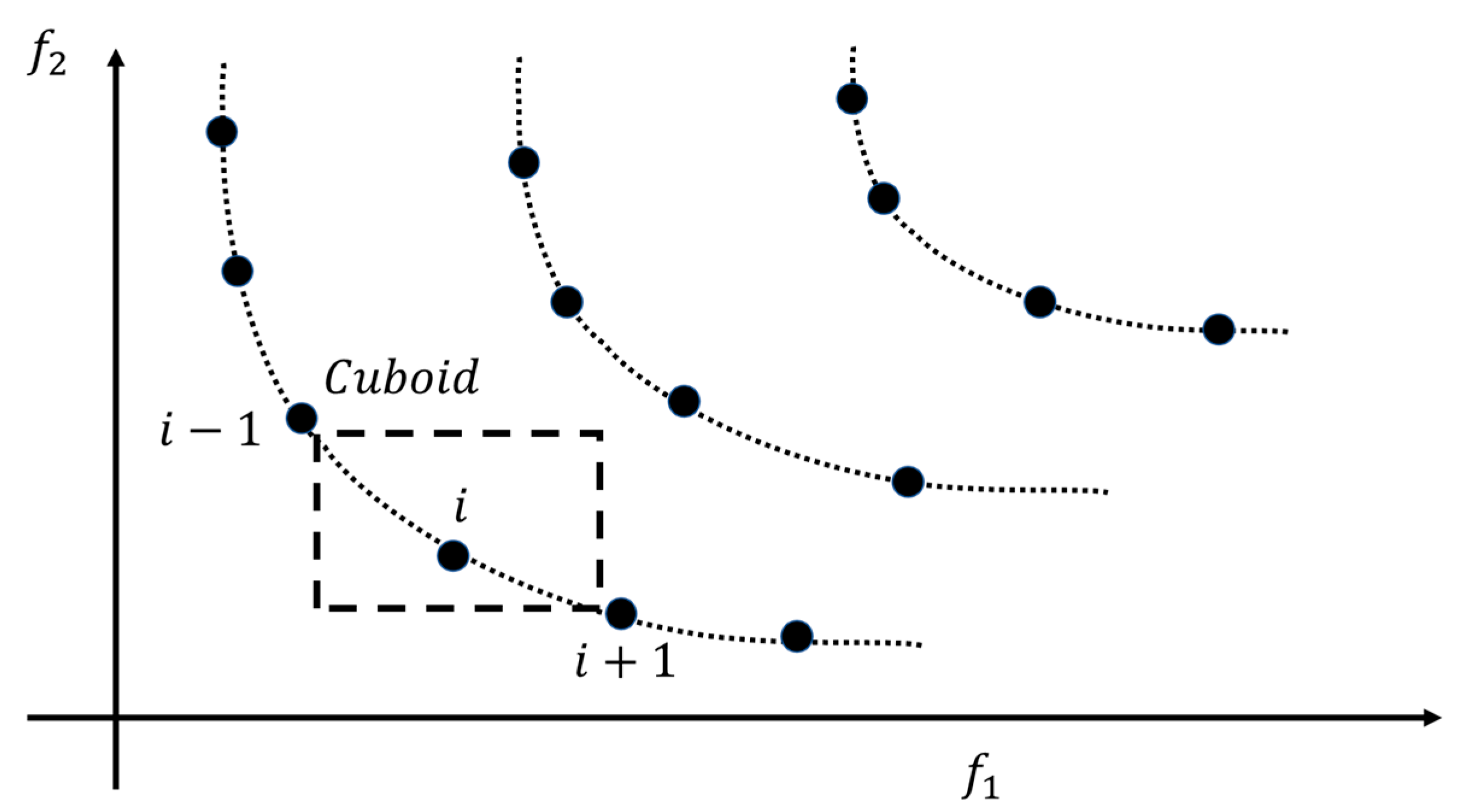
Figure 4 shows the calculation of the crowding distance of the solution
i, which is an estimate of the size of the largest cuboid enclosing
i without including any other solution. The algorithm used in this implementation is a normalized version of the original algorithm with the minimum (
) and maximum (
) values per objective (
) [
12]; this algorithm is calculated for each generation for the current population. The algorithm requires a set of non-dominated individuals (
) to calculate their distance.
4. Experimental Results
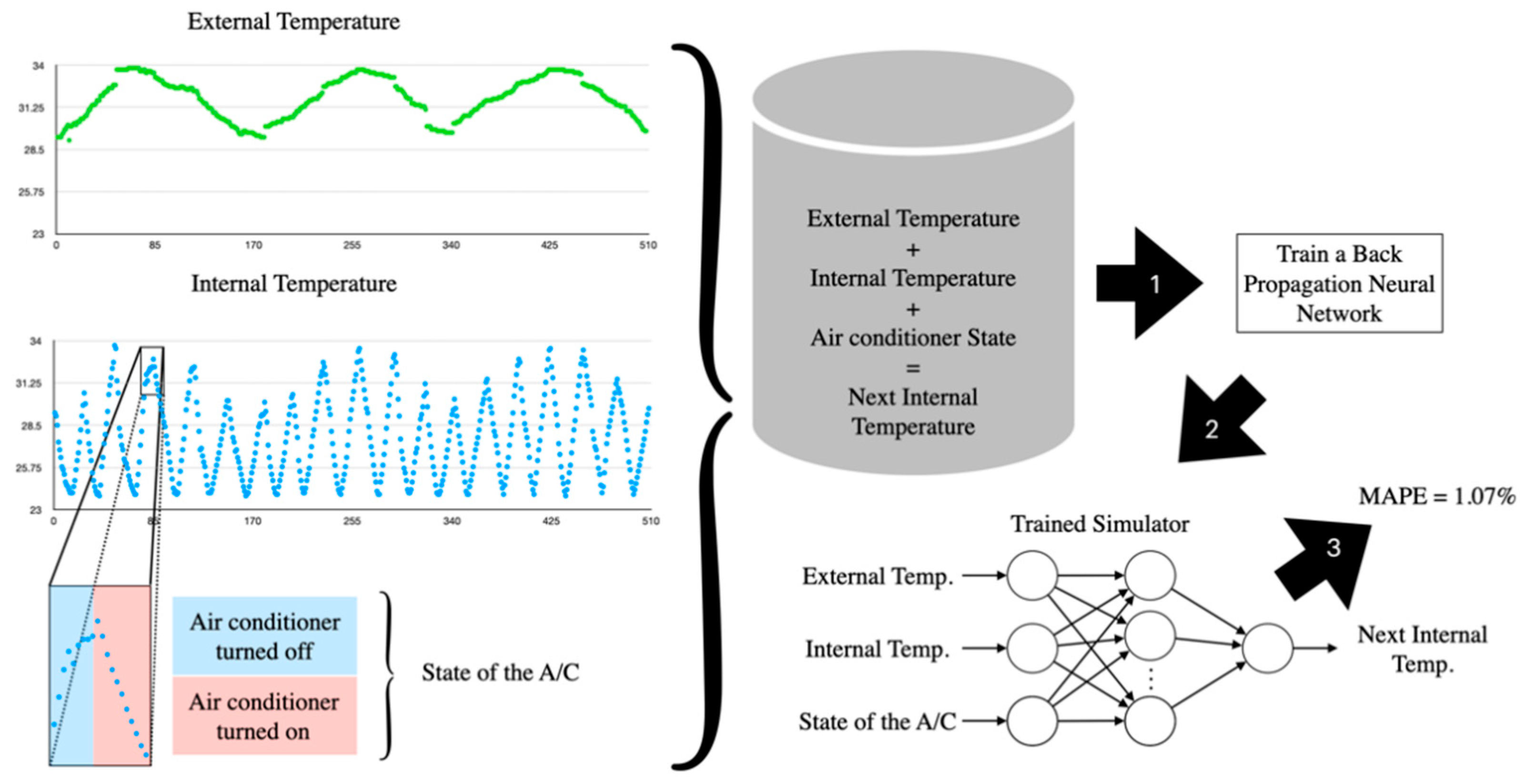
This experimentation aims to assess energy-saving and user satisfaction for five whole days. To do this, we executed both algorithms independently and used the neural network to simulate the temperature changes, given each algorithm’s recommendation.
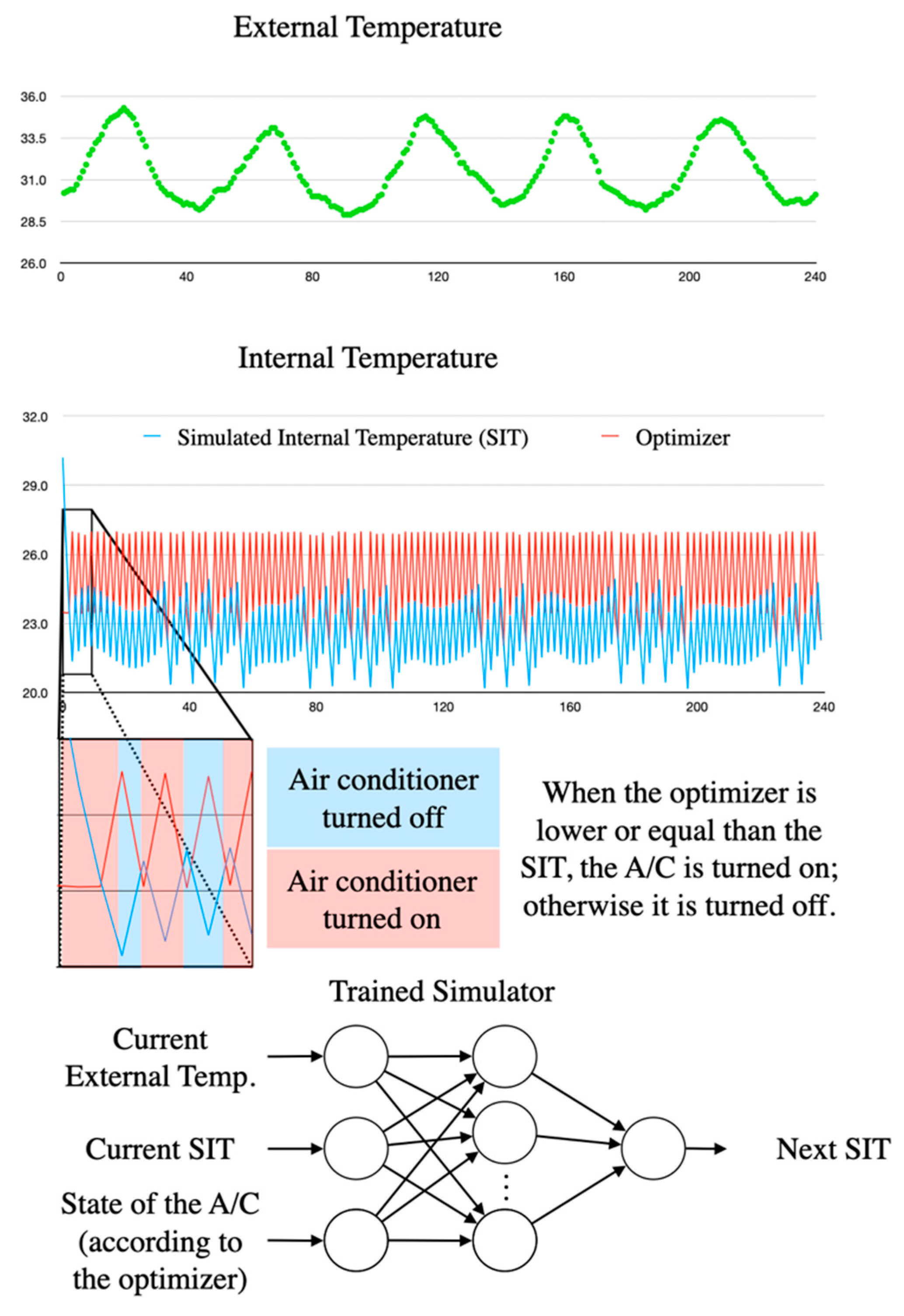
Figure 6 shows the external temperature acquired for five days and the simulated internal temperature obtained by the neuronal-network-based simulator. The simulator requires three parameters to forecast the new internal temperature: current external temperature, current internal temperature, and the state of the air conditioner system; the latest is obtained according to the optimizer recommendation, i.e., if the optimizer recommendation is lower or equal to the internal temperature, the air conditioning system is turned on; otherwise, it is turned off.
To avoid increasing computational costs, we execute the optimization algorithms once every half hour. These experimentations consider three configurations (see
Table 1): prioritizing energy-savings (A), a balance between energy-saving and user satisfaction (B), and prioritizing user satisfaction (C). These three configurations constitute the three primary user profiles within our laboratory and, roughly, in any conventional home.
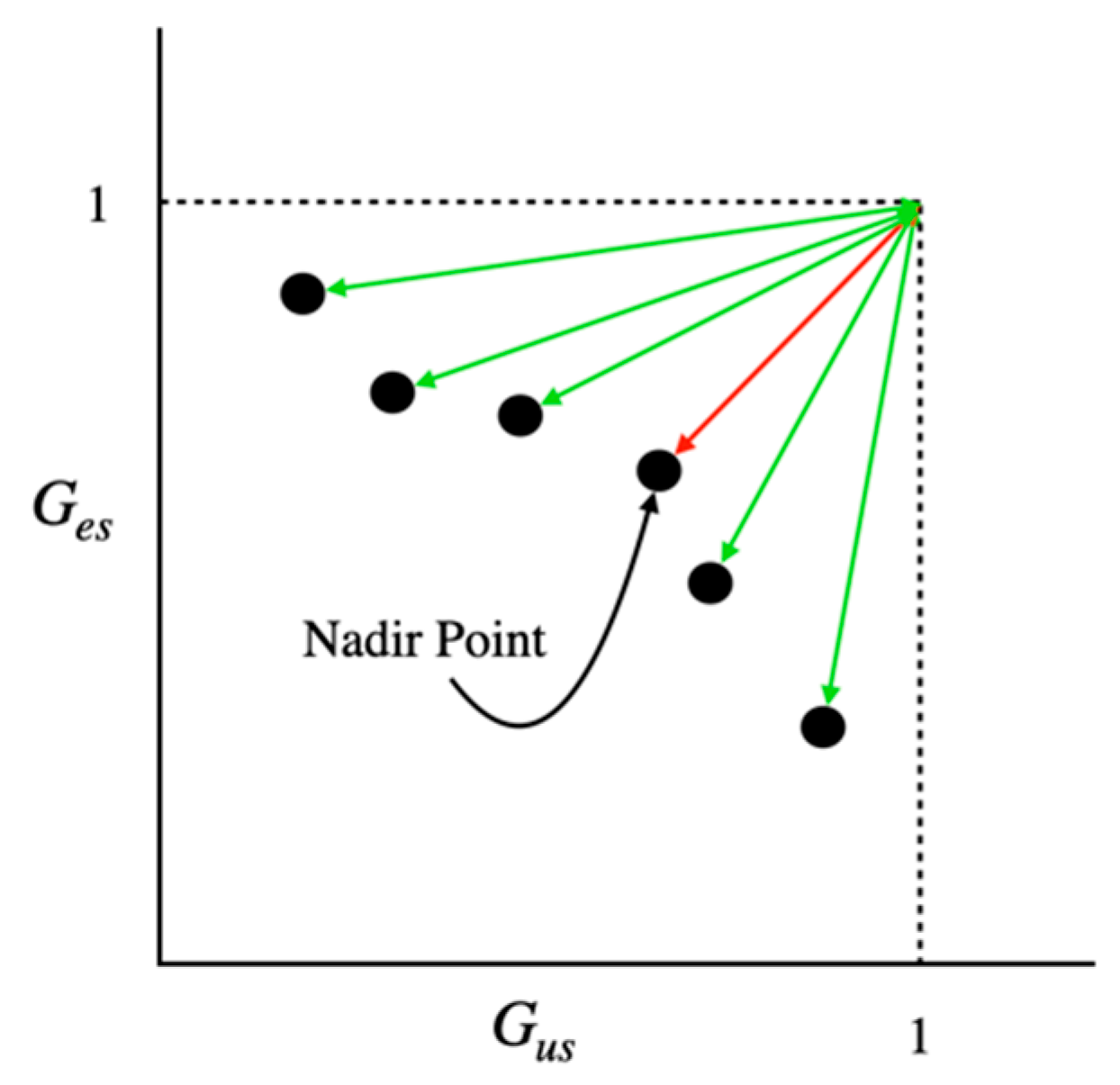
We configured the algorithms with the values from
Table 1; then, the algorithms produce their recommendations for five simulated days; where we use as a recommendation the best solution produced by GA, and a single solution from the first Pareto front for the NSGA II. To keep a fair comparison, we used the nadir point of the Pareto front, which is the solution with the lowest Euclidian distance to a hypothetical optimal point in the space. This hypothetical optimal point is (1, 1) because both objectives intend to maximize their gain, and 1 is the largest possible value for both objectives; see
Figure 7.
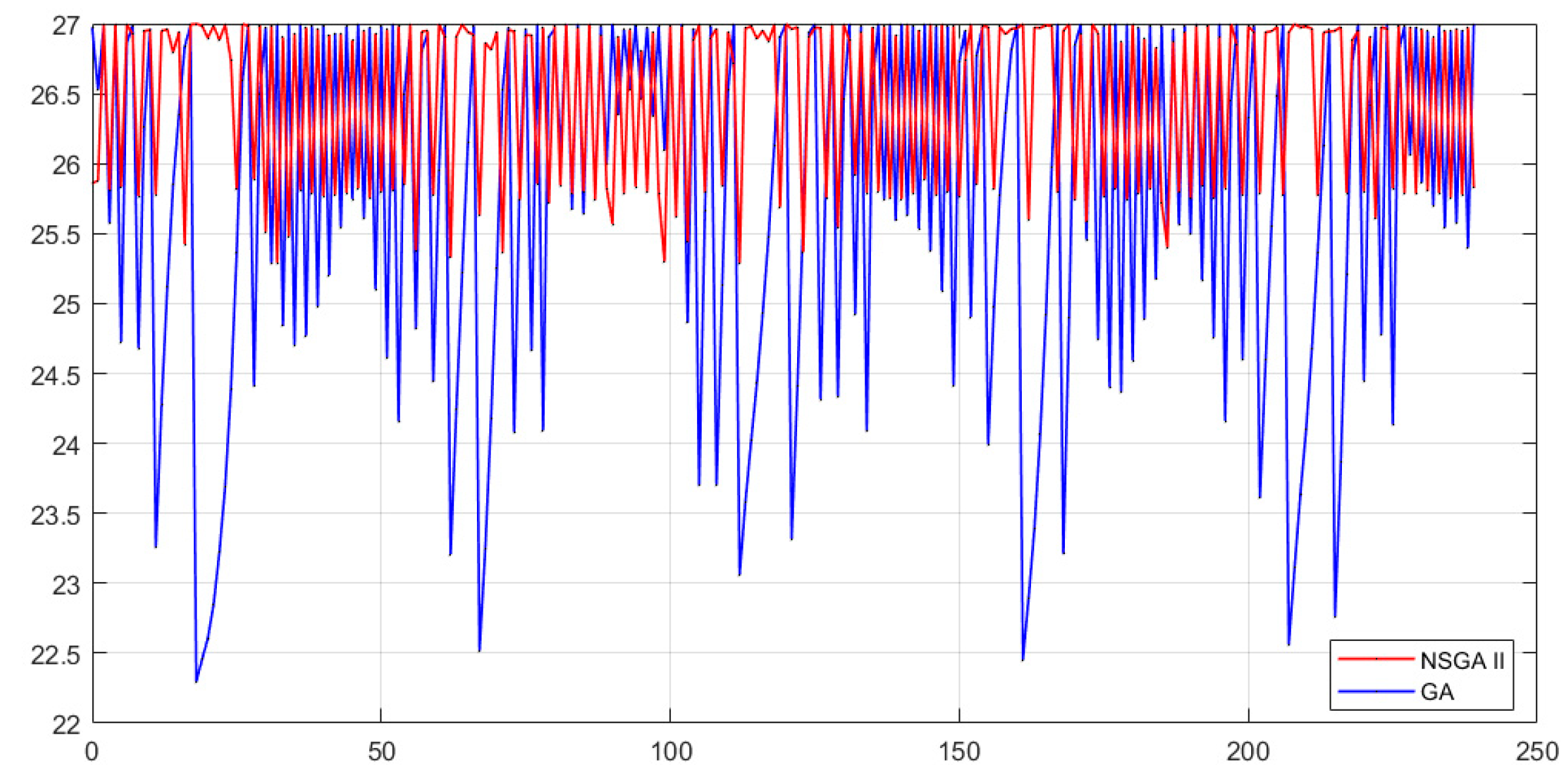
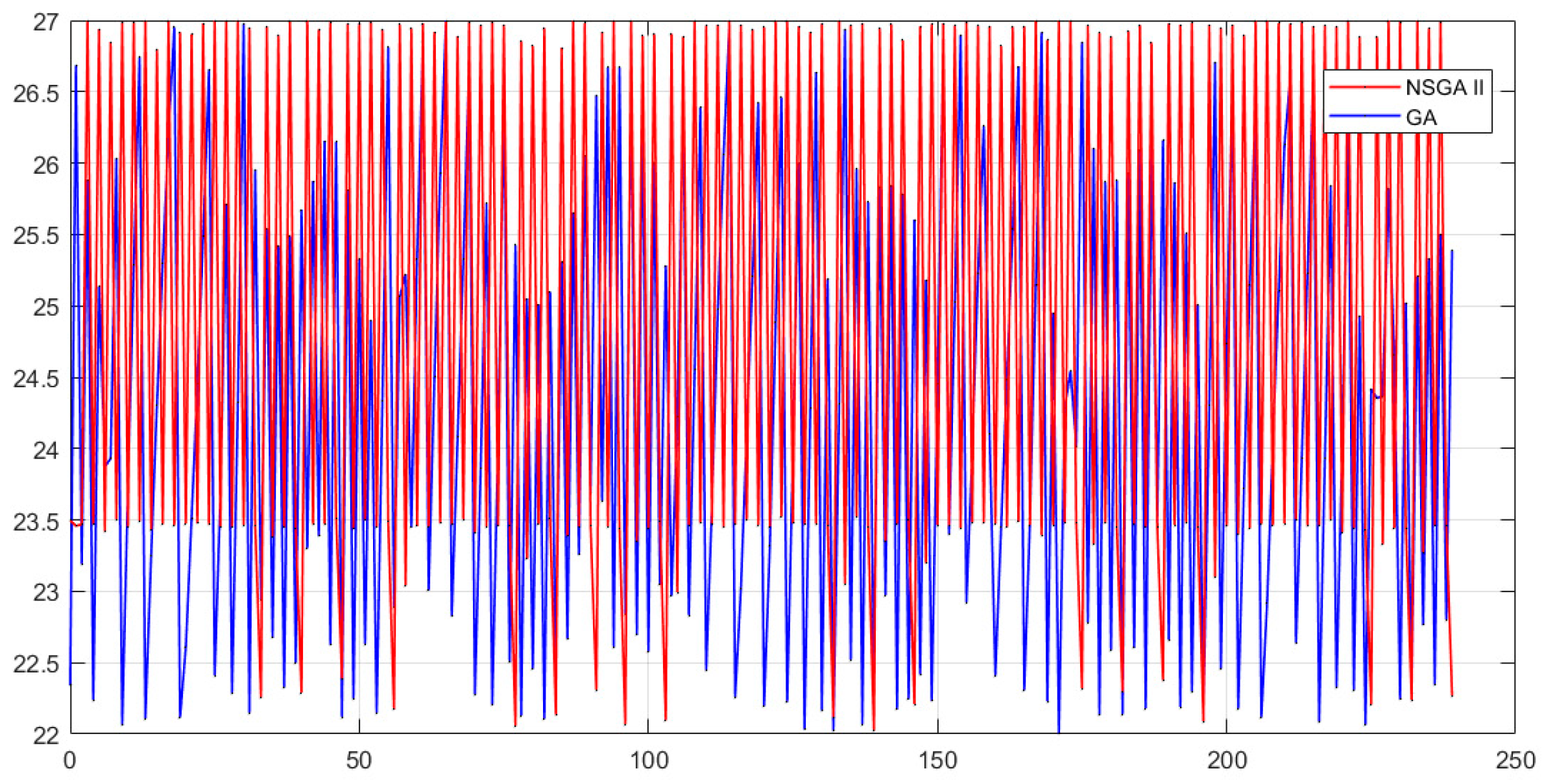
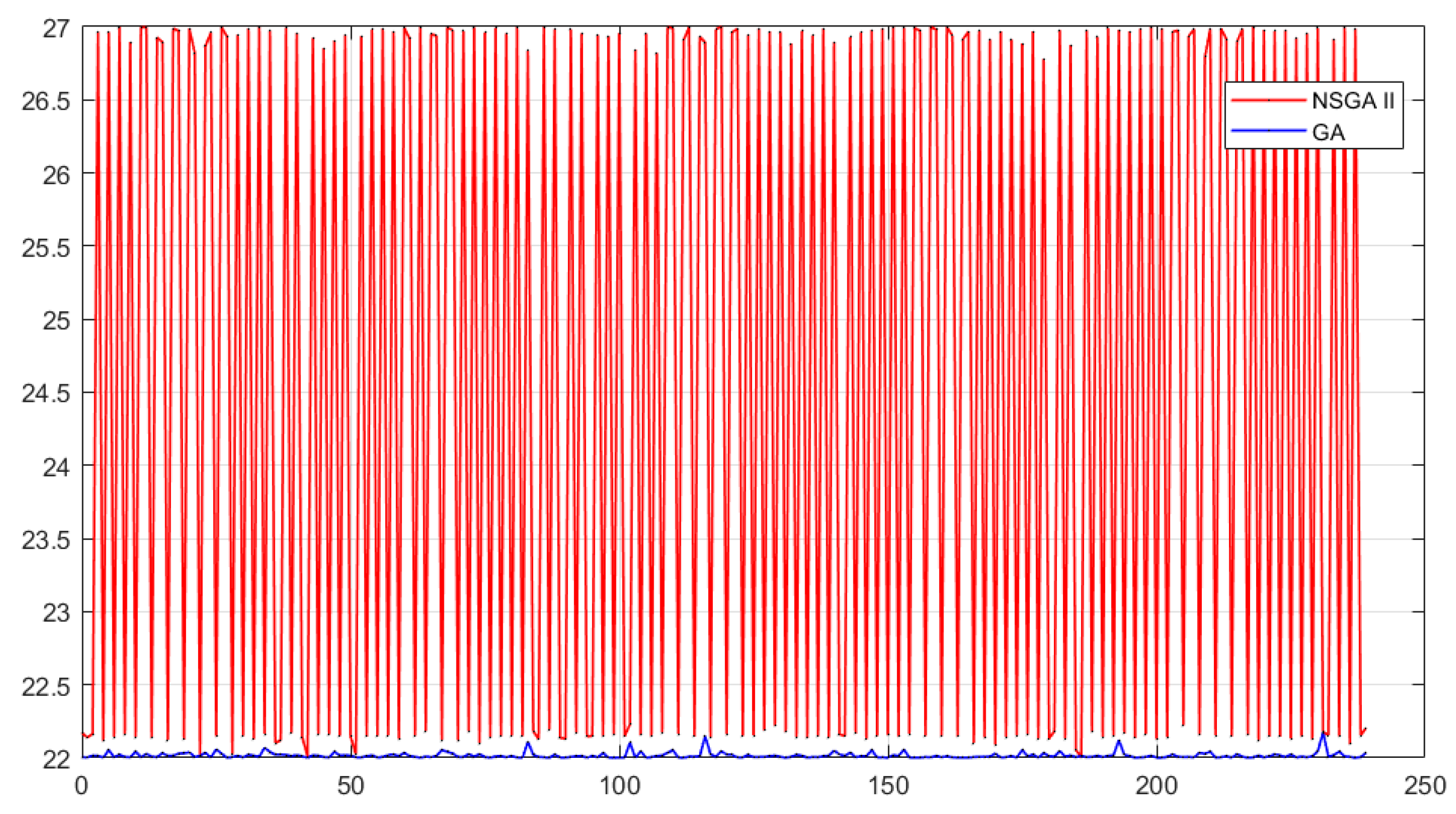
Figure 8,
Figure 9 and
Figure 10 show the temperature recommended by GA and NSGA II for each moment of the day analyzed (every half an hour) for each of the configurations.
Here, we can see that for configuration A, both algorithms recommend higher temperatures than the other configurations. However, GA does recommend lower values than NSGA II. For configuration B, GA’s recommendations have larger fluctuations than NSGA II, which mainly maintains its recommendations from 27 to 23.5 °C. Finally, for configuration C, GA recommends the lowest temperature, about 22 °C, while NSGA II increases its fluctuation.
Based on each algorithm’s recommended temperature, the simulator turns the air conditioning on or off for half an hour to adjust the room temperature.
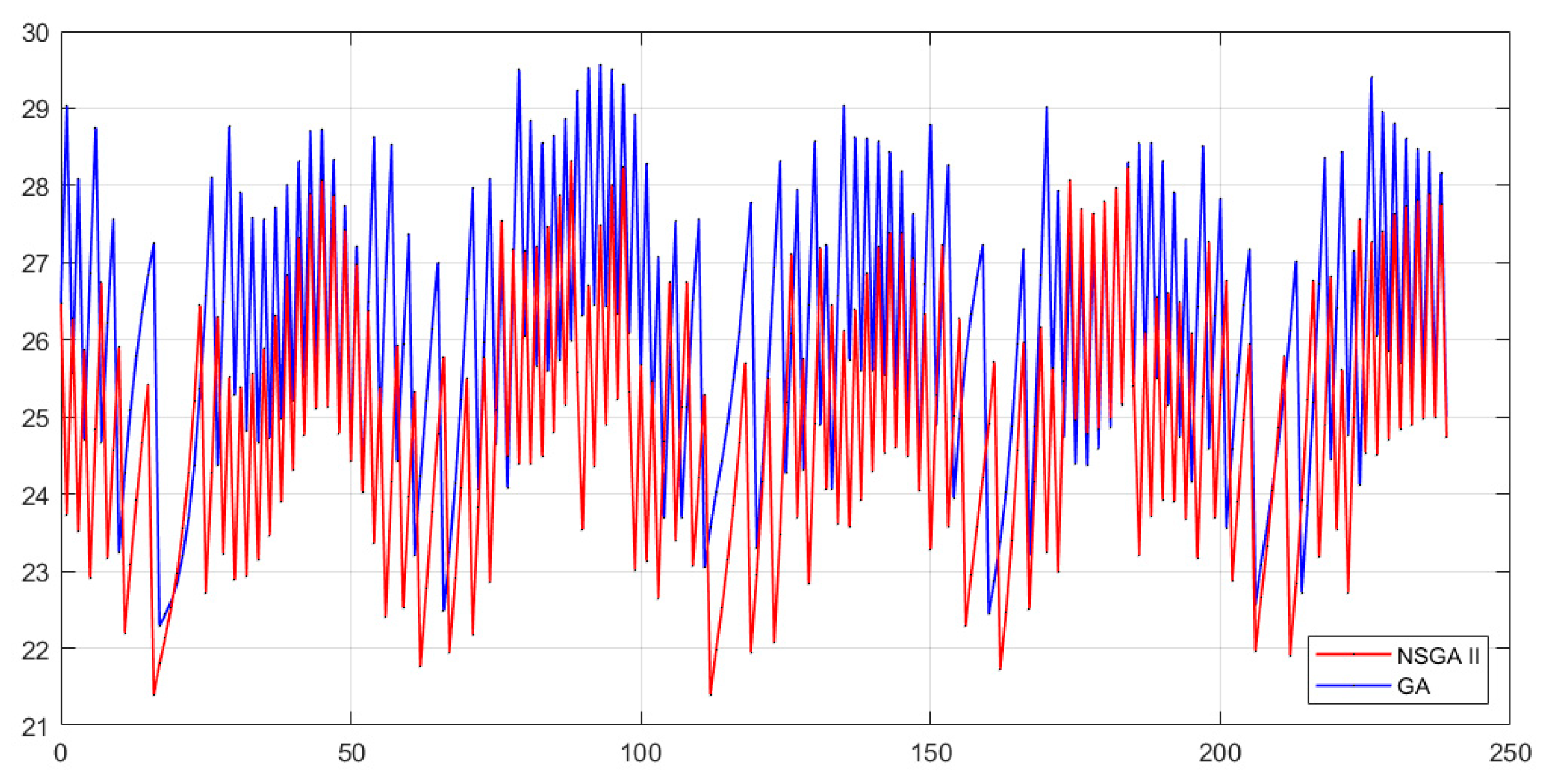
Figure 11,
Figure 12 and
Figure 13 show the room temperature simulation results by applying the algorithms’ recommendation for each configuration.
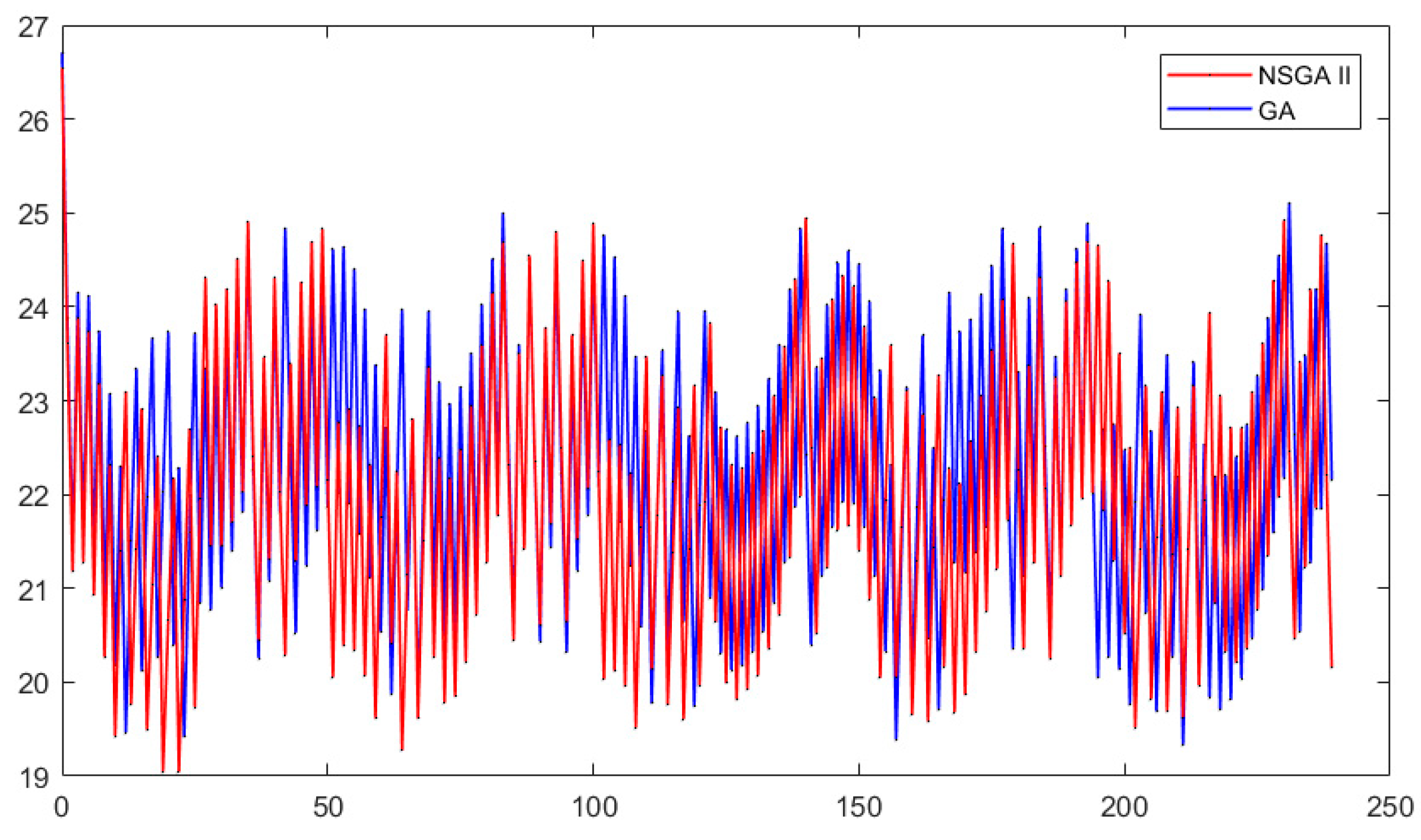
In
Figure 11, configuration A, both algorithms have similar behavior. However, NSGA II produces lower values than GA.
Figure 12, configuration B, shows that NSGA II has lower temperature values than GA and both algorithms have considerably different behavior. Finally,
Figure 13 shows an almost identical behavior for both algorithms with a slight tendency for the NSGA II to produce lower temperatures than GA.
The satisfaction level increases when the room temperature is closer to the minimum user desired temperature . As stated before, we live in a warm environment; thus, we require a cooling scheme for the air conditioning system. Therefore, the algorithm that keeps closer to provides greater satisfaction for the user.
Therefore, to measure user satisfaction, we created a satisfaction ratio, defined as the sum of the absolute differences between the current simulated temperature and for each moment of the day; this is because values lower than are unwanted.
A lower satisfaction ratio implies a higher level of satisfaction.
Table 2 presents the satisfaction ratios calculated for each algorithm for all the configurations.
As we can see, the NSGA II algorithm achieves better performance over the GA in maintaining the room temperature according to the user preferences. For the configuration where the algorithm prioritizes energy-saving (A), the NSGA II outperformed the GA’s satisfaction rate by about 295 units. Furthermore, for the second configuration (B), which prioritizes a balance between energy-saving and user satisfaction, the NSGA II outperformed the GA’s satisfaction rate by about 741 units. Finally, for the last configuration (C), which prioritizes user satisfaction, both algorithms produced almost the same satisfaction rate.
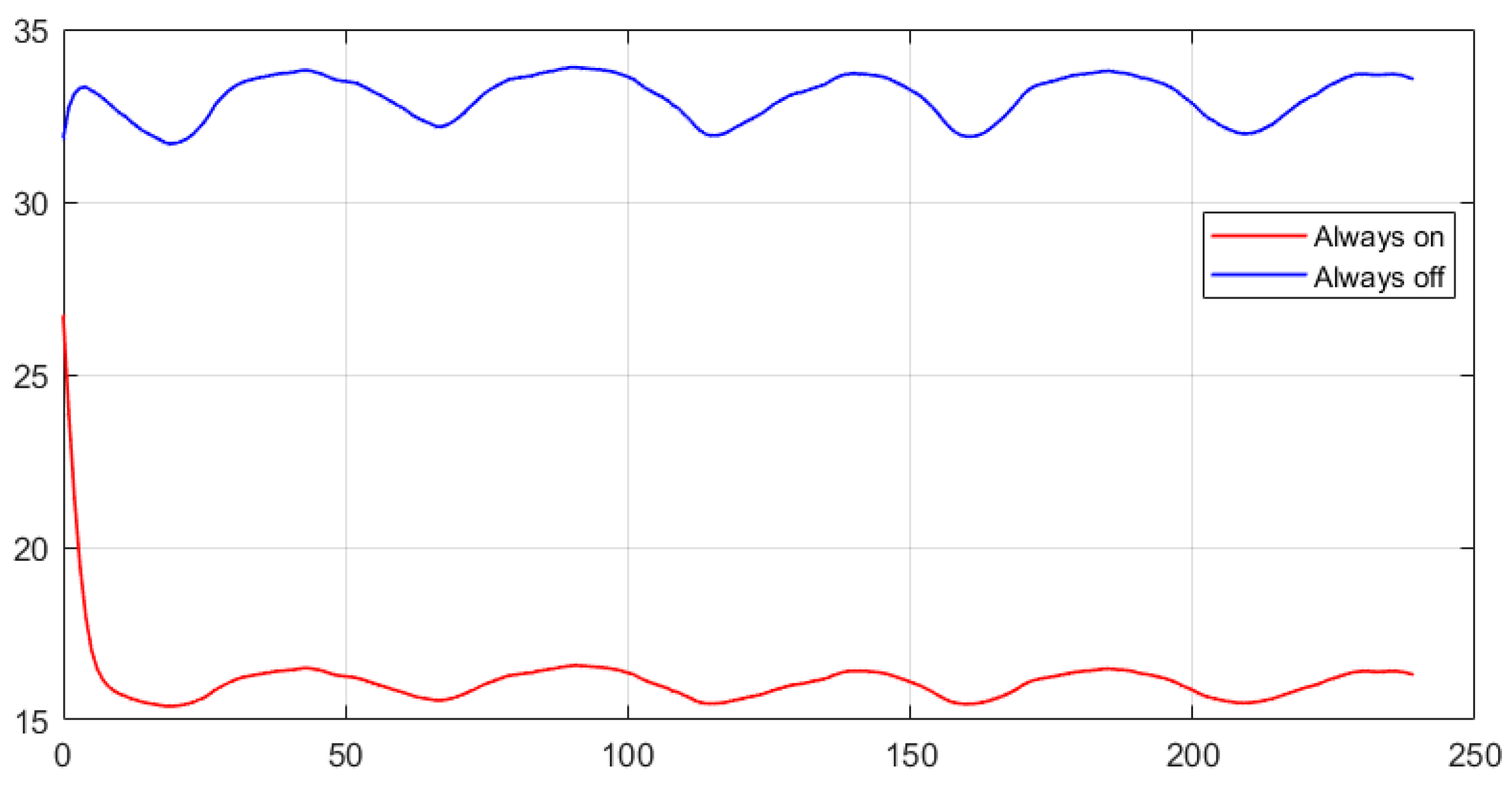
To measure the energy consumption, we evaluate the maximum and minimum energy consumption by simulating two extreme scenarios for the whole test. The first with the air conditioning system turned off and the second with the air conditioning system turned on (see
Figure 14). According to this simulation and during its execution, there was an electrical energy use of 0 and 105 kWh, respectively.
Table 3 shows calculations of the number of kWh used by all the configurations from
Table 1 for both algorithms. Additionally, we estimated the cost of
$2.997 Mexican pesos for each kWh consumed. We took this electric cost from the Mexican Federal Electricity Commission (CFE). Therefore, for the previous extreme scenario, where the air conditioning system is turned on for the whole test, the cost produced would be
$314.69.
Table 3 shows that NSGA II outperformed GA in the total cost of the electrical energy consumption in two of the three configurations. However, in the non-winning configuration, GA improves by a smaller margin to NSGA II than in the other cases.
5. Discussion
As we can see, NSGA II achieved a better performance than GA regarding user preferences while also outperforming GA in two of three configurations regarding the energy cost.
Although both algorithms adapt to the user preferences and the energy-saving, the NSGA II algorithm provides greater satisfaction. The neural-network-based simulator showed that the room temperature values of the NSGA II were closer to the user ideal temperature for two of three configurations. In this sense, we can conclude that the NSGA II algorithm produced better results than GA to control the air conditioning systems.
It is worth noting that the experimentation results were on a period of five days with a single room in our laboratory. However, by extending the experimentation to a longer time span and more laboratories/rooms, we can easily reach a cost of about $3700 for just two rooms with the air conditioning turned on for one month. On the other hand, we can decrease this cost to about $3000 with the NSGA II configured for energy-saving for the same amount of time. This comparison shows that we can reach an energy-saving of about nineteen percent by using the NSGA II optimizer, highlighting the impact of using an intelligent system on electrical energy consumption.
6. Conclusions
In this paper, we tackle the problem of controlling an air conditioning system using evolutive algorithms to increase energy-saving while considering user satisfaction.
Therefore, we assessed the performance of two genetic algorithms to control an air conditioning system. The first algorithm was an implementation of a genetic algorithm (GA) proposed in [
8], while the second was our proposed NSGA II algorithm, which is a multi-objective optimization algorithm. We considered the NSGA II an appropriate alternative because the air conditioning system intends to increase energy-saving while considering the user preference. Thus, both objectives are directly opposed, which is a key identifier of a multi-objective problem, making NSGA II an excellent alternative for solving.
Additionally, we proposed a modification to the definition of the problem, enhancing it to consider new elements, including the cost of maintaining the same temperature and the cancellation of the cost of returning to a warmer temperature, which occurs if the room is colder than the desired temperature.
Furthermore, we designed and implemented a neural-network-based simulator to measure both algorithms’ performance in equal circumstances. This simulator showed a relatively low mean average percentage error of 1.07.
Regarding the comparison between GA and NSGA II, the latter showed better energy-savings and user satisfaction than GA. Therefore, our assumption that a multi-objective algorithm would produce better results for controlling an air conditioning system with two objectives proved right.
Finally, we are currently working on expanding the experimentation by adding other services. As future work, we encourage researchers to develop an intelligent system prototype using NSGA II as a decision-making engine, integrating different configurations of user preferences and profiles and further studying the air conditioning system’s energy cost.