Abstract
Data modeling and dimensionality reduction are important research points in the field of big data. At present, there is no effective model to realize the consistent representation and fusion of different types of data of students in unstructured campus big data. In addition, in the process of big data processing, the amount of data is too large and the intermediate results are too complex, which seriously affects the efficiency of big data dimension reduction. To solve the above problems, this paper proposes an incremental high order singular value decomposition dimensionality (icHOSVD) reduction algorithm for unstructured campus big data. In this algorithm, the characteristics of audio, video, image and text data in unstructured campus student data are tensioned to form a sub-tensor model, and the semi-tensor product is used to fuse the sub-tensor model into a unified model as the individual student tensor model. On the basis of individual model fusion, the campus big data fusion model was segmented, and each segmented small tensor model was dimensioned by icHOSVD reduction to obtain an approximate tensor as the symmetric tensor that could replace the original tensor, so as to solve the problem of large volume of tensor fusion model and repeated calculation of intermediate results in data processing. The experimental results show that the proposed algorithm can effectively reduce the computational complexity and improve the performance compared with traditional data dimension reduction algorithms. The research results can be applied to campus big data analysis and decision-making.
1. Introduction
With the continuous penetration of information technology, the type and size of campus data is growing at an unprecedented rate. The term “Big Data” originated from the massive amount of data produced every day [1]. Since the beginning of the 21 century, information technology in the field of education has been developing rapidly, and more and more colleges and universities have begun to build digital campuses and campus big data platforms. The construction of big data platforms has greatly enhanced the management, teaching and research, and teacher-student services of colleges and universities, has accelerated the process of building smart campuses, and improved the level of education modernization [2]. Although the amount of data on campus is huge, most of the data belong to unstructured data. In campus big data, the data that cannot be expressed in a unified structure is campus unstructured big data, mainly including images, text, audio, video, etc. This kind of data is not convenient to be represented by the two-dimensional logical table of the database. Its format is very diverse and its standards are also diverse. In application, unstructured data are more difficult to be standardized and understood. The rise of the era of big data provides a platform for integration, mining and sharing of heterogeneous data. Students’ daily study and life will produce a large number of increasingly complex data. How to deal with and manage these massive information resources in an orderly and efficient manner and obtain useful data for analysis has become a great challenge for modern scientific research.
At present, colleges and universities all over the country are promoting information construction and forming massive data in school management, which greatly enriches the campus big data repository. However, there is a common phenomenon, that is, the degree of information data structure is not enough, and most of them are pictures, audio, video, text, and so on, and there kinds of semi-structured or unstructured information resources are difficult to be used to form an effective resource chain and provide effective decision support for campus management [3]. Traditional data mining technology is difficult to meet the needs of multi-source heterogeneous high-dimensional campus data when the data dimension and scale are expanded. However, the information content and application value of unstructured campus big data make it very important to use data efficiently. Therefore, it is necessary to study an effective and simple data representation method. How to fuse different types of data in unstructured campus big data into a unified model so as to eliminate data redundancy and obtain high-quality datasets is a big problem in data analysis.
Big data management includes data model construction, data storage, data cleaning, data application and other aspects. The main problem of big data processing is the complexity caused by the existence of multidimensional attributes and heterogeneous attributes [4,5]. Among them, how to establish a concise data model is the most basic link. A big data fusion model aims to merge or inherit different types of data at different abstract levels, so as to get a model that can fuse massive high-dimensional data together. The fused model is already highly usable and consists of complex structures and high dimensions. However, the traditional data model has been unable to handle data with a high dimension and a large volume. In order to achieve accurate classification and analysis of data, we need to identify and remove irrelevant and unimportant dimensions. Dimension reduction can improve the classification accuracy of datasets, computational efficiency, accuracy and time complexity of machine learning algorithms such as classification and clustering. These are the most important processing steps in data analysis and mining. Therefore, the most important task at present is how to design a data model that can fuse various types of unstructured data together, and implement an effective dimensionality reduction algorithm to obtain high-quality core data.
Aiming at the modeling of massive high-dimensional data, Luo et al. propose a mass data extraction model, which used fuzzy clustering to construct the model. The data with same or similar characteristics would be consolidated and data with different characteristics would be split during data extraction processes. Although the model can extract large amounts of data and reduce data redundancy and noise, there is no unified data representation model [6]. For unstructured data management, Li et al. propose a tetrahedron model. The model represents unstructured data with four facets, and the four facets are a basic attribute facet, a semantic feature facet, a low level feature facet and a raw data facet, and the links among data objects on each facet represent their correlations. To facilitate uniform classification and search, the top of the model adds a data identification. However, the model is complex and its expansibility is not better [7,8]. On the basis of the tetrahedron model, Han et al. propose a galaxy model. The model is optimized by the usage of attributes in the statistical file system. Unstructured data are described according to the set of attribute, but the model relies too much on the subject behavior [9]. Kuang et al. proposed a big data representation model based on a tensor. This model brings the multi-source data together and makes a unified representation of structured, semi-structured and unstructured data. Compared to the tetrahedron and the galaxy model, this model is simple, intuitive, and has good expansibility. However, the model does not fully consider the diversity of unstructured campus data [10,11].
One of the most important characteristics of big data is velocity, and the value of data decreases with time. Therefore, real-time is very important for big data. In recent years, domestic and foreign scholars have done a lot of work on how to deal with the huge amount of high-dimensional data as soon as possible. Nitika Sharma summarized several common dimensionality reduction algorithms, such as principal component analysis (PCA), linear discriminant analysis (LDA), feature clustering and so on, and concluded that the type of dataset should be considered to select the dimensionality reduction algorithm [12]. Yanxia Li proposed an automatic encoder-learning nonlinear mapping for data dimensionality reduction, which reduces the dimensionality and retains the nonlinear structure of high-dimensional data [13]. Some researchers have applied knowledge discovery and artificial intelligence technology to the flow data [14], and some scholars have used the theory of singular value decomposition in data dimensionality reduction [15,16,17]. The core data of historical data is obtained by performing the singular value decomposition of historical data. The core data of historical data are quickly integrated with the new data to achieve the purpose of providing services quickly [18]. Some scholars have applied a high order singular value decomposition method and a tensor decomposition method (Truck decomposition, Canonical Polyadic (CP) decomposition, etc.) to tensor flow to extract high-quality data [19,20,21,22]. Jouni, Mohamad used CP decomposition to reduce the dimensionality of the high-dimensional tensor of the image, and verified its effectiveness [23].
At present, in order to achieve the effective representation of a large-scale high dimensional dataset, researchers have mainly improved the traditional data representation model by optimizing the parameter setting. On the other hand, data of different structures are represented by building new data models [24,25,26,27]. The data extraction method is still used in small datasets, and cannot be used in a large data environment. These methods have the following defects:
(1) The unified representation of massive high dimensional data. At present, the representation model of some specific domain can only be applied to a specific domain, and cannot be used to represent all big data. This makes it difficult to build a data fusion model.
(2) The intermediate results are repeated. In the process of big data processing, the fast growing intermediate result obviously reduces the performance and efficiency of a big data processing system. However, the intermediate result is also crucial, and the loss of an intermediate result may result in the recomputation of all raw data. Therefore, the calculation of an intermediate result will directly affect the overall performance of the algorithm.
Therefore, in view of massive unstructured campus big data, this paper proposes an incremental High-Order Singular Value Decomposition (icHOSVD) dimensionality reduction algorithm for unstructured campus big data. In our algorithm, firstly, the video, audio and image of unstructured campus data are represented as a unified sub tensor model by tensor, and a campus big data fusion model based on a semi tensor product is proposed. Secondly, in the process of dimensionality reduction of the unified representation data model, the traditional data dimensionality reduction method was improved, and the big data icHOSVD dimensionality reduction method based on tensor block was proposed. The new data were used to quickly update the core dataset that had been calculated, so as to improve the efficiency of the big data dimensionality reduction algorithm.
We summarize our main contributions as follows:
- We construct the fusion model of unstructured campus data. The representation model for specific types of data has been very mature, but there is no method to integrate the video, audio, image and so on of unstructured campus data into one model. This paper proposes a fusion model of heterogeneous campus data. The model transforms a variety of heterogeneous campus student data into a corresponding vector form, and establishes corresponding sub tensor models according to students’ class video, class image, answer audio, evaluation text, etc. Then, the semi tensor product method is used to fuse tensors of different orders to realize the fusion of individual sub tensor models of students and abstract the labeled student model.
- Extraction of core tensors. After the fusion of a sub-tensor model, heterogeneous data can be utilized by various algorithms. Due to the large amount of data, this can cause huge time consumption for subsequent analysis. This paper proposes a core tensor extraction method. The original tensor is decomposed using singular value decomposition, and a smaller core tensor is extracted from the original tensor, which can reduce the data storage capacity and the computation time.
The remainder of this paper is organized as follows. In Section 2, we give an overview of relevant background knowledge. In Section 3, the system overview of the algorithm framework is given. The content of the algorithm is introduced in two parts, including the fusion model of heterogeneous campus data, icHOSVD dimension reduction algorithm. Section 4 will carry out experimental analysis of the mentioned methods. Finally, we summarize the whole paper and look forward to the future work.
2. Related Background Knowledge
In this paper, we will give the basic theoretical methods, definitions, concepts and theorems that need to be understood before the algorithms. A basic theoretical method of tensor is introduced first. A tensor is a multiple linear mapping that is defined in some vector space and some cartesian product in a dual space.
In this article, the letter is used to represent the initial tensor. Its related operations and symbols are as follows:
- is mode-m unfolded matrix;
- is the frobenius norm of tensor ;
- is n-mode product of a tensor;
- is Kronecker product;
- is semi-tensor product.
is a P-order tensor, and its p-mode unfolded matrix is .
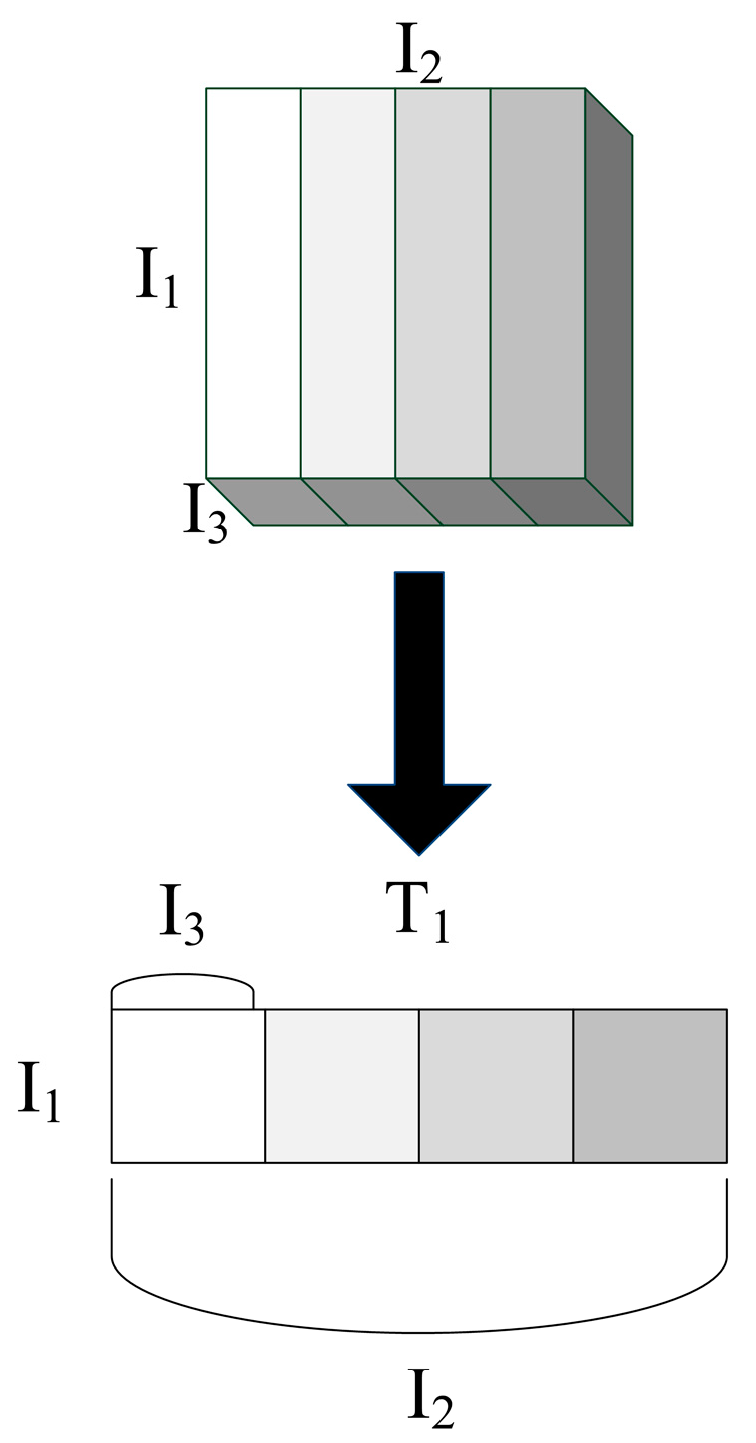
For example, the third order tensor T is expanded into a matrix, which is to rearrange the tensor T into a matrix according to n-norm. The 1-norm expansion matrix of the third-order tensor t is shown Figure 1, where , and represent the three dimensions of the third-order tensor, .
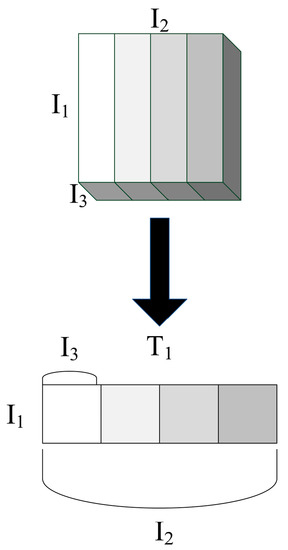
Figure 1.
1-norm unfolding of third order tensors.
The tensor is multiplied by the matrix U along the p-th order to obtain a new tensor. As shown in Formula (1), the dimension reduction of the p-th order of the tensor can be realized.
is a left singular vector matrix. It can help reduce the tensor dimension from to .
The Kronecker product of matrix is defined as Formula (2).
where matrix is ; matrix is .
Semi-tensor product of matrices is a new matrix product. The semi-tensor product of a matrix refers to the fact that even if the front array of two matrices is different from the back array, the matrix can also be multiplied.
The semi-tensor product of matrix and matrix is defined as Formula (3).
where T the least common multiple of n and p is t and .
Theorem 1.
Supposeis amatrix,is amatrix. The leftcolumns of matrixis matrix, and. That is,,,. The singular value decomposition ofandare defines as
where() refers to the left (right) singular vector space ofor;a diagonal matrix with non-negative real numbers on the diagonal.
Corollary 1.
If,then the two matrices have the same left singular vector basis.
Theorem 2.
Supposeandare P-order tensors, and r is a nonnegative integer.is a expansion matrix. Then tensorand tensormeet the conditions:
whereis p-mode product of a tensor by a matrix.
3. icHOSVD Algorithm for Unstructured Campus Big Data Fusion
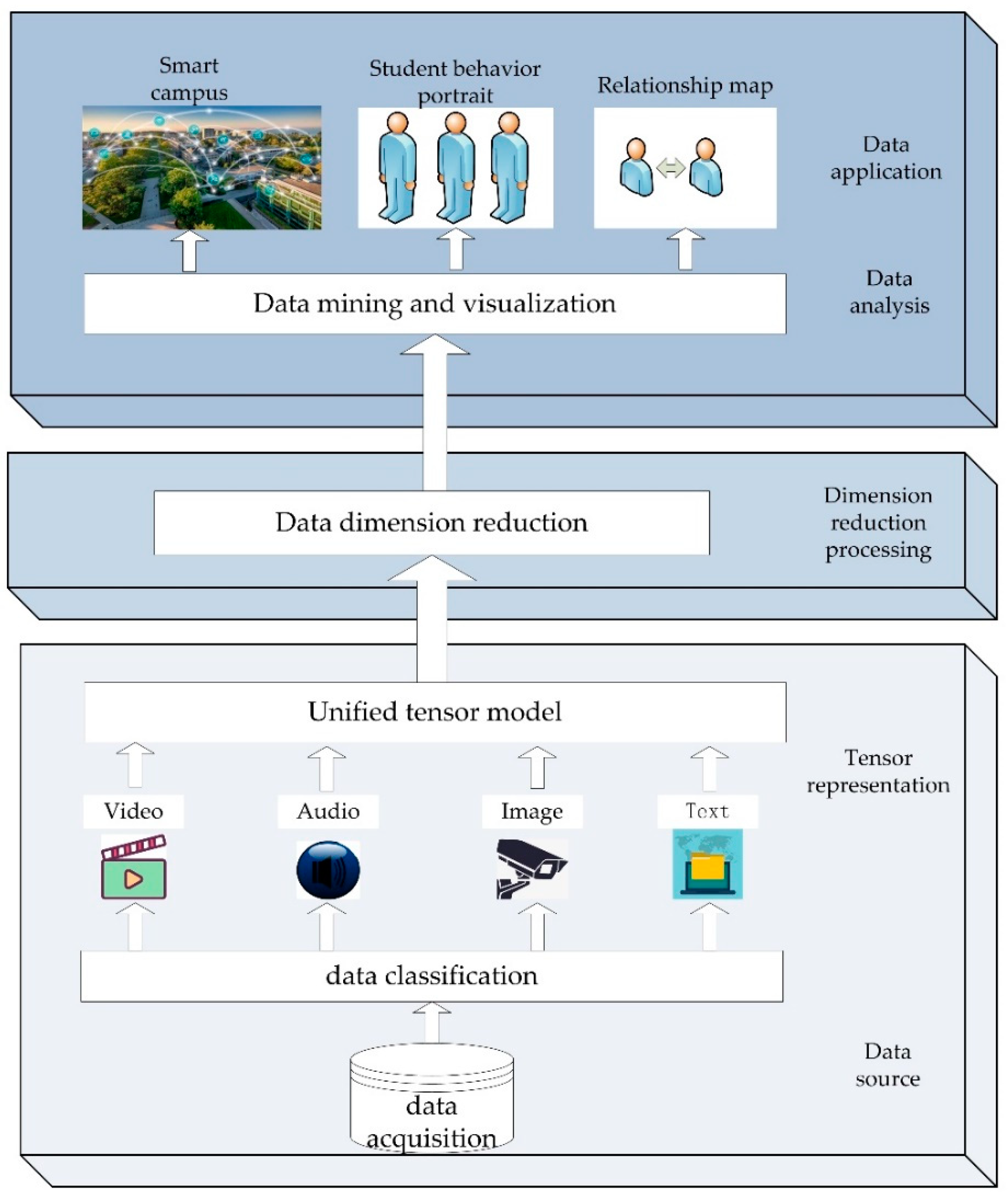
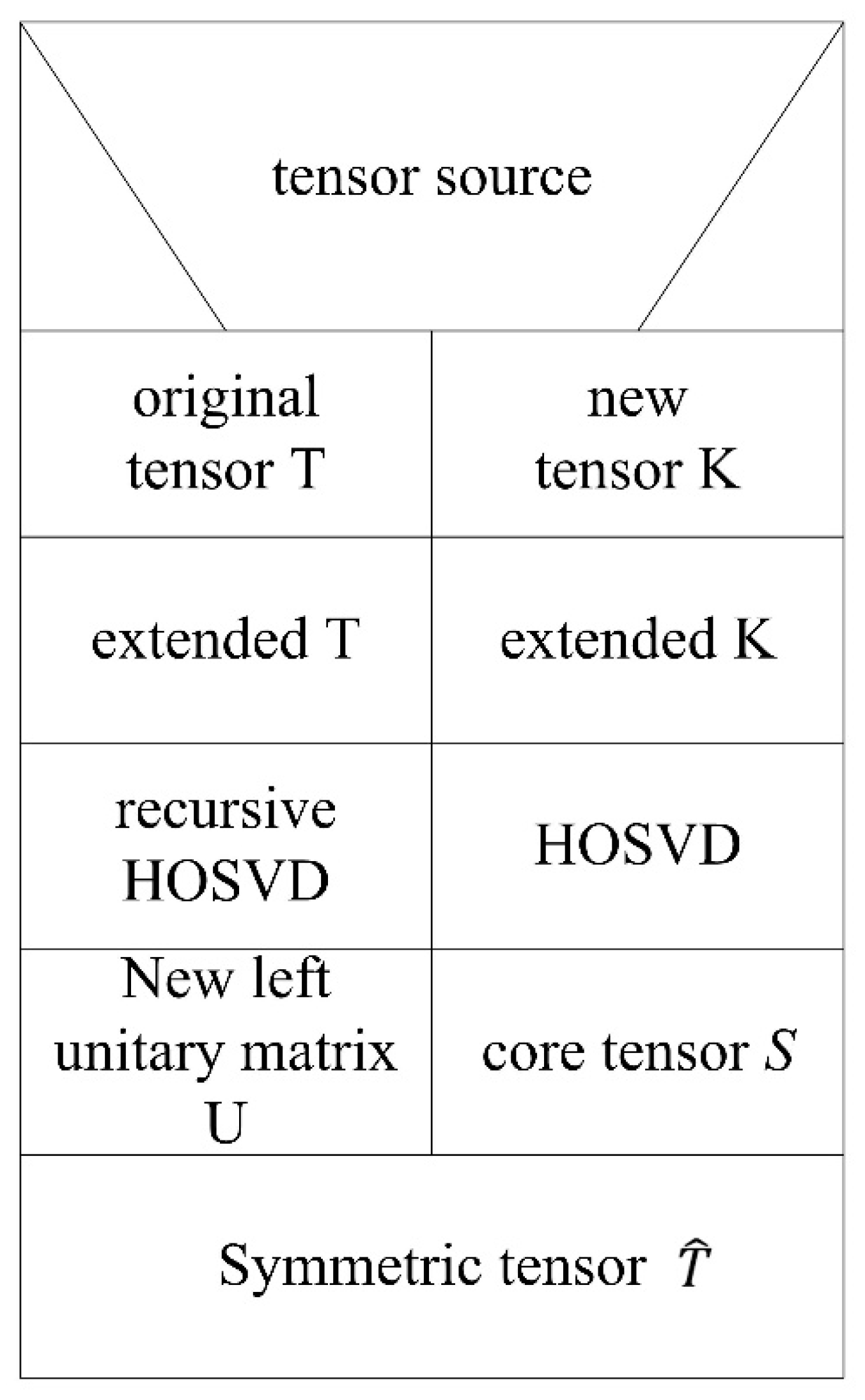
In this chapter, icHOSVD dimension reduction algorithm for unstructured campus big data will be introduced in detail. The overall process framework is shown in Figure 2. The overall framework is divided into three layers, each layer has its own task. After obtaining various kinds of data from data sources, the lowest level presents the data tensor to form a unified tensor model, and then the second level reduces the dimension of the data model, and then the results can be used for data analysis and application.
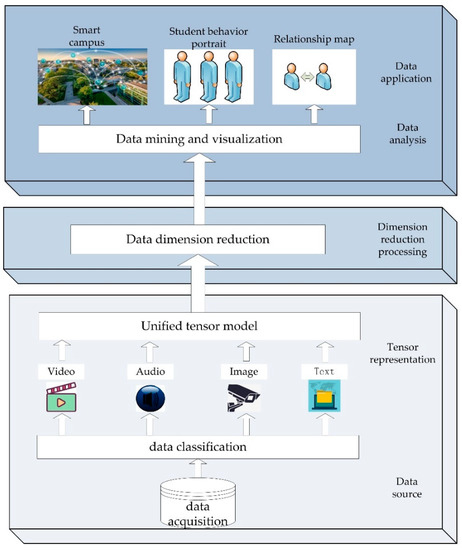
Figure 2.
Overall process framework.
This chapter first gives the overall framework flow chart and the unstructured campus big data icHOSVD dimension reduction algorithm framework. Then it describes the construction of the fusion model of heterogeneous campus data. Finally, the icHOSVD dimension reduction algorithm is described.
3.1. Framework of the icHOSVD Algorithm
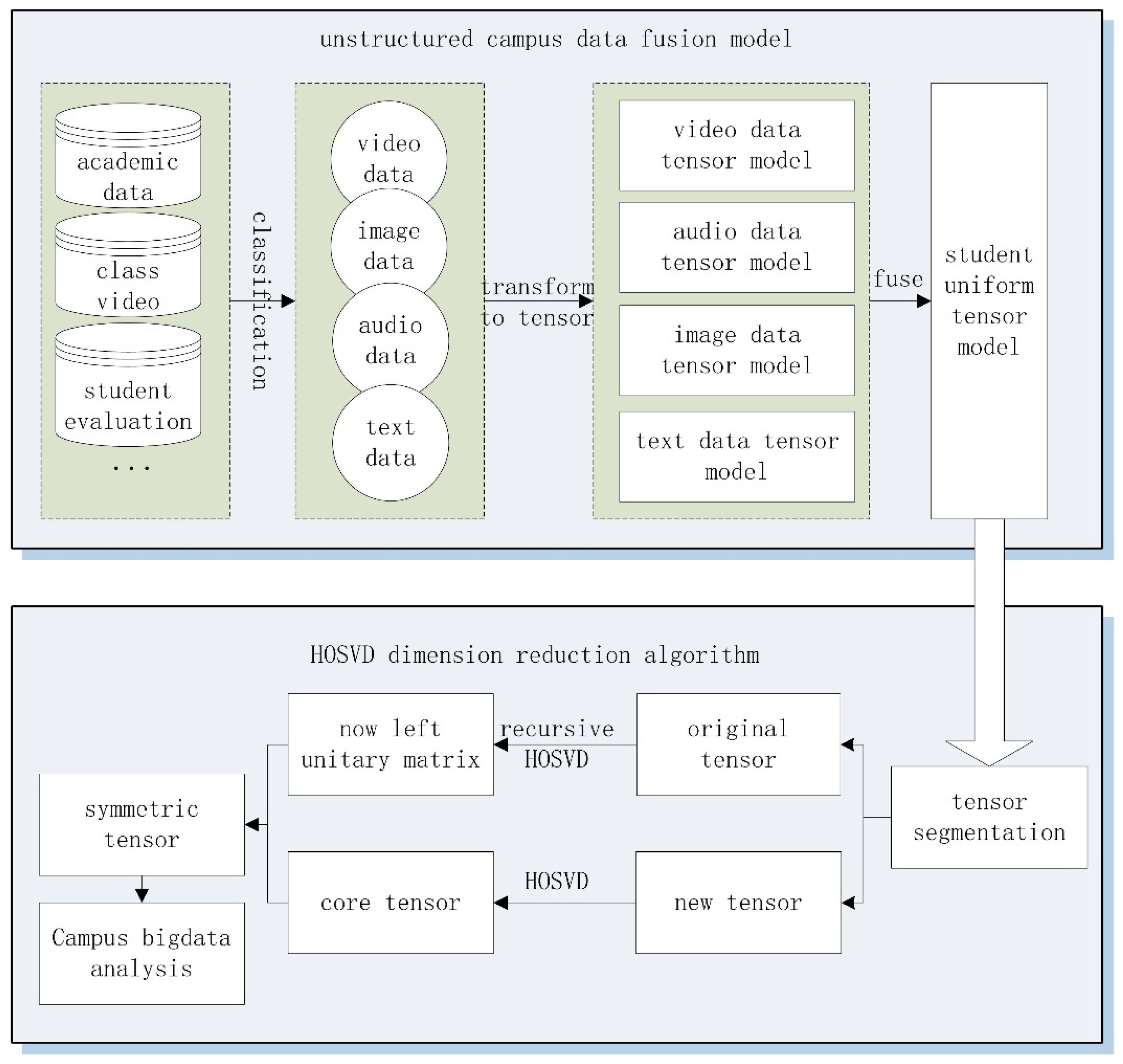
The icHOSVD algorithm for unstructured campus big data mainly includes the construction of heterogeneous campus data fusion model and icHOSVD dimension reduction. The algorithm framework is shown in Figure 3. In view of the problem of mass data unified representation, the heterogeneous campus data fusion model converts heterogeneous campus data into a corresponding vector, and the corresponding subtensor model is established. In order to realize the fusion of sub-tensor models of a variety of data, the tensors with different orders are fused by a semi-tensor product.
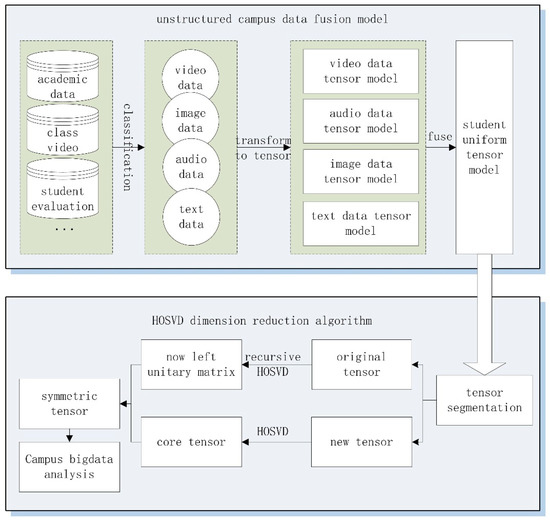
Figure 3.
The framework of the algorithm.
After the fusion of heterogeneous campus data, not only is the volume of the tensor fusion model too large, but also a recalculation problem is encountered in the process of extracting core tensor. In the icHOSVD dimensionality reduction part, the singular value decomposition method is used to decompose the original tensor to extract the core tensor from original tensor. The core dataset that has been calculated is updated quickly using the recursive singular value decomposition method of new data. Then, we can obtain the approximate tensor of original data as a symmetric tensor. In turn, the data storage capacity and computing time are reduced.
3.2. Fusion Model of Unstructured Campus Data
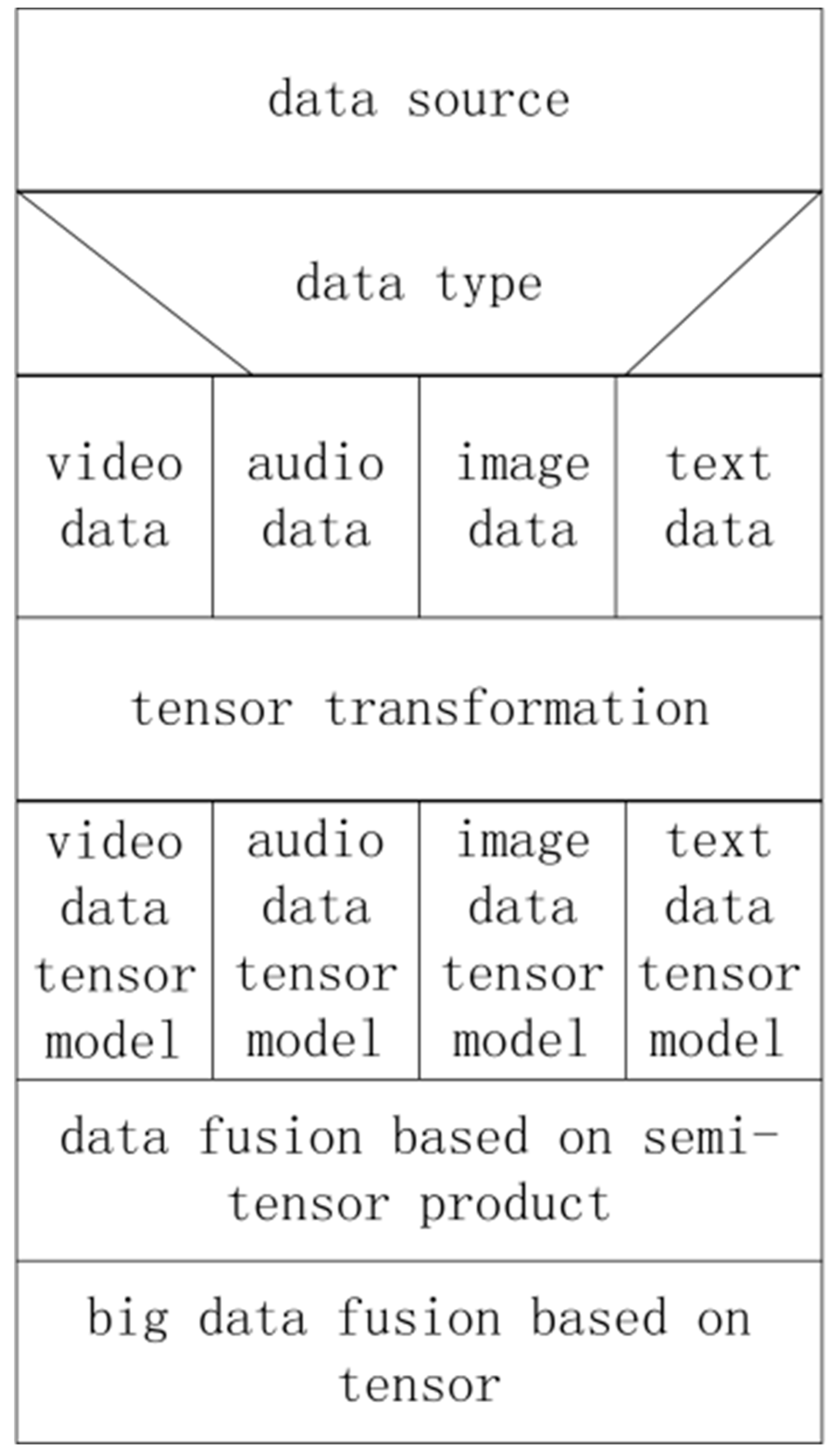
The representation model in some specific domain can only be applied to a specific domain and cannot represent heterogeneous massive campus data. The audio, video, image and other data in unstructured campus data have their own characteristics in the encoding scheme. Their encoding schemes are different. Therefore, the data features are different. All this makes data fusion difficult. In this section, our model uses tensors to quantize the audio, video, image and other data in unstructured campus data.
Then, by using the semi-tensor product, each sub-tensor model is fused into a unified tensor model, which is the student’s tensor model. The model N-S diagram is shown in Figure 4.
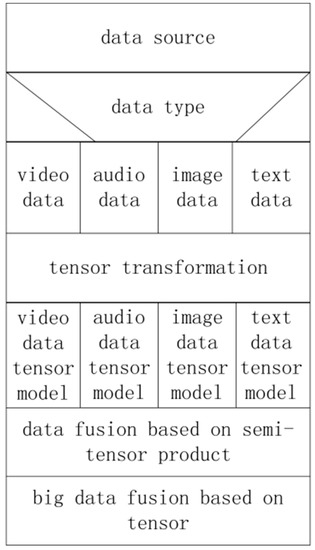
Figure 4.
N-S diagram of heterogeneous data fusion model.
As the audio, video, image data and text data in unstructured campus data are different in the form of feature encoding, different quantitative methods should be adopted for the processing of different types of data. Firstly, the encoding and dimension are provided as the transformation criteria, and different transformation functions are constructed. Different types of data are transformed uniformly to ensure that the internal structure and characteristics of the data remain unchanged. The data feature is mapped to the order of tensor according to the tensor’s advantage that each order represents a feature. The same features are merged to reduce the size of data and to improve the quality of the core set in coding. After encoding the massive heterogeneous data, the data are divided into the raw data part and the expandable part. In the tensor model, each order of the tensor represents the different properties of the data. In order to realize the expansion of tensors, one order of the tensor can be expanded by semi-tensor product operation with a certain order of another tensor.
In real situations, the audio, video, image data and text data in unstructured campus data are represented as a low order tensor model. Tensor extension operation can be used to realize the unification of the number of tensor order. When two tensors have the same number of attributes, they can be combined by a tensor extension operation.
3.2.1. Subtensor Model of Heterogeneous Data from Multiple Sources
In the traditional method, a new tensor can be obtained through multiplying two tensors. This process does not need to consider its internal data link. In the process of representing data with a tensor, the new tensor is obtained. In the meantime, the characteristics of the data in each tensor should be kept unchanged. Unstructured campus data mainly includes three kinds of data: (1) image data, such as student staff photos and campus images; (2) audio data, for example, classroom recording; (3) video data, such as video recorded during the class; (4) text data, for example, textual data about student evaluations and rewards and punishment information.
This section, according to its different characteristics, the audio, video and image data in audio, video, image data will be represented by a tensor first. Then, the corresponding tensor models are to be constructed by the tensors of each data. The specific process is as follows:
- (1)
- The sub-tensor representation method of video data.
The main features of video data are time frame, width, height and color space. Therefore, we use a four-order tensor to represent a video data, as shown in Formula (6).
where is the frame of time; is video width; is video height and is Red-Green-Blue (RGB) color.
- (2)
- The sub-tensor representation method of audio data.
Audio data such as recordings of lectures are encoded using PCM pulses to produce a series of voltage-varying signals. Then, audio data are represented by sampling frequency and amplitude. An audio data can be expressed as a second order subtensor, as shown in Formula (7).
where is sampling frequency; is amplitude.
- (3)
- The sub-tensor representation method of image data.
In unstructured campus data, a campus image is common data that are primarily used for image analysis of a lesion. In this paper, the campus image is represented as a third-order tensor, as shown in Formula (8).
where the width of image; is the height of image; is the space of color.
- (4)
- The sub-tensor representation method of text data.
Textual data such as student evaluation and reward and punishment information are converted into tensor composed of feature weights. In a vector space model, text can be expressed as , where represents each feature item. In order to express the importance of feature items in text, each feature item is given a weight W. The common weight calculation methods include Boolean weighting, term frequency-inverse document frequency (TF-IDF) weighting and entropy weight. The vector space is extended in a high dimension, and the text is expressed as a second-order tensor
where is the weight of feature .
3.2.2. A Tensor Space Fusion Method Based on Semi-Tensor Product
Through the description in the previous section, we have converted video, audio, video and text data of unstructured campus data into sub-tensor models with a lower order. In this section, the subtensor models with a lower order are fused by semi-tensor products, and the unified tensor model of a high order is obtained.
Suppose , and . Tensor extension multiplication follows the following functions, as shown in Formula (10).
The operator satisfies the associative law, that is . The order of the tensor can be extended to the existing tensor model in different directions through the semi-tensor product operation.
Unstructured campus big data usually includes video data , audio data , image data and text data , and a unified tensor model can be expressed as:
In Formula (11), the independent variables represent video data, audio data, image data and text data in unstructured campus data. These different types of data are represented as low-order subtensors, and then subtensors are integrated into a unified higher order tensor model by a tensor expansion operator based on the semi-tensor product.
3.3. An icHOSVD Algorithm Based on Tensor
After the data fusion, the video data, audio data, image data and text data in the unstructured campus data have been merged into a unified model by the tensor fusion. In view of large volume of heterogeneous data contained in the model, the traditional dimensionality reduction algorithm cannot effectively reduce the dimensionality of the model. During the calculation of the core data of the tensor, the tensor is expanded by the mode, and the core tensor is obtained by applying a high order singular value method to decompose the mode of the unfolded matrix. However, the raw data and the new data will produce a large number of intermediate results, which will be repeatedly calculated in the process of extracting the core tensor. The calculation of intermediate results will affect the calculation efficiency and the accuracy of the results. In view of the above problems, this section presents an icHOSVD dimensionality reduction algorithm based on tensor partitioning. This algorithm mainly consists of two parts: one part is a tensor partitioning after data fusion; another part is the icHOSVD algorithm that is used to form the high quality core tensor of the original tensor.
3.3.1. Tensor Segmentation
Tensor partition is the partition of a tensor along a certain order of the tensor. When dividing the tensor, divide it as evenly as possible, so that the size of each small piece is about the same.
Suppose that T is an N-order tensor, that is . The tensor is divided into n-blocks along a certain order, and the smaller tensor block can be represented by the following formula. As shown in Formulas (12) and (13).
where is the i-th slice; is the superscript of the i-th slice; is the subscript of the i-th slice.
3.3.2. icHOSVD Algorithm
The tensor is divided into tensor blocks. Then the tensor block is expanded according to the mode, and the mode matrix expansion is processed. How to combine the last calculation result with the new data in the process to reduce the computation is a problem that needs to be solved. Therefore, this paper proposes a recursive HOSVD dimensionality reduction algorithm.
First, the decomposition of high order singular values is introduced. The high order singular value decomposition is to decompose a tensor into a core tensor and several unitary matrices. As shown in Formula (14):
where is the core tensor of tensor T; is the left unitary matrix of tensor.
The specific algorithm description of the recursive High Order Singular Value Decomposition (HOSVD) algorithm is shown in Algorithm 1 below.
| Algorithm 1. The recursive HOSVD algorithm. |
| Input: matrix , matrix Output: new left unitary matrix , positive semi-definite diagonal matrix , right unitary matrix |
| 1. if then |
| 2. ; |
| 3. ; |
| 4. ; |
| 5. else if |
| 6. |
| 7. end |
| 8. end |
| 9. return; |
In the recursive process, the function f continuously calls itself to decompose the matrix and . The final result of the singular value decomposition will be obtained by calling the function f. Finally, we can get the matrix . As shown in Formula (15):
if is greater than one, the function f will be repeated and the result will be merged through function blend; if is equal to one, the matrix is decomposed by high order singular values.
In the recursive HOSVD algorithm, the main function of function blend is to combine the decomposition results of matrix and matrix , and matrix will be projected onto the orthogonal basis. The main process is as follows: firstly, the decomposition results of matrix and matrix is combined with matrix and matrix as the new input original matrix and incremental matrix. Then, the incremental matrix is projected onto the orthogonal space . The orthogonal matrix of is calculated and the unit orthogonal basis of orthogonal matrix . We can get a new matrix by combining with . We can get the new left unitary matrix , the semi-positive diagonal matrix , and the right unitary matrix by decomposing the new matrix with the high order singular values. In this way, the new matrix is combined with the original matrix, and then the dynamic update decomposition is completed.
The process of the icHOSVD algorithm is found by supposing the original tensor is and the new tensor is . According to the Theorem 1 and Corollary 1, the incremental tensor and the original tensor will be expanded to the same dimension. The tensor with different dimensions can get the mode unfolded matrix with different dimensions. Due to the different dimension, the mode unfolded matrix may not be merged.
After extending the original tensor and the new tensor to the same dimension, we can get the mode unfolded matrix of tensor by unfolding the tensor . The mode unfolded matrix of tensor can be updated by calling the recursive HOSVD algorithm. For the original tensor, HOSVD is used to obtain the core tensor and the left unitary matrix . Finally, a new symmetric tensor is obtained by combining the model unfolded matrix, which is updated by the recursive matrix HOSVD algorithm and the core tensor of the original tensor . The flow chart is shown in Figure 5.
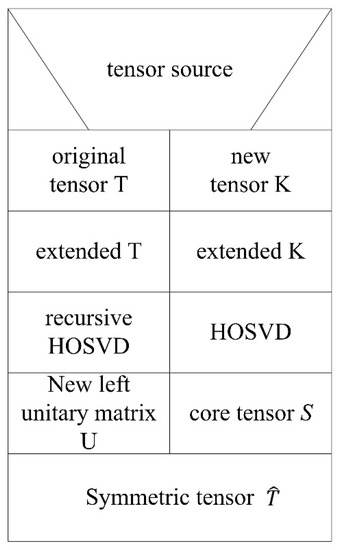
Figure 5.
N-S graph of icHOSVD algorithm.
4. Experiment Analysis
In this chapter, the proposed algorithm is verified and analyzed. This chapter consists of three sections: the time complexity of the algorithm theory analysis, the theoretical and experimental analysis of the original tensor and symmetric tensor error ratio and reduction ratio, as well as for the dimension reduction method as the most important means of time efficiency evaluation, by comparing the proposed method and the traditional HOSVD dimension reduction algorithm and other dimensionality reduction algorithms in the real campus data contrast to verify the performance of the algorithm is given in this paper. The experimental results are deeply analyzed.
- (1)
- Time complexity.
In the recursive icHOSVD process, time complexity mainly consists of three parts, which are matrix unfolding time , incremental singular value decomposition time of each unfolded matrice , and product time of a tensor by the truncated bases .
The total time used in the three processes is shown in Formula (16):
In the process of updating the left unitary matrix with function , the model unfolded matrix is decomposed by a singular value decomposition. According to Formula (16), the time complexity of updating the left unitary matrix can be obtained by Formula (17).
where C1 and C2 are constants. To begin by adding columns to raw matrix, the time complexity of one unfolded matrix decomposed by a singular value decomposition is , whereas is the number of truncated left singular vectors. After unfolding, a p-order tensor has p-mode unfolding matrixes. The matrix unfolding time is . The semi-product time of a tensor by a truncated base is . The total semi-product time is . The total time of icHOSVD algorithm is , which is .
- (2)
- Computation accuracy.
The main idea of the icHOSVD dimensionality reduction algorithm is to obtain the core tensor by decomposing the original tensor first, and then to combine the core tensor with the left unitary matrix updated by the recursive HOSVD, and finally to form an approximate tensor that can be substituted for the original tensor. The approximate tensor is a combination of the core tensor and the update left unitary matrix.
In this paper, the reconstruction error between the original tensor and the approximate tensor is used to verify whether the approximate tensor can replace the original tensor. In order to measure an approximation ratio between the original tensor and the approximate tensor, we define two variables.
Reconstruction error rate: the formula of reconstruction error rate is shown in Formula (18).
where and are Frobenius Norms.
Dimensionality Reduction Ratio: the formula of dimensionality reduction ratio is shown in Formula (19).
where is the core tensor; is the mode-i truncated orthogonal basis space; and nnz is the abbreviation of number of nonzero matrix elements. It is a function that returns the number of non-zero elements of a matrix. The dimensionality reduction ratio can effectively represent the degree of big data reduction.
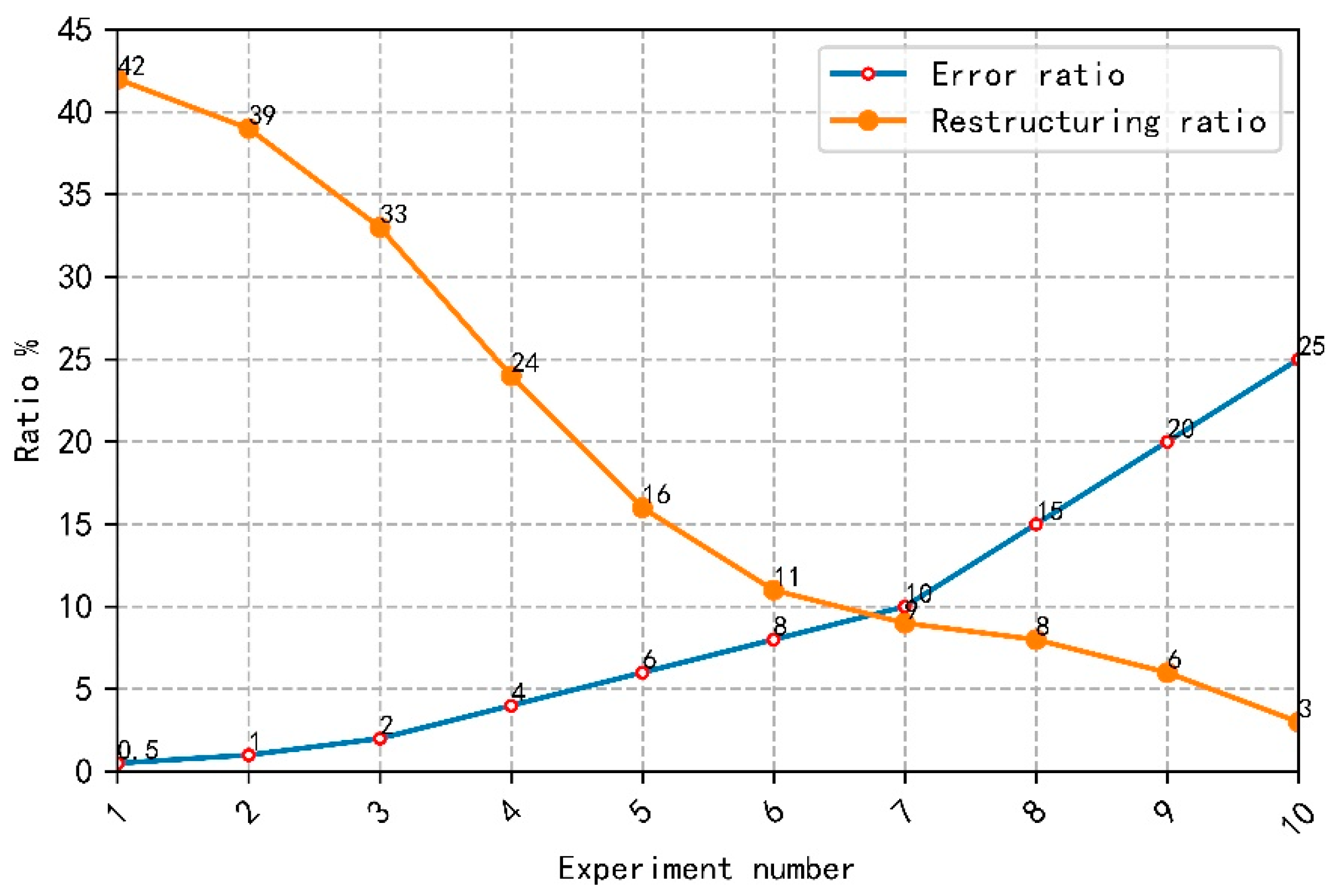
In this paper, we use to reflect the relationship between a dimensionality reduction ratio and a reconstruction error rate. The relationship between a dimensionality reduction ratio and a reconstruction error rate is shown in Figure 6. The abscissa is the number of experiments and the ordinate is the ratio value. We selected the same unstructured image data and set the error rate as 0.5%, 1%, 2%, 4%, 6%, 8%, 10%, 15%, 20% and 25% successively. The larger the error rate, the greater the difference between the symmetric tensor and the original tensor, and the larger the error means that the similarity between the approximate tensor and the original tensor is low.
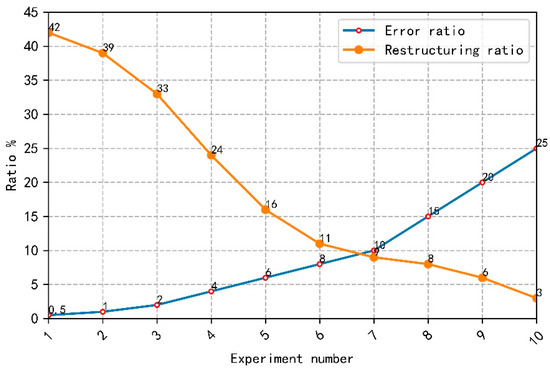
Figure 6.
The relationship between dimensionality reduction ratio and reconstruction error rate.
As can be seen from Figure 6, the lower the dimensionality reduction ratio is, the higher the reconstruction error rate is. This means that we cannot blindly pursue a low dimension in the process of dimensionality reduction. The dimensionality reduction ratio and the reconstruction error rate can achieve a balance, so that the approximate tensor is closest to the original tensor in the case of maximum dimensionality reduction. Because different types of data have different forms when constructing symmetric tensors, different error reduction rates and dimensionality reduction rates will be generated. Therefore, the balance between dimensionality reduction and error should be maintained according to the demand.
- (3)
- Comparison with other methods.
In this section, the algorithm is verified by contrasting icHOSVD algorithm and the traditional high order singular value, Tucker and a singular value decomposition (SVD) decomposition method.
The experimental data source of this paper comes from the historical data of a digital campus shared database. The original data includes 58,621 h of video and audio data of students in the main campus classroom in a week; 268,347 images of students in class; and 32,042 pieces of text data of student evaluation. All kinds of attribute data belonging to the same student are extracted and classified, including the student’s image, class video and audio, evaluation text, and the unusable data are cleaned up.
The methods in Section 3.2.1 are used to convert the various types of data into subtensors. The image data are transformed into a third-order sub-tensor, audio data into a second-order sub-tensor, video data into a fourth-order sub-tensor, and text data into a second-order sub-tensor. The tensor space fusion method based on the half-tensor product is used to combine the sub-tensors to form a unified tensor, that is, the individual student tensor. Because the students’ classroom images are obtained from the class video, the third order of the images in this experiment are included in the fourth order of the video, and a tensor model with a total of eight orders is constructed. Each order represents the video frame, video width, video height, video RGB color, audio sampling frequency, audio amplitude, number of text feature items and the number of text weight. All kinds of data are embedded together according to the rules. Individual tensors are obtained by fusing subtensors to eliminate ambiguity and redundancy. Due to the high dimension of individual tensors, it is difficult to carry out further processing. The icHOSVD algorithm proposed by us is used to reduce the unified tensors to lower-order tensors, so as to obtain the simplified individual tensor model.
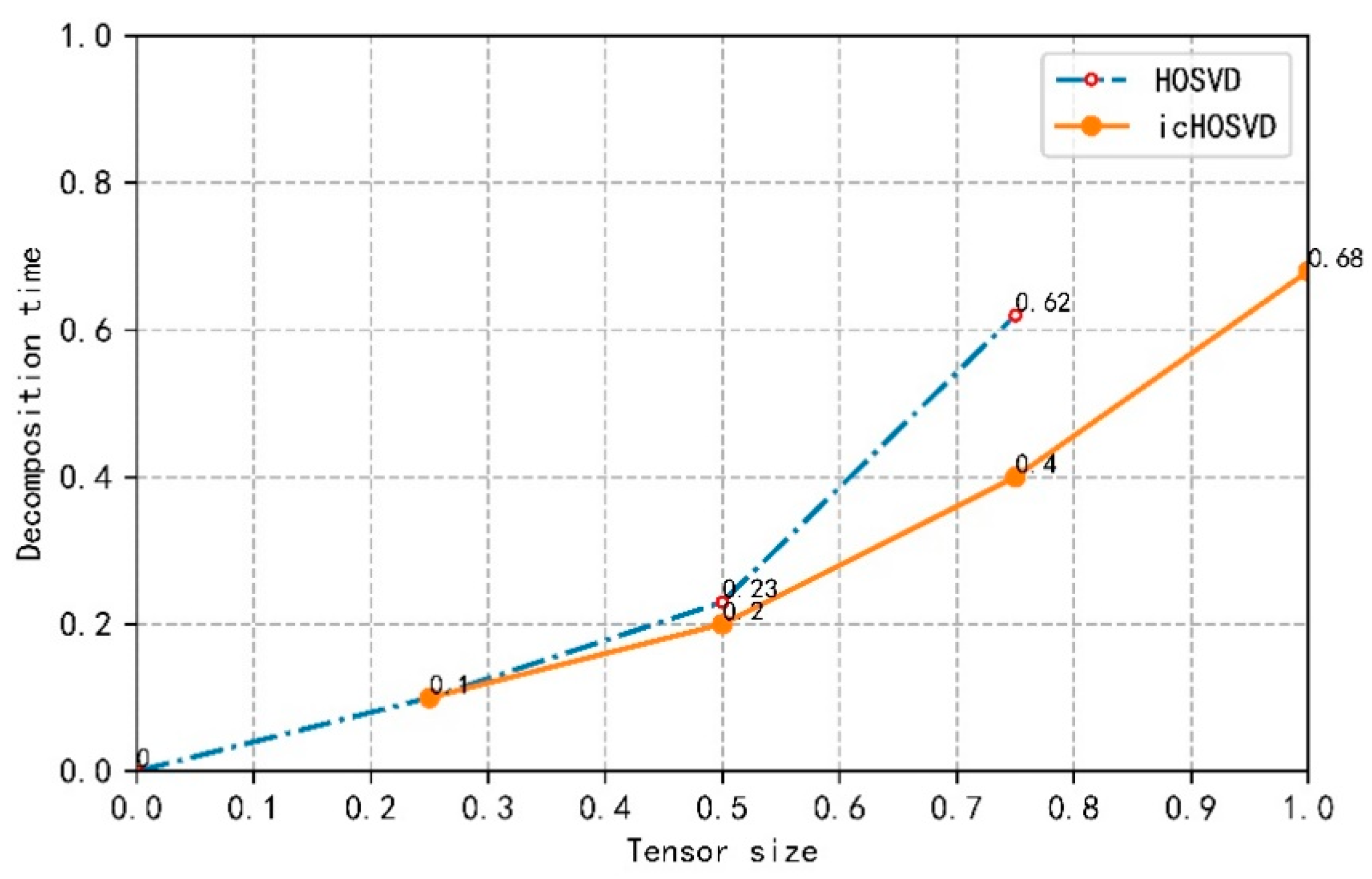
In order to evaluate the icHOSVD dimensionality reduction method, we use unstructured video data to construct a tensor model for experiments, and standardize the tensor decomposition time and tensor size to facilitate a comparison. The tensor model is divided into four parts. Under the same hardware conditions, the size and time of each method are calculated respectively. Comparing the efficiency of the decomposition algorithm of icHOSVD and traditional HOSVD, our experimental results are shown in Figure 7.
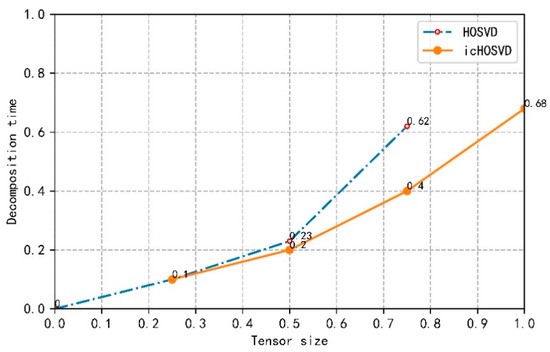
Figure 7.
Comparison between traditional dimensionality reduction methods and icHOSVD.
Figure 7 shows the performance comparison between the method based on icHOSVD and the traditional HOSVD method. In Figure 7, for HOSVD, there is a steep rise in the curve from the normalized tensor value of 0.75, which has greatly exceeded icHOSVD in time. In the icHOSVD method, the rise of time is relatively gentle. Because the HOSVD decomposition method can only reach the standard value of 0.75, there will be memory overflow, so the curve of HOSVD will be cut off to 0.75. In terms of decomposition time, icHOSVD decomposes a tensor of the same size, which takes less time than the traditional HOSVD decomposes. In terms of throughput, icHOSVD can process more data under the same hardware conditions.
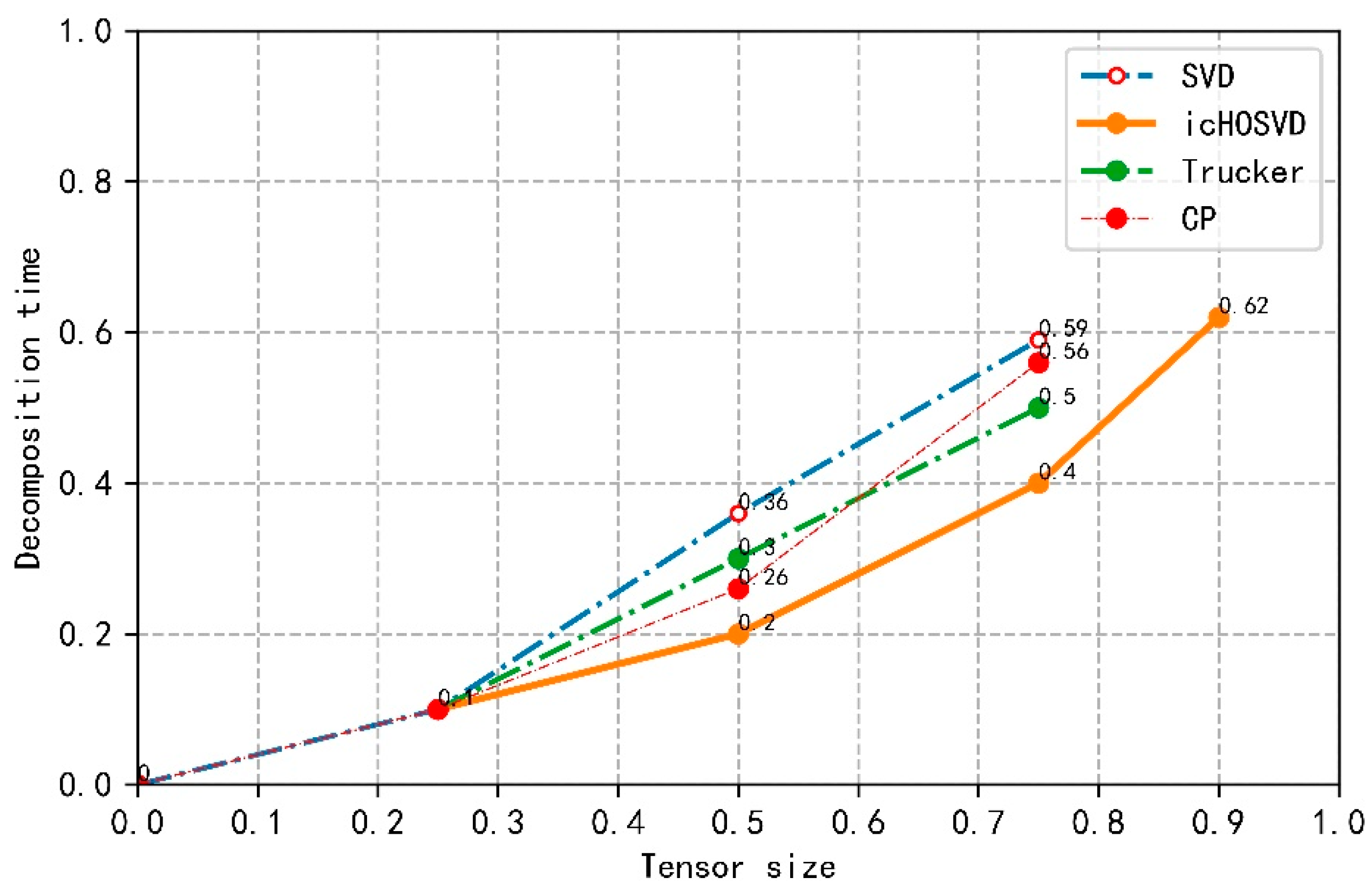
In Figure 8, we select several other common dimensionality reduction decomposition algorithms, namely SVD, trucker, CP decomposition algorithm, and use the same tensor model for experiments. Under the same conditions, we compare the time taken by each method to process the tensor size. As can be seen from Figure 8, the decomposition time of icHOSVD is relatively stable from the tensor size 0.25, but the decomposition time of traditional decomposition method and other decomposition methods increase rapidly. Under the same conditions, icHOSVD can decompose a larger tensor, whereas traditional SVD and Trucker and CP decomposition methods can only decompose half of the size of a tensor. Currently, the popular HOSVD decomposition method can only reach the tensor size 0.75, and then run out of memory. Through the above experimental analysis, the icHOSVD decomposition method based on tensor segmentation is more efficient.
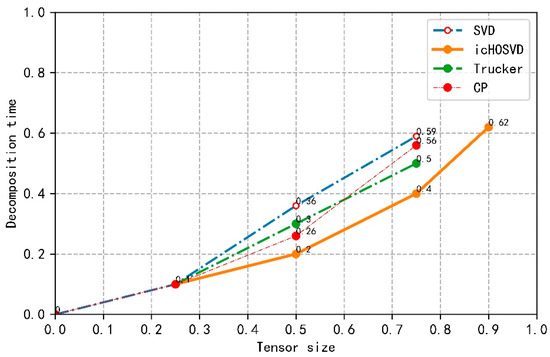
Figure 8.
Comparison of icHOSVD with SVD, Trucker decomposition and CP decomposition algorithms.
5. Summary and Outlook
With the rapid development of information technology, the data scale is growing exponentially, and the value of big data is getting more and more attention. In view of the complex campus heterogeneous big data types, and in the process of obtaining the core tensor, a large number of intermediate computation results will be generated between the original data and the newly added data, which will affect the performance of the algorithm. This paper proposes a dimensionality reduction algorithm based on icHOSVD for unstructured campus big data. Firstly, the video data, audio data, image data and text data in unstructured campus big data are represented as sub tensor models, and the semi tensor product is used to fuse the sub tensor models. Finally, the proposed dimensionality reduction algorithm icHOSVD is applied to the unified tensor for dimensionality reduction. Experiments show that the dimensionality reduction method is more efficient than the traditional dimensionality reduction method, which first divides the tensor into blocks, and then merges the new tensor and the original tensor, and achieves a higher dimensionality reduction effect while maintaining a lower error rate. In this paper, the representation method of heterogeneous data fusion and the icHOSVD dimension reduction algorithm are proposed to solve the problem of a huge data scale after fusion, which broadens the research field and the depth of heterogeneous data fusion and tensor dimension reduction.
The current model can fuse different types of unstructured data and reduce the dimension. After dimensionality reduction, it can improve the accuracy and time complexity of machine-learning algorithms such as dataset classification accuracy, computational efficiency, classification and clustering, and provide a theoretical basis for the subsequent analysis and mining of campus big data and student portraits. However, how to connect the data of various departments and analyze student data mining needs to be further studied. In addition, we also need a set of classification, clustering, prediction, anomaly detection and other methods suitable for tensor models. Through the continuous innovation and development of big data technology, students’ work and management are optimized, so that people can make full use of data resources and tap the value of data, and provide strong support for the development of intelligent management of campus students. At the same time, for different data sources, our proposed dimensionality reduction algorithm can also be applied to different data sources, and the application effect is not the same. Therefore, the tensor model needs to be improved and unified in research.
Author Contributions
Conceptualization, Z.W. and Y.W.; methodology, Z.W.; software, L.Z.; validation, Z.W., Y.W. and L.Z.; formal analysis, Y.W.; investigation, C.Z.; resources, X.Z.; data curation, L.Z.; writing, original draft preparation, Z.W.; writing, review and editing, L.Z.; visualization, Y.W.; supervision, L.Z.; project administration, X.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Key R&D Program of China (2018YFC0824401) and the National Natural Science Foundation of China (61872324).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article due to privacy.
Acknowledgments
This work was supported by the National Key Research and Development Program (2018YFC0824401) and the National Natural Science Foundation of China(61872324). The authors would like to thank the anonymous reviewers for their valuable suggestions and constructive criticism.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abdel-Basset, M.; Mohamed, M.; Smarandache, F.; Chang, V. Neutrosophic Association Rule Mining Algorithm for Big Data Analysis. Symmetry 2018, 10, 106. [Google Scholar] [CrossRef]
- Liu, K.; Ni, Y.; Li, Z.; Duan, B. Data Mining and Feature Analysis of College Students’ Campus Network Behavior. In Proceedings of the 2020 5th IEEE International Conference on Big Data Analytics (ICBDA), Xiamen, China, 6–9 March 2020; pp. 231–237. [Google Scholar] [CrossRef]
- Liu, W. Campus Management Strategy Research under the Environment of Big Data. In Proceedings of the 2016 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Changsha, China, 17–18 December 2016; pp. 195–199. [Google Scholar] [CrossRef]
- Ranjan, R.; Wang, L.; Zomaya, A.Y.; Tao, J.; Jayaraman, P.P.; Georgakopoulos, D. Advances in Methods and Techniques for Processing Streaming Big Data in Datacentre Clouds. IEEE Trans. Emerg. Top. Comput. 2016, 4, 262–265. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, L.; Ranjan, R.; Choo, K.-K.R.; He, J. Geographical information system parallelization for spatial big data processing: A review. Clust. Comput. 2015, 19, 139–152. [Google Scholar] [CrossRef]
- Luo, E.; Hu, Z.; Lin, H. Big data era development model research of huge amounts of data extraction. Appl. Res. Comput. 2013, 30, 3269–3275. [Google Scholar]
- Li, W.; Lang, B. A tetrahedron data model of unstructured database. SSI 2010, 40, 1039–1053. [Google Scholar]
- Lang, B.; Zhang, B. Key Techniques for Building Big-Data-Oriented Unstructured Data Management Platform. Inf. Technol. Stand. 2013, 10, 53–56. [Google Scholar]
- Han, J.; E, H.-H.; Song, M.N.; Song, J.D. Model for unstructured data based on subject behavior. Comput. Eng. Des. 2013, 34, 904–908. [Google Scholar]
- Kuang, L.; Hao, F.; Yang, L.T.; Lin, M.; Luo, C.; Min, G. A Tensor-Based Approach for Big Data Representation and Dimensionality Reduction. IEEE Trans. Emerg. Top. Comput. 2014, 2, 280–291. [Google Scholar] [CrossRef]
- Kuang, L.; Yang, L.T.; Liao, Y. An Integration Framework on Cloud for Cyber-Physical-Social Systems Big Data. IEEE Trans. Cloud Comput. 2015, 8, 363–374. [Google Scholar] [CrossRef]
- Sharma, N.; Saroha, K. Study of dimension reduction methodologies in data mining. In Proceedings of the International Conference on Computing, Communication & Automation, New Delhi, India, 15–16 May 2015; pp. 133–137. [Google Scholar]
- Li, Y.; Chai, Y.; Zhou, H.; Yin, H. A novel dimension reduction and dictionary learning framework for high-dimensional data classification. Pattern Recognit. 2021, 112, 107793. [Google Scholar] [CrossRef]
- He, J.; Ding, L.; Li, Z.; Hu, Q. Margin Discriminant Projection for Dimensionality Reduction. J. Softw. 2014, 25, 826–838. [Google Scholar] [CrossRef]
- Xiao, J.; Gao, W.; Peng, H.; Tang, L.; Yi, B. Detail Enhancement for Image Super-Resolution Algorithm Based on SVD and Local Self-Similarity. Chin. J. Comput. 2016, 39, 1393–1406. [Google Scholar]
- Zhan, C.; Wang, D.; Shen, C.; Cheng, H.; Chen, L.; Wei, S. Separable Compressive Image Method Based on Singular Value Decomposition. J. Comput. Res. Dev. 2016, 53, 2816–2823. [Google Scholar]
- Cuomo, S.; Galletti, A.; Marcellino, L.; Navarra, G.; Toraldo, G. On GPU–CUDA as preprocessing of fuzzy-rough data reduction by means of singular value decomposition. Soft Comput. 2018, 22, 1525–1532. [Google Scholar] [CrossRef]
- Pan, Y.; Hamdi, M. Computation of singular value decomposition on arrays with pipelined optical buses. J. Netw. Comput. Appl. 1996, 19, 235–248. [Google Scholar] [CrossRef][Green Version]
- García-Magariño, A.; Sor, S.; Velazquez, A. Data reduction method for droplet deformation experiments based on High Order Singular Value Decomposition. Exp. Therm. Fluid Sci. 2016, 79, 13–24. [Google Scholar] [CrossRef]
- Naskovska, K.; Haardt, M.; Tichavsky, P.; Chabriel, G.; Barreré, J. Extension of the semi-algebraic framework for approximate CP decompositions via non-symmetric simultaneous matrix diagonalization. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2971–2975. [Google Scholar]
- Ding, H.; Chen, K.; Yuan, Y.; Cai, M.; Sun, L.; Liang, S.; Huo, Q. A Compact CNN-DBLSTM Based Character Model for Offline Handwriting Recognition with Tucker Decomposition. In Proceedings of the 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), Kyoto, Japan, 9–15 November 2017; IEEE: Piscataway, NJ, USA, 2017; Volume 1, pp. 507–512. [Google Scholar]
- Wang, D.; Wang, H.; Zou, X. Identifying key nodes in multilayer networks based on tensor decomposition. Chaos 2017, 27, 063108. [Google Scholar] [CrossRef]
- Mohanmad, J.; Mauro Dalla, M.; Pierre, C. Hyperspectral Image Classification Using Tensor CP Decomposition. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 5328–5331. [Google Scholar]
- Liu, J.; Xu, H.; Tang, H.; Jia, Y.; Cheng, X. Model and Construction Method on Dynamic Knowledge Network in Big Data. J. Comput. Res. Dev. 2014, 51 (Suppl. 2), 86–93. [Google Scholar]
- Mao, G.; Hu, D.; Xie, S. Models and Algorithms for Classfying Bid Data Based on Distributed Data Streams. Chin. J. Comput. 2017, 40, 161–175. [Google Scholar]
- Sarasquete, N.C. A common data representation model for customer behavior tracking. Icono 2017, 15, 55–91. [Google Scholar]
- Chen, X.; Huang, L.; Tao, G. Big data representation method of power system based on random matrix theory. Hongshui River 2017, 36, 35–38. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).