1. Introduction
The logit model is a model that is often used for modeling categorical data in various research fields. Several studies have recently developed logit models for multiple correlated responses. McCullagh and Nelder [
1] introduced a multivariate logistic transform used to construct logit models with two or more correlated responses. A multivariate logistic transform, including the numerical optimization methods, has been proposed in [
2,
3,
4,
5,
6]. Lipsitz, Laird, and Harrington [
7] examined the maximum likelihood (ML) method for binary data models, which connects the probability of success at each time point to a set of covariates. Liang, Zeger, and Qaqish [
8] discussed the regression modeling of the marginal means of the responses using the generalized estimating equation approach, wherein there are dependencies between responses. An alternating logit model for jointly regressing the responses on covariates and modeling the dependencies among responses in the framework of pairwise odds ratios was proposed by [
9]. Cessie and Houwelingen [
10] modeled regression for correlated binary responses, in which the form of marginal response probabilities is the logit link function. Lang and Agresti [
11] considered the model-fitting methods for analyzing the parameters simultaneously and parsimoniously. The ML estimator properties of the kappa coefficient in the bivariate binary logistic model using the small and moderate sized samples through Monte Carlo simulation were investigated by [
12,
13]. Molenberghs and Lesaffre [
14] presented a simple generalized linear model formulation for marginal and association modeling of multivariate categorical data. The specifications of the association models in [
15], in which the dependence ratios contrast with other models for a multivariate binary response that is specified by odds ratios or correlation coefficients, were employed by [
16].
Studies have also proposed both the conditional and marginal models. A flexible conditional model for a multivariate binary response vector with covariates was examined by [
17]. Islam, Chowdhury, and Briollais [
18] developed a new simple procedure to construct the conditional and marginal models for the bivariate binary responses. The marginal and conditional probabilities of the responses were expressed as functions of covariates. El-Sayed, Islam, and Alzaid [
19] provided the estimation and test procedures for association measures in the correlated binary data. A generalized approach using both the conditional and marginal models was demonstrated by [
20,
21]. The responses of the model have a bivariate Bernoulli distribution. The ML and Newton–Raphson methods were used to estimate the model’s parameters, whereas the likelihood ratio test method was used to test the parameters’ significance. The properties of the ML estimators of the regression parameters have also been investigated.
Other models have also been developed. Sinha, Laird, and Fitzmaurice [
22] extended the univariate logit model in [
23] to the case of a logit model for multivariate-correlated responses with missing covariates and observed auxiliary information. A robust model for misclassified correlated binary responses was described by [
24]. O’Brien and Dunson [
25] provided an exact Bayesian analysis of a marginal logistic model. The multivariate logistic regression model in a framework of the geographically-weighted regression was proposed by [
26,
27].
Corresponding to the previous studies, in this study we constructed a logit model, namely, the bivariate binary logit (BBL) model, which has two correlated binary responses. Following [
1,
2], the BBL model’s responses follow a multinomial distribution. Therefore, the ML method can be used to estimate the BBL model’s parameters. The ML estimator is not closed-form, and it needs an iterative procedure using a numerical optimization method. We used the Berndt–Hall–Hall–Hausman (BHHH) iterative method [
28]. However, the BHHH method has not been used in previous studies. On the other hand, the BHHH method can be used as an alternative to the numerical optimization method when the elements of the Hessian matrix are unavailable. Following [
29], the maximum likelihood ratio test (MLRT) method was used to test the significance of parameters both simultaneously and partially. The performance of the BBL model was evaluated using an empirical study.
This article is organized as follows. In
Section 2, we describe the BBL model specifically.
Section 3 investigates the estimation of the BBL model’s parameters using the ML and BHHH methods. Hypothesis testing of the BBL model is discussed in
Section 4.
Section 5 demonstrates an application of the BBL model to real data. The conclusions are given in
Section 6.
2. Bivariate Binary Logit Model
Bivariate binary logit (BBL) models are one of the families of multivariate logit models and are used to model the relationships between two correlated binary responses with one or more covariates. Let
and
be two bivariate binary responses and
be a vector of responses. The elements of
have the probabilities of
,
,
, and
, respectively, which are presented in
Table 1.
According to Fathurahman, Purhadi, Sutikno, and Ratnasari [
27], the BBL model responses in
Table 1 follow a multinomial distribution. Therefore, the joint probability function of the responses can be defined as follows:
where
;
;
;
; and
.
and
are the values of the responses.
is the value of
, which represents the elements of the vector of responses.
is the joint probability of the responses.
and
are the marginal probabilities of
and
, respectively.
Let
be the vector of covariates, which is
-dimensional. Then the BBL model is expressed as follows:
where
,
, and
are vectors of parameters,
and
are marginal probabilities of responses, and
is the odds ratio of responses depending on covariates, which shows that the responses are correlated.
The vectors of parameters are symbolized by
The marginal probabilities of responses are defined as follows:
The joint probability of
in Equation (2) is defined by
where
and
If
, then the responses are independent [
30].
Based on
Table 1 and Equation (5), the probabilities of
,
, and
in Equation (2) are as follows:
3. Estimation of the BBL Model
The estimation of the BBL model’s parameters is one of the main results of this study. The BBL model in Equation (2) has
parameters, where
parameters show the dependencies among responses, and
parameters describe the relationships between responses and covariates. The BBL model’s parameters are denoted by
and expressed as
where
,
, and
are given by Equation (3).
To obtain the parameters estimator of the BBL model in Equation (7), the ML method was employed. Based on the ML method, the estimator of is the value of , maximized by the likelihood function and the log-likelihood function. The ML estimator can be obtained by determining the first partial derivatives of the log-likelihood function, then equating them to zero.
Based on Equation (2), the likelihood equation contains the interdependence equations, which have a non-explicit form. Therefore, the ML estimator of the BBL model’s parameters was not obtained analytically. The ML estimator was approximated by the likelihood equation’s roots, which were obtained via an iterative process using the BHHH method. Determining the ML estimator of the BBL model’s parameters using the BHHH method needs the gradient vector and the Hessian matrix. In the following, we present Lemmas 1 and 2 for the gradient vector and Hessian matrix, respectively.
Lemma 1. Let be a random vector sample that is mutually independent and identical with a multinomial distribution denoted by, where,,, andare probabilities of the random variables of,,, andthat contain the parameter. If the likelihood function of the BBL model is denoted by, whereis as in Equation (7), then the gradient vector is
where
Proof of Lemma 1. Suppose that
is a vector of the random sample that is independently and identically multinomial distributed; then the joint probability is defined by
As in Equation (9), the likelihood function is as follows:
For simplicity, let
for
; then the likelihood function in Equation (10) can be rewritten as
To obtain the log-likelihood function of the BBL model, both sides of the likelihood function in Equation (11) were transformed by the natural logarithm, which gives
The log-likelihood function in Equation (12) is that the vector of
has
dimensions. Following the definition in Greene [
31], the gradient vector of the log-likelihood function in Equation (12) is
where the vector of
is given by Equation (7).
Regarding the BBL model in Equation (2), we define the vector of
, which is denoted by
, where
,
, and
. The vector of the joint probability of
is defined by
. Furthermore, the derivative of
with respect to
is denoted by
. To get a symmetrical matrix of
, suppose
with
; then the vector of
is
. Thus, the matrix of
is
The inverse matrix of
in Equation (14) is as follows:
where
and
The gradient vector of the log-likelihood function in Equation (12) can be written as
In relation to Equations (13)–(15) and the chain rule of derivatives, the elements of the gradient vector in Equation (16) can be obtained as follows:
where
and
, for
, given in Equation (15). □
Lemma 2. If the log-likelihood function of the BBL model is and the vector ofis the BBL model’s parameters, then the Hessian matrix of is
where is the sample size. Proof of Lemma 2. The BBL model’s parameters
and the log-likelihood function
were given in Equations (7) and (12), respectively. Based on Lemma 1, the gradient vector of the log-likelihood function
is
. According to Greene [
31], the Hessian matrix can be obtained by the Berndt–Hall–Hall–Hausman (BHHH) method. On the other hand, the Hessian matrix depends on the gradient vector [
31], which is shown below:
Meanwhile, the gradient vector and the Hessian matrix associated with the information matrix and can be expressed by
The information matrix in Equation (22) is also referred to as the Fisher information matrix [
32]. Based on Equations (21) and (22), the Hessian matrix is
Regarding Lemmas 1 and 2, an iteration process can be carried out using the BHHH method. Following [
33], the BHHH algorithm in this study is as follows:
Determine the initial value for .
Determine the tolerance value for the BHHH iteration process stopping.
Start the BHHH iteration process using the formula:
The iteration stops at the -th iteration if the condition of convergence is satisfied, which is . The estimator values of the parameters are obtained in the last iteration.
Akaike’s information criterion (AIC) and the Bayesian information criterion (BIC) determine the best model in this study. The AIC and BIC values can be obtained by
where
is the log-likelihood value of the parameter’s estimate,
is the number of covariates, and
is the sample size. The best model is the BBL model, which has the smallest values of AIC and BIC. □
5. Application
The BBL model was applied to model the factors influencing the status of the human development index (HDI) and public health development index (PHDI) of regencies/municipalities in Kalimantan, Indonesia, in 2018. The HDI is an index measured from four components of the essential dimensions of human development: life expectancy, the average length of schooling, expected length of schooling, and adjusted per-capita income. Life expectancy represents an indicator of health, the average length of schooling and the expected length of schooling represent educational indicators, and adjusted per capita income represents an economic indicator [
34]. The PHDI is an index that measures the health of the regencies/municipalities and provinces in the Republic of Indonesia [
35].
The HDI status data and covariates’ data were collected from the National Bureau of Statistics of the Republic of Indonesia, whereas the PHDI data were collected from the Republic of Indonesia’s Ministry of Health. The variables in this study consist of two responses and five covariates. The responses are the HDI status and the PHDI status of regencies/municipalities, denoted by
and
. The covariates are the economic growth (
), the net enrollment rate of the junior high school (
), the percentage of people that have the minimum level of education in junior high school (
), the number of doctors per 1000 people (
), and the number of public health centers (
). The regencies and municipalities’ HDI status has four categories: low HDI, medium HDI, high HDI, and very high HDI [
34]. Regencies/municipalities in Kalimantan, Indonesia, in 2018, had HDI in the medium and high categories. Therefore, the HDI status (
) has two categories: the medium HDI coded by 0 and the high HDI coded by 1.
Meanwhile, the Ministry of Health of the Republic of Indonesia classifies regencies/municipalities’ health status based on the PHDI into two categories. Regencies/municipalities with a low PHDI have health problems, and vice versa [
36]. Therefore, the PHDI status (
) has two categories: the regencies/municipalities with low PHDI values are coded by 0, and the regencies/municipalities with high PHDI values are coded by 1. This study’s observation unit is the regency/municipality. Five provinces in Kalimantan, Indonesia were used (2018 data), including 47 regencies and nine municipalities. Therefore, the sample size is 56.
The descriptive statistics of the responses HDI status (
) and PHDI status (
), consisting of observed frequencies, are presented in
Table 2.
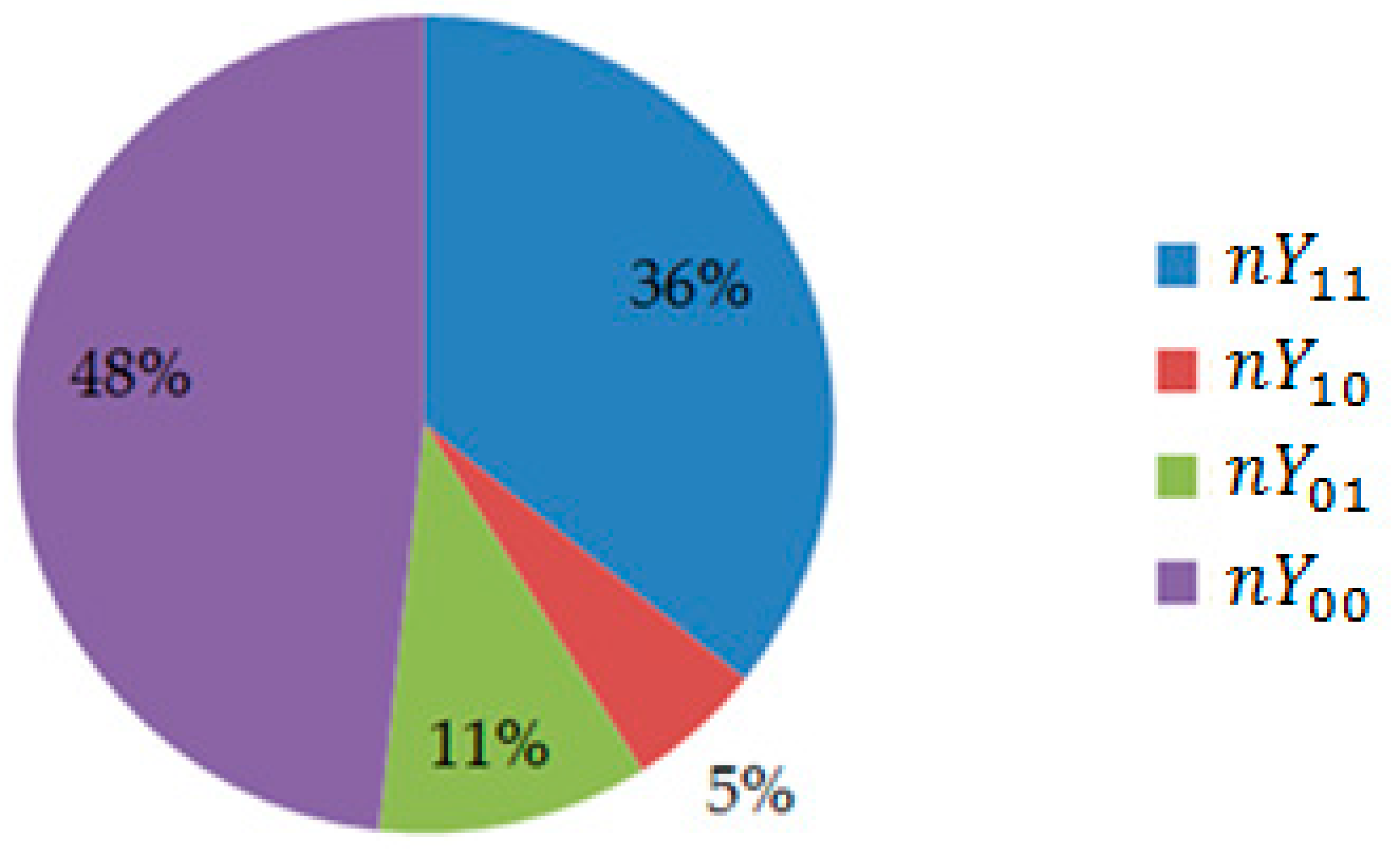
Table 2 shows that 20 regencies/municipalities had high HDI and PHDI, and six regencies/municipalities had high HDI and low PHDI. We also see that three regencies/municipalities had medium HDI and high PHDI. Finally, 27 regencies/municipalities had medium HDI and low PHDI. The HDI status (
) and PHDI status (
) of regencies/municipalities are displayed in
Figure 1.
The descriptive statistics of the responses show that the majority of regencies/municipalities in Kalimantan, Indonesia, in 2018, had medium HDI and low PHDI. The descriptive statistics of the covariates are summarized in
Table 3.
The HDI status (
) and PHDI status (
) are correlated. Based on the observed frequencies in
Table 2, the odds ratio (OR) value of HDI status (
) and PHDI status (
) was 30 with a 95% confidence interval of 6.6826 ≤ OR ≤ 134.6783. This result indicates that the responses are highly positively correlated. Meanwhile, we also employed the dependence test of the responses HDI status (
) and PHDI status (
), provided in
Table 4.
Three statistical tests demonstrated a dependence test of HDI status (
) and PHDI status (
). The result in
Table 4 shows that all of the statistical test values had greater than the chi-square table value (i.e.,
) and
p-values less than the significance level value (i.e.,
α = 0.05). Therefore, the conclusion was to reject the null hypothesis (
), and the HDI status (
) and PHDI status (
) are dependencies. Based on the OR value and the dependence test, the HDI status (
) and PHDI status (
) are appropriate for the BBL model.
The variance inflation factor detected the multicollinearity of the covariates. The variance inflation factor values of all covariates in
Table 5 are less than ten, which indicates that the covariates are independent of each other (i.e., no multicollinearity). Therefore, all covariates can be used in the BBL model.
The estimation of the BBL model’s parameters using the ML and BHHH methods was employed.
Table 6 provides the bias values and the numbers of BHHH iterations of the parameter estimation process for the BBL model with the single and multiple covariates.
The BBL model with the single covariate of economic growth (
) and public health centers (
) in
Table 6 was not convergent. Therefore, both covariates, economic growth (
) and public health centers (
), were not used in the BBL model. Based on
Table 6, the BBL model for modeling the factors that affect the HDI status and PHDI status of regencies/municipalities in Kalimantan, Indonesia, in 2018 was obtained.
Table 7 displays the ML estimates of the BBL model with multiple covariates (i.e.,
,
,
), giving the parameter estimates, the LR statistic of the simultaneous test (
), the degrees of freedom (df), and the
p-value.
The LR statistic value in
Table 7 is 99.739, and the
p-value is 1.7685 × 10
−21 (
p < 0.001). Meanwhile, the chi-square table’s value with nine degrees of freedom and a 5% significance level was 16.919. The LR statistic value is greater than the chi-square table’s value, and the
p-value is less than the 5% significance level. Therefore, the null hypothesis was rejected, and we conclude that the net enrollment rate of the junior high school, the percentage of people that have the minimum level of education in junior high school, and the number of doctors per 1000 people were jointly significantly affecting the HDI status and the PHDI status of regencies/municipalities in Kalimantan, Indonesia, in 2018. The BBL model for the HDI status and the PHDI status of regencies/municipalities can be written as follows:
The partial test using the MLRT method was used to obtain the covariates that individually affect the HDI status and the PHDI status of regencies/municipalities.
Table 8 describes the BBL model with the single covariate, which covers the parameter estimates, the LR statistic value (
), the degrees of freedom (df), and the
p-value.
The LR statistic’s value of the estimated parameter for each covariate (the net enrollment rate of the junior high school, the percentage of people that have the minimum level of education in junior high school, and the number of doctors per 1000 people;
Table 8) was greater than the chi-square table’s value; the chi-square table’s value with three degrees of freedom and 5% significance level was 7.8147. Meanwhile, the
p-value of each covariate was less than the 5% significance level. Therefore, we concluded that the net enrollment rate of the junior high school, the percentage of people that have the minimum level of education in junior high school, and the number of doctors per 1000 people individually significantly influenced the HDI status and the PHDI status of regencies/municipalities in Kalimantan, Indonesia, in 2018.
The BBL model with a single covariate (e.g.,
) for the HDI status and the PHDI status of regencies/municipalities can be expressed as follows:
The AIC and BIC methods in Equations (25) and (26) were used for the evaluation of the BBL model’s performance. The AIC and BIC values of the BBL models are shown in
Table 9.
The BBL model with the single covariate in
Table 9 has the smallest AIC and BIC values compared to the BBL model with the multiple covariates. Therefore, the BBL model with the single covariate is the best model for modeling the relationships between the responses (i.e., the HDI status and the PHDI status) and the covariates (i.e., the net enrollment rate of the junior high school, the percentage of people that have the minimum level of education in junior high school, and the number of doctors per 1000 people) of regencies/municipalities in Kalimantan, Indonesia, in 2018. Furthermore, the net enrollment rate of the junior high school, the percentage of people that have the minimum level of education in junior high school, and the number of doctors per 1000 people individually significantly affected the HDI status and the PHDI status of regencies/municipalities in Kalimantan, Indonesia, in 2018.
However, some recommendations and future research from this work are possible. Firstly, the logit models in this research are limited to two responses. The BBL model, with more than two responses, should be considered for future research. Secondly, other numerical optimization methods that improve the performance of the BBL model should also be considered for future research.