Finite-Size Effects with Boundary Conditions on Bose-Einstein Condensation
Abstract
1. Introduction
2. The Ideal Bose Gases in the Cubic Box
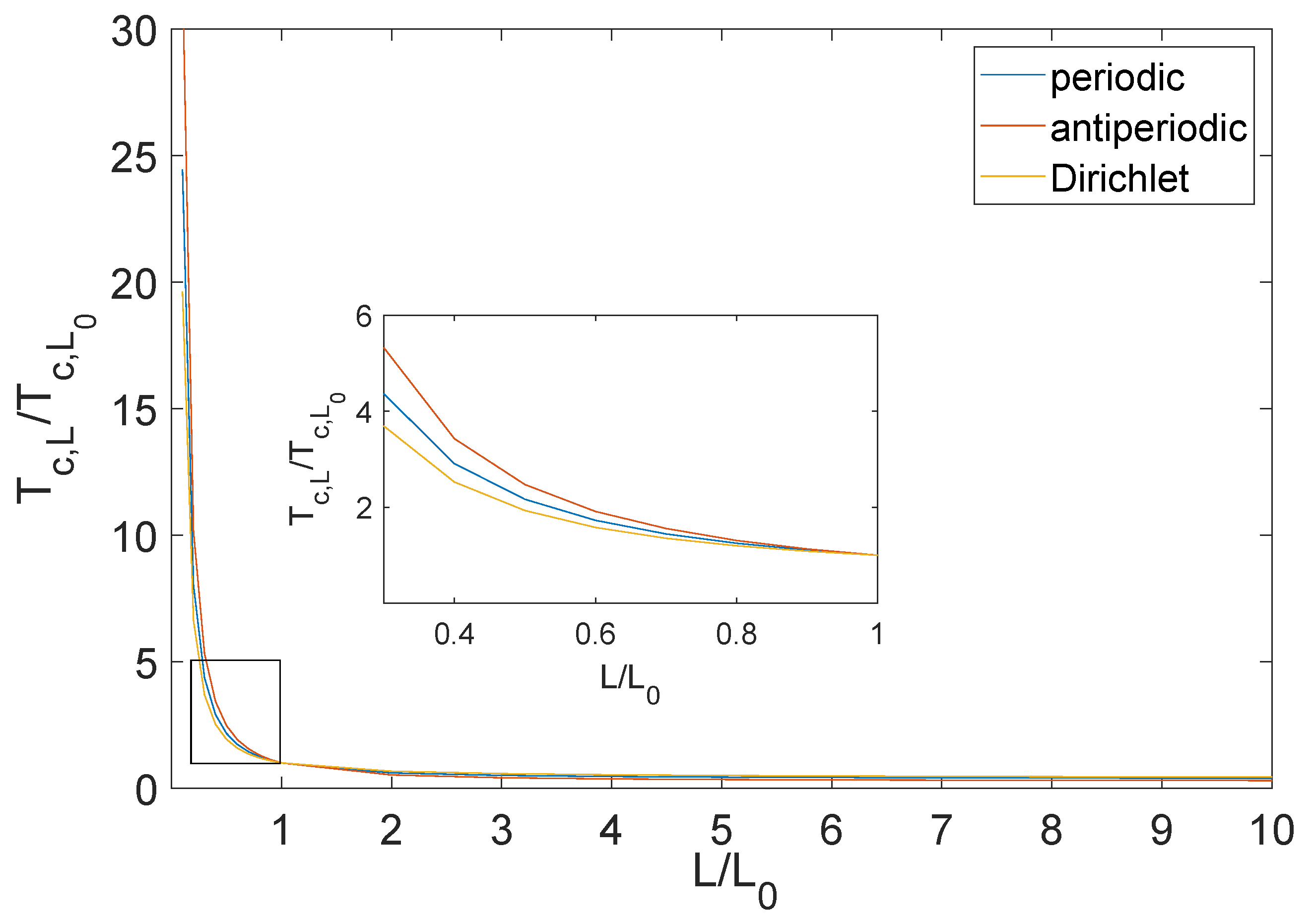
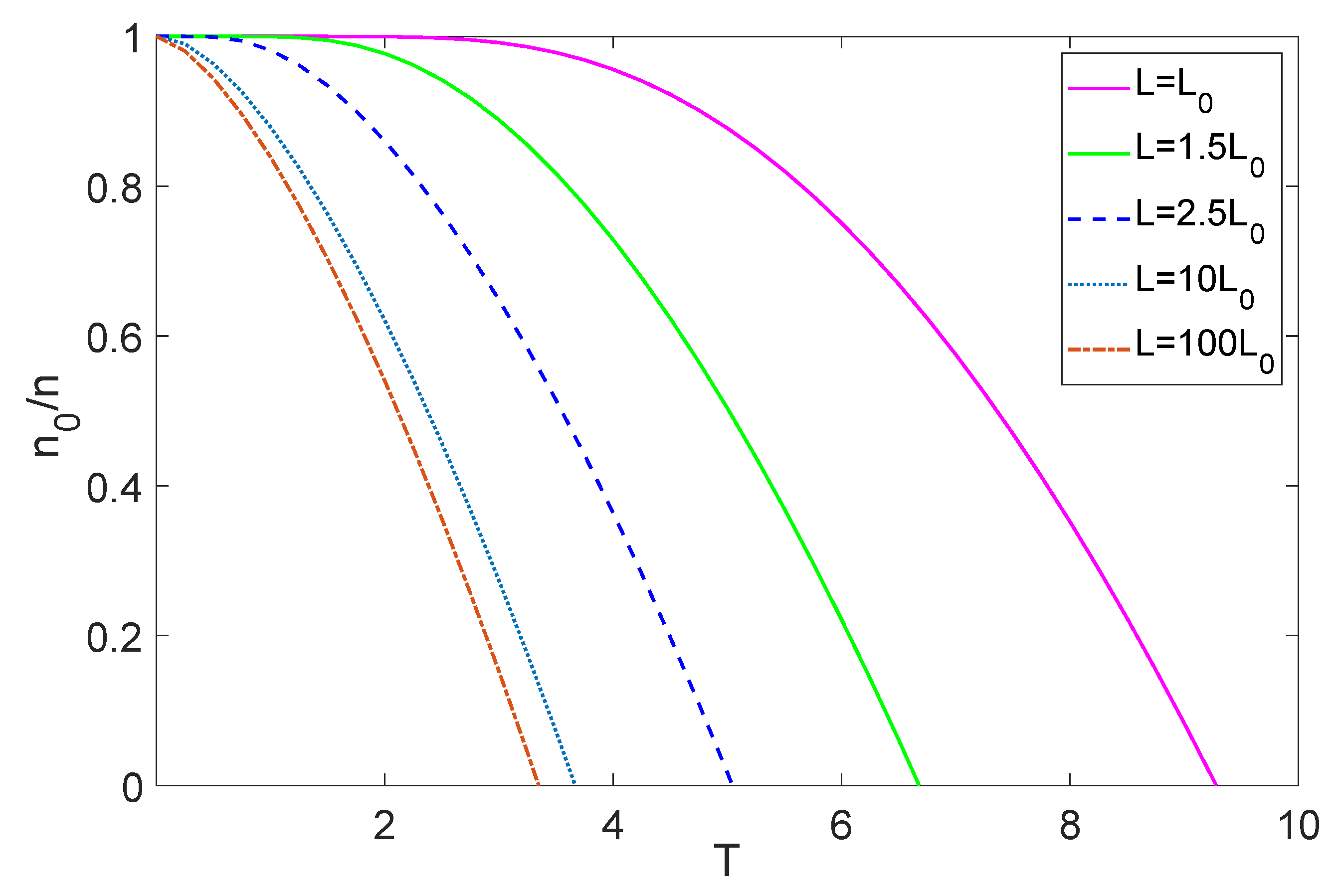
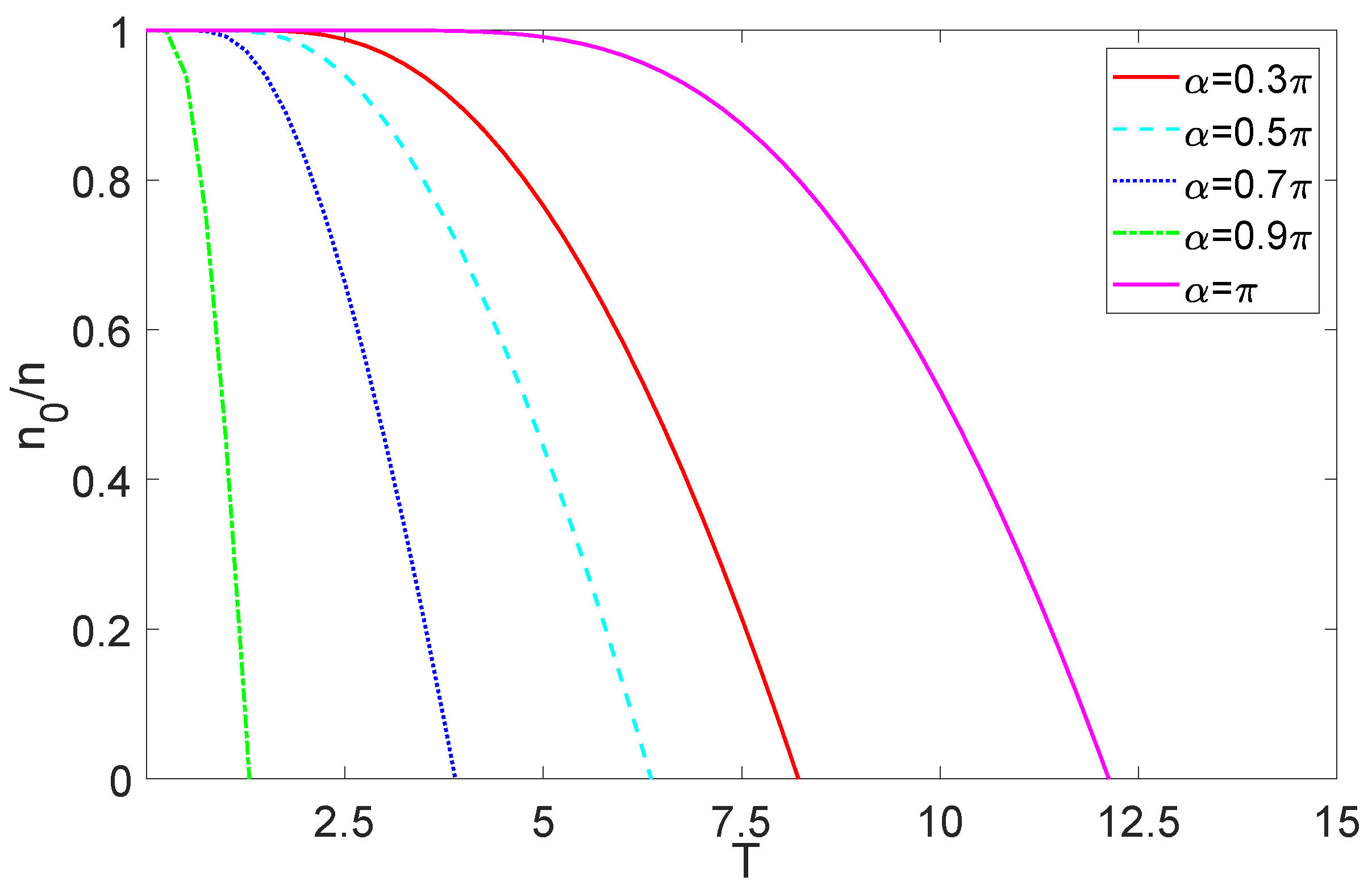
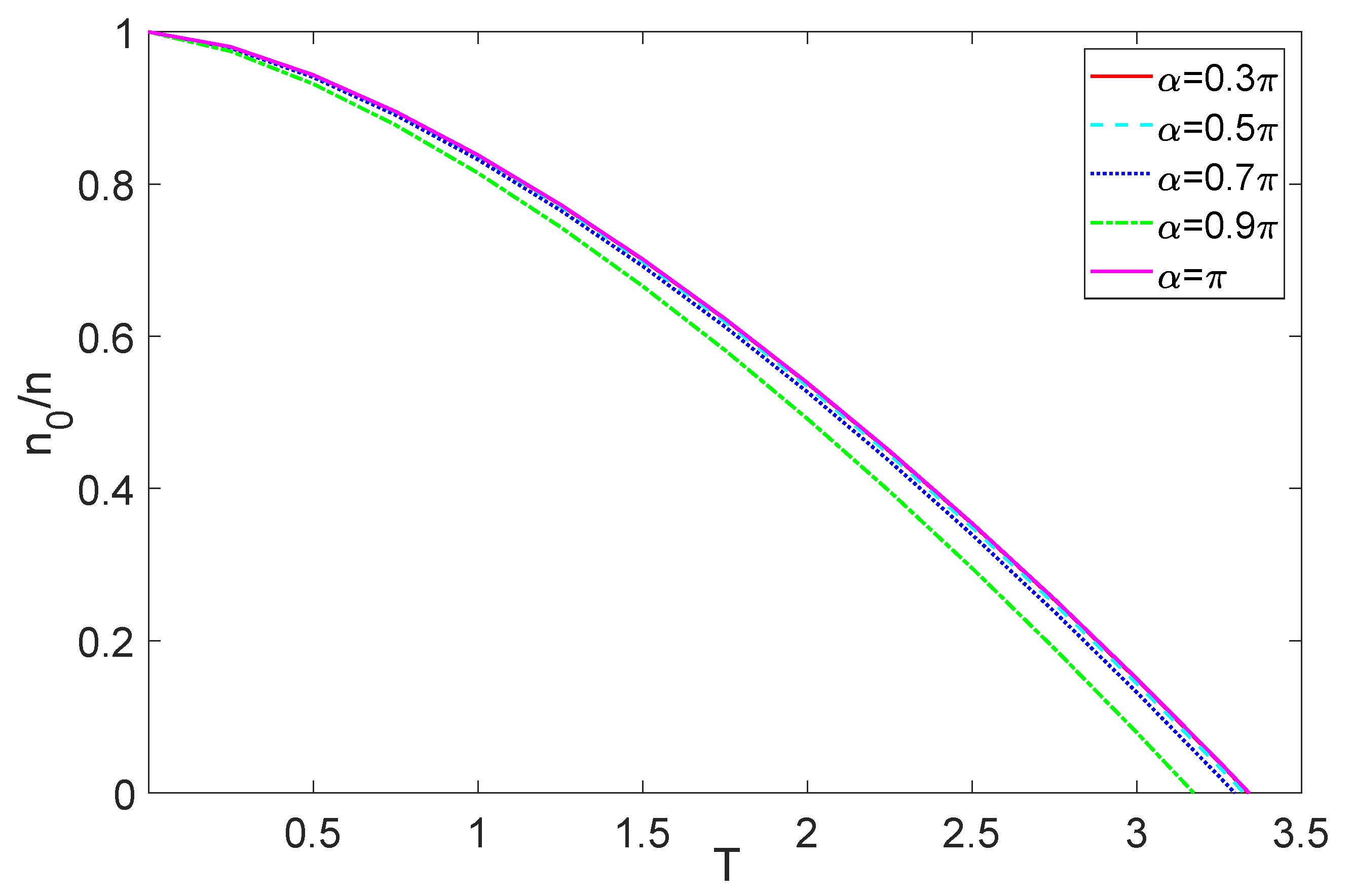
3. Finite-Size Effects on Bose–Einstein Condensation in the Cubic Box
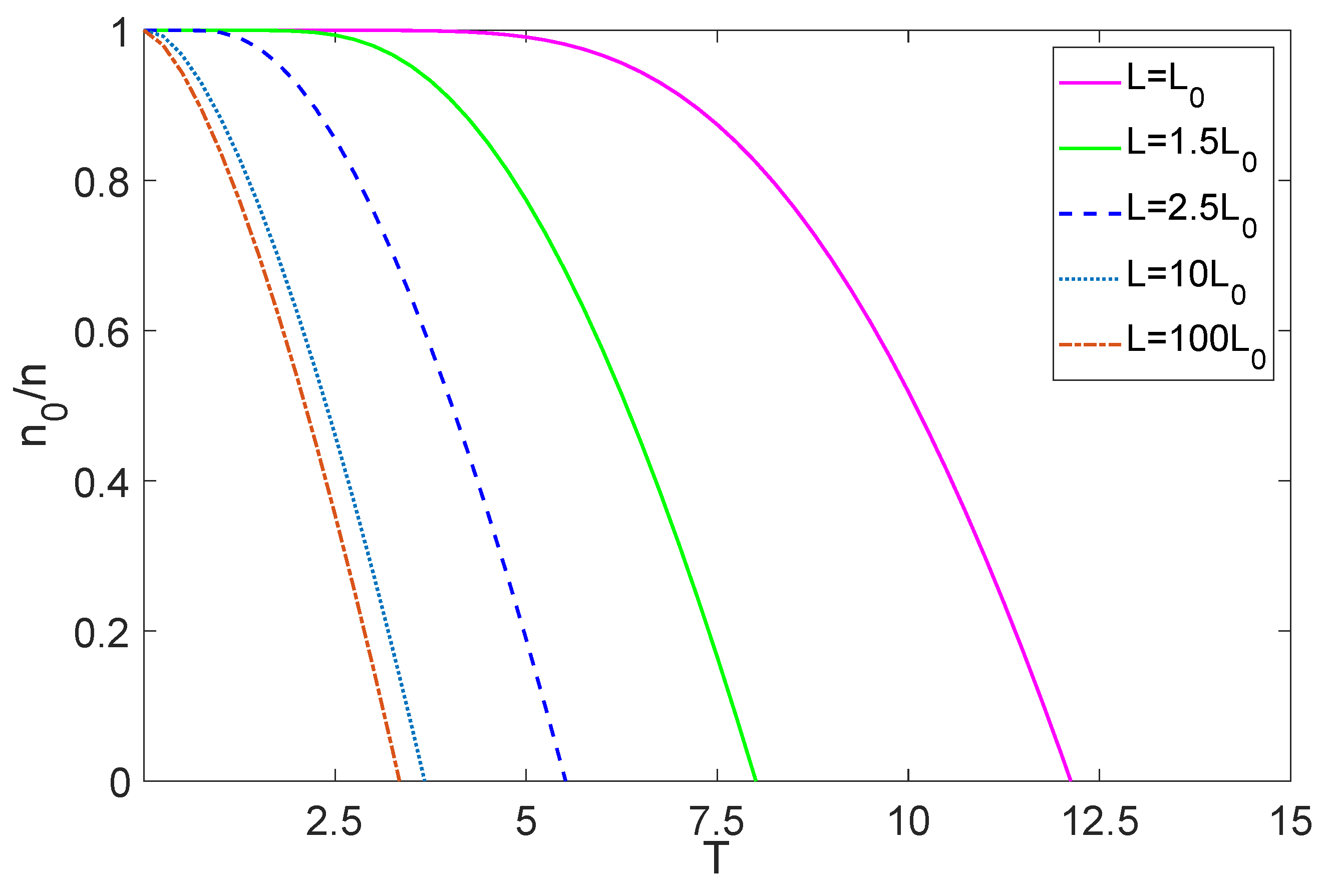
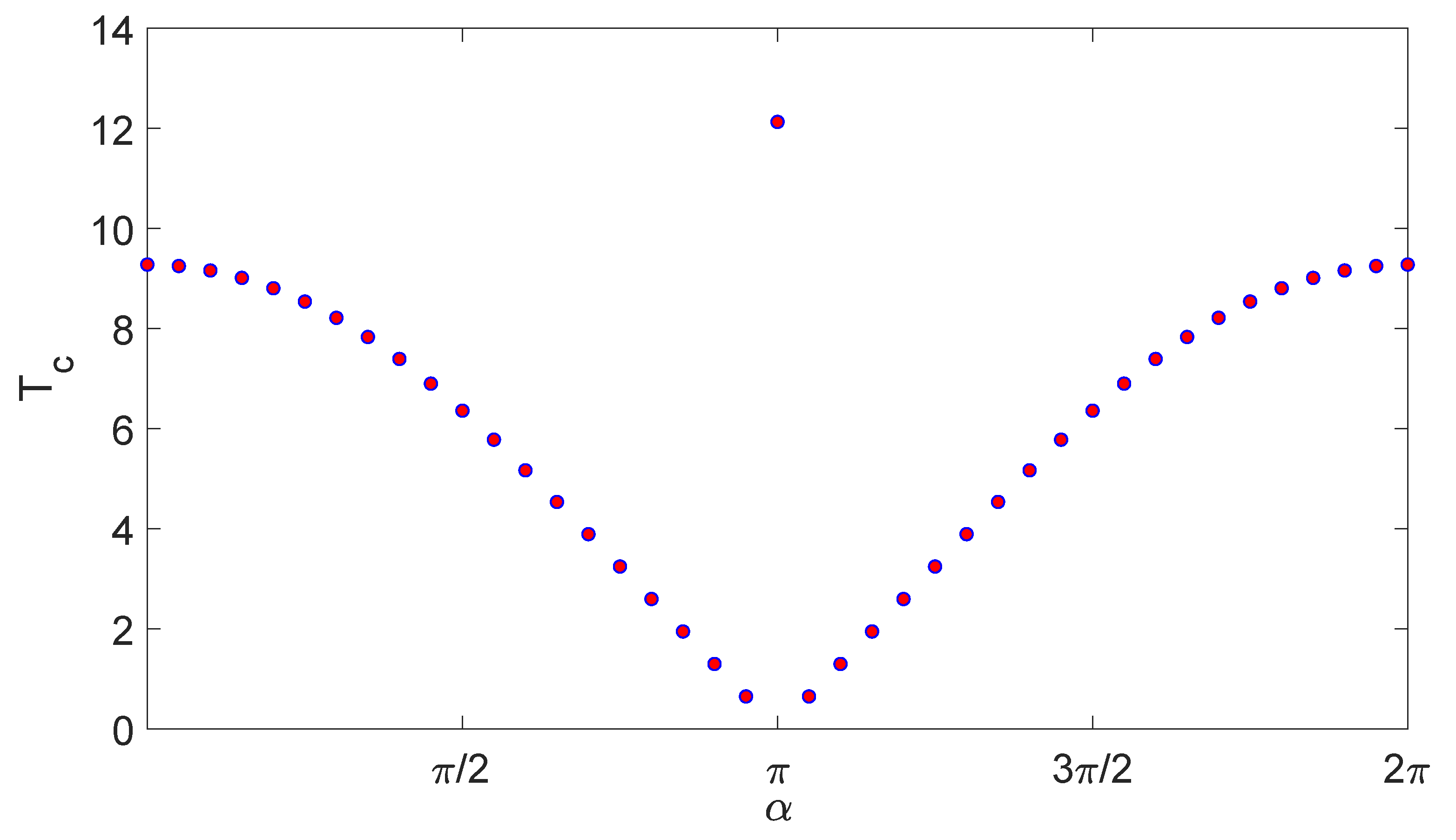
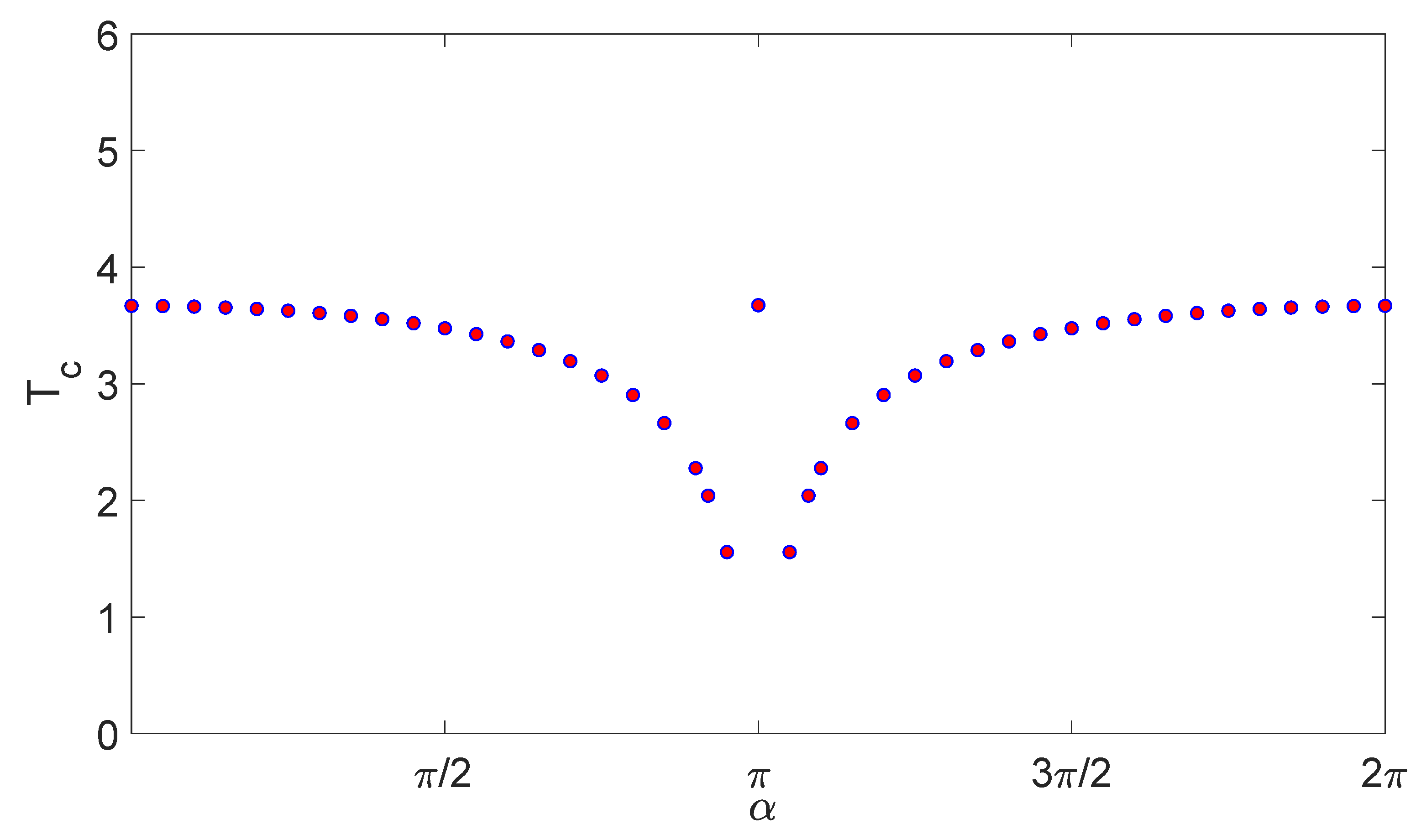
4. The Influences of Boundary Conditions on Bose–Einstein Condensation in a Cubic Box
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cataliotti, F.S.; Burger, S.; Fort, C.; Maddaloni, P.; Minardi, F.; Trombettoni, A.; Smerzi, A.; Inguscio, M. Josephson Junction Arrays with Bose-Einstein Condensates. Science 2001, 293, 843. [Google Scholar] [CrossRef] [PubMed]
- Inguscio, M.; Stringari, S.; Bassani, F.; Liedl, G.L.; Wyder, P. Bose-Einstein Condensation. In Encyclopedia of Condensed Matter Physics; Elsevier: Oxford, UK, 2005; pp. 131–141. [Google Scholar]
- Roati, G.; D’Errico, C.; Fallani, L.; Fattori, M.; Fort, C.; Zaccanti, M.; Modugno, G.; Modugno, M.; Inguscio, M. Anderson localization of a non-interacting Bose-Einstein condensate. Nature 2008, 453, 895. [Google Scholar] [CrossRef]
- Wu, C.J.; Mondragon-Shem, I.; Zhou, X.F. Unconventional Bose—Einstein Condensations from Spin-Orbit Coupling. Chin. Phys. Lett. 2011, 28, 097102. [Google Scholar] [CrossRef]
- Adhikari, S. Vortex-lattice in a uniform Bose-Einstein condensate in a box trap. J. Phys. Cond. Matter. 2019, 31, 275401. [Google Scholar] [CrossRef]
- Deuchert, A.; Seiringer, R.; Yngvason, J. Bose-Einstein Condensation in a Dilute, Trapped Gas at Positive Temperature. Commun. Math. Phys. 2019, 368, 723–776. [Google Scholar] [CrossRef]
- Urvoy, A.; Vendeiro, Z.; Ramette, J.; Adiyatullin, A.; Vuletić, V. Direct Laser Cooling to Bose-Einstein Condensation in a Dipole Trap. Phys. Rev. Lett. 2019, 122, 203202. [Google Scholar] [CrossRef]
- Schneider, M.; Brächer, T.; Breitbach, D.; Lauer, V.; Pirro, P.; Bozhko, D.A.; Musiienko-Shmarova, H.Y.; Heinz, B.; Wang, Q.; Meyer, T. Bose-Einstein condensation of quasiparticles by rapid cooling. Nat. Nanotechnol. 2020, 15, 457–461. [Google Scholar] [CrossRef]
- Georgescu, I. 25 years of BEC. Nat. Rev. Phys. 2020, 2, 396. [Google Scholar] [CrossRef]
- Klaers, J.; Schmitt, J.; Vewinger, F.; Weitz, M. Bose-Einstein condensation of photons in an optical microcavity. Nature 2010, 468, 545–548. [Google Scholar] [CrossRef]
- Hansen, A.; Schultz, J.T.; Bigelow, N.P. Singular atom optics with spinor Bose-Einstein condensates. Optica 2016, 3, 355–361. [Google Scholar] [CrossRef]
- Goldstein, E.V.; Meystre, P. Quasiparticle instabilities in multicomponent atomic condensates. Phys. Rev. A 1997, 55, 2935–2940. [Google Scholar] [CrossRef]
- Jochim, S.; Bartenstein, M.; Altmeyer, A.; Hendl, G.; Riedl, S.; Chin, C.; Hecker Denschlag, J.; Grimm, R. Bose-Einstein Condensation of Molecules. Science 2003, 302, 2101. [Google Scholar] [CrossRef]
- Zwierlein, M.; Stan, C.; Schunck, C.; Raupach, S.; Gupta, S.; Hadzibabic, Z.; Ketterle, W. Observation of Bose-Einstein Condensation of Molecules. Phys. Rev. Lett. 2003, 91, 250401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, L.; Yao, K.; Chin, C. Atomic Bose-Einstein condensate to molecular Bose-Einstein condensate transition. arXiv 2020, arXiv:2006.15297. [Google Scholar]
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor. Science 1995, 269, 198. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.B.; Mewes, M.O.; Joffe, M.A.; Andrews, M.R.; Ketterle, W. Evaporative Cooling of Sodium Atoms. Phys. Rev. Lett. 1995, 74, 5202–5205. [Google Scholar] [CrossRef] [PubMed]
- Ketterle, W.; Van Druten, N.J. Bose-Einstein condensation of a finite number of particles trapped in one or three dimensions. Phys. Rev. A 1996, 54, 656. [Google Scholar] [CrossRef]
- Bradley, C.; Sackett, C.; Hulet, R. Bose-Einstein Condensation of Lithium: Observation of Limited Condensate Number. Phys. Rev. Lett. 1997, 78, 985–989. [Google Scholar] [CrossRef]
- Brankov, J.; Dantchev, D.; Tonchev, N. Theory of Critical Phenomena in Finite-Size Systems: Scaling and Quantum Effects; World Scientific: Singapore, 2000. [Google Scholar]
- Kristensen, M.; Christensen, M.; Gajdacz, M.; Iglicki, M.; Pawłowski, K.; Klempt, C.; Sherson, J.F.; Rzążewski, K.; Hilliard, A.J.; Arlt, J.J. Observation of Atom Number Fluctuations in a Bose-Einstein Condensate. Phys. Rev. Lett. 2019, 122, 163601. [Google Scholar] [CrossRef] [PubMed]
- Andrews, M.; Townsend, C.; Miesner, H.J.; Durfee, D.; Kurn, D.; Ketterle, W. Observation of Interference between Two Bose Condensates. Science 1997, 275, 637. [Google Scholar] [CrossRef]
- Myatt, C.; Burt, E.; Ghrist, R.; Cornell, E.; Wieman, C. Production of Two Overlapping Bose-Einstein Condensates by Sympathetic Cooling. Phys. Rev. Lett. 1997, 78, 586–589. [Google Scholar] [CrossRef]
- Hall, D.S.; Matthews, M.R.; Ensher, J.R.; Wieman, C.E.; Cornell, E.A. Dynamics of Component Separation in a Binary Mixture of Bose-Einstein Condensates. Phys. Rev. Lett. 1998, 81, 1539–1542. [Google Scholar] [CrossRef]
- Miesner, H.J.; Stamper-Kurn, D.; Stenger, J.; Inouye, S.; Chikkatur, A.; Ketterle, W. Observation of Metastable States in Spinor Bose-Einstein Condensates. Phys. Rev. Lett. 1999, 82, 2228–2231. [Google Scholar] [CrossRef]
- Matthews, M.; Anderson, B.; Haljan, P.; Hall, D.; Wieman, C.; Cornell, E. Vortices in a Bose-Einstein Condensate. Phys. Rev. Lett. 1999, 83, 2498–2501. [Google Scholar] [CrossRef]
- Papp, S.B.; Pino, J.M.; Wieman, C.E. Tunable Miscibility in a Dual-Species Bose-Einstein Condensate. Phys. Rev. Lett. 2008, 101, 040402. [Google Scholar] [CrossRef]
- McCarron, D.; Cho, H.; Jenkin, D.; Köppinger, M.; Cornish, S. Dual-species Bose-Einstein condensate of 87Rb and 133Cs. Phys. Rev. A 2011, 84, 011603. [Google Scholar] [CrossRef]
- Grossmann, S.; Holthaus, M. Bose-Einstein condensation in a cavity. Z. Phys. B Condens. Matter 1995, 97, 319–326. [Google Scholar] [CrossRef]
- Ziff, R.M.; Uhlenbeck, G.E.; Kac, M. The ideal Bose-Einstein gas, revisited. Phys. Rep. 1977, 32, 169–248. [Google Scholar] [CrossRef]
- Franzosi, R.; Giampaolo, S.M.; Illuminati, F. Quantum localization and bound-state formation in Bose-Einstein condensates. Phys. Rev. A 2010, 82, 063620. [Google Scholar] [CrossRef]
- London, F. On the Bose-Einstein Condensation. Phys. Rev. 1938, 54, 947–954. [Google Scholar] [CrossRef]
- Krueger, D.A. Finite Geometries and Ideal Bose Gases. Phys. Rep. 1968, 172, 211–223. [Google Scholar] [CrossRef]
- Greenspoon, S.; Pathria, R.K. Bose-Einstein condensation in finite noninteracting systems: A new law of corresponding states. Phys. Rev. A 1974, 9, 2103. [Google Scholar] [CrossRef]
- Holthaus, M.; Kapale, K.T.; Scully, M.O. Influence of boundary conditions on statistical properties of ideal Bose-Einstein condensates. Phys. Rev. E 2002, 65, 036129. [Google Scholar] [CrossRef]
- Brankov, J.G.; Danchev, D.M.; Tonchev, N.S. Theory of Critical Phenomena in Finite-Size Systems; World Scientific: Singapore, 2020; Volume 9, p. 460. [Google Scholar] [CrossRef]
- Byers, N.; Yang, C.N. Theoretical Considerations Concerning Quantized Magnetic Flux in Superconducting Cylinders. Phys. Rev. Lett. 1961, 7, 46–49. [Google Scholar] [CrossRef]
- Zawadzki, K.; D’Amico, I.; Oliveira, L.N. Symmetries and Boundary Conditions with a Twist. Braz. J. Phys. 2017, 47, 488–511. [Google Scholar] [CrossRef]
- Sachrajda, C.T.; Villadoro, G. Twisted boundary conditions in lattice simulations. Phys. Lett. B 2005, 609, 73–85. [Google Scholar] [CrossRef]
- Könenberg, M.; Moser, T.; Seiringer, R.; Yngvason, J. Superfluid behavior of a Bose-Einstein condensate in a random potential. New J. Phys. 2015, 17, 013022. [Google Scholar] [CrossRef]
- Könenberg, M.; Moser, T.; Seiringer, R.; Yngvason, J. Superuidity and BEC in a Model of Interacting Bosons in a Random Potential. J. Phys. Conf. Ser. 2016, 691, 012016. [Google Scholar] [CrossRef]
- Kleman, M.; Friedel, J. Disclinations, dislocations, and continuous defects: A reappraisal. Rev. Mod. Phys. 2008, 80, 61–115. [Google Scholar] [CrossRef]
- Karbowski, J.; Turski, L. The Bose-Einstein condensation in random box. Phys. A 2000, 276, 489–494. [Google Scholar] [CrossRef]
- Dalfovo, F.; Pitaevskii, L.; Stringari, S. Bose Einstein Condensates. Uspekhi Fiz. Nauk. 2005, 167. [Google Scholar] [CrossRef]
- Kirsten, K.; Toms, D.J. Bose-Einstein condensation under external conditions. Phys. Lett. A 1998, 243, 137–141. [Google Scholar] [CrossRef][Green Version]
- Bagnato, V.; Pritchard, D.E.; Kleppner, D. Bose-Einstein condensation in an external potential. Phys. Rev. A 1987, 35, 4354–4358. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, S.; Kocharovsky, V.; Kocharovsky, V. Anomalous Statistics of Bose-Einstein Condensate in an Interacting Gas: An Effect of the Trap’s Form and Boundary Conditions in the Thermodynamic Limit. Entropy 2018, 20, 153. [Google Scholar] [CrossRef] [PubMed]

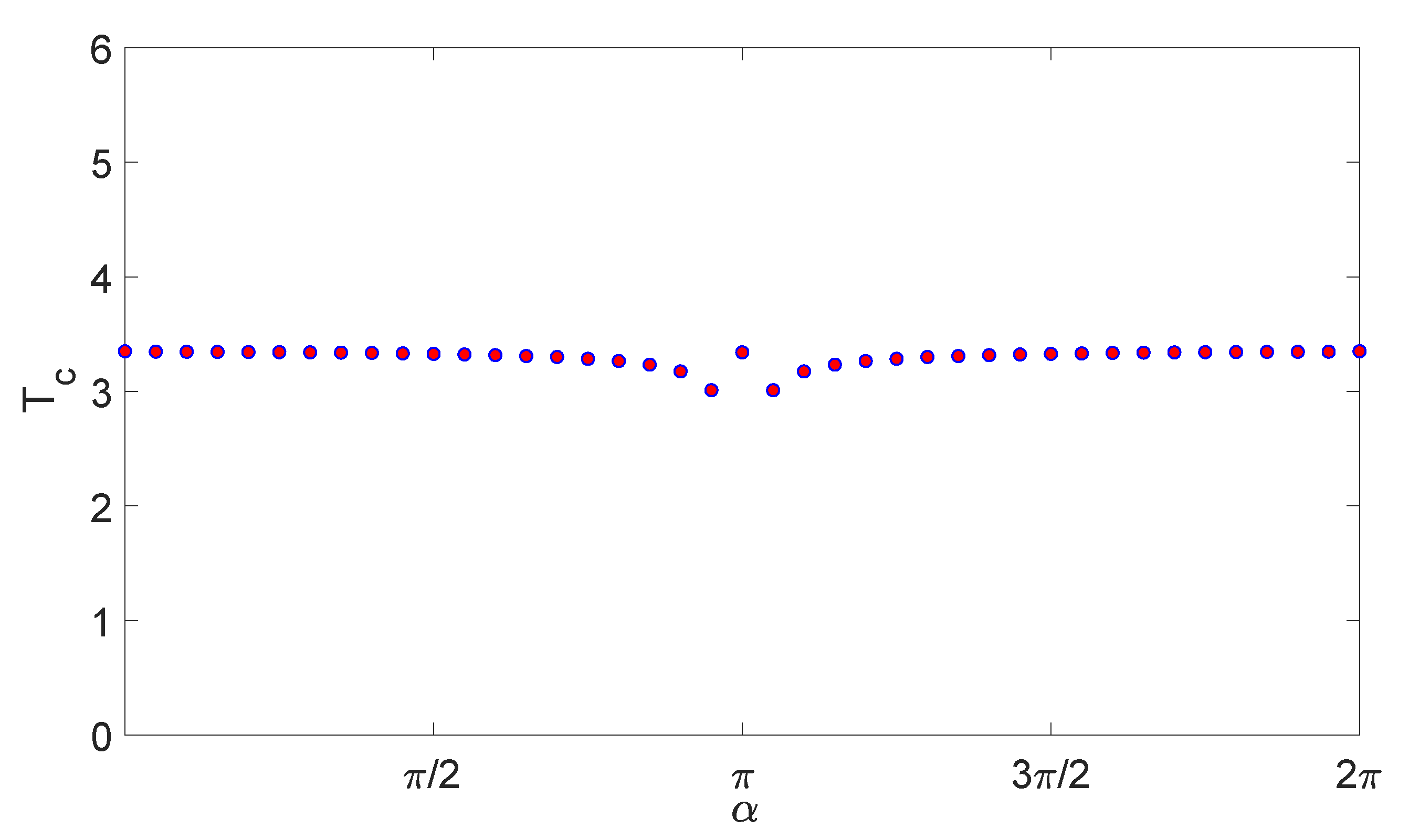

| 0.2 | 0.5 | 1 | 10 | 50 | 100 | |
|---|---|---|---|---|---|---|
| (a) | 74.5 | 20.1 | 9.279 | 3.67 | 3.38 | 3.35 |
| (b) | 123.3 | 30 | 12.13 | 3.68 | 3.37 | 3.34 |
| (c) | 62.4 | 18.2 | 9.42 | 4.168 | 3.57 | 3.463 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, R.; Wang, Q.-Y.; Wang, Y.-L.; Zong, H.-S. Finite-Size Effects with Boundary Conditions on Bose-Einstein Condensation. Symmetry 2021, 13, 300. https://doi.org/10.3390/sym13020300
Cheng R, Wang Q-Y, Wang Y-L, Zong H-S. Finite-Size Effects with Boundary Conditions on Bose-Einstein Condensation. Symmetry. 2021; 13(2):300. https://doi.org/10.3390/sym13020300
Chicago/Turabian StyleCheng, Run, Qian-Yi Wang, Yong-Long Wang, and Hong-Shi Zong. 2021. "Finite-Size Effects with Boundary Conditions on Bose-Einstein Condensation" Symmetry 13, no. 2: 300. https://doi.org/10.3390/sym13020300
APA StyleCheng, R., Wang, Q.-Y., Wang, Y.-L., & Zong, H.-S. (2021). Finite-Size Effects with Boundary Conditions on Bose-Einstein Condensation. Symmetry, 13(2), 300. https://doi.org/10.3390/sym13020300





