Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations
Abstract
1. Introduction
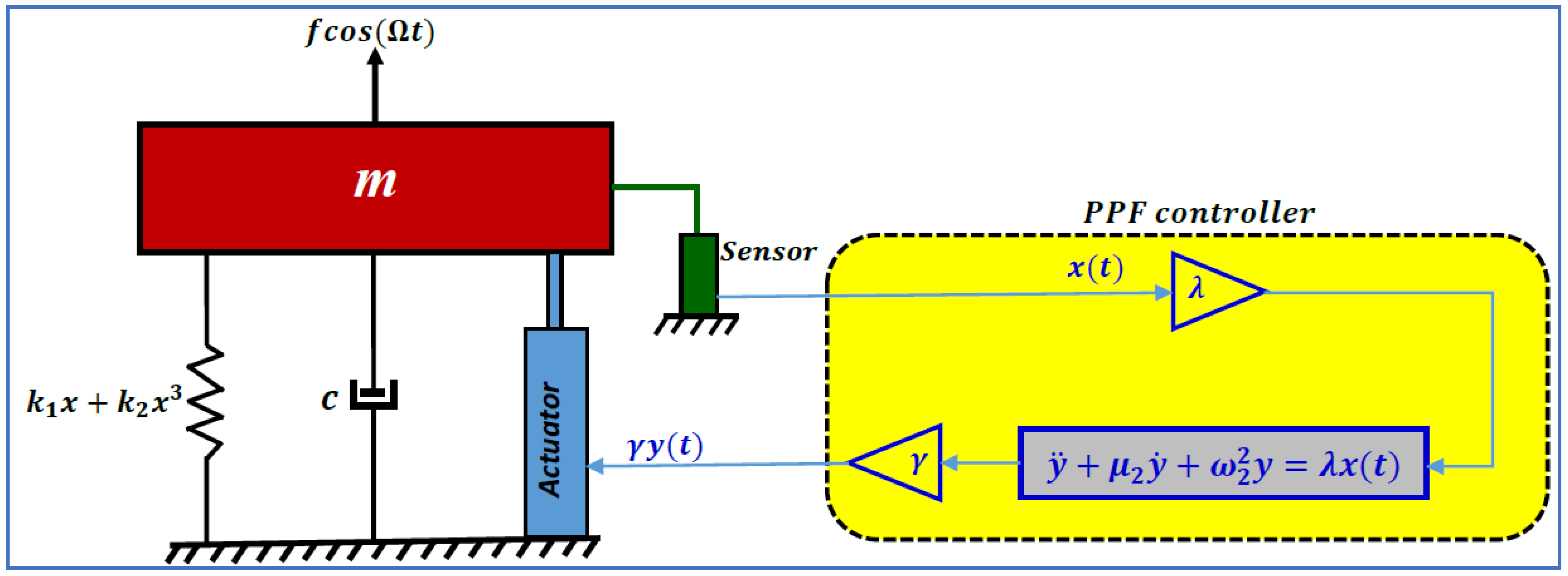
2. Positive Position Feedback (PPF) Controller
2.1. Mathematical Analysis
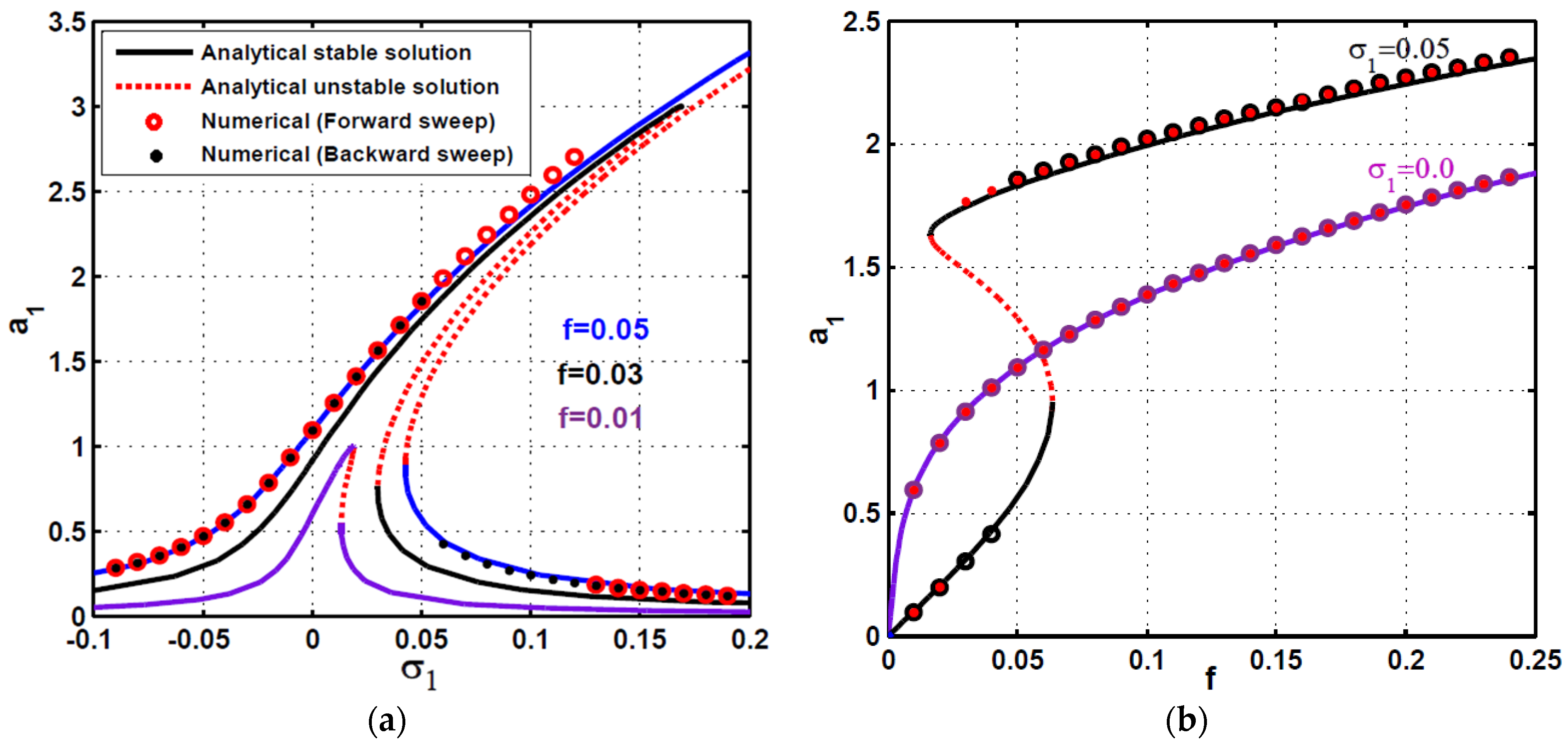
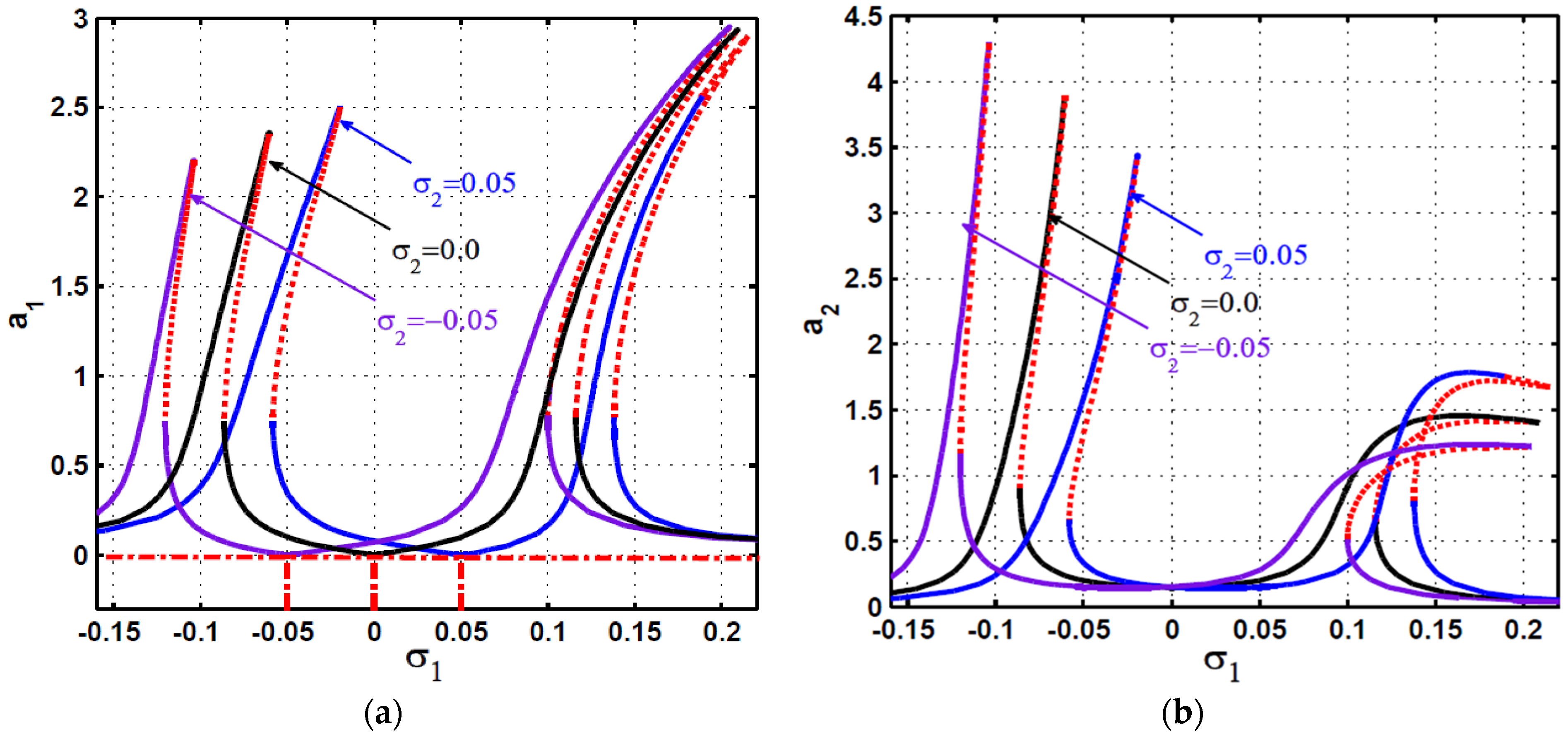
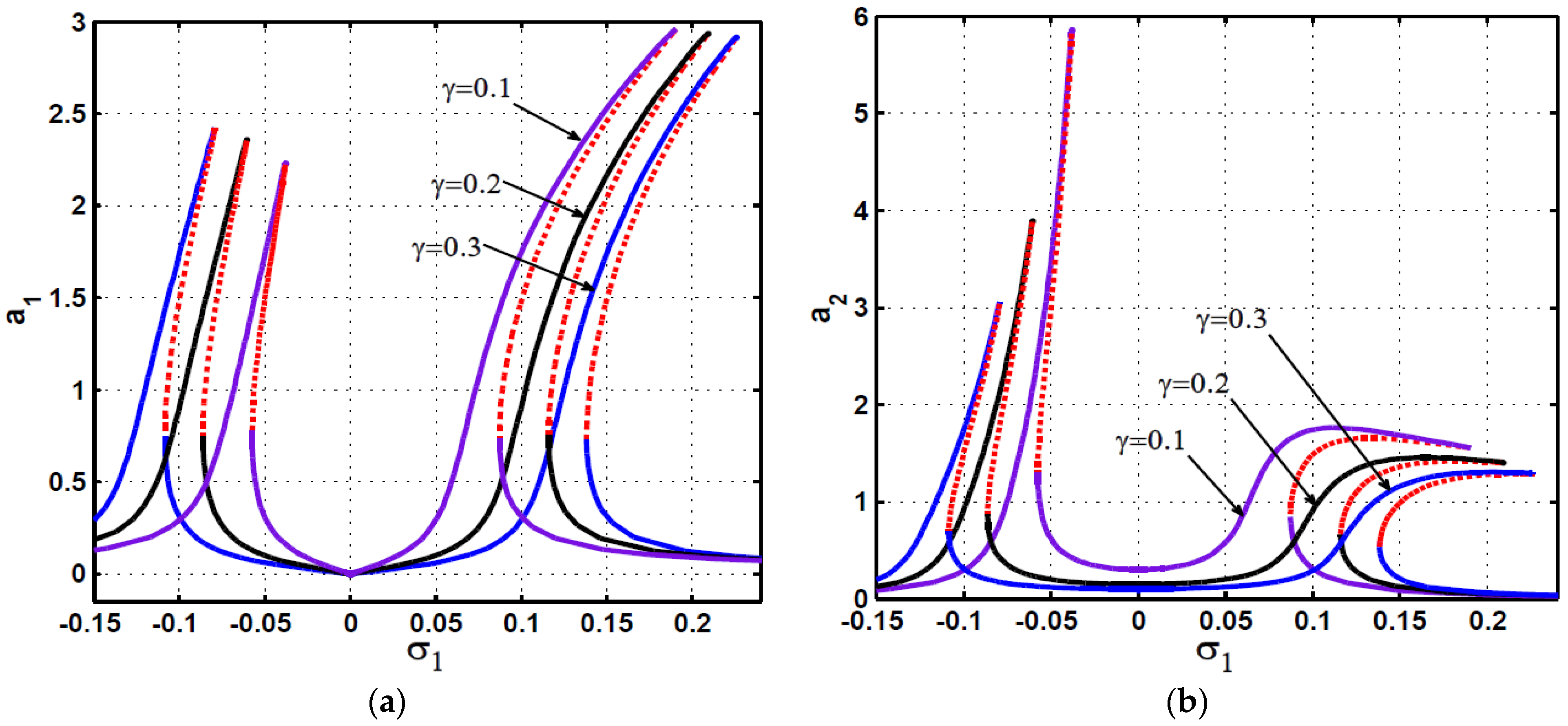
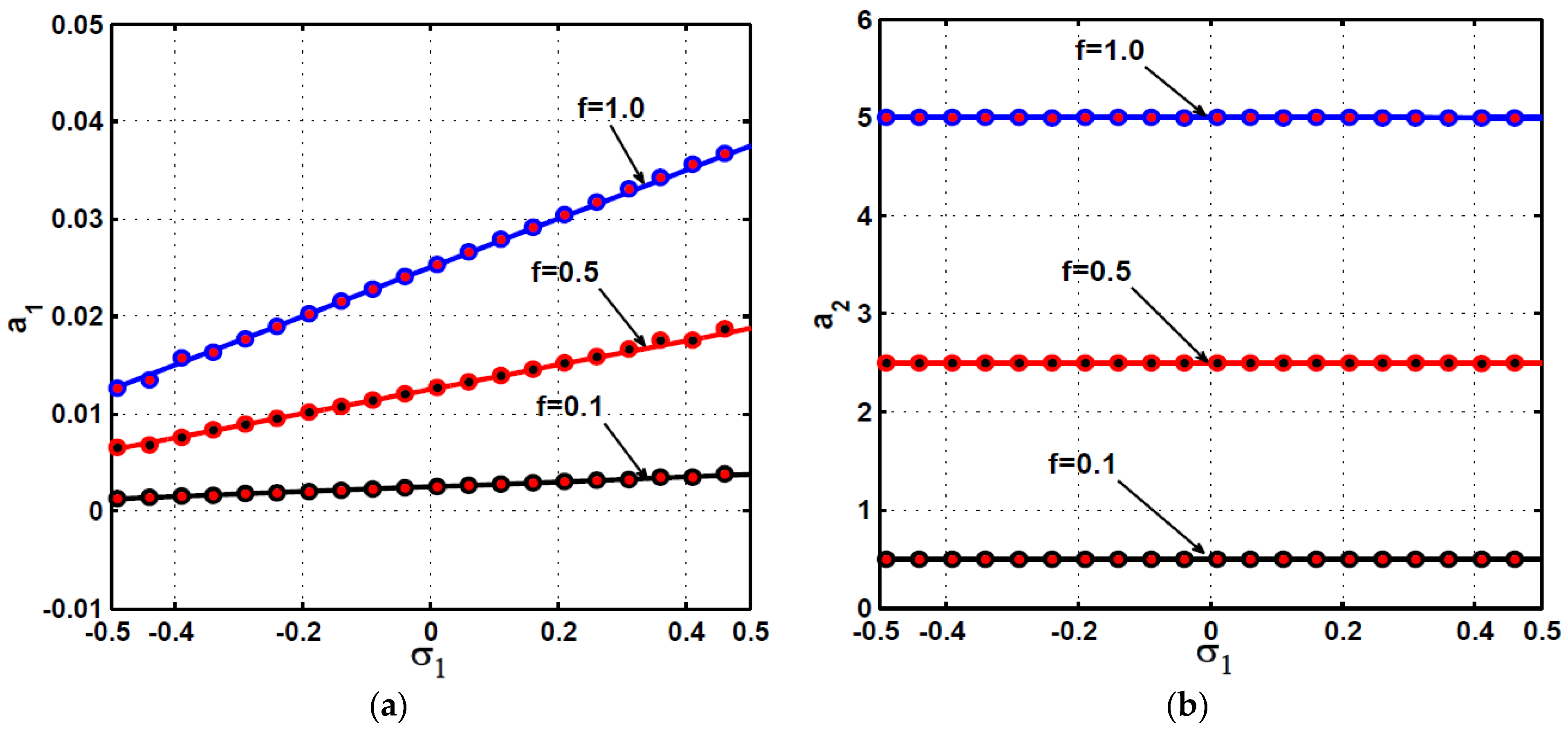
2.2. Steady-State Vibration and Stability Investigations
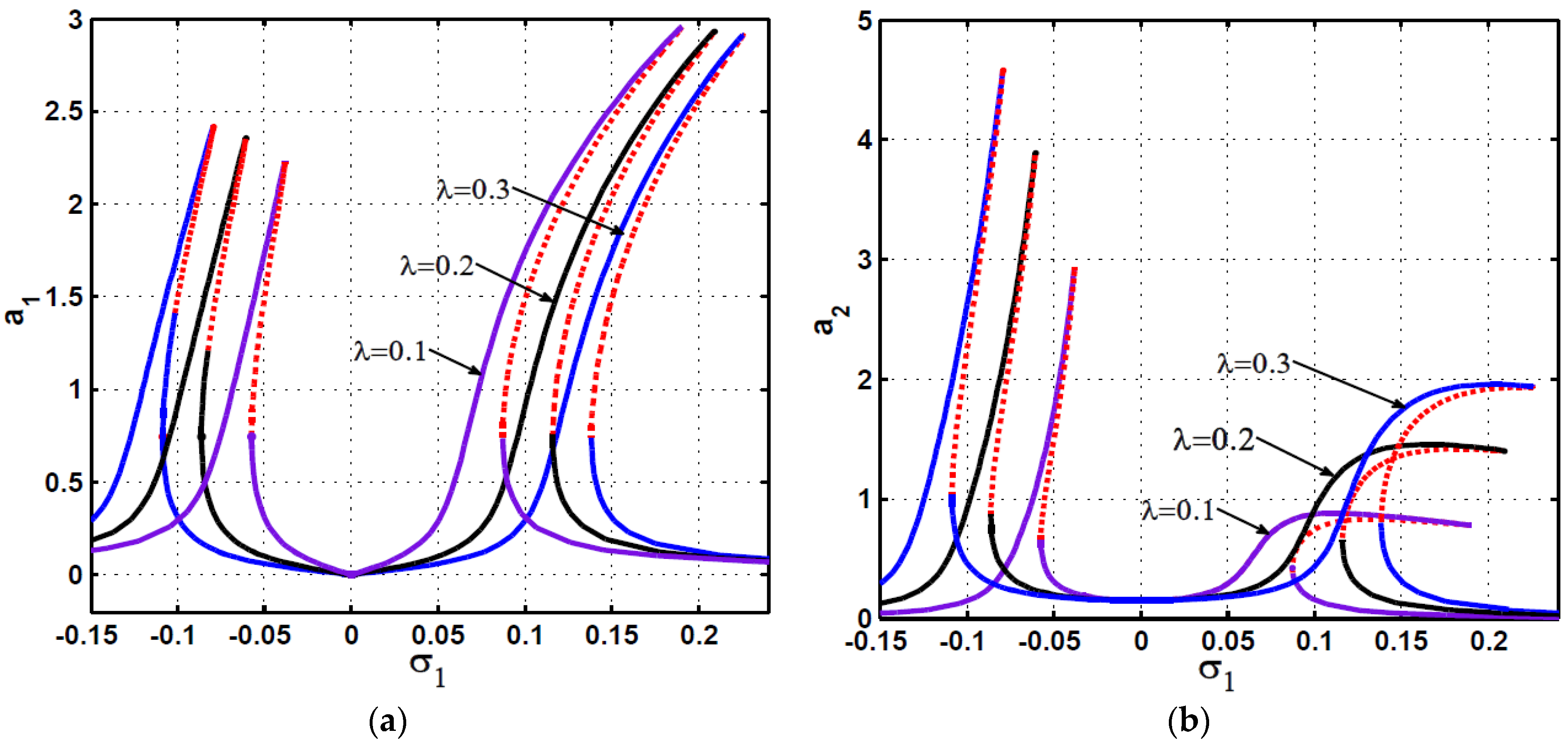
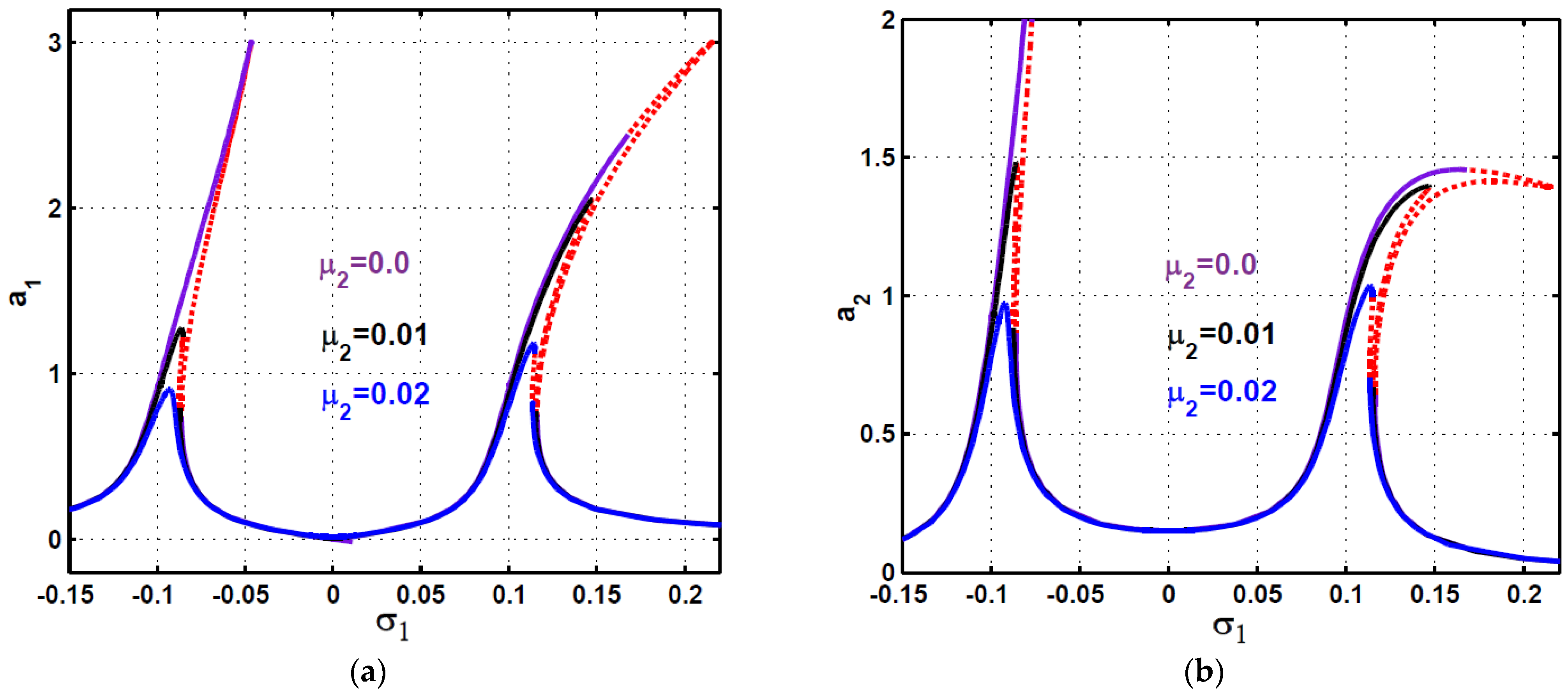
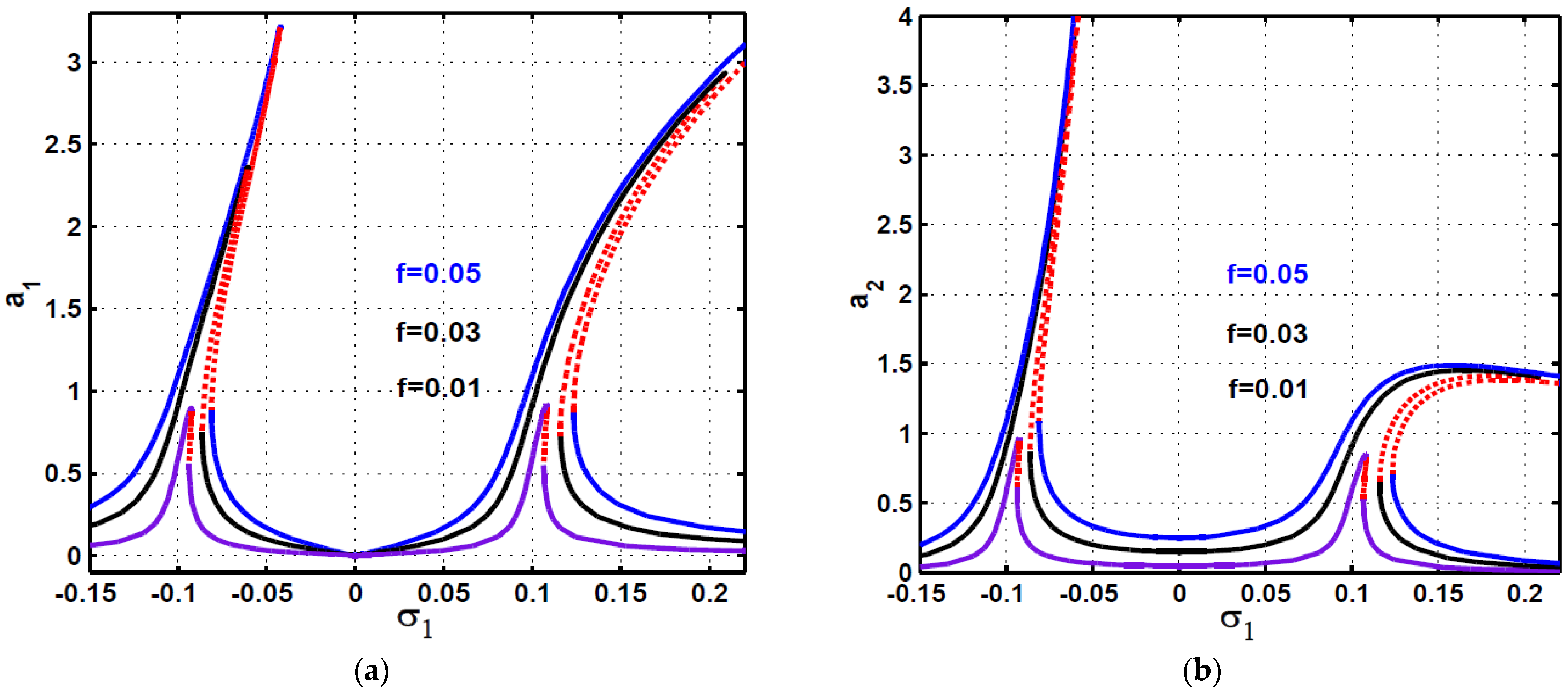
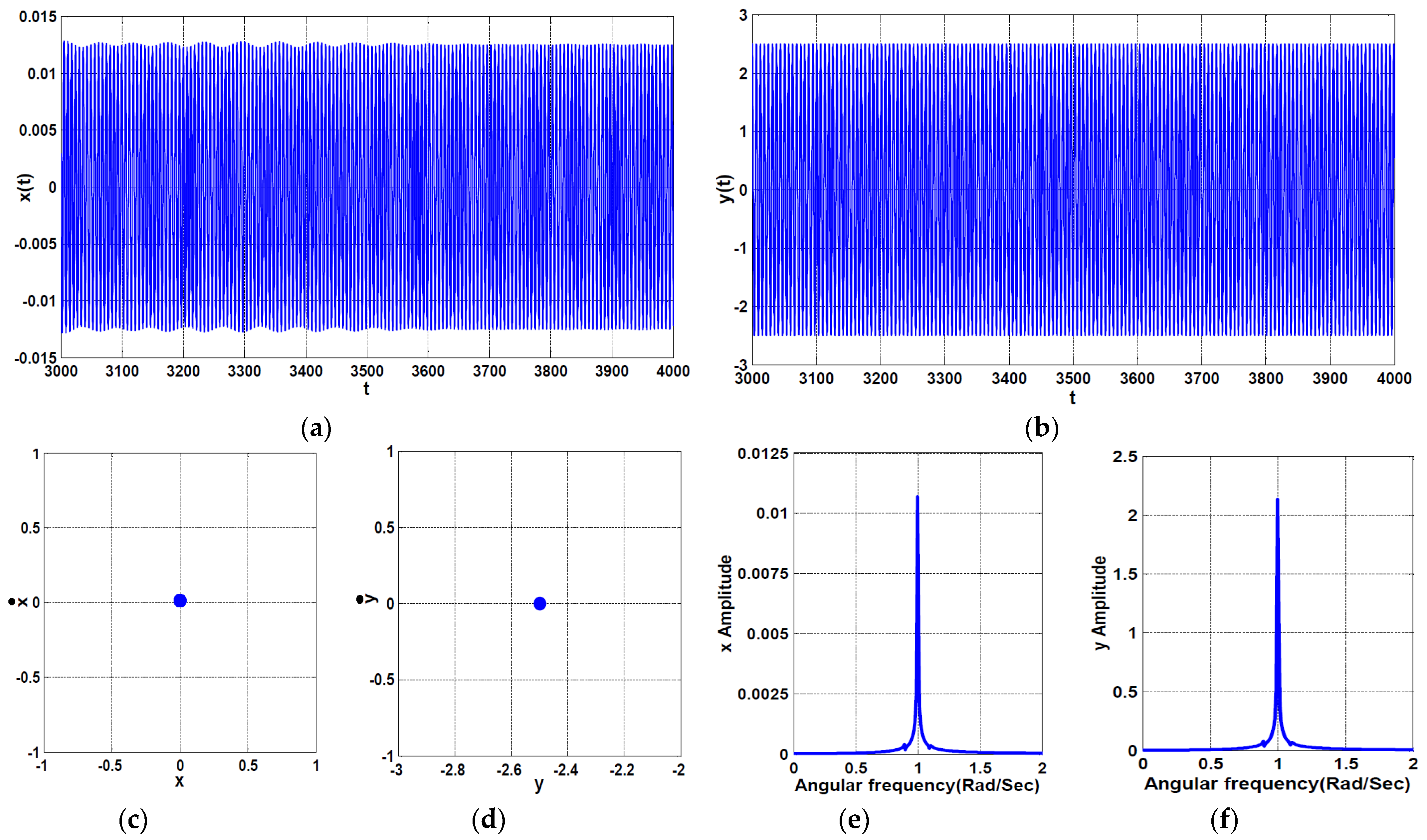
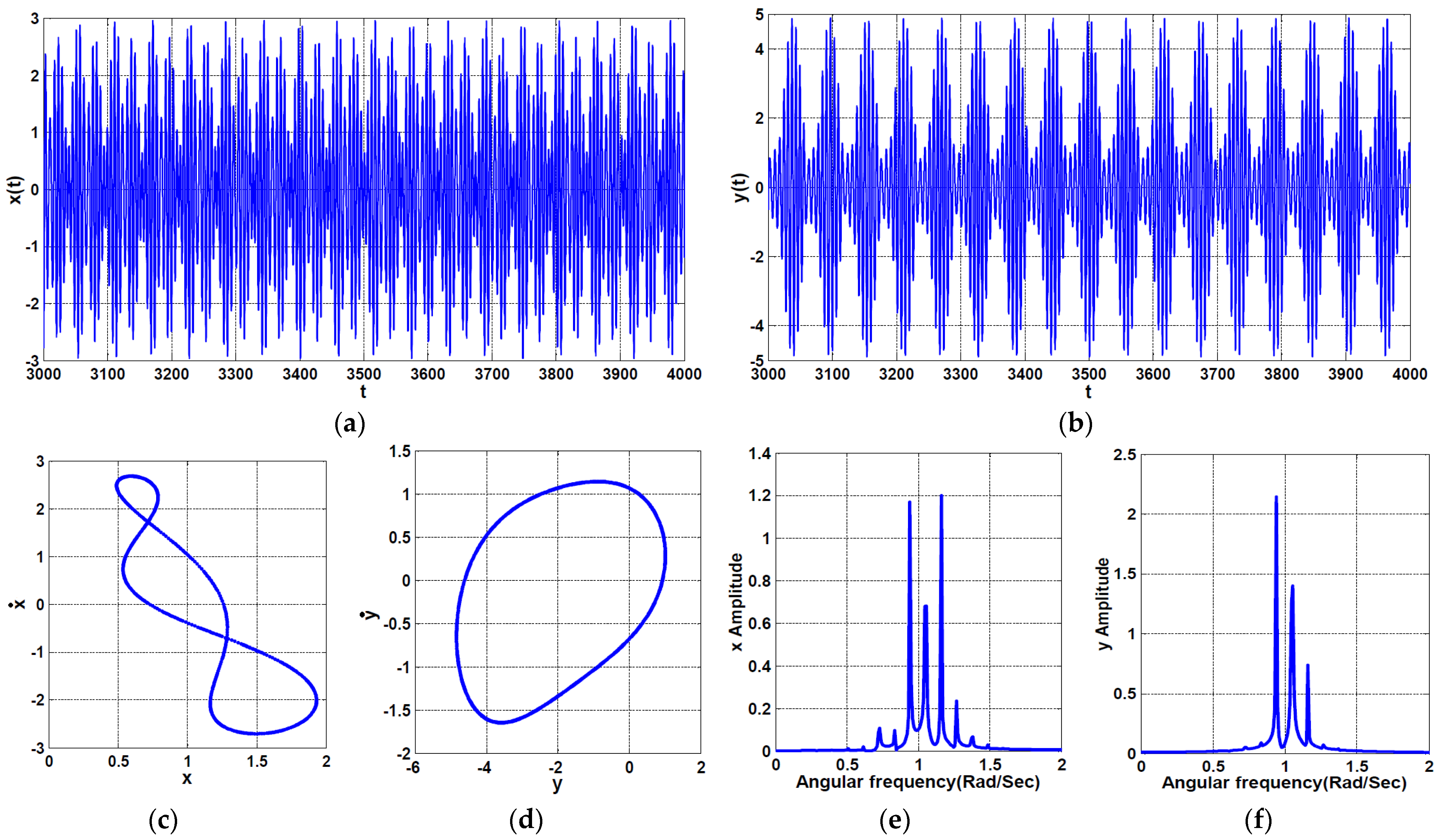
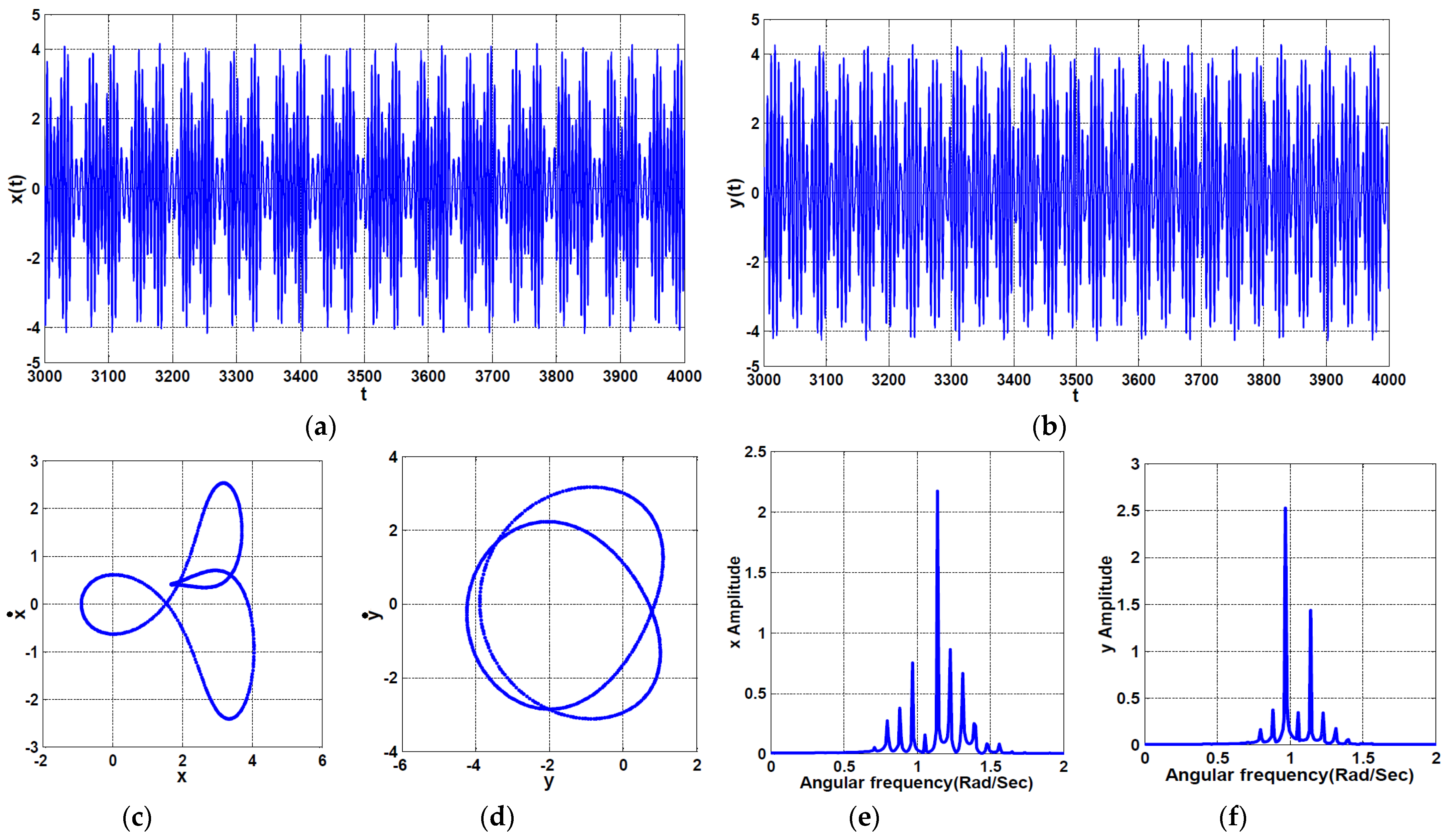
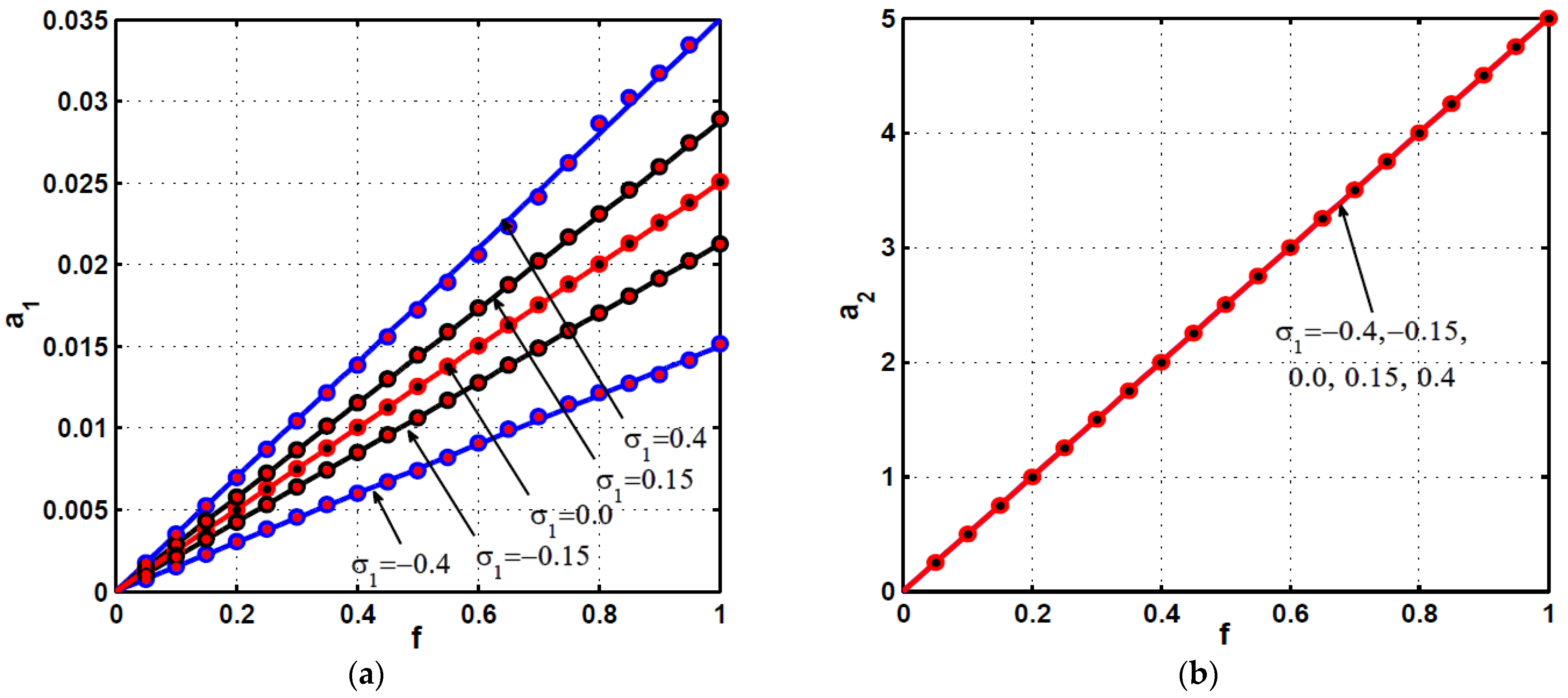
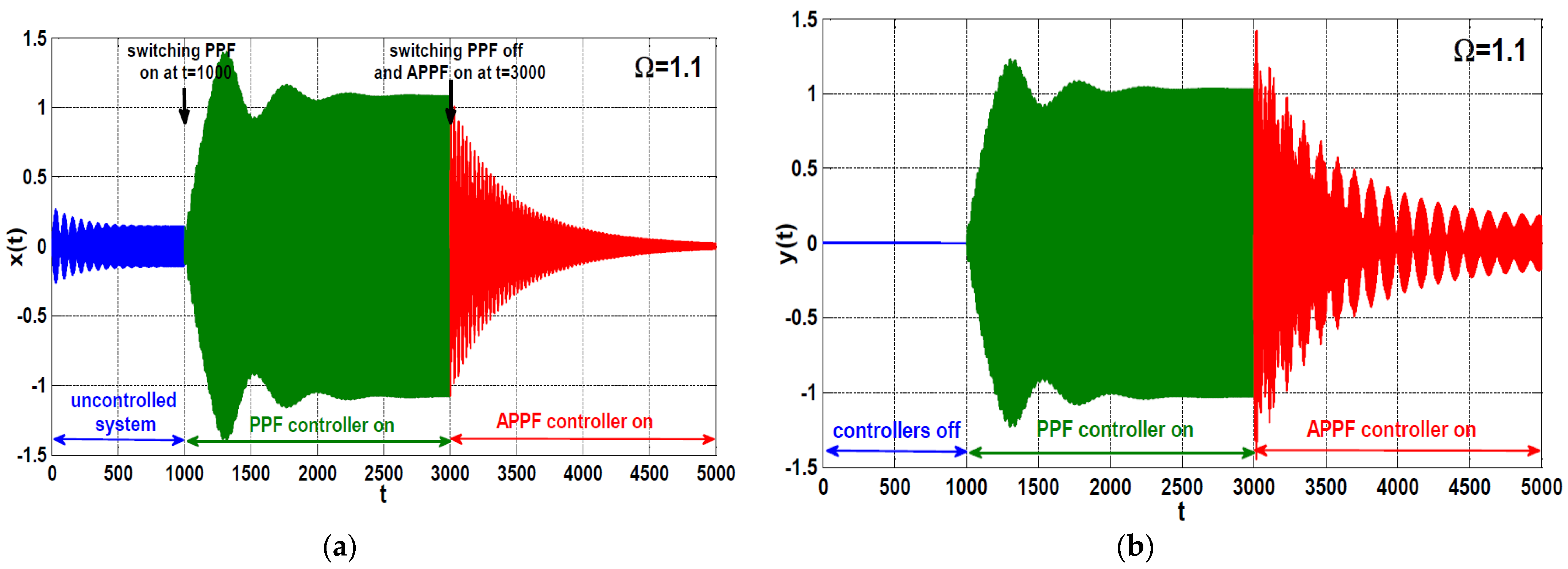
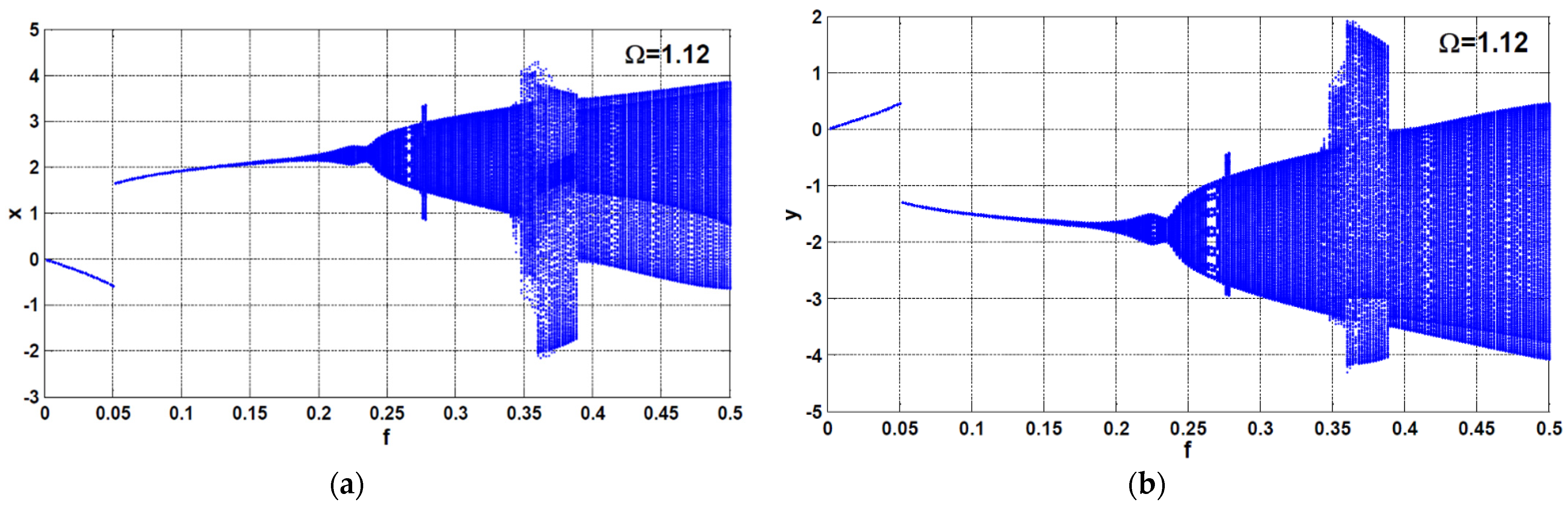
2.3. Response Curves and Numerical Validations
3. Adaptive Positive Position Feedback (APPF) Controller
Frequency-Response Equation of APPF Controller
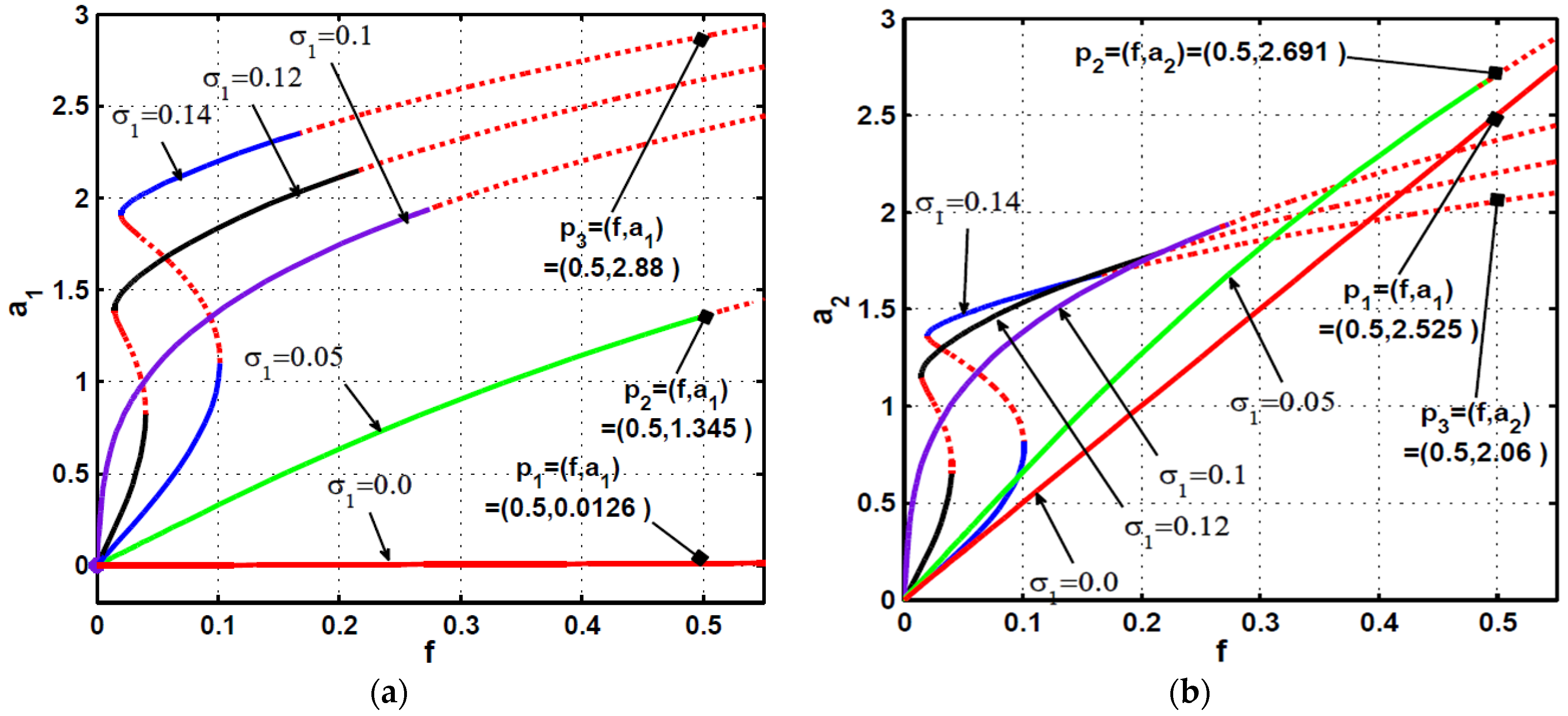
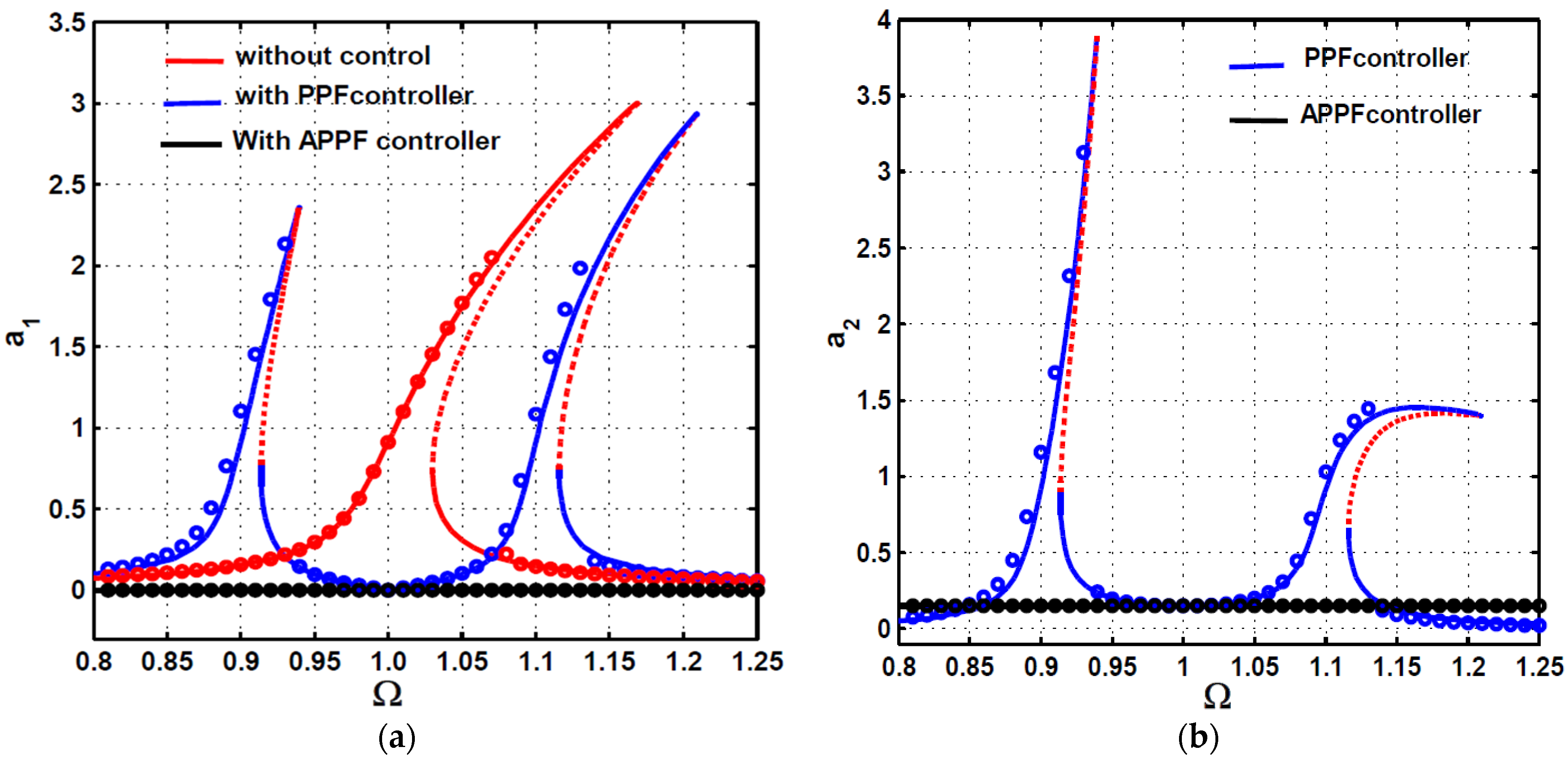
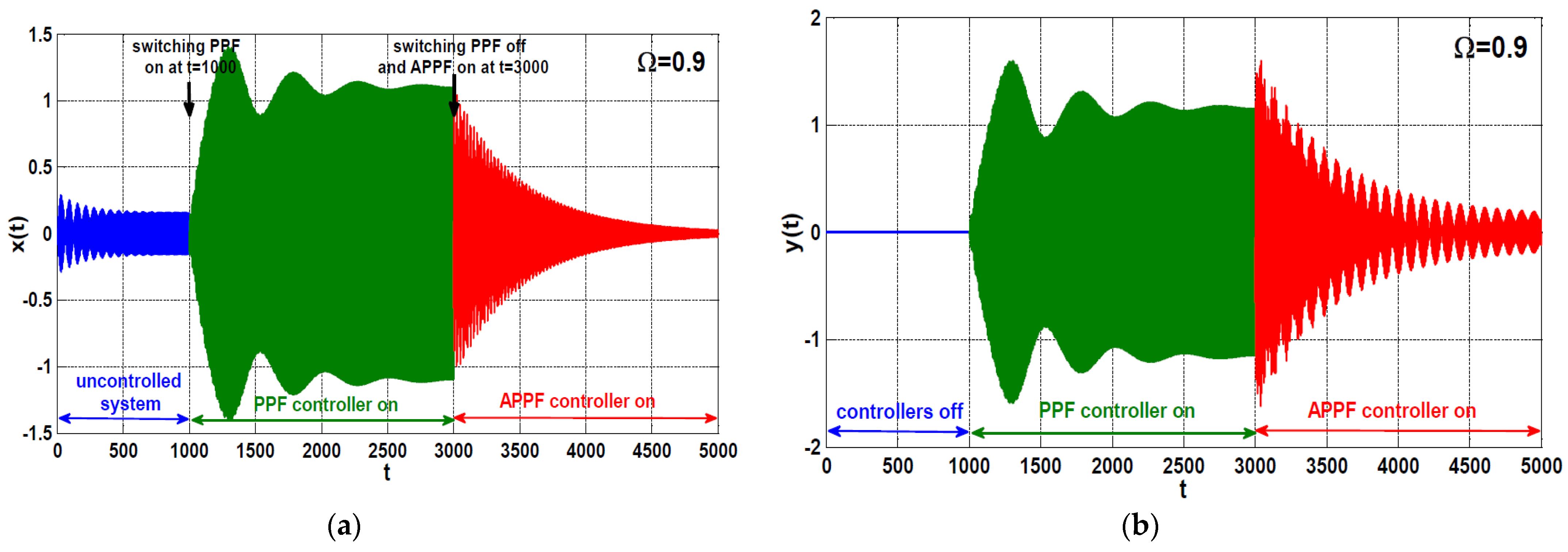
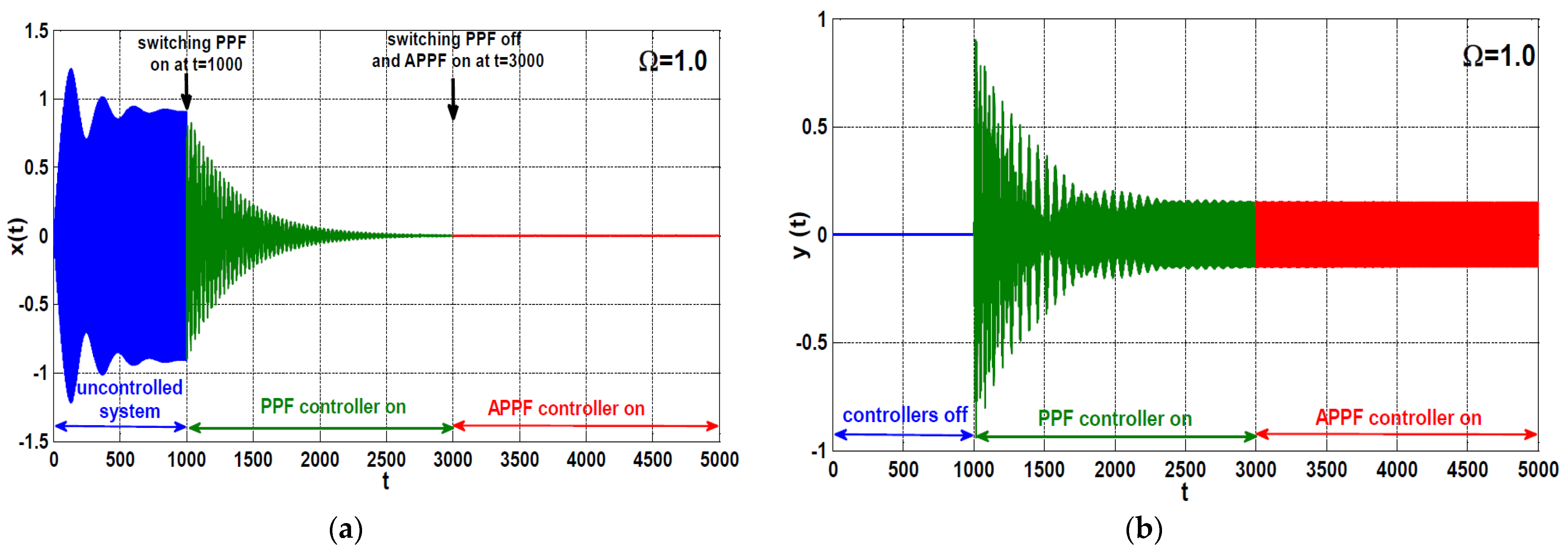
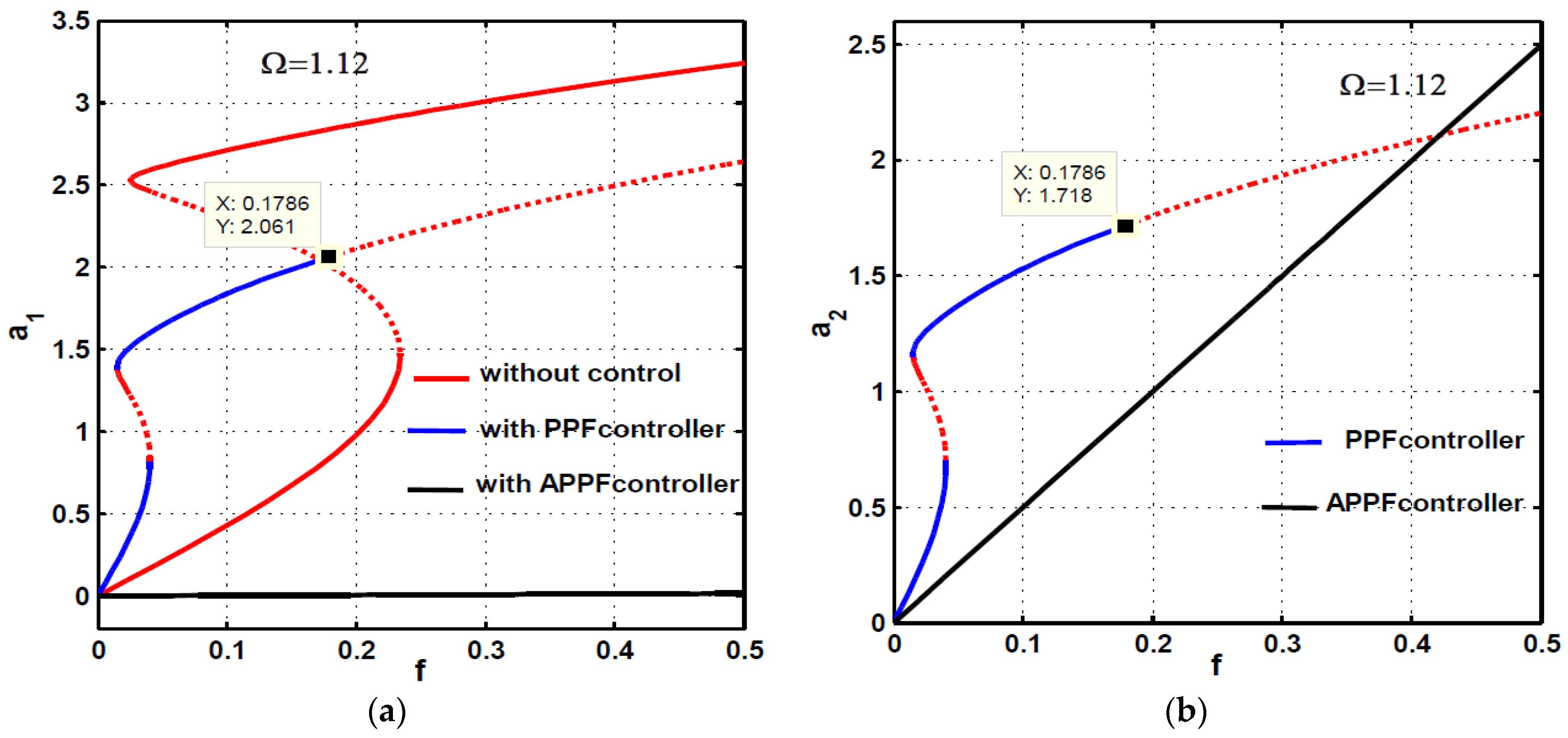
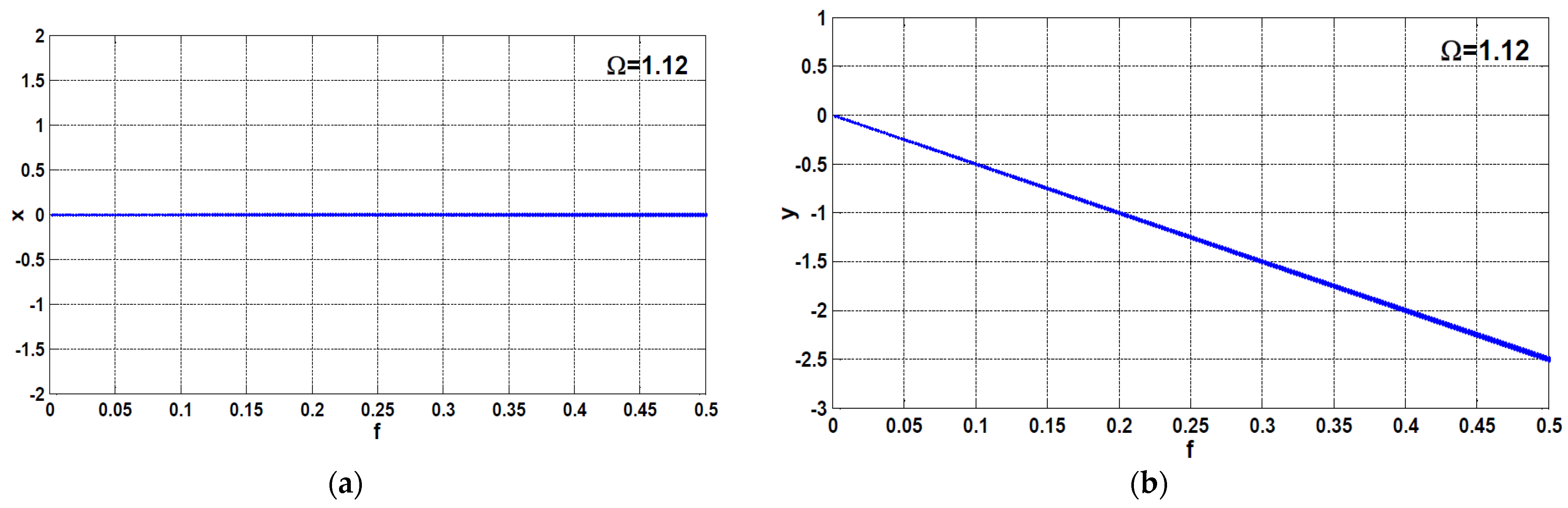
4. Comparison between the PPF and APPF Controllers
5. Conclusions
- The conventional PPF controller can eliminate the primary resonance vibrations of the considered system in the presence of 1:1 internal resonance.
- Once the resonance conditions between the main system and the PPF controller are lost, the controller adds excessive vibrational energy to the main system rather than suppressing it.
- At the large excitation force amplitudes, the main system may lose its stability to respond with a quasiperiodic motion when the resonance condition between the main system and the PPF controller is lost.
- Regardless of the main system natural frequency, once the controller natural frequency is properly tuned to be the same value as the excitation frequency (), the controller can suppress the main system vibrations when subjected to any excitation force amplitude and/or any excitation frequency.
- According to point (4) of the conclusion, the adaptive positive position feedback controller is the best control strategy that can eliminate the main system vibrations regardless of the excitation frequency and excitation force amplitude.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Dimensionless displacement, velocity, and acceleration of the main system. | |
| Dimensionless displacement, velocity, and acceleration of the controller. | |
| Dimensionless linear damping coefficients of the main system and controller, respectively. | |
| Dimensionless linear natural frequencies of the main system and controller, respectively. | |
| Dimensionless cubic nonlinear stiffness coefficient. | |
| Dimensionless excitation force amplitude. | |
| Excitation force angular frequency. | |
| Dimensionless control signal gain. | |
| Dimensionless feedback signal gain. | |
| The detuning parameter | |
| Dimensionless steady-state oscillation amplitudes of the main system and controller, respectively. |
References
- Baz, A.; Poh, S. Short communications optimal vibration control with modal positive position feedback. Optim. Control Appl. Methods 1996, 17, 141–149. [Google Scholar] [CrossRef]
- Baz, A.; Hong, J.-T. Adaptive control of flexible structures using modal positive position feedback. Int. J. Adapt. Control Signal Process. 1997, 11, 231–253. [Google Scholar] [CrossRef]
- Friswell, M.I.; Inman, D.J. The relationship between positive position feedback and output feedback controllers. Smart Mater. Struct. 1999, 8, 285–291. [Google Scholar] [CrossRef]
- Rew, K.-H.; Han, J.-H.; Lee, I. Multi-Modal Vibration Control Using Adaptive Positive Position Feedback. J. Intell. Mater. Syst. Struct. 2002, 13, 13–22. [Google Scholar] [CrossRef]
- Song, G.; Schmidt, S.; Agrawal, B. Experimental robustness study of positive position feedback control for active vibration suppression. J. Guid. Control Dyn. 2002, 25, 179–182. [Google Scholar] [CrossRef][Green Version]
- Song, G.; Qiao, P.; Binienda, W.; Zou, G. Active vibration damping of composite beam using smart sensors and actuators. J. Aerosp. Eng. 2002, 15, 97–103. [Google Scholar] [CrossRef]
- Shan, J.; Liu, H.; Sun, D. Slewing and vibration control of a single-link flexible manipulator by positive position feed-back (PPF). Mechatronics 2005, 15, 487–503. [Google Scholar] [CrossRef]
- Moon, K.; Seokn, H. Active vibration control of smart grid structure by multiinput and multioutput positive position feedback controller. J. Sound Vib. 2007, 304, 230–245. [Google Scholar]
- Kumar, R. Effective active vibration control of single link flexible manipulator with modified positive position feed-back control in the presence of instrumentation phase lead/lag. J. Vib. Control 2012, 19, 1538–1560. [Google Scholar] [CrossRef]
- Shin, C.; Hong, C.; Jeong, W. Active vibration control of clamped beams using positive position feedback controllers with moment pair. J. Mech. Sci. Technol. 2012, 26, 731–740. [Google Scholar] [CrossRef]
- Jun, L. Positive Position Feedback Control for High-Amplitude Vibration of a Flexible Beam to a Principal Resonance Excitation. Shock. Vib. 2010, 17, 187–203. [Google Scholar] [CrossRef]
- El-Ganaini, W.A.; Saeed, N.; Eissa, O.M. Positive position feedback (PPF) controller for suppression of nonlinear system vibration. Nonlinear Dyn. 2013, 72, 517–537. [Google Scholar] [CrossRef]
- Ferrari, G.; Amabili, M. Active vibration control of a sandwich plate by non-collocated positive position feedback. J. Sound Vib. 2015, 342, 44–56. [Google Scholar] [CrossRef]
- Omidi, E.; Mahmoodi, S. Nonlinear vibration suppression of flexible structures using nonlinear modified positive po-sition feedback approach. Nonlinear Dyn. 2015, 79, 835–849. [Google Scholar] [CrossRef]
- Omidi, E.; Mahmoodi, S. Sensitivity analysis of the Nonlinear Integral Positive Position Feedback and Integral Resonant controllers on vibration suppression of nonlinear oscillatory systems. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 149–166. [Google Scholar] [CrossRef]
- Syed, H.H. Comparative study between positive position feedback and negative derivative feedback for vibration control of a flexible arm featuring piezoelectric actuator. Int. J. Adv. Robot. Syst. 2017, 14, 1–9. [Google Scholar] [CrossRef]
- Saeed, N.; Kamel, M. Active magnetic bearing-based tuned controller to suppress lateral vibrations of a nonlinear Jeffcott rotor system. Nonlinear Dyn. 2017, 90, 457–478. [Google Scholar] [CrossRef]
- Saeed, N.A.; Eissa, M. Nonlinear vibration control of a horizontally supported Jeffcott-rotor system. J. Vib. Control 2018, 24, 5898–5921. [Google Scholar]
- Saeed, N.; Kandil, A. Lateral vibration control and stabilization of the quasiperiodic oscillations for rotor-active magnetic bearings system. Nonlinear Dyn. 2019, 98, 1191–1218. [Google Scholar] [CrossRef]
- Zhao, G.; Paknejad, A.; Raze, G.; Deraemaeker, A.; Kerschen, G.; Collette, C. Nonlinear positive position feedback control for mitigation of nonlinear vibrations. Mech. Syst. Signal Process. 2019, 132, 457–470. [Google Scholar] [CrossRef]
- Eissa, M.; Kamel, M.; Saeed, N.A.; El-Ganaini, W.A.; El-Gohary, H.A. Time-delayed positive-position and velocity feedback controller to suppress the lateral vibrations in nonlinear Jeffcott-rotor system. Menoufia J. Electron. Eng. Res. 2018, 27, 261–278. [Google Scholar] [CrossRef]
- Marinangeli, L.; Alijani, F.; HosseinNia, S.H. Fractional-order positive position feedback compensator for active vibration control of a smart composite plate. J. Sound Vib. 2018, 412, 1–16. [Google Scholar] [CrossRef]
- Niu, W.; Li, B.; Xin, T.; Wang, W. Vibration active control of structure with parameter perturbation using fractional order positive position feedback controller. J. Sound Vib. 2018, 430, 101–114. [Google Scholar] [CrossRef]
- Ragusa, M.A.; Scapellato, A. Mixed Morrey spaces and their applications to partial diferential equation. Nonlinear Anal. Theory Methods Appl. 2017, 151, 51–65. [Google Scholar] [CrossRef]
- Paknejad, A.; Zhao, G.; Osee, M.; Deraemaeker, A.; Robert, F.; Collette, C. A novel design of positive position feed-back controller based on maximum damping and H2 optimization. J. Vib. Control 2020, 26, 1155–1164. [Google Scholar] [CrossRef]
- Bin, E.; Shan, J.; Khushnood, M.A.; Wang, X.; Cui, N. Determination of optimal positive position feedback parameters by using nonsmooth H∞ synthesis. J. Vib. Control. 2020, 1–13. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T.; Holmes, P. Nonlinear Oscillations. J. Appl. Mech. 1980, 47, 692. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Resolving Controversies in the Application of the Method of Multiple Scales and the Generalized Method of Averaging. Nonlinear Dyn. 2005, 40, 61–102. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Craft, M.J.; Southward, S.C.; Ahmadian, M. Active vibration control using optimized modified acceleration feedback with Adaptive Line Enhancer for frequency tracking. J. Sound Vib. 2011, 330, 1300–1311. [Google Scholar] [CrossRef]
- Mahmoodi, S.N.; Ahmadian, M.; Inman, D.J. Vibration control of microcantilever using adaptive modified positive position feedback. J. Intell. Mater. Smart Struct. 2010, 21, 571–580. [Google Scholar] [CrossRef]



| The Main System Parameters | PPF Controller Parameters | ||
|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeed, N.A.; Awwad, E.M.; Abdelhamid, T.; El-Meligy, M.A.; Sharaf, M. Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations. Symmetry 2021, 13, 255. https://doi.org/10.3390/sym13020255
Saeed NA, Awwad EM, Abdelhamid T, El-Meligy MA, Sharaf M. Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations. Symmetry. 2021; 13(2):255. https://doi.org/10.3390/sym13020255
Chicago/Turabian StyleSaeed, N. A., Emad Mahrous Awwad, Talaat Abdelhamid, Mohammed A. El-Meligy, and Mohamed Sharaf. 2021. "Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations" Symmetry 13, no. 2: 255. https://doi.org/10.3390/sym13020255
APA StyleSaeed, N. A., Awwad, E. M., Abdelhamid, T., El-Meligy, M. A., & Sharaf, M. (2021). Adaptive versus Conventional Positive Position Feedback Controller to Suppress a Nonlinear System Vibrations. Symmetry, 13(2), 255. https://doi.org/10.3390/sym13020255







