Review of Shape Phase Transition Studies for Bose-Fermi Systems: The Effect of the Odd-Particle on the Bosonic Core

Abstract

The quantum phase transition studies we have done during the last few years for odd-even systems are reviewed. The focus is on the quantum shape phase transition in Bose-Fermi systems. They are studied within the Interacting Boson-Fermion Model (IBFM). The geometry is included in this model by using the intrinsic frame formalism based on the concept of coherent states. First, the critical point symmetries E(5/4) and E(5/12) are summarized. E(5/4) describes the case of a single $j=3/2$ particle coupled to a bosonic core that undergoes a transition from spherical to $\gamma$-unstable. E(5/12) is an extension of E(5/4) that describes the multi-j case ($j=1/2,3/2,5/2$) along the same transitional path. Both, E(5/4) and E(5/12), are formulated in a geometrical context using the Bohr Hamiltonian. Similar situations can be studied within the IBFM considering the transitional path from U${}^{BF}$(5) to O${}^{BF}$(6). Such studies are also presented. No critical points have been proposed for other paths in odd-even systems as, for instance, the transition from spherical to axially deformed shapes. However, the study of such shape phase transition can be done easily within the IBFM considering the path from U${}^{BF}$(5) (spherical) to SU${}^{BF}$(3) (axial deformed). Thus, in a second part, this study is presented for the multi-j case. Energy levels and potential energy surfaces obtained within the intrinsic frame formalism of the IBFM Hamiltonian are discussed. Finally, our recent works within the IBFM for a single-j fermion coupled to a bosonic core that performs different shape phase transitional paths are reviewed. All significant paths in the model space are studied: from spherical to $\gamma$-unstable shape, from spherical to axially deformed (prolate and oblate) shapes, and from prolate to oblate shape passing through the $\gamma$-unstable shape. The aim of these applications is to understand the effect of the coupled fermion on the core when moving along a given transitional path and how the coupled fermion modifies the bosonic core around the critical points.

1. Introduction

An interesting aspect of modern nuclear physics is the study of the quantum shape phase transition in atomic nuclei. Phase transitions are usually discussed and well defined for macroscopic systems. However, in the last few years, precursors of phase transitions have been observed in mesoscopic systems and then one talks about quantum phase transitions. Classical phase transitions are usually classified into two classes, called first-order and continuous phase transitions depending on the behavior of the order parameter at the critical point. At this point, the order parameter changes typically from zero to a finite value. When this variation is discontinuous at the critical point it is said that the transition is first order. On the contrary, when the variation of the order parameter is smooth at the critical point, the transition is said to be continuous. The same ideas can be translated to quantum phase transitions. It is clear that the concept of critical point is intimately linked to the subject of phase transitions. In this context, about twenty years ago, Iachello introduced the concept of the critical point symmetry [1] in relation to quantum systems as atomic nuclei. Iachello worked out two critical point symmetries within the geometrical model using the Bohr Hamiltonian [2]. One of them, called E(5), describes the critical point in the shape transition from spherical to deformed $\gamma$-unstable shapes [1] and is appropriate for continuous shape phase transitions. The other symmetry proposed by Iachello, called X(5), describes the critical point in the transition from spherical to axially deformed shapes [3] and is a benchmark for first order phase transitions.

Although the Interacting Boson Model (IBM) [4] is formulated from the beginning in a second quantization formalism, one can obtain a geometric image of the model using the idea of coherent state and intrinsic state formalism. In this way, one finds geometrical shapes, as in the Bohr model, linked to the different dynamical symmetries of the model. Thus, the U(5) limit corresponds to spherical shapes, the SU(3) ($\overline{\mathrm{SU}\left(3\right)}$) limit produces prolate (oblate) axially symmetric shapes, and the O(6) limit generates deformed $\gamma$-unstable shapes. Therefore, one can look for the equivalent to E(5) or X(5) symmetries in the IBM. In this case, the critical points are called $e\left(5\right)$ and $x\left(5\right)$ and correspond to the transitional paths from U(5) to O(6) and from U(5) to SU(3), respectively. Many experimental and theoretical studies have been performed for quantum phase transitions especially for even-even nuclei within the IBM [4], as reported in different review papers [5,6,7,8,9].

Relatively less attention has been devoted to the parallel topic of quantum phase transitions in Bose-Fermi systems. In addition to the above mentioned critical point symmetries for even-even systems, Iachello, also within the Bohr Hamiltonian, proposed to extend the concept of critical point symmetry to Bose-Fermi systems for using it in odd-even nuclei. Iachello worked out the case of an odd $j=3/2$ particle coupled to a bosonic core that undergoes a transition from spherical to $\gamma$-unstable shapes [10]. Soon after, an extension to multi-j case, called E(5/12), including $j=1/2,3/2$, and $5/2$ also within the Bohr Hamiltonian was proposed [11]. No other critical point symmetries have been proposed for odd-even systems. As in the case of even-even nuclei, the Interacting Boson-Fermion Model (IBFM) [12] can be used to study similar transitional situations as those described in the Bohr model and through any of the relevant transitional paths. Special relevance have the paths from spherical to deformed $\gamma$-unstable and from spherical to axially deformed shapes [11,13,14]. Although the E(5/4) and E(5/12), in the geometric model, and the corresponding critical point in the IBFM (spherical to deformed $\gamma$-unstable) are different, the results obtained within the IBFM and those from E(5/12) show a remarkable agreement for the energy levels spectrum and electromagnetic transitions.

The transition from spherical to axially deformed shape in Bose-Fermi systems has also been considered in the framework of the IBFM, where the odd fermion occupies the set of $j=1/2,3/2,5/2$ orbitals [15]. The energy levels and the electromagnetic transitions of the odd-even system have been calculated within the IBFM Hamiltonian and also the intrinsic frame formalism was employed to describe this quantum phase transition.

During the last decade, we have developed a systematic investigation of the quantum shape phase transition in Bose-Fermi systems for the case of a single-j fermion coupled to a bosonic core [16,17,18,19,20], making use of the intrinsic frame formalism to associate a given shape to the solution of a IBFM Hamiltonian. Transitions from spherical to $\gamma$–unstable shape [16], from spherical to prolate shape [18], from spherical to oblate shape [19] have been studied up to now, with the aim of understanding the effect of the coupled fermion on the core when moving to the transition paths and around the critical points. More recently, we have closed the circle, by investigating the phase transition from prolate to oblate shape passing through the $\gamma$-unstable shape in odd-even systems [20]. The different paths are marked in Figure 1.

We would like to mention that other relevant contributions to the topic of shape phase transitions in odd-even nuclei have been presented in the last 15 years in Refs. [10,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].

In this review paper, we present a summary of the most important results we have obtained within the IBFM for shape phase transitions in odd-even nuclei, namely the critical point symmetries for the specific E(5/4) [13] and E(5/12) [11,14] cases; the U${}^{BF}$(5)-SU${}^{BF}$(3) transition in odd nuclei for multi-j orbits, $j=1/2,3/2,5/2$ [15]; the results of our recent works related to the case of a single-j fermion coupled to the bosonic core that performs different transitions mentioned in previous paragraph [16,18,19,20]. The paper is organized as follows. The IBFM model with its Hamiltonian and the intrinsic frame formalism for Bose-Fermi systems are revised in Section 2. In Section 3, the E(5/4) and E(5/12) critical point symmetries and some results for equivalent situations in IBFM are discussed. In Section 4, the IBFM U${}^{BF}$(5) to SU${}^{BF}$(3) phase transition in odd nuclei for multi-j orbits is briefly outlined and results are presented for energy levels and energy surfaces. The results of the phase transitions in Bose-Fermi systems investigated within the intrinsic frame formalism of the IBFM for the case of a single-j fermion coupled to a bosonic core are reviewed in Section 5. General conclusions are drawn in the final section.

2. Methods: The IBFM Hamiltonian and the Intrinsic Frame Formalism

The IBM model [4] is designed to describe collective properties of medium and heavy mass even-even nuclei. The model has three basic approximations: (i) only valence particles are taken into account, (ii) these fermions are coupled to angular momentum $L=0$ and $L=2$, and (iii) those coupled fermions are treated as bosons (s-bosons with $L=0$ and d-bosons with $L=2$). With these approximations, many studies have been done for even-even nuclei. The boson hamiltonian in terms of s- and d-bosons can be written as,

$$H_B=(1-x){\widehat{n}}_d-\frac{x}{\alpha N_B}{\widehat{Q}}_B^{\left(\chi \right)}·{\widehat{Q}}_B^{\left(\chi \right)},$$

(1)

where $N_B$ is the number of bosons, $\alpha$ is a parameter, ${\widehat{n}}_d$ is the d-boson number operator,

$${\widehat{n}}_d=\sum _{\mu }{d}_{\mu }^{†}{d}_{\mu },$$

(2)

and ${\widehat{Q}}_B^{\left(\chi \right)}$ is the boson quadrupole operator given by

$${\widehat{Q}}_B^{\left(\chi \right)}={(s^{†}\times \tilde{d}+d^{†}\times \tilde{s})}^{\left(2\right)}+\chi {(d^{†}\times \tilde{d})}^{\left(2\right)}.$$

(3)

The control parameters of the model are x, and $\chi$. In Figure 1, the IBM model space is schematically plotted. There are four dynamical symmetries in the model: U(5), SU(3), $\overline{\mathrm{SU}\left(3\right)}$, and O(6). Shapes can be obtained in the model by using the intrinsic state formalism based on a coherent state (Refs. [37,38,39])

$$|{\Phi }_{gs}(\beta ,\gamma )\rangle =\frac{1}{\sqrt{N_B!}}{\left[b_{gs}^{†}(\beta ,\gamma )\right]}^{N_B}|0\rangle ,$$

(4)

where $N_B$ is the number of bosons for a particular nucleus, $|0\rangle$ is the boson vacuum, and $b_{gs}^{†}(\beta ,\gamma )$ is the ground state boson condensate creation operator given by

$$b_{gs}^{†}(\beta ,\gamma )=\frac{1}{\sqrt{1+{\beta }^2}}\left[s^{†}+\beta cos\gamma d_0^{†}+\frac{\beta }{\sqrt{2}}sin\gamma (d_2^{†}+d_{-2}^{†})\right].$$

(5)

$\beta$ and $\gamma$ are shape variables that are related to the quadrupole deformation parameters of the geometric collective model of Bohr-Mottelson [2]. The ground state energy surface is established by calculating the expectation value of the given bosonic $H_B$ Hamiltonian (1) in the intrinsic state (4)

$$E_{gs}(\beta ,\gamma )=\langle {\Phi }_{gs}(\beta ,\gamma )|H_B|{\Phi }_{gs}(\beta ,\gamma )\rangle .$$

(6)

Mathematically, $\beta$ and $\gamma$ are variational parameters in the intrinsic formalism of IBM model in the classical limit [37,38,39] that can be determined by minimizing the energy surface (6). This connection has been done and the correspondence with the IBM dynamical symmetries is: U(5) corresponds to $x=0$ and then $\beta =0$, spherical shape, SU(3) ($\overline{\mathrm{SU}\left(3\right)}$) corresponds to $x=1$ and $\chi =-\sqrt{7}/2$ ( $\chi =+\sqrt{7}/2$) and produces $\beta =\sqrt{2}$ and $\gamma =0$ ($\gamma ={60}^{\circ }$), axially deformed prolate (oblate) shape, and, finally, O(6) corresponds to $x=1$ and $\chi =0$, and gives a deformed $\gamma$-unstable shape. See Figure 1.

The IBFM model [12] is the extension of the IBM model [4] for the description of the properties of a system of $N_B$ bosons plus one fermion, the typical application being represented by an odd-even nuclei. The general model Hamiltonian for the coupling of an single fermion to the bosonic core is written as follows:

$$H=H_B+H_F+V_{BF},$$

(7)

where H${}_B$ is the pure bosonic Hamiltonian Equation (1), H${}_F$ is the fermion Hamiltonian

$$H_F=\sum _j{\epsilon }_j{a}_j^{†}·{\tilde{a}}_j,$$

(8)

where ${\epsilon }_j$ are the single-particle energies for the orbits j allowed for the fermion, and the third term in (7), V${}_{BF}$, couples the bosonic and fermionic parts. Usually, a quadrupole-quadrupole boson-fermion interaction is assumed:

$${\widehat{V}}_{BF}=-2\frac{x}{\alpha N_B}{\widehat{Q}}_B^{\left(\chi \right)}·{\widehat{q}}_F,$$

(9)

where $Q_B^{\left(\chi \right)}$ is the boson quadrupole operator given in Equation (3) and ${\widehat{q}}_F$ is the fermion quadrupole operator

$${\widehat{q}}_F=\sum _j{t}_j{(a_j^{†}\times {\tilde{a}}_j)}^{\left(2\right)},$$

(10)

where j indicates the single particle orbitals. In the case of a single-j shell, the coefficients $t_j$ can be set to one without loss of generality. Notice that, in the case of $j=1/2$, this operator cannot be defined.

The intrinsic frame formalism for odd-even systems [40,41,42] leads itself to the description of the shapes involved in a quantum phase transition. A potential energy surface, depending on the shape variables, can be associated to a given model Hamiltonian, such as (7), in this formalism. To consider the intrinsic frame states of the mixed boson-fermion system, the single-fermion states have to be coupled to the bosonic intrinsic ground-state $|{\Phi }_{gs}(\beta ,\gamma )\rangle$ given by Equation (4). To obtain the lowest states of the odd-even nucleus, we first construct the coupled states as follows

$$|{\Psi }_{jK}(\beta ,\gamma )\rangle =|{\Phi }_{gs}(\beta ,\gamma )\rangle \otimes |jK\rangle ,$$

(11)

and then diagonalize the total boson-fermion Hamiltonian in this basis, thus obtaining a set of energy eigenvalues $E_n$($\beta ,\gamma$), that are functions of the variational parameters, where n is an index that counts the solutions of the odd-even system.

In the following, we will use this formalism to study different transitional situations in IBFM, starting with path 1 in Figure 1 and the comparison with the proposed critical point symmetries.

3. The E(5/4) and E(5/12) Critical Points of the Boson-Fermion System

The concept of critical point symmetries in boson-fermion systems was fist proposed by Iachello [10]. He studied the case of an odd particle moving in a single $j=3/2$ shell coupled to an E(5) bosonic core, and called the corresponding symmetry E(5/4). The analytic solution of the E(5/4) model was first obtained from the Bohr Hamiltonian. Later on, the IBFM Hamiltonian was used to study the corresponding phase transition, called e(5/4), along the U(5)-O(6) line [13] for the even-even part, and the results are in good agreement with those of Bohr Hamiltonian for E(5/4) model. A more complex case of the critical point symmetry so-called as E(5/12) model [11,14] has been described for the case of multi-j orbitals, again starting from the Bohr Hamiltonian. In addition, in this case, comparable results are obtained within the IBFM model, called e(5/12). In this richer case, the fermion that can occupy a set of single-particle states with angular momenta j = $1/2$, $3/2$, $5/2$ and is coupled to a bosonic core undergoing the transition (path 1) from spherical to deformed $\gamma$-unstable situation.

These two cases are discussed below.

3.1. The E(5/4) Critical Point of the Boson-Fermion System

For the bosonic part of both mentioned E(5/4) and E(5/12) critical point symmetries, the bosonic Hamiltonian used is (7) with $\alpha =1$ (the selection of other $\alpha$ value displaces the critical point in x but all the characteristics remain the same). Since the transition in the bosonic core is from spherical to deformed $\gamma$-unstable shapes (path 1 in Figure 1), the value of $\chi =0$ is fixed along the path. Thus, there is a single control parameter, x, that changes in the interval $[0,1]$. For $x=0$, the system is in the U(5) dynamical symmetry (spherical), and, for $x=1$, the system is in the O(6) dynamical symmetry (deformed $\gamma$-unstable). All along the path, the system is $\gamma$-independent. Notice that the quadrupole operator does not show for this path the term with the coupling of two d bosons, since $\chi =0$ for this leg of the Casten triangle. The critical point occurs at $x_c=N_B/\left(5N_B-8\right)$. This result is obtained analytically by using the intrinsic frame formalism [13].

The Hamiltonian (7) within the IBFM model [12], where a single fermion is coupled to the even-even bosonic core, can be used to discuss the energy spectra evolution in odd nuclei and the corresponding behavior around the critical point. The bosonic part for this case is $\gamma$-independent, consequently, the Hamiltonian is only a function of $\beta$. The pure fermion part (8) in Equation (7) is just a constant for a single fermion: $H_F=constant$. The fermion quadrupole operator for this single-j case ($j=3/2$) is

$$q_F={(a_{3/2}^{†}\times {\tilde{a}}_{3/2})}^{\left(2\right)},$$

and the coupling term for the boson-fermion interaction is given by Equation (9) with $\alpha =1$.

The intrinsic frame states of the mixed boson-fermion system can be built by coupling the $j=3/2$ orbital with the ground state $|{\Phi }_{gs}(\beta ,\gamma )\rangle$ of the boson condensate given in Equation (4) obtaining $|{\Phi }_{gs}(\beta ,\gamma )\rangle \otimes |jK\rangle$, Equation (11). The fermionic part, as mentioned above, is just a constant because of the single-j, and so only the ${\widehat{V}}_{BF}$ coupling term has to be diagonalized in this basis. The doubly degenerate eigenvalues $E_{\pm }\left(\beta \right)$ are given by

$$E_{\pm }(x,\beta )=\pm 2\frac{x\beta }{1+{\beta }^2}.$$

(12)

Here, the coupled fermion does not destroy or alter the $\gamma$-instability of the system and the energy surfaces obtained for the different intrinsic states of the odd system are still $\gamma$-independent [42]. This special case of supersymmetry is known from the work of Bayman and Silverberg [43].

The corresponding evolution of the spectrum is displayed as a function of the control parameter x given in Hamiltonian (1) in Figure 2. The levels in the even-even system (left side) are compared with those in the odd-even system (right panel). The number of bosons is $N_B=7$ for both cases and the odd particle is assumed to be in the $j=3/2$ orbital. The critical point is $x_c=N_B/\left(5N_B-8\right)=7/27$ ≈ $0.26$ for seven bosons as marked in Figure 2. The level evolution of the odd-even system exhibits quite a similar behavior to that of the even-even system. In the odd system, the group Spin${}^{BF}$(5) replaces the group O${}^B$(5) of the bosonic case and leads to a richer pattern for the fermionic case. In particular, the multiplet $(3/2,1/2)$ plays the role of the $\tau =1$ multiplet of the even-even case, and leads to a larger set of degenerate angular momenta, namely $j=1/2,5/2$ and $7/2$. This is a clear signature for the occurrence of this symmetry: there should be a relatively well isolated multiplet with these quantum numbers, in order to speak of an underlying Spin${}^{BF}$(5) symmetry. The energy ratios of the odd-even case are also slightly different from that of even-even case. In the $x=0$ limit, the ground-band with maximum $\sigma$ values for both systems are obtained ($\sigma$ = $N_B$ for even-even nuclei and ${\sigma }_1=N_B+1/2$ for odd-even nuclei). The energy ratio E${}_{(5/2,1/2)}$/E${}_{(3/2,1/2)}$ of ground band is 2.4 and close to the ratio R${}_{4/2}$=2.5 of O${}^B$(6) symmetry.

To better evidence the peculiarity of the $j=3/2$ case, we compare in Figure 3 the evolution of the spectrum in the single-j cases, $j=3/2$ and $j=5/2$, as a function of the control parameter x. As seen in this figure, the spectrum of the $j=5/2$ case (right panel) is more complex because of the degeneracies are broken, even though it exhibits a qualitatively similar behavior with respect to that of the $j=3/2$ case, displayed in the left panel.

To summarize this subsection, we reviewed the results obtained within the IBFM model for the coupling of a $j=3/2$ particle to a bosonic core that undergoes a transition from spherical to $\gamma$-unstable shapes. The energy levels of the odd-even system display qualitatively similar behaviors with respect to levels of the even-even system. A more detailed investigation can be found in Ref. [13], including a comparison of these results with the E(5/4) model [10] based on the Bohr Hamiltonian.

3.2. The E(5/12) Critical Point of the Boson-Fermion System

The E(5/12) critical point within the collective Bohr hamiltonian for the multi-j case [11,14] is an extension of the E(5/4) critical point [10,13]. In this subsection, we review the corresponding results for the equivalent critical point within the IBFM model, called e(5/12), for the coupling of a single fermion moving in the $j=1/2,3/2,5/2$ single-particle orbits to the bosonic core undergoing a transition from spherical to $\gamma$-unstable shape (path 1 in Figure 1). It is worth mentioning that the Bohr Hamiltonian in this multi-j case has two extra parameters as given explicitly in (Ref. [11], Equation (1)).

The bosonic term in the general IBFM Hamiltonian (7), parametrized as in Equation (1), can be recasted into a combination of Casimir operators as follows [11,14];

$$H_B=(1-x)C_1\left[{\mathrm{U}}^B\left(5\right)\right]-\frac{x}{2\alpha N_B}\{C_2\left[{\mathrm{O}}^B\left(6\right)\right]-C_2\left[{\mathrm{O}}^B\left(5\right)\right]\},$$

(13)

where $C_1$[U${}^B$(5)] is the linear Casimir operator of the U${}^B$(5) algebra, and $C_2$[O${}^B$(6)] and $C_2$[O${}^B$(5)] are the quadratic Casimir operators of the O${}^B$(6) and O${}^B$(5) algebras. For the following results, we used $\alpha =1$. This bosonic Hamiltonian can produce a phase transition from spherical to $\gamma$-unstable case along the U(5)–O(6) line by sweeping the control parameter x from 0 to 1, and the critical point occurs at $x_c=N_B/\left(5N_B-8\right)$ [11,13,14].

The remaining pure fermionic term and the boson-fermion interaction term, that are needed in the general Hamiltonian (7), have been parametrized as follows, in Refs. [11,14],

$$H_F+V_{BF}=\frac{k^{\prime }}{2N_B}{C}_2\left[{\mathrm{O}}^F\left(5\right)\right]+\frac{k}{2N_B}\{C_2\left[{\mathrm{O}}^{BF}\left(5\right)\right]-C_2\left[{\mathrm{O}}^B\left(5\right)\right]-C_2\left[{\mathrm{O}}^F\left(5\right)\right]\},$$

(14)

where $C_2$[O${}^F$(5)] and $C_2$[O${}^{BF}$(5)] are the quadratic Casimir operators of the O${}^F$(5) and O${}^{BF}$(5) algebras, respectively. k and $k^{\prime }$ are the new parameters of the multi-j E(5/12) model, that were fixed to $k=-1/4$ and $k^{\prime }=5/2$ in Ref. [11]. For the IBFM comparison to the geometric E(5/12), the same values for $k=-1/4$ and $k^{\prime }=5/2$ have been used.

The general Hamiltonian (7) can be thus rewritten in terms of Casimir operators as

$$\begin{array}{cc}\hfill H=(1-x)& C_1\left[{\mathrm{U}}^B\left(5\right)\right]-\frac{x}{2N_B}\{C_2\left[{\mathrm{O}}^B\left(6\right)\right]-C_2\left[{\mathrm{O}}^B\left(5\right)\right]\}\hfill \\ & +\frac{k}{2N_B}\{C_2\left[{\mathrm{O}}^{BF}\left(5\right)\right]-C_2\left[{\mathrm{O}}^B\left(5\right)\right]-C_2\left[{\mathrm{O}}^F\left(5\right)\right]\}+\frac{k^{\prime }}{2N_B}{C}_2\left[{\mathrm{O}}^F\left(5\right)\right].\hfill \end{array}$$

(15)

This Hamiltonian is designed to mimic the corresponding Hamiltonian in the geometrical E(5/12) model [11].

The energy spectrum of the odd-even system corresponding to the results of the IBFM calculation with the Hamiltonian (15) at the critical point, given in the lower panel of Figure 4 is compared with the corresponding energy spectrum of the odd-even system obtained within the E(5/12) model (upper panel). The critical point $x_c$ is roughly 0.26 for the choice of $N_B=7$ bosons. As seen in this figure, the energy spectrum obtained in both approaches are structurally analogous with each other, even though small differences remain in the energies and transition rates.

The above IBFM Hamiltonian (15) has been specifically designed to match the E(5/12) Hamiltonian. An alternative way for checking the results of the E(5/12) model is to apply the Hamiltonian (1) used in the previous subsection for the U(5)-O(6) transition in even-even system and to select the critical point under these conditions. For the odd-even system, the odd fermion, allowed to span the set of $j=1/2,3/2,5/2$ orbitals, is coupled to the bosonic core using the standard form of quadrupole-quadrupole boson-fermion interaction. In this case, the single-particle energies in Equation (8) are taken as ${\epsilon }_{1/2}$ = 0, and ${\epsilon }_{3/2}$ = ${\epsilon }_{5/2}$ = $(1-x)+4x/N_B$. For the boson-fermion part, the usual form Equation (9) is used with the fermion quadrupole operator given in this situation as [14]

$${\widehat{q}}_F=t_F^{\left(2\right)}\left[-\sqrt{\frac{4}{5}}{(a_{1/2}^{†}\times {\tilde{a}}_{3/2}+h.c.)}^{\left(2\right)}-\sqrt{\frac{6}{5}}{(a_{1/2}^{†}\times {\tilde{a}}_{5/2}+h.c.)}^{\left(2\right)}\right].$$

(16)

With these choices, the total Hamiltonian (7) can be recast in a way that is formally equivalent to that given in Equation (13) for the boson part, namely

$$H_{BF}=(1-x)C_1\left[{\mathrm{U}}^{BF}\left(5\right)\right]-\frac{x}{2N_B}\{C_2\left[{\mathrm{O}}^{BF}\left(6\right)\right]-C_2\left[{\mathrm{O}}^{BF}\left(5\right)\right]\}.$$

(17)

The evolution of the spectrum as a function of the control parameter x is shown in Figure 5. The boson number used is $N_B=7$, and the critical point is $x_c=N_B/\left(5N_B-8\right)\approx 0.26$ as marked by a line. Energies are normalized to the energy difference between the first excited state (which is always a $3/2-5/2$ doublet) and the $J_{BF}=1/2$ ground state. Each state is characterized by the $({\tau }_1,{\tau }_2)$ quantum numbers, and the set $[N_1,N_2]({\sigma }_1,{\sigma }_2,{\sigma }_3)$, different for each band, is given for each state on the right side of the figure.

The comparison of results obtained at the critical point for both the E(5/12) and this new IBFM model is displayed in Figure 6. The IBFM states are labeled by the $[N_1,N_2]({\sigma }_1,{\sigma }_2,{\sigma }_3)$ quantum numbers and labels $({\tau }_1,{\tau }_2)$ are given beside each level for each band. The structure of the spectrum obtained within the IBFM model given in lower panel resembles quite closely the spectrum of E(5/12) given in the upper panel.

For the shape phase transition in odd nuclei in a multi-j model, two IBFM Hamiltonians have been designed. The first one is produced to mimic the situation studied in the E(5/12) model for the case of the coupling of a single fermion moving in the $j=1/2,3/2,5/2$ orbitals to a bosonic core at the critical point appearing in the transition from spherical to $\gamma$-unstable shapes. In a second one, the IBFM model was considered for the case of the coupling of a single fermion moving in the same multi-j orbitals to a bosonic core undergoing a transition from U(5) to O(6) via a more realistic quadrupole-quadrupole boson-fermion interaction. In this subsection, we reviewed both IBFM models and results for the energy spectrum obtained by the IBFM calculations have been compared with the analytical results of the E(5/12) model. Both IBFM models show a remarkable agreement with each other and with the E(5/12) critical point symmetry. One can find a detailed investigations in Refs. [11,14] including all formulations of both models and some other comparisons for the results concerning the electromagnetic transitions and moments (E2 and M1).

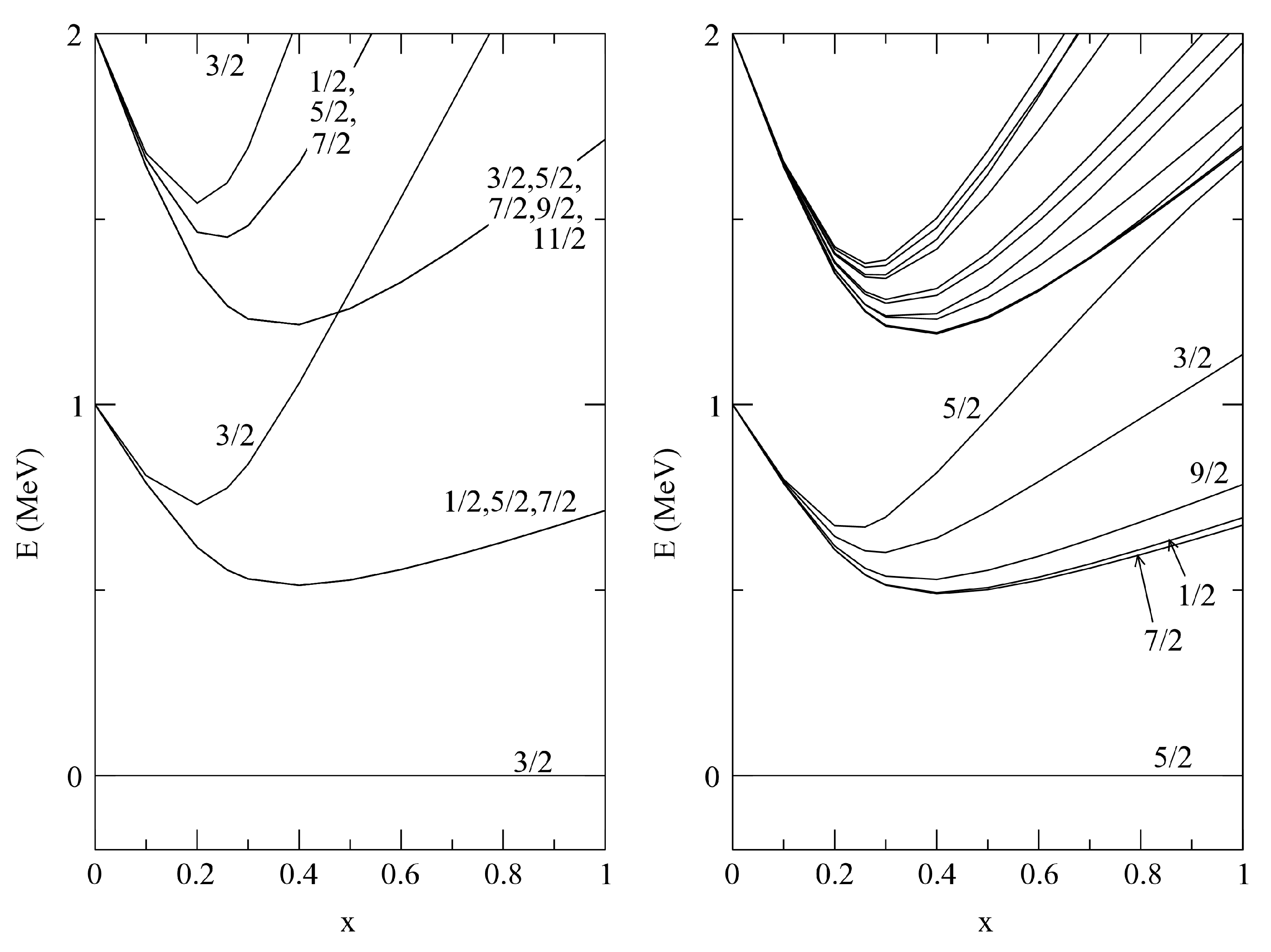
4. U^BF(5) to SU^BF(3) Shape Phase Transition in Odd Nuclei for Multi-j Orbits (j = 1/2, 3/2, 5/2): The Role of the Odd Particle at the Critical Point

In this section, we review some of the results obtained with the IBFM model for a transition from sphericity to axial deformation, with the single fermion still occupying the set of $j=1/2,3/2,5/2$ orbitals. No critical point symmetry has been proposed for this path in the case of odd-even systems (path 2 in Figure 1). However, the critical point in this transitional path can be studied within the IBFM. For this case, the bosonic part of the Hamiltonian, Equation (1), along the transition path from U(5) to SU(3) has a fixed value for the $\chi$ parameter, i.e., $\chi =-\sqrt{7}/2$. Thus, in this case, the only control parameter is x that changes from zero (U(5)-spherical limit) to 1 (SU(3) -prolate axially deformed limit). In addition, for the calculations in this section, $\alpha =4$ in Equations (1) and (9) (this is just to have the critical point around the middle of the interval for the parameter x). In fact, with this $\alpha$ value, the phase transition along this path occurs the critical point $x_c=16N_B/(34N_B-27)$, as shown in Ref. [15].

The boson Hamiltonian (1) can be recast into the Casimir form ($C_i$ with $i=1,2$ for linear or quadratic Casimir operator of the listed Lie algebra) as follows [15];

$$H_B=(1-x)C_1\left[{\mathrm{U}}^B\left(5\right)\right]-\frac{x}{8N_B}\left\{\frac{3}{2}{C}_2\left[{\mathrm{SU}}^B\left(3\right)\right]-\frac{3}{8}{C}_2\left[{\mathrm{O}}^B\left(3\right)\right]\right\}.$$

(18)

A similar Casimir form can be used for the boson-fermion Hamiltonian to describe the transition from spherical to axially deformed odd-even system within the IBFM by

$$H_{BF}=(1-x)C_1\left[{\mathrm{U}}^{BF}\left(5\right)\right]-\frac{x}{8N_B}\left\{\frac{3}{2}{C}_2\left[{\mathrm{SU}}^{BF}\left(3\right)\right]-\frac{3}{8}{C}_2\left[{\mathrm{O}}^{BF}\left(3\right)\right]\right\}.$$

(19)

where the label $BF$ stands for boson-fermion. The bosonic Casimir operators and the Bose-Fermi Casimir operators are explained in detail in Refs. [4,12]. This boson-fermion Hamiltonian is rewritten for the present problem as follows:

$$H_{BF}=(1-x)(n_d+n_{3/2}+n_{5/2})-\frac{x}{4N_B}{Q}_{BF}·Q_{BF},$$

(20)

where $n_{j=3/2(5/2)}$ is the fermion number operator, and $Q_{BF}$ is the sum of the boson and fermion quadrupole operators given by

$$Q_{BF}=Q_B^{(\chi =-\sqrt{7}/2)}+q_F,$$

(21)

where $Q_B$ is the boson quadrupole operator (3) with $\chi =-\sqrt{7}/2$, and $q_F$ is the fermion quadrupole operator (10), given in this case by [15]

$$\begin{array}{cc}\hfill q_F& =-\sqrt{\frac{4}{5}}\left[{(a_{1/2}^{†}\times {\tilde{a}}_{3/2})}^{\left(2\right)}-{(a_{3/2}^{†}\times {\tilde{a}}_{1/2})}^{\left(2\right)}\right]-\sqrt{\frac{6}{5}}\left[{(a_{1/2}^{†}\times {\tilde{a}}_{5/2})}^{\left(2\right)}-{(a_{1/2}^{†}\times {\tilde{a}}_{1/2})}^{\left(2\right)}\right]\hfill \\ & -\frac{\sqrt{7}}{2}\left[-\sqrt{\frac{14}{25}}{(a_{3/2}^{†}\times {\tilde{a}}_{3/2})}^{\left(2\right)}+\sqrt{\frac{6}{25}}\left[{(a_{3/2}^{†}\times {\tilde{a}}_{5/2})}^{\left(2\right)}-{(a_{5/2}^{†}\times {\tilde{a}}_{3/2})}^{\left(2\right)}\right]-\sqrt{\frac{24}{25}}{(a_{5/2}^{†}\times {\tilde{a}}_{5/2})}^{\left(2\right)}\right].\hfill \end{array}$$

(22)

With particular choice of the control parameter x in Hamiltonian (20), one can obtain the U${}^{BF}$(5) and SU${}^{BF}$(3) dynamical symmetries. The values are $x=0$ for U${}^{BF}$(5) and $x=1$ for SU${}^{BF}$(3). Changing this x parameter in the Hamiltonian, one moves between these symmetries following the transitional path from spherical (U(5)) to axially deformed (SU(3)) shapes. In this case, calculations were done for a bosonic core with $N_B=9$ bosons to which a single fermion ($N_F=1$) is coupled. 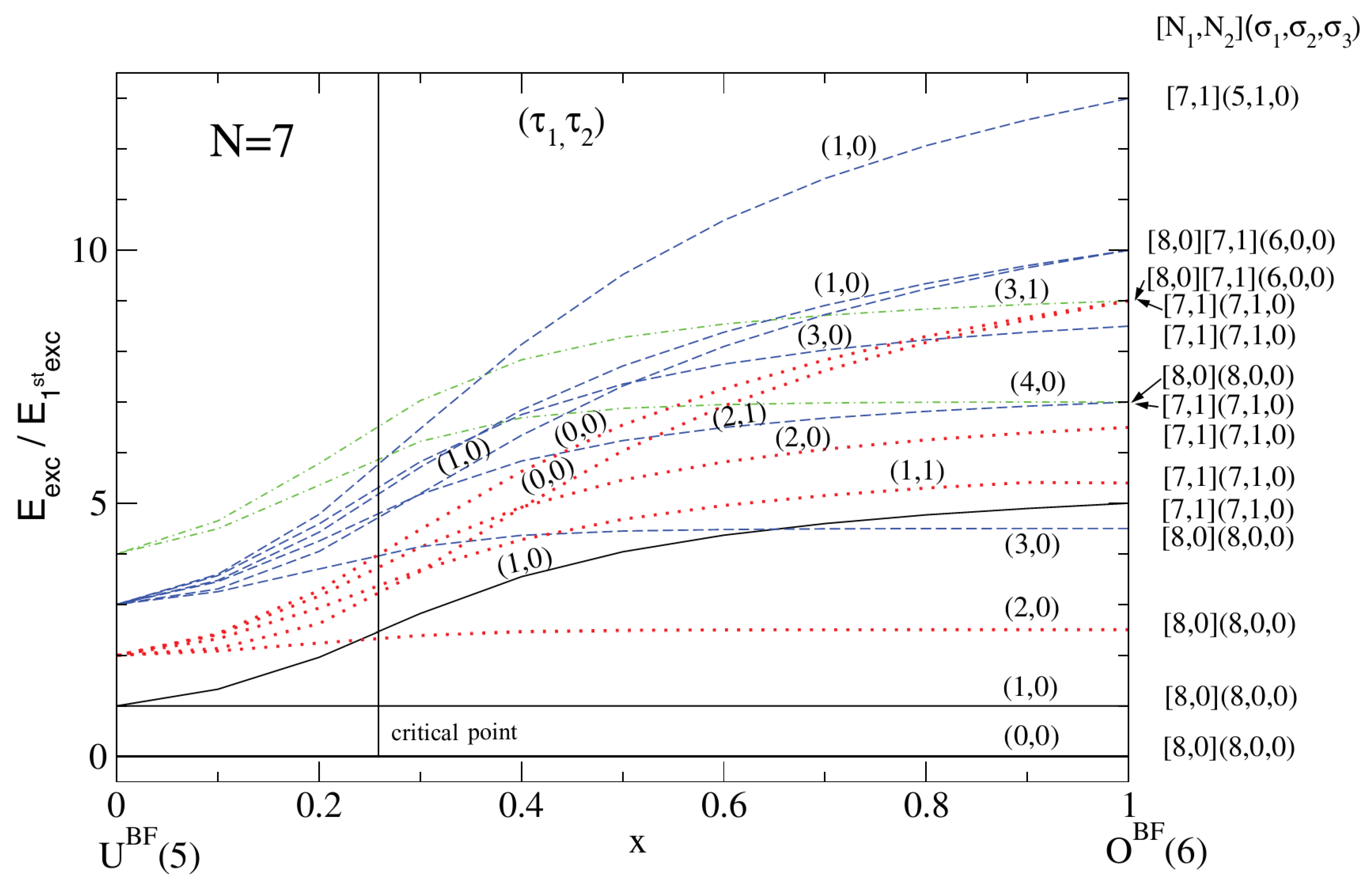The critical value of the control parameter for the even-even system is $x_c\approx 0.516$ for 9 bosons since the phase transition occurs at $x_c=16N_B/(34N_B-27)$, and the critical point of the odd-even case is $x_c\approx 0.485$ [15]. The full evolution of some selected energy levels, normalized to the energy of the first excited state, along the U${}^{BF}$(5) to SU${}^{BF}$(3) transitional path is shown in Figure 7. Each state is characterized by the SU${}^{BF}$(3) quantum numbers ($\lambda ,\mu$), which are strictly valid only at $x=1$, and the O${}^{BF}$(3) quantum number, L. As seen in this figure, the general behavior of the energy levels is rather smooth close to the U${}^{BF}$(5) and SU${}^{BF}$(3) dynamical symmetries and changes rapidly in the neighborhood of the critical point, indicated by a dashed vertical line. This flat behavior close to the dynamical symmetries has been observed before, also in even systems, and called quasi-dynamical symmetry by Rowe [44].

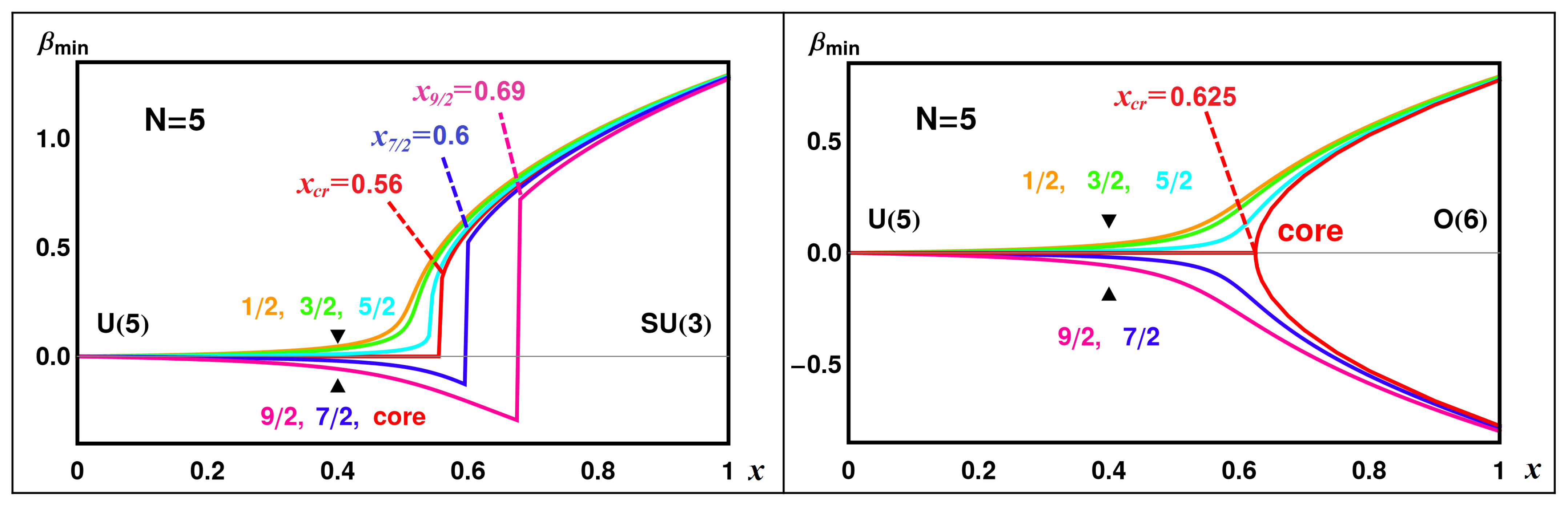
The concept of intrinsic states and associated energy surfaces can be used to better understand the quantum shape phase transition from U${}^{BF}$(5) to SU${}^{BF}$(3). The intrinsic frame formalism has been discussed in Section 2. In this specific case, for the U${}^{BF}$(5)-SU${}^{BF}$(3) transition, the energy surface has a well-defined minimum for any value of the control parameter x, as a function of the parameter $\beta$ (for $\gamma =0$). Detailed explanation and formalism for the even-even system is discussed in Ref. [15]. Intrinsic frame states for odd systems can be built by coupling the odd single-particle states (each with a given angular momentum j and magnetic component K) to the intrinsic states of the even core as formulated at the end of Section 2. For the specific U${}^F$(12) algebra, a total of 12 components appears, due to the multi-j space given by $j=1/2,3/2,5/2$, but this is restricted to 6 because of the symmetry $K\leftrightarrow -K$. For $\gamma =0$, the Hamiltonian (20) conserves the quantum number K and the diagonalization is independently done for each K-value. Thus, two states with $K=1/2$, one degenerate pair with $K=1/2,3/2$ and the degenerate pair with $K=3/2,5/2$ have been obtained in this case. Notice that one of the $K=1/2$ states merges with the $K=3/2,5/2$ pair in the strict $x=1$ limit.

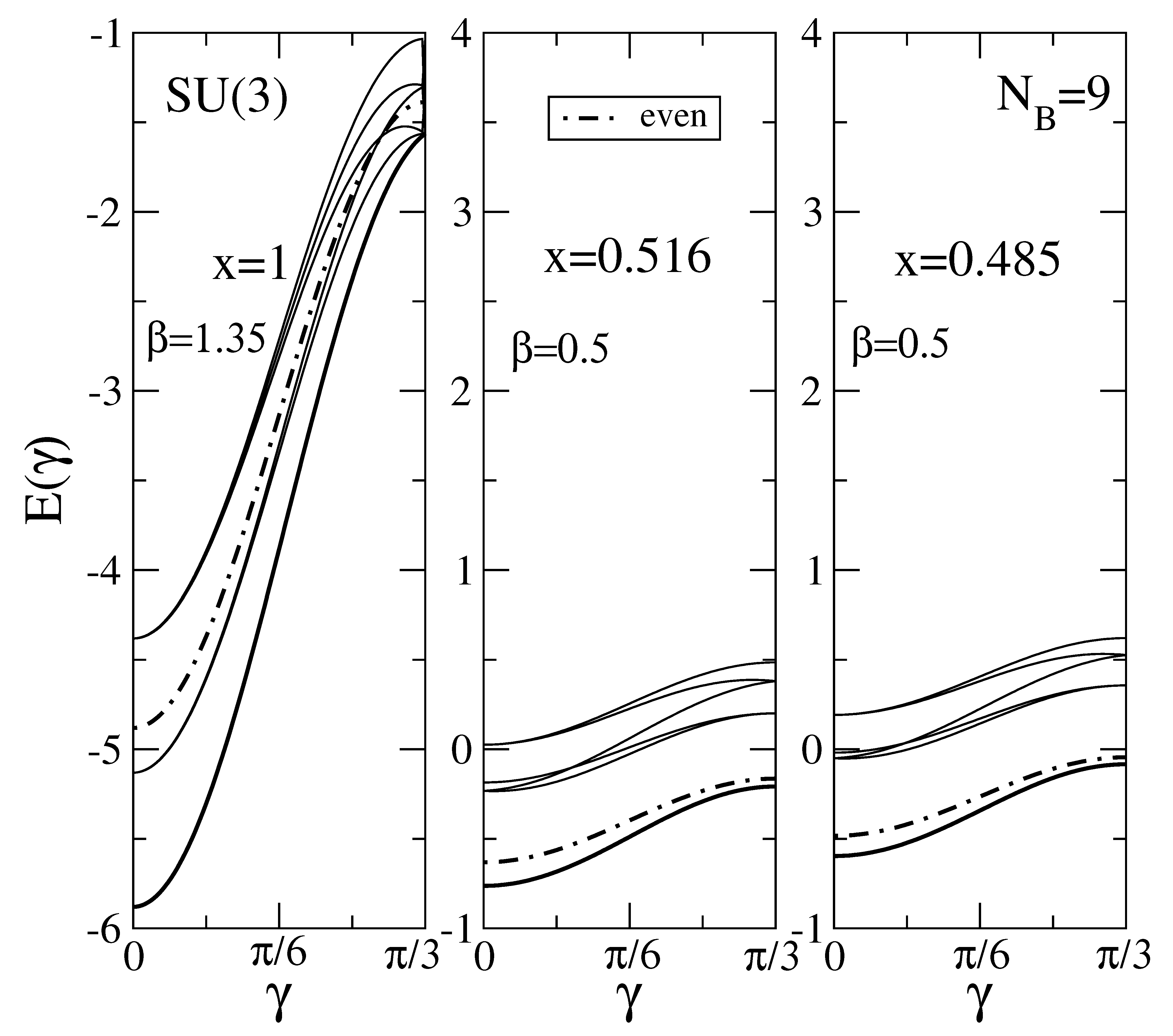
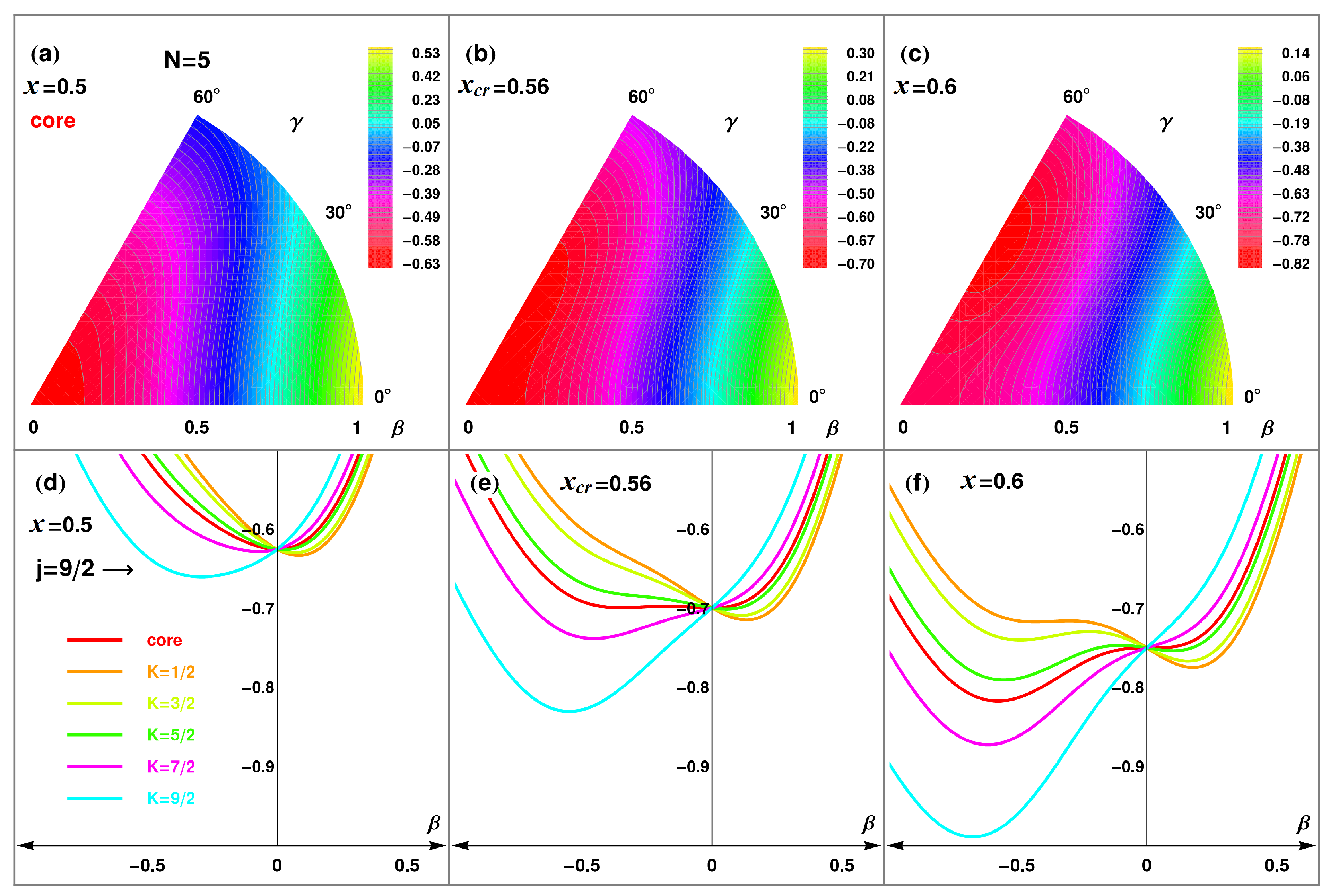
The boson-fermion energy surfaces as a function of the deformation parameter $\beta$ for $\gamma =0$ are shown in Figure 8, in comparison with the energy surfaces for the even–even core with $N_B=9$ bosons (dashed lines). In left panel of this figure, we consider a well-deformed case, corresponding to the SU${}^{BF}$(3) dynamical symmetry, by taking the control parameter as $x=1$. Here, it is clearly seen that all energy surfaces display the minimum at about the same value of the deformation parameter, namely $\beta \approx 1.35$. Therefore, the coupling with the fermion is not changing the behavior of the system in the well-deformed case.

The other panels of Figure 8 correspond to the critical points in the even-even case (x = 0.516) and the odd-even case (x = 0.485), respectively. As seen in the middle panel, the situation is different around the critical point of the bosonic core: the coupled fermion drives the system toward deformed or spherical shapes depending on the different states of the odd-even system. This gives rise to an effective shift of the critical point. In the right panel of this figure, the corresponding energy surface becomes flat for the critical point $x=0.485$.

The ground-state energy surfaces as a function of $\gamma$ for minimum $\beta$ are shown in Figure 9 for the odd-even cases (solid line) and the even-even system (dot-dashed) with 9 bosons taken as reference. In the left panel, the control parameter is taken as $x=1$, corresponding to the SU${}^{BF}$(3) of a well-deformed case, and $\beta$ is $1.35$ close to the minimum of the energy surface in the odd-even nucleus as seen in the first panel of Figure 8. Other panels display the critical points, $x_c=0.516$ of the even-even case and $x=0.485$ of the odd-even ones, with $\beta =0.5$, close to the minima of the ground-state energy surfaces given in the middle and right panels of Figure 8. As evidently seen in Figure 9, the minimum at $\gamma =0$ is quite deep for the well-deformed case (left panel), indicating axial deformation, but the minima at the critical points of either the even-even or the odd-even systems become rather shallow, and the system tends to be more $\gamma$-soft.

To summarize this section, we considered within the intrinsic frame formalism of the IBFM model the case of the coupling of a single fermion moving in the $j=1/2,3/2,5/2$ orbitals to a boson core undergoing a transition from spherical to axially deformed shape. We reviewed some results including the energy levels along the given transitional path, the energy surfaces as a function of $\beta$ (for $\gamma =0$) and the ground-state energy surfaces as a function of $\gamma$ (for selected minimal $\beta$). According to these results, obtained by resorting to the intrinsic fermion-boson states, the position of the critical point is shifted by the presence of the coupled fermion. More detailed results can be found in Ref. [15].

5. Quantum Shape Phase Transition in Bose-Fermi Systems for a Single-j Orbit: The Effect of the Coupled Fermion

In this part, we review our recent works for the cases of one fermion in a single-j orbital coupled to a bosonic core that performs different transitional paths: from spherical to $\gamma$-unstable shape, from spherical to axially deformed (prolate and oblate) shapes, and from prolate to oblate shapes passing through the $\gamma$-unstable shape. These results are obtained within the IBFM model. We will take as example the case of the $j=9/2$ orbital, but we expect analog results for other values of j, except for the already mentioned case of $j=3/2$.

For the quantum shape phase transitions in this section, the boson part of the general model Hamiltonian (7) is taken as given in Equation (1) and the boson-fermion interaction as in Equation (9), both with $\alpha =4$. The fermion quadrupole operator in this section has just one term (single-j), and the corresponding coefficient $t_j$ can be set to one without loss of generality since a single-j shell case is considered. Notice that, in the case of $j=1/2$, this operator cannot be defined. The pure fermion part of the general IBFM Hamiltonian, given in Equation (7), is just a constant for the single-j shell case. Thus, the IBFM Hamiltonian used is

$$H=H_B+V_{BF}=(1-x){\widehat{n}}_d-\frac{x}{4N_B}{\widehat{Q}}_B^{\chi }·{\widehat{Q}}_B^{\chi }-\frac{x}{2N_B}{\widehat{Q}}_B^{\chi }·{\widehat{q}}_F.$$

(23)

Consequently, there are two control parameters in the Hamiltonian: x and $\chi$. Changing appropriately these control parameters, one can explore the full IBM model space (see Figure 1) to which the fermion is coupled in IBFM. Each dynamical symmetry of the model corresponds to specific values of x and $\chi$.

The intrinsic formalism discussed in Section 2 is used for the present applications. For the single angular momentum $j=9/2$ cases, the possible magnetic components are $K=-9/2,...,9/2$ and there are ten different states in total. However, these states can be restricted to five due to the symmetry involving the K↔$-K$ components.

5.1. Quantum Phase Transition in Bose-Fermi Systems for a Single-j Orbit: From Spherical to γ-Unstable Shapes

In this subsection, we discuss the effect of the coupling of a single fermion with $j=9/2$ to a bosonic core with $N_B=5$ bosons that performs a transition from spherical to $\gamma$-unstable shape. Spherical and $\gamma$-unstable shapes are obtained by taking all along the path $\chi =0$ in the boson quadrupole operator and selecting $x=0$ and $x=1$, respectively, in the Hamiltonian (23). The critical point is found at $x_c=N_B/(2N_B-2)$ for this second-order shape phase transition and its value is $0.625$ for $N_B=5$ bosons. Please note that, in preceding Section 3, the critical point in the even-even system for the transitional path from spherical to γ-unstable shapes was $x_c=N_B/(5N_B-8)$, but that was the case with $\alpha =1$ in the Hamiltonian. In this section, as in Section 4, we are using $\alpha =4$ in the Hamiltonian so as to have the critical point around the middle of the x interval.

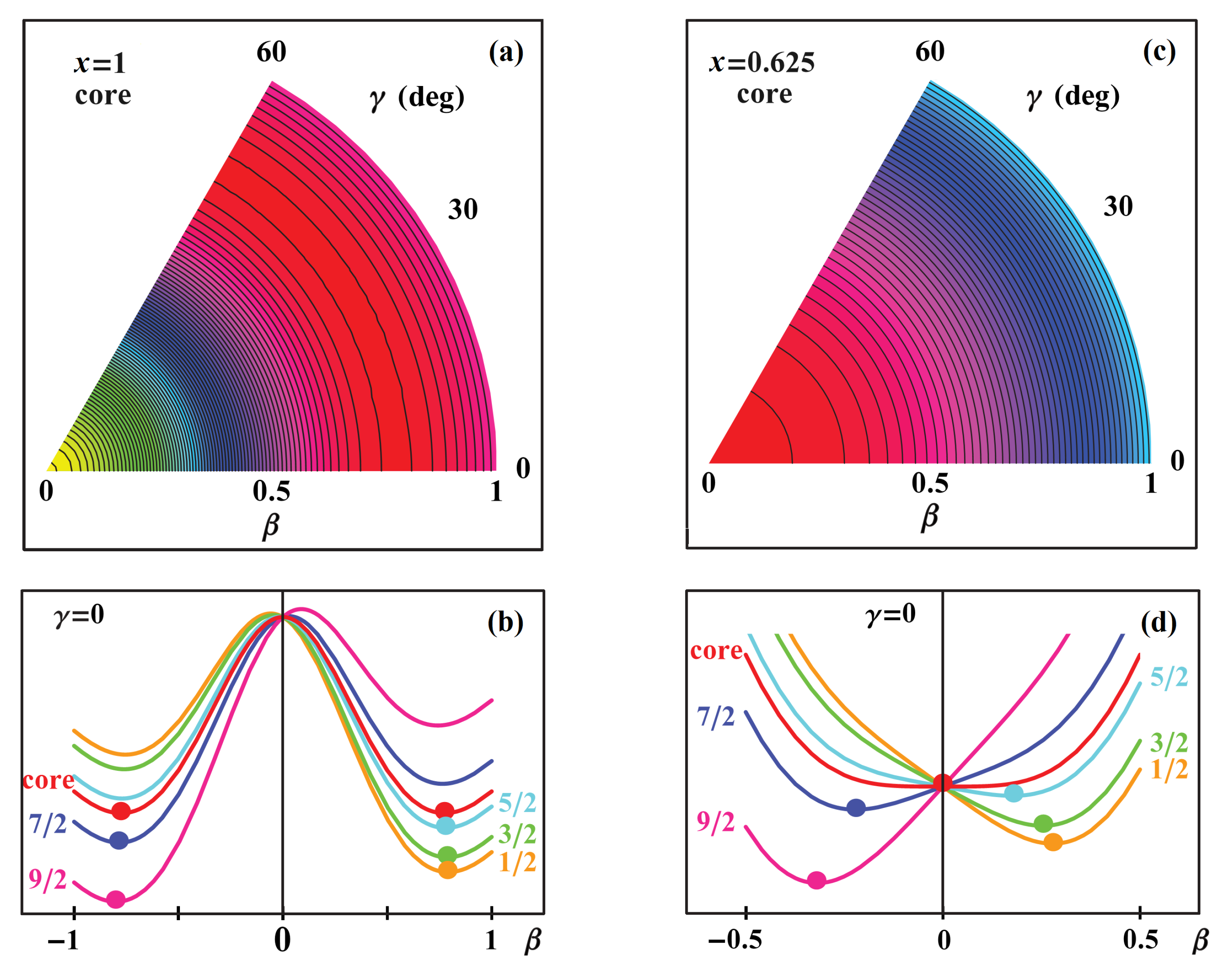
In the right side of Figure 10, the bosonic energy surface is plotted in the $\beta$-$\gamma$ plane at the critical point ($x=0.625$ for $N_B=5$ bosons). As seen from Figure 10c, the even-even core is $\gamma$-unstable and has a spherical minimum. The single fermion with $j=9/2$ is coupled to this core using the boson-fermion interaction in Equation (23). Then, the five fermionic energy surfaces are plotted as a function of $\beta$ for $\gamma =0^{\circ }$ in Figure 10d including also the bosonic one as reference, plotted as a red color line. The positive and negative $\beta$ values indicate prolate and oblate shapes, respectively. As it is clearly seen in this figure, the even-even energy surface is very flat, and this is a clue that indicates that it is the critical point of a continuous phase transition. However, the odd-even system prefers prolate shapes for $K=1/2,3/2,5/2$, while it prefers to be oblate for $K=7/2,9/2$. The left side of Figure 10 includes the bosonic energy surface of a purely $\gamma$-unstable core in the $\beta$-$\gamma$ plane, and the energy surfaces as a function of $\beta$ are obtained by coupling a $j=9/2$ particle to this bosonic core (again shown as a reference marked by red in Figure 10b). It is seen from this panel that the even-even energy surface has two degenerate minima with the same deformation value ${\beta }_{min}=\pm 0.78$ in both prolate and oblate sides. This suggests $\gamma$-independence. The behavior of the odd-even energy surfaces are similar to the ones in Figure 10d. The states with $K=1/2,3/2,5/2$ have prolate minima, and the other K-states have oblate minima, for roughly the same $\pm {\beta }_{min}$ of the bosonic core.

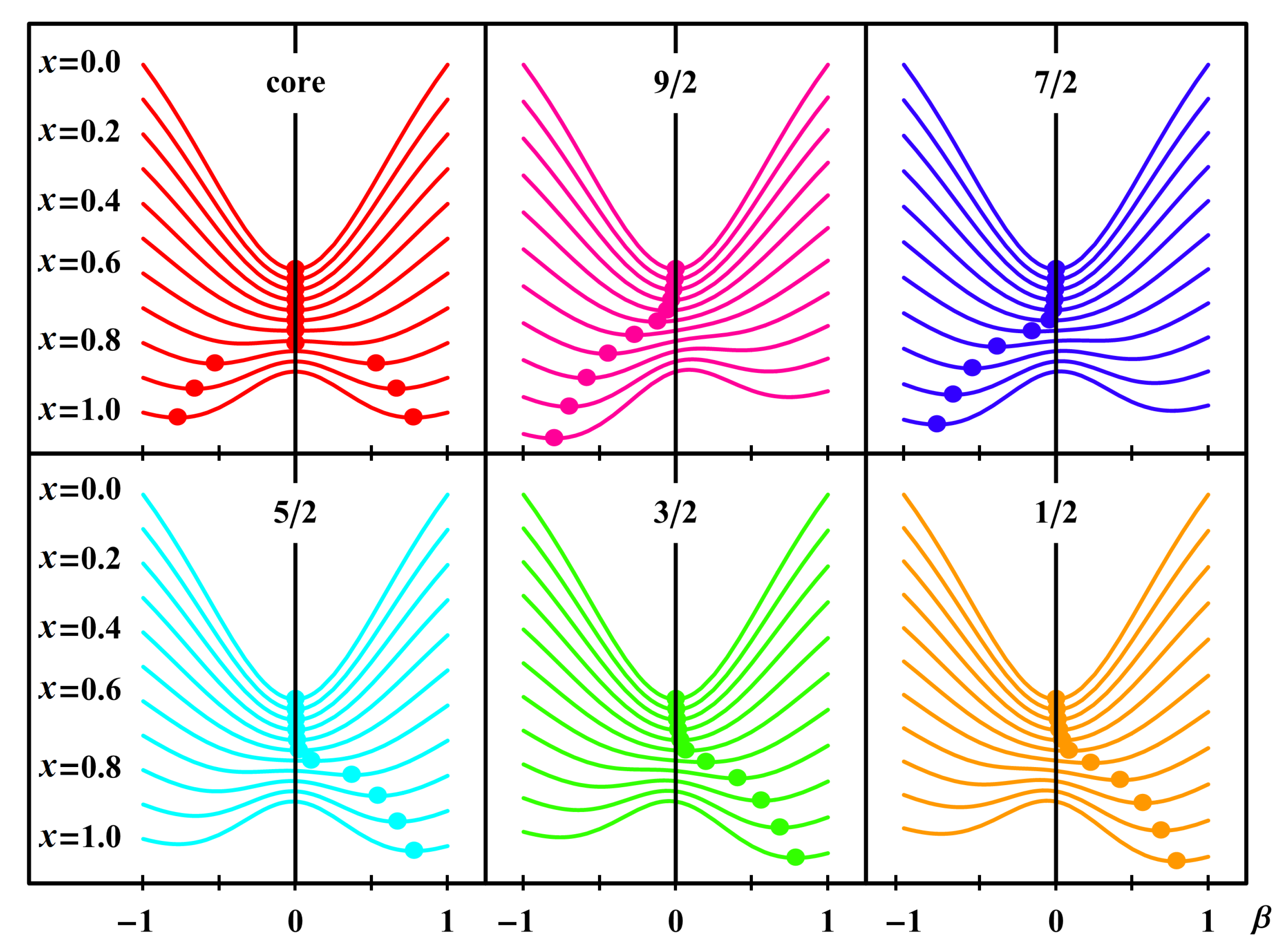
In Figure 11, the evolution of the bosonic and fermionic energy surfaces as a function of $\beta$ deformation for $\gamma =0^{\circ }$ is given for a set of x values along the transitional region. When the core is inside the spherical region ($\beta$ minimum in zero), the preference of $K=1/2,3/2,5/2$ states is for the prolate side shapes, and the preference of others K-states is for oblate shapes with quite small values of deformation. When the core jumps into deformed $\gamma$-unstable at the critical point and moves to more β-deformed $\gamma$-unstable shapes, the behavior of all K-states remains similar, but the modulus of their $\beta$ values at the energy minimum increases, showing the differences more appreciably.

5.2. Quantum Phase Transition in Bose-Fermi Systems for a Single-j Orbit: From Spherical to Prolate Shapes

In this part, we discuss the effect of the coupling of a single $j=9/2$ fermion to a bosonic core with $N_B=5$ that performs a transition from spherical to prolate shapes, in particular, at and around the critical point. To obtain pure prolate shape, one has to choose $\chi =-\sqrt{7}/2$ and $x=1$ in the Hamiltonian (23). In this situation, the phase transition occurs at the critical point $x_{cr}=16N_B/(34N_B-27)$ along the transition spherical-prolate shapes, as discussed in Section 4. For $N_B=5$, the value of the critical point is $x_{cr}=0.56$, and the transition in the even-even system is known to be first-order [3].

To study the effect of the coupled fermion on the core around the U(5)-SU(3) critical point, the control parameter values are taken as $x=0.5$, $x_{cr}=0.56$, $x=0.6$ in the Hamiltonian (23). Their ground state energy surface is obtained by calculating the expectation value of this Hamiltonian in the intrinsic state. The bosonic energy surfaces as a function of $\beta$ and $\gamma$ are plotted around the critical point as seen Figure 12. Later, the single fermion with $j=9/2$ is coupled to the core using the boson-fermion interaction $V_{BF}$ in Equation (23). The behavior of the fermionic energy surfaces as a function of $\beta$ (for $\gamma =0^{\circ }$) is illustrated around the critical point in the right side of each panel in Figure 12, where the bosonic core is marked with red color as a reference. As seen in the middle panel, the bosonic surface has two minima at $x_{cr}=0.56$. The even-even core is spherical before this point (in the first panel) and then it jumps to prolate (in the last panel). The intrinsic states of the odd-even system have a tendency to show prolate or oblate shapes, while the bosonic core is located at critical point or in its close surroundings.

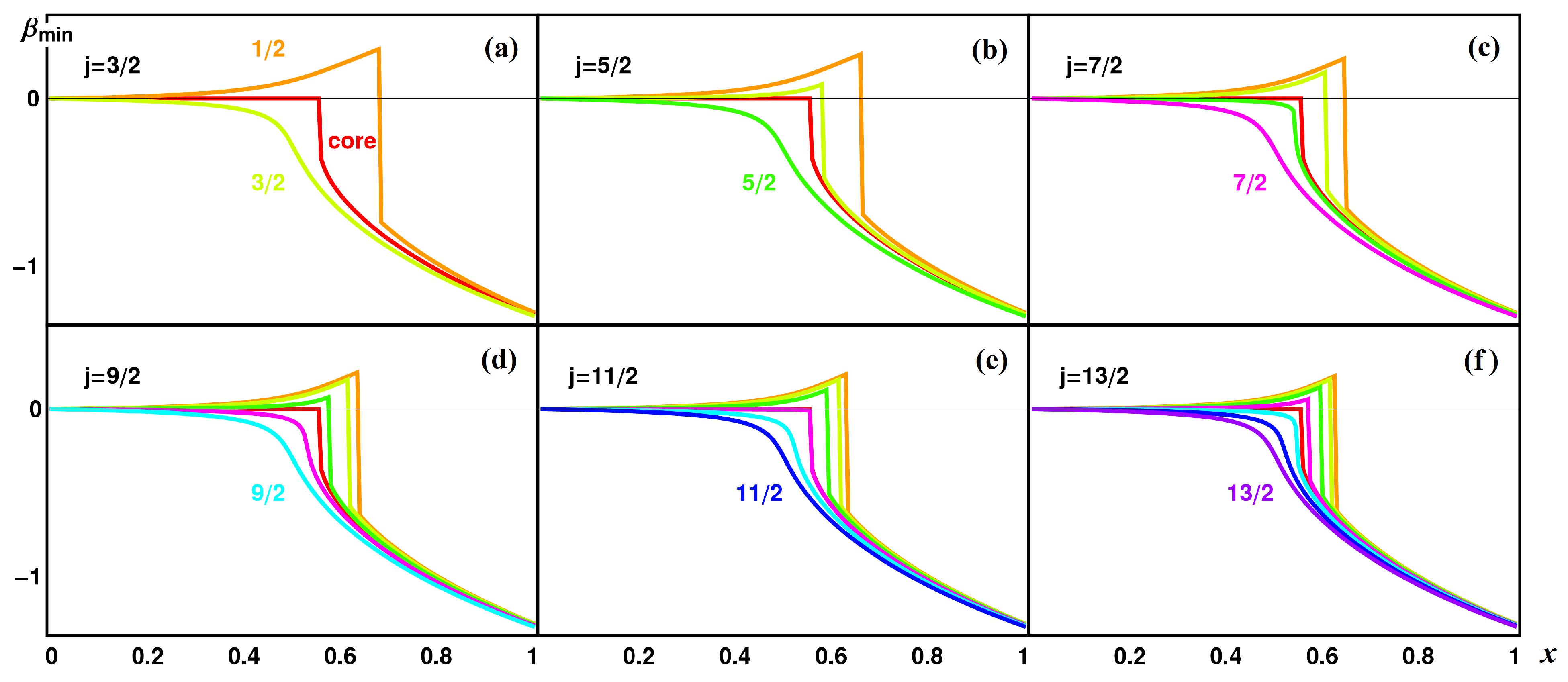
The evolution of the equilibrium deformation parameter for the bosonic core and five fermionic states is illustrated in Figure 13 along the transition from spherical to prolate shape (left panel). Fermionic states with smaller $K=1/2,3/2,5/2$ always favor the prolate shapes, while states with $K=7/2,9/2$ are oblate up to $x_{7/2}\simeq 0.6$ and $x_{9/2}\simeq 0.69$. Later, these states with larger K suddenly jump to prolate shapes. It is clearly seen that both states, $K=7/2,9/2$, show first order transitions at certain specific values of the control parameter. In the prolate region, the core drives all K states into the prolate side and they have roughly the same ${\beta }_{min}\simeq 1.28$. The case of U(5) to O(6) transition discussed in the previous subsection is also given in the right panel of Figure 13 for the comparison. Here, the tendency of the states with smaller K’s is always to be prolate, while states with higher K’s always tend to oblate shapes.

5.3. Quantum Phase Transition in Bose-Fermi System for a Single-j Orbit: From Spherical to Oblate Shapes

The effect of the coupling of a fermion moving in a single $j=9/2$ shell to a bosonic core with $N_B=5$ that performs the transition from spherical to oblate shapes is discussed. The aim is to see how the coupled fermion modifies the shape of the coupled odd system and how each of the odd states behaves along the given transition path (path 3 in Figure 1). We show the case of j = 9/2, but the overall results for the effect of the coupled fermion are also presented for a set of different values of j ranging from $3/2$ to $13/2$ along the same transitional region. This case is similar to the preceding case, and we discuss it for the sake of completeness.

The spherical shape is obtained for the control parameter $x=0$ in the Hamiltonian (23), while $x=1$ and $\chi =+\sqrt{7}/2$ produce a pure well deformed oblate shape. The critical point is found at $x_{cr}=16N_B/(34N_B-27)$ in between spherical and oblate shapes, which correspond to the value $x_{cr}=0.56$ in the case of five bosons. This value is exactly the same value of the critical point that occurs in between spherical and prolate shapes. The bosonic energy surfaces are plotted as a function of the deformation parameters ($\beta$, $\gamma$) for $N_B=5$ around the critical point as shown in upper panels of Figure 14. As seen in the middle panel (b), the bosonic surface has two degenerate minima (one spherical and one oblate) at the critical point value $x_{cr}=0.56$. Before this point, the even-even system is spherical and after it jumps to oblate shape. Comparing Figure 12 and Figure 14, one sees that the two bosonic cases are completely symmetric with respect of the sign change in chi, as expected. As seen in the lower panels of Figure 14, the fermionic intrinsic states prefer either prolate or oblate shapes depending on their K value; hence, their behavior around the critical point is quite different from that illustrated in Figure 12.

The evolution of the equilibrium deformation parameter for the fermionic states and the bosonic case along the transitional path from spherical to oblate shape is illustrated in Figure 15. As seen in fourth panel (d) of Figure 15 for the case of $j=9/2$, the states with $K=7/2,9/2$ always favor oblate shapes, while states with the lower $K=1/2,3/2,5/2$ are prolate up to their specific critical x values. After these values, they suddenly jump from prolate to oblate shapes. They present two degenerate minima for these values and as a result the components with lower K’s show first-order phase transitions. On the contrary, in the case of phase transitions along the U(5) → SU(3) path, as illustrated in the first panel of Figure 13, the states that show first order characteristics are those with higher $K=7/2,9/2$. As seen in the panels of Figure 15 for the different single-j from $3/2$ to $13/2$, the lower K states always prefer to be prolate up to their specific critical point, then they jump to oblate shape at these specific x values, while the higher K states always prefer oblate shapes along the full transitional path. In the well deformed oblate region, close to $x=1$, once again we see that the oblate core drives all states to the oblate shape, with approximately the same ${\beta }_{min}\simeq -1.28$.

5.4. Quantum Phase Transition in Bose-Fermi System for a Single-j Orbit: From Prolate to Oblate Shapes

Recently, we investigated [20] the case of a single-$j=9/2$ fermion coupled to a bosonic core with $N_B=5$ that performs a transition from prolate to oblate shapes. We focused on the effect of the coupled fermion on the whole system along the transitional path from prolate to oblate shapes, passing through the $\gamma$-unstable shape. For this transition, one can move in between the SU(3) → O(6) →$\overline{\mathrm{SU}\left(3\right)}$ symmetries (path 4 in Figure 1) in the deformed region by taking a fixed value of $x=1$ and changing the $\chi$ parameter from $\chi =-\sqrt{7}/2$, through $\chi =0$ to $\chi =+\sqrt{7}/2$ in the Hamiltonian (23).

The deformed prolate, $\gamma$-unstable, and oblate shapes of the even-even core with $N_B=5$ bosons are produced for different $\chi$ values as in the previous subsections of the Section 5. Their ground state energy surface for each shape is obtained by calculating the expectation value of the corresponding Hamiltonian (23) in the intrinsic state given in Equation (4). These energy surfaces in the $\beta$ and $\gamma$ plane are presented for deformed prolate shape in Figure 8 left panel. In this case, the bosonic energy surface has the minimum at $\gamma =0$. The projection of this energy surface on the $\gamma =0$ plane is the dashed line. In the same plot, the energy surfaces of the odd-even system are displayed. All of them follow the behavior of the core with approximately the same deformation. The case for the deformed oblate shape is similar to the prolate case but the deformations are for negative $\beta$ (or alternatively for $\gamma ={60}^{\circ }$). Thus, one could conclude that all the magnetic substates of the coupled single-fermion with $j=9/2$ would be driven by the shape of the bosonic core. However, for the $\gamma$-unstable case, Figure 10 (panel a) presents the bosonic energy surface in the $(\beta ,\gamma )$ plane. This figure also include, in panel b, the odd-even energy surfaces of a single fermion with angular momentum $j=9/2$ coupled to it using the boson-fermion interaction given in Equation (23). Now, we will show that, in the surroundings of the O(6) point, the odd-fermion system follows some unexpected and unique paths.

The energy surfaces as a function of $\beta$ and $\gamma$ are calculated for the obtained odd-even states. The notation with $n=1,...,5$ is used instead of K, for the five magnetic substates of $j=9/2$ because K is not a good quantum number along this transition (it is still a good quantum number at the extreme points where axial symmetry is recovered). 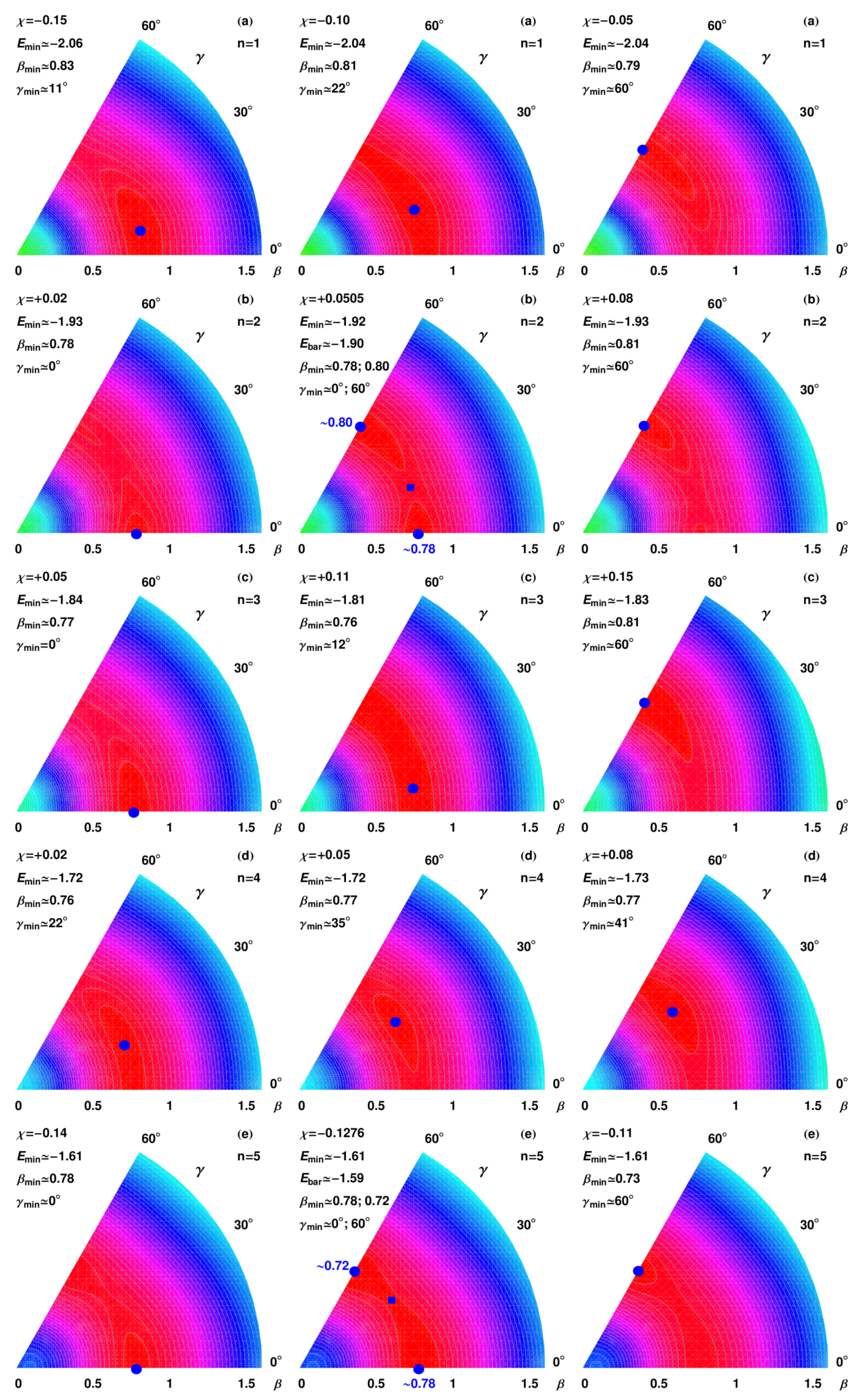These calculated odd-even energy surfaces in ($\beta$, $\gamma$) are shown in Figure 16 for each n state for different $\chi$ values. The three rows in the figure refer to three $\chi$ values selected around the critical region for each n-state. The energy minimum is denoted by a blue dot in each panel also including the values ${\beta }_{min}$, ${\gamma }_{min}$, and $E_{min}$. In the middle panels of $n=2$ and $n=4$ states, there are two blue circles since prolate and oblate minima are degenerate for slightly different $\beta$-deformations separated by a small barrier with the $E_{bar}$ marked with blue squares.

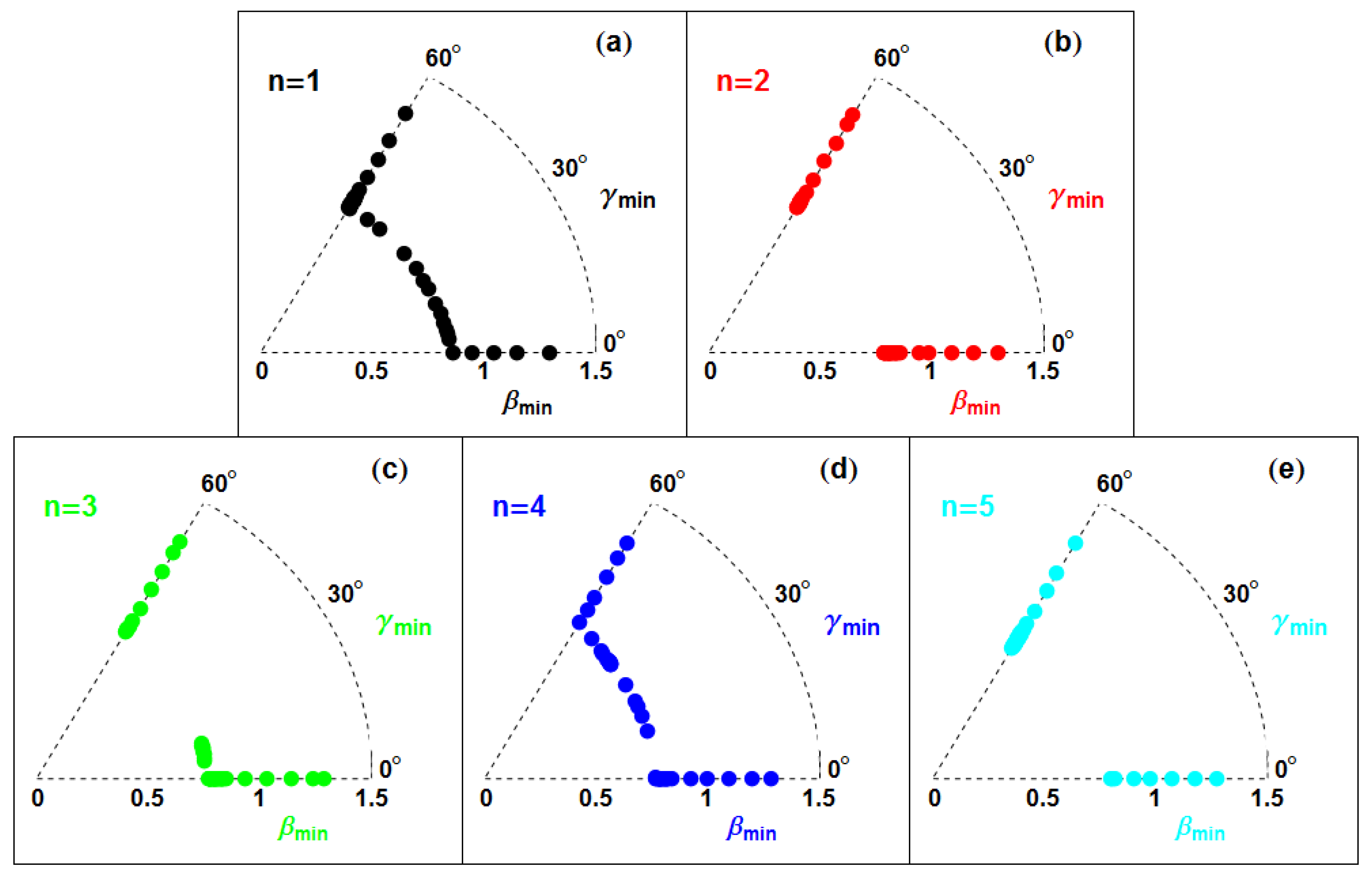
For the complete analysis of the absolute minimum evolution for each n-state, polar plots in the $(\beta ,\gamma )$ plane are presented in Figure 17. Each panel corresponds to a different n-state and the $\beta$ and $\gamma$ values provide the absolute minima of the energy surface for different $\chi$-values. It is clearly seen that the five components of the $j=9/2$ orbital seem to show quite interesting and unexpected behavior. Two odd-states ($n=1,4$) move slowly from the prolate ($\gamma =0$) to the oblate ($\gamma ={60}^{\circ }$) shape by venturing into the triaxial region, showing $\gamma$-softness around their slow shape-changing region. The other three odd-states ($n=2,3,5$) show sudden jumps (critical point) at some ${\chi }_{crit}$ from prolate side to oblate side without passing through triaxial structures what generates shape coexistence, although one of them ($n=3$) is fairly close to $\gamma$-instability. Of course, care has been used here to ensure that the jump is not a numerical artifact due to scales changing too slowly or too rapidly.

6. Summary and Conclusions

In this contribution, our works on quantum phase transition for Bose-Fermi systems within the intrinsic frame formalism associated with the IBFM model have been reviewed. The main aim of these studies is to understand the effect of the coupled fermion on the core when moving along a given transitional path and how the coupled fermion modifies the characteristics of the bosonic core around the critical points.

First, we presented some IBFM results trying to mimic the situation described by the E(5/4) critical point symmetry, for the case of a single $j=3/2$, and its extended version, the E(5/12) critical point symmetry, for multi-j orbits ($j=1/2,3/2,5/2$). A possible example of the E(5/4) is ${}^{133}$Ba built on the single particle level d${}_{3/2}$. The multi-j situation of E(5/12) can occur in odd-neutron Pt isotopes with the active orbits 3$p_{1/2}$, 3$p_{3/2}$, 2$f_{5/2}$ and in odd-proton Ir isotopes with active orbits 2$d_{5/2}$, 2$d_{3/2}$, 3$s_{1/2}$ around the $A\simeq 190$ mass region and also in odd-neutron Ba isotopes with relevant orbits 2$d_{5/2}$, 2$d_{3/2}$, 3$s_{1/2}$ around the $A\simeq 130$ mass region. Later, we recapitulated the IBFM results for the U${}^{BF}$(5) to SU${}^{BF}$(3) transition in odd nuclei for the same multi-j orbits. These results include the energy levels along the transition from spherical to the axially deformed shape and also the energy surfaces for the even-even and odd-even cases. According to these results, the main effect of the coupled fermion is to produce a systematic shift of the critical point location in the odd-even system with respect to the one characterizing the even-even core.

Finally, in Section 5, we reviewed our systematic studies for the case of a single-j fermion coupled to a bosonic core that performs different transitions: from spherical to $\gamma$-unstable shape, from spherical to axially deformed (prolate and oblate) shapes, and from prolate to oblate shape passing through the $\gamma$-unstable shape. As a specific test case, we took into account a single-j fermion with angular momentum $j=9/2$ coupled to a bosonic core with small number of bosons ($N_B=5$). When the bosonic system exhibits a second-order phase transition moving from spherical and $\gamma$-unstable shapes, the fermionic states with lower $K=1/2,3/2,5/2$ values show oblate shapes, while the $K=7/2,9/2$ states prefer prolate ones. However, when the even-even system performs the transition from spherical to prolate shape for the bosonic core, the fermionic states with smaller K’s always favor prolate shapes, and the states with $K=7/2,9/2$ are oblate up to a certain point beyond the critical point for the bosonic system, but then these states also jump to the prolate side, showing first-order phase transitions. When the bosonic core moves from spherical shape to oblate shape, states with the lower $K=1/2,3/2,5/2$ show first-order phase transitions, jumping to oblate at some value of the control parameter x beyond the bosonic critical point. States with higher $K=7/2,9/2$ always favor oblate shapes. For this transitional path, we also presented the results for different single-j values from $3/2$ to $13/2$ to show that their behavior is similar, and we can thus take just one (say the $j=9/2$) as a representative for any of them. Finally, the results of our last work on the prolate to oblate phase transition in Bose-Fermi systems show quite interesting and unexpected behavior. Two states in the odd-even system move slowly from the prolate to the oblate shape by venturing into the triaxial region, also showing a $\gamma$-softness behavior in the middle, while the other three states show sudden jumps from prolate to oblate shapes.

Evidence of quantum phase transitions in odd systems were reported in recent works [27,28,29,30,31,32,33,34]. The experimental evidence for transition from spherical to the $\gamma$-unstable shapes in odd-mass ${}^{127-137}$Ba and ${}^{101-109}$Rh, and ${}^{123-135}$Xe nuclei was presented in Refs. [27,28,32] and analyzed by calculating their nuclear properties, such as B(E2) values and two-neutron separation energies, within the IBFM model for the U${}^{BF}$(5)–O${}^{BF}$(6) transition along the isotopic chain. The signatures of the quantum shape phase transition in odd-mass ${}^{129-137}$Ba, ${}^{129-137}$La, ${}^{127-135}$Xe, and ${}^{127-135}$Cs nuclei in the A ≈ 130 mass region were studied by taking into account their bosonic cores ${}^{128-136}$Ba for ${}^{129-137}$Ba, ${}^{129-137}$La, and ${}^{126-134}$Xe [30,31]. These cores empirically exhibit a transition from nearly spherical to $\gamma$-soft shape. The calculations of the low-energy states and the electromagnetic transition rates of given $\gamma$-soft odd-mass nuclei provide a reasonable agreement with the experimental data along the isotopic chain [30,31]. A microscopic description of the quantum shape phase transition was performed for the the axially-deformed odd-mass ${}^{147-155}$Sm and ${}^{147-155}$Eu nuclei [29] by taking into consideration their common bosonic cores ${}^{148-154}$Eu that show the transition from spherical to axially-deformed shape. Another description along the same transition path was carried out for odd-mass ${}^{149-155}$Eu isotopes and their even-even neighbors, ${}^{148-154}$Sm and ${}^{150-156}$Gd nuclei [33]. In this study, the energy surfaces were presented for even-even nuclei, later the energy spectra of odd-mass ${}^{149-155}$Eu isotopes were analyzed and their two-neutron separation energies, isotope shifts, quadrupole moments, and E2 reduced transition matrix elements were calculated along the isotopic chain and the results show good agreement with experimental data [33]. The prolate to oblate shape phase transition was studied in neutron-rich odd-mass ${}^{185-193}$Os, ${}^{185-195}$Ir, and ${}^{185-199}$Pt nuclei in the A ≈ 190 mass region to see the effect of the odd particle [34]. Their even-even neighboring nuclei ${}^{186-200}$Pt and ${}^{186-194}$Os were also taken into account and their energy surfaces were plotted as a function deformation parameters ($\beta$, $\gamma$) exhibiting good examples for the transition from prolate to oblate shape and also including $\gamma$-soft shape. Spectroscopic properties of given odd-mass Os, Ir, and Pt nuclei were calculated within the effective IBFM Hamiltonian based on the nuclear energy density functional theory [45]. More recently, a description of the quantum shape phase transition has been simultaneously performed in the even-even ${}^{94-102}$Zr and the odd-even ${}^{95-103}$Zr nuclei [46]. Their spectroscopic properties, related to the quantum shape phase transitions, are calculated within the IBFM model, and the results are in good agreement with the experimental data.