Abstract
Isospin symmetry breaking effects on the mass-radius relation of a cold, non-accreting neutron star are studied on the basis of two Skyrme Energy Density Functionals (EDFs). One functional contains isospin symmetry breaking terms other than those typically included in Skyrme EDFs while its counterpart is of standard form. Both functionals are based on the same fitting protocol except for the observables and pseudo-observables sensitive to the isospin symmetry breaking channel. The quality of those functionals is similar in the description of terrestrial observables but choosing either of them has a non-negligible effect on the mass-radius relation and tidal deformability of a neutron star. Further investigations are needed to clarify the effects of isospin symmetry breaking on these and other observables of neutron stars that are, and will become, available.
1. Introduction
The nuclear Equation of State (EoS) is one of the fundamental ingredients to describe the mass-radius relation in neutron stars [1,2,3,4,5]. The neutron star core is believed to cover the largest portion of the neutron star radius and mass. Despite the effect of the crust is non-negligible to properly determine such quantities (for more details see, e.g., Refs. [6,7]), relative effects might be safely studied neglecting the crust. It is customary to assume the core of a neutron star as made of -stable neutrons, protons and electrons [8,9,10,11,12,13]. This allows easily calculating the mass-radius relation and compare to observational data in order to detect deviations from such an approximation. Different effects that may influence such a relation have been studied in the literature, e.g., three-neutron forces at high densities or the plausible appearance of new degrees of freedom such as hyperons or quarks. While models with hyperonic degrees of freedom predict a soft equation of state for the star, not being able to explain the largest masses observed to date (see, for example, [14]), models that account for a phase-transition to quark deconfined matter do not suffer from such problem [15].
Nuclear energy density functionals (EDFs) were proven to predict with a good accuracy the ground state as well as some excited state properties in terrestrial nuclei and have been also applied to predict the limits of nuclear existence [16,17]. The use of these models to the study of neutron-star matter may be regarded as strong extrapolation due to the difference in average density within the interior of a neutron star (over ) and the interior of the atomic nucleus (). Currently, EDFs are the only type of models that can be used to consistently predict the structure and composition of a neutron star outer core and of the neutron star crust at the same time [18]. Hence, to study how different physical effects may influence the mass-radius relation of a neutron-star by using EDFs is well justified.
Isospin symmetry breaking (ISB) effects, other than those originated from direct and exchange part of the Coulomb interaction, are not commonly included in the fitting of current EDFs. This is because assuming isospin symmetry of the nuclear strong interaction and neglecting Coulomb corrections beyond the direct and exchange terms is known to be a very good approximation for the study of many observables in atomic nuclei. The most paradigmatic counter example is the excitation energy of the Isobaric Analog State (IAS) that has been measured for many nuclei with exquisite accuracy (cf. the compilation in Ref. [19]). The IAS energy depends only on ISB terms in the nuclear Hamiltonian. Specifically,
where is the ground state wave function of the nucleus and are the raising and lowering isospin operators. Hence, it is now clear that terms in the Hamiltonian not commuting with the isospin operator will contribute to . In the early literature it was already shown that only the Coulomb interaction is not enough to explain available experimental data—this is known as the Nolen-Schiffer anomaly [20]—pointing to the fact that ISB of the nuclear strong interaction should play a non-negligible role.
In addition, it was shown that the energy of the IAS is intimately correlated with the neutron skin thickness of a heavy neutron-rich nucleus such as Pb [21] and, thus, with the so-called symmetry energy [22,23]. The symmetry energy is a quantity very much studied in the context of neutron stars since it gives the penalty energy as a function of the density to convert all protons into neutrons in symmetric nuclear matter. Specifically, an approximate formula for has been derived [21]. This formula explains in simple yet physical terms the relation of the with the neutron skin thickness
where N and Z are the neutron and proton numbers, respectively; e the elementary electric charge; and () the proton (neutron) root mean square radius. The neutron skin thickness is customarily defined as . In EDFs is commonly well constrained by experimental data on the electric charge radius of the nucleus while or remains quite elusive and highly correlated with the neutron pressure inside nuclei or, which is the same, to the density dependence of the nuclear symmetry energy. The last simple equation predicts that the IAS energy should decrease with increasing neutron skin thickness. For example, for the case of Pb Equation (2) is in reasonable agreement with the result of Hartree-Fock plus Random Phase approximation calculations presented in Ref. [21].
In this contribution, we will briefly analyze the possible ISB effects on the mass-radius relation of a neutron star by comparing two EDFs of the Skyrme type. The first one, SAMi [24], is of standard form and assumes exact isospin symmetry in the nuclear channel. The second one, SAMi-ISB [21], is identical to SAMi but contains all important ISB terms for a better description of the IAS energy. It is important to note that both functionals essentially use the same fitting protocol except for the fact that SAMi-ISB includes some extra information on ISB observables such as the in Pb and pseudo-observables such as the ISB contributions to the symmetric matter equation of state as calculated by using the realistic nucleon-nucleon AV18 interaction within the Brueckner-Hartree-Fock (BHF) approach [25].
The paper is organized as follows. In Section 2, we recall the basic form of ISB terms adopted here and although this has been published elsewhere [26], we deem it important to include it also here for the sake of completeness. In Section 3, we will show the main results of the present investigation while our conclusions are laid in Section 4.
2. Theory
We calculate the mass-radius relation of a cold non-accreting neutron star—neglecting the contribution from the crust—by solving the Tolman-Oppenheimer-Volkoff equation using as input neutron-proton-electron -equilibrated matter. This procedure has been extensively used in the literature and further details can be found by the reader in Ref. [27]. To calculate the nuclear contribution assuming this model of neutron-star matter, we will use a nuclear Skyrme functional. Below we overview the main terms for our purposes here.
The isospin conserving form of the Skyrme functional adopted in this work can be easily found in the literature (see for example Equation (2.6) in Ref. [28]). Regarding the ISB contributions included in the SAMi-ISB functional [21] and neglected in the SAMi functional, we give a brief account here since those correspond to the main topic covered in this work. The contributions related to the Coulomb interaction discussed below will not contribute to the calculation of the neutron star mass-radius relation but definitely affect the fine tuning of the model in the fitting procedure that includes data on finite nuclei and, hence, will affect in an indirect way the results presented in Section 3.
2.1. Finite Size Effects
The electric charge distribution in momentum space is calculated by taking into account the effect of the proton and neutron electromagnetic form factors convoluted by using the proton and neutron point like densities, respectively, i.e., up to order where m stands for the mass of the nucleon and assuming spherical symmetry [29]
where are the electric (E) and magnetic (M) form factors [30], is the radial single particle wave function, t refers to the isospin state of the nucleon and n, l, j and s to the principal, orbital, total and spin quantum numbers. The sums run over all occupied states. The density calculated in such a way is then used for the calculation of the Coulomb energy functional. Finite size effects are frequently neglected and the proton density distribution is used instead in many EDF calculations of the Coulomb terms.
2.2. Electromagnetic Spin-Orbit
The electromagnetic spin-orbit correction to the nucleon single-particle (sp) energy can be written within a non-relativistic approximation as follows,
where i labels the i-th nucleon quantum numbers, is the neutron or proton mass, is the Coulomb energy potential—calculated at the Hartree-Fock level– and is equal to for protons and for neutrons; and are the neutron and proton g-factors, respectively [31]. The total energy correction to the binding energy of a nucleus will be then . The effect of this term can be treated perturbatively since it produces a change in the nucleon single particle energies of tens of keV and, thus, negligible in the single particle wave functions.
As an exercise, assuming a uniformly charged sphere of radius one can estimate the energy correction to the single particle energies [32],
where is the fine structure constant.
2.3. Coulomb Exchange
In connection with the Skyrme interaction, it is customary to adopt the so-called Slater approximation for the calculation of the Coulomb exchange. The mean-field corresponding to such an approximation can be written as,
where e is the elementary electric charge, is the proton density and is the single particle wave function of the i-th nucleon. The exact exchange has instead the well-known non-local form,
Since the early pioneering calculations done with the Skyrme force, the Slater approximation has been known to work quite well. In particular, the relative difference between the exact total energy and that calculated with the Slater approximation has been found to be of the order of 3–6% in Ref. [33]. As a consequence, single-particle energies undergo small changes of about hundreds of keV at most (see, e.g., Ref. [34] for numerical details).
2.4. Vacuum Polarization Correction
The lowest order correction in the fine-structure constant to the Coulomb potential is estimated via the vacuum polarization correction. The vacuum polarization modifies the charge of the proton over a range of the order of the electron Compton wavelength. The virtual emission and absorption of an electron-positron pair gives rise to a repulsive potential that corrects the Coulomb repulsion of two protons. Taking into account the finite size of the nucleus, the correction potential can be written as follows [35],
where e is the fundamental electric charge, the fine-structure constant, the reduced Compton electron wavelength and
2.5. Charge Symmetry Breaking and Charge Independence Breaking Potentials
A charge symmetry breaking potential can be generally defined as while a charge independence breaking potential can be generally defined as . So an effective nucleon-nucleon potential can be build on three parts: the charge independent part (isospin symmetry is fully preserved) plus the two previously defined breaking terms.
Following [36] (cf. Equations (18)–(21)) one can define Skyrme-like CSB and CIB potentials as follows,
and
where acts on the right, is its complex conjugate acting on the left and are the usual projector operators in isospin/spin spaces.
The Hartree-Fock energy density associated with the CSB and CIB potentials is (see appendix in Ref. [37])
where , and are the total, neutron and proton kinetic densities, respectively, and J, and are the total, neutron and proton spin-orbit densities, respectively.
For the case of SAMi-ISB only the terms in and have been considered by setting and to . The momentum-dependent terms were not considered since the information that we have at our disposal might not be sufficient to pin down the values of all parameters of a general interaction with several partial waves. We remind here that those terms set to zero in the Hamiltonian ((Equations (12a) and (12b)) will affect the neutron and proton effective masses as well as the central mean-field potential and spin-orbit potential [37]. Hence, we kept the model simple and with just a couple of extra parameters since the Coulomb corrections previously described are model independent. This is enough for SAMi-ISB to satisfactorily fit the IAS energy of Pb and the symmetric matter EoS predicted by the AV18 potential when solved within the BHF approach.
The energy densities in Equations (12a) and (12b), needed for the calculation of the neutron star mass-relation, simplify as follows,
being MeV fm3 and MeV fm3 determined from nuclear data and pseudo-data as previously explained. Summing and re-writing the previous terms,
where and . Neutron star matter is characterized by values of , and therefore,
if were exactly equal to , a situation allowed from the statistical errors reported in the determination of the parameters. It is also interesting to note that for pure neutron matter (), the resulting energy density will be,
with a statistical error in the determination of these parameters in the fitting protocol of SAMi-ISB that would be compatible with no ISB contribution to the neutron matter equation of state (as seen already in Equation (15)). Hence, it is important to note the relevance of the fine tuning of the parameters since the cancellation for this phenomenological choice of the CSB and CIB terms seems to be very large. The resulting energy contribution is negative and small, indicating a slight attractive overall behavior in pure neutron matter of ISB terms. The sign of this result is consistent with the neutron-neutron scattering length in the vacuum (cf. Table 1 in Ref. [38]). Since is included in the fitting protocol of the self-consistent SAMi-ISB functional, the isospin conserving part of the functional will be slightly modified with respect to that of SAMi in order to accommodate an accurate reproduction of the nuclear data (cf. Table 1). The effect on the observables such as the neutron matter EoS of such refit of the parameters can overcome, and will be shown to overcome, the genuine ISB effects. To which extent this cancellation effect depends on the uncertainties associated with the EDF fitting procedure, is an interesting subject for further investigation.

Table 1.
Some selected neutron-rich nuclei observables and nuclear matter properties of the SAMi [24] and SAMi-ISB [21] functionals. Quantities within parenthesis correspond to the statistical theoretical error.
3. Results
In this section, we first compare the results of SAMi and SAMi-ISB for some ground and excited state properties of different nuclei as well as some relevant properties of the nuclear equation of state.
In Table 1, the binding energies and charge radii of some selected neutron-rich nuclei are given. The accuracy of both models is very good for the medium-heavy and heavy nuclei shown and never worse than a few ‰ for binding energies and 1% for charge radii. In the same table, some key nuclear matter properties at saturation density are given. These values, although non-observable, are thought to be in a reasonable range to properly describe not only binding energies and charge radii as briefly discussed above but also collective excited states such as the Giant Monopole, Dipole or Quadrupole Resonances (cf. Table 2 in Ref. [16]).
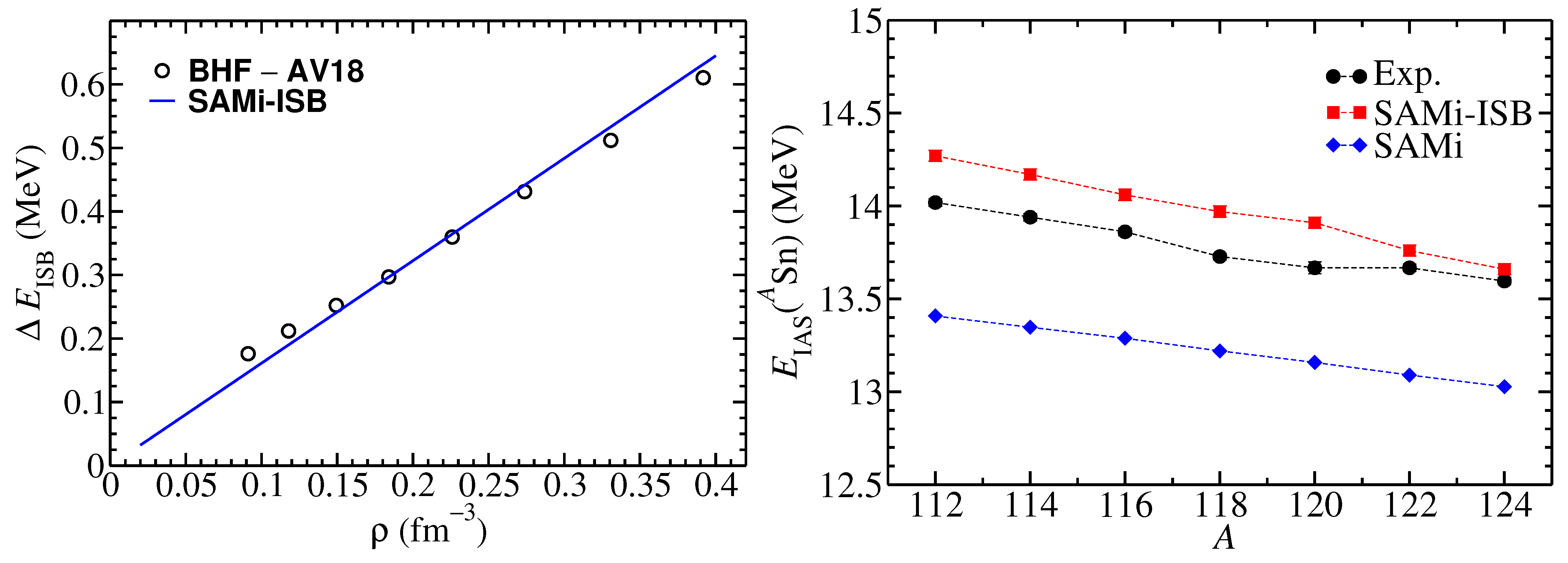
In Figure 1, left panel, we show ISB contributions predicted by a Brueckner-Hartree-Fock (BHF) calculation using the AV18 realistic nucleon-nucleon potential to the energy per particle of symmetric nuclear matter as a function of the density [25]. We also show in the same panel the result from the SAMi-ISB functional that has been fitted to these pseudo-data.
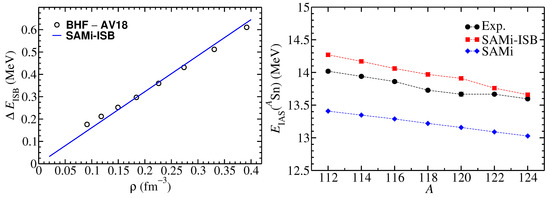
Figure 1.
(Left panel) ISB contributions to the symmetric matter equation of state as predicted by the BHF calculations based on AV18 potential (black circles) of Ref. [25]. The solid line corresponds to SAMi-ISB. (Right panel) IAS energy for Sn isotopes as predicted by SAMi and SAMi-ISB, compared to experimental data. Figure taken from the supplemental material of Ref. [21].
As discussed in the introduction, the energy of the IAS is particularly sensitive to ISB effects. In Figure 1, right panel, we show the IAS energy for Sn isotopes as predicted by SAMi and SAMi-ISB, compared to experimental data. These results correspond to a prediction of the model since SAMi-ISB has been fitted to the IAS energy in Pb alone. From that figure it is clear that ISB terms help in reproducing the absolute value of IAS energies along the Sn isotopic chain.
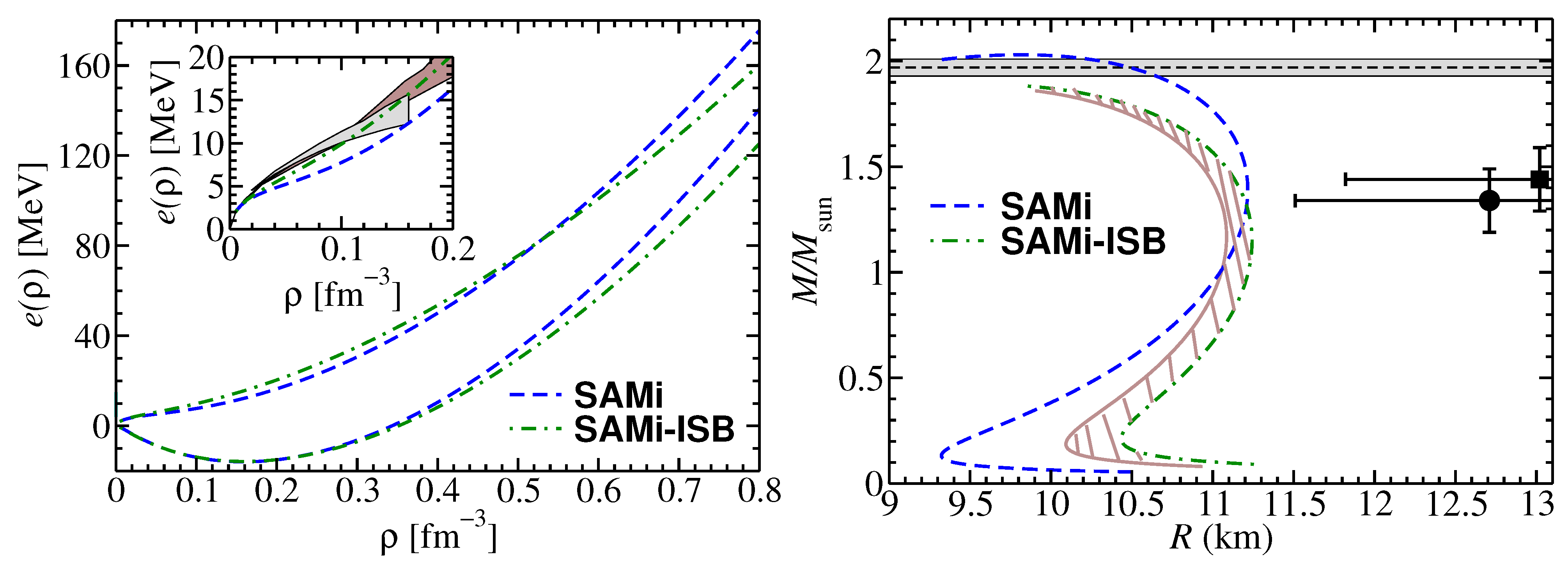
In Figure 2, left panel, we compare the neutron matter and symmetric matter EoS as predicted by SAMi and SAMi-ISB. Symmetric matter EoS are very similar from the low density region to where they start to separate, with SAMi-ISB giving a softer increase of the energy per particle with density. The pure neutron matter EoS predicted by SAMi-ISB is slightly larger for densities up to about ∼0.5 fm−3, where it becomes smaller, but still its trend is softer than SAMi for most of the density range shown. This behaviour is due to the fine-tuning of the SAMi-ISB parameters since ISB terms alone would produce attraction in neutron matter (cf. Equation (16)) and, thus, the opposite trend for 0.5 fm−3. Hence, the small ISB contributions cannot be disentangled from the effect resulting from the re-fit of the parameters between SAMi and SAMi-ISB (cf. previous Section). In the inset, the same neutron matter EoSs are shown and compared with the results of two representative ab initio approaches for the low density part. The details of those calculations can be found in Refs. [39,40]. It is seen from the figure that SAMi-ISB agrees better than SAMi with the ab initio calculations shown here.
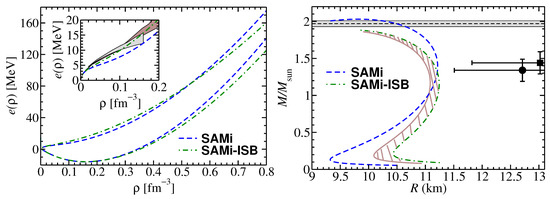
Figure 2.
(Left panel) EoS of pure neutron and symmetric nuclear matter as predicted by SAMi (dashed) and SAMi-ISB (dash-dotted). In the inset only the neutron matter EoSs are shown and compared with the results from the ab initio approaches of Ref. [39] (brown shaded area) and Ref. [40] (grey shaded area). (Right panel) Mass-Radius relation of a neutron star as predicted by SAMi and SAMi-ISB. The brown shaded area encloses SAMi-ISB predictions with the predictions of the same model if . The maximum observed mass of the millisecond pulsar J1614-2230 () is also shown (grey horizontal band) [41] as well as the simultaneous estimation of the mass and radius of the millisecond pulsar PSR J0030+0451 [43] (dot) and [44] (square). Errors correspond to the 1 estimation.
In the right panel of the same figure, the mass-radius relation of a neutron star is shown for the same models. The maximum observed mass of the J1614-2230 pulsar () is also shown (grey horizontal band) [41]. In Ref. [42] an observation of the pulsar J0348 + 0432 allowed to estimate its mass as which essentially sets the same maximum mass constraint (not shown in the figure). For completeness, we also show the simultaneous estimation (with 1 error bars) of the mass and radius of the millisecond pulsar PSR J0030 + 0451 [43,44,45]. It is seen that both neutron star EoSs predict a radius that would be compatible with this observation at the 2 level and that the SAMi-ISB model does not reproduce a maximum mass of 2. On the other side, it is worth noting that both models are fully consistent with GW170817 [46] and GW190425 [47] radii constraints. In addition, the inclusion of a realistic crust is expected to increase the predicted radius for low and, to a lesser extent, medium mass stars while keeping the maximum mass prediction much less affected (cf. right panel of Figure 2.1 in Ref. [7]) and, thus, both models would likely be in better agreement with the radius observations of the PSR J0030+0451 pulsar. The brown shaded area encloses SAMi-ISB predictions with the predictions of the same model if . Those could be regarded as pure ISB effects while the difference between SAMi and SAMi-ISB is also affected by the result of the fitting procedure. Hence, even though large systematic uncertainties exist, it is clear from the figure that ISB effects that are known to be small in nuclei, may entail non-negligible effects on observables that are sensitive to large densities as those associated with the core of a neutron star. These results should be confirmed and tested on the bases of other models for neutron star matter.
For completness, in Table 2, we report on some basic properties of a neutron star as predicted by SAMi, SAMi-ISB and SAMi-ISB with functionals. Specifically, the maximum mass and radius where for SAMi-ISB the maximum mass is reduced by ∼7% with respect to the one predicted by SAMi. The central density of a 1.4 neutron star is ∼10% larger for SAMi-ISB and the corresponding radius has only slightly decreased. The sensitivity of the radius to nuclear ISB effects (see table and compare green dash-dotted and brown solid curves in the left panel of Figure 2) seems to be around hundreds of meters for a wide range of neutron star masses. The tidal deformability (see, e.g., [46,48,49,50]) predicted by SAMi-ISB shows a decrease with respect to SAMi that is larger than ∼10%. The range deduced from GW170817 is 800 [46]. The tidal deformability is customarily written as a function of the compactness parameter (also shown in Table 2) and of the quadrupole tidal Love number [51] as .

Table 2.
Some basic properties of a neutron star as predicted by SAMi, SAMi-ISB and SAMi-ISB with functionals. Specifically, the maximum mass (), radius () and central density (), radius (), tidal deformability () and compactness () for a neutron star.
In summary, according to SAMi-ISB results, we shall expect an influence of ISB terms originated from the nuclear strong interaction for properties related to very high densities –easily found in a neutron star interior– as well as a small to moderate effect on the radius and tidal deformability. The properties of the crust, not studied here, might also be affected by ISB effects whenever competing configurations are close enough in energy since ISB effects at normal densities are expected to be of the order of hundreds of keV.
4. Conclusions
In this contribution, we present a preliminary study of the effect of ISB on the mass-radius relation of a neutron star and a few related observables such as the tidal deformability. Since densities expected along the core of the star are thought to be well above , ISB terms that are commonly small and frequently negligible for the study of finite nuclear properties, may become relevant for the study of neutron star matter and specifically its mass-radius relation (see brown area in the right panel of Figure 2). We compared the predictions of two models based on the same fitting protocol, one containing non-standard ISB terms (SAMi-ISB) and the other neglecting them (SAMi). Some differences appear even though there is a large cancellation between the CSB and CIB parts of the proposed phenomenological interaction. The extrapolation of our model to very large densities should be further investigated and complemented with other type of calculations in order to confirm or dismiss the effects of ISB on the mass-radius relation of a neutron star and, whenever possible, study the large cancellation predicted here for the CSB and CIB terms. The study of ISB effects on other observable properties of neutron stars might also be envisaged.
Author Contributions
Conceptualization, X.R.-M. and G.C.; Formal analysis, G.S.; Investigation, X.R.-M., G.C. and G.S.; Software, G.S.; Writing—original draft, X.R.-M. All authors have read and agreed to the published version of the manuscript.
Funding
Funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 654002 is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Chamel, N.; Haensel, P. Physics of Neutron Star Crusts. Living Rev. Relativ. 2008, 11, 10. [Google Scholar] [CrossRef]
- Steiner, A.W.; Lattimer, J.M.; Brown, E.F. The Neutron Star Mass-Radius Relation and the Equation of State of Dense Matter. Astrophys. J. Lett. 2013, 765, L5. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Constraints on the symmetry energy using the mass-radius relation of neutron stars. Eur. Phys. J. A 2014, 50, 40. [Google Scholar] [CrossRef]
- Oertel, M.; Hempel, M.; Klähn, T.; Typel, S. Equations of state for supernovae and compact stars. Rev. Mod. Phys. 2017, 89, 015007. [Google Scholar] [CrossRef]
- Ferreira, M.; Providência, C.M.C. Effect of the crust on neutron star empirical relations. Phys. Rev. D 2020, 102, 103003. [Google Scholar] [CrossRef]
- Carreau, T. Modeling the (Proto)Neutron Star Crust: Toward a Controlled Estimation of Uncertainties. Ph.D. Thesis, Normandie Université, Caen, France, 2020. [Google Scholar]
- Prakash, M.; Ainsworth, T.L.; Lattimer, J.M. Equation of State and the Maximum Mass of Neutron Stars. Phys. Rev. Lett. 1988, 61, 2518–2521. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef]
- Todd-Rutel, B.G.; Piekarewicz, J. Neutron-Rich Nuclei and Neutron Stars: A New Accurately Calibrated Interaction for the Study of Neutron-Rich Matter. Phys. Rev. Lett. 2005, 95, 122501. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Constraints on Neutron Star Radii Based on Chiral Effective Field Theory Interactions. Phys. Rev. Lett. 2010, 105, 161102. [Google Scholar] [CrossRef]
- Gandolfi, S.; Carlson, J.; Reddy, S. Maximum mass and radius of neutron stars, and the nuclear symmetry energy. Phys. Rev. C 2012, 85, 032801. [Google Scholar] [CrossRef]
- Chen, W.C.; Piekarewicz, J. Building relativistic mean field models for finite nuclei and neutron stars. Phys. Rev. C 2014, 90, 044305. [Google Scholar] [CrossRef]
- Vidaña, I. Hyperons in Neutron Stars. J. Phys. Conf. Ser. 2016, 668, 012031. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Nattila, J.; Vuorinen, A. Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 2020, 16, 907–910. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Paar, N. Nuclear equation of state from ground and collective excited state properties of nuclei. Prog. Part. Nucl. Phys. 2018, 101, 96–176. [Google Scholar] [CrossRef]
- Erler, J.; Birge, N.; Kortelainen, M.; Nazarewicz, W.; Olsen, E.; Perhac, A.M.; Stoitsov, M. The limits of the nuclear landscape. Nature 2012, 486, 509–512. [Google Scholar] [CrossRef]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, 584, A103. [Google Scholar] [CrossRef]
- Antony, M.; Pape, A.; Britz, J. Coulomb displacement energies between analog levels for 3<A<239. At. Data Nucl. Data Tables 1997, 66, 1–63. [Google Scholar] [CrossRef]
- Nolen, J.A.; Schiffer, J.P. Coulomb Energies. Annu. Rev. Nucl. Sci. 1969, 19, 471–526. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Colò, G.; Sagawa, H. Nuclear Symmetry Energy and the Breaking of the Isospin Symmetry: How Do They Reconcile with Each Other? Phys. Rev. Lett. 2018, 120, 202501. [Google Scholar] [CrossRef]
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef] [PubMed]
- Danielewicz, P.; Lee, J. Symmetry energy II: Isobaric analog states. Nucl. Phys. A 2014, 922, 1–70. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Colò, G.; Sagawa, H. New Skyrme interaction with improved spin-isospin properties. Phys. Rev. C 2012, 86, 031306. [Google Scholar] [CrossRef]
- Muther, H.; Polls, A.; Machleidt, R. Isospin symmetry breaking nucleon-nucleon potentials and nuclear structure. Phys. Lett. B 1999, 445, 259–264. [Google Scholar] [CrossRef][Green Version]
- Roca-Maza, X.; Colò, G.; Sagawa, H. The nuclear symmetry energy and the breaking of the isospin symmetry: How do they reconcile with each other? EPJ Web Conf. 2018, 194, 01002. [Google Scholar] [CrossRef][Green Version]
- Lattimer, J.M.; Trache, L.; Chesneanu, D.; Ur, C.A. Introduction to neutron stars. AIP Conf. Proc. 2015, 1645, 61–78. [Google Scholar] [CrossRef]
- Chabanat, E.; Bonche, P.; Haensel, P.; Meyer, J.; Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities. Nucl. Phys. A 1997, 627, 710–746. [Google Scholar] [CrossRef]
- Ray, L. Neutron isotopic density differences deduced from 0.8 GeV polarized proton elastic scattering. Phys. Rev. C 1979, 19, 1855–1872. [Google Scholar] [CrossRef]
- Friedrich, J.; Walcher, T. A coherent interpretation of the form factors of the nucleon in terms of a pion cloud and constituent quarks. Eur. Phys. J. A Hadron. Nucl. 2003, 17, 607–623. [Google Scholar] [CrossRef]
- Mohr, P.J.; Newell, D.B.; Taylor, B.N. CODATA recommended values of the fundamental physical constants: 2014. Rev. Mod. Phys. 2016, 88, 035009. [Google Scholar] [CrossRef]
- Bentley, M.; Lenzi, S. Coulomb energy differences between high-spin states in isobaric multiplets. Prog. Part. Nucl. Phys. 2007, 59, 497–561. [Google Scholar] [CrossRef]
- Titin-Schnaider, C.; Quentin, P. Coulomb exchange contribution in nuclear Hartree-Fock calculations. Phys. Lett. B 1974, 49, 397–400. [Google Scholar] [CrossRef]
- Roca-Maza, X.; Cao, L.G.; Colò, G.; Sagawa, H. Fully self-consistent study of charge-exchange resonances and the impact on the symmetry energy parameters. Phys. Rev. C 2016, 94, 044313. [Google Scholar] [CrossRef]
- Fullerton, L.W.; Rinker, G.A. Accurate and efficient methods for the evaluation of vacuum-polarization potentials of order Zα and Zα2. Phys. Rev. A 1976, 13, 1283–1287. [Google Scholar] [CrossRef]
- Sagawa, H.; Giai, N.V.; Suzuki, T. Isospin mixing and the sum rule of super-allowed fermi beta decay. Phys. Lett. B 1995, 353, 7–12. [Google Scholar] [CrossRef]
- Sagawa, H.; Colò, G.; Roca-Maza, X.; Niu, Y. Collective excitations involving spin and isospin degrees of freedom. Eur. Phys. J. A 2019, 55, 227. [Google Scholar] [CrossRef]
- Suzuki, T.; Sagawa, H.; Van Giai, N. Charge independence and charge symmetry breaking interactions and the Coulomb energy anomaly in isobaric analog states. Phys. Rev. C 1993, 47, R1360–R1363. [Google Scholar] [CrossRef]
- Drischler, C.; Hebeler, K.; Schwenk, A. Asymmetric nuclear matter based on chiral two- and three-nucleon interactions. Phys. Rev. C 2016, 93, 054314. [Google Scholar] [CrossRef]
- Tews, I.; Gandolfi, S.; Gezerlis, A.; Schwenk, A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys. Rev. C 2016, 93, 024305. [Google Scholar] [CrossRef]
- Demorest, P.B.; Pennucci, T.; Ransom, S.M.; Roberts, M.S.E.; Hessels, J.W.T. A two-solar-mass neutron star measured using Shapiro delay. Nature 2010, 467, 1081–1083. [Google Scholar] [CrossRef]
- Antoniadis, J.; Freire, P.C.C.; Wex, N.; Tauris, T.M.; Lynch, R.S.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A Massive Pulsar in a Compact Relativistic Binary. Science 2013, 340, 1233232. [Google Scholar] [CrossRef] [PubMed]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. 2019, 887, L21. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef]
- Raaijmakers, G.; Riley, T.E.; Watts, A.L.; Greif, S.K.; Morsink, S.M.; Hebeler, K.; Schwenk, A.; Hinderer, T.; Nissanke, S.; Guillot, S.; et al. A NICER View of PSR J0030+0451: Implications for the Dense Matter Equation of State. Astrophys. J. 2019, 887, L22. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M ⊙. Astrophys. J. 2020, 892, L3. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Effective one body description of tidal effects in inspiralling compact binaries. Phys. Rev. D 2010, 81, 084016. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).