A Parallel Hybrid Bregman Subgradient Extragradient Method for a System of Pseudomonotone Equilibrium and Fixed Point Problems

Abstract

We introduce a new parallel hybrid subgradient extragradient method for solving the system of the pseudomonotone equilibrium problem and common fixed point problem in real reflexive Banach spaces. The algorithm is designed such that its convergence does not require prior estimation of the Lipschitz-like constants of the finite bifunctions underlying the equilibrium problems. Moreover, a strong convergence result is proven without imposing strong conditions on the control sequences. We further provide some numerical experiments to illustrate the performance of the proposed algorithm and compare with some existing methods.

1. Introduction

In this paper, we consider the Equilibrium Problem (EP) in the framework of a real reflexive Banach space. Let E be the real reflexive Banach space, and consider its subset C, which is nonempty, closed and convex. Let g: $C\times C\to \mathbb{R}$ be a bifunction. The task of the EP with respect to g is to find a point $p^{*}\in C$ such that:

$$g(p^{*},y)\ge 0,\forall y\in C.$$

(1)

We denote the set of solutions of (1) by $EP\left(g\right)$. In the literature, it is common knowledge that numerous fascinating and complicated problems in nonlinear analysis, like the complementarity, the fixed point, Nash equilibrium, optimization, saddle point and variational inequality, can be written as an EP [1]. In view of the immense utilization of the EP, it has gained the interest of numerous researchers as of late (see, for example, [2,3,4,5], and the references therein).

On the other hand, let $T:C\to C$ be an operator. A point $x\in C$ is called a fixed point of T if $x=Tx.$ We denote the set of fixed points of T by $F\left(T\right).$ Fixed point theory has numerous applications both in pure and applied science. The largest category for its application is differential equations, and others are in economics, control theory, optimization and game theory. Different techniques have been presented for assessing and estimating the fixed points of nonexpansive and quasi-nonexpansive mappings; see [6,7,8,9,10,11], and the references therein.

The problem of finding a common solution of the EP and the fixed point problem, i.e.:

$$\mathrm{Find}{p}^{*}\in C\mathrm{such}\mathrm{that}{p}^{*}\in EP\left(g\right)\cap F\left(T\right),$$

(2)

has become an important area of research due to its possible applications in applied science. This happens mainly in image processing, network distribution, signal processing, etc. [12,13,14,15].

Tada and Takahashi [16] presented the following hybrid technique for finding the said element $p^{*}$ of the set of solutions of the monotone EP and the set of fixed points of a nonexpansive mapping T in the framework of Hilbert spaces:

$$\left\{\begin{array}{c}{x}_0\in C_0=Q_0=C,{\pi }_n\in (0,1),{\lambda }_n\in (0,\infty )\hfill \\ z_n\in C\mathrm{such}\mathrm{that}g(z_n,y)+\frac{1}{{\lambda }_n}⟨y-z_n,z_n-x_n⟩\ge 0,\forall y\in C,\hfill \\ {\beta }_n={\pi }_n{x}_n+(1-{\pi }_n)T{z}_n,\hfill \\ C_n=\left\{v\in C:∥{\beta }_n-v∥\le ∥x_n-v∥\right\},\hfill \\ Q_n=\left\{v\in C:⟨x_0-x_n,v-x_n⟩\le 0\right\},\hfill \\ x_{n+1}=P_{C_n\cap Q_n}{x}_0.\hfill \end{array}\right.$$

Note that at each step for finding the intermediate approximation $z_n$, we need to solve a strongly monotone regularized equilibrium problem, i.e.,

$$\mathrm{Find}{z}_n\in C\mathrm{such}\mathrm{that}g(z_n,y)+\frac{1}{{\lambda }_n}⟨y-z_n,z_n-x_n⟩\ge 0,\forall y\in C.$$

(3)

If the bifunction g is not monotone, then subproblem (3) is not necessarily strongly monotone; hence, the regularization method cannot be applied to the problem. To overcome this predicament, Anh [17] presented the following iterative scheme for finding a common element of the set of fixed points of a nonexpansive mapping T and the set of solutions of the EP involving a pseudomonotone bifunction g in Hilbert spaces:

$$\left\{\begin{array}{c}{x}_0\in C_0=Q_0=C,{\pi }_n\in (0,1),{\sigma }_n\in (0,\infty )\hfill \\ y_n=\mathrm{argmin}\left\{{\sigma }_{n}g(x_n,y)+\frac{1}{2}{∥x_n-y∥}^2:y\in C\right\}\hfill \\ t_n=\mathrm{argmin}\left\{{\sigma }_{n}g(x_n,y)+\frac{1}{2}{∥y_n-y∥}^2:y\in C\right\}\hfill \\ z_n={\pi }_n{x}_n+(1-{\pi }_n)T{t}_n,\hfill \\ C_n=\left\{v\in C:∥z_n-v∥\le ∥x_n-v∥\right\}\hfill \\ Q_n=\left\{v\in C:⟨x_0-x_n,v-x_n⟩\le 0\right\}\hfill \\ x_{n+1}=P_{C_n\cap Q_n}{x}_0.\hfill \end{array}\right.$$

(4)

In order to establish the strong convergence of the sequences $\left\{x_n\right\}$ generated by (4) to $x^{*}=P_{EP\left(g\right)\cap F\left(T\right)}{\pi }_0$, the author required that the positive sequences $\left\{{\sigma }_n\right\}$ of the stepsize satisfy a Lipschitz-like condition, i.e.,

$$0<{\sigma }_n\le \min \left\{\frac{1}{2c_1},\frac{1}{2c_2}\right\},$$

(5)

where $c_1$ and $c_2$ are the Lipschitz-like constants of g, that is $c_1$ and $c_2$ satisfy the following inequality: $g(x,y)+g(y,z)\ge g(x,z)-c_1{D}_f(y,x)-c_2{D}_f(z,y),\forall x,y,z\in C$, where $D_f$ is the associated Bregman distance of the convex function f.

In 2016, Hieu et al. [18], following a similar trend, introduced the following parallel hybrid method, called the Parallel Modified Extragradient Method (PMEM), for solving the finite family of equilibrium problems and the common fixed point of nonexpansive mappings in the framework of real Hilbert spaces:   

$$\left\{\begin{array}{c}{y}_n^i=\mathrm{argmin}\left\{\rho g_i(x_n,y)+\frac{1}{2}{∥x_n-y∥}^2:y\in C\right\}i=1,\cdots ,N,\hfill \\ z_n^i=\mathrm{argmin}\left\{\rho g_i(y_n^i,y)+{∥{\rho }_n-y∥}^2:y\in C\right\}i=1,\cdots ,N,\hfill \\ i_n=\mathrm{Argmax}\left\{∥z_n^i-x_n∥:i=1,2,\cdots ,N\right\},{\overline{z}}_n:=z_n^{i_n},\hfill \\ u_n^j={\alpha }_n{x}_n+(1-{\alpha }_n)T_j\overline{z},j=1,\cdots ,M,\hfill \\ j_n=\mathrm{Argmax}\left\{∥u_n^j-x_n∥:j=1,2,\cdots ,M\right\}{\overline{u}}_n:=u_n^{j_n}\hfill \\ C_n=\left\{v\in C:∥{\overline{u}}_n-v∥\le ∥x_n-v∥\right\},\hfill \\ Q_n=\left\{v\in C:⟨x_0-x_n,v-x_n⟩\le 0\right\},\hfill \\ x_{n+1}=P_{C_n\cap Q_n}{x}_0.\hfill \end{array}\right.$$

(6)

They also proved a strong convergence result for the sequence $\left\{x_n\right\}$ generated by (6) provided the stepsize $\rho$ satisfies the following condition:

$$0<\rho <\min \left\{\frac{1}{2c_1},\frac{1}{2c_2}\right\},$$

(7)

where $c_1=\max \{c_{1,i}:i=1,2,\cdots ,N\}$ and $c_2=\max \{c_{2,i}:i=1,2,\cdots ,N\}$, such that $c_{1,i}$ and $c_{2,i}$ are the Lipschitz-like constants for $g_i$ for $i=1,2,\cdots ,N.$

In 2014, Shahzad and Zegeye [11], in the framework of real reflexive Banach spaces and for approximating the common fixed point of multi-valued Bregman relatively nonexpansive mappings, presented the following iterative scheme:

$$\left\{\begin{array}{c}u,x_0\in E,{\alpha }_n\in (0,1),{\left\{{\beta }_{n,i}\right\}}_{i=0}^N\subset (0,1)\hfill \\ w_n=Pro{j}_C^f({\alpha }_n\nabla f\left(u\right)+(1-{\alpha }_n)\nabla f\left(x_n\right)),\hfill \\ x_{n+1}=\nabla f^{*}({\beta }_{n,0}\nabla f\left(w_n\right)+\sum _{i=1}^N{\beta }_i\nabla f\left(u_{i,n}\right)),\hfill \end{array}\right.$$

where $u_{i,n}\in T_i{w}_n$ and C is a nonempty closed convex subset of int domf (i.e., the interior of the domain of f). Under some mild conditions on the parameters, the authors proved the strong convergence of the sequence $\left\{x_n\right\}$ to $Pro{j}_F^{f}u$, where $F={\bigcap }_{i=1}^{N}F\left(T_i\right)$.

Very recently, Eskandani et al. [19], using the Hybrid Parallel extragradient method (HPA), introduced a Bregman–Lipschitz-type condition for a pseudomonotone bifunction. For estimating this common point $p^{*}$ for a finite family of multi-valued Bregman relatively nonexpansive mappings in reflexive Banach spaces, the following algorithm, called HPA, was presented:

$$\left\{\begin{array}{c}{x}_0\in C,{\alpha }_n\in (0,1),{\left\{{\beta }_{n,r}\right\}}_{r=0}^M\subset (0,1),\hfill \\ w_n^i=\mathrm{argmin}\left\{{\sigma }_n{g}_i(x_n,\beta )+D_f(\beta ,x_n):\beta \in C\right\}i=1,\cdots ,N,\hfill \\ z_n^i=\mathrm{argmin}\left\{{\sigma }_n{g}_i(w_n^i,\beta )+D_f(\beta ,x_n):\beta \in C\right\}i=1,\cdots ,N,\hfill \\ j_n\in \mathrm{Argmax}\left\{D_f(z_n^i,x_n),j=1,2,\cdots ,N\right\},{\overline{z}}_n:=z_n^{i_n},\hfill \\ y_n=\nabla f^{*}\left({\beta }_{n,0}\nabla f\left({\overline{z}}_n\right)\right)+\sum _{r=1}^M{\beta }_{n,r}\nabla f\left(z_{n,r}\right)),z_{n,r}\in T_r{\overline{z}}_n,\hfill \\ {\rho }_{n+1}=Pro{j}_C^f(\nabla f\left(u_n\right)+(1-{\alpha }_n)\nabla f\left(y_n\right))),\hfill \end{array}\right.$$

where $D_f$ is the related Bregman distance of a function f. Under specific suppositions, they established that the sequence $\left\{x_n\right\}$ converges strongly to $Pro{j}_{\Omega }^{f}u$, where $\mathsf{\Omega }={\bigcap }_{r=}^{M}F\left(T_r\right)\cap {\bigcap }_{i=1}^{N}EP\left(g_i\right)\ne \varnothing$ provided that the stepsize ${\sigma }_n$ satisfies the condition:

$$\left\{{\sigma }_n\right\}\subset \left[a,b\right]\subset (0,q),\mathrm{where}q=\min \left\{\frac{1}{c_1},\frac{1}{c_2}\right\},$$

(8)

where $c_1$ = ${\displaystyle \underset{1\le i\le N}{\max }}\left\{c_{i,1}\right\}$, $c_2={\displaystyle \underset{1\le i\le N}{\max }}\left\{c_{i,1}\right\}$ and $c_{i,2},c_{i,2}$ are the Bregman–Lipschitz coefficients of bifunction $g_i$ for $i=1,2,\cdots ,N.$

It is worth noting that the results of Anh, Hieu and Eskandani et al., mentioned above, and other similar ones (see, e.g., [20,21,22]) involve prior knowledge of the Lipschitz-like constants, which have been proven to be very strenuous to approximate piratically. In fact, when it is possible, the estimates are often too small, which slows down the rate of convergence of the algorithms. Thus, it becomes very important to find an algorithm that does not depend on the prior knowledge of the Lipschitz-like constants. Recently, the authors of [23,24,25], introduced some modified extragradient algorithms for solving the pseudomonotone EP (when $N=1$), which does not involve the prior estimate of the Lipschitz-like constants $c_1$ and $c_2$. Furthermore, related to our work are several methods such as [26], where the stepsize is the variable stepsize formula, that is the bifunction has a Lipschitz-like condition defined on it, and the algorithm also operates without the prior estimation of Lipschitz-type constants. The authors in [27,28] considered algorithms for solving the mixed equilibrium problem, split variational inclusion and fixed point theorems. Lastly, we also mention in passing that the authors in [29] considered a convex feasibility problem, that is finding a common element in the finite intersection of a finite family of convex sets $C_i$; whereas, in our work, we consider a finite family of pseudomonotone bifunctions, and our C is fixed.

Persuaded by the outcomes above, in this present paper, we provide another subgradient extragradient technique for finding a common element of the set of solutions of equilibrium problems for a finite family of pseudomonotone bifunctions and the set of common fixed points of a finite family of Bregman relatively nonexpansive mappings in the framework of reflexive Banach spaces. Our algorithm is designed in a way that its convergence does not need prior knowledge of the Lipschitz-like constants of the bifunctions $g_i$ for $i=1,2,\cdots ,N.$ Under specific mild assumptions, we prove a strong convergence result for the sequence generated by our algorithm. Furthermore, we give some numerical examples to demonstrate the proficiency, competitiveness and efficiency of our algorithm with respect to other algorithms in the literature.

2. Preliminaries

Throughout this work, E and C are as defined in the Introduction, and we denote the dual space of E by $E^{*}$. Let $f:E\to (-\infty ,\infty ]$ be a proper convex and lower semicontinuous function. We denote the domain of f by dom f, which is the set $\{x\in E:f\left(x\right)<\infty$}. Letting $x\in$ int dom f, we define the subdifferential of the function f at x as the convex set such that:

$$\partial f\left(x\right)=\{\varsigma \in E^{*}:f\left(x\right)+⟨y-x,\varsigma ⟩\le f\left(y\right),\forall y\in E\}.$$

We also define the Fenchel conjugate of f, as the function:

$$f^{*}:E^{*}\to (-\infty ,\infty ],\mathrm{such}\mathrm{that}{f}^{*}\left(\varsigma \right)=\sup \{⟨\varsigma ,x⟩-f\left(x\right):x\in E\}.$$

It is easy to note that $f^{*}$ is a proper convex and lower semicontinuous function. A function f on E is said to be coercive [30] if:

$$\underset{∥x∥\to +\infty }{\lim }f\left(x\right)=+\infty$$

(9)

Now, considering any convex mapping $f:E\to (-\infty ,\infty ]$, the directional derivative of f, denoted by $f^{\circ }(x,y)$, at $x\in$ int domf in the direction of y, is given by:

$$f^{\circ }(x,y):=\underset{t\to 0^{+}}{\lim }\frac{f(x+ty)-f\left(y\right)}{t}.$$

(10)

Suppose that the limit in (10) subsists for every $y\in E$, f is called G$\widehat{a}$teaux differentiable at x. The function f is referred to as G$\widehat{a}$teaux differentiable if it is G$\widehat{a}$teaux differentiable at each point x in the domain of f. When the limit t approaching zero in (10) is procured throughout for any point $y\in E$ where $\parallel y\parallel =1$, we say that f is Fr$\widehat{e}$chet differentiable at x. In the sequel, we assume that f is an admissible function, i.e., f is proper, convex, lower semicontinuous and Gâteaux differentiable. In this case, f is continuous in the interior of the domain of f (int dom f) (see [31,32]). Also, f is said to be Legendre if it satisfies the following two conditions:

L1.

int dom $f\ne \varnothing$, and the subdifferential $\partial f$ is single-valued on its domain;

L2.

int dom $f^{*}\ne \varnothing$, and $\partial f^{*}$ is single-valued on its domain.

According to ([33], p. 83), it is notable that in a reflexive Banach space $E,$$\nabla f^{*}={\left(\nabla f\right)}^{-1}$, where $\nabla f$ denotes the gradient of f. At the point when this reality is blended together with (L1) and (L2), we get:

$$\mathrm{ran}\nabla f=\mathrm{dom}\nabla f^{*}{=\mathrm{int}(\mathrm{dom}f)}^{*}\mathrm{and}\mathrm{ran}\nabla f^{*}=\mathrm{dom}\nabla f=\mathrm{int}\mathrm{dom}f.$$

Likewise, according to ([34], Corollary 5.5, p. 634), f is Legendre if and only if $f^{*}$ is Legendre and the functions f and $f^{*}$ are G$\widehat{a}$teaux differentiable and strictly convex on int domf and int dom$f^{*}$, respectively.

In 1967, Bregman [35] introduced an exquisite and efficacious tool for designing and dissecting the feasibility of optimization algorithms. In what follows, we presume that $f:E\to (-\infty ,\infty ]$ is a Gâteaux differentiable function. The Bregman distance is defined as the bifunction $D_f:\mathrm{dom}f\times \mathrm{int}\mathrm{dom}f\to [0,+\infty )$, where:

$$D_f(y,x)=f\left(y\right)-f\left(x\right)-⟨\nabla f\left(x\right),y-x⟩,y\in \mathrm{dom}f,x\in \mathrm{int}\mathrm{dom}f.$$

The Bregman distance satisfies the following important property called the three point identity: for any $x\in \mathrm{dom}f$ and $y,z\in \mathrm{int}\mathrm{dom}f$,

$$D_f(x,y)+D_f(y,z)-D_f(x,z)=⟨\nabla f\left(z\right)-\nabla f\left(y\right),x-y⟩.$$

(11)

According to ([36], Section 1.2, p. 17), the modulus of total convexity at $x\in \mathrm{int}\mathrm{dom}f$ f is the function $v_f(x,.):[0,+\infty )\to [0,\infty ]$, defined by:

$$v_f(x,s):=\inf \{D_f(y,x):y\in \mathrm{int}\mathrm{dom}f,\parallel y-x\parallel =s\}.$$

The function f is called totally convex at $x\in \mathrm{int}\mathrm{dom}f$ if $v_f(x,s)>0$ for any $t>0$. The function f is said to be totally convex when it is totally convex at every point $x\in \mathrm{int}\mathrm{dom}f$. We mention in passing that f is totally convex on bounded subsets if and only if f is uniformly convex on bounded subsets (see [36], cf.). According to [37], we are reminded that given any bounded sequence $\left\{{\sigma }_n\right\}$ and any other sequence, say $\left\{{\psi }_n\right\}$ in E, then f is referred to as being sequentially consistent if:

$$\underset{n\to \infty }{\lim }{D}_f({\sigma }_n,{\psi }_n)=0\Rightarrow \underset{n\to \infty }{\lim }\parallel {\sigma }_n-{\psi }_n\parallel =0.$$

(12)

Lemma 1

([31]). If $f:E\to \mathbb{R}$ is uniformly Fr$\widehat{e}$chet differentiable and bounded on subsets of E, then $\nabla f$ is uniformly continuous on bounded subsets of E from the strong topology E to the strong topology of $E^{*}$.

Lemma 2

([36]). If domf contains at least two points, then the function f is totally convex on bounded sets if and only if the function f is sequentially consistent.

Lemma 3

([32]). Let $f:E\to \mathbb{R}$ be a G$\widehat{a}$teaux differentiable and totally convex function. If ${\pi }_0\in E$ and the sequence $D_f({\sigma }_n,{\pi }_0)$ is bounded, then the sequence $\left\{{\sigma }_n\right\}$ is also bounded.

The Bregman projection (cf. [35]) with respect to f of $x\in \mathrm{int}\mathrm{dom}f$ onto $C\subset \mathrm{int}\mathrm{dom}f$ is characterized as the essentially exceptional vector ${\mathrm{Proj}}_C{}^f\left(x\right)\in C$, which satisfies the following:

$$D_f({\mathrm{Proj}}_C{}^f\left(x\right),x)=\inf \{D_f(y,x):y\in C\}.$$

Similar to the metric projection in Hilbert spaces, the Bregman projection with respect to totally convex and G$\widehat{a}$teaux differentiable functions has a variational characterization ([38], Corollary 4.4, p. 23).

Lemma 4

([38]). Assume that f is G$\widehat{a}$teaux differentiable and totally convex on int domf. Let $x\in \mathrm{int}\mathrm{dom}f$ and $C\subset \mathrm{int}\mathrm{dom}f$ be a nonempty, closed, and convex set. If $\widehat{x}\in C$, then the following conditions are equivalent:

M1. 

The vector $\widehat{x}\in C$ is the Bregman projection of x onto C with respect to f.

M2. 

The $\widehat{x}\in C$ is the unique solution of the variational inequality:

$$⟨z-y,\nabla f\left(x\right)-\nabla f\left(z\right)⟩\ge 0,\forall y\in C.$$

(13)

M3. 

The vector $\widehat{x}$ is the unique solution of the inequality:

$$D_f(y,z)+D_f(z,x)\le D_f(y,x),\forall y\in C.$$

Definition 1.

Let $T:C\to C$ be a mapping. A point x is called a fixed point of T if $Tx=x$. The set of fixed points of T is denoted by $F\left(T\right)$. Furthermore, a point $x^{*}\in C$ is said to be an asymptotic fixed point of T if C contains a sequence ${\left\{x_n\right\}}_{n=1}^{\infty }$ that converges weakly to $x^{*}$, and ${\lim }_{n\to \infty }\parallel x_n-T{x}_n\parallel =0$. The set of asymptotic fixed points of T is denoted by $\widehat{F}\left(T\right)$.

Definition 2.

Let C be a nonempty, closed and convex subset of E. A mapping $T:C\to \mathrm{int}\mathrm{dom}f$ is called:

i. 

Bregman firmly nonexpansive (BFNE) if:

$$⟨\nabla f\left(Tx\right)-\nabla f\left(Ty\right),Tx-Ty⟩\le ⟨\nabla f\left(x\right)-\nabla f\left(y\right),Tx-Ty⟩,\mathit{for}\mathit{all}x,y\in C.$$

ii. 

Bregman strongly nonexpansive (BSNE) with respect to a nonempty $\widehat{F}$(T) if:

$$D_f(p,Tx)\le D_f(p,x),$$

for all $p\in \widehat{F}\left(T\right)$ and $x\in C$, and if whenever ${\left\{x_n\right\}}_{n=1}^{\infty }\subset C$ is bounded, $p\in \widehat{F}\left(T\right)$ and:

$$\underset{n\to \infty }{\lim }(D_f(p,x_n)-D_f(p,T{x}_n))=0,\mathit{it}\mathit{follows}\mathit{that}\underset{n\to \infty }{\lim }{D}_f(p,x_n)=0,$$

iii. 

Bregman relatively nonexpansive (BRNE) if:

$$D_f(p,Tx)\le D_f(p,x),\forall x\in C,p\in F\left(T\right),\mathit{and}\widehat{F}\left(T\right)=F\left(T\right).$$

iv. 

Quasi-Bregman nonexpansive (QBNE) if $F\left(T\right)\ne 0$ and:

$$D_f(p,Tx)\le D_f(p,x),\mathit{for}\mathit{all}x\in C,p\in F\left(T\right).$$

It was mentioned in [39] that in the instance where $\widehat{F}\left(T\right)=F\left(T\right)$, the following inclusion holds:

$$\mathrm{BFNE}\subset \mathrm{BSNE}\subset \mathrm{QBNE}.$$

In this case, QBNE is called a Bregman relatively nonexpansive mapping.

Following [40,41], we define a map $V_f:E\times E^{*}\to [0,+\infty ]$ with respect to f by:

$$V_f(\mu ,{\mu }^{*})=f\left(\mu \right)-⟨x,{\mu }^{*}⟩+f^{*}\left({\mu }^{*}\right),\forall \mu \in E,{\mu }^{*}\in E^{*}.$$

Then:

$$V_f(\mu ,{\mu }^{*})=D_f(\mu ,\nabla f^{*}\left({\mu }^{*}\right)),\forall \mu \in E,{\mu }^{*}\in E^{*}.$$

(14)

More so, by the subdifferential inequality, we have:

$$V_f(\mu ,{\mu }^{*})+⟨\nabla f^{*}\left({\mu }^{*}\right)-x,y^{*}⟩\le V_f(\mu ,{\mu }^{*}+y^{*}),$$

(15)

for all $\mu \in E,{\mu }^{*},y^{*}\in E^{*}$ (see [42]). In addition, if $f:E\to (-\infty ,\infty ]$ is a proper lower semicontinuous function, then $f^{*}:E^{*}\to (-\infty ,\infty ]$ is proper weak lower semicontinuous and convex. Hence, $V_f$ is convex in the second variable. Then, for all $z\in E$, we have:

$$D_f\left(z,\nabla f^{*}\left(\sum _{i=1}^N{t}_i\nabla f\left(x_i\right)\right)\right)\le \sum _{i=1}^N{D}_f(z,x_i),$$

(16)

where ${\left\{x_i\right\}}_{i=1}^N\subset E$ and ${\left\{t_i\right\}}_{i=1}^N\subset (0,1)$ with ${\sum }_{i=1}^N{t}_i=1$.

Let B and S be the closed unit ball and the unit sphere of a Banach space E, respectively. Then, the function $f:E\to \mathbb{R}$ is said to be uniformly convex on bounded subsets (see [43]) if ${\nu }_r>0$ for all $r,t>0$, where ${\nu }_r:[0,\infty )\to [0,\infty ]$ is defined by:

$${\nu }_r=\underset{x,y\in rB,\parallel x-y\parallel =t,\kappa \in (0,1)}{\inf }\frac{\alpha f\left(x\right)+(1-\kappa )f\left(y\right)-f(\kappa x+1-\alpha )y}{\kappa (1-\kappa )},$$

$\forall t\ge 0$. The function ${\nu }_r$ is called the gauge of uniform convexity of f. It is known that ${\nu }_r$ is a nondecreasing function. If f is uniformly convex, then the following lemma is known:

Lemma 5

([44]). Let E be a Banach space, $r>0$ be a constant and $f:E\to \mathbb{R}$ be a uniformly convex function on bounded subsets of E. Then:

$$f\left(\sum _{k=0}^n{a}_k{x}_k\right)\le \sum _{k=0}^n{a}_{k}f\left(x_k\right)-a_i{a}_j{\rho }_r(\parallel x_i-x_j\parallel ),$$

for all $i,j\in (0,1,2,\cdots ,n)$, $x_k\in rB$, $a_k\in (0,1)$ and $k=0,1,2,\cdots ,n$ with ${\sum }_{k=0}^n{a}_k=1$, where ${\rho }_r$ is the gauge of the uniform convexity of f.

Lemma 6

([45]). Suppose that $f:E\to (-\infty ,+\infty ]$ is a Legendre function. The function f is totally convex on bounded subsets if and only if f is uniformly convex on bounded subsets.

Lemma 7

([46]). Let C be a nonempty convex subset of E and $f:C\in \mathbb{R}$ be a convex and subdifferentiable function on C. Then, f attains its minimum at $x\in C$ if and only if $0\in \partial f\left(x\right)+N_C\left(x\right)$, where $N_C\left(x\right)$ is the normal cone of C at x, that is:

$$N_C\left(x\right):=\{x^{*}\in E^{*}:⟨x-z,x^{*}⟩\ge 0,\forall z\in C\}.$$

Throughout this paper, we assume that the following assumptions hold on any $g:C\times C\to \mathbb{R}$:

A1.

g is pseudomonotone, i.e., $g(x,y)\ge 0\mathrm{and}g(y,x)\le 0$ for all $x,y\in C$,

A2.

g is a Bregman–Lipschitz-type condition, i.e., there exist two positive constants $c_1,c_2$, such that:

$$g(x,y)+g(y,z)\ge g(x,z)-c_1{D}_f(y,x)-c_2{D}_f(z,y),\forall x,y,z\in C.$$

(17)

A3.

$g(x,x)=0$ for all $x\in C$,

A4.

$g(·,y)$ is continuous on C for every $y\in C$,

A5.

$g(x,·)$ is convex, lower semicontinuous and subdifferentiable on C for every fixed $x\in C$.

3. Results

In this section, we introduce a new parallel hybrid subgradient extragradient algorithm for finding a common element of the set of solutions of equilibrium problems for pseudomonotone bifunctions and the common fixed point of Bregman relatively nonexpansive mappings.

Let E be a real reflexive Banach space, C be a nonempty, closed and convex subset of E and $f:E\to \mathbb{R}$ be a uniformly Fréchet differentiable function, which is coercive, Legendre, totally convex and bounded on subsets of E such that $C\subset \mathrm{int}\mathrm{dom}f.$ For $i=1,2,\cdots ,N,$ let $g_i:E\times E\to \mathbb{R}$ be a finite family of bifunctions satisfying Assumptions (A1)–(A5). Furthermore, for $j=1,2,\cdots ,M,$ let $T_j:E\to E$ be a finite family of Bregman relative nonexpansive mappings. Assume that the solution set:

$$Sol=\left({\cap }_{i=1}^{N}EP\left(g_i\right)\right)\bigcap \left({\cap }_{j=1}^{M}F\left(T_j\right)\right)\ne \varnothing .$$

Furthermore, the control sequence ${\left\{{\alpha }_n\right\}}_{n=0}^{\infty }\subset (0,1)$ satisfies the condition:

$$0<a\le \underset{n\to \infty }{\mathrm{lim\; inf}}{\alpha }_n\le \underset{n\to \infty }{\mathrm{lim\; sup}}{\alpha }_n\le b<1.$$

(18)

Now, we present our algorithm (Algorithm 1) as follows.

Algorithm 1 Parallel hybrid Bregman subgradient extragradient method (PHBSEM).

Step 0.      Pick $x_0\in E$, $\mu \in (0,1),{\lambda }_0>0$, and set $n=0.$ Step 1.      Solve N strongly convex programs: $$\begin{array}{cc}\hfill & y_n^i=argmin\left\{g_i(x_n,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y):y\in C\right\},\hfill \\ \hfill & z_n^i=argmin\left\{g_i(y_n^i,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y):y\in T_n^i\right\},\hfill \end{array}$$ (19)      where $T_n^i=\left\{z\in E:⟨\nabla f\left(x_n\right)-{\lambda }_n{w}_n^i-\nabla f\left(y_n^i\right),z-y_n^i⟩\le 0\right\}$ and $w_n^i\in \partial g_i(x_n,y_n^i).$ Step 2.      Find the farthest element of $z_n^i$ from $x_n$ by: $$i_n=Argmax\left\{D_f(x_n,z_n^i):i=1,\cdots ,N\right\}.$$ (20)      Set ${\overline{z}}_n=z_n^{i_n}.$ Step 3.      Compute in parallel for $j=1,\cdots ,M$: $$u_n^j=\nabla f^{*}({\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)).$$ (21)      Find the farthest element of $u_n^j$ from $x_n$ by: $$j_n=Argmax\left\{D_f(x_n,u_n^j):j=1,\cdots ,M\right\}.$$      Set ${\overline{u}}_n=u_n^{j_n}.$ Step 4.      Construct two half-spaces $C_n$ and $Q_n$ as follows: $$\begin{array}{ccc}\hfill C_n& =& \left\{z\in E:D_f(z,{\overline{u}}_n)\le D_f(z,x_n)\right\},\hfill \\ \hfill Q_n& =& \left\{z\in E:⟨\nabla f\left(z\right)-\nabla f\left(x_n\right),x_n-x_0⟩\ge 0\right\}.\hfill \end{array}$$ (22) Step 5.      Compute $x_{n+1}$ and ${\lambda }_{n+1}$ by: $$x_{n+1}=Pro{j}_{C_n\cap Q_n}\left(x_0\right)$$      and: $${\lambda }_{n+1}=\left\{\begin{array}{cc}\min \left\{{\lambda }_0,\underset{1\le i\le N}{\min }\left\{\frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{g(x_n,z_n^i)-g(x_n,y_n^i)-g(y_n^i,z_n^i)}\right\}\right\}\hfill & \\ \mathrm{if}g(x_n,z_n^i)-g(x_n,y_n^i)-g(y_n^i,z_n^i)\ge 0,\hfill \\ {\lambda }_0,\mathrm{otherwise}.\hfill \end{array}\right.$$ (23)

Before we start with the proof of Algorithm 1, we discuss some contributions of the algorithm compared with other methods in the literature.

(i)

Firstly, Algorithm 1 solves two strongly convex optimization problems in parallel for $i=1,2,\cdots ,N,$ with the second convex problem solving over the half-spaces $T_n^i$, which is simpler than the entire feasible set used in Eskandani et al. [19].

(ii)

Moreover, the stepsize in Eskandami et al. [19] required finding the prior estimates of the Lipschitz-like constants of the finite bifunctions, which is very cumbersome for computation. Meanwhile, in Algorithm 1, the stepsize is chosen self-adaptively and does not require the prior estimates of the Lipschitz-like constant of the finite bifunctions.

(iii)

Furthermore, when E is the real Hilbert space, our Algorithm 1 improves the algorithms of [18,47,48,49,50] in the setting of real Hilbert spaces.

(iv)

Furthermore, when E is a real Hilbert space and $N=1$, $M=1$, our Algorithm 1 improves and compliments the algorithms of [17,20,22,24,25,51].

Now, to prove the strong convergence of the algorithm parallel hybrid Bregman subgradient extragradient method (PHBSEM), we need the following results.

Lemma 8.

The sequence $\left\{{\lambda }_n\right\}$ is bounded by:

$$\min \left\{{\lambda }_0,\underset{1\le i\le N}{\min }\left\{\frac{\mu }{\max \left\{c_{1,i},c_{2,i}\right\}}\right\}\right\},$$

(24)

where $\left\{c_{1,i}\right\},\left\{c_{2,i}\right\}$ are the Lipschitz-like constants of the bifunctions $g_i$ for $i=1,2,\cdots ,N.$

Proof. 

From the Lipschitz-like condition (17), we have:

$$g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)\le c_{1,i}{D}_f(y_n^i,x_n)+c_{2,i}{D}_f(z_n^i,y_n^i),\mathrm{for}\mathrm{all}i=1,2,\cdots ,N.$$

It follows that:

$$\frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)}\ge \frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{c_{1,i}{D}_f(y_n^i,x_n)+c_{2,i}{D}_f(z_n^i,y_n^i)}$$

for $i=1,2,\cdots ,N.$ Hence, for $i=1,2,\cdots ,N,$ we have:

$$\begin{array}{c}\hfill \frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)}\ge \frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{\max \left\{c_{1,i},c_{2,i}\right\}\left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}.\end{array}$$

Thus, for $i=1,2,\cdots ,N,$ we have:

$$\begin{array}{c}\hfill \frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)}\ge \frac{\mu }{\max \left\{c_{1,i},c_{2,i}\right\}}.\end{array}$$

This implies that:

$$\begin{array}{c}\hfill \frac{\mu \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)}{g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)}\ge \underset{1\le i\le N}{\min }\left\{\frac{\mu }{\max \left\{c_{1,i},c_{2,i}\right\}}\right\}\end{array}$$

Therefore, we have that $\left\{{\lambda }_n\right\}$ is bounded by:

$$\begin{array}{c}\hfill \min \left\{{\lambda }_0,\underset{1\le i\le N}{\min }\left\{\frac{\mu }{\max \left\{c_{1,i},c_{2,i}\right\}}\right\}\right\}.\end{array}$$

   □

Lemma 9.

Suppose $x^{*}\in Sol$ and $x_n,y_n^i,z_n^i,$ where $i=1,\cdots ,N$ are as defined in Step 1 and Step 2 of the algorithm PHBSEM. Then:

$$D_f(x^{*},z_n^i)\le D_f(x^{*},x_n)-(1-\sigma )D_f(x_n,y_n^i)-(1-\sigma )D_f(y_n^i,z_n^i).$$

(25)

Proof. 

Since $z_n^i\in T_n^i$, we have:

$$⟨\nabla f\left(x_n\right)-\nabla f\left(y_n^i\right),z_n^i-y_n^i⟩\le {\lambda }_n⟨w_n^i,z_n^i-y_n^i⟩.$$

(26)

Furthermore, $w_n^i\in \partial g_i(x_n,y_n^i)$; thus:

$$g_i(x_n,z)-g_i(x_n,y_n^i)\le ⟨w_n^i,z-y_n^i⟩,\forall z\in T_n^i,i=1,2,\cdots ,N.$$

(27)

By (26) and (27), we have:

$$⟨\nabla f\left(x_n\right)-\nabla f\left(y_n^i\right),z_n^i-y_n^i⟩\le {\lambda }_n\left(g_i(x_n,z_n^i)-g_i(x_n,y_n^i)\right).$$

(28)

Furthermore, since $z_n^i=\mathrm{argmin}\left\{g_i(y_n^i,y)+\frac{1}{2{\lambda }_n}{D}_f(x_n,y):y\in T_n^i\right\},$ it follows from (7) that:

$$0\in \partial \left({\lambda }_n^i{g}_i(y_n^i,y)+D_f(x_n,y)\left(z_n^i\right)+N_{T_n}^i\left(z_n^i\right)\right).$$

This implies that for $i=1,2,\cdots ,N,$ there exists ${w_n}^i\in \partial g_i(y_n^i,z_n^i)$ and ${\xi }^i\in N_{T_n^i}\left(z_n^i\right)$ such that:

$${\lambda }_n{w}_n^i+D_f\left(z_n^i\right)-\nabla f\left(x_n\right)+{\xi }^i=0.$$

Since ${\xi }^i\in N_{T_n^i}\left(z_n^i\right),$ then $⟨{\xi }^i,z-z_n^i⟩\le 0,\forall z\in T_n^i.$ Hence:

$${\lambda }_n⟨{\overline{w_n}}^i,z-z_n^i⟩\ge ⟨\nabla f\left(x_n\right)-\nabla f\left(z_n^i\right),z-z_n^i⟩.$$

(29)

Furthermore, ${\overline{w_n}}^i\in \partial g_i(y_n^i,z_n^i)$, then:

$$g_i(y_n^i,z)-g_i(y_n^i,z_n^i)\ge ⟨\overline{w_n},z-z_n^i⟩,\forall z\in E.$$

Thus,

$${\lambda }_n\left(g_i(y_n^i,z)-g_i(y_n^i,z_n^i)\right)\ge {\lambda }_n⟨{\overline{w_n}}^i,z-z_n^i⟩,z\in E.$$

(30)

By (29) and (30), we have:

$$⟨\nabla f\left(x_n\right)-\nabla f\left(z_n^i\right),z-z_n^i⟩\le {\lambda }_n\left(g_i(y_n^i,z)-g_i(y_n^i,z_n^i)\right).$$

(31)

Let $z=x^{*}\in EP\left(g_i\right)$. From (31), we get:

$$⟨\nabla f\left(x_n\right)-\nabla f\left(z_n^i\right),x^{*}-z_n^i⟩\le {\lambda }_n\left(g_i(y_n^i,x^{*})-g_i(y_n^i,z_n^i)\right).$$

Since each $g_i$ is pseudomonotone, $g_i(y_n^i,x^{*})\le 0$. Therefore:

$$⟨\nabla f\left(x_n\right)-\nabla f\left(z_n^i\right),x^{*}-z_n^i⟩\le -{\lambda }_n\left(g_i(y_n^i,z_n^i)\right).$$

(32)

Adding (28) and (32), we have:

$$\begin{array}{cc}\hfill ⟨\nabla f\left(x_n\right)-\nabla f\left(y_n^i\right),z_n^i-y_n^i⟩& +⟨\nabla f\left(x_n\right)-\nabla f\left(z_n^i\right),x^{*}-z_n^i⟩\hfill \\ \hfill & \le {\lambda }_n\left(g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)\right).\hfill \end{array}$$

(33)

By the three point identity, i.e., (11), we get:

$$\begin{array}{cc}\hfill D_f(x^{*},z_n^i)+D_f(y_n^i,x_n)& +D_f(z_n^i,y_n^i)-D_f(x^{*},x_n)\hfill \\ \hfill & \le {\lambda }_n\left(g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g_i(y_n^i,z_n^i)\right).\hfill \end{array}$$

Using (23), we have:

$$\begin{array}{ccc}\hfill D_f(x^{*},z_n^i)& \le & D_f(x^{*},x_n)-D_f(y_n^i,x_n)-D_f(z_n^i,y_n^i)+\frac{{\lambda }_n}{{\lambda }_{n+1}}{\lambda }_{n+1}\left(g_i(x_n,z_n^i)-g_i(x_n,y_n^i)-g(y_n^i,z_n^i)\right)\hfill \\ & \le & D_f(x^{*},x_n)-D_f(y_n^i,x_n)-D_f(z_n^i,y_n^i)+\frac{{\lambda }_n}{{\lambda }_{n+1}}\sigma \left(D_f(y_n^i,x_n)+D_f(z_n^i,y_n^i)\right)\hfill \\ & =& D_f(x^{*},x_n)-(1-\sigma )D_f(y_n^i,x_n)-(1-\sigma )D_f(z_n^i,y_n^i).\hfill \end{array}$$

Thus, we obtain (25). This completes the proof.    □

Lemma 10.

For any $x^{*}\in Sol$, the following inequality holds:

$$\begin{array}{c}\hfill D_f(x^{*},u_n^j)\le D_f(x^{*},x_n)-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right),\end{array}$$

where $j=1,2,\cdots ,M$ and ${\rho }_s^{*}:E^{*}\to \mathbb{R}$ is the gauge of uniform convexity of the conjugate function $f^{*}.$

Proof. 

From (21) and Lemma 5, we have:

$$\begin{array}{ccc}\hfill D_f(x^{*},u_n^j)& =& D_f(x^{*},\nabla f^{*}({\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)))\hfill \\ & =& V_f(x^{*},{\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right))\hfill \\ & =& f\left(x^{*}\right)-⟨x^{*},{\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)⟩+f^{*}\left({\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)\right)\hfill \\ & \le & f\left(x^{*}\right)-{\alpha }_n⟨x^{*},\nabla f\left({\overline{z}}_n\right)⟩-(1-{\alpha }_n)⟨x^{*},\nabla f\left(T_j{\overline{z}}_n\right)⟩\hfill \\ & & +{\alpha }_n{f}^{*}\left(\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)\right)-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\hfill \\ & =& {\alpha }_n\left(f\left(x^{*}\right)-⟨x^{*},\nabla f\left({\overline{z}}_n\right)⟩+\nabla f^{*}\left(\nabla f\left({\overline{z}}_n\right)\right)\right)\hfill \\ & & +(1-{\alpha }_n)\left(f\left(x^{*}\right)-⟨x^{*},\nabla f\left(T_j{\overline{z}}_n\right)⟩+f^{*}\left(\nabla f\left(T_j{\overline{z}}_n\right)\right)\right)\hfill \\ & & -{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\hfill \\ & =& {\alpha }_n{V}_f(x^{*},\nabla f\left({\overline{z}}_n\right))+(1-{\alpha }_n)V_f(x^{*},\nabla f\left(T_j{\overline{z}}_n\right))-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\hfill \\ & =& {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},T_j{\overline{z}}_n)-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\hfill \\ & \le & {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},{\overline{z}}_n)-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\hfill \\ & =& D_f(x^{*},{\overline{z}}_n)-{\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right).\hfill \end{array}$$

Since $\sigma \in (0,1),$ then the desired result follows from Lemma 9.    □

Lemma 11.

The sequence $\left\{x_n\right\}$ generated by the algorithm PHBSEM is well defined and $Sol\subset C_n\cap Q_n$.

Proof. 

Let $x^{*}\in Sol$, then from Lemma 9 and the definition of $u_n^j$ and ${\overline{z}}_n$, we have:

$$\begin{array}{cc}\hfill D_f(x^{*},u_n^j)& =D_f(x^{*},\nabla f^{*}({\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right))\hfill \\ \hfill & \le {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},T_j{\overline{z}}_n)\hfill \\ \hfill & \le {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},{\overline{z}}_n)\hfill \\ \hfill & \le D_f(x^{*},{\overline{z}}_n)\hfill \\ \hfill & \le D_f(x^{*},x_n).\hfill \end{array}$$

(34)

Therefore, $D_f(x^{*},u_n^j)\le D_f(x^{*},x_n)$, and this implies that $x^{*}\in C_n$. Hence, $Sol\subset C_n,$ for all $n\ge 0.$

By induction, for $n\ge 0$, we have $Q_0=E,$ and thus, $Sol\subset C_0\cap Q_0$. Suppose $x_k$ is given and $Sol\subset C_k\cap Q_k$, for some $n=k>0$. There exits $x_{k+1}\subset C_k\cap Q_n$ such that $x_{k+1}=Pro{j}_{C_k\cap Q_k}\left(x_1\right)$. By (13), we have:

$$⟨x_{k+1}-y,\nabla f\left(x_1\right)-\nabla f\left(x_{k+1}\right)⟩\ge 0,\forall y\in C_K\cap Q_k.$$

Since $Sol\subset C_k\cap Q_k$, we get $Sol\subset C_{k+1}$. Therefore, $Sol\subset C_{k+1}\cap Q_{k+1}$. Thus, the sequence $\left\{x_n\right\}$ is well defined.    □

Lemma 12.

Let $\left\{x_n\right\},\left\{y_n^i\right\},\left\{z_n^i\right\},\left\{u_n^j\right\}$ be the sequences generated by the algorithm PHBSEM. Then, the following relations hold:

$$\underset{n\to \infty }{\lim }\parallel x_n-x_{n+1}\parallel =\underset{n\to \infty }{\lim }\parallel u_n^j-x_n\parallel =\underset{n\to \infty }{\lim }\parallel z_n^i-x_n\parallel =\underset{n\to \infty }{\lim }\parallel y_n^i-x_n\parallel =\underset{n\to \infty }{\lim }\parallel u_n^j-T_j{\overline{z}}_n\parallel =0.$$

(35)

Proof. 

Since $Sol\subset C_n\cap Q_n$ for all $n\ge 0$ and from the definition of $x_{n+1},$ then:

$$D_f(x_{n+1},x_0)\le D_f(x^{*},x_0),\forall n\ge 0,x^{*}\in Sol.$$

Hence, $\left\{D_f(x_n,x_0)\right\}$ is bounded, and from Lemma 3, we have that $\left\{x_n\right\}$ is bounded. Moreover, from the definition of $Q_n$ and $x_n=Pro{j}_{Q_n}^f\left(x_0\right)$ and since $x_{n+1}\in C_n\cap Q_n\subset Q_n,$ we have:

$$\begin{array}{cc}\hfill D_f(x_{n+1},x_0)& \ge D_f(x_{n+1},Pro{j}_{Q_n}^f\left(x_0\right))+D_f(Pro{j}_{Q_n}^f\left(x_0\right),x_0)\hfill \\ \hfill & \ge D_f(x_{n+1},x_n)+D_f(x_n,x_0).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill D_f(x_n,x_0)& \le D_f(x_{n+1},x_0)-D_f(x_{n+1},x_n)\hfill \\ \hfill & \le D_f(x_{n+1},x_0).\hfill \end{array}$$

Thus,

$$D_f(x_n,x_0)-D_f(x_{n+1},x_0)\ge 0.$$

Hence, $\left\{x_n\right\}$ is increasing, and since it is also bounded, ${\lim }_{n\to \infty }{D}_f(x_n,x_0)$ exists. Thus, it follows that:

$$\underset{n\to \infty }{\lim }{D}_f(x_{n+1},x_n)=0.$$

(36)

Then, from (12), we get:

$$\underset{n\to \infty }{\lim }\parallel x_{n+1}-x_n\parallel =0.$$

Furthermore, since $x_{n+1}\in C_n$, then $D_f(x_{n+1},{\overline{u}}_n)\le D_f(x_{n+1},x_n).$ Thus, taking the limits of both sides as $n\to \infty$ and by (36), we get:

$$\underset{n\to \infty }{\lim }{D}_f(x_n,{\overline{u}}_n)=0.$$

(37)

This implies that:

$$\underset{n\to \infty }{\lim }{D}_f(x_n,u_n^j)=0,\forall j=1,2,\cdots ,M.$$

It follows from Lemma 2 that:

$$\underset{n\to \infty }{\lim }∥x_n-u_n^j∥=0.$$

(38)

By the uniform continuity and Fréchet differentiability of f, we have:

$$\underset{n\to \infty }{\lim }∥f\left(x_n\right)-f\left(u_n^j\right)∥=\underset{n\to \infty }{\lim }∥\nabla f\left(x_n\right)-\nabla f\left(u_n^j\right)∥=0.$$

(39)

Moreover:

$$\begin{array}{cc}\hfill D_f(x^{*},x_n)-D_f(x^{*},u_n^j)& =f\left(x^{*}\right)-f\left(x_n\right)-⟨\nabla f\left(x_n\right),x^{*}-x_n⟩-f\left(x^{*}\right)+f\left(u_n^j\right)+⟨\nabla f\left(u_n^j\right),x^{*}-u_n^j⟩\hfill \\ \hfill & =f\left(u_n^j\right)-f\left(x_n\right)-⟨\nabla f\left(x_n\right),x^{*}-x_n⟩+⟨\nabla f\left(u_n^j\right),x^{*}-u_n^j⟩\hfill \\ \hfill & =f\left(u_n^j\right)-f\left(x_n\right)-⟨\nabla f\left(x_n\right),x^{*}-u_n^j⟩-⟨\nabla f\left(x_n\right),u_n^j-x_n⟩\hfill \\ \hfill & +⟨\nabla f\left(u_n^j\right),x^{*}-u_n^j⟩\hfill \\ \hfill & =f\left(u_n^j\right)-f\left(x_n\right)-⟨\nabla f\left(x_n\right)-\nabla f\left(u_n^j\right),x^{*}-u_n^j⟩-⟨\nabla f\left(x_n\right),u_n^j-x_n⟩.\hfill \end{array}$$

Therefore, from (38) and (39), we get:

$$\underset{n\to \infty }{\lim }\left(D_f(x^{*},x_n)-D_f(x^{*},u_n^j)\right)=0$$

(40)

Then, from Lemma 10, we have:

$${\alpha }_n(1-{\alpha }_n){\rho }_s^{*}\left(∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥\right)\le D_f(x^{*},x_n)-D_f(x^{*},u_n^j).$$

(41)

Thus, from (18), we obtain:

$$\underset{n\to \infty }{\lim }∥\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)∥=0,$$

(42)

which implies that:

$$\underset{n\to \infty }{\lim }∥{\overline{z}}_n-T_j{\overline{z}}_n∥=0.$$

(43)

Moreover, by Lemma 9, we have:

$$\begin{array}{cc}\hfill D_f(x^{*},u_n^j)& =D_f(x^{*},\nabla f^{*}({\alpha }_n\nabla \left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{\overline{z}}_n\right)))\hfill \\ \hfill & \le {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},T_j{\overline{z}}_n)\hfill \\ \hfill & \le {\alpha }_n{D}_f(x^{*},{\overline{z}}_n)+(1-{\alpha }_n)D_f(x^{*},z_n^i)\hfill \\ \hfill & \le {\alpha }_n{D}_f(x^{*},x_n)+(1-{\alpha }_n)\left(D_f(x^{*},x_n)-(1-\sigma )D_f(x_n,y_n^i)-(1-\sigma )D_f(y_n^i,z_n^i)\right)\hfill \\ \hfill & =D_f(x^{*},x_n)-(1-{\alpha }_n)(1-\sigma )\left(D_f(x_n,y_n^i)+D_f(y_n^i,z_n^i)\right).\hfill \end{array}$$

Thus,

$$\begin{array}{cc}\hfill (1-{\alpha }_n)(1-\sigma )\left(D_f(x_n,y_n^i)+D_f(y_n^i,z_n^i)\right)& \le D_f(x^{*},x_n)-D_f(x^{*},u_n^j)\hfill \end{array}$$

Therefore, taking the limits as $n\to \infty$ and by (40), we have:

$$\underset{n\to \infty }{\lim }{D}_f(x_n,y_n^i)=\underset{n\to \infty }{\lim }{D}_f(y_n^i,z_n^i)=0,\forall i=1,\cdots ,N.$$

Then:

$$\underset{n\to \infty }{\lim }\parallel y_n^i-x_n\parallel =\underset{n\to \infty }{\lim }\parallel y_n^i-z_n^i\parallel =0.$$

Hence:

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\parallel x_n-z_n^i\parallel =0.\end{array}$$

(44)

In addition, from (21), we have:

$$\begin{array}{ccc}\hfill \nabla f\left(u_n^j\right)-\nabla f\left(T_j{\overline{z}}_n\right)& =& {\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T_j{z}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)\hfill \\ & =& {\alpha }_n(\nabla f\left({\overline{z}}_n\right)-\nabla f\left(T_j{\overline{z}}_n\right)).\hfill \end{array}$$

Therefore, from (42), we get:

$$\begin{array}{c}\hfill \underset{n\to \infty }{\lim }\parallel \nabla f\left(u_n^j\right)-\nabla f\left(T_j{\overline{z}}_n\right)\parallel =0.\end{array}$$

This implies that:

$$\underset{n\to \infty }{\lim }\parallel u_n^j-T_j{\overline{z}}_n\parallel =0.$$

This completes the proof.    □

Now, we prove that the sequence $\left\{x_n\right\}$ generated by Algorithm 1 converges strongly to an element in $Sol.$

Theorem 1.

Let E be a real reflexive Banach space, C be a nonempty, closed and convex subset of E and function $f:E\to \mathbb{R}$ be a uniformly Fréchet differentiable function, which is coercive, Legendre, totally convex and bounded on subsets of E such that $C\subset int\left(domf\right).$ For $i=1,2,\cdots ,N,$ let $g_i:E\times E\to \mathbb{R}$ be a finite family of bifunctions satisfying Assumptions (A1)–(A5). Furthermore, for $j=1,2,\cdots ,M,$ let $T_j:E\to E$ be a finite family of Bregman relatively nonexpansive mappings. Suppose that $Sol=\left({\cap }_{i=1}^{N}EP\left(g_i\right)\right)\bigcap \left({\cap }_{j=1}^{M}F\left(T_j\right)\right)\ne \varnothing .$ Let $\left\{{\alpha }_n\right\}$ be a sequence in $(0,1)$ such that $0<a\le {\mathrm{lim\; inf}}_{n\to \infty }{\alpha }_n\le {\mathrm{lim\; sup}}_{n\to \infty }{\alpha }_n\le b<1.$ Then, the sequences $\left\{x_n\right\},\left\{y_n^i\right\},\left\{z_n^i\right\}$ generated by Algorithm 1 converge strongly to a solution $x^{*},$ where $x^{*}=Pro{j}_{Sol}^f\left(x_0\right).$

Proof. 

First, we show that every sequential weak limit point of $\left\{x_n\right\}$ belongs to $Sol.$ From the previous results, we see that $Pro{j}_{C_n\cap Q_n}^f{x}_0$ is well defined and $Sol\subset C_n\cap Q_n$ for all $n\ge 0.$ Furthermore, from Lemma 12, $\left\{x_n\right\}$ is bounded. Then, there exists a subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ converging weakly to p. By (43) and (44), we obtain that $p\in F\left(T_j\right)$ for $j=1,2,\cdots ,M.$ Hence, $p\in {\bigcap }_{j=1}^{M}F\left(T_j\right).$ Since:

$$y_n^i=argmin\left\{g_i(x_n,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y):y\in C\right\},\mathrm{for}i=1,2,\cdots ,N.$$

By Lemma 7, we obtain:

$$0\in {\partial }_2\left(g_i(x_n,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y)\right)\left(y_n^i\right)+N_C\left(y_n^i\right),\mathrm{for}i=1,2,\cdots ,N.$$

This implies that:

$${\lambda }_n{w}_n^i+\nabla f\left(x_n\right)-\nabla f\left(y_n^i\right)+{\overline{w}}_n^i=0,$$

where $w_n^i\in \partial g_i(x_n,y_n^i)$ and ${\overline{w}}_n^i\in N_C\left(y_n^i\right)$ for $i=1,2,\cdots ,N.$ This implies that:

$$⟨{\lambda }_n{w}_n^i,y-y_n^i⟩+⟨{\overline{w}}_n^i,y-y_n^i⟩=⟨\nabla f\left(y_n^i\right)-\nabla f\left(x_n\right),y-y_n^i⟩.$$

Note that $⟨{\overline{w}}_n^i,y-y_n^i⟩\le 0,$$\forall y\in C,i=1,2,\cdots ,N.$ Hence,

$${\lambda }_n⟨w_n^i,y-y_n^i⟩\ge ⟨\nabla f\left(y_n^i\right)-\nabla f\left(x_n\right),y-y_n^i⟩,\mathrm{for}i=1,2,\cdots ,N.$$

Furthermore, since $w_n^i\in {\partial }_2{g}_i(x_n,y_n^i),$ then:

$$g_i(x_n,y)+g_i(x_n,y_n^i)\ge ⟨w_n^i,y-z_n^i⟩,\forall y\in C,\mathrm{for}i=1,2,\cdots ,N.$$

Then:

$${\lambda }_n\left(g_i(x_n,y)-g_i(x_n,y_n^i)\right)\ge ⟨\nabla f\left(y_n^i\right)-\nabla f\left(x_n\right),y-y_n^i⟩,\mathrm{for}i=1,2,\cdots ,N.$$

Therefore:

$${\lambda }_{n_k}\left(g_i(x_{n_k},y)-g_i(x_{n_k},y_{n_k}^i)\right)\ge ⟨\nabla f\left(y_{n_k}^i\right)-\nabla f\left(x_{n_k}\right),y-y_{n_k}^i⟩,\mathrm{for}i=1,2,\cdots ,N.$$

(45)

Passing the limit as $k\to \infty$ to the expression in (45), since $x_{n_k}\rightharpoonup p$, $\parallel \nabla f\left(x_{n_k}\right)-\nabla f\left(y_{n_k}^i\right)\parallel \to 0$ and ${\lambda }_{n_k}\to \lambda >0,$ it follows from (45) that:

$$g_i(p,y)\ge 0,\forall y\in C,i=1,2,\cdots ,N.$$

Hence, $p\in EP\left(g_i\right)$ for $i=1,2,\cdots ,N.$ This means that $p\in {\bigcap }_{i=1}^{N}EP\left(g_i\right).$ Consequently, $p\in Sol.$

Now, we show that $\left\{x_n\right\}$ converges strongly to $Pro{j}_{Sol}^f{x}_0.$ Since $x_n=Pro{j}_{C_n}^f{x}_0,$ then we have:

$$⟨x_n-z,\nabla f\left(x_0\right)-\nabla f\left(x_n\right)⟩\ge 0\forall z\in C_n.$$

Furthermore, $Sol\subset C_n,$ thus:

$$⟨x_n-z,\nabla f\left(x_0\right)-\nabla f\left(x_n\right)⟩\ge 0\forall z\in Sol.$$

(46)

Passing the limit as $n\to \infty$ into (46), we get:

$$⟨p-z,\nabla f\left(x_0\right)-p⟩\ge 0\forall z\in Sol.$$

From (13), $p=Pro{j}_{Sol}^f\left(x_0\right).$ This implies that $\left\{x_n\right\}$ converges strongly to $p=Pro{j}_{Sol}^f\left(x_0\right).$ Lemma 12 ensures that $\left\{y_n^i\right\},\left\{z_n^i\right\}$ also converges strongly to $p=Pro{j}_{Sol}^f\left(x_0\right).$ This completes the proof.    □

The following results can be obtained as consequences of our main result.

Corollary 1.

Let E be a real reflexive Banach space, C be a nonempty, closed and convex subset of E and function $f:E\to \mathbb{R}$ be a uniformly Fréchet differentiable function, which is coercive, Legendre, totally convex and bounded on subsets of E such that $C\subset int\left(domf\right).$ For $i=1,2,\cdots ,N,$ let $g_i:E\times E\to \mathbb{R}$ be a finite family of bifunctions satisfying Assumptions (A1)–(A5). Furthermore for $j=1,2,\cdots ,M,$ let $T_j:E\to E$ be a finite family of Bregman strongly nonexpansive (BSNE) mappings. Suppose that $Sol=\left({\cap }_{i=1}^{N}EP\left(g_i\right)\right)\bigcap \left({\cap }_{j=1}^{M}F\left(T_j\right)\right)\ne \varnothing .$ Let $\left\{{\alpha }_n\right\}$ be a sequence in $(0,1)$ such that $0<a\le {\mathrm{lim\; inf}}_{n\to \infty }{\alpha }_n\le {\mathrm{lim\; sup}}_{n\to \infty }{\alpha }_n\le b<1.$ Then, the sequences $\left\{x_n\right\},\left\{y_n^i\right\},\left\{z_n^i\right\}$ generated by Algorithm 2 converges strongly to a solution $x^{*},$ where $x^{*}=Pro{j}_{Sol}^f\left(x_0\right).$

Furthermore, by setting $N=M=1,$ we obtain the following result, which extends the results of [24,25,51] to a real reflexive Banach space.

Corollary 2.

Let E be a real reflexive Banach space, C be a nonempty, closed and convex subset of E and function $f:E\to \mathbb{R}$ be a uniformly Fréchet differentiable function, which is coercive, Legendre, totally convex and bounded on subsets of E such that $C\subset int\left(domf\right).$ Let $g:E\times E\to \mathbb{R}$ be a bifunction satisfying Assumptions (A1)–(A5) and $T:E\to E$ be a Bregman relatively nonexpansive mapping. Suppose that $Sol=EP\left(g\right)\cap F\left(T\right)\ne \varnothing .$ Let $\left\{{\alpha }_n\right\}$ be a sequence in $(0,1)$ such that $0<a\le {\mathrm{lim\; inf}}_{n\to \infty }{\alpha }_n\le {\mathrm{lim\; sup}}_{n\to \infty }{\alpha }_n\le b<1.$ Then, the sequences $\left\{x_n\right\},\left\{y_n\right\},\left\{z_n\right\}$ generated by the following Algorithm 2 converge strongly to a solution $x^{*},$ where $x^{*}=Pro{j}_{Sol}^f\left(x_0\right).$

Algorithm 2 Hybrid Bregman subgradient extragradient algorithm (HBSEA).

Step 0. Pick $x_0\in E$, $\mu \in (0,1),{\lambda }_0>0$, and set $n=0.$ Step 1. Solve the strongly convex programs: $$\begin{array}{cc}\hfill & y_n=argmin\left\{g(x_n,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y):y\in C\right\},\hfill \\ \hfill & z_n=argmin\left\{g(y_n,y)+\frac{1}{{\lambda }_n}{D}_f(x_n,y):y\in T_n\right\},\hfill \end{array}$$ (47)      where $T_n=\left\{z\in E:⟨\nabla f\left(x_n\right)-{\lambda }_n{w}_n-\nabla f\left(y_n\right),z-y_n⟩\le 0\right\}$ and $w_n\in \partial g(x_n,y_n).$ Step 2.      Compute: $$u_n=\nabla f^{*}({\alpha }_n\nabla f\left({\overline{z}}_n\right)+(1-{\alpha }_n)\nabla f\left(T{z}_n\right)).$$ (48) Step 3.      Construct two half-spaces $C_n$ and $Q_n$ as follows: $$\begin{array}{ccc}\hfill C_n& =& \left\{z\in E:D_f(z,u_n)\le D_f(z,x_n)\right\},\hfill \\ \hfill Q_n& =& \left\{z\in E:⟨\nabla f\left(z\right)-\nabla f\left(x_n\right),x_n-x_0⟩\ge 0\right\}.\hfill \end{array}$$ (49) Step 4.      Compute $x_{n+1}$ and ${\lambda }_{n+1}$ by: $$x_{n+1}=Pro{j}_{C_n\cap Q_n}\left(x_0\right)$$      and: $${\lambda }_{n+1}=\left\{\begin{array}{cc}\min \left\{{\lambda }_0,\frac{\mu \left(D_f(y_n,x_n)+D_f(z_n,y_n)\right)}{g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)}\right\}\hfill & \\ \mathrm{if}g(x_n,z_n)-g(x_n,y_n)-g(y_n,z_n)\ge 0,\hfill \\ {\lambda }_0,\mathrm{otherwise}.\hfill \end{array}\right.$$ (50)

Furthermore, when E is a real Hilbert space, our Algorithm 1 becomes the following algorithm, which improves the algorithm in [18,50], and the references therein.

Algorithm 3 Parallel Subgradient Extragradient Algorithm (PSEA).

Step 0.      Pick $x_0\in E$, $\mu \in (0,1),{\lambda }_0>0$, and set $n=0.$ Step 1.      Solve N strongly convex programs: $$\begin{array}{cc}\hfill & y_n^i=argmin\left\{g_i(x_n,y)+\frac{1}{{\lambda }_n}{\parallel x_n-y\parallel }^2:y\in C\right\},\hfill \\ \hfill & z_n^i=argmin\left\{g_i(y_n^i,y)+\frac{1}{{\lambda }_n}{\parallel x_n-y\parallel }^2:y\in T_n^i\right\},\hfill \end{array}$$ (51)      where $T_n^i=\left\{z\in E:⟨x_n-{\lambda }_n{w}_n^i-y_n^i,z-y_n^i⟩\le 0\right\}$ and $w_n^i\in \partial g_i(x_n,y_n^i).$ Step 2.      Find the farthest element of $z_n^i$ from $x_n$ by: $$i_n=Argmax\left\{\parallel x_n-z_n^i\parallel :i=1,\cdots ,N\right\}.$$ (52)      Set ${\overline{z}}_n=z_n^{i_n}.$ Step 3.      Compute in parallel for $j=1,\cdots ,M$: $$u_n^j={\alpha }_n{\overline{z}}_n+(1-{\alpha }_n)T_j{\overline{z}}_n.$$      Find the farthest element of $u_n^j$ from $x_n$ by: $$j_n=Argmax\left\{\parallel x_n-u_n^j\parallel :j=1,\cdots ,M\right\}.$$      Set ${\overline{u}}_n=u_n^{j_n}.$ Step 4.      Construct two half-spaces $C_n$ and $Q_n$ as follows: $$\begin{array}{ccc}\hfill C_n& =& \left\{z\in E:\parallel {\overline{u}}_n-z\parallel \le \parallel x_n-z\parallel \right\},\hfill \\ \hfill Q_n& =& \left\{z\in E:⟨z-x_n,x_n-x_0⟩\ge 0\right\}.\hfill \end{array}$$ (53) Step 5.      Compute $x_{n+1}$ and ${\lambda }_{n+1}$ by: $$x_{n+1}=P_{C_n\cap Q_n}\left(x_0\right)$$      and: $${\lambda }_{n+1}=\left\{\begin{array}{cc}\min \left\{{\lambda }_0,\underset{1\le i\le N}{\min }\left\{\frac{\mu \left(\parallel y_n^i-x_n{\parallel }^2+{\parallel z_n^i-y_n^i\parallel }^2\right)}{2\left((x_n,z_n^i)-g(x_n,y_n^i)-g(y_n^i,z_n^i)\right)}\right\}\right\}\hfill & \\ \mathrm{if}g(x_n,z_n^i)-g(x_n,y_n^i)-g(y_n^i,z_n^i)\ge 0,\hfill \\ {\lambda }_0,\mathrm{otherwise}.\hfill \end{array}\right.$$ (54)

4. Numerical Examples

In this section, we give some numerical examples to show the performance and efficiency of the proposed algorithm. We compare the the efficiency of Algorithm 1 (namely PHBSEM) with that of Algorithm (23) of [19] (namely HPA) using different types of convex functions and with Algorithm 1 of [18] (PMEM)). All computations were performed using MATLAB (2019b) programming on a PC with specifications: processor AMD Ryzen 53500 U and 2.10 GHz, 8.00 GB RAM.

We employ the following convex functions:

(1)

$f\left(x\right)=\frac{1}{2}{\parallel x\parallel }^2,\forall x\in {\mathbb{R}}^m:$ in this case, $\nabla f\left(x\right)=\nabla f^{*}\left(x\right)=x$ and $D_f(x,y)=\frac{1}{2}{\parallel x-y\parallel }^2$ (i.e., the Euclidean squared norm);

(2)

$f\left(x\right)=\sum _{i=1}^m{x}_i\log \left(x_i\right)$ with $x\in {\mathbb{R}}_{+}^m:=\{x\in {\mathbb{R}}^m:x_i>0\}:$ in this case, $\nabla f\left(x\right)={\left(1+\log \left(x_1\right),1+\log \left(x_2\right),\cdots ,1+\log \left(x_m\right)\right)}^T,$$\nabla f^{*}\left(x\right)={\left(\exp (x_1-1),\exp (x_2-1),\cdots ,\exp (x_m-1)\right)}^T$ and

$$D_f(x,y)=\sum _{i=1}^m\left(x_i\log \left(\frac{x_i}{y_i}\right)+x_i-y_i\right),$$

for all $x=(x_1,x_2,\cdots ,x_m)\in {\mathbb{R}}_{+}^m$ and $y=(y_1,y_2,\cdots ,y_m)\in {\mathbb{R}}_{+}^m$ (i.e., the Kullback–Leibler distance).

Example 1.

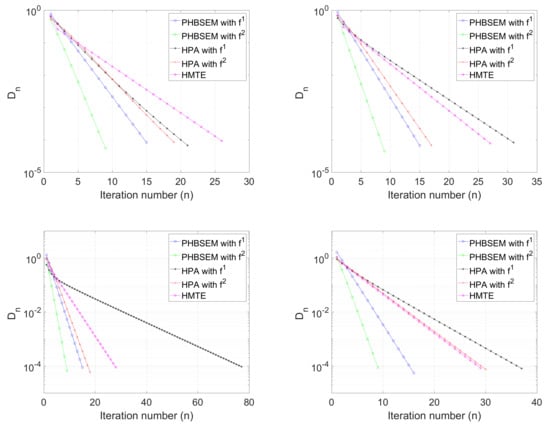
Let $H={\mathbb{R}}^m$ with induced norm $\parallel x\parallel =\sqrt{{\sum }_{i=1}^m{\left|x_i\right|}^2}$ and inner product $⟨x,y⟩={\sum }_{i=1}^m{x}_i{y}_i,$ for all $x=(x_1,x_2,\cdots ,x_m)\in {\mathbb{R}}^m$ and $y=(y_1,y_2,\cdots ,y_m)\in {\mathbb{R}}^m.$ The feasible set C is given by:

$$C=\left\{(x_1,x_2,\cdots ,x_m)\in {\mathbb{R}}_{+}^m:\left|x_k\right|\le 1,\mathit{where}k=1,2,\cdots ,m\right\}.$$

Consider the following problem:

$$\mathrm{Find}{x}^{*}\in Sol:=\left(\bigcap _{i=1}^{N}EP\left(g_i\right)\right)\cap \left(\bigcap _{j=1}^{M}F\left(S_j\right)\right),$$

where $g_i:E\times E\to \mathbb{R}$ is defined by:

$$g_i(x,y)=\sum _{k=1}^m(q_{ik}{y}_k^2-q_{ik}{x}_k^2),i=1,2,\cdots ,N,$$

where $q_{ik}\in (0,1)$ is randomly generated $\forall i=1,2,\cdots ,N,$$k=1,2,\cdots ,m$; and $T_j:E\to E$ is defined by:

$$T_j\left(x\right)=\frac{x}{j+1},\forall j=1,2,\cdots ,M.$$

It is easy to see that Conditions (A1)–(A5) are satisfied and $T_j$ is a Bregman relatively nonexpansive mapping for $j=1,2,\cdots ,M.$ Moreover, $Sol=\left\{0\right\}$. In what follows, for each $n\in \mathbb{N},$ we choose ${\alpha }_n=\frac{3n}{10(n+1)},\mu =0.36,{\lambda }_0=0.24.$ The initial value $x_0\in C$ is generated randomly, and using $D_n=\parallel x_n-0\parallel <{10}^{-4}$ as the stopping criterion, we compare the performance of the algorithms PHBSEM and HPA using the convex functions defined above and the algorithm HPEM for the following values of $m,M$ and $N:$

• Case I: $m=5,N=5,M=2;$
• Case II: $m=10,N=6,M=4;$
• Case III: $m=20,N=10,M=5;$
• Case IV: $m=30,N=5,M=10.$

The numerical results are shown in Table 1 and Figure 1.

Table 1. Computational result for Example 1. PHBSEM, parallel hybrid Bregman subgradient extragradient method.

		Case I	Case II	Case III	Case IV
PHBSEM with $f^1$	Iter.	15	15	15	16
	Time (s)	1.0343	1.7926	4.7522	2.6533
PHBSEM with $f^2$	Iter.	9	9	9	9
	Time (s)	0.8500	1.1863	3.5812	2.4625
HPA with $f^1$	Iter.	21	32	77	37
	Time (s)	1.1719	6.5847	38.7433	11.6689
HPA with $f^2$	Iter.	19	17	18	30
	Time (s)	1.2669	3.7743	9.0533	9.3293
HPEM	Iter.	26	27	28	29
	Time (s)	1.4189	5.1728	12.5232	8.0773

Figure 1. Example 1. Top left: I; top right: Case II; bottom left: Case III; bottom right: Case IV.

Next, we consider the Nash–Cournot oligopolistic market equilibrium model.

Example 2.

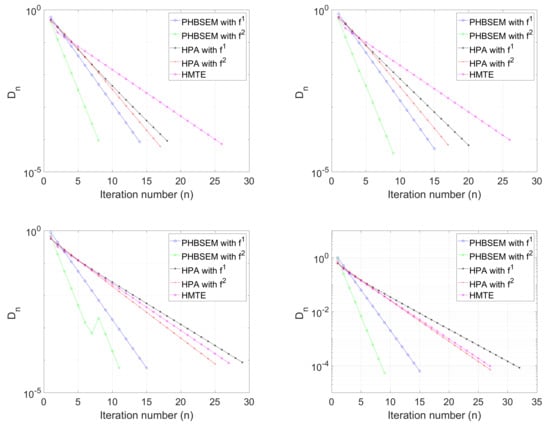
Let $E={\mathbb{R}}^m.$ For $i=1,2,\cdots ,N,$ let $g_i:E\times E\to \mathbb{R}$ be defined by:

$$g_i(x,y)=⟨P_{i}x+Q_{i}y+q_i,y-x⟩,$$

where $q_i$ are vectors in ${\mathbb{R}}^m$ for $i=1,2,\cdots ,N,$$P_i,Q_i$ are matrices of order $m\times m$ such that $Q_i$ are symmetric positive semidefinite and $Q_i-P_i$ are symmetric negative semidefinite. Clearly, $g_i$ are pseudomonotone and satisfy a Lipschitz-like condition with $c_{1,i}=c_{2,i}=\frac{1}{2}\parallel Q_i-P_i\parallel .$ We define the feasible set C by:

$$C=\{x\in {\mathbb{R}}^m:-2\le x_i\le 5,i=1,2,\cdots ,m\}.$$

Now, for $j=1,2,\cdots ,M,$ let $T_j:{\mathbb{R}}^m\to {\mathbb{R}}^m$ be defined by:

$$T_{j}x=\left(P_{{\Delta }_j}\right)\left(x\right)=\left\{\begin{array}{cc}{d}_j+r\frac{x-d_j}{\parallel x-d_j\parallel },\hfill & \mathit{if}x\notin {\Delta }_j,\hfill \\ x,\hfill & \mathit{if}x\in {\Delta }_j,\hfill \end{array}\right.$$

(55)

where ${\Delta }_j$ are the closed balls in ${\mathbb{R}}^m$ centred at $d_j\in {\mathbb{R}}^m$ with radius $r>0,$ i.e., ${\Delta }_j=\{x\in {\mathbb{R}}^m:\parallel x-d_j\parallel \le r\}.$ It is easy to see that $T_j$ are nonexpansive and, thus, Bregman relatively nonexpansive. More over, $Sol=\left\{0\right\}.$ We chose the following parameters: ${\alpha }_n=\frac{2n}{5n+1}$${\lambda }_0=0.04,$$\mu =0.13$ and compare the performance of the algorithm PHBSEM with the algorithms HPA and HPEM for the following values of $m,M$ and N:

• Case I: $m=5,M=5,N=5;$
• Case II: $m=10,M=5,N=7;$
• Case III: $m=15,M=10,N=5;$
• Case IV: $m=20,M=20,N=10.$

We use $D_n=\parallel x_n-0\parallel <{10}^{-4}$ as the stopping criterion in each case. The computational results are shown in Table 2 and Figure 2.

Table 2. Computational result for Example 2.

		Case I	Case II	Case III	Case IV
PHBSEM with $f^1$	Iter.	14	15	15	15
	Time (s)	2.3438	3.7407	2.5454	7.7285
PHBSEM with $f^2$	Iter.	9	9	11	9
	Time (s)	2.0031	4.8016	3.6948	6.3261
HPA with $f^1$	Iter.	18	20	29	32
	Time (s)	6.1129	9.6401	10.9361	23.6825
HPA with $f^2$	Iter.	17	17	25	27
	Time (s)	6.0802	8.0388	9.2322	19.1269
HPEM	Iter.	26	26	27	27
	Time (s)	8.0451	13.0750	9.7936	18.2040

Figure 2. Example 1: Top left: I; top right: Case II; bottom left: Case III; bottom right: Case IV.

Finally, we consider the following example in an infinite-dimensional space. In this case, we chose $f\left(x\right)=\frac{1}{2}{\parallel x\parallel }^2.$

Example 3.

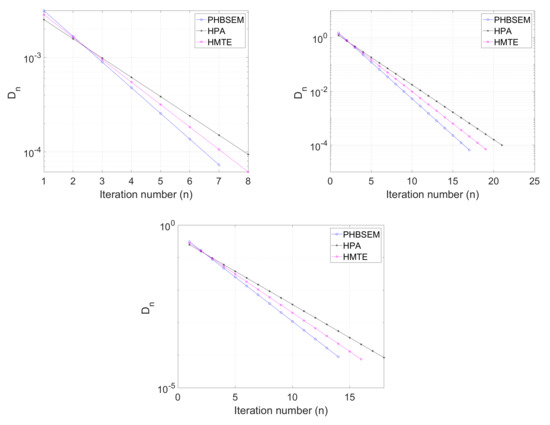
Let $E=L^2\left(\left[0,1\right]\right)$ with the inner product $⟨x,y⟩={\int }_0^{1}x\left(s\right)y\left(s\right)ds$ and the induced norm $∥x∥={\left({\int }_0^1{\left|x\left(s\right)\right|}^{2}ds\right)}^{\frac{1}{2}}$. The feasible set is defined as:

$$C=\left\{x\in H:∥x∥\le 1\right\}.$$

Let $g_i(x,y)$ be defined as $⟨A_{i}x,y-x⟩$ with the operator $A_i:L^2\left(\left[0,1\right]\right)\to L^2\left(\left[0,1\right]\right)$ given as $A_i\left(x\left(s\right)\right)=\max \left\{0,\frac{x\left(s\right)}{i}\right\}$, for $i=1,2,\cdots ,N,$$s\in [0,1].$ It is easy to see that each $g_i$ is monotone, thus pseudomonotone on C for $i=1,2,\cdots ,N.$ For $j=1,2,\cdots ,N,$ we define the mapping $T_j:L^2\left(\left[0,1\right]\right)\to L^2\left(\left[0,1\right]\right)$ by $T_{j}x=P_{C}x,$ where:

$$P_C\left(x\right)=\left\{\begin{array}{cc}\frac{x}{\parallel x\parallel }\hfill & \mathit{if}\parallel x\parallel >1,\hfill \\ x\hfill & \mathit{if}\parallel x\parallel \le 1.\hfill \end{array}\right.$$

(56)

Then, $T_j$ is a Bregman relatively nonexpansive mapping for $j=1,2,\cdots ,M$ and $Sol=\left\{0\right\}.$ We take ${\alpha }_n=\frac{2n}{7n+1},\mu =0.5,\lambda =0.02,$$N=5,M=1$ and study the performance of the algorithms PHBSEM, HPA and HPEM for the following initial value:

• Case I: $x_0=\frac{\cos \left(3s\right)}{7};$
• Case II: $x_0=\exp \left(2s\right);$
• Case III: $x_0=s^2-1.$

We use $D_n=\parallel x_n-0\parallel <{10}^{-4}$ as the stopping criterion and plot the graphs of $D_n$ against the number of iterations in each case. The computation results are shown in Table 3 and Figure 3.

Table 3. Computational result for Example 3.

		Case I	Case II	Case III
PHBSEM	Iter.	7	17	14
	Time (s)	2.9028	1.1050	1.1554
HPA	Iter.	8	21	18
	Time (s)	3.0987	2.8468	1.9877
HPEM	Iter.	8	19	16
	Time (s)	2.9476	2.0084	1.9088

Figure 3. Example 1: Top left: I; top right: Case II; bottom: Case III.

5. Conclusions

In this paper, we present a new parallel hybrid Bregman subgradient extragradient method for finding a common solution of a finite family of the pseudomonotone equilibrium problem and common fixed point problem for Bregman relatively nonexpansive mappings in real Hilbert spaces. The algorithm is designed such that its convergence does not require prior estimates of the Lipschitz-like constant of the pseudomonotone bifunctions. Furthermore, a strong convergence result is proven under mild conditions. Some numerical examples are presented to show the efficiency and accuracy of the proposed method. This result improves and extends the results of [17,18,19,20,22,25,47,49,50,51] and many other results in the literature.