Abstract
FeSe is classed as a Hund’s metal, with a multiplicity of d bands near the Fermi level. Correlations in Hund’s metals mostly originate from the exchange parameter J, which can drive a strong orbital selectivity in the correlations. The Fe-chalcogens are the most strongly correlated of the Fe-based superconductors, with the most correlated orbital. Yet little is understood whether and how such correlations directly affect the superconducting instability in Hund’s systems. By applying a recently developed ab initio theory, we show explicitly the connections between correlations in and the superconducting critical temperature . Starting from the ab initio results as a reference, we consider various kinds of excursions in parameter space around the reference to determine what controls . We show small excursions in J can cause colossal changes in . Additionally we consider changes in hopping by varying the Fe-Se bond length in bulk, in the free standing monolayer M-FeSe, and M-FeSe on a SrTiO substrate (M-FeSe/STO). The twin conditions of proximity of the state to the Fermi energy, and the strength of J emerge as the primary criteria for incoherent spectral response and enhanced single- and two-particle scattering that in turn controls . Using c-RPA, we show further that FeSe in monolayer form (M-FeSe) provides a natural mechanism to enhance J. We explain why M-FeSe/STO has a high , whereas M-FeSe in isolation should not. Our study opens a paradigm for a unified understanding what controls in bulk, layers, and interfaces of Hund’s metals by hole pocket and electron screening cloud engineering.
1. Introduction
Iron-pnictogen and iron-chalcogen based superconductors (IBS) are classed as Hund’s metals, meaning correlations mostly originate from the Hund’s exchange parameter J. In recent years a consensus has evolved that strong Hund’s correlations drive the ubiquitous bad metallicity observed in their phase diagrams [1,2]. Such metals have a multiplicity of bands near the Fermi level ; in particular FeSe [3,4,5] has all five Fe d states active there. Correlations are observed to be highly orbital-selective [5,6] (a signature of “Hundness”) with the most strongly correlated orbital. In recent years, the role of Hund’s exchange J is explored in determining the orbital-selectivity [7] and triplet pairing in Uranium based superconductors [8]. However, very little is known whether Hund’s correlation can generate glue for superconducting pairing and control in singlet-pairing channel.
is a mere 9 K in bulk, but it has been observed to increase to ∼75 K when grown as a monolayer on SrTiO[9] (M-FeSe/STO), and 109 K on doped SrTiO [10]. Thus while “Hundness” has been found to be important in controlling the single- and two-particle spectral properties of bulk FeSe, the multiplicity of factors (orbital character, spin-orbit coupling, shape of Fermi surface and dispersion of states around it, differences in susceptibilities, nematicity, electron-phonon interaction) obfuscate to what extent Hundness, or other factors, drive superconductivity, and whether ‘Hundness’ can at all explain the jump in going from bulk to M-FeSe/STO.
In this work we calculate the superconducting instability using a new high fidelity, ab initio approach [11,12]. For the one-particle Green’s function it combines the quasiparticle self consistent GW (QSGW) approximation [13] with CTQMC solver [14,15] based dynamical mean field theory (DMFT) [16]. This framework [17,18] is extended by computing the local vertex from the two-particle Green’s function by DMFT [19,20], which is combined with nonlocal bubble diagrams to construct a Bethe-Salpeter equation [21,22,23]. The latter is solved to yield the essential two-particle spin and charge susceptibilities and — physical observables which provide an important benchmark. Moreover they supply ingredients needed for the particle–particle Bethe–Salpeter equations, which yields eigenvalues and eigenfunctions that describe instabilities to superconductivity. We will denote QSGW++ as a shorthand for the four-tier QSGW+DMFT+BSE.
The numerical implementation is discussed in Pashov et al. [12].
QSGW++ has high fidelity because QSGW captures non-local dynamic correlation particularly well in the charge channel [12,24], but cannot adequately capture effects of spin fluctuations. DMFT does an excellent job at the latter, which are strong but mostly controlled by a local effective interaction given by Hubbard parameters U and J. These are calculated within the c-RPA [25] from the QSGW Hamiltonian using an approach [12] similar to that of Ref. [26]. That it can well describe superconductivity in a parameter-free manner has now been established in several Hund’s materials [21,22]. In FeSe, we have also shown [27] that it reproduces the main features of neutron structure factor [28,29].
SrRuO was the first system where we implemented our QSGW++ ability. We found a dense spectrum of triplet and singlet superconducting instabilities therein [21]. Lacking at that time the ability to calculate U, J, we borrowed values from an earlier LDA+DMFT study [30]. Later we were able to build our own c-RPA calculated from QSGW (QSGW+cRPA), and found U, J to be approximately 2/3 of the original values. Our initial study concluded that the triplet instability was slightly stronger than the B − d singlet in unstrained SrRuO. Redoing the procedure with U, J calculated from QSGW+cRPA [31] the conclusions did not qualitatively change, except the singlet eigenvalue became larger than the triplet. Thus the original study [21] did not predict the correct ground state. From a prior study we discovered that the superconducting instability can be sensitive to the exact choices of U, J. Here we show small changes in J have a dramatic effect on spin susceptibility and superconductivity in FeSe. For that reason we recalculate QSGW+cRPA for for all cases we report here, on bulk and layered variants of FeSe. This is a step forward in making the calculations as ab-initio as possible, and as we discuss later in the paper, this provides us with a remarkable unified understanding of both bulk and layered variants of FeSe, the correlations and superconducting instabilities therein.
To isolate the effect of Hundness we make excursions about the ab initio reference point, by treating J as a free parameter. One of our primary conclusions is that intense and broad low energy spin fluctuations in the vicinity of an antiferromagnetic ordering vector is the primary glue for pairing and the controlling element for in several variants of FeSe (both bulk and layered); and that this in turn is controlled by J. We further show, using c-RPA, that J can be tuned by varying the screening through, e.g., changes in the geometry such as the change from bulk to monolayer. We also consider excursions in Fe-Se bond length, and can find correlation can be enhanced or suppressed by changes in it. For Hund’s coupling to be effective in driving it needs a certain ‘universal’ band feature: the Fe state must be in close proximity to the Fermi energy.
The paper organised as follows. We:
- Present the mathematical formulation and implementation of different susceptibilities in spin, charge and superconducting channels;
- List the structural and Hubbard parameters used for different materials, and present ab initio results bulk FeSe;
- By treating J and the Se height as free parameters, show how they affect correlations and superconductivity in bulk FeSe;
- Show results for a standing monolayer of FeSe (M-FeSe);
- Show results for a monolayer of FeSe on SrTiO (M-FeSe/STO);
- Interpret these results to explain what controls T.
2. Methodology
The QSGW+DMFT implementation is discussed in our method paper [12]. The one-body part of QSGW is performed on a k-mesh and charge has been converged up to accuracy, while the (relatively smooth) many-body static self-energy is constructed on a k-mesh from the dynamical . is iterated until convergence (RMS change in Ry). DMFT is solved for all five Fe- orbitals using a Continuous time Quantum Monte Carlo technique (CTQMC) [14] on a rotationally invariant Coulomb interaction. From CTQMC-DMFT we sample the local full and connected two-particle Green’s functions. The DMFT for the dynamical self energy is iterated, and converges in ∼20 iterations. Calculations for the single particle response functions are performed with QMC steps per core and the statistics is averaged over 64 cores. The two particle Green’s functions are sampled over a larger number of cores (30,000-50,000) to improve the statistical error bars. We compute the local polarisation bubble from the local single-particle Green’s function. In order to extract , we employ the local Betlpeter equation which relates the local two-particle Green’s function () sampled by CTQMC, with both the local polarisation function () and .
is the local irreducible two-particle vertex functions computed in magnetic (m) and density (d) channels. is a function of two fermionic frequencies and and the bosonic frequency .
The non-local polarisation bubble in the p-h channel is computed from single-particle DMFT Green’s functions embedded into the QSGW bath.
Spin () and charge () susceptibilities are computed from momentum dependent Bethe-Salpeter in magnetic (spin) and density (charge) channels.
The susceptibilities are computed by closing with spin or charge bare vertex (=1/2 for spin and =1 for charge) and summing over frequencies (,) and orbitals ().
The superconducting pairing susceptibility is computed by dressing the non-local pairing polarisation bubble with the pairing vertex using the Bethe-Salpeter equation in the particle–particle channel.
The particle–particle vertex in the singlet channel has odd-symmetry under exchange of two external spins (and even symmetry in the triplet channel),
The irreducible particle–particle vertex function channel which provides the pairing glue to form Cooper pairs, consists of the fully irreducible vertex function and the reducible vertex functions computed in the particle-hole channels
The reducible magnetic/charge vertex is obtained from the non-local magnetic/charge susceptibilities and magnetic/charge irreducible vertex functions by
The irreducible particle–particle vertex function is finally written in terms of the reducible magnetic/charge vertex functions.
Finally, exploiting the Equations (6) and (7) and Equations (10) and (11) we obtain the in the singlet (s) and triplet (t) channels from the magnetic and density particle-hole reducible vertices,
With in hand we can solve the p-p BSE to compute the p-p susceptibility .
The critical temperature is determined by the temperature where diverges. The pairing susceptibility diverges when the leading eigenvalue approaches unity. The corresponding eigenfunction represents the momentum structure of . For such divergence the sufficient condition is that at least one eigenvalue of the pairing matrix approaches unity. Hence , eigenvalues and eigenfunctions associated with different superconducting gap symmetries (in the singlet channel) can all be computed by solving the eigenvalue equation,
The gap function can be written in a symmetric and Hermitian form by
However, it can also be explicitly shown that the eigenvalues of the non-Hermitian gap equation are the same as eigenvalues of the Hermitian gap equation.
Finally, can be represented in terms of eigenvalues and eigenfunctions of the Hermitian particle–particle pairing matrix.
To solve this eigenvalue equation, the most important approximation we make is to take the static limit of in the bosonic frequency i = 0 (real frequency axis). The explicit dependence on the fermion frequencies are kept, as are all the orbital and momentum indices.
As is apparent from Equations (13) and (14) at what wave vector spin and charge fluctuations are strong is of central importance to the kind of superconducting pairing symmetry they can form. The entire momentum, orbital and frequency dependence of the vertex functions are computed explicitly and the BSE equations are solved with them. The crucial point is that the vertex structure has no predefined form-factor, so the emergent superconducting gap symmetry is calculated in an unbiased manner. This provides an unbiased insight into the superconducting gap symmetries, the strength of the leading eigenvalues in different systems and, most importantly, allows for a fair comparison of the relative strength of the leading superconducting instabilities in bulk FeSe and the monolayer of FeSe/STO. Thus, our ability to predict these properties is limited mostly by the fidelity of the Green’s functions that determine the vertices and .
There is a practical limitation, however. Since we compute the vertex functions from CTQMC, which limits the temperatures down to which the vertex can be computed. We have observed in different materials that the leading eigenvalue does not have a simple, analytic dependence on temperature [22], and hence can not be reliably extrapolated to very low temperatures. For that reason, we avoid estimating (the temperature at which reaches 1) for different systems from our method, rather, we compare the strength of for a given temperature in different materials, which is free from any ambiguities.
In some recent studies [32,33,34,35,36], the shortcomings of the standard Eliashberg formalism in explaining some of the fundamental observation related to unconventional superconductivity has been highlighted and alternative formulation for a better theory is proposed. While our particle–particle ladder approximation does not use the standard Eliashberg formalism, it is an important task for future efforts, also for our own approach, to see how these proposed formulations can be adapted for better description of unconventional superconductivity.
3. Results and Discussion
3.1. Structural Parameters and c-RPA Estimates for U and J
Table 1 provides structural parameters used for simulating different systems, and the correlation parameters calculated using QSGW+constrained-RPA. In the bulk crystal, Se sits above and below the Fe plane with height Å and bond length Å. cRPA yields U = 3.4 eV and J = 0.6 eV, calculated from the QSGW band structure.

Table 1.
Structural parameters, chalcogen height and computed U and J for the correlated many body Hamiltonian from our QSGW+c-RPA implementation. We also list the bare electronic bandwidths from QSGW which show how electronic correlations enhance in M-FeSe/STO in comparison to the bulk as the bands get narrower. References indicate where the structural inputs were taken.
Over the large variety on iron based superconductors it is observed [6] that larger chalcogen/pnictogen height ( in our case) reduces the Fe-chalcogen/pnictogen-Fe hopping and hence makes the systems more strongly correlated. We observe that is reduced in both M-FeSe/STO and free-standing monolayer M-FeSe relative to the bulk FeSe (B-FeSe), however, the Fe-Se bond lengths remain almost invariant in both monolayer variants in comparison to the bulk (as a increases in layer). It suggests that the monolayer variants have similar or less electronic correlations (larger electronic hopping). However, as we will show, the free standing monolayer is non-superconducting while both the bulk FeSe and M-FeSe/STO are superconducting. Further, the c-RPA calculations for each materials indicate that both U and J increase in the monolayer variants relative to the bulk.
As we will show below, the degree of correlation and resulting superconductivity are highly sensitive to small changes in both quasiparticle levels and the Hubbard parameters driving the correlations. Thus, the electronic origins of unconventional superconductivity in FeSe can only be understood when the interplay between crystal structure, one-particle properties, and Hubbard parameters is taken into account.
3.2. Fermi Surfaces and Spectral Functions
QSGW Fermi surfaces are generally smaller than DFT Fermi surfaces in the Fe superconductors [39]. However, in FeSe, both DFT and QSGW predict the band to cross the Fermi level forming a pocket around (see Figure 1), apparently in contradiction to ARPES measurements which place it at approximately meV [40,41,42]. When is further dressed by DMFT this pocket shrinks further, but it still remains, leaving a discrepancy with ARPES of ∼20 meV. The orbital character emerges as the most incoherent (see Figure 2a) but its position is slightly higher than where ARPES places it.

Figure 1.
Fermi surfaces are shown in the -M (z = 0) plane for both bulk FeSe and monolayer FeSe/STO from DFT + DMFT, and QSGW + DMFT. In each case the the U and J are used from respective C-RPA calculations.
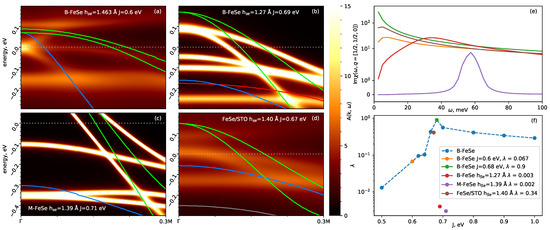
Figure 2.
The QSGW band structure and QSGW+DMFT spectral functions are shown on a section of the -M path for: (a) bulk-FeSe (J = 0.6 eV); (b) bulk FeSe with reduced Se height above the Fe plane (h = 1.27 Å); (c) M-FeSe, a free standing monolayer of FeSe; (d) M-FeSe/STO. In all four panels, the Fe- state calculated by QSGW is depicted in blue and the Fermi energy is at 0. Note the strongly marked incoherence in (a,d). In all cases DMFT narrows the width of relative to QSGW as is typical of narrow-band d systems [11,39], but incoherence is highly sensitive to the position of . In (a,d) is proximate to and a high degree of incoherence is present. while in (b,c) is pushed far below : and the system has properties similar to a normal Fermi liquid. Panel (e) shows the imaginary part of the spin susceptibility , at the AFM nesting vector = (1/2, 1/2, 0) for the four geometries (a):orange, (b): red, (c): purple, (d): brown. Shown also in green is Im for bulk FeSe with J = 0.68–the highest found among parameterised hamiltonians. The more intense Im is, the larger the superconducting instability. Panel (f) shows how the leading eigenvalue of the linearised particle–particle ladder BSE equation treating J as a free parameter (blue circles). The extreme sensitivity to J is apparent. Shown also are for the four ab initio calculations (a–d), using the colour scheme in panel e. For (a) B-FeSe and (d), FeSe/STO, falls near and approximately coincides with the blue line; (b,c) do not.
3.3. Bulk FeSe
The most direct way to isolate the contributors to superconductivity is to make parametric adjustments to the ab initio results. Thus to assess the role of ‘Hundness’ we consider, in addition to the ab initio QSGW++ calculations, how excursions in J between 0 and 1 eV affect the single-particle scattering rate , and the inverse Z factor, a measure of mass or bandwidth normalisation.
The single-site DMFT Im is fit to a fourth order polynomial in for low energies (first 6 matsubara points at = 1/40 eV = 290 K). The mass enhancement, related to the coefficient () of the linear term in the expansion [43], and the intercept = . m/m = is resolved in different intra-orbital channels. is found to be insensitive to J for eV, while for eV it increases monotonically for all orbitals (see Figure 3). The size of the local moment also increases steadily and reaches a value of 2.2 for eV which is the atomic moment experimentally observed in Fe. This observed moment in bulk FeSe is also very close to the spin local moment estimated from NMR, INS and x-ray emission spectroscopy studies [44]. Thus there is smooth transition from coherence to incoherence with increasing J. increases from 1.33 at , reaching a maximum of 4.5 in the channel at eV. Correlation increases for all states, but is the heaviest and most incoherent, followed by (see Figure 3). For still larger J, both and begin to slowly decrease (see Figure 3). A similar non-monotonic behaviour was observed in a previous study of Hund’s metals [45] Similar conclusions were drawn in a recent orbitally-resolved quasi-particle scattering interference measurement by Kostin et al. [5] in the low temperature orthorhombic phase of FeSe, and the orbital selectivity was emphasised in Ref. [46].
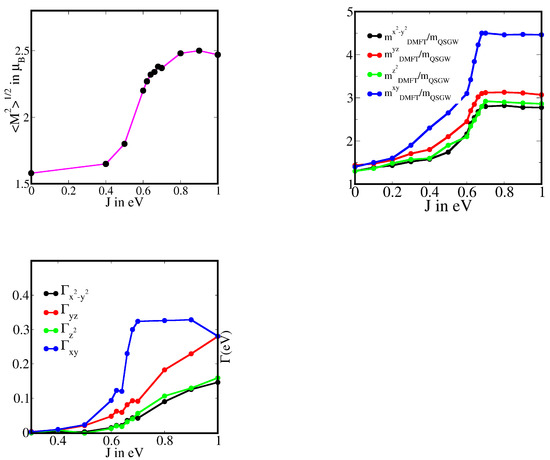
Figure 3.
We compute the net local moment and its evolution with J. Orbitally resolved single-particle scattering rate () and mass enhancement m/m for Bulk FeSe with varying Hund’s coupling strength.
Small increases in J induce remarkable changes in the transverse spin susceptibility (see Figure 4a,b). The peak near the antiferromagnetic nesting vector (in 2-Fe unit cell) and = 0 becomes markedly more intense as shown in Figure 2e and Figure 4b. In Figure 4, Im is plotted along the lines in the FeSe unit cell. The energy dispersion in Im also becomes strongly compressed. Elsewhere [27] we perform a rigorous benchmarking of against inelastic neutron scattering measurements [28,29,47] where we show that our calculations reproduce all intricate structures of for all energies and momenta. Resolving Im into orbital channels, is seen to be the leading component. Along it contributes about 50% of the total with , and combining to contribute the rest.
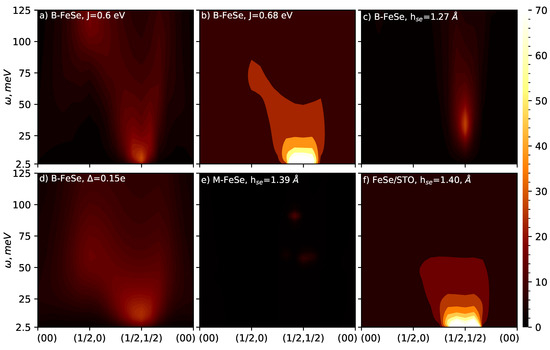
Figure 4.
Energy and momentum resolved spin susceptibility Im shown for (a) bulk FeSe (B-FeSe) (J = 0.6 eV), (b) bulk FeSe with increased Hund’s correlation (J = 0.68 eV), (c) reduced Fe-Se height ( = 1.27 Å), (d) 0.15 electron doped bulk FeSe (a section on uniformly electron doped FeSe is included in the SM), (e) free standing monolayer of FeSe, M-FeSe [38] (f) M-FeSe/STO [38]. The q-path (H,K,L = 0) chosen is along (0,0) − () − () − (0,0) in the Brillouin zone corresponding to the two Fe-atom unit cell. The intensity of the spin fluctuations at () is directly related to the presence of the Fe- state at Fermi energy and its incoherence. The more incoherent the A(k,) is the more intense is the Im .
How do these striking changes in Im correlate with superconductivity? We compute the full two particle scattering amplitude in the particle–particle channel within our DMFT framework, and solve Equation (17) in the BCS low energy approximation [19,20,21,22]. Resolving the eigenfunctions of the gap equation into inter- and intra-orbital channels, two dominant eigenvalues are found. Both of them increase with J up to the point of maximum intensity in (J = 0.68 eV) and then begin to decrease, as shown in Figure 2f. The corresponding eigenfunctions have extended s-wave- cos()+cos() (leading eigenvalue) and − cos() − cos() structures (second eigenvalue) [48]. Calculations show that these instabilities reside primarily in the intra-orbital − channel and the inter-orbital components are negligible. In the bulk crystal, varying J from the ab initio value ( = 0.067 at J = 0.60 eV), we find reaches its maximum 0.9 at the point where the spin susceptibility is most intense, J=0.68 eV (see Figure 2f). We attribute the decrease for eV to the softening of electron masses and loss of spin fluctuations at as can be seen in local moment plotted in Figure 3.
3.4. Excursion in Fe-Se bond length in Bulk FeSe
We next consider how parametric changes in the one-body Hamiltonian alter the spectral function, and . We first vary the Fe-Se bond length . When it is reduced from its experimental value of 2.39 Å, the band initially near at , gets pushed down well below . It is particularly easy to see at the QSGW level (blue band in Figure 2b), reaching about meV when h = 1.27 or = 2.275 Å. From c-RPA we compute the corresponding U and J as 3.9 eV and 0.69 eV respectively. A similar shift is found in the spectral function calculated by QSGW+DMFT (Figure 2b). Further, quasi-particles become more coherent: orbital-selective values range between 1.6 and 1.3 and scattering rates become small (○, Figure 5). The system behaves as an itinerant metal, and the peak in Im at shifts to higher and becomes gapped (see Figure 4c). It also becomes very weak and broad (Figure 2e). The leading eigenvalue of Equation (17) become negligibly small (see Figure 2f and Figure 5e), suggesting extremely weak or no superconducting instability. also becomes completely insensitive to J. A similar observation was made in our recent work on LaFeAs [22], where the collapsed tetragonal phase with lesser in comparison to its uncollapsed phase, loses superconductivity [49] as bands become itinerant due to increased Fe-Fe hopping mediated via As. It suggests that a small pnictogen/chalcogen height over the Fe-Fe square plane is not conducive for superconductivity as the system gains significant amount of kinetic energy and electronic scatterings are remarkably reduced. Similar observations are made for Fe based pnictides containing Phosphorus, where the system has a Fermi liquid normal phase with dispersive electrons and either they do not superconduct or have extremely small ’s [20].
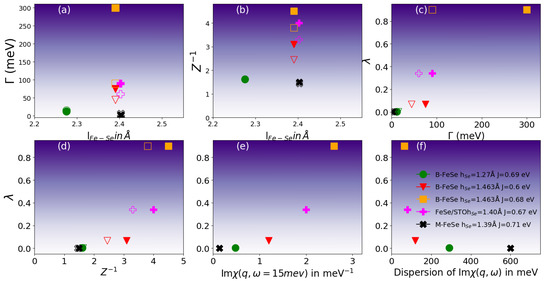
Figure 5.
(a,b) Inverse Z factors and scattering rates for Fe 3 (filled symbols) and 3 (empty symbols) orbitals in three configurations of bulk FeSe (▽, ○, □) ▽ is the ab initio result (h = 1.463 Å, J = 0.60 eV); while □ changes J to 0.68 eV; ○ changes h and J to 1.27 Å and 0.69 eV. Shown also are an isolated FeSe monolayer with h = 1.39 Å and J = 0.71 eV (×), a monolayer on STO with h = 1.40 Å and J = 0.67 eV (+). Correlation is sensitive to changes in and J. (c–f) leading eigenvalue of the superconducting instability calculated at 290 K drawn against various measures of correlation: is approximately proportional to and (c), and it is monotonic in and (d), and also in the strength of Im (e) and suppression of the dispersion of the paramagnon branches (f). The graded intense purple background separates the most strongly correlated systems with large from the weakly correlated systems with small in weaker purple background.
3.5. Free Standing Monolayer of FeSe
We next turn to a free standing monolayer of FeSe, M-FeSe. For this study we take the structural inputs from recent work by Mondal et al. [38] which finds the minimum-energy value for h to be 1.39 Å within a combined DFT+DMFT framework, while the lattice parameter a is somewhat larger, close to that of SrTiO. As a benchmark, the same work found the equilibrium h to be close to the measured value in bulk crystalline FeSe [50]. DFT has a tendency to underestimate h; the error is not easily fixed by other kinds of density-functionals. However, DFT does predict a similar change in between bulk and monolayer which gives us some confidence in the value of h.
At the QSGW level, the band is pushed to meV on the –M line (band structure in Figure 2c and SM, bottom panel). c-RPA calculations yield U = 4.3 eV and J = 0.71 eV, the increase arising from reduced screening. is found from QSGW+DMFT to be 1.5, 1.35, 1.3, 1.25 on , , , respectively (Figure 5b); also a negligible scattering rate is found (Figure 5a). As a further indicator of a good metal, Im shows negligible spin fluctuations in the channel; and at spin excitations are gapped and vanishingly small (see Figure 2e and Figure 4e). The superconducting instability is almost entirely suppressed (see Figure 2f and Figure 5f). It is noteworthy that the reduction in electronic screening reflects in a marked increment in J. Unfortunately, this beneficial effect is more than counterbalanced by the fact that is pushed far below on the scale of magnetic excitation energies. Suppression of low energy one- and two-particle scattering is not conducive for superconductivity.
3.6. Monolayer of FeSe/SrTiO
How does the effect of a SrTiO substrate modify superconductivity in M-FeSe? M-FeSe/STO is a subject of intense debate, since as noted above, of M-FeSe/STO has been measured to be an order of magnitude higher than bulk FeSe (In the Supplementary Materials we include a small section on uniformly electron doped bulk FeSe). Many explanations have been put forward, e.g., that superconductivity is boosted by large electron-phonon coupling [51,52,53] as SrTiO is close to a ferroelectric instability (for a contrary view see [54]), but the simplest explanation is that SrTiO modifies M-FeSe to restore to be proximate to . M-FeSe/STO is a partially formed Schottky barrier; we can expect the Fermi level to sit in the SrTiO bandgap. SrTiO modifies M-FeSe in two important ways: the interfacial dipole controls the Schottky barrier height and changes the electron count in M-FeSe; also the STO (especially the O-p-derived bonding states) couple to the Fe-d in an orbital-selective manner. Both effects are accurately incorporated by a direct QSGW calculation of M-FeSe/STO. We consider 5-ML slab of SrTiO terminated on the Sr side by M-FeSe. The structure is relaxed with DFT, subject to the constraint that h is fixed to 1.40 Å, as predicted in Ref. [38]. This value is close to h = 1.39 Å ( = 2.403 Å) found for free-standing M-FeSe. Its value is critical, as we have seen in the bulk case, and we cannot rely on DFT for it.
A c-RPA calculation for M-FeSe/STO yields U = 3.8 eV and J = 0.67 eV. Using QSGW + DMFT, we extract the Fermi surfaces spectral functions (see Figure 1d and Figure 2d). Remarkably, while is pushed far below in M-FeSe, its position returns near to in the M-FeSe/STO case ( to meV in QSGW and meV in QSGW + DMFT as shown in Figure 2d). This is fully consistent with ARPES studies [55]. Furthermore, its bandwidth is slightly reduced relative to bulk, in keeping with a stretched a.
In the QSGW++ calculation, the hole pockets of character survive although are significantly narrowed. This is a discrepancy with ARPES, which finds no such pockets. However, their small size suggests that they should be sensitive to electron-phonon coupling that can further renormalise them and push them down.
Using QSGW+DMFT we compute the orbital dependent (4, 3.3, 3.2 2.7 on , , , ) and , which show significantly enhanced incoherence in the quasiparticle spectrum relative to M-FeSe (see Figure 5a,b). Further, the dispersion in Im is significantly narrower than the bulk, and the intensity is spread over momenta in the region around (see Figure 2e and Figure 4f). These signatures suggest that M-FeSe/STO is more correlated than either the bulk or free standing monolayer. The leading extended-s wave instability from the particle–particle ladder BSE equation survives but the second () instability gets suppressed. Whenever the state is pushed below at and yet continues to be present at the electron pockets, the only surviving superconducting instability is the state, consistent with earlier predictions [56,57,58].
Experimentally, the superconducting gap of FeSe/STO show maxima on the bands with character [59]. Furthermore, in surface doped bulk FeSe where superconductivity enhances, the appearance of the electron pocket on the Fermi surface coincides with the beginning of the second superconducting dome with higher [60]. The leading for superconducting instability is 0.34, which is five times larger that the estimate for bulk FeSe. These ab initio results do not support a recently published results from Eliashberg theory where it is claimed that spin fluctuations can, at most, account for only two fold increment in . [61] We also find that suppressing the contributions in Equation (17) lead to only 6% reduction in . Thus, the orbital is the determinative one.
Our estimate of five-fold increment is less than the eight-fold increment in = 75 K observed for M-FeSe/STO, but there can be many reasons for this. The comparison to experiment is not direct: experimentally M-FeSe/STO has a buffer layer between M-FeSe and STO, which our calculation omits. Furthermore, the calculated is extremely sensitive to J and h. Both are theoretically calculated; moreover h is assumed to be the same for the Se planes above and below Fe, while there should be small differences. Finally the interface can have several other effects we omitted such as an enhanced phonon contribution to , as others have suggested [51,52,53].
We close with a note on the origins of the discrepancies in QSGW++ spectral function with ARPES. We have recently developed the ability to incorporate the electron-phonon self-energy into QSGW++ via a field-theoretic technique. While initial results are very preliminary, they suggest that much of the discrepancy we see with ARPES in bulk FeSe, originates from this interaction. It is perhaps not surprising, given that the electron-phonon interaction is expected to be stronger when pockets are small. These new findings, however, are beyond the scope of this work.
4. Conclusions
To summarise, a unified picture of the origins of superconductivity in FeSe emerges from evidence drawn from several parametric studies of FeSe around a high-fidelity ab initio theory. Superconducting glue mainly originates from low-energy spin fluctuations concentrated in a region near the antiferromagnetic ordering vector. The instability and the single- and two-particle correlations characterised by the band renormalisations , scattering rate and Im are all closely linked as summarised in Figure 2 and Figure 5. The Fe orbital is the most strongly correlated and contributes maximally to the pairing glue as long as it is auspiciously near the Fermi level and further, that the Hund’s J is sufficiently large to induce a high degree of ‘bad metallic’ behaviour. Further, the superconducting instability is found to lie predominately in the channel.
We show that in the bulk, is extremely sensitive to J over a certain energy window. At the optimum J increases by nearly 15 times its value at the ab initio J, even though the increment in J is only 10–15%. This indicates that a possible way to enhance is to reducing the electron screening. We presented two scenarios where a structural modification induces a change in J (M-FeSe and M-FeSe/STO), and further that this enhancement drives a five fold enhancement in , in M-FeSe/STO relative to the bulk. M-FeSe and M-FeSe/STO differ in the latter preserves the proximity of the channel to while M-FeSe does not. This provides a natural explanation for the enchantment in superconducting M-FeSe/STO as a purely electronic one: the two dominant factors are J and the proximity of the band to .
Controlling number of layers, applying pressure to tune Fe-chalcogenide bond length, doping and intercalation are some other possibilities. At the same time it is important to realise it is necessary to control both the screening and specific features of the single-particle spectrum. Our calculations show that one promising directions for reaching an optimised appears to be controlling number of layers and interfaces to simultaneously satisfy both conditions: lesser electron screening leading to a larger Hund’s correlation and larger contribution to the Fermiology.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-8994/13/2/169/s1.
Author Contributions
S.A. conceived and designed the work. S.A., D.P. and M.v.S. performed calculations. F.J. built the c-RPA ability. S.A., M.v.S., D.P., F.J. contributed codes. S.A., D.P. prepared figures. S.A. and M.v.S. drafted the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study does not involve humans and animals.
Informed Consent Statement
This study does not involve humans and animals.
Data Availability Statement
All codes are available on https://questaal.gitlab.io/. Separately all input/output data files relevant for the calculations can be provided on reasonable request.
Acknowledgments
This work was supported by the Simons Many-Electron Collaboration. For computational resources, MvS, SA and DP acknowledge PRACE for awarding us access to SuperMUC at GCS@LRZ, Germany and Irene-Rome hosted by TGCC, France. SA acknowledges the Cambridge Tier-2 system operated by the University of Cambridge Research Computing Service (www.hpc.cam.ac.uk) funded by EPSRC Tier-2 capital Grant No. EP/P020259/1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Georges, A.; Medici, L.d.; Mravlje, J. Strong Correlations from Hund’s Coupling. Ann. Rev. Cond. Matt Phys. 2013, 4, 137–178. [Google Scholar] [CrossRef]
- Yin, Z.P.; Haule, K.; Kotliar, G. Fractional power-law behavior and its origin in iron-chalcogenide and ruthenate superconductors: Insights from first-principles calculations. Phys. Rev. B 2012, 86, 195141. [Google Scholar] [CrossRef]
- Lanata, N.; Strand, H.U.; Giovannetti, G.; Hellsing, B.; de’Medici, L.; Capone, M. Orbital selectivity in Hund’s metals: The iron chalcogenides. Phys. Rev. B 2013, 87, 045122. [Google Scholar] [CrossRef]
- Yin, Z.; Haule, K.; Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nat. Mater. 2011, 10, 932. [Google Scholar] [CrossRef] [PubMed]
- Kostin, A.; Sprau, P.O.; Kreisel, A.; Chong, Y.X.; Böhmer, A.E.; Canfield, P.C.; Hirschfeld, P.J.; Andersen, B.M.; Davis, J.S. Imaging orbital-selective quasiparticles in the Hund’s metal state of FeSe. Nat. Mater. 2018, 17, 869. [Google Scholar] [CrossRef] [PubMed]
- Yi, M.; Zhang, Y.; Shen, Z.X.; Lu, D. Role of the orbital degree of freedom in iron-based superconductors. Npj Quantum Mater. 2017, 2, 57. [Google Scholar] [CrossRef]
- Zwicknagl, G.; Yaresko, A.; Fulde, P. Microscopic description of origin of heavy quasiparticles in UPt 3. Phys. Rev. B 2002, 65, 081103. [Google Scholar] [CrossRef]
- Kądzielawa-Major, E.; Fidrysiak, M.; Kubiczek, P.; Spałek, J. Spin-triplet paired phases inside a ferromagnet induced by Hund’s rule coupling and electronic correlations: Application to UGe2. Phys. Rev. B 2018, 97, 224519. [Google Scholar] [CrossRef]
- Wang, Q.-Y.; Li, Z.; Zhang, W.-H.; Zhang, Z.-C.; Zhang, J.-S.; Li, W.; Ding, H.; Ou, Y.-B.; Deng, P.; Chang, K.; et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 2012, 29, 037402. [Google Scholar] [CrossRef]
- Ge, J.-F.; Liu, Z.-L.; Liu, C.; Gao, C.-L.; Qian, D.; Xue, Q.-K.; Liu, Y.; Jia, J.-F. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 2015, 14, 285. [Google Scholar] [CrossRef]
- Sponza, L.; Pisanti, P.; Vishina, A.; Pashov, D.; Weber, C.; van Schilfgaarde, M.; Acharya, S.; Vidal, J.; Kotliar, G. Self-energies in Itinerant Magnets: A Focus on Fe and Ni. Phys. Rev. B 2017, 95, 041112. [Google Scholar] [CrossRef]
- Pashov, D.; Acharya, S.; Lambrecht, W.R.L.; Jackson, J.; Belashchenko, K.D.; Chantis, A.; Jamet, F.; van Schilfgaarde, M. Questaal: A package of electronic structure methods based on the linear muffin-tin orbital technique. Comput. Phys. Commun. 2019. [Google Scholar] [CrossRef]
- Kotani, T.; van Schilfgaarde, M.; Faleev, S.V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. Phys. Rev. B 2007, 76, 165106. [Google Scholar] [CrossRef]
- Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 2007, 75, 155113. [Google Scholar] [CrossRef]
- Gull, E.; Millis, A.J.; Lichtenstein, A.I.; Rubtsov, A.N.; Troyer, M.; Werner, P. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 2011, 83, 349. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13. [Google Scholar] [CrossRef]
- Acharya, S.; Weber, C.; Plekhanov, E.; Pashov, D.; Taraphder, A.; van Schilfgaarde, M. Metal-Insulator Transition in Copper Oxides Induced by Apex Displacements. Phys. Rev. X 2018, 8, 021038. [Google Scholar] [CrossRef]
- Baldini, E.; Sentef, M.A.; Acharya, S.; Brumme, T.; Sheveleva, E.; Lyzwa, F.; Pomjakushina, E.; Bernhard, C.; van Schilfgaarde, M.; Carbone, F.; et al. Electron–phonon-driven three-dimensional metallicity in an insulating cuprate. Proc. Natl. Acad. Sci. USA 2020, 117, 6409–6416. [Google Scholar] [CrossRef]
- Park, H. The Study of Two-Particle Response Functions in Strongly Correlated Electron Systems within the Dynamical Mean Field Theory. Ph.D. Thesis, Rutgers University-Graduate School, New Brunswick, NJ, USA, 2011. [Google Scholar]
- Yin, Z.; Haule, K.; Kotliar, G. Spin dynamics and orbital-antiphase pairing symmetry in iron-based superconductors. Nat. Phys. 2014, 10, 845. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; Weber, C.; Park, H.; Sponza, L.; van Schilfgaarde, M. Maximization of Tc via Conspired Even-Parity Spin and Charge Collective Excitations in Strained Sr2RuO4. Commun. Phys. 2019, 2. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; Jamet, F.; van Schilfgaarde, M. Controlling Tc through Band Structure and Correlation Engineering in Collapsed and Uncollapsed Phases of Iron Arsenides. Phys. Rev. Lett. 2020, 124, 237001. [Google Scholar] [CrossRef] [PubMed]
- Boehnke, L.; Hafermann, H.; Ferrero, M.; Lechermann, F.; Parcollet, O. Orthogonal polynomial representation of imaginary-time Green’s functions. Phys. Rev. B 2011, 84, 075145. [Google Scholar] [CrossRef]
- Tomczak, J.M.; Liu, P.; Toschi, A.; Kresse, G.; Held, K. Merging GW with DMFT and non-local correlations beyond. Eur. Phys. J. Spec. Top. 2017, 226, 2565–2590. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Imada, M.; Georges, A.; Kotliar, G.; Biermann, S.; Lichtenstein, A. Frequency-dependent local interactions and low-energy effective models from electronic structure calculations. Phys. Rev. B 2004, 70, 195104. [Google Scholar] [CrossRef]
- Şaşıoğlu, E.; Friedrich, C.; Blügel, S. Effective Coulomb interaction in transition metals from constrained random-phase approximation. Phys. Rev. B 2011, 83, 121101. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; van Schilfgaarde, M. Role of nematicity in controlling spin fluctuations and superconducting Tc in bulk FeSe. arXiv 2020, arXiv:2005.07729. [Google Scholar]
- Wang, Q.; Shen, Y.; Pan, B.; Zhang, X.; Ikeuchi, K.; Iida, K.; Christianson, A.D.; Walker, H.C.; Adroja, D.T.; Abdel-Hafiez, M.; et al. Magnetic ground state of FeSe. Nat. Commun. 2016, 7, 12182. [Google Scholar] [CrossRef]
- Rahn, M.C.; Ewings, R.A.; Sedlmaier, S.J.; Clarke, S.J.; Boothroyd, A.T. Strong (π,0) spin fluctuations in β-FeSe observed by neutron spectroscopy. Phys. Rev. B 2015, 91, 180501. [Google Scholar] [CrossRef]
- Deng, X.; Haule, K.; Kotliar, G. Transport Properties of Metallic Ruthenates: A DFT+DMFT Investigation. Phys. Rev. Lett. 2016, 116. [Google Scholar] [CrossRef]
- Acharya, S.; Pashov, D.; Chachkarova, E.; van Schilfgaarde, M.; Weber, C. Electronic structure correspondence of singlet-triplet scale separation in strained Sr2RuO4. Appl. Sci. 2021, 11, 508. [Google Scholar] [CrossRef]
- Hirsch, J. BCS theory of superconductivity: It is time to question its validity. Phys. Scr. 2009, 80, 035702. [Google Scholar] [CrossRef]
- Hirsch, J. Inconsistency of the conventional theory of superconductivity. EPL Europhys. Lett. 2020, 130, 17006. [Google Scholar] [CrossRef]
- Koizumi, H. Reversible superconducting-normal phase transition in a magnetic field and the existence of topologically protected loop currents that appear and disappear without Joule heating. EPL Europhys. Lett. 2020, 131, 37001. [Google Scholar] [CrossRef]
- Koizumi, H.; Ishikawa, A. Theory of supercurrent in superconductors. Int. J. Mod. Phys. B 2020, 34, 2030001. [Google Scholar] [CrossRef]
- Koizumi, H. Explanation of Superfluidity Using the Berry Connection for Many-Body Wave Functions. J. Supercond. Nov. Magn. 2020, 33, 1697–1707. [Google Scholar] [CrossRef]
- Kumar, R.S.; Zhang, Y.; Sinogeikin, S.; Xiao, Y.; Kumar, S.; Chow, P.; Cornelius, A.L.; Chen, C. Crystal and electronic structure of FeSe at high pressure and low temperature. J. Phys. Chem. B 2010, 114, 12597–12606. [Google Scholar] [CrossRef]
- Mandal, S.; Zhang, P.; Ismail-Beigi, S.; Haule, K. How Correlated is the FeSe/SrTiO3 System? Phys. Rev. Lett. 2017, 119, 067004. [Google Scholar] [CrossRef]
- Tomczak, J.M.; van Schilfgaarde, M.; Kotliar, G. Many-body effects in iron pnictides and chalcogenides – non-local vs dynamic origin of effective masses. Phys. Rev. Lett. 2012, 109, 237010. [Google Scholar] [CrossRef]
- Watson, M.D.; Kim, T.K.; Rhodes, L.C.; Eschrig, M.; Hoesch, M.; Haghighirad, A.A.; Coldea, A.I. Evidence for unidirectional nematic bond ordering in FeSe. Phys. Rev. B 2016, 94, 201107. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, L.; He, S.; He, J.; Liu, D.; Mou, D.; Shen, B.; Hu, Y.; Huang, J.; Zhou, X. Electronic structure and superconductivity of FeSe-related superconductors. J. Physics: Condens. Matter 2015, 27, 183201. [Google Scholar] [CrossRef]
- Rhodes, L.; Watson, M.; Haghighirad, A.; Eschrig, M.; Kim, T. Strongly enhanced temperature dependence of the chemical potential in FeSe. Phys. Rev. B 2017, 95, 195111. [Google Scholar] [CrossRef]
- Han, Q.; Dang, H.T.; Millis, A. Ferromagnetism and correlation strength in cubic barium ruthenate in comparison to strontium and calcium ruthenate: A dynamical mean-field study. Phys. Rev. B 2016, 93, 155103. [Google Scholar] [CrossRef]
- Gretarsson, H.; Lupascu, A.; Kim, J.; Casa, D.; Gog, T.; Wu, W.; Julian, S.; Xu, Z.; Wen, J.; Gu, G.; et al. Revealing the dual nature of magnetism in iron pnictides and iron chalcogenides using x-ray emission spectroscopy. Phys. Rev. B 2011, 84, 100509. [Google Scholar] [CrossRef]
- Dasari, N.; Yamijala, S.R.K.C.S.; Jain, M.; Dasgupta, T.S.; Moreno, J.; Jarrell, M.; Vidhyadhiraja, N.S. First-principles investigation of cubic BaRuO3: A Hund’s metal. Phys. Rev. B 2016, 94, 085143. [Google Scholar] [CrossRef]
- Nica, E.M.; Yu, R.; Si, Q. Orbital-selective pairing and superconductivity in iron selenides. Npj Quantum Mater. 2017, 2, 24. [Google Scholar] [CrossRef]
- Lynn, J.W.; Dai, P. Neutron studies of the iron-based family of high Tc magnetic superconductors. Phys. C Supercond. 2009, 469, 469–476. [Google Scholar] [CrossRef]
- Kreisel, A.; Hirschfeld, P.J.; Andersen, B.M. On the Remarkable Superconductivity of FeSe and Its Close Cousins. Symmetry 2020, 12, 1402. [Google Scholar] [CrossRef]
- Iyo, A.; Ishida, S.; Fujihisa, H.; Gotoh, Y.; Hase, I.; Yoshida, Y.; Eisaki, H.; Kawashima, K. Superconductivity in Uncollapsed Tetragonal LaFe2As2. J. Phys. Chem. Lett. 2019, 10, 1018–1023. [Google Scholar] [CrossRef]
- Haule, K.; Pascut, G.L. Forces for structural optimizations in correlated materials within a DFT+embedded DMFT functional approach. Phys. Rev. B 2016, 94, 195146. [Google Scholar] [CrossRef]
- Xiang, Y.Y.; Wang, F.; Wang, D.; Wang, Q.H.; Lee, D.H. High-temperature superconductivity at the FeSe/SrTiO3 interface. Phys. Rev. B 2012, 86, 134508. [Google Scholar] [CrossRef]
- Li, B.; Xing, Z.W.; Huang, G.Q.; Xing, D.Y. Electron-phonon coupling enhanced by the FeSe/SrTiO3 interface. J. Appl. Phys. 2014, 115, 193907. [Google Scholar] [CrossRef]
- Lee, J.J.; Schmitt, F.T.; Moore, R.G.; Johnston, S.; Cui, Y.T.; Li, W.; Yi, M.; Liu, Z.K.; Hashimoto, M.; Zhang, Y.; et al. Interfacial mode coupling as the origin of the enhancement of Tc in FeSe films on SrTiO3. Nat. Vol. 2014, 515, 245. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Sawatzky, G.A. Electron Phonon Coupling versus Photoelectron Energy Loss at the Origin of Replica Bands in Photoemission of FeSe on SrTiO3. Phys. Rev. Lett. 2018, 120, 237001. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhang, W.; Mou, D.; He, J.; Ou, Y.-B.; Wang, Q.-Y.; Li, Z.; Wang, L.; Zhao, L.; He, S.K.; et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 2012, 3, 1–6. [Google Scholar] [CrossRef]
- Zeng, B.; Mu, G.; Luo, H.; Xiang, T.; Mazin, I.; Yang, H.; Shan, L.; Ren, C.; Dai, P.; Wen, H.H. Anisotropic structure of the order parameter in FeSe 0.45 Te 0.55 revealed by angle-resolved specific heat. Nat. Commun. 2010, 1, 112. [Google Scholar] [CrossRef]
- Hanaguri, T.; Niitaka, S.; Kuroki, K.; Takagi, H. Unconventional s-wave superconductivity in Fe (Se, Te). Science 2010, 328, 474–476. [Google Scholar] [CrossRef]
- Nourafkan, R.; Kotliar, G.; Tremblay, A.M.S. Correlation-Enhanced Odd-Parity Interorbital Singlet Pairing in the Iron-Pnictide Superconductor LiFeAs. Phys. Rev. Lett. 2016, 117, 137001. [Google Scholar] [CrossRef]
- Zhang, Y.; Lee, J.; Moore, R.; Li, W.; Yi, M.; Hashimoto, M.; Lu, D.; Devereaux, T.; Lee, D.H.; Shen, Z.-X. Superconducting Gap Anisotropy in Monolayer FeSe Thin Film. Phys. Rev. Lett. 2016, 117, 117001. [Google Scholar] [CrossRef]
- Ye, Z.R.; Zhang, C.F.; Ning, H.L.; Li, W.; Chen, L.; Jia, T.; Hashimoto, M.; Lu, D.-H.; Shen, Z.-X.; Zhang, Y. Simultaneous emergence of superconductivity, inter-pocket scattering and nematic fluctuation in potassium-coated FeSe superconductor. arXiv 2015, arXiv:1512.02526. [Google Scholar]
- Schrodi, F.; Aperis, A.; Oppeneer, P.M. Eliashberg theory for spin fluctuation mediated superconductivity: Application to bulk and monolayer FeSe. Phys. Rev. B 2020, 102, 014502. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).