Abstract
SrRuO and Fe-pnictide superconductors belong to the same point group symmetry . Many experimental data confirm odd pairs in SrRuO and even pairs in Fe-pnictides, but opposite conclusions also exist. Recent NMR results of Pustogow et al., which revealed even Cooper pairs in SrRuO, require reconsideration of symmetry treatment of its SOP (superconducting order parameter). In the present work making use of the Mackey–Bradley theorem on symmetrized squares, a group theoretical investigation of possible pairing states in symmetry is performed. It is obtained for , i.e., space group of SrRuO, that triplet pairs with even spatial parts are possible in direction and in points M and Y. For the two latter cases pairing of equivalent electrons with nonzero total momentum is proposed. In space group of Fe- pnictides in point M, even and odd pairs are possible for singlet and triplet cases. It it shown that even and odd chiral states with angular momentum projection have nodes in vertical planes, but is nodal , whereas is nodeless in the basal plane. It is also shown that the widely accepted assertion that the parity of angular momentum value is directly connected with the spatial parity of a pair is not valid in a space-group approach to the wavefunction of a Cooper pair.
1. Introduction
Pnictide superconductors [1] and SrRuO [2] have been characterized in a great number of experiments [3,4] whose results are in some cases mutually excluding, and no consensus is currently achievable. The absence of changes in the Knight shift in the O NMR spectrum on passing through confirms oddness of the SOP (superconducting order parameter) of SrRuO [5]. Phase-sensitive measurements indicate that the phase of the SOP in SrRuO changes by under inversion and confirmed the odd nature of pairing [6]. Odd superconductivity in SrRuO is also in agreement with the results of penetration measurements [7,8]. A slight increase in the spin susceptibility originating from the Ru- electrons in superconducting state of SrRuO was connected with a triplet pairing [9]. However, a dramatic increase in from 1.5 K to 3.5 K and increase in ( by a factor of 20 ) in strained samples of SrRuO [10] was connected with singlet phase.
A reduction in O Knight shift observed for all strain values and temperatures T [11,12] suggests even SOP and singlet pairs, which were represented by even chiral function:
On the other hand, for the unstrained samples the reduction in Knight shift of approximately 50% is not inconsistent with helical states of or symmetry, which were written as [11]
where and stand for the components of triplet spin in the ESP (equal spin pairing) case, and and represent the continuous wavevector. However, by means of the NMR spectroscopy of normal state SrRuO under uniaxial stress and corresponding density-functional calculations, it was demonstrated that there are two different effects associated with the strain-induced the enhancement of the DOS associated with the -band FS (Fermi surface ) passing the Y point of the BZ (Brillouin zone), and a substantial Stoner enhancement [13]. The enhancement of the DOS through the Stoner factor boosts ferromagnetic spin fluctuations, which favors triplet states and seems to disfavor singlet pairing [13]. Thus, the singlet or triplet nature of pairing in SrRuO is still under debate.
Nevertheless, there is no doubt about other unusual properties of this superconductor. The results of SR (muon spin relaxation) experiments on superconducting SrRuO indicate the presence of spontaneous internal magnetic fields, i.e., TRSB (time-reversal symmetry breaking) [14]. More resent SR experiments established splitting between and temperature of TRSB, which rules out any mechanism based on interaction of magnetic fluctuations and conventional superconductivity [15]. Observed Kerr rotation below implies TRSB [16] and is consistent with the SOP of the form [17]:
where stands for the component of triplet spin vector in OSP (opposite spin pairing case). The measurements of the specific heat resulted in lines of gap minima or zeros in planes and [18]. High-resolution inelastic neutron scattering measurements and random phase approximation calculations suggest horizontal line nodes [19]. The results of angle-resolved study of ultrasonic attenuation in SrRuO suggest that the gap function has nodes in vertical or horizontal planes [20]. Thermal conductivity measurements on single crystals of SrRuO revealed vertical line nodes of SOP [21]. Recent results of sound velocity experiments are compatable with two-component d-wave SOP [22]. The authors [20,21,22] noticed the inconsistency between chiral p- wave or d-wave superconductivity and vertical line nodes. However, it was shown that group theoretical vertical line nodes are inherent to real and complex forms of SOP [23]. Recent field-angle-dependent specific-heat measurements [24] revealed the presence of horizontal line nodes in the gap consistent with SOP of (1) structure. Chiral even SOP nodeless in the basal plane was represented in polynomial form as
Transport properties of the planar and corner Josephson junctions formed between SrRuO and Nb revealed time-reversal invariant superconductivity, with most probably helical p-wave symmetry [25]. Using the results of resonant ultrasound spectroscopy measurements, the structure of SOP was proposed [26]. Thus, the above-mentioned model representations of SOP in SrRuO [11,17,22] reflect experimental features, but the inconsistency between their theoretical nodal structure [11,17] and experimental data on vertical line nodes in the chiral case [18,20,21] exists.
The electron band structure of pnictide superconductors is quite unusual resulting in some unconventional features of their SOP. According to the calculations the FS of pnictides consists of two electronic parts: and near point and a hole part near M point [27]. The results of scanning tunneling microscopy on Fe(Se,Te) single crystals indicate that the sign is reversed between the hole and the electron FS pockets (-wave), favoring the unconventional pairing mechanism associated with spin fluctuations [28]. ARPES (angle-resolved photoelectron spectroscopy) investigations of NdFeAsOF detected some angular fluctuations of gap at FS, but the results do not exclude p-wave or d-wave pairing states with nodes of the gap [29]. ARPES of BaKFeAs revealed nodeless superconducting gaps of different values, opening simultaneously at the bulk on all three observed FS sheets [30]. The results are consistent with the SOP of s-wave symmetry, although the authors cannot rule out the possibility of nontrivial relative phases between the pairing order parameters on the different FS sheets. ARPES with laser excitation showed that KFeAs ( = 3.4 K) is an s-wave superconductor with unusual multigap structure, i.e., internal and external FS have no zeroes, whereas octet point nodes are located on the middle FS at an angular distance from coordinate axes, and gap symmetry was suggested [31]. However, tunneling conductance spectra of stoichiometric FeSe crystalline films in their superconducting state revealed evidence for a gap function with nodal lines, manifesting symmetry breaking from to [32]. Summarizing experimental results of combinatorial microwave measurements, it was concluded that LiFeAs has nodeless gaps with moderate anisotropy and that BaFe(AsP) has highly anisotropic gaps containing at least one line-nodal gap [33]. A constant Knight shift in As in NMR investigation of a single crystal of superconducting LiFeAs was considered as a signs of triplet pairing [34]. In addition, the observed anomalous hysteresis at high fields is compatible with the existence of chiral gap wave functions similar to the forms (4) or (5) [35]. Making use of SR, symmetry analysis and first principles band structure calculation chiral d-wave SOP was proposed for weakly correlated pnictide compound LaPtP [36].
Both types of compounds SrRuO and Fe- pnictides have the same point group symmetry, but belong to different space groups: ( ,139) and (, 129), respectively, and the symmetry analysis of pair symmetry inside the BZ is the same for them. The BZs for these space groups are presented in Figure 1.
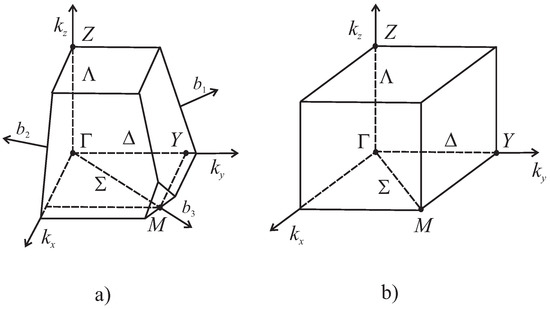
Figure 1.
1/8 parts of BZ for two space groups of symmetry (a) (), (b) ().
Representations of experimental data (1)–(4) are based on phenomenological point group approach [17,37,38], in which possible SOP functions are obtained by reduction of spherical harmonics to a point group. According to Anderson ansatz [39] wavefunction of a singlet pair is even and that of a triplet pair is odd. It was shown, making use of the space-group approach to the wavefunction of a Cooper pair, that this direct relation between multiplicity and parity of a pair is violated in symmetrical points and directions in a BZ [40,41]. Since the spherical functions are taken for the representation of SOP in phenomenological approaches, it was assumed that singlet pairs have even value of angular momentum l and triplet pairs have odd value of angular momentum [42]. It should be noted that in a general case, for each IR (irreducible representation) of a rotation group there are even and odd extensions on the rotation group with space inversion [43]. Hence, the direct relation between the parity of angular momentum value and the spatial parity of pair function is a consequence of the basis function choice, but not of the symmetry requirements. Usually the accepted formula (4) for triplet chiral states is nodeless in vertical planes, but making use of the space-group approach the examples of p-wave SOP with group-theoretical vertical lines of nodes were obtained [23]. Recent results on even nature of the SOP in SrRuO [11] require also investigations of vertical nodes of singlet chiral states. It was mentioned that the concept of s-wave, p-wave, etc., has to be taken with a grain of salt because of the presence of a crystalline lattice that breaks translational symmetry [44]. By virtue of the fact that there are many experimental results on the symmetry of SOP of SrRuO and Fe- pnictides, which apparently contradict with each other and with model representation, its group theoretical analysis independent on the models is required.
In the present work the space group theory [45] for one-electron states, Anderson ansatz [39] and Mackey–Bradley theorem [46,47] for two-electron states, are used to investigate spatial structures of singlet and triplet pairs in distinct points of a BZ. Symmetrical points in a BZ are identified, where direct connection between multiplicity and parity of a pair function is violated. Even and odd chiral states with angular momentum projection are built, and their nodal structure is investigated.
2. Symmetry of Two-Electron States
One-electron states in a crystal with symmetry group G are labeled by the wavevector k, its symmetry group H (little group) and the index of small IR of H [45] . For brevity the second index for one-electron states will be dropped. The IR of the space group is an induced representation [45]. In a general point of a BZ the dimension of IR equals the number n of point group elements of (central extension of G). Two-electron space is a Kronecker square of this space, and its dimension in a general point equals to . This space can be easily decomposed into physically different parts making use of double coset decomposition of G with respect to H [46,47]:
The double coset representatives denote different terms in a Kronecker square decomposition. The notation × for direct (Kronecker) product is used throughout. For each double coset a representation is considered, whose character is written as:
where . For self-inverse double cosets, i.e., if there are two extensions of on group :
and
where the coset representative a is chosen from the relation:
According to the Mackey–Bradley theorem [46,47] symmetrized (superscript +) and antisymmetrized (superscript −) parts of a Kronecker square are written as:
The symmetrization (antisymmetrization) in the first item is performed by standard point group technique, sum in the second item runs over self-inverse double cosets, and the sum in the third item runs over not self-inverse double cosets, i.e., if .
Total momentum of a pair is written as:
where is a reciprocal lattice vector. In the case of Cooper pairs the double coset representative is a space inversion I, and in some symmetrical points on the surface of a BZ is an identity element E. It should be noted that since in a space-group approach one-electron wavefunction is multidimensional, there are states of two equivalent electrons with nonzero total momentum K. Some such states will be considered later on.
According to the Pauli exclusion principle, the symmetrized square of a spatial part of the wavefunction corresponds to a singlet pair and antisymmetrized square corresponds to a triplet pair. For the induced representation is a reducible representation of a point group . The frequency of appearance of any IR of in the decomposition of induced representation is given by Frobenius reciprocity theorem [45], i.e., by the formula:
Inside the BZ in the majority of cases (but not in all) the spatial part of a singlet pair is even and spatial part of a triplet pair is odd. If IR is two-dimensional, one obtains from (7)–(9) that , and Hence, it follows that in this case even and odd IRs are mixed in the decomposition of symmetrized and antisymmetrized squares. The mixing of even and odd IRs takes place also in nonsymmorphic space groups on the surface of a BZ [40,41,48,49] due to non-trivial factor-system [41,48]. In the case of group the wavevector group H in point M is a group (see Figure 1b)), and IRs are projective [50]. In the case of projective IRs symmetrized (antisymemtrized) characters in the first item in r.h.s. of formula (11) are written as [41,49]:
where stands for the factor system of projective representation.
In addition, it may be derived from formula (11) that a usually accepted assertion that triplet (singlet) pairs have odd (even) angular momentum value is violated. For example, consider group and k a general point in a BZ. In this case all even (odd) IRs appear in the decomposition for singlet (triplet) pairs with frequencies equal to their dimensions. Consider IR for a singlet pair and and for triplet pairs. It is known that the even spatial part of the wavefunction of atomic term () transforms as in symmetry. In addition, the odd spatial part of atomic term splits in crystal field into and . Hence, it follows that the angular momentum should be assigned to a singlet pair of symmetry, and the angular momentum should be assigned to eventual pairs of and symmetry.
The decompositions of symmetrized and antisymmetrized squares of IRs of the space group are presented in Table 1. The notations of points in a BZ are according to Figure 1. The results for points inside the BZs for groups and are the same and differ on their surfaces. The important point M for group is also considered. It is seen in Table 1 that in direction , even IR appears in the decomposition of antisymmetrized square of . Additionally, appears in the decomposition of symmetrized square of . Hence, it follows that in this case triplet pair with spatial part and singlet pair with spatial part are possible. In point Z, where , double coset defined by the identity element results in zero total momentum of a pair. In this case, spatial parts of singlet and triplet pairs are even. However, since SrRuO is almost a two-dimensional superconductor, these examples unlikely correspond to pairing in it, and we consider symmetry points in basal plane. Because the space inversion is an element of group of the wavevector M of BZ, the left coset defined by the space inversion is absent. Since all IRs of are one-dimensional, in the left coset defined by the identity element antisymmetrized square vanishes, and only singlet pairs are possible. Hence, in this case triplet Cooper pairs are forbidden by symmetry.

Table 1.
Possible IRs of singlet and triplet pairs for group () depending on the wavevector in a BZ (see Figure 1a) and IR of wavevector group H. Double coset representatives and the pair’s wavevectors K are presented in last two columns. The results for point M of group () are also included. Since, in a general point of a BZ all even IRs are possible for singlet pairs and all odd IRs are possible for triplet pairs, the absence of any IR on line (plane) corresponds to a point node (line of nodes).
However, in point M of BZ nontrivial triplet and singlet pairs are possible. Let us consider double coset defined by the rotation (see Figure 2a). In this case the relation (12) results in a two-electron wavevector , whose group is . In this case IRs of singlet and triplet pairs are different, but they all are even. However, in this case translations by some lattice vectors result in a phase factor , and this state does not correspond to the definition of a Cooper pair completely. Nevertheless, since many other symmetries in topological superconductors are broken, this unusual case may be considered in the theories of unconventional superconductivity.
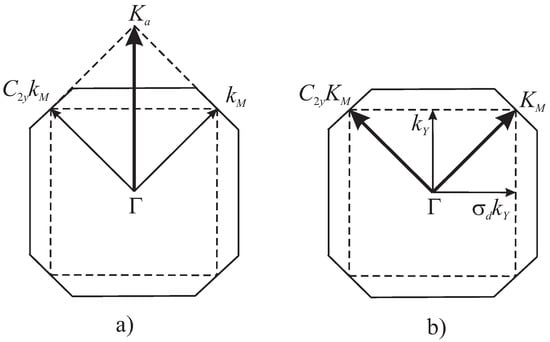
Figure 2.
Nontrivial pair functions in two symmetrical points of BZ. (a) electron wavevector k in point M, pair wavevector (b) electron wavevector k in pont Y, pair wavevector .
In point Y IRs and double coset, defined by the space inversion are the same as for direction (see Table 1), consequently possible pair functions are the same also. Though there is a non-trivial wavevector relation, corresponding to double coset, defined by (see Figure 2b). It is seen in Figure 2b), that in this case two-electron state in M has a star, consisting of two prongs. Since space inversion is an element of the wavevector group, this state is characterized by a parity. However, this state is also not completely symmetrical with respect to lattice translation, and some lattice translations result in a phase factor .
3. Nodal Structure and Chirality of Cooper Pair Wavefunction
General group theoretical results of the previous section may be envisaged by introducing a Cooper pair basis set as follows. According to Anderson ansatz [39] for k a general point in a BZ spatial parts of singlet and triplet pairs are written by the two following formulas, respectively:
and
where and denote electron coordinates, and represents the action of the space inversion on k. According to the space-group representation theory [45] the one-electron state in crystal is represented by the wavevector star , consisting of prongs. When acting by left coset representatives in the decomposition of relative to on basis functions (15) or (16) one obtains total basis set for singlet or triplet Cooper pair, whose dimension equals to . One can choose pure rotation subgroup of or any other subgroup of index 2, which contains only one of the two elements connected by the space inversion. Singlet (triplet) functions form a basis of induced representation of point group . The projection of this reducible basis, sets on the rows of IR of the whole group may be obtained making use of the standard projection operator technique [43], i.e., making use of formula:
In the case of group there are eight basis pair functions for the singlet case and eight functions for the triplet case. Taking three rotations about the z axis (, and = ) and four reflections in vertical planes (, , and as left coset representatives, one obtains reducible Cooper pair basis set for a general k-point in a Brillouin zone, shown in Figure 3. Basis functions or are obtained by the action of left coset representatives on the functions or (see formulas (15) and (16)). Note that in Figure 3 all vectors have the same nonzero projection.
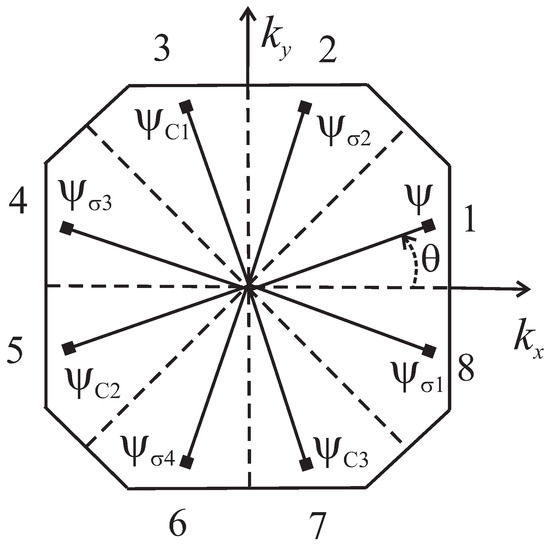
For one-dimensional IRs the linear combinations of the basis set are unique, and Table 1 defines their nodal structure completely. The nodal structure of two-dimensional IRs depends on additional quantum numbers and was considered for triplet pairs elsewhere [23]. It was also shown that chiral basis functions for triplet pairs constructed making use complex form of IR [50] have vertical nodes. However, chiral even functions were not considered in a framework of a space-group approach, and one of the aims of the present work is to consider such states. On vertical planes each one of the two-dimensional IRs appears ones. It follows from formula (13) that for k a general point in a BZ and appear twice for triplet and singlet cases, respectively. Hence, it follows that for each vertical plane, two-dimensional IRs may be nodal or nodeless.
Chiral forms of IRs and on subgroup [50] are presented in Table 2. Since IRs are characterized by parity, their matrices for all groups can be easily obtained. It can be easily verified that direct product equals to Consequently, there are two extensions of these matrices on the left coset defined by , labeled by the sign of matrix of the left coset representative as a superscript. The matrices of element with corresponding superscripts are also presented in Table 2.

Table 2.
Matrices D of IRs and for the rotation subgroup elements (, , ) and two forms of matrix for the left coset representative .
The pairs’ functions of and symmetry constructed from the basis set shown in Figure 3 making use of projection operators (17) are presented in Table 3. It is seen from Table 3 that the basis functions , and of the first row of , obtained by the action of , and rotations on the initial function , acquire phase factors i, and , respectively, i.e., correspond to magnetic quantum number . Basis functions of the second row, obtained by the action of the same rotations on the function , acquire phase factors , and i and correspond to magnetic quantum number . In the Ginzburg–Landau theory the SOP is identified with the wavefunction of a Cooper pair, which includes all pairs in the condensate. In the space-group approach this general pair function is obtained when the electron wavevector k runs in the sector (see Figure 3), and other sectors are brought about by left coset representatives. Suppose, that there is a phase winding in the first sector. It is natural to suppose that due to topological reasons In this case the functions in the sectors labeled by odd numbers in Figure 3 may be considered as possessing angular momentum projection . It is clear that reflection changes the direction of phase winding in sector 8 relative to sector 1, and the functions of even sectors possess angular momentum projection . In this technique the basis functions and their phases in the other sectors are obtained group theoretically by the action of left coset representatives.

Table 3.
Pair functions for two-dimensional IRs and of group . is a pair function corresponding to Anderson ansatz [39] in a basis domain of a BZ (see formulas (15) and (16) for singlet and triplet cases, respectively). The other functions are obtained by the action of point group elements on (see Figure 3). The superscript corresponds to the sign of matrix of left coset representative (see Table 2).
Basis functions of two rows of two-dimensional IRs are localized at different sectors in k-space and meet at vertical planes, where interference of pair functions occurs. In order to envisage such interference, the wave functions of pairs in a finite number of points were represented by normalized sum of real and imaginary Gaussians. Within the sectors the phases at neighboring points almost coincide, and constructive interference takes place. At the boundaries of the sectors, both constructive and destructive interference of the wavefunctions is possible. When squaring modulus of the complex function at every point we obtain the structure of SOP in the plane normal to the -axis. Nodal structures of IRs and , obtained by this numerical method presented in Figure 4, have nodes in plane and deeps in diagonal planes. Figure 5 shows the same for and , where line of nodes is in plane . Nodes in vertical coordinate planes are defined by additional quantum number, i.e., the sign of matrix (see Table 2). Nodes and deeps in diagonal vertical planes are the result of phase differences between two complex functions. In order to envisage the origin of these peculiarities, the phases of basis functions with and for and are presented in Figure 6 and Figure 7, respectively. Due to the same choice of left coset representative (denoted by superscript “+” or “−”) the results for and with the same superscripts coinside, and subscripts are dropped in Figure 6 and Figure 7. In Figure 6 near the positive direction of x- axis the phases of functions at and at are the same ( denotes small positive angle) and the phase was added to the function for convenience. On a clockwise path from 360 to 90 the phase winding of function is , and the total phase is The phase winding on the counter-clockwise of the function on the path from to 90 is . Thus, the total phase difference is , and interference is destructive at 90. Similar estimation at 45 results in phases of the first and second function and , respectively, resulting in constructive interference of real parts, destructive interference of imaginary parts and deep (not node) of SOP. Figure 7 shows the case in which reflection changes the phase, and the interference pattern is rotated by 90. Note that a similar interference pattern was obtained for complex odd IR without phase winding [23].
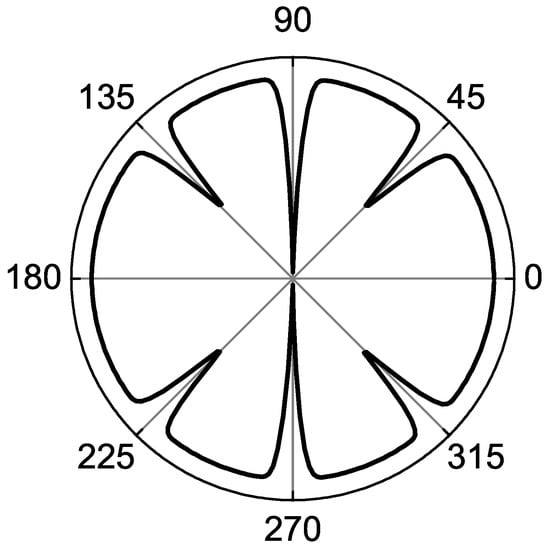
Figure 4.
SOP of chiral and pair functions (see Table 3) Note that is nodal and is nodeless in basal plane.
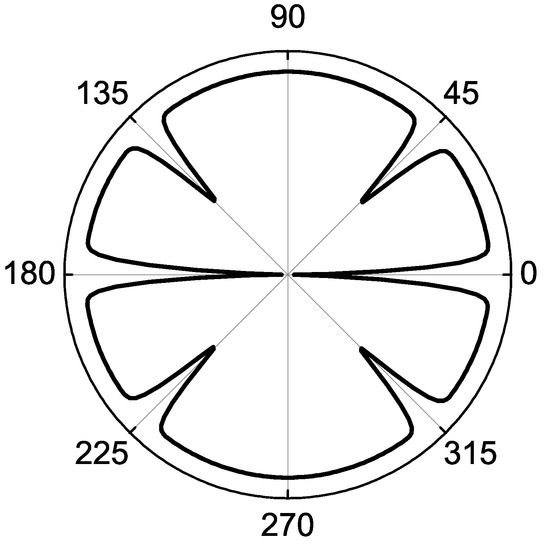
Figure 5.
SOP of chiral and pair functions (see Table 3). Note that is nodal and is nodeless in basal plane.
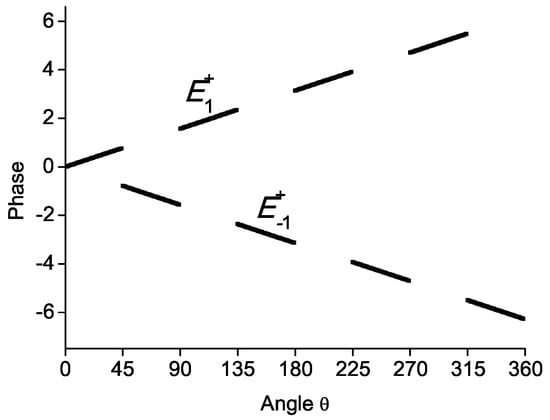
Figure 6.
Phases of two basis functions of IR . Superscript + corresponds to the superscript of matrix (see Table 2) Subscripts in figure correspond to magnetic quantum numbers.
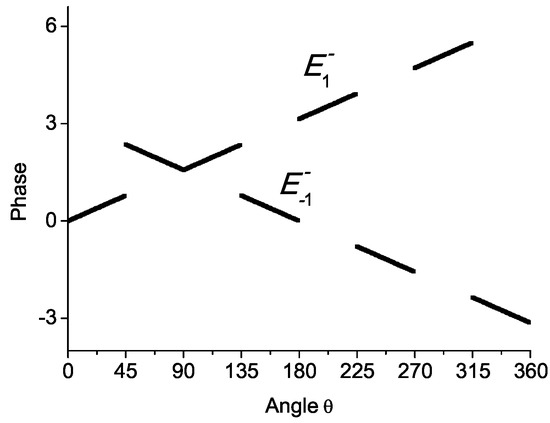
Figure 7.
Phases of two basis functions of IR . Superscript − corresponds to the superscript of matrix (see Table 2) Subscripts in figure correspond to magnetic quantum numbers.
Thus, even and odd two-dimensional complex IRs have one vertical nodal plane or . The nodal and nodeless planes are interchanged when multiplying by characters of IR , so the vertical nodal planes of and are topologically unstable according to the definition of Kobayashi et al. [51]. The basis functions of and symmetry in chiral representations have angular momentum projection . The essential difference between the structures of and appears in the basal plane (see Table 1), where is nodeless, and nodes of are topologically stable.
4. Weak Spin-Orbit Coupling
In a weak spin orbit coupling case total pair function is a direct product of its spin and spatial parts. In symmetry OSP spin function belongs to IR . Multiplication of by results in also. Since characters of equal for all elements of the left coset with respect to , it follows that such a multiplication results in an interchange of and cases. The ESP spin functions and belong to in its standard form. In chiral representation of [50] its basis triplet spin functions are linear combinations and . Decomposition of direct product results in the states , which are similar to helical states (2), (3). Multiplication of the spin part by the spatial part belonging to any odd one-dimensional IR results in , which corresponds to chiral ESP state. In the case of SrRuO singlet spin state of symmetry and triplet OSP state of symmetry are considered. Thus, in symmetry total functions of chiral singlet and triplet OSP pairs belong to IRs and , respectively.
5. Discussion
Group theoretical basis functions with topological phase winding of the present work are similar to commonly used chiral functions (1), (4) and (5), and it is important to establish the reasons for the appearance of significant differences, namely vertical line nodes and nonunitary structure. It should be noted that authors of these models did not consider matrices, whose basis is formed by these functions. However, to define nodal structures of multi-dimensional IRs, additional quantum numbers, specifying the matrix, are required [52]. Consider the application of the technique of the present work to the functions (1). It is immediately verified that reflection interchanges two functions (1). The function is a good basis function for phase winding in the first sector with . In addition, the action of rotational elements of on this function result in the same phase factors as elements of the first row and first column of in chiral form [50] (see also Table 2). Continuing to apply the method of projection operators, we pass to the element , which transforms the function into and interchanges rows of IR (see Table 2). Thus, we obtain the function with in the 8 sector. Hence, it follows that application of the standard projection operator technique [43] and chiral form of IR [50] to the first of functions (1) results in the same phase structure as shown in Figure 6 and Figure 7 and, consequently, the same nodal structure, as obtained in the present work in a space-group basis set. It should be noted that according to the Mackey–Bradley theorem, two-dimensional IRs appear twice in a total two-electron basis decomposition. It is immediately verified that multiplication of by results in also, but the magnetic quantum numbers are swapped. Thus, starting projection on the first row from we obtain that functions with are in the first row of matrix and in odd sectors in k-space (see Figure 2). In this case a total phase structure is opposite to that shown in Figure 6 and Figure 7. Hence, it follows that the sum of these two basis sets results in nodeless and unitary (i.e., probabilities of and are equal in all k- space) SOP structures. However, since experimental results indicate that SOP of SrRuO is chiral, nodal and nonunitary, we may conclude that this case corresponds to one chiral two-dimensional IR considered in the present work. The structure (4) is similar to (1) , but the chiral model form (5) , which is also written as , consists of two different IRs and has no group theoretic analog.
Since the primary detected odd spatial parity [5,6] of unconventional superconductor SrRuO is under debate [11,13], the establishing of a connection between parity and multiplicity is very essential. In the present work, making use of Anderson ansatz [39] and the Mackey–Bradley theorem [46,47], possible pair symmetries on the dependence of the wavevector k in a BZ are obtained for symmetry group . In the majority of cases the wavefunction of a singlet pair is even, and that of a triplet pair is odd (see Table 1). Since in the space-group theory one-electron states are characterized by a wavevector star [45,47], possible pair states with the certain parity may also include states with nonzero total momentum K. In point M for group, in the case of pairing of electrons and , possible symmetries of singlet pairs are + and of triplet pairs are . The wavevector K of these states equals (. These states are not completely translation invariant, i.e., some lattice translations result in a phase factor 1, but some translations result in a phase factor . In addition, for k in point Y there are pair states denoted as and for singlet case and and for triplet case. These pairs are not translation invariant, but characterized by parity. In addition to the symmetries broken in unconventional superconductors such two-electron states represent another possibility, i.e., pairs states with partially broken translation symmetry. Thus, triplet pairs in symmetry, being odd in general points of a BZ, may exhibit even spatial part in some symmetrical points of a BZ. Hence, it follows that recent experiments [11] manifesting the contribution of even pairs in SrRuO may be explained in a triplet pairing scenario. The even triplet pairing and odd singlet pairing cases are referred to as odd frequency pairing [53].
In point M for non-symmorphic space group in addition to the standard relation between multiplicity and parity of a Cooper pair, singlet odd pairs and triplet even pairs are possible.
Chiral states constructed making use of the complex form of IRs [50] have a nodal plane in one of the vertical coordinate planes and deeps in diagonal planes. The position of the vertical nodal plane depends on an additional quantum number—the sign of matrix for reflection . In these states the basis functions connected by rotations about the axis acquire phase factors corresponding to magnetic quantum numbers . When adding a continuous gauge phase in the range 0 one obtains total phase winding group theoretically. The transformations of and pairs by rotations of the subgroup are the same. This assertion is in agreement with the general conclusion of the present work, that parity and angular momentum of a pair are not connected with each other. For example, in symmetry singlet pairs of symmetry are possible, but it is also the symmetry of term of configuration with angular momentum . This result differs from the assertion of phenomenological approaches based on spherical functions, that even (odd) values of momentum correspond to even (odd) inversion symmetry. However the present result does not contradict with general group theory [43]. Phenomenological chiral functions (1) and (4) arise from spherical function in k-space and are nodeless in vertical planes. Group theoretical chiral functions have vertical lines of node and deeps and agree with experimental results [20,21,22]. Thus, the only robust difference between nodal structures of and states is nodal structure in the basal plane.
6. Conclusions
Making use of the Mackey–Bradley theorem on symmetrized squares and Anderson ansatz for the Cooper pair, group theoretical investigation of possible pairing states in symmetry was performed. It was obtained that for non-symmorphic group of Fe-pnictide superconductors at point M of a BZ, odd singlet and even triplet pairs are possible. It was also obtained that triplet pairs with an even spatial part are possible in direction and in points M and Y of a BZ for the space group . For the two latter cases, pairing of equivalent electrons with total pair momentum in symmetry points of BZ other than is proposed. Thus, the recent results [11,12,13], which revealed even features of previously considered as odd SOP of SrRuO, may be explained by the presence of triplet pairs with even spatial structure in some points of a BZ. It was shown that even and odd chiral states with angular momentum projection have nodes and deeps in vertical planes, which corresponds to the experimental data. The only robust difference between nodal structures of and takes place in the basal plane, where is nodal and is nodeless.
Funding
The work was supported by IGIC RAS state assignment.
Conflicts of Interest
The author declares no conflict of interest.
References
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La[O1-xFx]FeAs (x = 0.05–0.12) with Tc = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
- Maeno, Y.; Hashimoto, H.; Yoshida, K.; Nishizaki, S.; Fujita, T.; Bednorz, J.D.; Lichtenberg, F. Superconductivity in a layered perovskite without copper. Nature 1994, 372, 532–534. [Google Scholar] [CrossRef]
- Maeno, Y.; Kittaka, S.; Nomura, T.; Yonezava, S.; Ishida, K. Evaluation of spin-triplet superconductivity in Sr2RuO4. J. Phys. Soc. Jpn. 2012, 81, 011009. [Google Scholar] [CrossRef] [Green Version]
- Shibauchi, T.; Hanaguri, T.; Matsuda, Y. Exotic Superconducting States in FeSe-based Materials. J. Phys. Soc. Jpn. 2020, 89, 102002. [Google Scholar] [CrossRef]
- Ishida, K.; Mukuda, H.; Kitaoka, Y.; Asayama, K.; Mao, Z.Q.; Mori, Y.; Maeno, Y. Spin-triplet superconductivity in Sr2RuO4 identified by 17O Knight shift. Nature 1998, 396, 658–660. [Google Scholar] [CrossRef]
- Nelson, K.D.; Mao, Z.Q.; Maeno, Y.; Liu, Y. Odd-parity superconductivity in Sr2RuO4. Science 2004, 306, 1151–1154. [Google Scholar] [CrossRef]
- Anwar, M.S.; Lee, S.R.; Ishiguro, R.; Sugimoto, Y.; Tano, Y.; Kang, S.J.; Shin, Y.J.; Yonezawa, S.; Manske, D.; Takayanagi, H.; et al. Direct penetration of spin-triplet superconductivity into a ferromagnet in Au/SrRuO3/Sr2RuO4 junctions. Nat. Commun. 2016, 7, 13220. [Google Scholar] [CrossRef] [PubMed]
- Terrade, D.; Gentile, P.; Cuoco, M.; Manske, D. Proximity effects in a spin-triplet superconductor–ferromagnet heterostucture with a spin-active interface. Phys. Rev. B. 2013, 88, 054516. [Google Scholar] [CrossRef] [Green Version]
- Ishida, K.; Manago, M.; Yamanaka, T.; Fukazawa, H.; Mao, Z.Q.; Maeno, Y.; Miyake, K. Spin polarization enhanced by spin-triplet pairing in Sr2RuO4 probed by NMR. Phys. Rev. B. 2015, 92, 100502. [Google Scholar] [CrossRef]
- Steppke, A.; Zhao, L.; Barber, M.E.; Scaffidi, T.; Jerzembeck, F.; Rosner, H.; Gibbs, A.S.; Maeno, Y.; Simon, S.H.; Mackenzie, A.P.; et al. Strong peak in Tc of Sr2RuO4 under uniaxial pressure. Science 2017, 355, eaaf9398. [Google Scholar] [CrossRef] [Green Version]
- Pustogow, A.; Luo, Y.; Chronister, A.; Su, Y.S.; Sokolov, D.A.; Jerzembeck, F.; Mackenzie, A.P.; Hicks, C.W.; Kikugawa, N.; Raghu, A.P.; et al. Constraints on the superconducting order parameter in Sr2RuO4 from oxygen-17 nuclear magnetic resonance. Nature 2019, 574, 72–75. [Google Scholar] [CrossRef]
- Ishida, K.; Manago, M.; Maeno, Y. Reduction of the 17O Knight shift in the superconducting state and the heat-up effect by NMR pulses on Sr2RuO4. J. Phys. Soc. Jpn. 2020, 89, 034712. [Google Scholar] [CrossRef]
- Luo, Y.; Pustogow, A.; Guzman, P.; Dioguardi, A.P.; Thomas, S.M.; Ronning, F.; Kikugawa, N.; Sokolov, D.A.; Jerzembeck, F.; Mackenzie, A.P.; et al. Normal state 17O NMR studies of Sr2RuO4 under uniaxial stress. Phys. Rev. X 2019, 9, 021044. [Google Scholar]
- Luke, G.M.; Fudamoto, Y.; Kojima, K.M.; Larkin, M.I.; Merrin, J.; Nachumi, B.; Uemura, Y.J.; Maeno, Y.; Mao, Z.Q.; Mori, Y.; et al. Time-reversal symmetry breaking superconductivity in Sr2RuO4. Nature 1998, 394, 558–561. [Google Scholar] [CrossRef] [Green Version]
- Grinenko, V.; Ghosh, S.; Sarkar, R.; Orain, J.-C.; Nikitin, A.; Elender, M.; Das, D.; Guguchia, Z.; Brückner, F.; Barber, M.E.; et al. Split superconducting and time-reversal symmetry-breaking transitions in Sr2RuO4 under stress. Nat. Phys. 2021, 17, 748–754. [Google Scholar] [CrossRef]
- Xia, J.; Maeno, Y.; Beyersdorf, P.T.; Fejer, M.M.; Kapitulnik, A. High resolution polar kerr effect measurements of Sr2RuO4: Evidence for broken time reversal symmetry in the superconducting state. Phys. Rev. Lett. 2006, 97, 167002. [Google Scholar] [CrossRef] [Green Version]
- Rice, T.M.; Sigrist, M.J. Sr2RuO4: An electronic analogue of 3He? J. Phys. Cond. Matter 1995, 7, L348–L643. [Google Scholar] [CrossRef]
- Deguchi, K.; Mao, Z.Q.; Maeno, Y.J. Determination of the superconducting gap structure in all bands of the spin-triplet Superconductor Sr2RuO4. J. Phys. Soc. Jpn. 2004, 73, 1313–1321. [Google Scholar] [CrossRef] [Green Version]
- Iida, K.; Kofu, M.; Suzuki, K.; Murai, N.; Ohira-Kawamura, S.; Kajimoto, R.; Inamura, Y.; Ishikado, M.; Hasegawa, S.; Masuda, T.; et al. Horizontal line nodes in Sr2RuO4 proved by spin resonance. J. Phys. Soc. Jpn. 2020, 89, 053702. [Google Scholar] [CrossRef] [Green Version]
- Lupien, C.; MacFarlane, W.A.; Proust, C.; Taillefer, L.; Mao, Z.Q.; Maeno, Y.U. ltrasound attenuation in Sr2RuO4: An angle-resolved study of the superconducting gap function. Phys. Rev. Lett. 2001, 86, 5986–5989. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hassinger, E.; Bourgeois-Hope, P.; Taniguchi, H.; Rene de Cotret, S.; Grissonnanche, G.; Anwar, M.S.; Maeno, Y.; Doiron-Leyraud, N.; Taillefer, L. Vertical line nodes in the superconducting gap structure of Sr2RuO4. Phys. Rev. X 2017, 7, 011032. [Google Scholar] [CrossRef] [Green Version]
- Benhabib, S.; Lupien, C.; Paul, I.; Berges, L.; Dion, M.; Nardone, M.; Zitouni, A.; Mao, Z.Q.; Maeno, Y.; Georges, A.; et al. Ultrasound evidence for a two-component superconducting order parameter in Sr2RuO4. Nat. Phys. 2021, 17, 194–198. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G. Group theoretical lines of nodes in triplet chiral superconductor Sr2RuO4. J. Phys. Soc. Jpn. 2018, 87, 114711. [Google Scholar] [CrossRef]
- Kittaka, S.; Nakamura, S.; Sakakibara, T.; Kikugawa, N.; Terashima, T.; Uji, S.; Sokolov, D.A.; Mackenzie, A.P.; Irie, K.; Tsutsumi, Y.; et al. Searching, for, gap, zeros, in, Sr2RuO4 via field-angle-dependent specific-heat measurement. J. Phys. Soc. Jpn. 2018, 87, 093703. [Google Scholar] [CrossRef]
- Kashiwaya, S.; Saitoh, K.; Kashiwaya, H.; Koyanagi, M.; Sato, M.; Yada, K.; Tanaka, Y.; Maeno, Y. Time-reversal invariant superconductivity of Sr2RuO4 revealed by Josephson effects. Phys. Rev. B 2019, 100, 094530. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Shekhter, A.; Jerzembeck, F.; Kikugawa, N.; Sokolov, D.A.; Brando, M.; Mackenzie, A.P.; Hicks, C.W.; Ramshaw, B.J. Thermodynamic evidence for a two-component superconducting order parameter in Sr2RuO4. Nat. Phys. 2021, 17, 199–204. [Google Scholar] [CrossRef]
- Singh, D.J.; Du, M.-H. Density functional study of LaFeAsO1-xFx: A low carrier density superconductor near itinerant magnetism. Phys. Rev. Lett. 2008, 100, 237003. [Google Scholar] [CrossRef] [Green Version]
- Hanaguri, T.; Niitaka, S.; Kuroki, K.; Takagi, H. Unconventional s-wave superconductivity in Fe(Se,Te). Science 2010, 328, 474–476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kondo, T.; Santer-Syro, A.F.; Copie, O.; Liu, C.; Tillman, M.E.; Mun, E.D.; Schmalian, J.; Bud’ko, S.L.; Tanatar, M.A.; Canfield, P.C.; et al. Momentum dependence of the superconducting gap in NdFeAsO0.9F0.1 single crystals measured by angle resolved photoemission spectroscopy. Phys. Rev. Lett. 2008, 101, 147003. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Richard, P.; Nakayama, K.; Sugawara, T.; Arakane, T.; Sekiba, Y.; Takayama, A.; Souma, S.; Sato, T.; Takahashi, T.; et al. Observation of Fermi-surface–dependent nodeless superconducting gaps in Ba0.6K0.4Fe2As2. Europhys. Lett. 2008, 83, 47001. [Google Scholar] [CrossRef] [Green Version]
- Okazaki, K.; Ota, Y.; Kotani, Y.; Malaeb, W.; Ishida, Y.; Shimojima, T.; Kiss, T.; Watanabe, S.; Chen, C.-T.; Kihou, K.; et al. Octet-line node structure of superconducting order parameter in KFe2As2. Science 2012, 337, 1314–1317. [Google Scholar] [CrossRef]
- Song, C.-L.; Wang, Y.-L.; Cheng, P.; Jiang, Y.-P.; Li, W.; Zhang, T.; Li, Z.; He, K.; Wang, L.; Jia, J.-F.; et al. Direct observation of nodes and twofold symmetry in FeSe superconductor. Science 2011, 332, 1410–1413. [Google Scholar] [CrossRef] [Green Version]
- Okada, T.; Imai, Y.; Kitagawa, K.; Matsubayashi, K.; Nakajima, M.; Iyo, A.; Uwatoko, Y.; Eisaki, H.; Maeda, A. Superconducting-gap anisotropy of iron pnictides investigated via combinatorial microwave measurements. Sci. Rep. 2020, 10, 7064. [Google Scholar] [CrossRef]
- Baek, S.-H.; Harnagea, L.; Wurmehl, S.; Buchner, B.; Grafe, H.-J. Anomalous superconducting state in LiFeAs implied by the 75As Knight shift measurement. J. Phys. Condens. Matter 2013, 25, 162204. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Urbano, R.R.; Goswami, P.; Tarantini, C.; Lv, B.; Kuhns, P.; Reyes, A.P.; Chu, C.W.; Balicas, L. Anomalous hysteresis as evidence for a magnetic-field-induced chiral superconducting state in LiFeAs. Phys. Rev. B 2013, 87, 024512. [Google Scholar] [CrossRef] [Green Version]
- Biswas, P.K.; Ghosh, S.K.; Zhao, J.Z.; Mayoh, D.A.; Zhigadlo, N.D.; Xu, X.; Baines, C.; Hillier, A.D.; Balakrishnan, G.; Lees, M.R. Chiral singlet superconductivity in the weakly correlated metal LaPt3P. Nat. Commun. 2021, 12, 2504. [Google Scholar] [CrossRef]
- Sigrist, M.; Ueda, K. Phenomenological theory of unconventional superconductivity. Rev. Mod. Phys. 1991, 63, 239–311. [Google Scholar] [CrossRef]
- Volovik, G.E.; Gor’kov, L.P. Superconducting classes in heavy-fermion systems. Sov. Phys. JETP 1985, 61, 843–854. [Google Scholar]
- Anderson, P.W. Structure of “triplet” superconducting energy gaps. Phys. Rev. B. 1984, 30, 4000–4002. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G.; Murav’ev, E.N. Space group approach to the wavefunction of a Cooper pair. J. Phys. Cond. Matter 1992, 4, 3525–3532. [Google Scholar] [CrossRef]
- Yarzhemsky, V.G. Induced representation method in the theory of electron structure and superconductivity. Adv. Math. Phys. 2019, 4873914. [Google Scholar] [CrossRef] [Green Version]
- Sato, M.; Ando, Y. Topological superconductors: A review. Rep. Prog. Phys. 2017, 80, 076501. [Google Scholar] [CrossRef] [Green Version]
- Hamermesh, M. Group Theory and Its Application to Physical Problems; Adison-Wesley: Boston, MA, USA, 1964. [Google Scholar]
- Norman, M.R. The challenge of unconventional superconductivity. Science 2011, 332, 196–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bradley, C.J.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids. Representation Theory of Point Groups and Space Groups; Clarendon: Oxford, UK, 1972. [Google Scholar]
- Mackey, G.W. Symmetric and anti symmetric Kronecker squares and intertwining numbers of induced representations of finite groups. Am. J. Math. 1953, 75, 387–405. [Google Scholar] [CrossRef]
- Bradley, C.J.; Davies, B.L. Kronecker products and symmetrized squares of irreducible representations of space groups. J. Math. Phys. 1970, 11, 1536–1552. [Google Scholar] [CrossRef]
- Micklitz, T.; Norman, M.R. Odd parity and line nodes in nonsymmorphic superconductors. Phys. Rev. B 2009, 80, 100506R. [Google Scholar] [CrossRef] [Green Version]
- Yarzhemsky, V.G.; Izotov, A.D.; Izotova, V.O. Structure of the order parameter in iron pnictide-based superconducting materials. Inorg. Mater. 2017, 53, 923–929. [Google Scholar] [CrossRef]
- Kovalev, O.V. Irreducible Representations of the Crystallographic Space Groups: Irreducible Representations, Induced Representations and Corepresentations; Gordon & Breach: New York, NY, USA, 1993. [Google Scholar]
- Kobayashi, S.; Shiozaki, K.; Tanaka, Y.; Sato, M. Topological Blount’s theorem of odd-parity superconductors. Phys. Rev. B 2014, 90, 024516. [Google Scholar] [CrossRef] [Green Version]
- Yarzhemsky, V.G. Nodal quantum numbers for two-electron states in solids. Few-Body Syst. 2012, 53, 499–504. [Google Scholar] [CrossRef]
- Tanaka, Y.; Sato, M.; Nagaosa, N. Symmetry and topology in superconductors–odd-frequency pairing and edge states. J. Phys. Soc. Jpn. 2012, 81, 011013. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).