Abstract
The spread of a computer virus among the Internet of Things (IoT) devices can be modeled as an Epidemic Containment (EC) game, where each owner decides the strategy, e.g., installing anti-virus software, to maximize his utility against the susceptible-infected-susceptible (SIS) model of the epidemics on graphs. The EC game’s canonical solution concepts are the Minimum/Maximum Nash Equilibria (MinNE/MaxNE). However, computing the exact MinNE/MaxNE is NP-hard, and only several heuristic algorithms are proposed to approximate the MinNE/MaxNE. To calculate the exact MinNE/MaxNE, we provide a thorough analysis of some special graphs and propose scalable and exact algorithms for general graphs. Especially, our contributions are four-fold. First, we analytically give the MinNE/MaxNE for EC on special graphs based on spectral radius. Second, we provide an integer linear programming formulation (ILP) to determine MinNE/MaxNE for the general graphs with the small epidemic threshold. Third, we propose a branch-and-bound (BnB) framework to compute the exact MinNE/MaxNE in the general graphs with several heuristic methods to branch the variables. Fourth, we adopt NetShiled (NetS) method to approximate the MinNE to improve the scalability. Extensive experiments demonstrate that our BnB algorithm can outperform the naive enumeration method in scalability, and the NetS can improve the scalability significantly and outperform the previous heuristic method in solution quality.
1. Introduction
Diffusion processes in small networks can model the explosive spread of computer viruses (e.g., WananCry ransomware 2017 [1]) in an IoT network or Cyber–Physical Systems (CPS) network. Efficient investment (secure firewall, etc.) can contain the spread of such adverse events, which involves a specific cost for individuals. Most owners of a device prefer to benefit from their neighbors as their security depends on the strategies of the entire population. These dilemmas with the following properties can be modeled as Interdependent Security (IDS) games: (1) a bad event happens suddenly within a population of devices, whose security depends on the entire population; (2) individuals can reduce these risks by the investment [2].
Researches propose many models in this area [3,4,5,6]. A large part of models involve individual utility functions that are difficult to compute, and some models cannot be extended to heterogeneous networks, which are not close to realistic scenarios. Thus, Saha et al. [7] used the characterization of spectral radius to simplify the utility function, and present a general dynamics SIS model for arbitrary graphs as an Epidemic Containment (EC) game. When an epidemic dies out in an EC game, every individual prefers not to change its strategy under a Nash Equilibrium (NE).
The study of computing equilibria is challenging. Minimum Nash Equilibria (MinNE) and Maximum Nash Equilibria (MaxNE) are essential parts of understanding NE. Several algorithms can be used to find MinNE/MaxNE for the EC game. High Degree (HDG) and Low Degree (LDG) are heuristic algorithms for MinNE and MaxNE, respectively [7]. They generate the strategy in a degree order, which will pick a node that does not belong to any secured node set of MinNE/MaxNE, leading to a big loss with the exact solution. Neighbors Information (NI) [8] is a heuristic MaxNE algorithm which performs better. NI decides with too much information: information of nodes, strategy of their neighborhood, and spectral radius of networks. On the one hand, the algorithms mentioned above perform poorly, as shown in Section 3. On the other hand, big complex networks are hard to estimate NE cost. Thus, company managers are interested in the small networks in which LDG/HDG/NI cannot give the exact MinNE/MaxNE.
To fill this gap, we provide a thorough analysis of some special graphs and propose exact and scalable algorithms for general graphs, and our contributions are four-fold. First, we give the MinNE/MaxNE for EC on special graphs based on spectral radius. For several important classes of network topologies (star-shaped graphs, complete graphs, and path graphs), MinNE and MaxNE are equal in most cases. Second, we provide an integer linear programming formulation (ILP) to compute MinNE/MaxNE for the general graphs with the small epidemic threshold. Third, we propose a Branch-and-Bound (BnB) framework to compute the exact MinNE/MaxNE in the general graphs with several heuristic methods to branch the variables. We speed up the search with information of degree, reduction of spectral radius, and neighborhood of nodes. We also adopt the NetShiled (NetS) method to approximate the MinNE to improve the scalability. Fourth, we test our methods empirically by comparing our algorithms with the enumeration method on a random tree, Erdoős–Rényi (ER) random networks, and Barabási–Albert (BA) scale-free networks, and extensive experiments demonstrate that our algorithm framework can outperform the naive enumeration method in scalability. The NetS algorithm can improve the scalability significantly and outperform previous heuristic method in solution quality.
2. Related Work
Security game is a game-theoretic model that captures essential characteristics of decision making to protect and self-insure resources within a network [9]. Kumar et al. [10] limit the amount of graph information needed in the utility function, and consider decisions restricted to the graph induced by nodes within a distance. Jiang et al. [11] consider a network security game where the utility function determine by a weighted topology which represents the positive externality between players. The utility function in the EC game also involves a global quantity in the form of the spectral radius, which can be a good proxy for estimating this cost from the characterization of Ganesh et al. [6]. Secure problems (infection, computer virus, etc.) with interdependent actions can formulate as Interdependent Security (IDS) games [12,13]. Kunreuther et al. [14] mainly focus on the IDS game limited to the simple case of two agents. Moreover, general IDS model makes decisions on the one-hop strategy limiting the information as a system. Aspnes et al. [5] give an inoculation game model, which is a propagation-based IDS assuming a restricted network topology. In this study, the infected individual will infect all its neighbors. In the EC game, the individual is cured with a fixed rate. It is more closely to the spread of epidemics in real life.
In the domain of immunization algorithm, Briesemeister et al. [15] give the random wiring immunization, which is typically overwhelmed on power-law graphs. Madar et al. [16] present an “acquaintance” immunization policy that picks a random person and immunizes one random neighbor. The analytical result shows that it is better than several immunization policies for scale-free graphs. Chen et al. [17] give an approximate algorithm (NetShiled) to immunize the top k node, using matrix perturbation theory to approximate the drop of the spectral radius. Some similar works also focus on an efficient vaccination algorithm without considering NE structure [18,19]. To find NE in EC game, High Degree (HDG) and Low Degree (LDG) [7] give a rough approximation for MinNE and MaxNE by picking nodes in degree orders and checking in reverse degree orders, respectively. Xu et al. [8] find that LDG performs poorly with small network scope, and gives a heuristic algorithm with neighbors’ degree and strategy. Saha et al. [20] propose GreedyWalk, which reduces the spectral radius by reducing the number of closed walks of length k. It spends too much time to determine the closed walks. However, all the works cannot give exact MinNE/MaxNE even in small networks.
3. Preliminaries
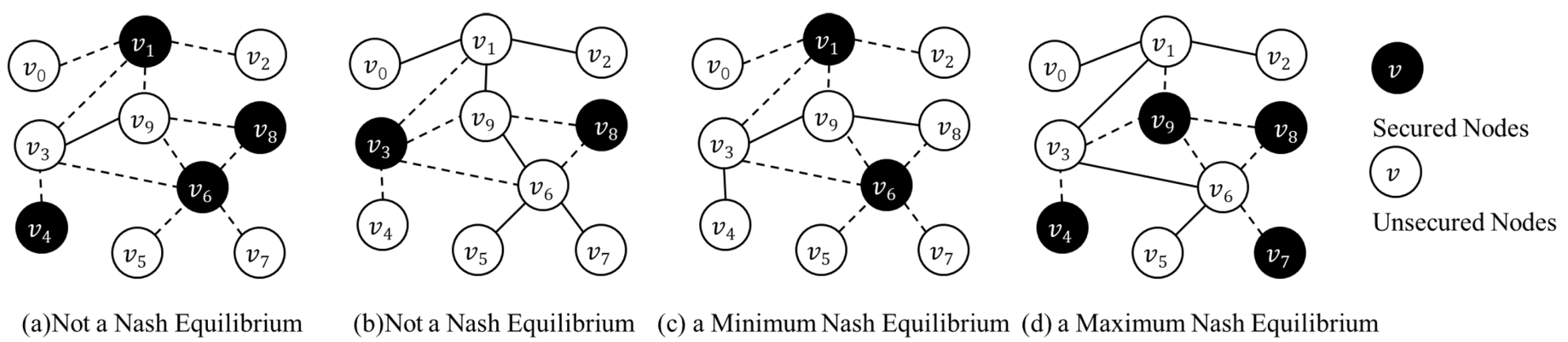
The Epidemic Containment (EC) game [7] is based on an undirected graph with the node set V and the edges set E. We use i as the index of the node, , . The neighbor set is denoted by and denotes the the adjacency matrix of G. An example of an Epidemic Containment (EC) game can be shown in Figure 1.
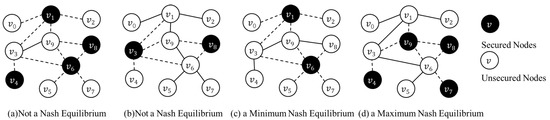
Figure 1.
An Example of an Epidemic Containment (EC) game , . (a) One kind of non-Nash Equilibria (NE) where but when some nodes change their strategies it still has , , . The spectral radius is determined by and , , . If node 8 switches its strategy from to , reducing cost from to , we get and . Now that and epidemic still dies out, is not NE. (b) Another kind of non-Nash Equilibria in which epidemic will spread around. (c) A Minimum Nash Equilibria with . If nodes 1 or 6 change their strategy, the epidemic spreads out. In addition, it is safe for the rest graph immunized from the secured node. We cannot find another NE strategy with a cost lower than . (d) A Maximum Nash Equilibria with , . No node can benefit from changing its strategy and there is no strategy with a cost bigger than .
Epidemic Model. We choose a spectral characterized susceptible-infected-susceptible (SIS, developed by Ganesh et al. [6]) model as epidemic model. In the SIS model, nodes are in states susceptible (S) or infected (I). Initially, some source nodes get infected, and all other nodes are susceptible. Each infected node i infects each of its neighbors j currently in state S at a transmission rate ; if neighbor j gets infected, it switches to state I. Each infected node i switches back to state S at rate . An epidemic dies out soon if , where is the spectral radius of the contact graph G or the largest eigenvalue of the . We define as the threshold which is smaller than , and implies the epidemic lasts long [7,21].
Game Model. Let denote the discrete strategy selected by the node i independently, whether to become secured (denoted by ) or not (denoted by ). denotes the strategy profile of all the nodes. We use to denote the strategy profile of the players other than node i. denotes secured node set with the strategy profile , and the graph induced by the set of unsecured nodes called attack graph. represents the unique connected component of that contains node i. A node will incur a cost (the cost for a vaccination), if node i chooses to be secured, i.e., . If node i is not secured, i.e., , it probably gets infected, and its cost depends on whether or not the epidemic dies out quickly in the connected component induced by the unsecured nodes. If , node i merely bears a cost (the cost of secured by its neighbor); if , node i in the susceptible state will suffer the cost (the cost of recovery, ). Given the strategy profile , the cost of each node is described as below:
is the cost of strategy . Nash Equilibrium is defined as below:
Definition 1.
For a strategy profile , , we have in which is the alternative strategy for node i and . The strategy profile is Nash Equilibrium (NE) in EC game if and only if , .
In an NE, node i cannot benefit by changing its strategy, given that is fixed [7]. If is NE, is the cost of Minimum Nash Equilibria (MinNE), and is the cost of Maximum Nash Equilibria (MaxNE). There is an example of EC game under . An instance of EC game can be defined as a tuple . For the rest of the paper, we will focus on instances where , and . Computing the Minimum Nash Equilibria (MinNE) is NP-complete [7]. We can prove complexity of Maximum Nash Equilibria (MaxNE) is NP-complete in the same way.
Lemma 1.
Finding the Maximum Nash Equilibria of an EC game is NP-complete.
Proof.
To prove this statement, we reduce the problem of finding vertex cover to this problem. Let and be two general instances of the two problems defined as follows: (1) : Given a graph , is there a vertex cover set of size or less? (2) : Given the EC game , is there a configuration with social cost P or less? We reduce to as follows: set , , where is arbitrarily close to 0, set , , choose such that and set . Clearly, the reduction takes polynomial time. Now we show this is a valid reduction. If there is a vertex cover set of size , then corresponds to a secured node set of yielding social cost . As a result that removing the vertex cover set, by definition, leaves no edge in the graph and so, the spectral radius of the attack graph is 0 which is less than . Therefore, all the unsecured nodes incur zero cost and NE cost is . On the other hand, if there is a secured node set of cardinality , and NE cost in , that means removing from G, leaves no edge in the graph. By definition, is a vertex cover to G of size P. Therefore, this is a valid polynomial time reduction and finding the corresponding social cost with P in EC game is NP complete. Set in a decreasing order, the first answer for is the MaxNE for the corresponding . □
4. Counterexample for HDG/LDG/NI
ITERATIVESECURE (IS) [7] is a method to generate an NE for the EC game with two nodes permutations and . HDG/LDG/NI [7,8] is based on ITERATIVESECURE and designed to obtain approximate MinNE or MaxNE for the EC game. According to nodes permutation in V, ITERATIVESECURE produces a secured node set S, and ends with , . Then, ITERATIVESECURE checks every node in set S by a nodes permutation in V. If node changes its strategy , delete the node from S. Permutation of nodes and in HDG are non-increasing and non-decreasing degree orders. LDG is also based on ITERITERATIVESECURE [7], permutation and are non-decreasing and non-increasing degree orders. In NI, permutation and are non-decreasing and non-increasing score orders. They have similar disadvantages: (1) pick a node too early but fail to delete it from the S (e.g., node 4 in Figure 2a); (2) fail to reach a node in permutation which is necessary for NE (e.g., node 4 in Figure 2c); (3) confuse the nodes with the same property (degree, reduction of spectral radius, etc.). Thus, previous algorithms cannot give the exact MinNE/MaxNE even in small networks, and we propose some algorithms to find exact MinNE/MaxNE.

Figure 2.
A network for EC game with , . (a) High Degree (HDG) picks nodes in non-increasing degree order with permutation , and check nodes with permutation . (a) HDG gets an NE with as MinNE, when exact MinNE (b) is with . (c) Low Degree (LDG) picks nodes in non-decreasing degree order with permutation , and check nodes with permutation . LDG gets an NE with as MinNE, NI (d) gets an NE with , when exact MaxNE (e) is with .
5. Approach to Find Nash Equilibria for Special Networks
In this section, we explore the NE based on characters of spectral radius for three network typologies: star-shaped graphs, complete graphs, and path graphs. Given the threshold T and a specific graph, we can give a strategy and find that MinNE/MaxNE are equal in some cases.
5.1. Star-Shaped Networks
The spreading on a large amount of power-law graphs is often determined by the spreading on the star-shaped subgraphs [6]. A star-shaped graph is a graph with N nodes where the only edges are , . The spectral radius of a star-shaped graph is [6]. Node has the same structure. When and , nodes around node 0 getting secured can reach an NE and . However, for , we have to immunize node 0 and to immunize the other nodes, respectively.
5.2. Complete Graph
The complete graph also plays a prominent role in networks. For example, the BGP routers, belonging to the Internet’s top-level autonomous systems, form an utterly connected component [6]. A complete graph is a connected graph with N vertices where all vertices are of degree . When the network is a complete graph, we have spectral radius [22]. A complete graph is a homogeneous network, and every node has the same importance to getting secured. No node needs to be secured under . For , we can reach NE by randomly picking nodes to immunize, .
5.3. Path Graphs
Paths graphs are simple and often crucial in their role as subgraphs of other graphs. A path graph is a graph whose vertices can be listed in the order such that the edges are where . The spectral radius of a path graph is [23]. A path graph has 2 pendant nodes and the other nodes of degree 2 which have similar importance. When , MinNE immunize last node every nodes, . Under this threshold, MaxNE immunize two nodes every nodes in a fixed order, .
6. Approach to Find Nash Equilibria for Small Threshold
We obtain MinNE/MaxNE structure based on the threshold for specific network topology. We find that it is a minimum vertex cover problem in the case () to finding MinNE. We extend integer linear programming formulation to finding MinNE/MaxNE in threshold , and .
6.1. MinNE/MaxNE for
When , it is a minimum vertex cover problem to finding MinNE. We can compute MaxNE by adding a constraint of neighborhood number. Every node is isolated from each other under this threshold, and spectral radius of graph is 0.
Proposition 1.
When threshold is small (), a strategy profile is NE that every node is isolated from each other.
Proof.
Every edge with two unsecured nodes () gets . Strategy is not an NE in which epidemic lasts long. In other words, every edge has at least one node immune to decline the . □
For a minimum vertex cover problem, MinNE can be formulated as Equation (2) according to Proposition 1. ensures Proposition 1 that every edge can immunize one node or two nodes.
6.2. MinNE/MaxNE for
For , we extend the integer linear programming formulation for MinNE/MaxNE from . The maximum connected component in the graph is an edge with two nodes, and spectral radius of graph is 1 in this situation.
Proposition 2.
When a strategy profile is an NE under , the maximum connected component in is a line with two unsecured nodes assuming G has at least one edge.
Proof.
Edge with two unsecured nodes () gets . For , maximum connected component in is three nodes with two edges , and epidemic lasts long. Hence, has maximum connected component containing no more than three nodes. On the other hand, has a edge with one secured end node i, , , . Node i can change its strategy that . Therefore, is NE, the maximum connected component in is a edge. □
Secured nodes consider to minimize the cost for MinNE. Every susceptible node i has at most one susceptible neighbor node j, , . Equation (4b) ensures the maximum connected component in the graph is one edge with two unsecured nodes according to Proposition 2.
7. Approach to Find Nash Equilibria for General Networks
To solve MinNE/MaxNE for the general networks, we first propose an enumeration method to solve the problem. Enumeration becomes time-consuming as node number increasing. We propose a Branch-and-Bound (BnB) algorithm to tackle it with several ways to improve searching speed and scalability. Our BnB speed up the search in degree order, reduction of spectral radius, and neighborhood information. Finally, NetS improves the scalability of our algorithm framework for approximation.
7.1. Enumeration
Enumeration (Enum) is brute force algorithm to find all the MaxNE/MinNE and helps visualizing the structure when the network is small. Let denote strategy with the strategy index B, which satisfies that , .
Here we merely give the Enum (Algorithm 1) to find all MaxNE. In step 1, Enum calculates all the , index of , and corresponding spectral radius and cost . In steps 2–4, Enum finds all the MaxNE with specific threshold T according to the definition of NE. Finding MinNE is to change the judging criterion in step 2 and record the cost of MinNE instead.
| Algorithm 1: Enum. |
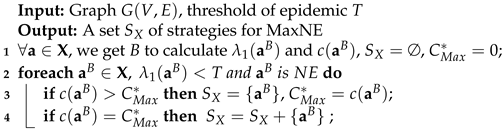 |
7.2. Branch-and-Bound
We develop an efficient Branch-and-Bound (BnB) algorithm (Algorithm 2) to search the exact MinNE/MaxNE in strategy profile space ().
Branch. For every node at level i (according to nodes permutation ) of the search tree, we have a corresponding pair , , . At every node , the tree is expanded by performing a branching operation. Two nodes are introduced: a left node where and a right node where . The check of NE in leaves is irreplaceable, and original BnB uses a random nodes permutation . We can choose an order to search the tree (node permutation ). In this way, it is possible to find a MinNE earlier. We proposed BnB-D/BnB-E/BnB-N from three different perspectives and speed up the pruning.
| Algorithm 2: Branch-and-Bound for MinNE. |
 |
(i) Degree order: Immunizing large degree nodes helps BnB find MinNE more quickly. For BnB-D, we use a non-increasing degree order permutation , .
(ii) Reduction of spectral radius: In our model, we compare spectral radius with threshold to determine epidemic dies out or not. Therefore, reducing spectral radius seems to be efficient to control epidemic. We adopt BnB-E based on drop of spectral radius orders, , node i is only node secured in . We have permutation , .
(iii) Neighborhood information: We find that secured node i will bring benefit for its neighborhood, i.e., its neighbor is more likely to not vaccinate. The BnB-N searches in nodes permutation that there are node and its adjacent node , . We have permutation that edge ,.
Bound. BnB keeps track of bounds by two constraints. One is lower bound: the cost of current should be less than , assuming all the rest nodes choose , . The other is upper bound: epidemic should not spread out even all the rest nodes choose to immunize themselves , , . Only if the search reaches the leaves (all nodes have their strategy) can we check the strategy is an NE with less cost .
In step 1, BnB (Algorithm 2) uses HDG [7] to get the upper bound of MinNE based on the breadth-first search (BFS). In steps 4–8, as every node has its strategy, BnB checks if is a MinNE. In 10–13, BnB checks the upper bound and lower bound of node i and decides to bound it or not. In 15–16, BnB changes searching nodes from left nodes to the right nodes and right nodes to its parent node. When the searching process finished, strategy is a MinNE.
7.3. NetShiled (NetS)
Finding a MinNE in the EC game can be divided into two steps:(1) finding an optimal set or permutation of nodes whose removal would maximally reduce the spectral radius of the network; (2) checking the set of the immunized nodes to NE for EC game.
For the first step, we can find the key nodes by circulating the drop of eigenvalue when deleting the set of nodes S from the original graph G, . As the size of nodes increases, computing the drop of eigenvalue is more difficult.
The NetShield [17] uses Shield-value score to precisely approximate the drop of eigenvalue by matrix perturbation theory. The original NetShield merely finds k nodes to immunize without taking equilibria into consideration. Therefore, we extend NetShield with ITERATIVESECURE to change strategy generated into equilibrium, called NetS (Algorithm 3). Let bold upper cases represent matrices, e.g., , . Bold lower cases stand for column vectors respectively, e.g., , . Let denotes the ith eigenvector for matrix . Let denotes the ith row of matrix , and the jth column of matrix . denotes the matrix of which contains columns in node set S. Shield-value score is defined as:
We also have Equation (7b) justifying the precision of . Algorithm 3 computes the largest eigenvalue and the corresponding eigenvector in steps 1–2. In step 4, the value measures the Shield-value score of each individual node. Then, in each iteration of steps 6–11, NetS greedily select one more node and add it into set S according to (step 10), generating the permutation until . Note that steps 11–12 are to exclude those nodes that are already in the selected set S. Step 11 makes sure that strategy with immunization of S is an NE. The time complexity of Algorithm 3 is .
| Algorithm 3: NetS. |
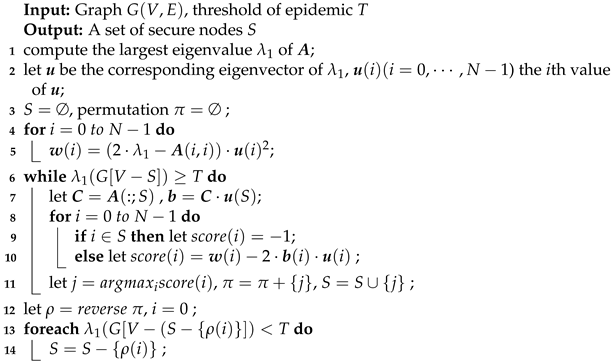 |
8. Empirical Results
We evaluate the performance of our approach through extensive experiments. We use CPLEX (version 12.9) to solve all integer linear programs (ILP). All computations are performed on a PC with a 2.60 GHz quad-core CPU and 16.00 GB memory. All values averaged over 40 instances unless otherwise specified. We conduct experiments on three types of graph structures which widely used to model connections between population: (i) Random trees (RT), where every new node is attached to a randomly picked incumbent; (ii) Barabási–Albert scale-free model, which is denoted by BA(m) where m represents the average node degree; (iii) Erdős–Rényi random graphs, which is denoted by ER(p) where p represents the existence probability of an edge between any pair of nodes [24]. We use BA scale-free networks with parameters , and use ER random graphs with parameters .
We compare the scalability and optimality of four versions of algorithms: (i) ILP: integer linear programming for small threshold (); (ii) BnB: branch and bound algorithm with random searching permutation; (iii) BnB-D/BnB-E/BnB-N: BnB algorithm which searches with permutation base on the degree of nodes, eigenvalues drop of nodes and neighborhood information of nodes; (iv) NetS: heuristic algorithm which generates NE by a node permutation according to the drop of eigenvalue. We use Enum as a benchmark for exact solution, HDG as benchmark for approximation. The HDG algorithm is a heuristic algorithm that obtained MinNE by running the IS procedure with and permutations of nodes in non-increasing and non-decreasing degree orders.
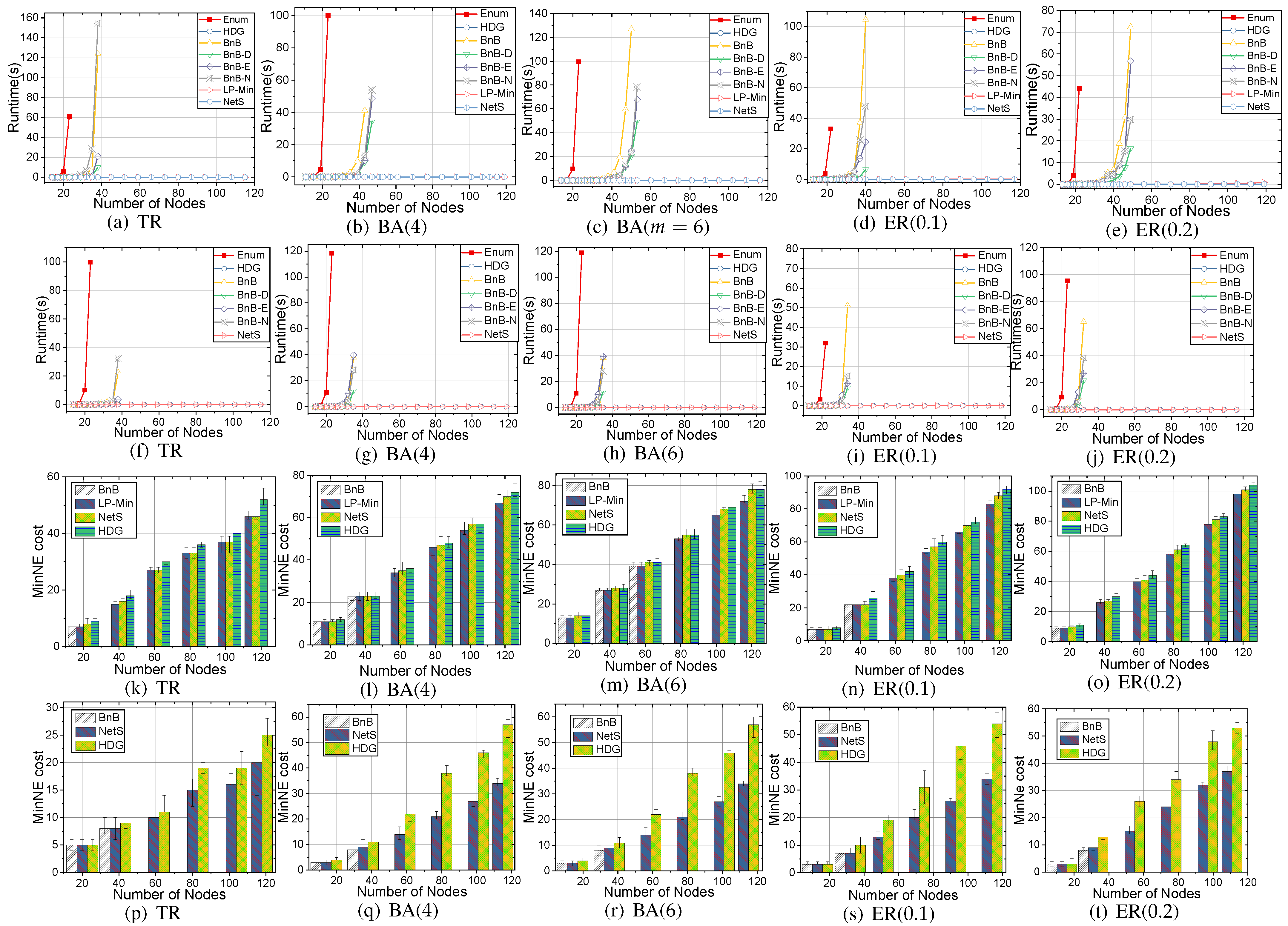
Runtime. In Figure 3a–e,f–j, we compare the scalability of the proposed algorithms on 5 types of networks under and , respectively. For small threshold (), ILP performs as fast as the heuristic algorithms. BnB-D/BnB-E/BnB-N are shown to improve the searching speed. BnB-D is better than BnB-E/BnB-N in BA scale-free network, and degree heterogeneity turns out to be extremely useful in searching. NetS extends the scalability of the algorithm as node size is increasing.
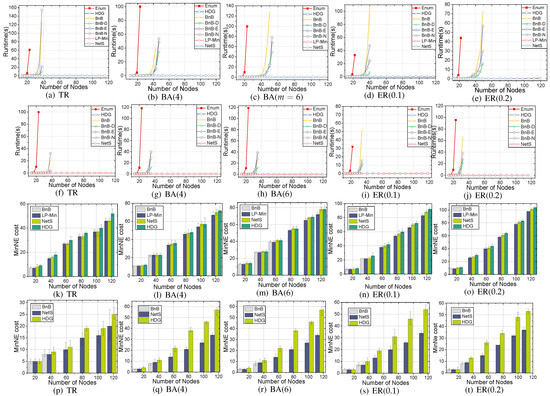
Figure 3.
Scalability: (a–e), T = 1.0; (f–j), T = 0.5λ1. Optimality: (k–o), T = 1.0; (p–t), T = 0.5λ1.
Solution Quality. We compare the cost of MinNE with HDG as the benchmark. The results are illustrated in Figure 3k–t, Enum/ILP/BnB give the exact NE. BnB-D works well under the small threshold and sparse network structure like the TR graph. NetS gives a near-optimal performance and outperforms HDG, especially under the larger threshold.
9. Conclusions and Future Research
This paper focuses on exploring the Nash Equilibria in Epidemic Containment game, representing the spread of epidemics among interdependent users. As the most practical EC game application scenarios are IoT networks, we find that the previous algorithms (HDG/LDG/NI) cannot give exact MinNE/MaxNE in small networks.
To study the structure of exact NE, this paper first explores the network typologies’ spectral radius. We can give the strategy directly for star-shaped graphs, complete graphs, and path graphs. By observing a single node’s degree information, we propose linear programming formulations to finding the exact MinNE/MaxNE in threshold as quick as heuristic algorithms. Secondly, we develop an efficient Branch-and-Bound (BnB) algorithm branching with the degree information to speed up the research. To extend the algorithm’s scalability, we propose the NetS which approximates the spectral radius’s drop. This algorithm extremely outperforms HDG to find MinNE in larger Barabási–Albert and Erdős–Rényi random graphs. The following inspirations can be obtained from the experiment results: heterogeneity of degree and spectral radius turn out to be extremely useful for extracting information from nodes. However, our research is limited to artificial networks, and we get more information on the real-world networks, e.g., AS (Oregon-1), P2P (Gnutella-6) [19,25], which can help us extend our experiments to more realistic scenarios in the following researches.
In the future work, we would consider Stackelberg strategies to reduce MaxNE, a more realistic scenario. Combining IDS gaming security and data security concepts, we can also extend EC game on the relevant relationship networks with different granularity levels [26,27].
Author Contributions
J.Z., H.D., Y.T., Z.W., and L.Y. wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Zhejiang Provincial Natural Science Foundation of China under Grant Nos. LQY19G030001 and LY20F0300.
Institutional Review Board Statement.
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used during the study are available from the corresponding author.
Acknowledgments
The authors like to appreciate the referee for their valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, M.S.; Ben-Othman, J.; Srinivasagan, K.G. An Investigation on Wannacry Ransomware and its Detection. In Proceedings of the IEEE ISCC 2018, Natal, Brazil, 25–28 June 2018; pp. 1–6. [Google Scholar]
- Heal, G.; Kunreuther, H. Interdependent Security: A General Model; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 2004. [Google Scholar]
- Omic, J.; Orda, A.; Van Mieghem, P. Protecting against network infections: A game theoretic perspective. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1485–1493. [Google Scholar]
- Lelarge, M.; Bolot, J. A local mean field analysis of security investments in networks. In Proceedings of the 3rd International Workshop on Economics of Networked Systems, Seattle, WA, USA, 22 August 2008; pp. 25–30. [Google Scholar]
- Aspnes, J.; Chang, K.; Yampolskiy, A. Inoculation strategies for victims of viruses and the sum-of-squares partition problem. J. Comput. Syst. Sci. 2006, 72, 1077–1093. [Google Scholar] [CrossRef]
- Ganesh, A.; Massoulié, L.; Towsley, D. The effect of network topology on the spread of epidemics. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 2, pp. 1455–1466. [Google Scholar]
- Saha, S.; Adiga, A.; Vullikanti, A.K.S. Equilibria in epidemic containment games. In Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, Quebec City, QC, Canada, 27–31 July 2014. [Google Scholar]
- Xu, J.H.; Wang, Z.; Cui, G.H.; Ren, Y.Z.; Ding, H.; Choo, K.K.R. An Extended Exploration to the Epidemic Containment Game. In Proceedings of the 2018 27th International Conference on Computer Communication and Networks (ICCCN), Hangzhou, China, 30 July–2 August 2018; pp. 1–7. [Google Scholar]
- Grossklags, J.; Christin, N.; Chuang, J. Secure or insure: A game-theoretic analysis of information security games. In Proceedings of the 17th International Conference on World Wide Web, Beijing, China, 1 April 2008; pp. 209–218. [Google Scholar]
- Kumar, V.A.; Rajaraman, R.; Sun, Z.; Sundaram, R. Existence Theorems and Approximation Algorithms for Generalized Network Security Games. In Proceedings of the 2010 IEEE 30th International Conference on Distributed Computing Systems, Genova, Italy, 21–25 June 2010; pp. 348–357. [Google Scholar]
- Jiang, L.; Anantharam, V.; Walrand, J. Efficiency of selfish investments in network security. In Proceedings of the 3rd International Workshop on Economics of Networked Systems, Seattle, WA, USA, 22 August 2008; pp. 31–36. [Google Scholar]
- Kearns, M.; Ortiz, L.E. Algorithms for interdependent security games. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004; pp. 561–568. [Google Scholar]
- Heal, G.; Kunreuther, H. IDS models of airline security. J. Confl. Resolut. 2005, 49, 201–217. [Google Scholar] [CrossRef]
- Kunreuther, H.; Heal, G. Interdependent security. J. Risk Uncertain. 2003, 26, 231–249. [Google Scholar] [CrossRef]
- Briesemeister, L.; Lincoln, P.; Porras, P. Epidemic profiles and defense of scale-free networks. In Proceedings of the 2003 ACM workshop on Rapid Malcode, Washington, DC, USA, 27 October 2003; pp. 67–75. [Google Scholar]
- Madar, N.; Kalisky, T.; Cohen, R.; Ben-avraham, D.; Havlin, S. Immunization and epidemic dynamics in complex networks. Eur. Phys. J. B 2004, 38, 269–276. [Google Scholar] [CrossRef]
- Chen, C.; Tong, H.; Prakash, B.A.; Tsourakakis, C.E.; Eliassi-Rad, T.; Faloutsos, C.; Chau, D.H. Node immunization on large graphs: Theory and algorithms. IEEE Trans. Knowl. Data Eng. 2015, 28, 113–126. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Y.; Yang, S. Efficient influence maximization in social networks. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; pp. 199–208. [Google Scholar]
- Van Mieghem, P.; Stevanović, D.; Kuipers, F.; Li, C.; Van De Bovenkamp, R.; Liu, D.; Wang, H. Decreasing the spectral radius of a graph by link removals. Phys. Rev. E 2011, 84, 016101. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.; Adiga, A.; Prakash, B.A.; Vullikanti, A.K.S. Approximation algorithms for reducing the spectral radius to control epidemic spread. In Proceedings of the 2015 SIAM International Conference on Data Mining, Vancouver, BC, Canada, 30 April–2 May 2015; pp. 568–576. [Google Scholar]
- Chakrabarti, D.; Wang, Y.; Wang, C.; Leskovec, J.; Faloutsos, C. Epidemic thresholds in real networks. ACM Trans. Inf. Syst. Secur. (TISSEC) 2008, 10, 1–26. [Google Scholar] [CrossRef]
- Godsil, C.; Royle, G.F. Algebraic Graph Theory; Springer Science & Business Media: Berlin, Germany, 2013; Volume 207. [Google Scholar]
- Cvetkovic, D.; Simic, S.; Rowlinson, P. An Introduction to the Theory of Graph Spectra; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- ERDdS, P.; R&wi, A. On random graphs i. Publ. Math. Debrecen 1959, 6, 18. [Google Scholar]
- Opsahl, T.; Panzarasa, P. Clustering in weighted networks. Soc. Netw. 2009, 31, 155–163. [Google Scholar] [CrossRef]
- Kayes, A.; Han, J.; Colman, A.; Islam, M.S. RelBOSS: A relationship-aware access control framework for software services. In OTM Confederated International Conferences “On the Move to Meaningful Internet Systems”; Springer: Berlin, Germany, 2014; pp. 258–276. [Google Scholar]
- Kayes, A.; Rahayu, W.; Watters, P.; Alazab, M.; Dillon, T.; Chang, E. Achieving security scalability and flexibility using Fog-Based Context-Aware Access Control. Future Gener. Comput. Syst. 2020, 107, 307–323. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).