Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry
Abstract
1. Introduction
2. Nonlinear Modeling for Multi-Converter Infeed System
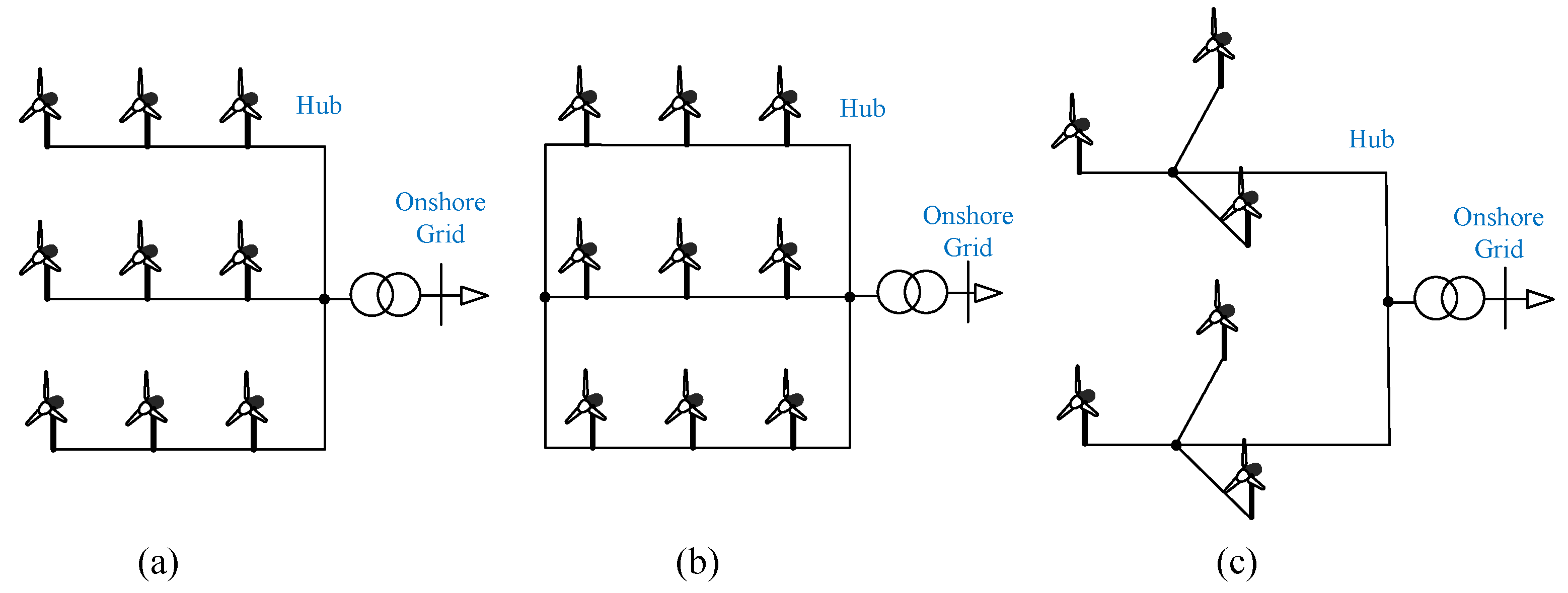
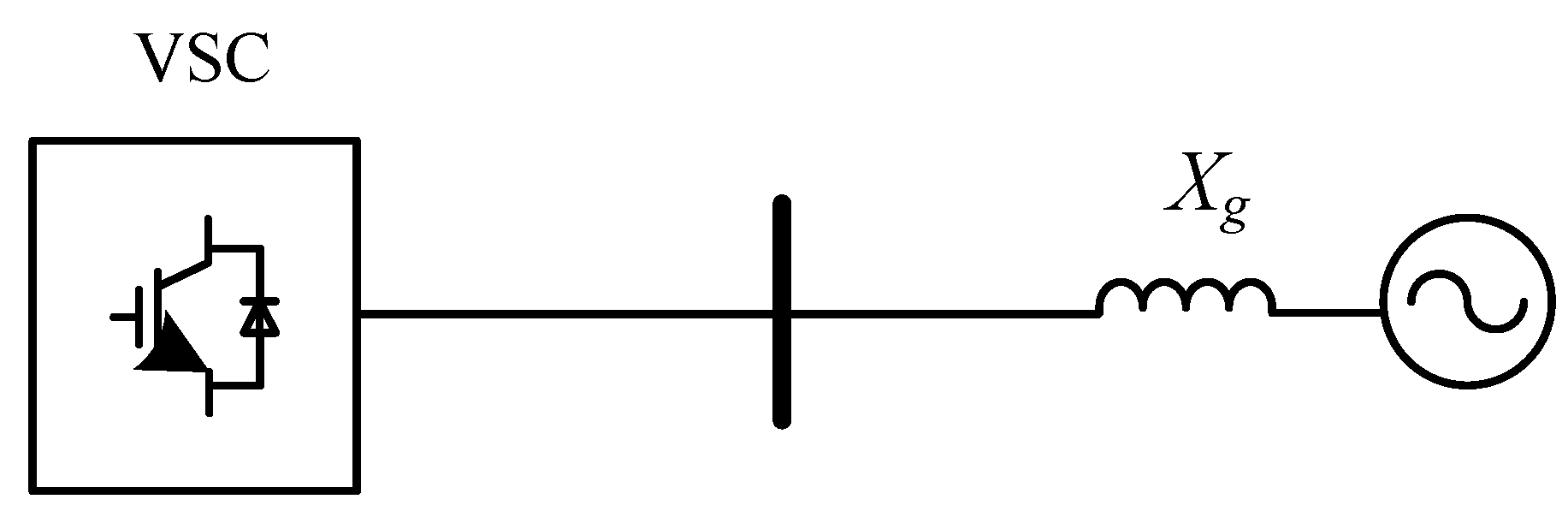
2.1. System Overview
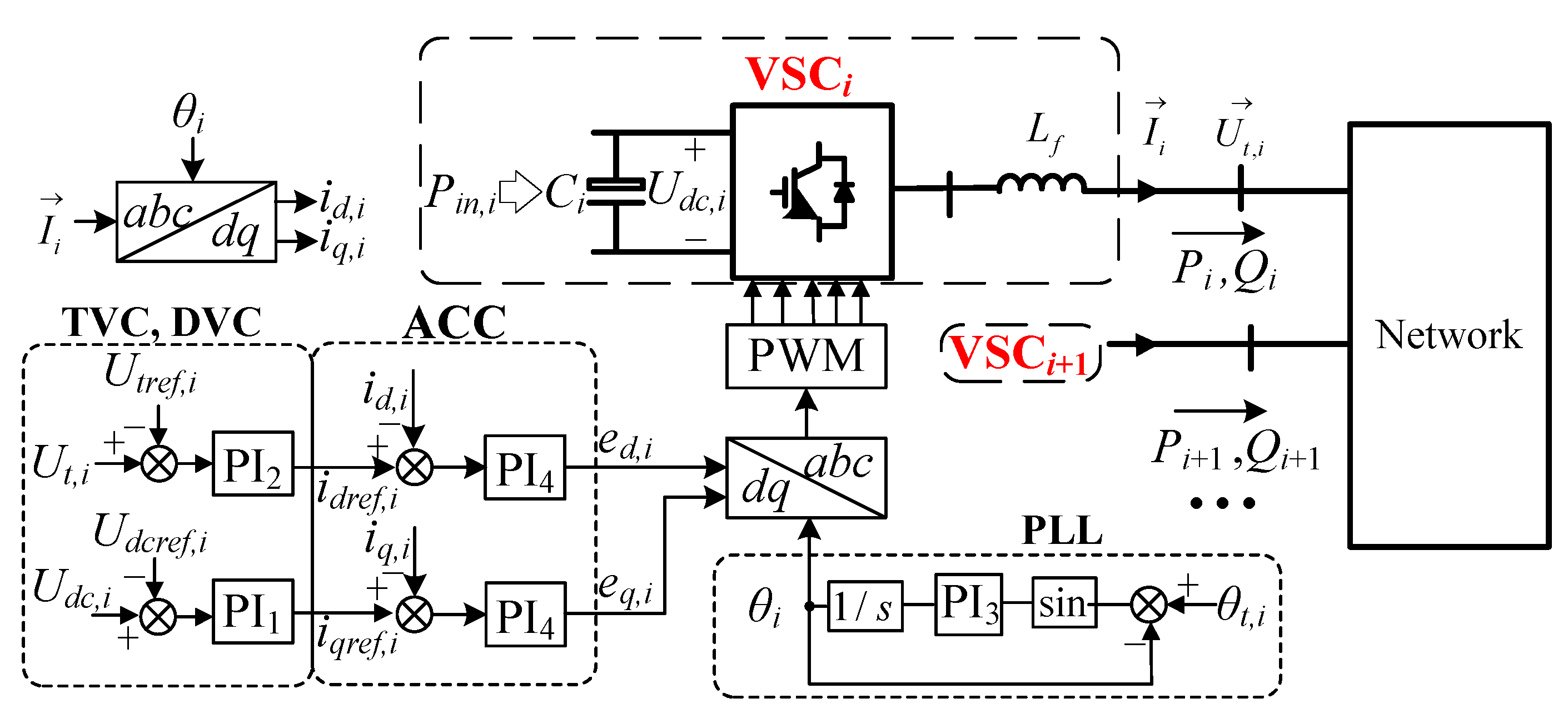
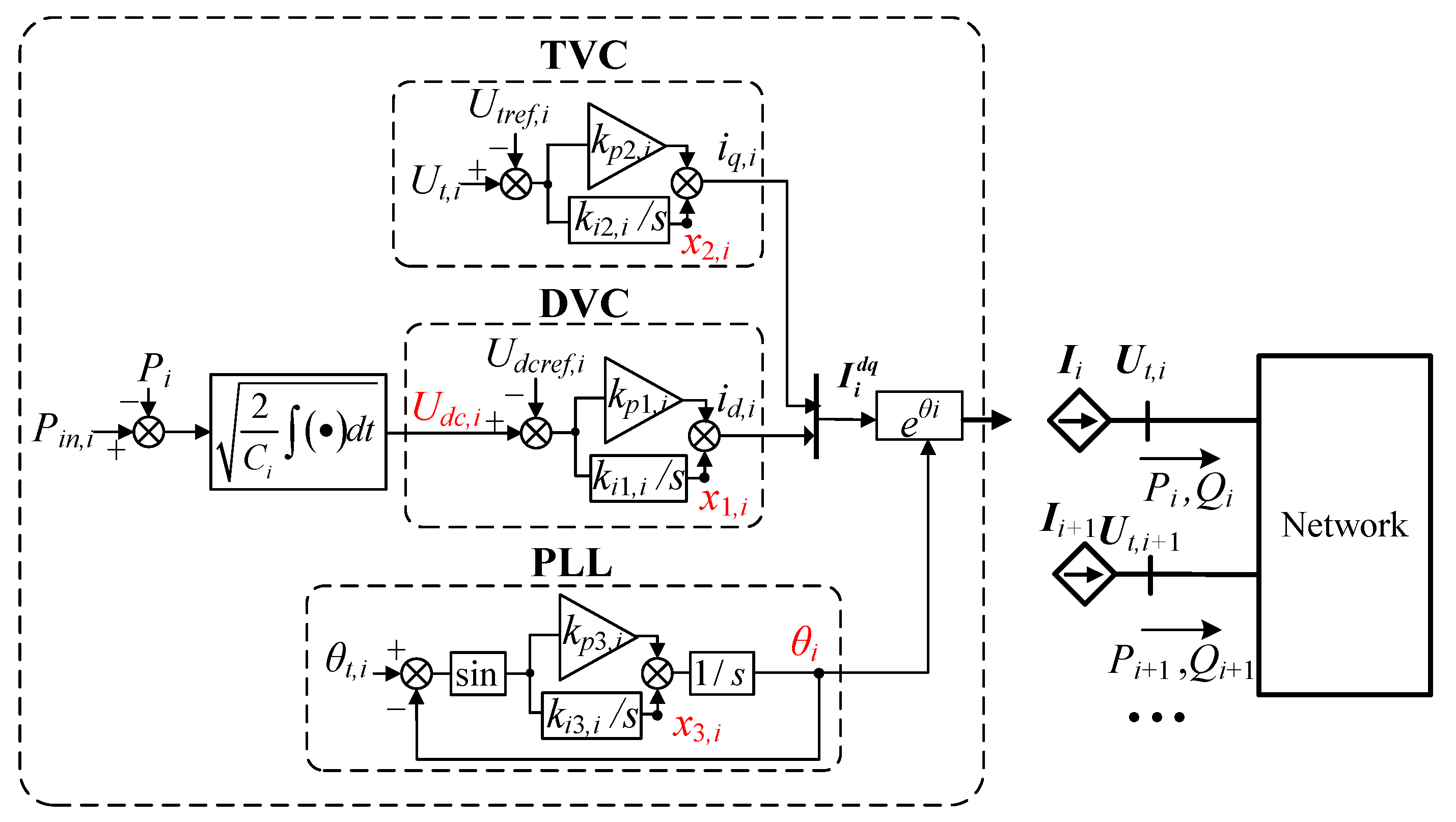
2.2. VSC Modeling
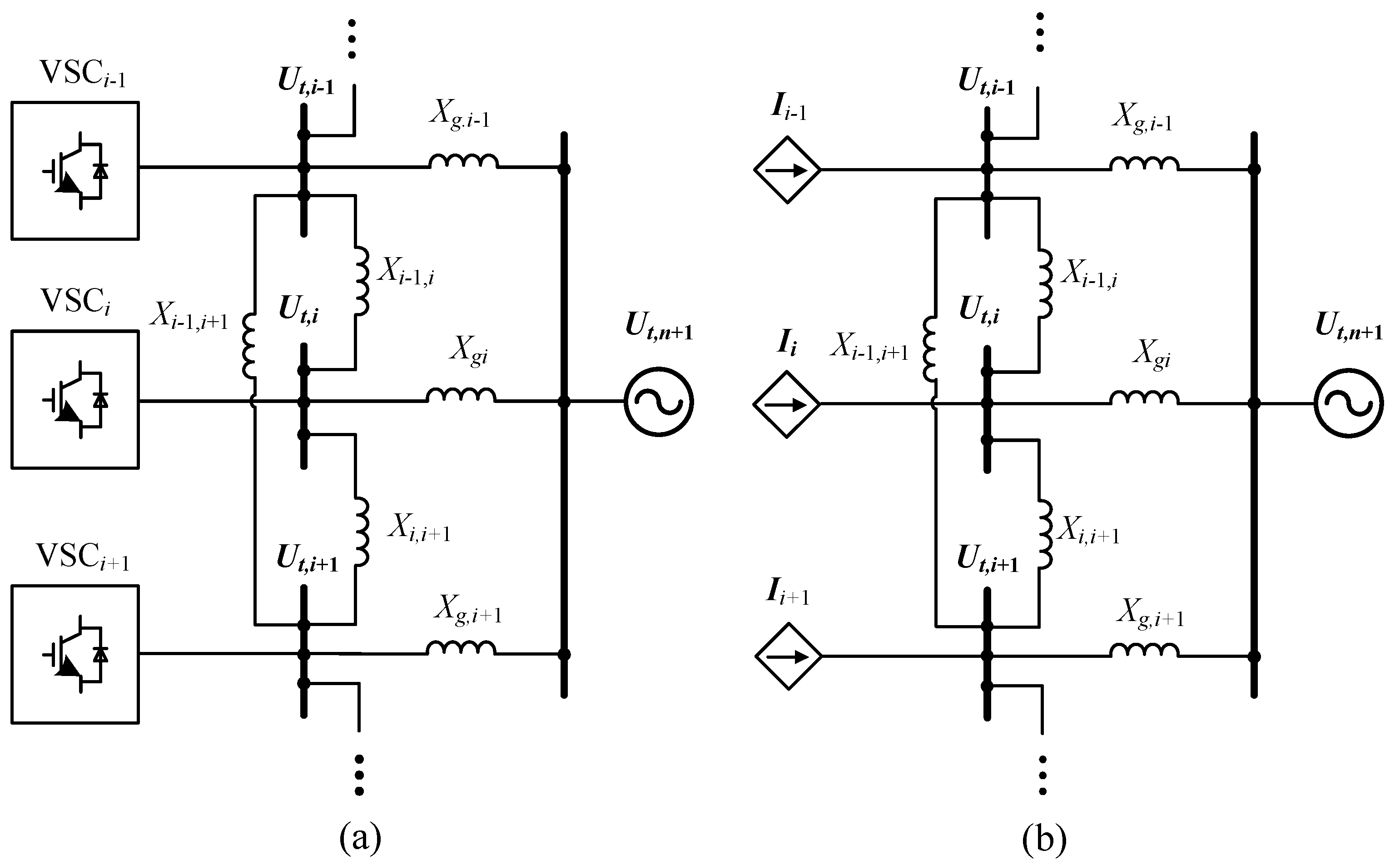
2.3. Network Modeling
2.4. Whole System Modeling
3. Linear Modeling for Multi-Converter Infeed System
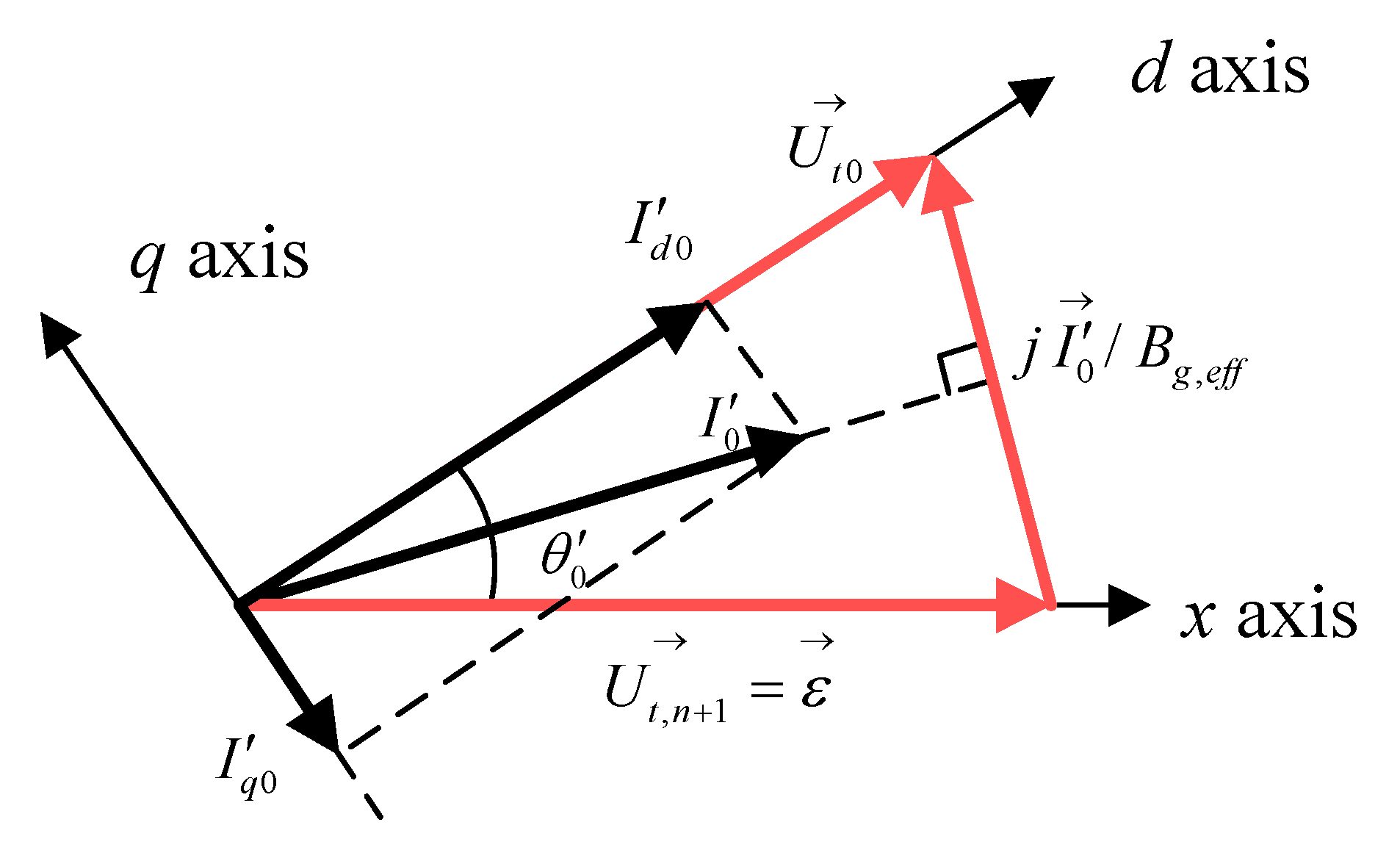
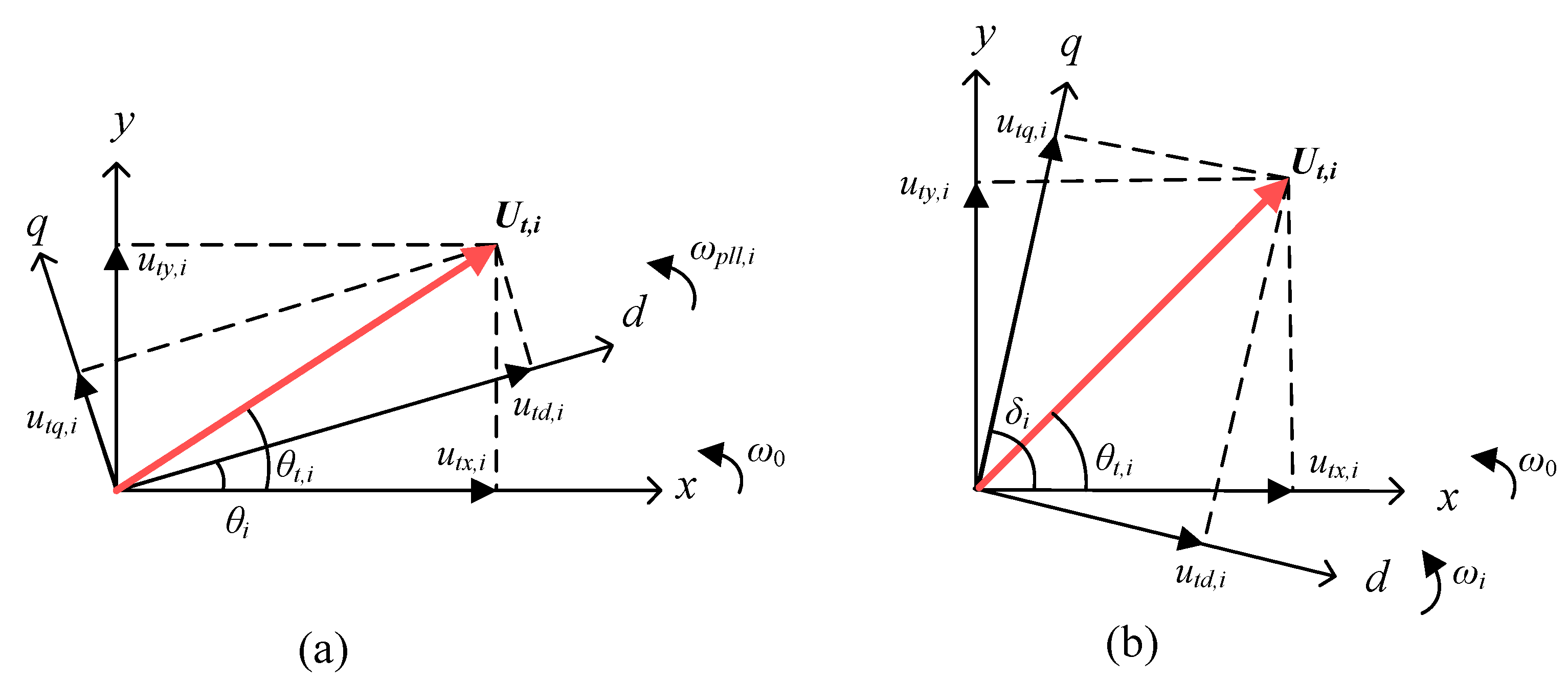
3.1. Operating Point
3.2. VSC Linearization
3.3. Network Linearization
3.4. Characteristic Equation for Linear System Modeling
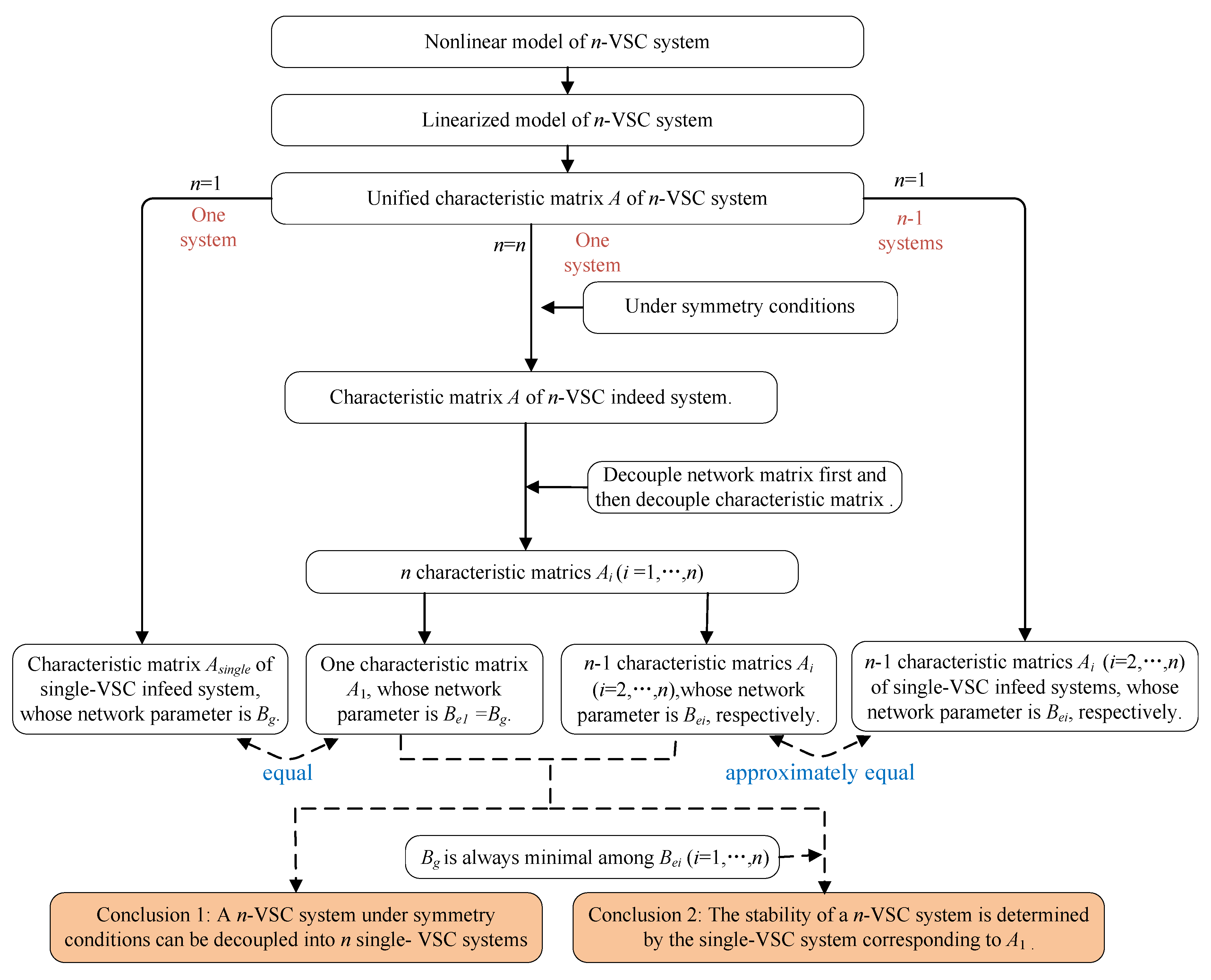
4. Small-Signal Stability Analysis for Multi-Converter Infeed System with Symmetry
4.1. Small-Signal Stability Analysis for a Single VSC System
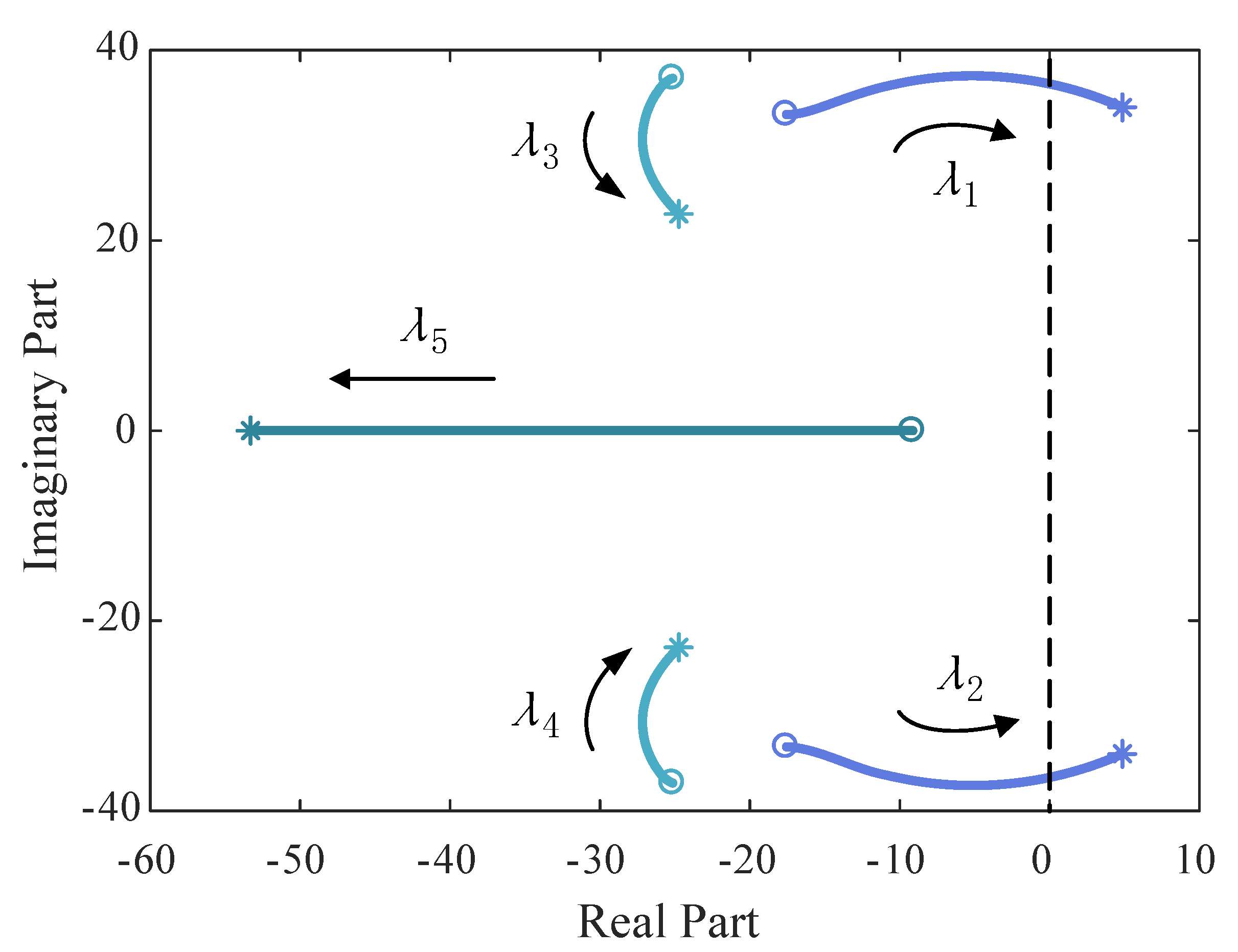
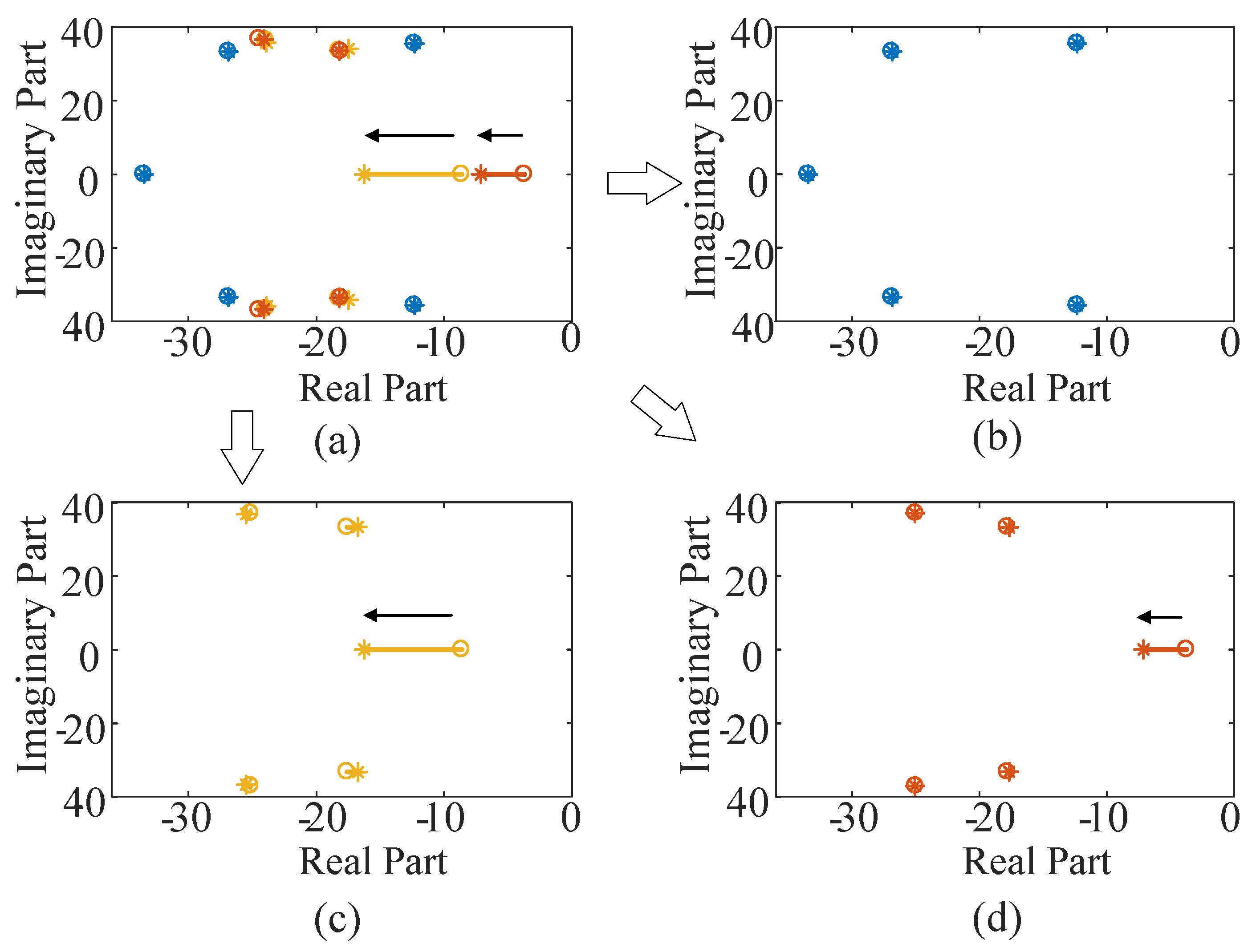
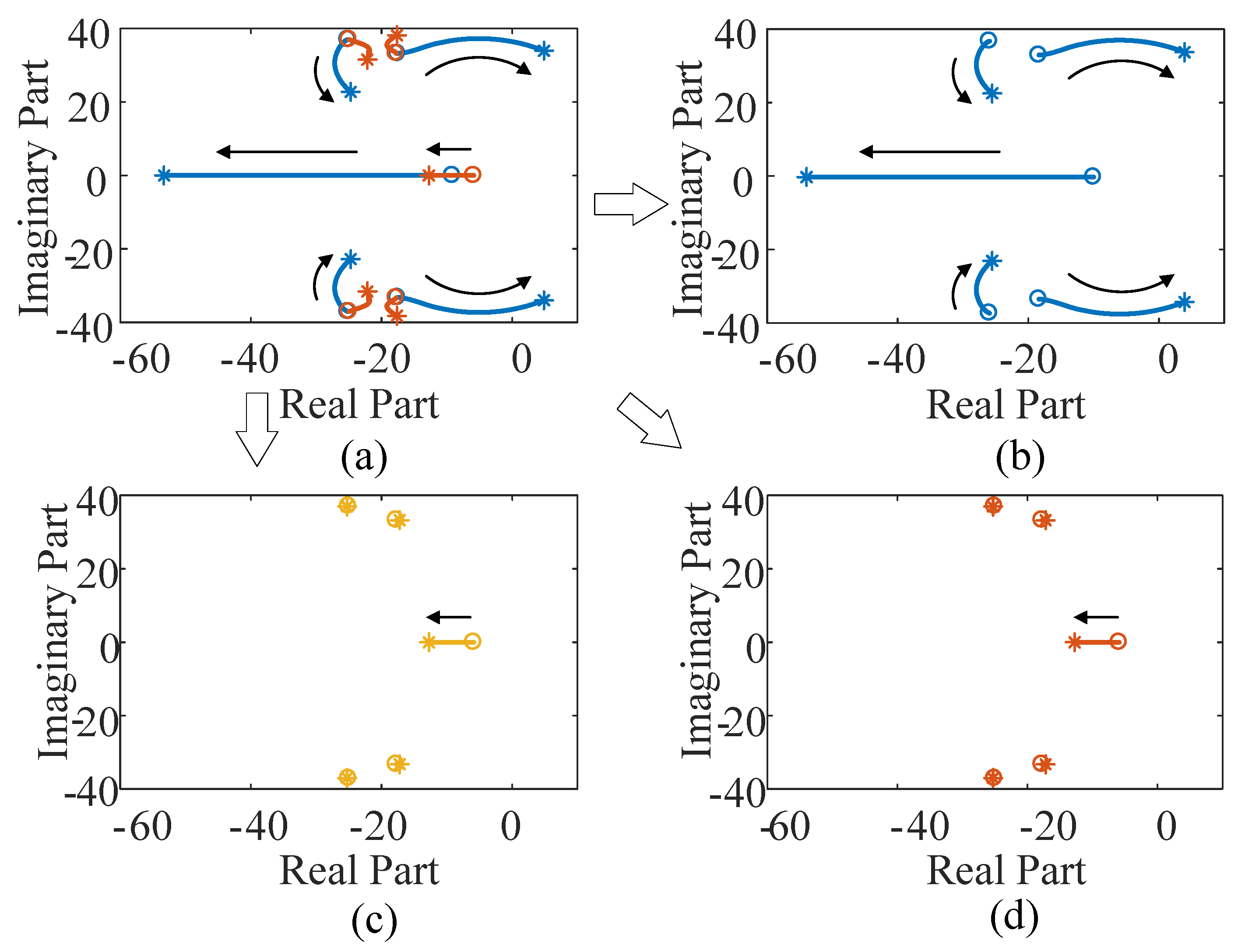
4.2. Decoupling of Multi-VSC Infeed System with Symmetry
4.3. Analysis for Subsystems
5. Test System and Simulation Results
5.1. Single-VSC Infeed System
5.2. Multi-VSC Infeed System
5.3. Time-Domain Simulation Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Converter Parameters
Appendix B. Details Derivations for Approximate Equivalence of the Network Matrices
Appendix C. The Detailed Eigenvalues Data of the Single-VSC System and the Three-VSC System
| Network Parameters | Stability | Eigenvalues |
|---|---|---|
| Stable | ||
| Critical stable | ||
| Unstable | ||
| Network Parameters of Three-VSC System | Stability | Eigenvalues | Network Parameters of Three Subsystems | Stability | Eigenvalues |
|---|---|---|---|---|---|
| Stable | Stable | ||||
| Stable | |||||
| Stable | |||||
| Stable | Stable | ||||
| Stable | |||||
| Stable | |||||
| Network Parameters of Three-VSC System | Stability | Eigenvalues | Network Parameters of Three Subsystems | Stability | Eigenvalues |
|---|---|---|---|---|---|
| Stable | Stable | ||||
| Stable | |||||
| Stable | |||||
| Critical stable | Critical stable | ||||
| Stable | |||||
| Stable | |||||
| Unstable | Unstable | ||||
| Stable | |||||
| Stable | |||||
References
- Blaabjerg, F.; Ma, K. Future on power electronics for wind turbine systems. IEEE J. Emerg. Select. Top. Power Electr. 2013, 1, 139–152. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F. Harmonic stability in power electronic-based power systems: Concept, modeling, and analysis. IEEE Trans. Smart Grid 2018, 10, 2858–2870. [Google Scholar] [CrossRef]
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef] [PubMed]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; McGraw-hill New York: New York, NY, USA, 1994; Volume 7. [Google Scholar]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Ni, Y.; Chen, S.; Zhang, B. Theory and Analysis of Dynamic Power System; Tsinghua University Publication: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Zhao, M.; Yuan, X.; Hu, J.; Yan, Y. Voltage dynamics of current control time-scale in a VSC-connected weak grid. IEEE Trans. Power Syst. 2015, 31, 2925–2937. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, Z.; Blaabjerg, F. Small-signal stability analysis of inverter-fed power systems using component connection method. IEEE Trans. Smart Grid 2017, 9, 5301–5310. [Google Scholar] [CrossRef]
- Yang, Z.; Ma, R.; Cheng, S.; Zhan, M. Nonlinear Modeling and Analysis of Grid-connected Voltage Source Converters Under Voltage Dips. IEEE J. Emerg. Select. Top. Power Electr. 2020, 8, 3281–3292. [Google Scholar] [CrossRef]
- Yang, Z.; Ma, R.; Cheng, S.; Zhan, M. Problems and Challenges of Power-electronic-based Power System Stability: A Case Study of Transient Stability Comparison. Acta Phys. Sin. 2020, 69, 1–14. [Google Scholar]
- Yang, Z.; Mei, C.; Cheng, S.; Zhan, M. Comparison of Impedance Model and Amplitude-Phase Model for Power-electronics-based Power System. IEEE J. Emerg. Select. Top. Power Electr. 2019, 8, 2546–2558. [Google Scholar] [CrossRef]
- Ji, Y.; He, W.; Cheng, S.; Kurths, J.; Zhan, M. Dynamic network characteristics of power-electronics-based power Systems. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- Qiu, Q.; Zhou, B.; Wang, P.; He, L.; Xiao, Y.; Yang, Z.; Zhan, M. Origin of amplitude synchronization in coupled nonidentical oscillators. Phys. Rev. E 2020, 101, 022210. [Google Scholar] [CrossRef]
- Beerten, J.; D’Arco, S.; Suul, J.A. Identification and small-signal analysis of interaction modes in VSC MTDC systems. IEEE Trans. Power Deliv. 2015, 31, 888–897. [Google Scholar] [CrossRef]
- Hu, J.; Yuan, X.; Cheng, S. Multi-time scale transients in power-electronized power systems considering multi-time scale switching control schemes of power electronics apparatus. Proc. Chin. Soc. Elect. Eng. 2019, 39, 5457–5467. [Google Scholar]
- Wang, L.; Xie, X.; Liu, H.; Zhan, Y.; He, J.; Wang, C. Review of emerging SSR/SSO issues and their classifications. J. Eng. 2017, 2017, 1666–1670. [Google Scholar] [CrossRef]
- Xie, X.; Wang, L.; He, J.; Liu, H.; Wang, C.; Zhan, Y. Analysis of subsynchronous resonance/oscillation types in power systems. Power Syst. Technol. 2017, 41, 1043–1049. [Google Scholar]
- Wang, X.; Du, W.; Wang, H. Stability analysis of grid-tied VSC systems under weak connection conditions. Proc. CSEE 2018, 26, 1593–1604. [Google Scholar]
- Huang, Y.; Zhai, X.; Hu, J.; Liu, D.; Lin, C. Modeling and stability analysis of VSC internal voltage in DC-link voltage control timescale. IEEE J. Emerg. Select. Top. Power Electr. 2017, 6, 16–28. [Google Scholar] [CrossRef]
- Zhu, J.; Hu, J.; Lin, L.; Wang, Y.; Wei, C. High-Frequency Oscillation Mechanism Analysis and Suppression Method of VSC-HVDC. IEEE Trans. Power Electr. 2020, 35, 8892–8896. [Google Scholar] [CrossRef]
- Barrat, A.; Barthelemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Menck, P.J.; Heitzig, J.; Marwan, N.; Kurths, J. How basin stability complements the linear-stability paradigm. Nat. Phys. 2013, 9, 89–92. [Google Scholar] [CrossRef]
- Menck, P.J.; Heitzig, J.; Kurths, J.; Schellnhuber, H.J. How dead ends undermine power grid stability. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef]
- Nitzbon, J.; Schultz, P.; Heitzig, J.; Kurths, J.; Hellmann, F. Deciphering the imprint of topology on nonlinear dynamical network stability. New J. Phys. 2017, 19, 033029. [Google Scholar] [CrossRef]
- Rohden, M.; Sorge, A.; Timme, M.; Witthaut, D. Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 2012, 109, 064101. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Nishikawa, T.; Motter, A.E. Small vulnerable sets determine large network cascades in power grids. Science 2017, 358. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, B.; Witthaut, D.; Timme, M.; Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun. 2018, 9, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Witthaut, D.; Timme, M. Braess’s paradox in oscillator networks, desynchronization and power outage. New J. Phys. 2012, 14, 083036. [Google Scholar] [CrossRef]
- Motter, A.E.; Myers, S.A.; Anghel, M.; Nishikawa, T. Spontaneous synchrony in power-grid networks. Nat. Phys. 2013, 9, 191–197. [Google Scholar] [CrossRef]
- Barzel, B.; Barabási, A.L. Universality in network dynamics. Nat. Phys. 2013, 9, 673–681. [Google Scholar] [CrossRef]
- Wolff, M.F.; Schmietendorf, K.; Lind, P.G.; Kamps, O.; Peinke, J.; Maass, P. Heterogeneities in electricity grids strongly enhance non-Gaussian features of frequency fluctuations under stochastic power input. Chaos Interdiscipl. J. Nonlinear Sci. 2019, 29, 103149. [Google Scholar] [CrossRef]
- Timme, M.; Kocarev, L.; Witthaut, D. Focus on networks, energy and the economy. New J. Phys. 2015, 17, 110201. [Google Scholar] [CrossRef]
- Ongena, J. Focus Point on the Transition to Sustainable Energy Systems. Eur. Phys. J. Plus 2018, 133, 82. [Google Scholar] [CrossRef]
- Anvari, M.; Hellmann, F.; Zhang, X. Introduction to Focus Issue: Dynamics of modern power grids. Chaos Interdiscipl. J. Nonlinear Sci. 2020, 30, 063140. [Google Scholar] [CrossRef]
- Ma, Y.; Yang, P.; Wang, Y.; Zhao, Z. Typical characteristics and key technologies of microgrid. Autom. Electr. Power Syst. 2015, 39, 168–175. [Google Scholar]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Shalwala, R.; Bleijs, J. Impact of Grid-Connected PV systems on voltage regulation of a residential area network in Saudi Arabia. In Proceedings of the IEEE 2010 1st International Nuclear & Renewable Energy Conference (INREC), Amman, Jordan, 21–24 March 2010; pp. 1–5. [Google Scholar]
- Du, W.; Fu, Q.; Wang, X.; Wang, H. Small-signal stability analysis of integrated VSC-based DC/AC power systems—A review. Int. J. Electr. Power Energy Syst. 2018, 103, 545–552. [Google Scholar] [CrossRef]
- Bahirat, H.J.; Mork, B.A.; Høidalen, H.K. Comparison of wind farm topologies for offshore applications. In Proceedings of the IEEE 2012 Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Wu, B.; Narimani, M. High-Power Converters and AC Drives; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ackermann, T. Wind Power in Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Jovcic, D. High Voltage Direct Current Transmission: Converters, Systems and DC Grids; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Nilsson, J.W. Electric Circuits; Pearson Education India: Chennai, India, 2008. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Yang, Z.; Kurths, J.; Zhan, M. Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry. Symmetry 2021, 13, 157. https://doi.org/10.3390/sym13020157
Yu J, Yang Z, Kurths J, Zhan M. Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry. Symmetry. 2021; 13(2):157. https://doi.org/10.3390/sym13020157
Chicago/Turabian StyleYu, Jiawei, Ziqian Yang, Jurgen Kurths, and Meng Zhan. 2021. "Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry" Symmetry 13, no. 2: 157. https://doi.org/10.3390/sym13020157
APA StyleYu, J., Yang, Z., Kurths, J., & Zhan, M. (2021). Small-Signal Stability of Multi-Converter Infeed Power Grids with Symmetry. Symmetry, 13(2), 157. https://doi.org/10.3390/sym13020157







