Abstract
Materials with nanoscale phase separation are considered. A system representing a heterophase mixture of ferromagnetic and paramagnetic phases is studied. After averaging over phase configurations, a renormalized Hamiltonian is derived describing the coexisting phases. The system is characterized by direct and exchange interactions and an external magnetic field. The properties of the system are studied numerically. The stability conditions define the stable state of the system. At a temperature of zero, the system is in a pure ferromagnetic state. However, at finite temperature, for some interaction parameters, the system can exhibit a zeroth-order nucleation transition between the pure ferromagnetic phase and the mixed state with coexisting ferromagnetic and paramagnetic phases. At the nucleation transition, the finite concentration of the paramagnetic phase appears via a jump.
1. Introduction
Phase transitions are commonly characterized by the appearance of non-analyticities in the system’s thermodynamic characteristics. The classification of phase transitions is usually connected with the non-analyticities in the derivatives of thermodynamic potentials. Thus, the non-analyticity in the first-order derivatives implies a first-order phase transition, the non-analyticity in the second-order derivatives of a thermodynamic potential defines a second-order phase transition [1].
Recently, the possible existence of zeroth-order phase transitions has been brought to attention [2]; it is possible when a thermodynamic potential itself exhibits a discontinuity. Zeroth-order phase transitions have been found in the physics of black holes [3,4,5,6,7,8,9,10,11], holographic superconductors [12,13,14,15], and holographic ferromagnets and antiferromagnets [16,17]. The zeroth-order phase transition was also found for some spin models with long-range interactions [18,19]. Note that for the systems with long-range interactions, microcanonical and canonical ensembles are not necessarily equivalent [20].
Metal-insulator phase transitions in some materials, such as VO, were classified as zeroth-order phase transitions, where the free energy is discontinuous [21,22]. These phase transitions exhibit the phase coexistence and ramified fractal-like nanoscale phase separation in the transition region [21,22,23].
In this way, the zeroth-order phase transitions can occur when at least one of the features is present: either long-range interactions or nanoscale phase separation. Under this kind of phase separation, the system represents a mixture of nanoscale regions of different phases. The probabilistic weights of the phases are self-consistently defined by the system parameters and thermodynamic variables. Such nanoscale mixtures are also called heterophase or mesoscopic, since the linear size of inclusions of one phase inside the matrix of the other is larger than the interparticle distance but much smaller than the system linear size. The appearance of mesoscopic heterophase mixtures under nanoscale phase separation is a very widespread phenomenon arising around many phase transitions that can be of first or second order. Numerous examples of materials exhibiting the existence of such mixtures are given in the review articles [24,25,26,27]. Recently, the possibility of superfluid dislocations inside quantum crystals has been discussed [28,29,30]. Different types of nanoscale phase separation occur in electrolytes [31,32,33,34,35].
Here we shall concentrate on a heterophase mixture of ferromagnetic and paramagnetic phases. There exist numerous examples of materials exhibiting the coexistence of magnetic (ferromagnetic or antiferromagnetic) and paramagnetic phases. Thus, using the Mössbauer effect, the coexistence of antiferromagnetic and paramagnetic phases is observed in FeF [36], in CaFeO [37], and in a number of orthoferrites, such as LaFeO, PrFeO, NdFeO, SmFeO, EuFeO, GdFeO, TbFeO, DyFeO, YFeO, HoFeO, ErFeO, TmFeO, and YbFeO [38,39]. Ferromagnetic cluster fluctuations, called ferrons or fluctuons, can arise inside a paramagnetic matrix of some semiconductors [40,41,42,43,44,45]. In some materials, magnetic cluster excitations can occur in the paramagnetic region above or above [46,47,48,49,50,51,52], causing the appearance of spin waves in the paramagnetic phase, for instance, in Ni, Fe, EuO, EuS, PdFe, and Gd [53,54,55,56,57,58]. The coexistence of ferromagnetic and nonmagnetic phases was also observed in YCo, YCo, Co(SSe), Co(TiAl), and Lu(CoAl) [59,60]. In colossal magnetoresistance materials, such as LaCaMnO and LaSrCoO, one observes the coexistence of a paramagnetic insulating, or semiconducting, phase and a ferromagnetic metallic phase [61,62,63], while in LaBiCaMnO, paramagnetic and antiferromagnetic phases coexist [64]. Nanoscale phase separation into ferromagnetic and paramagnetic regions has been observed in the colossal magnetoresistence compound, EuBC [65]. Many more examples can be found in the review articles [24,25,26,27].
In the present paper, we consider a heterophase system with random phase separation, where the regions of different phases are randomly distributed in space. By averaging the phase configurations, we derive a renormalized, effective Hamiltonian of the mixture. Keeping in mind a spin system, we pass to the quasi-spin representation. Specifically, we consider a mixture of ferromagnetic and paramagnetic phases. Long-range interactions are assumed, such that the mean-field approximation becomes, in the thermodynamic limit, asymptotically exact. The existence of the ferromagnetic–paramagnetic mixture is due to the competition between direct and exchange interactions. We treat the case when the system is placed in an external magnetic field. We show that for some system parameters, there occurs the following situation: at low temperatures, the system is a pure ferromagnet that, when rising in temperature, can transfer into a mixture of ferromagnetic and paramagnetic phases at a nucleation point. For some system parameters, this nucleation transition happens to be a zeroth-order transition.
The plan of the paper is as follows. In Section 2, we recall the Gibbs method of equimolecular surfaces that are used for describing the spatial phase separation. Section 3 explains how the statistical operator of the mixture with phase separation can be defined by minimizing the functional information.The random spatial distribution of competing phases requires the averaging over phase configurations. The results of this averaging are summarized in Section 4. In Section 5, we pass from the field-operator representation to spin representation. Although this conversion is based on the known Bogolubov canonical transformation, it is necessary to recall it in order to elucidate the importance of taking account of direct particle interactions, in addition to exchange interactions. Keeping in mind long-range interactions, in Section 6, we derive the free energy of the mixture. Section 7 formulates the stability conditions that make it straightforward to separate stable states from unstable ones. In Section 8, we present the results of the numerical calculations and accompany them with discussions and conclusions.
2. Spatial Phase Separation
The description of a two-phase system with spatial phase separation starts with the Gibbs method [66] of equimolecular separating surfaces, where the system of volume V and number of particles N is considered to be separated into two parts, with the total volumes and the particle numbers , so that
The regions occupied by different phases are assumed to be randomly distributed in space. Their spatial locations are described by the manifold indicator functions
where
The Hilbert space of microscopic states of the system is the tensor product
of the weighted Hilbert spaces [24,25,26] corresponding to the phases . The algebra of observables in this space is given by the direct sum of the algebra representations on the corresponding subspaces
For instance, the system energy Hamiltonian reads as
with the general form of the phase replica Hamiltonians
where is an interaction potential, is an external potential, and the field operators are columns with respect to internal degrees of freedom, such as spin. The number-of-particle operator is
with the number-of-particle operators of each phase
Here and below, we set the Planck and Boltzmann constants to one.
3. System Statistical Operator
The general procedure of defining the statistical operator for a system is by minimizing the information functional, taking account of the prescribed constraints. The latter is the normalization condition
the definition of the system energy
and of the total number of particles in the system
Here and in what follows, the trace operation is taken over the whole Hilbert space (3), and implies the averaging over phase configurations describing the random locations and shapes of separated phases.
The information functional in the Kullback–Leibler form [67,68] reads as
with the Lagrange multipliers , , and , and with a trial statistical operator characterizing some a priori information if any. If no a priori information is available, is a constant. Then minimizing the information functional over yields the statistical operator
with the grand Hamiltonian
and the partition function
Introducing the effective renormalized Hamiltonian by the relation
gives the partition function
Then we get the grand thermodynamic potential
This picture describes a heterophase system where the phase-separated regions are random in the sense that they are randomly located in space and can move and change their shapes. In that sense, strictly speaking, the system is in quasi-equilibrium. However, the averaging over phase configurations reduces the consideration to an effective system equilibrium on average [24,25,26].
4. Averaging over Phase Configurations
In order to explicitly accomplish the averaging over phase configurations, it is necessary to define the functional integration over the manifold indicator functions (2). This functional integration has been defined and explicitly realized in papers [24,69,70,71,72,73]. Here we formulate the main results of this functional integration over the manifold indicator functions with the differential measure , which realizes the averaging over phase configurations.
Theorem 1.
Let us consider the functional
The integration of this function over the manifold indicator functions gives
where
while
defines the geometric probability of an f-th phase.
Theorem 2.
The thermodynamic potential
after the averaging over phase configurations, becomes
where
and the renormalized Hamiltonian is
with the phase probabilitiesbeing the minimizers of the thermodynamic potential,
under the normalization condition
Theorem 3.
The observable quantities, given by the averages
of the operators from the algebra of observables (4),
withdefined as in (19), after the averaging over phase configurations, reduce to the form
where the renormalized operator of an observable is
withdefined as in (21), and the renormalized statistical operator is
with the partition function (17).
The proofs of these theorems are given in the papers [24,69,70,71,72,73].
5. Hamiltonian in Spin Representation
Since we aim to study the magnetic properties of a system with phase separation, it is useful to transform Hamiltonian (6) into spin representation. For this purpose, we assume that the system is periodic over a lattice with the lattice sites , where , and we expand the field operators over Wannier functions:
Keeping in mind well-localized Wannier functions [74], we retain in the Hamiltonian only the terms expressed through the matrix elements over Wannier functions containing not more than two lattice sites, since the overlap of Wannier functions located at three or four different lattice sites is negligibly small.
The remaining matrix elements are: the tunneling term
the term of direct interactions
and the term of exchange interactions
To exclude self-interactions, one sets
Then we introduce spin operators following the method of canonical transformations [75,76,77], generalized in the case of heterophase systems [78,79,80]. Keeping in mind the particles with spin one-half, the operators are to be treated as spinors
of two components, one with spin up and the other with spin down. When each lattice site is occupied by a single particle, the unipolarity condition is valid
The canonical transformations introducing spin operators , acting on the space , read as
Employing these canonical transformations and wishing to write the Hamiltonian in a compact form, we define the average direct interactions
the average exchange interactions
and the effective chemical potentials
For localized particles, the tunneling term is small and can be neglected. Hence, as is seen from expression (45), . Then the last term in Hamiltonian (46) becomes . Such linear scalar terms in can be omitted since they enter the Hamiltonian (26) as , which is as a constant shift. The value (47) characterizes an average potential acting on each particle in the system and is mainly due to direct interactions that are usually much larger than the exchange interactions. It is reasonable to assume that this average potential does not depend on the kind of magnetic phases, so that . For generality, it is also necessary to take into account an external magnetic field . As a result, we come to the Hamiltonian
The main feature of the paramagnetic phase is, clearly, the absence of long-range order. The direct way of taking this into account on the microscopic level is to notice that the term of exchange interactions (37) essentially depends on the localization of Wanier functions. From expression (37), it is evident that the better Wannier functions are localized, the smaller the exchange term. Therefore, accepting that the paramagnetic exchange term is very small, automatically degrades the long-range order. Keeping this in mind, we set to zero the paramagnetic exchange interactions, . Then the Hamiltonian (48) yields for the ferromagnetic phase
and for the paramagnetic phase
The external magnetic field is assumed to be directed along the z-axis
Recall that the total system Hamiltonian, according to (26), reads as
The order parameters can be defined by the averages
which lie in the interval
For the ferromagnetic phase, there exist such low temperatures where
while for the paramagnetic phase at all temperatures, one has
Accepting that interparticle interactions are of a long-range order, Hamiltonian (49) can be simplified by resorting to the mean-field approximation
where . This reduces that Hamiltonian to the form
6. Free Energy of Mixture
Defining the reduced free-energy in the standard way
introducing the dimensionless parameters
where
and measuring temperature in units of J, we come to the mixture free energy
Here the free energy of the magnetic component is
with the order parameter
and the free energy of the paramagnetic component is
with the order parameter
Studying the properties of the free energy, it is convenient to represent it in the form symmetric with respect to both phase components, introducing the quantity
By definition, , while . Then the partial free energy
becomes
with the order parameter
7. Stability Conditions
The statistical system is stable when it is in the state of the absolute minimum of the thermodynamic potential, which in the present case is the free energy. The system is in the mixed state, provided the free energy (62) corresponds to a minimum with respect to the variables , , and . The variable is expressed through the relation . For convenience, it is possible to use the notation
and consider only the variable w, instead of and connected by the normalization condition. The conditions of the extremum are
The first and second conditions give the expressions (64) and (66) for the order parameters and . The third equation, due to the normalization condition, can be written as
Using the derivative
results in the probability of the ferromagnetic component
The extremum is a minimum provided the principal minors of the Hessian matrix are positive. The Hessian matrix is expressed through the second derivatives
For the considered system, we have
The minimum of the free energy implies the stability conditions that for the present case become
We need to solve the system of equations for the order parameter , given in (64) and satisfying condition (55), for the order parameter , given in (66) and satisfying condition (56), and for the probability of ferromagnetic phase w, defined in (73) and satisfying conditions (28). If there occur several solutions, it is necessary to choose the solution that corresponds to the minimal free energy and satisfies the stability conditions (74).
Furthermore, it is necessary to choose the state with the minimal free energy between the free energy F of the mixture, free energy of the pure ferromagnetic phase
with the order parameter
and the free energy of the pure paramagnetic phase
with the order parameter
8. Results and Discussion
We have derived the model of a mixed system describing the coexistence of different phases when at least one of the phases represents nanoscale regions of a competing phase inside a host phase. The spatial distribution of the phases is random. This picture is often termed nanoscale phase separation. As a concrete example, we have studied the mixture of ferromagnetic and paramagnetic phases, modeling a ferromagnet with paramagnetic fluctuations. The choice of this example is dictated by the fact that spin models serve as typical illustrations of phase transitions of different nature.
After averaging over phase configurations, we obtain a renormalized Hamiltonian, taking into account the coexistence of mesoscopic phases. In the resulting effective picture, thermodynamic potentials are represented as the sums of replicas characterizing different phases. This, however, is not a simple sum of the terms corresponding to pure phases, as in the case of the Gibbs macroscopic mixture, where, for instance, free energy is a linear combination, in our case
The separation of phases is connected with the existence of surface free energy. The latter is not a microscopic notion and is not defined at the level of operators and microscopic states. The surface free energy is a thermodynamic notion defined by the difference between the actual free energy of the system and the free energy of the Gibbs macroscopic mixture [81,82,83]. That is, the surface free energy is defined by the difference
In our case, this is
Contrary to a pure phase needing a one-order parameter (that can be a vector or a tensor), the mixed state requires, for its correct description, a larger number of parameters. Thus, compared to the pure ferromagnetic phase, described by a single order parameter , the mixed ferromagnetic–paramagnetic state needs three parameters: the order parameter (reduced magnetization) of the ferromagnetic component, , the order parameter (reduced magnetization) of the paramagnetic component, , and the probability of one of the phases, say w, with the probability of the other phase given by .
In Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, we present the results of the numerical investigation for different parameters u and h. Only stable solutions are shown. The absence of F in a figure implies that F is unstable. Depending on the values of the parameters, there can exist two types of behavior.
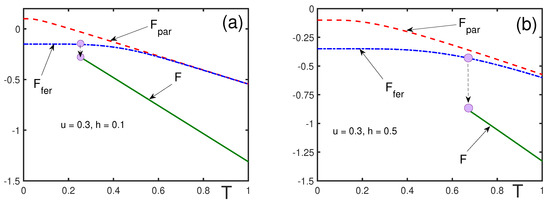
Figure 1.
Free energies of the mixed state, F (solid line), ferromagnetic state, (dash–dotted line), and of the paramagnetic state, (dashed line), for and different magnetic fields: (a) ; (b) .
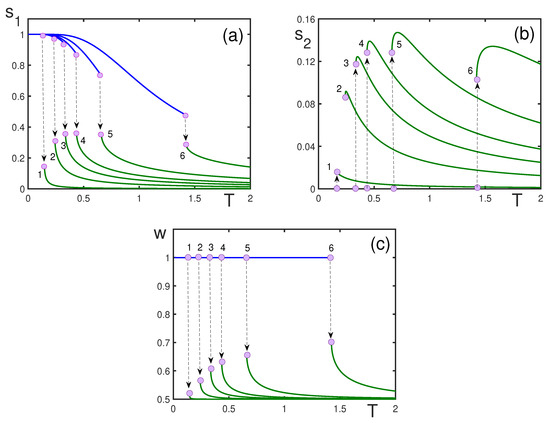
Figure 2.
Order parameters (a), (b), and w as functions of dimensionless temperature T (c), for and different fields: (1) ; (2) ; (3) ; (4) ; (5) ; (6) . The corresponding nucleation temperatures are: (1) ; (2) ; (3) ; (4) ; (5) ; (6) .
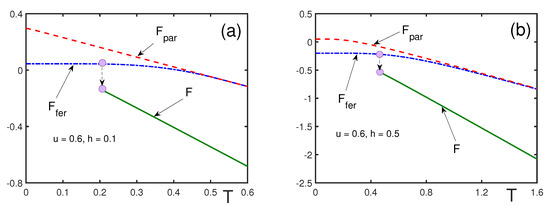
Figure 3.
Free energies of the mixed state, F (solid line), ferromagnetic state, (dash-dotted line), and of the paramagnetic state, (dashed line), for and different magnetic fields: (a) ; (b) .
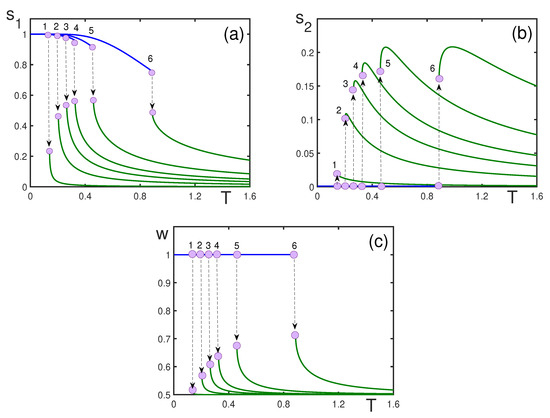
Figure 4.
Order parameters (a), (b), and w as functions of dimensionless temperature T (c), for and different fields: (1) ; (2) ; (3) ; (4) ; (5) ; (6) . The corresponding nucleation temperatures are: (1) ; (2) ; (3) ; (4) ; (5) ; (6) .
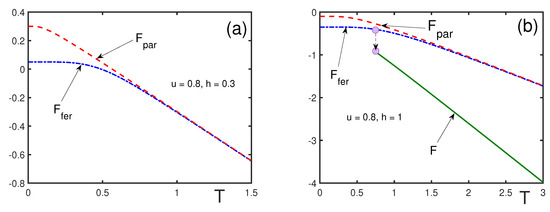
Figure 5.
Free energies of the mixed state, F (solid line), ferromagnetic state, (dash–dotted line), and of the paramagnetic state, (dashed line), for and different magnetic fields: (a) ; (b) . For , the mixed state is not stable. For , the zeroth-order nucleation transition occurs at the nucleation temperature .
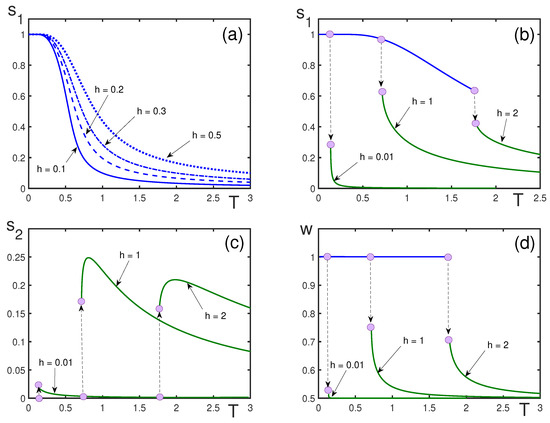
Figure 6.
Order parameters , , and w as functions of dimensionless temperature T, for and different fields: (a) (solid line), (dashed line); (dash–dotted line); (dotted line); (b) ; ; . The corresponding nucleation temperatures are , , and ; (c) ; ; ; (d) ; ; .
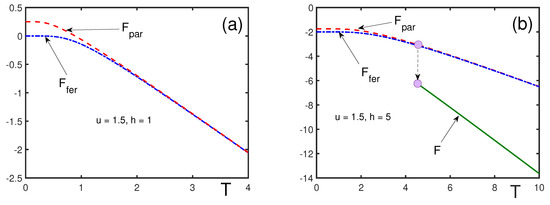
Figure 7.
Free energies of the mixed state, F (solid line), ferromagnetic state, (dash–dotted line), and of the paramagnetic state, (dashed line), for and different magnetic fields: (a) ; (b) . For , the mixed state is not stable. For , the zeroth-order nucleation transition occurs at the nucleation temperature .
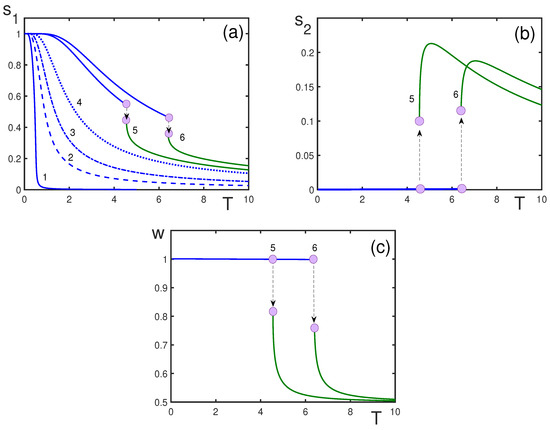
Figure 8.
Order parameters (a), (b), and w as functions of dimensionless temperature T (c), for and different fields: (1) ; (2) ; (3) ; (4) ; (5) ; (6) . The nucleation temperatures are for and for .
- (i)
- At low temperatures, the system is a pure ferromagnet described by the free energy and the order parameter , with . When increasing temperature, gradually approaches corresponding to a paramagnet. The order parameter has the form typical of the ferromagnetic magnetization. This behavior, for instance, happens for and all .
- (ii)
- For , at low temperatures, below the nucleation temperature , the system is a pure ferromagnet, with the free energy , the order parameter , and . At the nucleation temperature , there appears a solution for the mixed state with the free energy F and the order parameters and . The free energy F is lower than , but does not intersect it so that the nucleation is to be classified as a zeroth-order transition.
In this way, the nucleation transition is the transition of a system from a pure phase into a mixed phase. In the considered case, this is the transition between the pure ferromagnetic phase and a mixed state, where ferromagnetic regions start coexisting with paramagnetic fluctuations.
As follows from the figures, the zeroth-order nucleation transition is accompanied by the abrupt appearance inside the ferromagnetic phase of a finite concentration of nanoscale paramagnetic regions. Hence, when the concentration of the paramagnetic admixture does not continuously grow from zero but increases by a jump, this suggests the possible occurrence of a zeroth-order nucleation transition. The appearance of paramagnetic regions can be noticed by means of Mössbauer experiments.
We show, numerically, that the nucleation transition can be of zeroth order. From one side, this could be a consequence of approximations involved in the process of calculations. From the other side, strictly speaking, nucleation is not a typical phase transition, because of which, it is not compulsorily required to be classified as either first or second order. Although, as is discussed in the Introduction, there are works showing that even classical phase transitions could be of zeroth order. Even more so is allowed for such a non-classical transition as a nucleation transition.
Author Contributions
V.I.Y. and E.P.Y. equally contributed to this review. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kubo, R. Thermodynamics; North-Holland: Amsterdam, The Netherlands, 1968. [Google Scholar]
- Maslov, V.P. Zeroth-order phase transitions. Math. Notes 2004, 76, 697–710. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Kubiznak, D.; Mann, R.B. Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. J. High Energy Phys. 2012, 2012, 110. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B. Reentrant phase transitions in rotating anti-de Sitter black holes. Phys. Rev. D 2013, 88, 101502. [Google Scholar] [CrossRef]
- Altamirano, N.; Kubiznak, D.; Mann, R.B.; Sherkatghanad, Z. Kerr-AdS analogue of triple point and solid/liquid/gas phase transition. Class. Quantum Grav. 2014, 31, 042001. [Google Scholar] [CrossRef]
- Frassino, A.M.; Kubiznak, D.; Mann, R.B.; Simovic, F. Multiple reentrant phase transitions and triple points in Lovelock thermodynamics. J. High Energy Phys. 2014, 2014, 1–47. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Brenna, W.G.; Mann, R.B. P − V criticality in quasitopological gravity. J. High Energy Phys. 2015, 2015, 77. [Google Scholar] [CrossRef]
- Hennigar, R.A.; Mann, R.B. Reentrant phase transitions and van der Waals behaviour for hairy black holes. Entropy 2015, 17, 8056. [Google Scholar] [CrossRef]
- Kubiznak, D.; Simovic, F. Thermodynamics of horizons: De Sitter black holes and reentrant phase transitions. Class. Quantum Grav. 2016, 33, 245001. [Google Scholar] [CrossRef]
- Dehyadegari, A.; Sheykhi, A.; Montakhab, A. Novel phase transition in charged dilaton black holes. Phys. Rev. D 2017, 96, 084012. [Google Scholar] [CrossRef]
- Dehyadegari, A.; Sheykhi, A. Reentrant phase transition of Born-Infeld-AdS black holes. Phys. Rev. D 2018, 98, 024011. [Google Scholar] [CrossRef]
- Zeng, H.B. Possible Anderson localization in a holographic superconductor. Phys. Rev. D 2013, 88, 126004. [Google Scholar] [CrossRef]
- Cai, R.G.; Li, L.; Li, L.F. A holographic P-wave superconductor model. J. High. Energy Phys. 2014, 1401, 032. [Google Scholar] [CrossRef]
- Cai, R.G.; Li, L.; Li, L.F.; Yang, R.Q. Towards complete phase diagrams of a holographic P-wave superconductor model. J. High. Energy Phys. 2014, 1404, 016. [Google Scholar] [CrossRef]
- Zeng, H.B.; Zhang, H.Q. Zeroth order phase transition in a holographic superconductor with single impurity. Nucl. Phys. B 2015, 897, 276–288. [Google Scholar] [CrossRef][Green Version]
- Cai, R.G.; Yang, R.Q. Paramagnetism-ferromagnetism phase transition in a dyonic black hole. Phys. Rev. D 2014, 90, 081901. [Google Scholar] [CrossRef]
- Cai, R.G.; Yang, R.Q. Holographic model for the paramagnetism-antiferromagnetism phase transition. Phys. Rev. D 2015, 91, 086001. [Google Scholar] [CrossRef]
- Hou, J.X. Zeroth order phase transition induced by ergodicity breaking in a mean-field system. Eur. Phys. J. B 2021, 94, 6. [Google Scholar] [CrossRef]
- Hou, J.X. Zeroth-order phase transition in the Blume-Emery-Griffiths model without bilinear exchange coupling. Phys. Rev. E 2021, 104, 024114. [Google Scholar] [CrossRef]
- Touchette, H. Equivalence and nonequivalence of ensembles: Thermodynamic, macrostate, and measure levels. J. Stat. Phys. 2015, 159, 987–1016. [Google Scholar] [CrossRef]
- Bar, T.; Choudhary, S.K.; Ashraf, M.A.; Sujith, K.S.; Puri, S.; Raj, S.; Bansal, B. Kinetic spinodal instabilities in the Mott transition in V2O3: Evidence from hysteresis scaling and dissipative phase ordering. Phys. Rev. Lett. 2018, 121, 045701. [Google Scholar] [CrossRef]
- Kundu, S.; Bar, T.; Nayak, R.K.; Bansal, B. Critical slowing down at the abrupt Mott transition: When the first-order phase transition becomes zeroth order and looks like second order. Phys. Rev. Lett. 2020, 124, 095703. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Phillabaum, B.; Carlson, E.W.; Dahmen, K.A.; Vidhyadhiraja, N.S.; Qazilbash, M.M.; Basov, D.N. Random field driven spatial complexity at the Mott transition in VO2. Phys. Rev. Lett. 2016, 116, 036401. [Google Scholar] [CrossRef]
- Yukalov, V.I. Phase transitions and heterophase fluctuations. Phys. Rep. 1991, 208, 395–489. [Google Scholar] [CrossRef]
- Yukalov, V.I. Mesoscopic phase fluctuations: General phenomenon in condensed matter. Int. J. Mod. Phys. B 2003, 17, 2333–2358. [Google Scholar] [CrossRef]
- Yukalov, V.I. Systems with symmetry breaking and restoration. Symmetry 2010, 2, 40–68. [Google Scholar] [CrossRef]
- Kagan, M.Y.; Kugel, K.I.; Rakhmanov, A.L. Electronic phase separation: Recent progress in the old problem. arXiv 2021, arXiv:2109.12684. [Google Scholar] [CrossRef]
- Kuklov, A.B.; Prokof’ev, N.V.; Svistunov, B.V. How solid is supersolid? Physics 2011, 4, 109. [Google Scholar] [CrossRef]
- Boninsegni, M.; Prokof’ev, N.V. Supersolids: What and where are they? Rev. Mod. Phys. 2012, 84, 759–776. [Google Scholar] [CrossRef]
- Yukalov, V.I. Saga of superfluid solids. Physics 2020, 2, 6. [Google Scholar] [CrossRef]
- Buggy, N.C.; Du, Y.; Kuo, M.C.; Seifert, S.; Gasvoda, R.J.; Agarwal, S.; Coughlin, E.B.; Herring, A.M. Designing anion-exchange ionomers with oriented nanoscale phase separation at a Silver interface. J. Phys. Chem. C 2021, 125, 20592–20605. [Google Scholar] [CrossRef]
- Batys, P.; Fedorov, D.; Mohammadi, P.; Lemetti, L.; Linder, M.B.; Sammalkorpi, M. Self-assembly of silk-like protein into nanoscale bicontinuous networks under phase-separation conditions. Biomacromolecules 2021, 22, 690–700. [Google Scholar] [CrossRef]
- Park, J.; Zhao, H.; Kang, S.D. Fictitious phase separation in Li layered oxides driven by electro-autocatalysis. Nat. Mater. 2021, 20, 991–999. [Google Scholar] [CrossRef] [PubMed]
- Martin, E.W.; Harmon, T.S.; Hopkins, J.B. A multi-step nucleation process determines the kinetics of prion-like domain phase separation. Nat. Commun. 2021, 12, 4513. [Google Scholar] [CrossRef] [PubMed]
- Kyndiah, A.; Checa, M.; Leonardi, F.; Millan-Solsona, R.; Di, M.; Tanwar, S.; Fumagalli, L.; Mas-Torrent, M.; Gomila, G. Nanoscale mapping of the conductivity and interfacial capacitance of an electrolyte-gated organic field-effect transistor under operation. Funct. Mater. 2021, 31, 2008032. [Google Scholar] [CrossRef]
- Bertelsen, U.; Knudsen, J.; Krogh, H. Mössbauer effect in FeF3. Phys. Status Solidi 1967, 22, 59–64. [Google Scholar] [CrossRef]
- Yamamoto, H.; Osaka, T.; Watanabe, H.; Fukase, M. Mössbauer effect study of spin relaxation in CaFe2O4. J. Phys. Soc. Jpn. 1968, 24, 275–279. [Google Scholar] [CrossRef]
- Eibschütz, M.; Shtrikman, S.; Treves, D. Mössbauer studies of Fe57 in orthoferrites. Phys. Rev. 1967, 156, 562–577. [Google Scholar] [CrossRef]
- Levinson, L.; Luban, M.; Shtrikman, S. Mössbauer studies of Fe57 near the Curie temperature. Phys. Rev. 1969, 177, 864–870. [Google Scholar] [CrossRef]
- Krivoglaz, M.A. Fluctuon states of electrons. Phys. Usp. 1974, 16, 856–877. [Google Scholar] [CrossRef]
- Nagaev, E.L. Ferromagnetic and antiferromagnetic semiconductors. Phys. Usp. 1975, 18, 863–892. [Google Scholar] [CrossRef]
- Belov, K.P. Rare-Earth Magnets and Their Applications; Nauka: Moscow, Russia, 1980. [Google Scholar]
- Belov, K.P.; Tretyakov, Y.D.; Gordeev, I.V.; Koroleva, L.I.; Kesler, Y.A. Magnetic Semiconductors–Chalcogenide Spinels; Moscow State University: Moscow, Russia, 1981. [Google Scholar]
- Reissner, M.; Steiner, W.; Kappler, J.; Bauer, P.; Besnus, M. Magnetic behaviour of Y(FexAl1−x)2 alloys. J. Phys. F 1984, 14, 1249–1260. [Google Scholar] [CrossRef]
- Kumeishin, V.F.; Ivanov, O.A. Investigation of relaxation processes in nickel near the Curie temperature by means of nuclear gamma-resonance. Phys. Met. Metallogr. 1975, 40, 1295–1299. [Google Scholar]
- Baryakhtar, V.G.; Vitebsky, I.M.; Yablonsky, D.A. Theory of creation of nuclei at magnetic first order phase tarnsition between paramagnetic and magneto-ordered phases. Phys. Solid State. 1977, 19, 347–352. [Google Scholar]
- Goldman, M. Nuclear dipolar magnetic ordering. Phys. Rep. 1977, 32, 1–47. [Google Scholar] [CrossRef]
- Reimann, H.; Hagen, H.; Waldner, F.; Arend, H. Observation of excitation of the antiferromagnetic mode in the paramagnetic state of (C2H5NH3)2CuCl4. Phys. Rev. Lett. 1978, 40, 1344–1346. [Google Scholar] [CrossRef]
- Bhargava, S.; Zeeman, N. Mössbauer study of Ni0.25Zn0.75Fe2O4: Spin fluctuations. Phys. Rev. B 1980, 21, 1717–1724. [Google Scholar] [CrossRef]
- Uen, T.M.; Tseng, P.K. Mössbauer-effect studies on the magnetic properties of the Ni-Zn-ferrite system. Phys. Rev. B 1982, 25, 1848–1859. [Google Scholar] [CrossRef]
- Srivastava, J.; Muraleedharan, K.; Vijayaraghavan, R. On anomalous Mössbauer spectra in spinel ferrites. Phys. Lett. A 1984, 104, 482–486. [Google Scholar] [CrossRef]
- Hälg, B.; Furrer, A.; Vogt, O. Coexistence of different short-range-ordered spin fluctuations in Ce1−x(LaY)xSb. Phys. Rev. Lett. 1985, 54, 1388–1391. [Google Scholar] [CrossRef] [PubMed]
- Lynn, J.W. Temperature dependence of the magnetic excitations in iron. Phys. Rev. B 1975, 11, 2624–2637. [Google Scholar] [CrossRef]
- Liu, S.H. Magnetic excitations above the critical temperature. Phys. Rev. B 1976, 13, 2979–2985. [Google Scholar] [CrossRef]
- Lynn, J.W.; Mook, H.A. Temperature dependence of the dynamic susceptibiity of nickel. Phys. Rev. B 1981, 23, 198–206. [Google Scholar] [CrossRef]
- Cable, J.W.; Nicklow, R.M.; Wakabayashi, N. Temperature dependence of the magnetic excitations in gadolinium. Phys. Rev. B 1986, 32, 1710–1719. [Google Scholar] [CrossRef] [PubMed]
- Lynn, J.W.; Mook, H.A. Nature of the magnetic excitations above Tc in Ni anf Fe. J. Magn. Magn. Mater. 1986, 54, 1169–1170. [Google Scholar] [CrossRef]
- Cable, J.W.; Nicklow, R.M. Spin dynamics of Gd at high temperatures. Phys. Rev. B 1989, 39, 11732–11741. [Google Scholar] [CrossRef]
- Goto, T.; Sakakabara, T.; Yamaguchi, M. Coexistence of nonmagnetic and ferromagnetic Co in Y2Co7 and YCo3 hydrides. J. Magn. Magn. Mater. 1986, 54, 1085–1086. [Google Scholar] [CrossRef]
- Shinogi, A.; Saito, T.; Endo, K. Coexistence of nonmagnetic and magnetic Co in cubic Laves phase compounds Lu(Co1−xAlx)2. J. Phys. Soc. Jpn. 1987, 56, 2633–2636. [Google Scholar] [CrossRef]
- Jaime, M.; Lin, P.; Chun, S.H.; Salamon, M.B.; Dorsey, P.; Rubinshtein, M. Coexistence of localized and itinerant carriers near TC in calcium-doped manganites. Phys. Rev. B 1999, 60, 1028–1032. [Google Scholar] [CrossRef]
- Merithew, R.D.; Weissman, M.B.; Hess, F.M.; Spradling, P.; Nowak, E.R.; O’Donnell, J.; Ekstein, J.M.; Tokura, Y.; Tomioka, Y. Mesoscopic thermodynamics of an inhomogeneous colossal-magnetoresistive phase. Phys. Rev. Lett. 2000, 84, 3442–3445. [Google Scholar] [CrossRef]
- Baio, J.; Barucca, G.; Caciuffo, R.; Rinaldi, D.; Mira, J.; Rivas, J.; Senaris-Rodriguez, M.A.; Fiorani, D. Phase separation, thermal history and magnetic behavior of Sr dopped LaCoO3. J. Phys. Condens. Matter 2000, 12, 9761–9770. [Google Scholar] [CrossRef]
- Sun, J.R.; Shen, B.G.; Gao, J.; Fei, Y.; Nie, Y.P. Presence of a paramagnetic phase well below the ferromagnetic onset in La0.67−xBixCa0.33MnO3. Eur. Phys. Lett. 2003, 62, 732–738. [Google Scholar] [CrossRef][Green Version]
- Batko, I.; Batkova, M.; Tran, V.H.; Keiderling, U.; Filipov, V.B. Evidence for magnetic phase separation in colossal magnetoresistence compound EuB5.99C0.01. Solid State Commun. 2014, 190, 23–27. [Google Scholar] [CrossRef]
- Gibbs, J.W. Collected Works; Longmans: New York, NY, USA, 1928. [Google Scholar]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Yukalov, V.I. Theory of melting and crystallization. Phys. Rev. B 1985, 32, 436–446. [Google Scholar] [CrossRef]
- Yukalov, V.I. Effective Hamiltonians for systems with mixed symmetry. Physica A 1986, 136, 575–587. [Google Scholar] [CrossRef]
- Yukalov, V.I. Renormalization of quasi-Hamiltonians under heterophase averaging. Phys. Lett. A 1987, 125, 95–100. [Google Scholar] [CrossRef]
- Yukalov, V.I. Procedure of quasiaveraging for heterophase mixtures. Physica A 1987, 141, 352–374. [Google Scholar] [CrossRef]
- Yukalov, V.I. Lattice mixtures of fluctuating phases. Physica A 1987, 144, 369–389. [Google Scholar] [CrossRef]
- Marzari, N.; Mostofi, A.A.; Yates, J.R.; Souza, I.; Vanderbilt, D. Maximally localized Wannier functions: Theory and applications. Rev. Mod. Phys. 2012, 84, 1419–1475. [Google Scholar] [CrossRef]
- Bogolubov, N.N. Lectures on Quantum Statistics; Gordon and Breach: New York, NY, USA, 1967; Volume 1. [Google Scholar]
- Bogolubov, N.N. Lectures on Quantum Statistics; Gordon and Breach: New York, NY, USA, 1970; Volume 2. [Google Scholar]
- Bogolubov, N.N. Quantum Statistical Mechanics; World Scientific: Singapore, 2015. [Google Scholar]
- Yukalov, V.I. Microscopic theory of spin reorientations: General analysis. Physica A 1990, 167, 861–876. [Google Scholar] [CrossRef]
- Yukalov, V.I.; Yukalova, E.P. Statistics of multiscale fluctuations in macromolecular systems. J. Phys. Chem. B 2012, 116, 8435–8448. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yukalov, V.I.; Yukalova, E.P. Mesoscopic disorder in double well optical lattices. Laser Phys. 2011, 21, 1448–1458. [Google Scholar] [CrossRef]
- Ono, S.; Kondo, S. Molecular Theory of Surface Tension in Liquids; Springer: Berlin, Germany, 1960. [Google Scholar]
- Rusanov, A.I. Problems of surface thermodynamics. Pure Appl. Chem. 1992, 64, 111–124. [Google Scholar] [CrossRef]
- Kjelstrup, S.; Bedeaux, D. Non-Equilibrium Thermodynamics of Heterogeneous Systems; World Scientific: Singapore, 2008. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).