On the Semi-Analytical Solutions in Hydrodynamics of Ideal Fluid Flows Governed by Large-Scale Coherent Structures of Spiral-Type
Abstract
:1. Introduction, Equations of Motion
2. The General Form of Coherent Spiral-Type Fluid Structures Which Drive the Fluid of Incompressible Flows of Euler Equations via Rotation
3. Presentation of the Time-Dependent Part of Solution
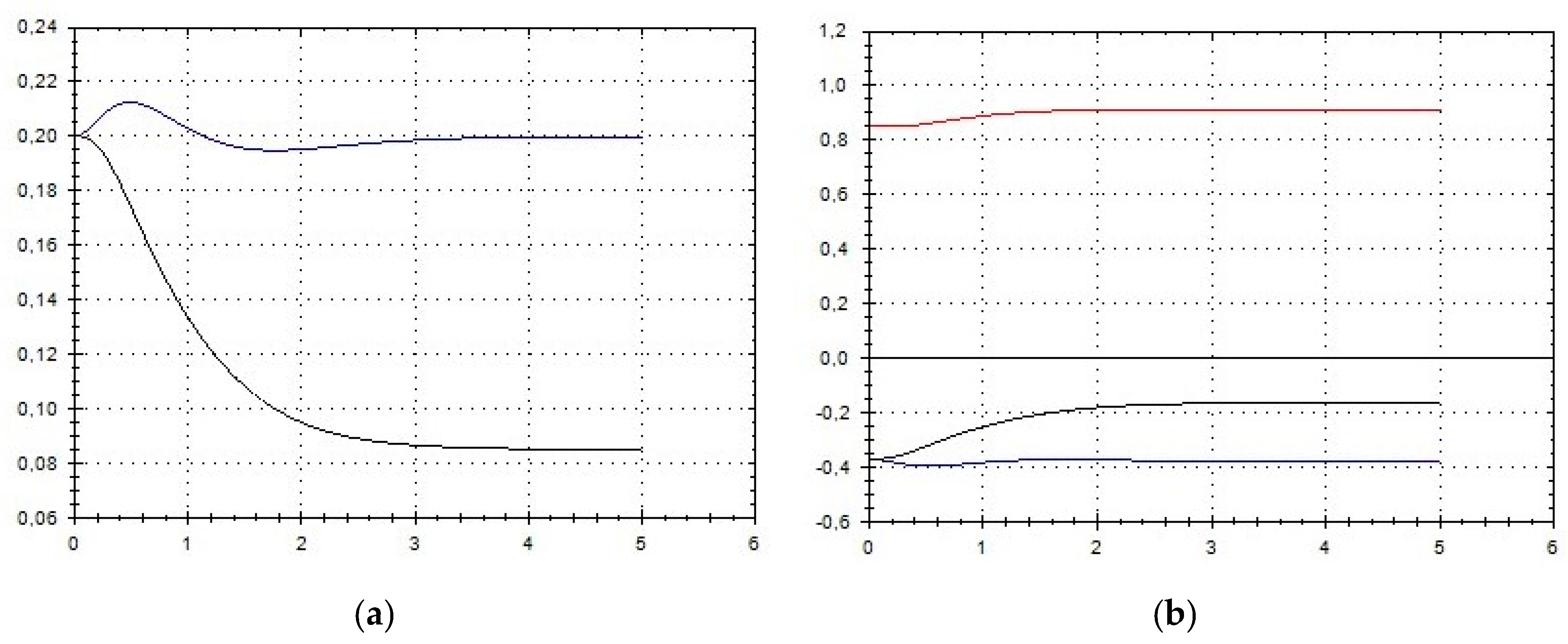
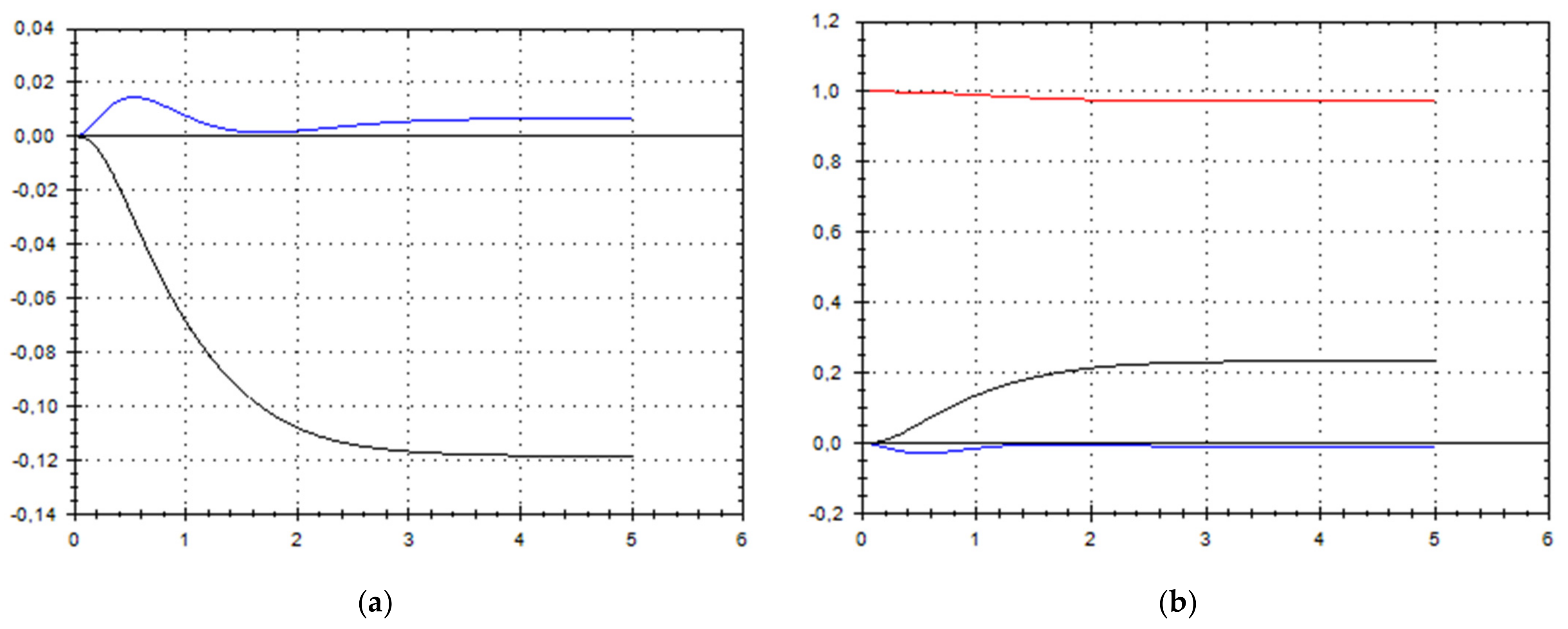
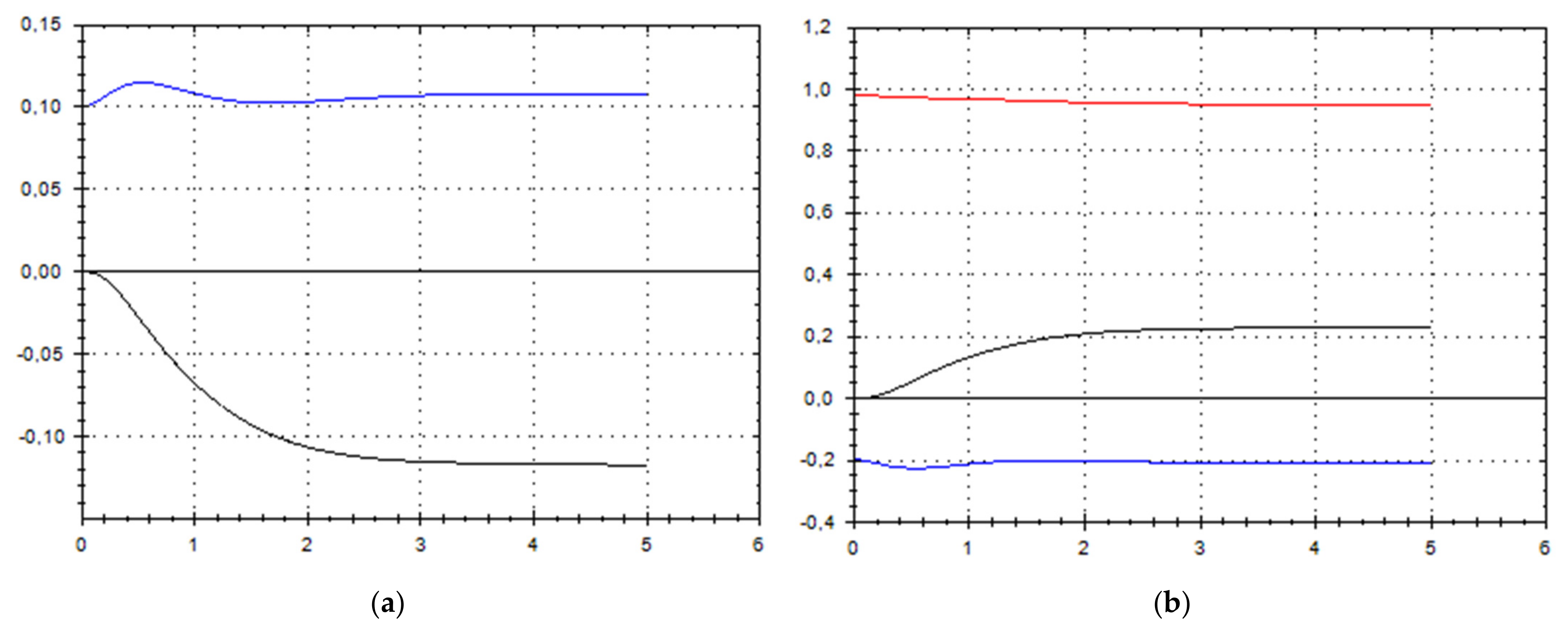
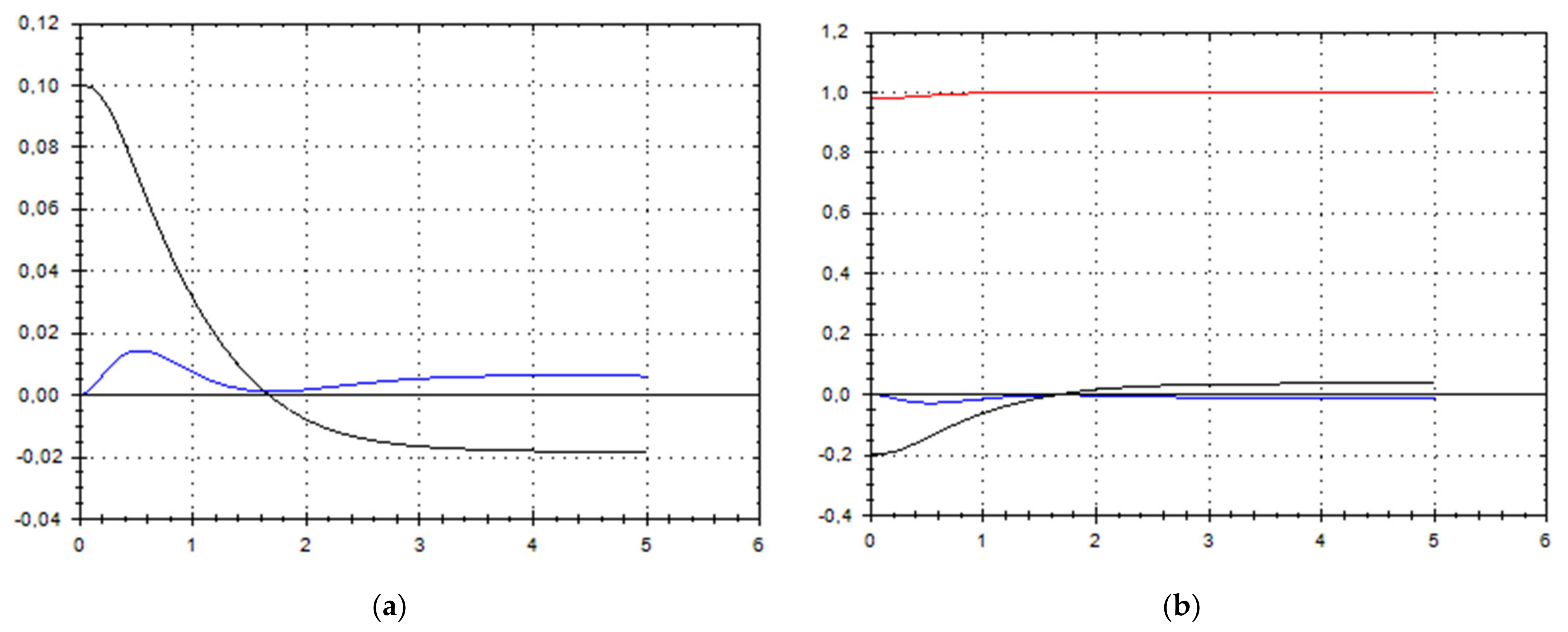
4. Final Presentation of the Solution
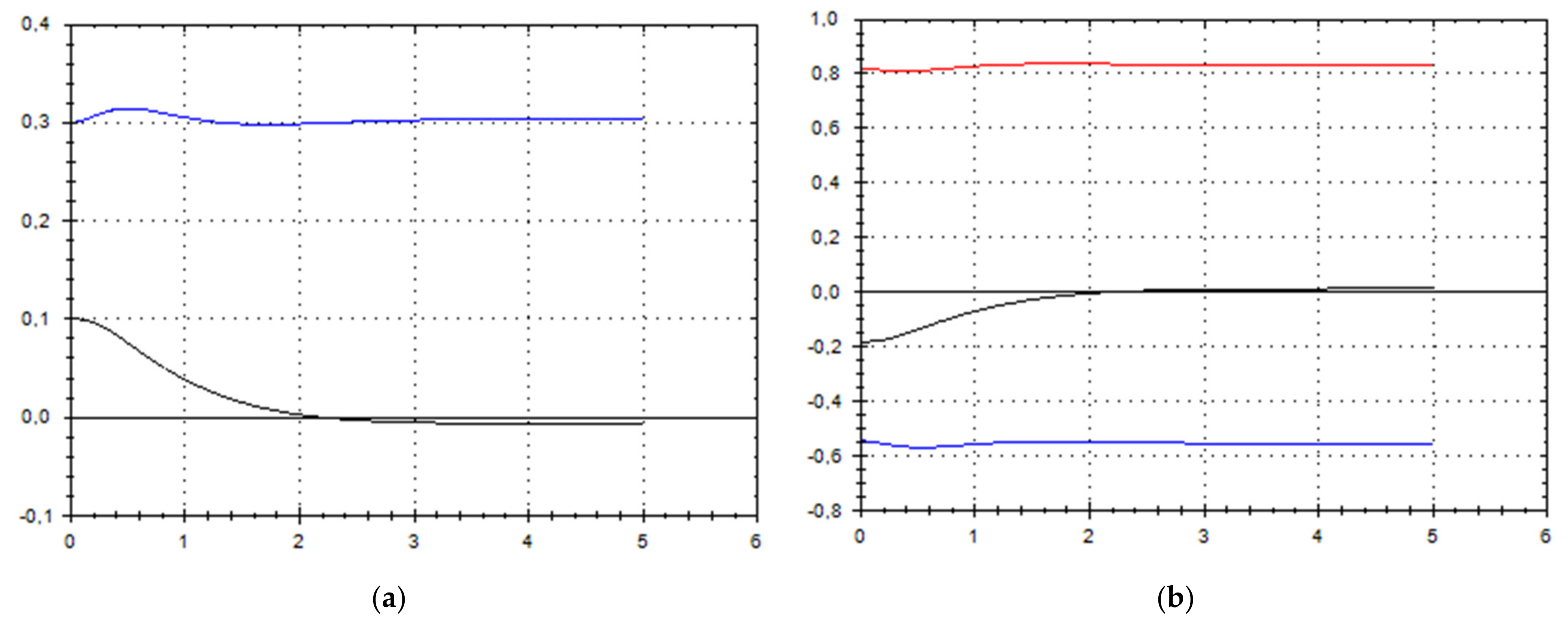
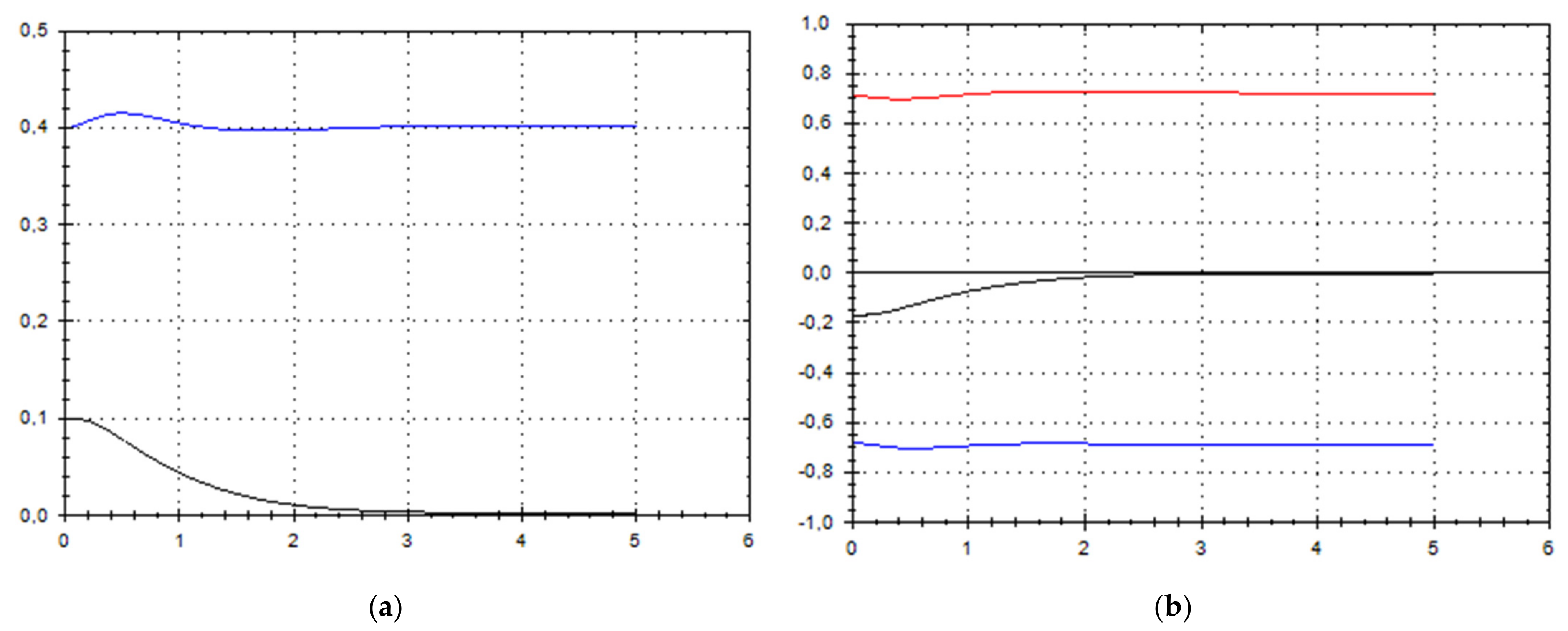
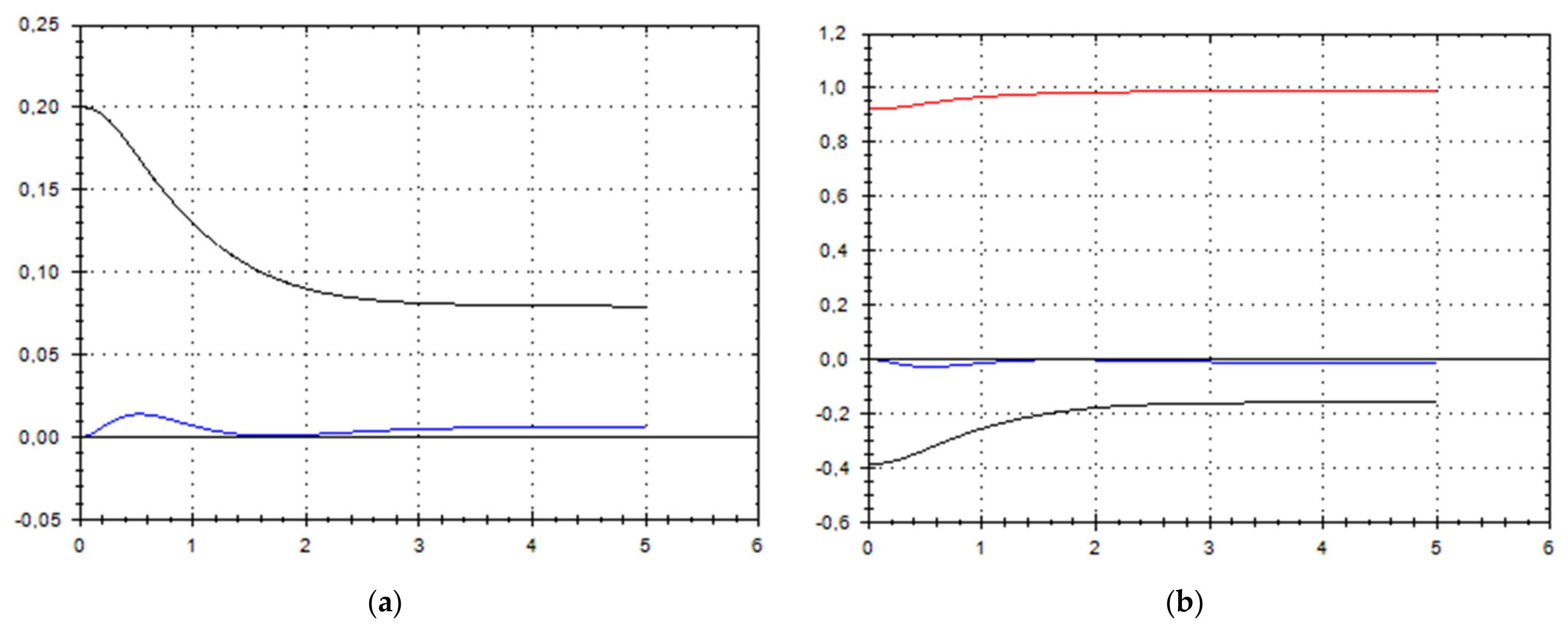
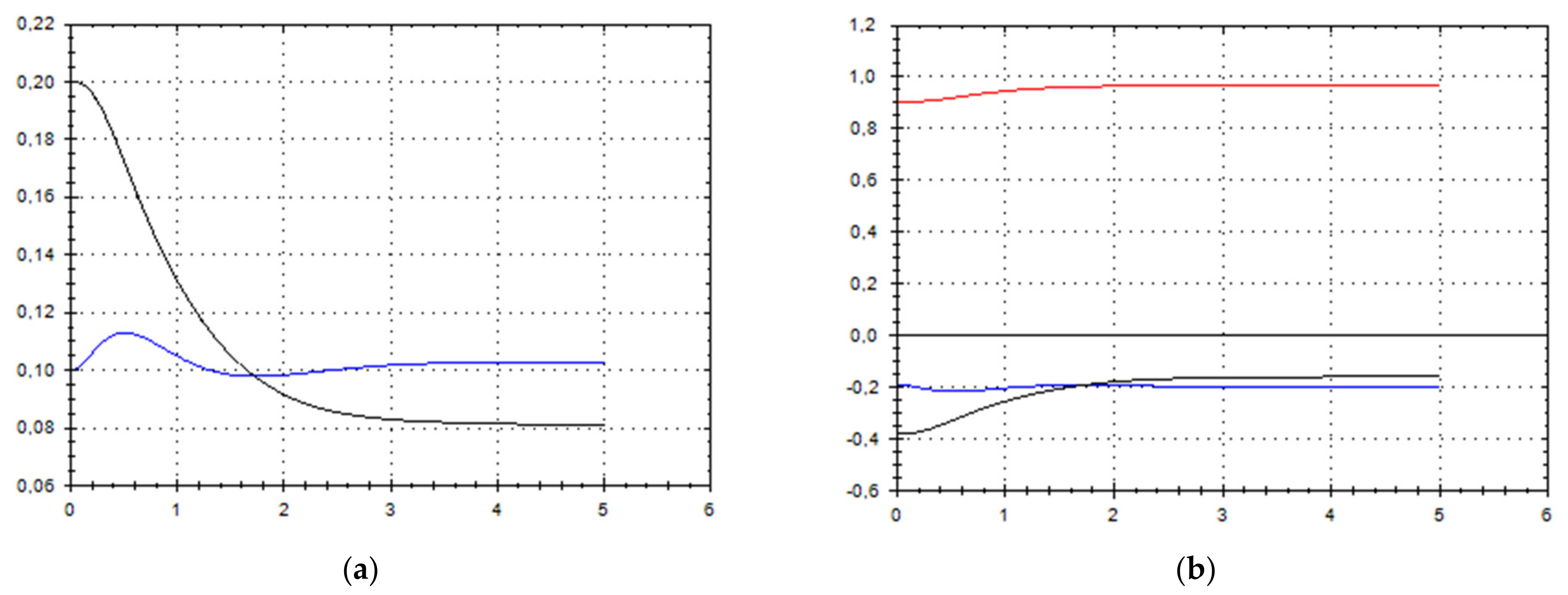
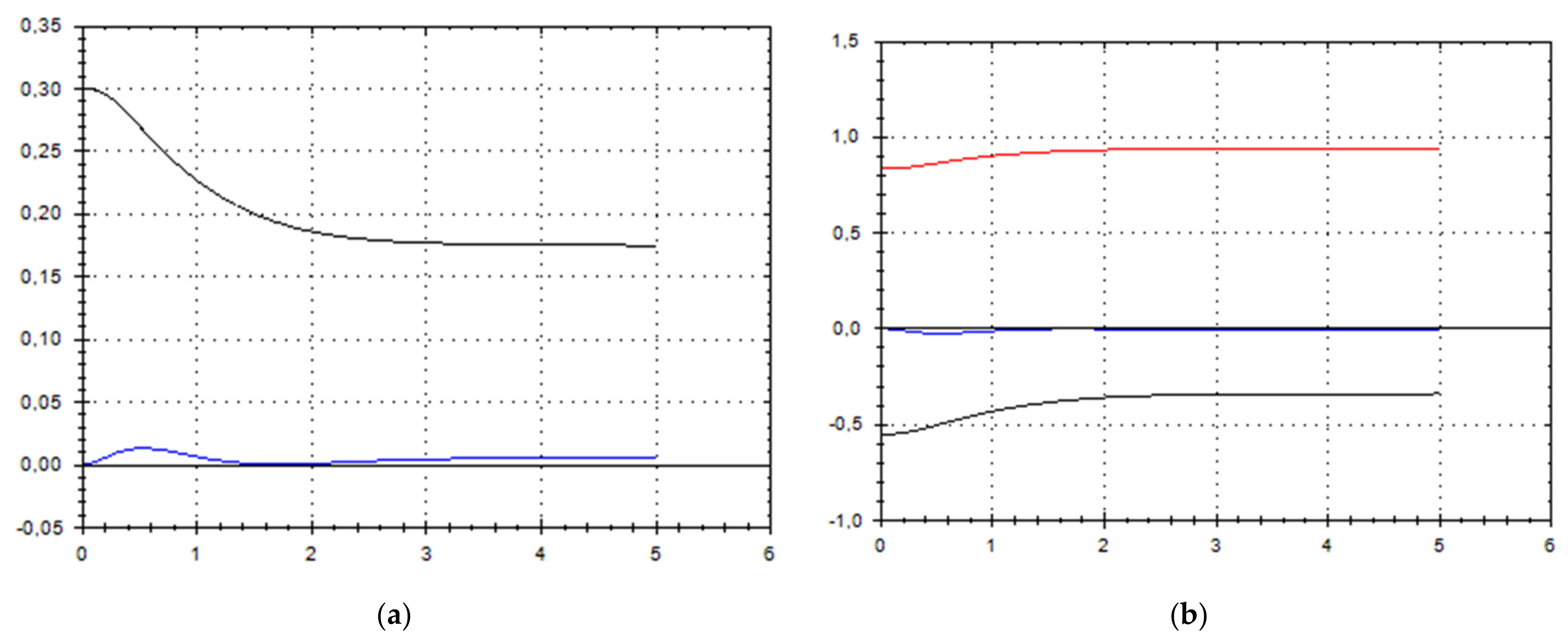
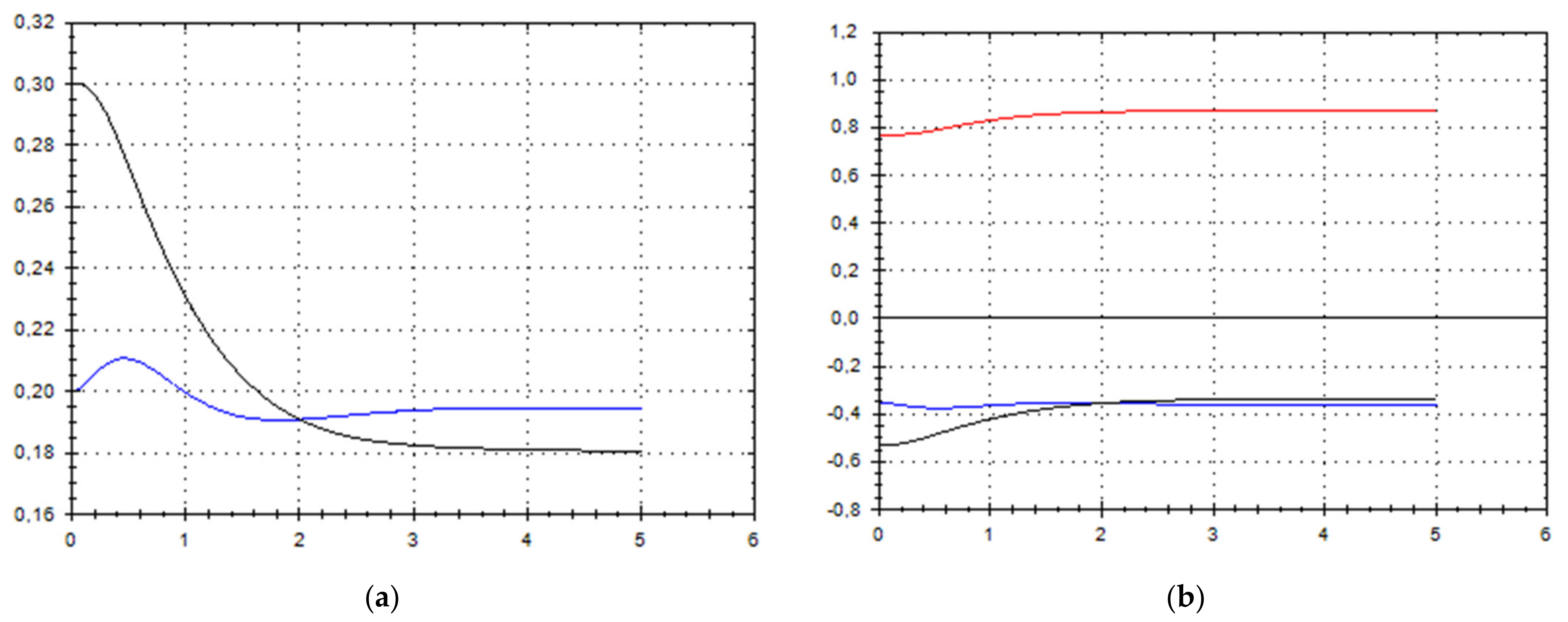
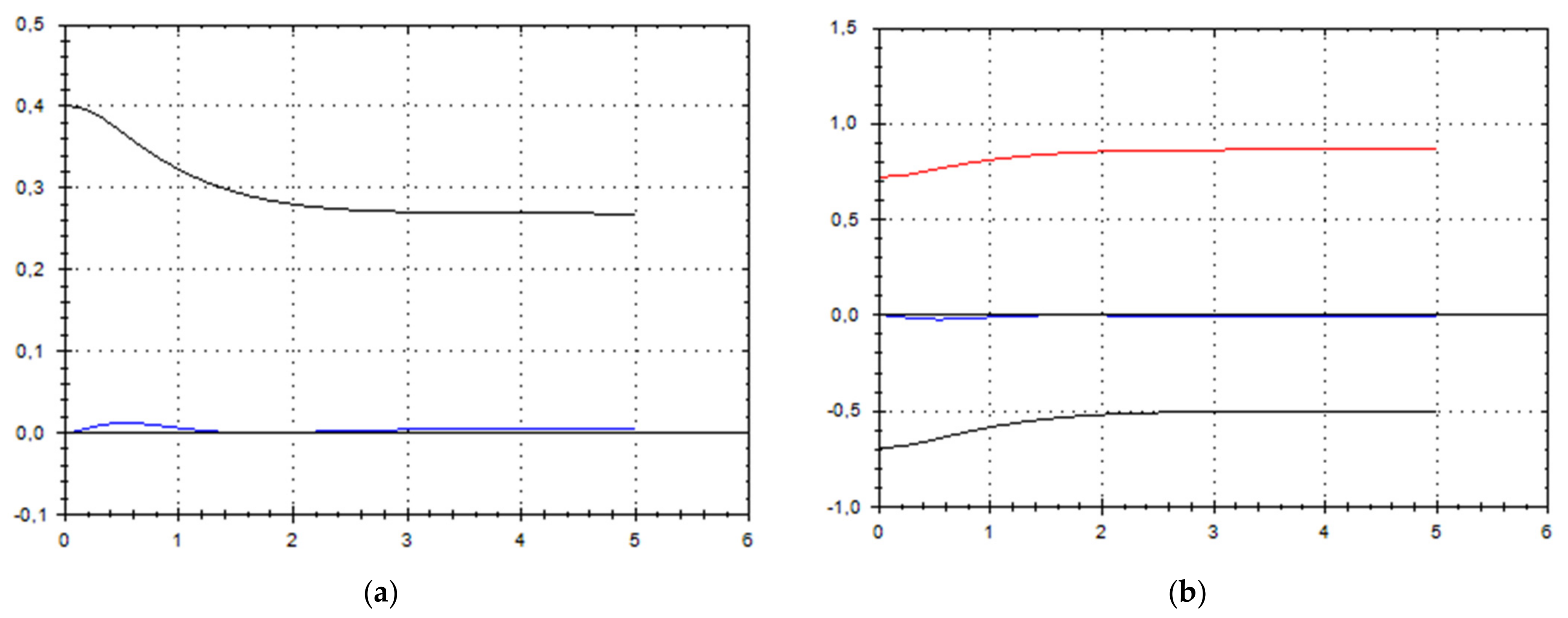
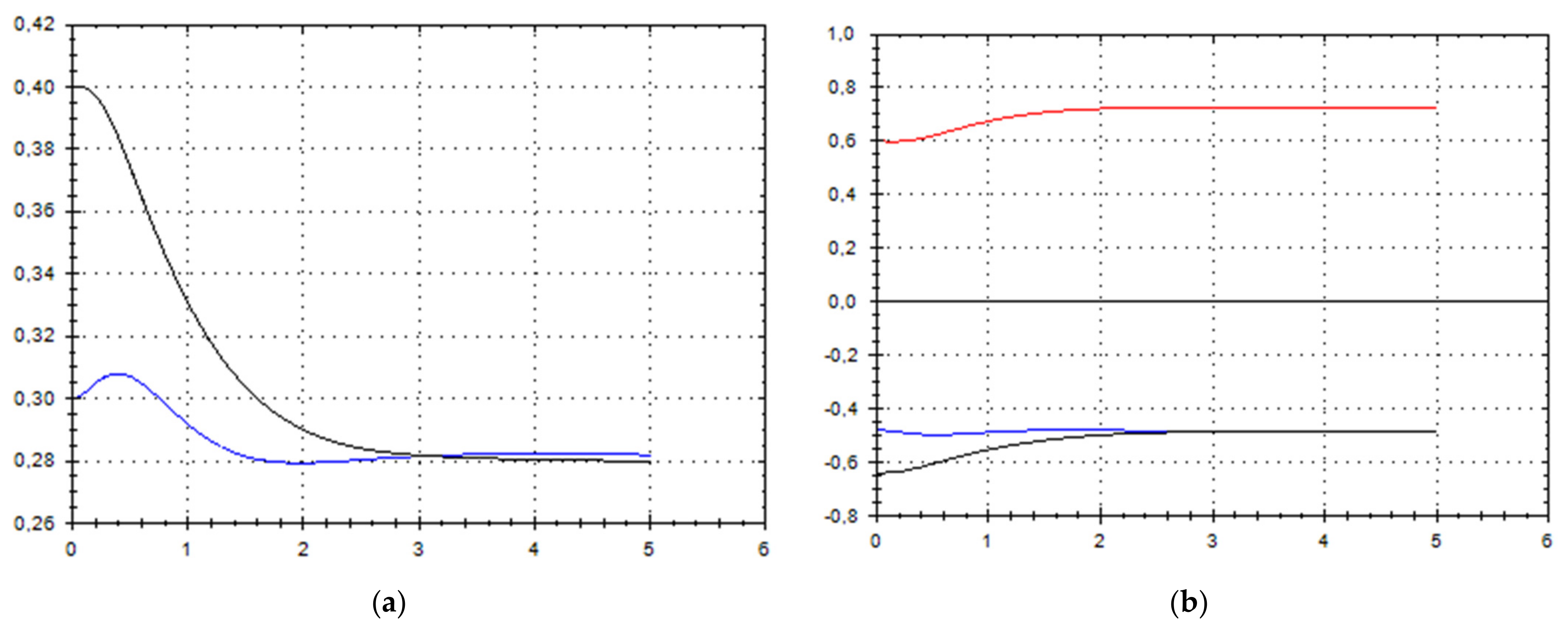
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| the flow velocity, m⋅s−1 | |
| p | internal pressure, Pa |
| F | external volumetric force acting per unit of mass of the fluid, m⋅s−2 |
| the curl field, s−1 | |
| B | Bernoulli-function, Pa |
| {U, V, W} | components of flows velocity of the large-scale coherent structure in a fluid flow, m⋅s−1 |
| A | angular velocity of spiral rotation, s−1 |
| {a, b} | the real-valued solutions of the mutual system of two Riccati ODEs, dimensionless |
| Greek symbols | |
| ρ | the density of fluid, kg⋅m−3 |
| φ | potential of external volumetric force F, Pa |
| σ | spiral factor, m⋅s−1 |
| γ | arbitrary function, m⋅s−1 |
| ξ | arbitrary function, m⋅s−1 |
| Ω | denotation for function, m−1⋅s−1 |
| α | positive constant, m⋅s−1 |
| β | positive constant, s−1 |
| Subscripts | |
| 1, 2, 3 | components of flow velocity in the Ox, Oy, Oz-directions |
References
- Samelson, R.M. Lagrangian Motion, Coherent Structures, and Lines of Persistent Material Strain. Annu. Rev. Mar. Sci. 2013, 5, 137–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Malhotra, N.; Mezić, I.; Wiggins, S. Patchiness: A new diagnostic for Lagrangian trajectory analysis in time-dependent fluid flows. Int. J. Bifurc. Chaos 1998, 8, 1053–1093. [Google Scholar] [CrossRef]
- Gnosh, A.; Suara, K.; Yu, Y.; Zhang, H.; Brown, R.J. Using Lagrangian Coherent Structures to Investigate Tidal Transport Barriers in Moreton Bay, Queensland. In Proceedings of the 21st Australasian Fluid Mechanics Conference Adelaide, Adelaide, Australia, 10–13 December 2018. [Google Scholar]
- Saffman, P.G. Vortex Dynamics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, Course of Theoretical Physics 6, 2nd ed.; Pergamon Press: Cambridge, UK, 1987; ISBN 0-08-033932-8. [Google Scholar]
- Ershkov, S.V.; Shamin, R.V. A Riccati-type solution of 3D Euler equations for incompressible flow. J. King Saud Univ.-Sci. 2020, 32, 125–130. [Google Scholar] [CrossRef]
- Ershkov, S.V. On Existence of General Solution of the Navier-Stokes Equations for 3D Non-Stationary Incompressible Flow. Int. J. Fluid Mech. Res. 2015, 42, 206–213. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.V. Non-stationary Riccati-type flows for incompressible 3D Navier-Stokes equations. Comput. Math. Appl. 2015, 71, 1392–1404. [Google Scholar] [CrossRef]
- Ershkov, S.V. A procedure for the construction of non-stationary Riccati-type flows for incompressible 3D Navier-Stokes equations. Rend. Circ. Mat. Palermo 2016, 65, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Ershkov, S.V.; Giniyatullin, A.R.; Shamin, R.V. On a new type of non-stationary helical flows for incompressible 3D Navier-Stokes equations. J. King Saud Univ.-Sci. 2020, 32, 459–467. [Google Scholar] [CrossRef]
- Ershkov, S.V.; Shamin, R.V. On a new type of solving procedure for Laplace tidal equation. Phys. Fluids 2018, 30, 127107. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Green, M.A. Detection and tracking of vortex phenomena using Lagrangian coherent structures. Exp. Fluids 2015, 56, 147. [Google Scholar] [CrossRef]
- Wang, N.; Dand, T.; Lei, I.; Wang, W.; Datta-Barrua, S. Alignment of High-Latitude Ionospheric and Thermospheric Lagrangian Coherent Structures. J. Geophys. Res.: Space Phys. 2021, 126, e2020JA029028. [Google Scholar] [CrossRef]
- Si, X.; Fang, L. Preferential alignment and heterogeneous distribution of active non-spherical swimmers near Lagrangian coherent structures. Phys. Fluids 2021, 33, 073303. [Google Scholar] [CrossRef]
- Wang, K.; Zou, L.; Zhang, I.; Jiang, Y.; Zhao, P. Lagrangian coherent structures and material transport in unsteady flow of vertical-axis turbine wakes. AIP Adv. 2021, 11, 085001. [Google Scholar] [CrossRef]
- Lin, S.-J.; Xiang, Y.; Li, Z.-Q.; Wang, F.-X.; Liu, H. Evolution of the Lagrangian drift and vortex added-mass of a growing vortex ring. J. Hydrodyn. 2021, 33, 725–735. [Google Scholar] [CrossRef]
- Verma, V.; Sarkar, S. Lagrangian three-dimensional transport and dispersion by submesoscale currents at an upper-ocean front. Ocean Model. 2021, 165, 101844. [Google Scholar] [CrossRef]
- Zhang, Y.-W.; Feng, Y.-L.; Feng, C.-A.; Wang, Z.-W.; Zhang, X.-Q. Study on Lagrangian Coherent Structure of tidal current field in Laizhou Bay. Shuidonglixue Yanjiu yu Jinzhan/Chin. J. Hydrodyn. Ser. A 2021, 36, 95–101. [Google Scholar]
- Koptev, A.V. Generator of solutions for 2D Navier-Stokes equations. J. Sib. Fed. Univ. 2014, 7, 324–330. [Google Scholar]
- Koptev, A.V. Integrals of Motion of an Incompressible Medium Flow. From Classic to Modern. In Handbook of Navier-Stokes Equations: Theory and Applied Analysis; Nova Science Publishers: New York, NY, USA, 2017; pp. 443–460. [Google Scholar]
- Koptev, A.V. Method for Solving the Navier-Stokes and Euler Equations of Motion for Incompressible Media. J. Math. Sci. 2020, 250, 10–21. [Google Scholar] [CrossRef]
- Koptev, A.V. Exact Solutions of 3D Navier-Stokes Equations. J. Sib. Fed. Univ. Math. Phys. 2020, 13, 306–313. [Google Scholar] [CrossRef]
- Semenov, V.I. Some new identities for solenoidal fields and applications. Mathematics 2014, 2, 29–36. [Google Scholar] [CrossRef] [Green Version]
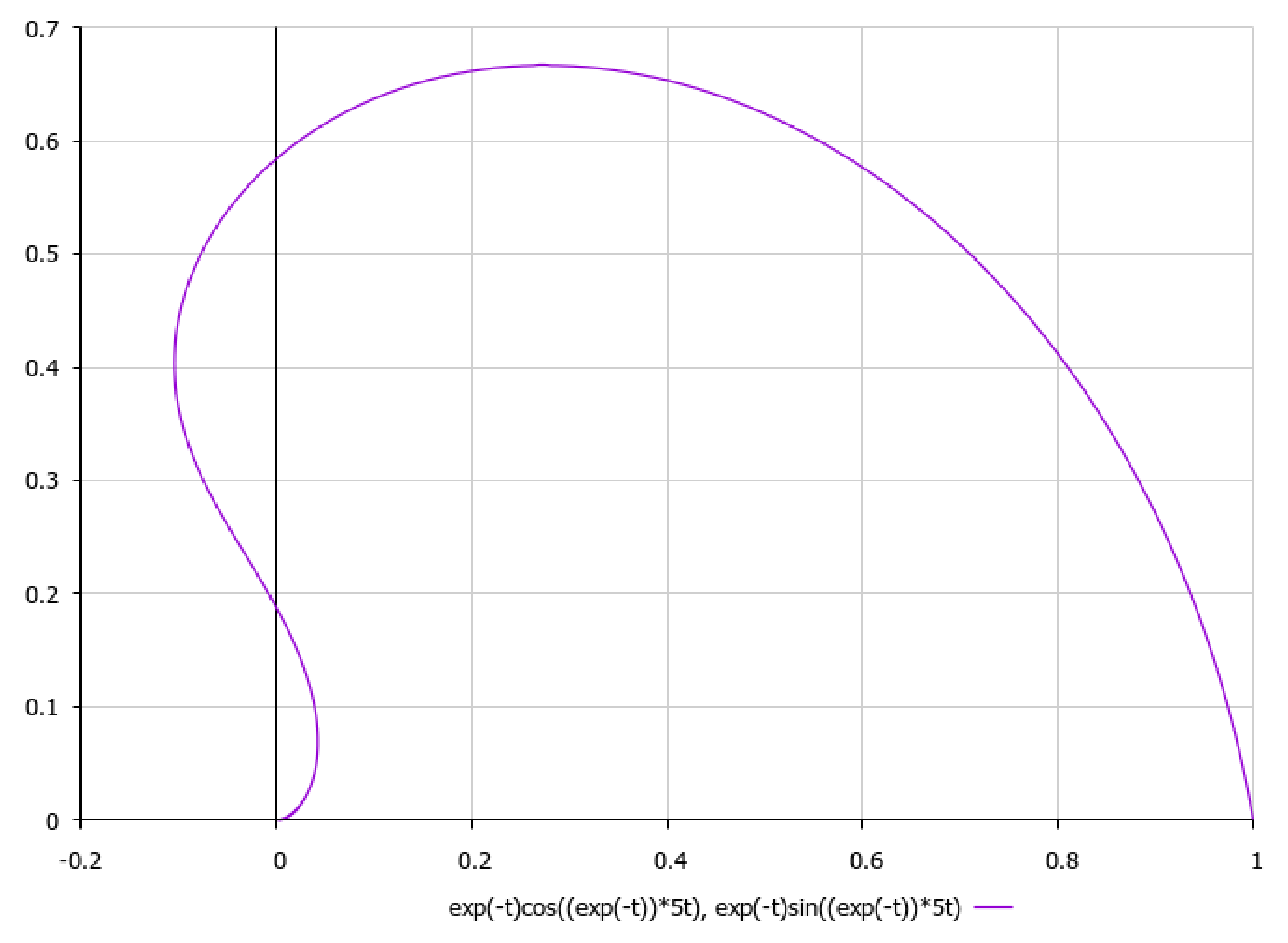
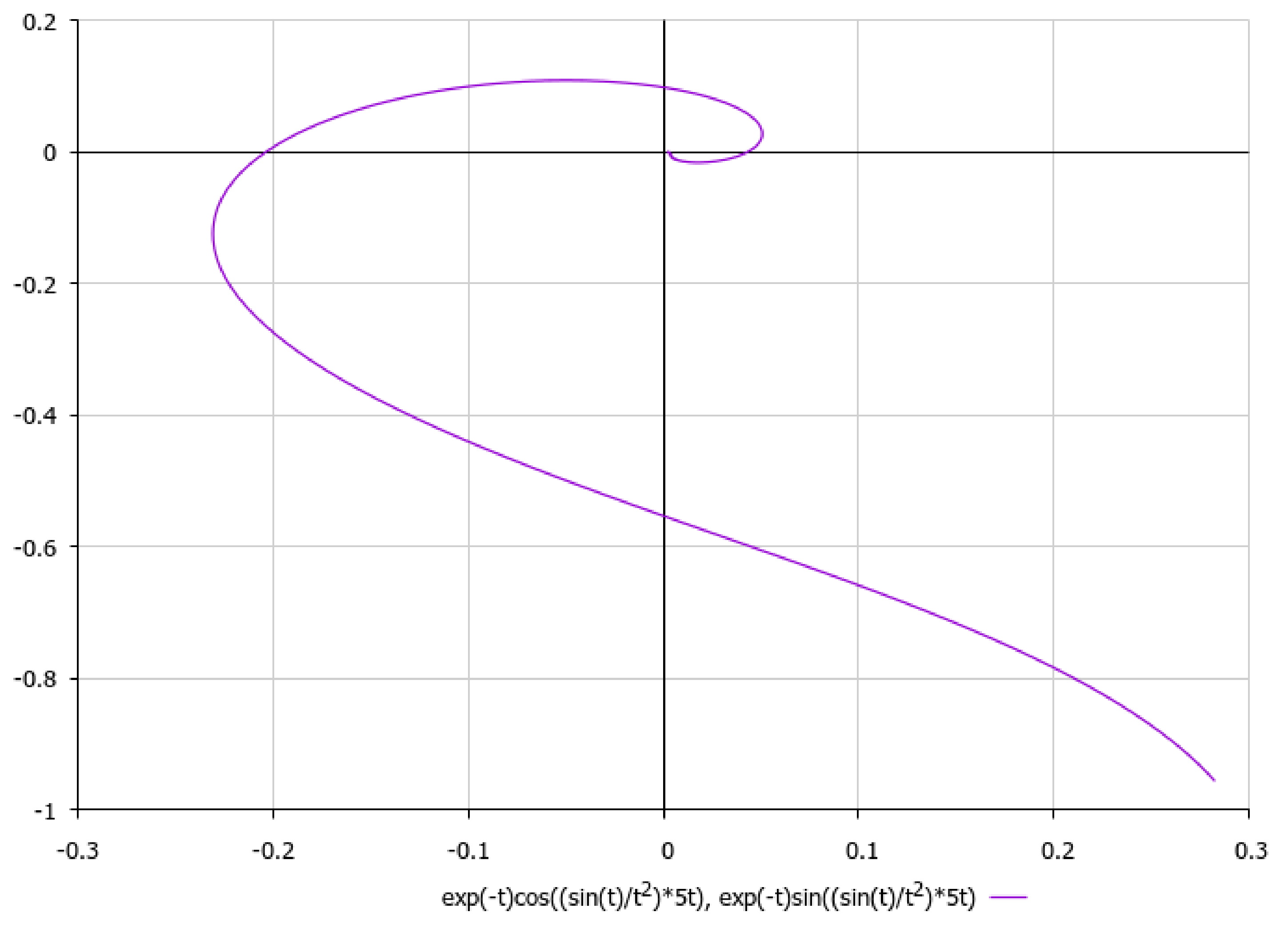
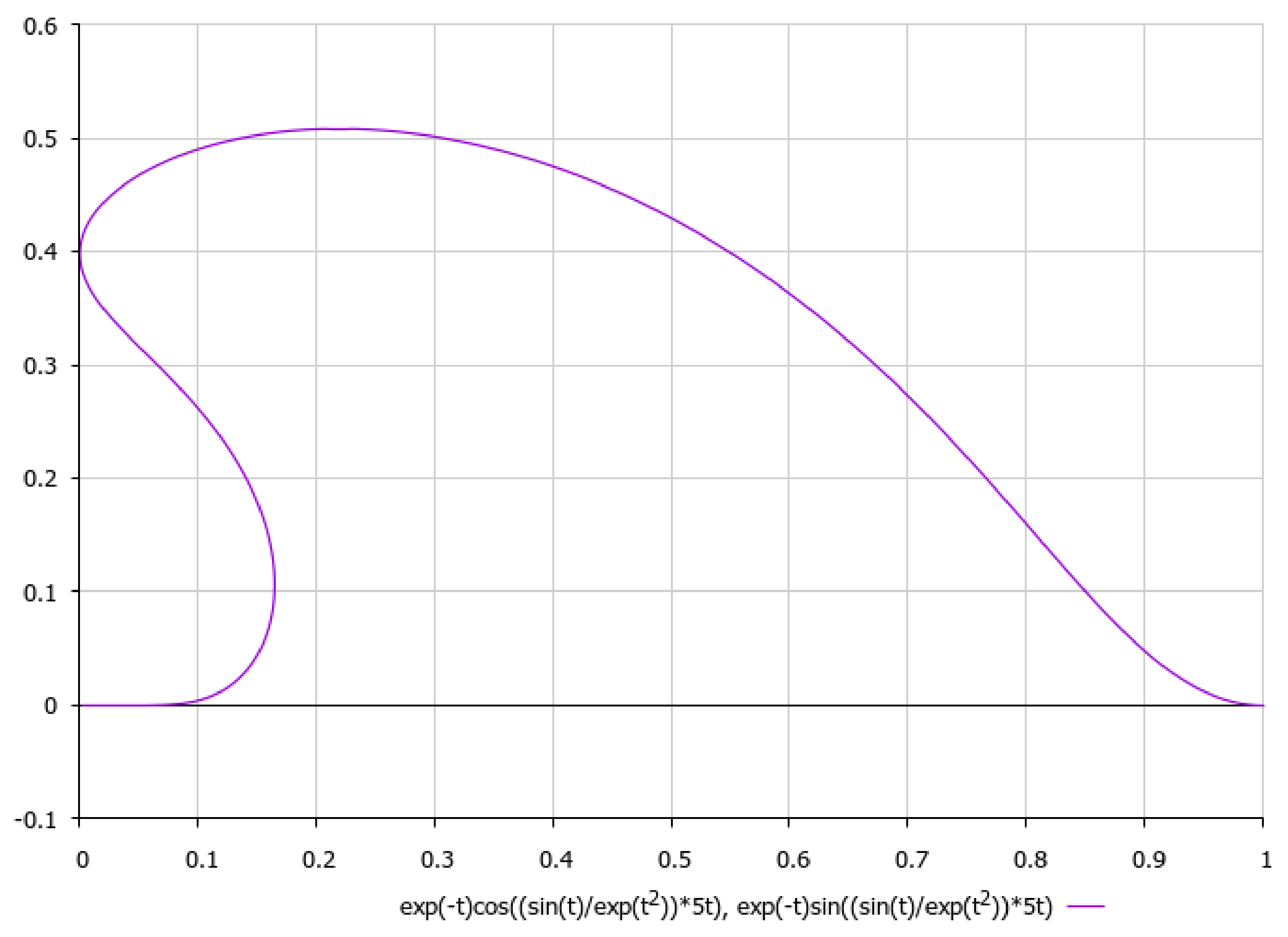
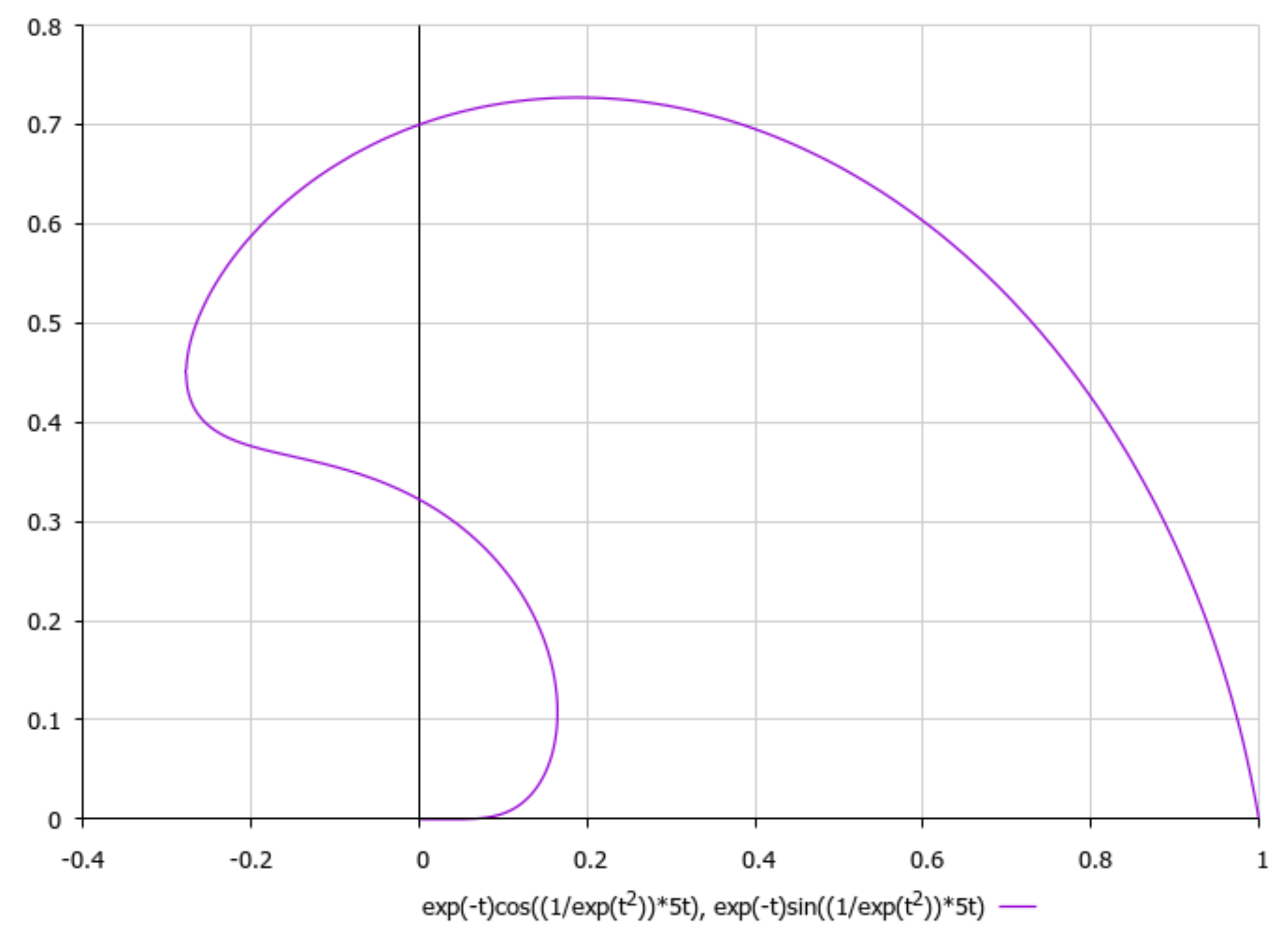

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ershkov, S.V.; Rachinskaya, A.; Prosviryakov, E.Y.; Shamin, R.V. On the Semi-Analytical Solutions in Hydrodynamics of Ideal Fluid Flows Governed by Large-Scale Coherent Structures of Spiral-Type. Symmetry 2021, 13, 2307. https://doi.org/10.3390/sym13122307
Ershkov SV, Rachinskaya A, Prosviryakov EY, Shamin RV. On the Semi-Analytical Solutions in Hydrodynamics of Ideal Fluid Flows Governed by Large-Scale Coherent Structures of Spiral-Type. Symmetry. 2021; 13(12):2307. https://doi.org/10.3390/sym13122307
Chicago/Turabian StyleErshkov, Sergey V., Alla Rachinskaya, Evgenii Yu. Prosviryakov, and Roman V. Shamin. 2021. "On the Semi-Analytical Solutions in Hydrodynamics of Ideal Fluid Flows Governed by Large-Scale Coherent Structures of Spiral-Type" Symmetry 13, no. 12: 2307. https://doi.org/10.3390/sym13122307
APA StyleErshkov, S. V., Rachinskaya, A., Prosviryakov, E. Y., & Shamin, R. V. (2021). On the Semi-Analytical Solutions in Hydrodynamics of Ideal Fluid Flows Governed by Large-Scale Coherent Structures of Spiral-Type. Symmetry, 13(12), 2307. https://doi.org/10.3390/sym13122307







