Analysis of Sound Absorption Characteristics of Acoustic Ducts with Periodic Additional Multi-Local Resonant Cavities
Abstract
:1. Introduction
2. Characteristics of Acoustic Pipe Added Multiple Local Resonant Cavities
2.1. Cell of Acoustic Pipe Added Multiple Local Resonant Cavities
2.2. Acoustic Pipe with Periodic Multiple Local Resonant Cavities
3. Transmission Loss of the Acoustic Duct with Periodic Multi-Local Resonant Cavity with Single Plate with Mass
3.1. Parameters for Simulation
3.2. Transmission Loss of Multi-Local Resonant Cavity Acoustic Duct with Periodic Plate with Mass
3.3. Band Structure Analysis of Multi-Local Resonant Cavity with Additional Plate and Mass
4. Transmission Loss of the Acoustic Duct with Periodic Multi-Local Resonant Cavity with Several Plates with Masses
4.1. Transmission Loss of Acoustic Duct with Periodic Multi-Local Resonant Cavity with Two Plates with Masses
4.1.1. Transmission Loss of Multi-Local Resonant Cavity with Two Plates with Masses
4.1.2. Transmission Loss of the Acoustic Duct with Periodic Multi-Local Resonant Cavity with Two Plates with Masses
4.2. Transmission Loss of Acoustic Duct with Periodic Multi-Local Resonant Cavity with Three Plates with Masses
4.2.1. Transmission Loss of Multi-Local Resonant Cavity with Three Plates with Masses
4.2.2. Transmission Loss of Acoustic Duct with Periodic Multi-Local Resonant Cavity with Three Plates with Masses
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, J.H.; Ma, F.Y.; Zhang, S.W.; Shen, L. Application of Acoustic Metamaterials in Low-frequency Vibration and Noise Reduction. J. Mech. Eng. 2016, 52, 68–78. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Z.F.; Yu, D.L.; Liu, J.W.; Wen, J.H. Properties of band gaps in phononic crystal pipe consisting of expansion chambers with extended inlet/outlet. Acta Phys. Sin. 2018, 67, 153–164. (In Chinese) [Google Scholar] [CrossRef]
- Chen, L.Q. The muffling principle and application of Helmholtz resonator. Phys. Bull. 1992, 4, 37–38. (In Chinese) [Google Scholar]
- Munjal, M.L. Acoustics of Ducts and Mufflers; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Cai, C.; Mak, C.M. Noise attenuation capacity of a Helmholtz resonator. Adv. Eng. Softw. 2018, 116, 60–66. [Google Scholar] [CrossRef]
- Cai, C.; Mak, C.M. Hybrid noise control in a duct using a periodic dual Helmholtz resonator array. Appl. Acoust. 2018, 134, 119–124. [Google Scholar] [CrossRef]
- Langfeldt, F.; Hoppen, H.; Gleine, W. Resonance frequencies and sound absorption of Helmholtz resonators with multiple necks. Appl. Acoust. 2019, 145, 314–319. [Google Scholar] [CrossRef]
- Ge, M.X.; Li, G. Acoustic Characteristics of Double Neck Helmholtz Resonators. Noise Vib. Control 2020, 40, 231–234. (In Chinese) [Google Scholar]
- Zhang, X.X.; Liu, Y.R.; Li, L.J. Research on acoustic metamaterial based on Helmholtz resonant cavity array. Chin. J. Eng. Des. 2020, 27, 441–447. (In Chinese) [Google Scholar]
- Guan, D.; Zhao, D.; Ren, Z. Aeroacoustic Attenuation Performance of a Helmholtz Resonator with a Rigid Baffle Implemented in the Presence of a Grazing Flow. Int. J. Aerosp. Eng. 2020, 2020, 1916239. [Google Scholar] [CrossRef]
- Zhou, R.; Wu, W.G.; Wen, Y.F. An acoustic metamaterial based on Helmholtz resonator with thin membrane. Tech. Acoust. 2017, 36, 297–302. (In Chinese) [Google Scholar]
- Zhou, C.G.; Liu, B.L.; Li, X.D.; Tian, J. Effect of elastic cavity walls on acoustic characteristics of a water-filled Helmholtz resonator: Equivalent lumped parameter model for cylindrical cavity. Acta Acust. 2007, 32, 426–434. [Google Scholar]
- Cui, S.; Harne, R.L. Acoustic-Structure Interaction in an Adaptive Helmholtz Resonator by Compliance and Constraint. J. Vib. Acoust. 2020, 142, 1–39. [Google Scholar] [CrossRef]
- Liu, J.B.; Lv, H.F.; Wang, P.H.; Ji, Y.L. Research on the pipeline silencing characteristics of membrane-type acoustic metamaterial. Tech. Acoust. 2019, 38, 206–211. (In Chinese) [Google Scholar]
- Li, Y.F.; Shen, H.J.; Zhang, L.K.; Su, Y.S. Sound propagation characteristics of a metamaterials-type periodic pipe and its low-frequency broadband control. Acta Acust. 2017, 42, 334–340. (In Chinese) [Google Scholar]
- Zhang, X.G.; Lv, H.F.; Lv, C.M.; Zhang, W.H. Double local resonance effect acoustic metamaterial muffling performance. J. Aerosp. Power 2020, 35, 52–59. (In Chinese) [Google Scholar]
- Hu, G.; Tang, L.; Cui, X. On the modelling of membrane-coupled Helmholtz resonator and its application in acoustic metamaterial system. Mech. Syst. Signal Process. 2019, 132, 595–608. [Google Scholar] [CrossRef]
- Shen, H.J.; Yu, D.L.; Tang, Z.Y.; Su, Y.S.; Li, Y.F.; Liu, J.W. Characteristics of low-frequency noise elimination in a fluid-filled pipe of dark acoustic metamaterial type. Acta Phys. Sin. 2019, 68, 144301. (In Chinese) [Google Scholar] [CrossRef]
- Catapane, G.; Magliacano, D.; Petrone, G.; Casaburo, A.; Franco, F.; De Rosa, S. Transmission Loss Analyses on Different Angular Distributions of Periodic Inclusions in a Porous Layer. Aerotec. Missili Spaz. 2021. [Google Scholar] [CrossRef]
- Weisser, T.; Groby, J.-P.; Dazel, O.; Gaultier, F.; Deckers, E.; Futatsugi, S.; Monteiro, L. Acoustic behavior of a rigidly backed poroelastic layer with periodic resonant inclusions by a multiple scattering approach. J. Acoust. Soc. Am. 2016, 139, 617–629. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Assouar, M.B.; Sun, J.-H.; Lin, F.-S.; Hsu, J.-C. Hybrid phononic crystal plates for lowering and widening acoustic band gaps. Ultrasonics 2014, 54, 2159–2164. [Google Scholar] [CrossRef]
- Song, Y.; Feng, L.; Liu, Z.; Wen, J.; Yu, D. Suppression of the vibration and sound radiation of a sandwich plate via periodic design. Int. J. Mech. Sci. 2019, 150, 744–754. [Google Scholar] [CrossRef]
- Du, G.H.; Zhu, Z.M.; Gong, X.F. Fundamentals of Acoustics; Nanjing University Press: Nanjing, China, 2012. [Google Scholar]
- Sugimoto, N.; Horioka, T. Dispersion characteristics of sound waves in a tunnel with an array of Helmholtz resonators. Acoust. Soc. Am. J. 1995, 97, 1446–1459. [Google Scholar] [CrossRef]





















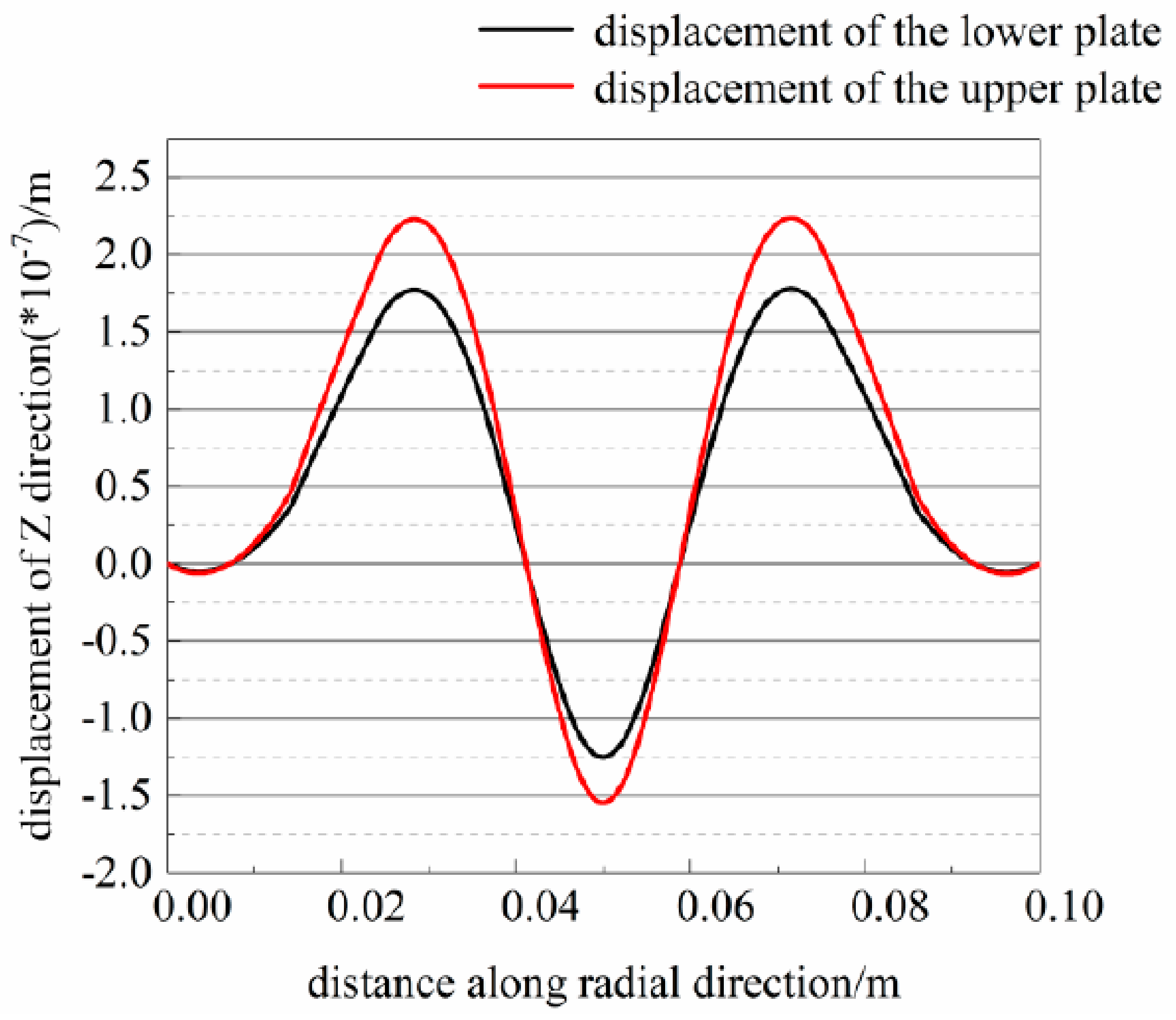













| Parameters/Units | Definition | Value |
|---|---|---|
| density of air | 1.25 | |
| sound speed in air | 343 | |
| d/m | length of cell | 0.5 |
| a/m | cross section length of duct | |
| /m | the neck radius | |
| /m | length of the neck | |
| /m | cavity radius | |
| /m | height of upper cavity | |
| /m | height of lower cavity | |
| density of plate | 1000 | |
| h/m | thickness of plate | 0.001 |
| μ | Possion’s ratio of plate | 0.4 |
| m/kg | mass of mass block |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Wang, T.; Chen, M. Analysis of Sound Absorption Characteristics of Acoustic Ducts with Periodic Additional Multi-Local Resonant Cavities. Symmetry 2021, 13, 2233. https://doi.org/10.3390/sym13122233
Liu J, Wang T, Chen M. Analysis of Sound Absorption Characteristics of Acoustic Ducts with Periodic Additional Multi-Local Resonant Cavities. Symmetry. 2021; 13(12):2233. https://doi.org/10.3390/sym13122233
Chicago/Turabian StyleLiu, Junyi, Ting Wang, and Meixia Chen. 2021. "Analysis of Sound Absorption Characteristics of Acoustic Ducts with Periodic Additional Multi-Local Resonant Cavities" Symmetry 13, no. 12: 2233. https://doi.org/10.3390/sym13122233
APA StyleLiu, J., Wang, T., & Chen, M. (2021). Analysis of Sound Absorption Characteristics of Acoustic Ducts with Periodic Additional Multi-Local Resonant Cavities. Symmetry, 13(12), 2233. https://doi.org/10.3390/sym13122233







