First Principles Calculation of the Topological Phases of the Photonic Haldane Model
Abstract
:1. Introduction
2. The Haldane Model
2.1. The Electronic Haldane Model
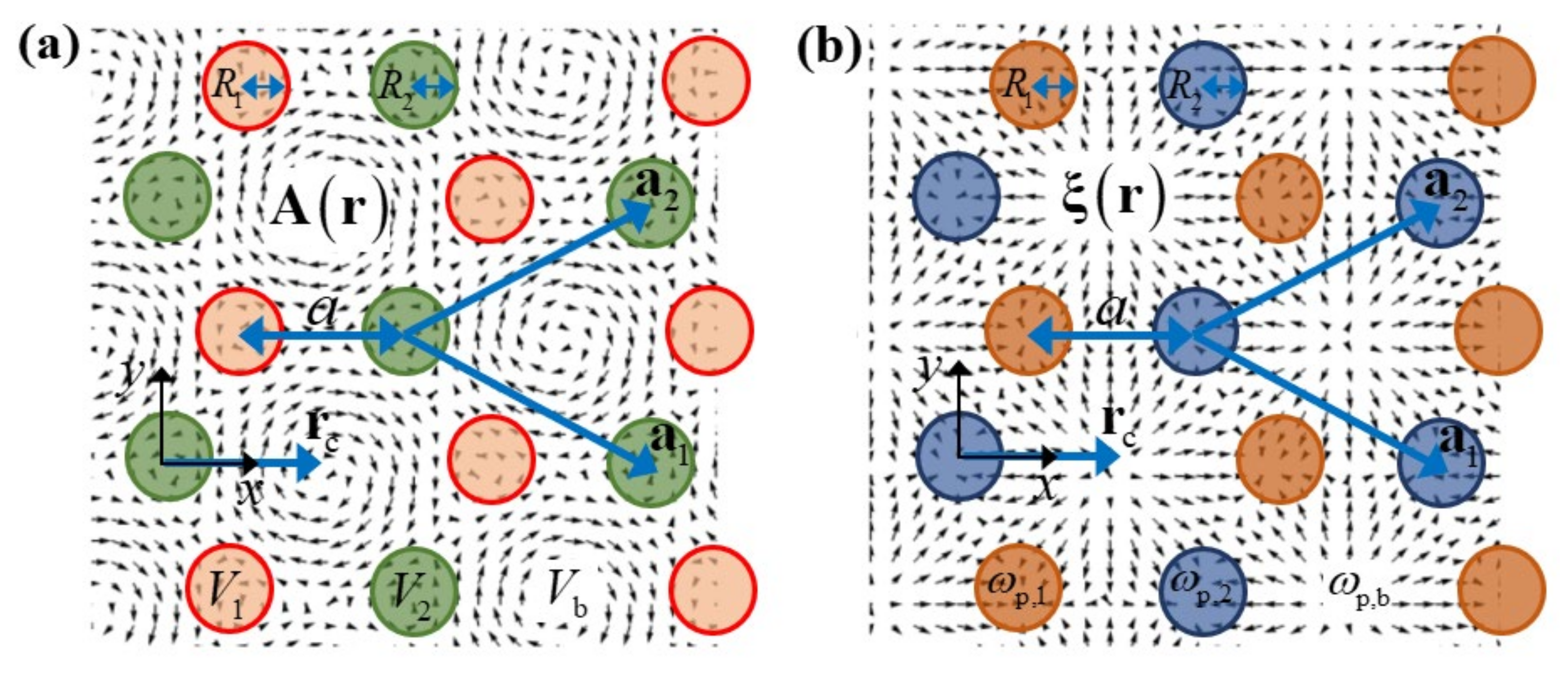
2.2. Photonic Analogue of the Haldane Model
3. Topological Classification with Green’s Function
3.1. Gap Chern Number for the Electronic Haldane Model
3.2. Topological Phases of the Photonic Haldane Model: Theory
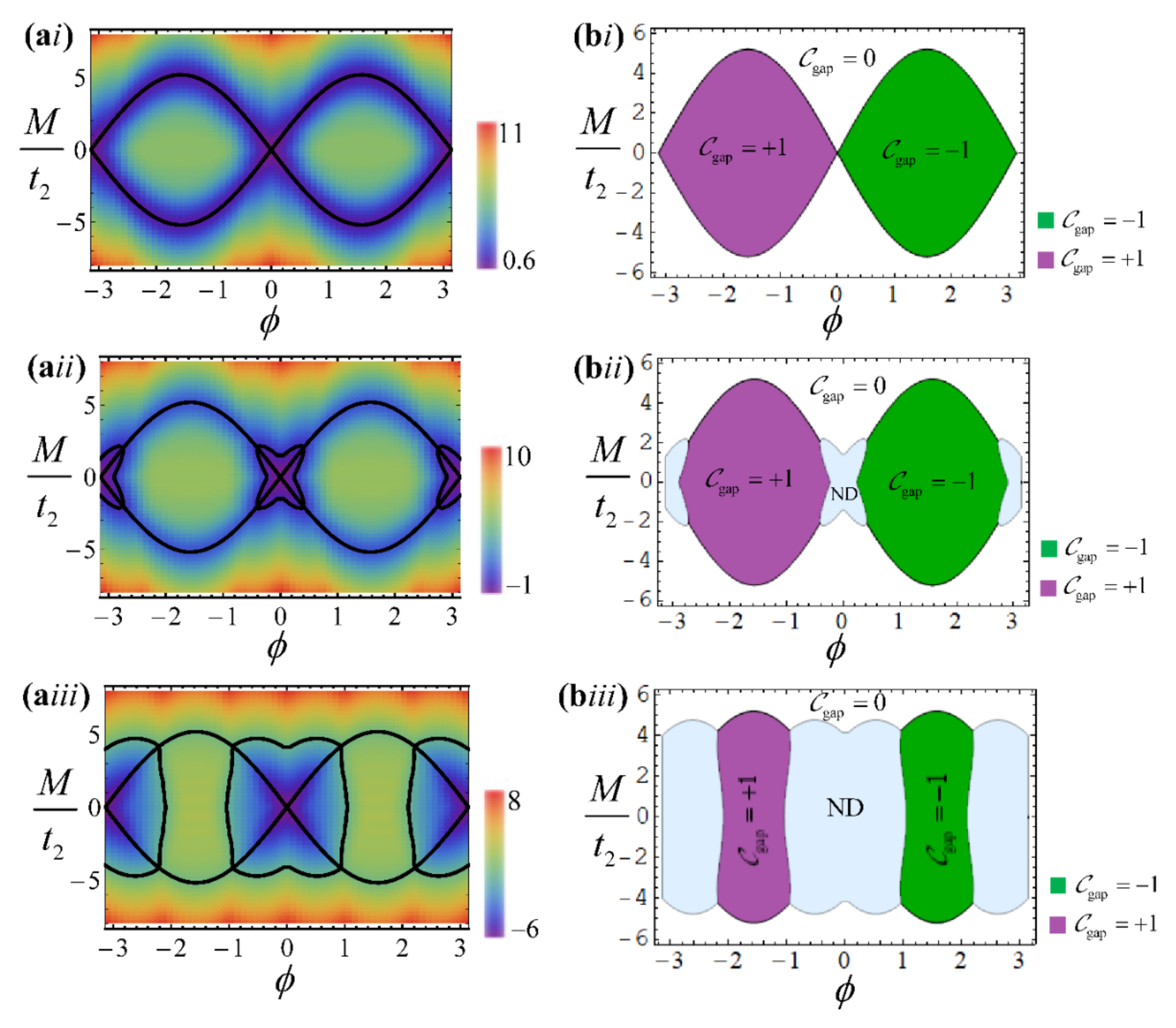
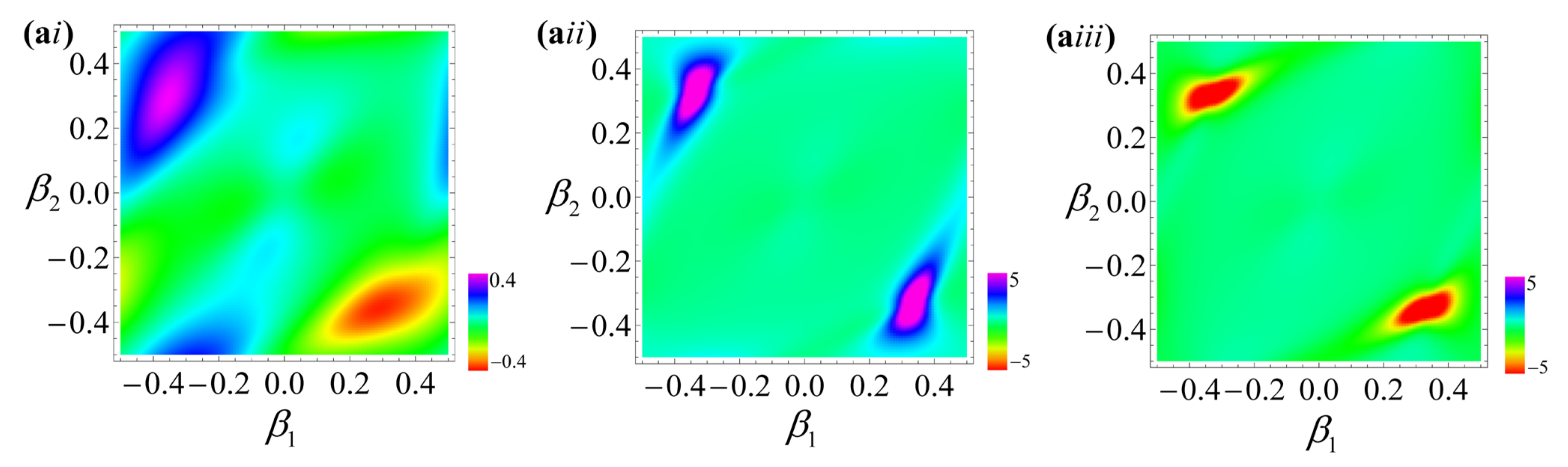
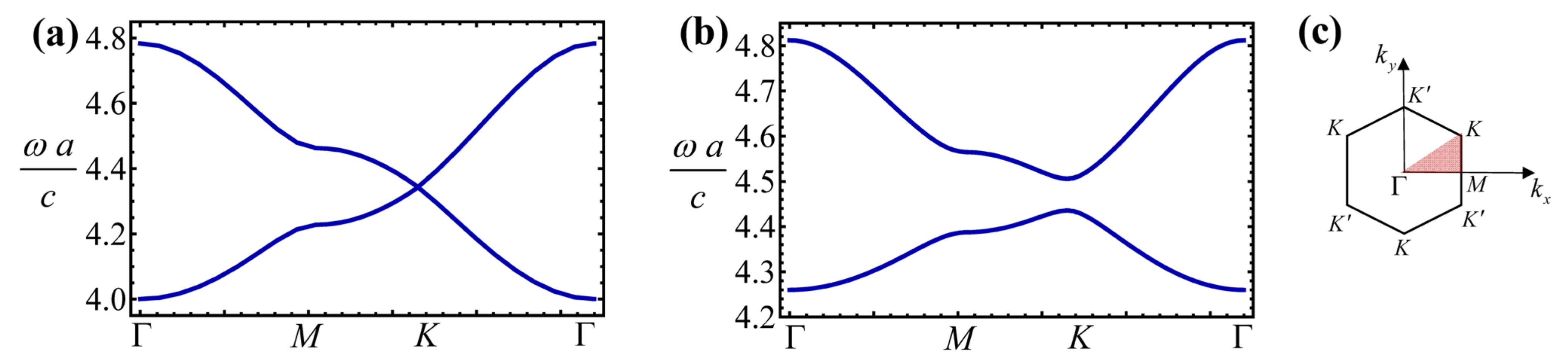
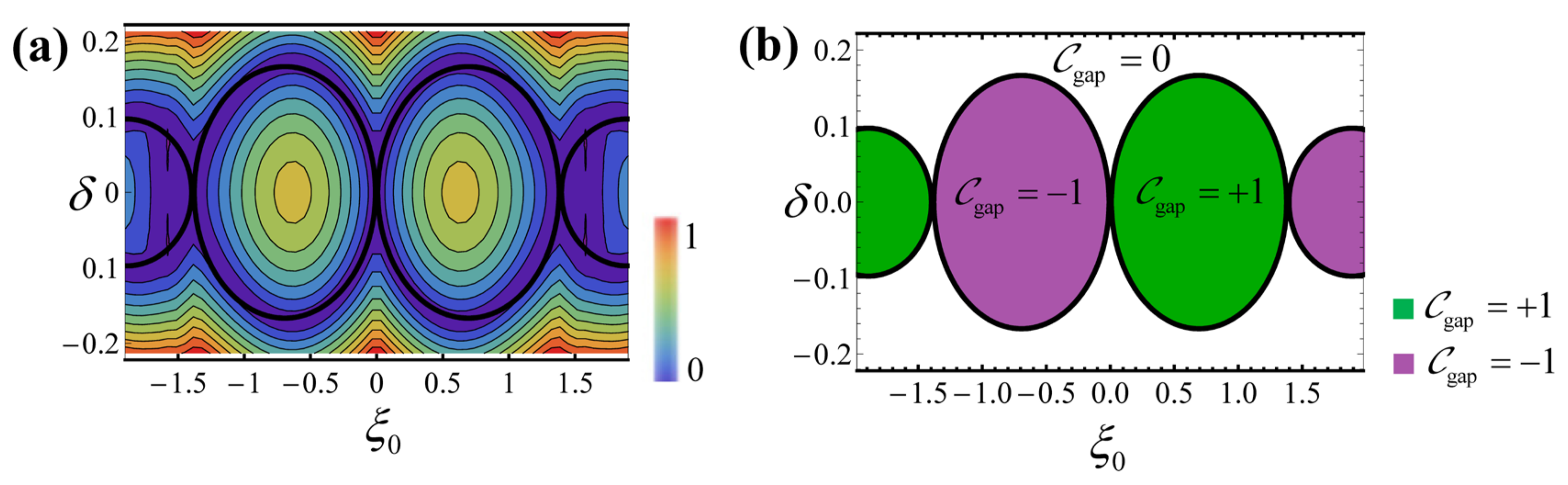
3.3. Topological Phases of the Photonic Haldane Model: Numerical Results
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 1988, 61, 2015–2018. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M. Nobel lecture: Topological quantum matter. Rev. Mod. Phys. 2017, 89, 040502. [Google Scholar] [CrossRef]
- Lu, L.; Joannopoulos, J.D.; Soljacic, M. Topological photonics. Nat. Photonics 2014, 8, 821. [Google Scholar] [CrossRef] [Green Version]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef] [Green Version]
- Haldane, F.D.M.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [Green Version]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nat. Cell Biol. 2009, 461, 772–775. [Google Scholar] [CrossRef] [Green Version]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2012, 12, 233. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nat. Cell Biol. 2013, 496, 196–200. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Chern invariants for continuous media. Phys. Rev. B 2015, 92, 125153. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Bulk-edge correspondence for topological photonic continua. Phys. Rev. B 2016, 94, 205105. [Google Scholar] [CrossRef] [Green Version]
- Silveirinha, M.G. Quantized angular momentum in topological optical systems. Nat. Commun. 2019, 10, 349. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Proof of the bulk-edge correspondence through a link between topological photonics and fluctuation-electrodynamics. Phys. Rev. 2019, 9, 011037. [Google Scholar] [CrossRef] [Green Version]
- Leykam, D.; Bliokh, K.; Huang, C.; Chong, Y.; Nori, F. Edge modes, degeneracies, and topological numbers in non-Hermitian systems. Phys. Rev. Lett. 2017, 118, 040401. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.; Zhen, B.; Fu, L. Topological band theory for non-Hermitian Hamiltonians. Phys. Rev. Lett. 2018, 120, 146402. [Google Scholar] [CrossRef] [Green Version]
- Yao, S.; Wang, Z. Edge states and topological invariants of non-Hermitian systems. Phys. Rev. Lett. 2018, 121, 086803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silveirinha, M.G. Topological theory of non-Hermitian photonic systems. Phys. Rev. B 2019, 99, 125155. [Google Scholar] [CrossRef] [Green Version]
- Lannebère, S.; Silveirinha, M.G. Effective Hamiltonian for electron waves in artificial graphene: A first principles derivation. Phys. Rev. B 2015, 91, 045416. [Google Scholar] [CrossRef] [Green Version]
- Lannebère, S.; Silveirinha, M.G. Link between the photonic and electronic topological phases in artificial graphene. Phys. Rev. B 2018, 97, 165128. [Google Scholar] [CrossRef] [Green Version]
- Lannebère, S.; Silveirinha, M.G. Photonic analogues of the Haldane and Kane-Mele models. Nanophotonics 2019, 8, 1387–1397. [Google Scholar] [CrossRef]
- Silveirinha, M.G. Topological classification of Chern-type insulators by means of the photonic Green function. Phys. Rev. B 2018, 97, 115146. [Google Scholar] [CrossRef] [Green Version]
- Prudêncio, F.R.; Silveirinha, M.G. First principles calculation of topological invariants of non-Hermitian photonic crystals. Comm. Phys. 2020, 3, 221. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L. Topological Insulators and Topological Superconductors; Princeton University Press: Oxford, UK, 2013. [Google Scholar]
- Jacobs, D.A.; Miroshnichenko, A.E.; Kivshar, Y.S.; Khanikaev, A.B. Photonic topological Chern insulators based on Tellegen metacrystals. New J. Phys. 2015, 17, 125015. [Google Scholar] [CrossRef] [Green Version]
- Serdyukov, A.; Semchenko, I.; Tretyakov, S.; Sihvola, A. Electromagnetics of Bi-Anisotropic Materials: Theory and Applications; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Astrov, D.N. Magnetoelectric effect in chromium oxide. Sov. Phys. JETP 1961, 13, 729. [Google Scholar]
- Qi, X.L.; Li, R.; Zang, J.; Zhang, S.C. Inducing a magnetic monopole with topological surface states. Science 2009, 323, 1184–1187. [Google Scholar] [CrossRef] [Green Version]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef] [Green Version]
- Coh, S.; Vanderbilt, D. Canonical magnetic insulators with isotropic magnetoelectric coupling. Phys. Rev. B 2013, 88, 121106. [Google Scholar] [CrossRef] [Green Version]
- Mong, R.S.K.; Essin, A.M.; Moore, J.E. Antiferromagnetic topological insulators. Phys. Rev. B 2010, 81, 245209. [Google Scholar] [CrossRef] [Green Version]
- Dziom, V.; Shuvaev, A.; Pimenov, A.; Astakhov, G.V.; Ames, C.; Bendias, K.; Böttcher, J.; Tkachov, G.; Hankiewicz, E.M.; Brüne, C.; et al. Observation of the universal magnetoelectric effect in a 3D topological insulator. Nat. Commun. 2017, 8, 15197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prudencio, F.; Matos, S.; Paiva, C.R. Exact image method for radiation problems in stratified isorefractive Tellegen media. IEEE Trans. Antennas Propag. 2014, 62, 4637–4646. [Google Scholar] [CrossRef]
- Prudencio, F.R.; Matos, S.A.; Paiva, C.R. A geometrical approach to duality transformations for Tellegen media. IEEE Trans. Microw. Theory Tech. 2014, 62, 1417–1428. [Google Scholar] [CrossRef]
- Prudêncio, F.R.; Matos, S.A.; Paiva, C.R. Asymmetric band diagrams in photonic crystals with a spontaneous nonreciprocal response. Phys. Rev. A 2015, 91, 063821. [Google Scholar] [CrossRef] [Green Version]
- Prudêncio, F.R.; Silveirinha, M.G. Optical isolation of circularly polarized light with a spontaneous magnetoelectric effect. Phys. Rev. A 2016, 93, 043846. [Google Scholar] [CrossRef]
- Zhao, R.; Xie, G.-D.; Chen, M.L.N.; Lan, Z.; Huang, Z.; Sha, W.E.I. First-principle calculation of Chern number in gyrotropic photonic crystals. Opt. Express 2020, 28, 4638–4649. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, M.L.N.; Jiang, L.J.; Zhang, S.; Zhao, R.; Lan, Z.; Sha, W.E.I. Comparative study of Hermitian and non-Hermitian topological dielectric photonic crystals. Phys. Rev. A 2021, 104, 033501. [Google Scholar] [CrossRef]
- Sakoda, K. Optical Properties of Photonic Crystals; Springer: Berlin, Germany, 2001. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prudêncio, F.R.; Silveirinha, M.G. First Principles Calculation of the Topological Phases of the Photonic Haldane Model. Symmetry 2021, 13, 2229. https://doi.org/10.3390/sym13112229
Prudêncio FR, Silveirinha MG. First Principles Calculation of the Topological Phases of the Photonic Haldane Model. Symmetry. 2021; 13(11):2229. https://doi.org/10.3390/sym13112229
Chicago/Turabian StylePrudêncio, Filipa R., and Mário G. Silveirinha. 2021. "First Principles Calculation of the Topological Phases of the Photonic Haldane Model" Symmetry 13, no. 11: 2229. https://doi.org/10.3390/sym13112229
APA StylePrudêncio, F. R., & Silveirinha, M. G. (2021). First Principles Calculation of the Topological Phases of the Photonic Haldane Model. Symmetry, 13(11), 2229. https://doi.org/10.3390/sym13112229





