Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation
Abstract
:1. Introduction
2. Preliminaries
3. Construction of the Method (AHPM)
4. Applications of AHPM
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shah, N.A.; El-Zahar, E.R.; Aljoufi, M.D.; Chung, J.D. An efficient approach for solution of fractional-order Helmholtz equations. Adv. Differ. Equ. 2021, 2021, 14. [Google Scholar] [CrossRef]
- Abuasad, S.; Moaddy, K.; Hashim, I. Analytical treatment of two-dimensional fractional Helmholtz equations. J. King Saud Univ. Sci. 2019, 31, 659–666. [Google Scholar] [CrossRef]
- Semin, A.; Delourme, B.; Schmidt, K. On the Homogenization of the Helmholtz Problem with Thin Perforated Walls of Finite Length. ESAIM 2018, 52, 29–67. [Google Scholar] [CrossRef] [Green Version]
- Seadawy, A.R. The solutions of the Boussinesq and generalized fifth-order KdV equations by using the direct algebraic method. Appl. Math. Sci. 2012, 6, 4081–4090. [Google Scholar]
- Noeiaghdam, S.; Dreglea, A.; Işik, H.; Suleman, M. A Comparative Study between Discrete Stochastic Arithmetic and Floating-Point Arithmetic to Validate the Results of Fractional Order Model of Malaria Infection. Mathematics 2021, 9, 1435. [Google Scholar] [CrossRef]
- Ali, Z.; Nia, S.N.; Rabiei, F.; Shah, K.; Tan, M.K. A Semianalytical Approach to the Solution of Time-Fractional Navier-Stokes Equation. Adv. Math. Phys. 2021, 2021, 13. [Google Scholar]
- Atangana, A.; Secer, A. A Note on Fractional Order Derivatives and Table of Fractional Derivatives of Some Special Functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef] [Green Version]
- Seadawy, A.R.; Lu, D. Ion acoustic solitary wave solutions of three-dimensional nonlinear extended Zakharov-Kuznetsov dynamical equation in a magnetized two-ion-temperature dusty plasma. Results Phys. 2016, 6, 590–593. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.; Shah, K.; Jarad, F. On stable iterative solutions for a class of boundary value problem of nonlinear fractional order differential equations. Math. Meth. Appl. Sci. 2018, 2018, 1–13. [Google Scholar]
- Alia, S.; Arifa, M.; Lateefb, D.; Akramc, M. Stable monotone iterative solutions to a class of boundary value problems of nonlinear fractional-order differential equations. J. Nonlinear Sci. Appl. 2019, 12, 376–386. [Google Scholar] [CrossRef]
- Ali, S.; Abdeljawad, T.; Shah, K.; Jarad, F.; Arif, M. Computation of iterative solutions along with stability analysis to a coupled system of fractional order differential equations. Adv. Differ. Equ. 2019, 2019, 215. [Google Scholar] [CrossRef] [Green Version]
- Gul, H.; Alrabaiah, H.; Ali, S.; Shah, K.; Muhammad, S. Computation of solution to fractional order partial reaction diffusion equations. J. Adv. Res. 2020, 25, 31–38. [Google Scholar] [CrossRef]
- Ali, S.; Bushnaq, S.; Shah, K.; Arif, M. Numerical treatment of fractional order cauchy reaction diffusion equations. Chaos Solitons Fractals 2017, 103, 578–587. [Google Scholar] [CrossRef]
- Bildik, N.; Konuralp, A. The use of variational iteration method, differential transform method and Adomian decomposition method for solving different types of nonlinear partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 2006, 7, 65–70. [Google Scholar] [CrossRef]
- Hashim, I.; Noorani, M.S.; Al-Hadidi, M.S. Al-Hadidi MRS, Solving the generalized Burgers Huxley equation using the Adomian decomposition method. Math. Comput. Model 2006, 43, 1404–1411. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Baleanu, D. Fractional Differences and Integration by Parts. J. Comput. Anal. Appl. 2011, 13, 10. [Google Scholar]
- Chohan, M.I.; Ali, S.; Shah, K. On Approximate solutions of fractional Order partial differential equations. Therm. Sci. 2018, 22, 287–299. [Google Scholar] [CrossRef]
- Bushnaq, S.; Ali, S.; Shah, K.; Arif, M. Approximate solutions to nonlinear factional order partial differential equations arising in ion-acoustic waves. AIMS Math. 2019, 4, 721–739. [Google Scholar] [CrossRef]
- Shah, K.; Khalil, H.; Khan, R.A. Analytical Solutions of Fractional Order Diffusion Equations by Natural Transform Method. Iran. J. Sci. Technol. (Trans. Sci. A) 2018, 42, 1479–1490. [Google Scholar] [CrossRef]
- Liao, S.J. On the Proposed Analysis Technique for Nonlinear Problems and Its Applications. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- He, J. An approximate solution technique depending on an artificial parameter: A special example. Commun. Nonlinear Sci. Numer. Simul. 1998, 3, 92–97. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Application of Optimal Homotopy Asymptotic Method for solving nonlinear equations arising in heat transfer. Int. Commun. Heat Mass Transf. 2008, 35, 710–715. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Optimal homotopy perturbation method for a non-conservative dynamical system of a rotating electrical machine. Z. Naturforsch. A 2012, 67, 509–516. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V.; Madescu, G. Dynamic response of a permanent magnet synchronous generator to a wind gust. Energies 2019, 12, 915. [Google Scholar] [CrossRef] [Green Version]
- Marinca, V.; Herisanu, N. On the flow of a Walters-type B’viscoelastic fluid in a vertical channel with porous wall. Int. J. Heat Mass Transf. 2014, 79, 146–165. [Google Scholar] [CrossRef]

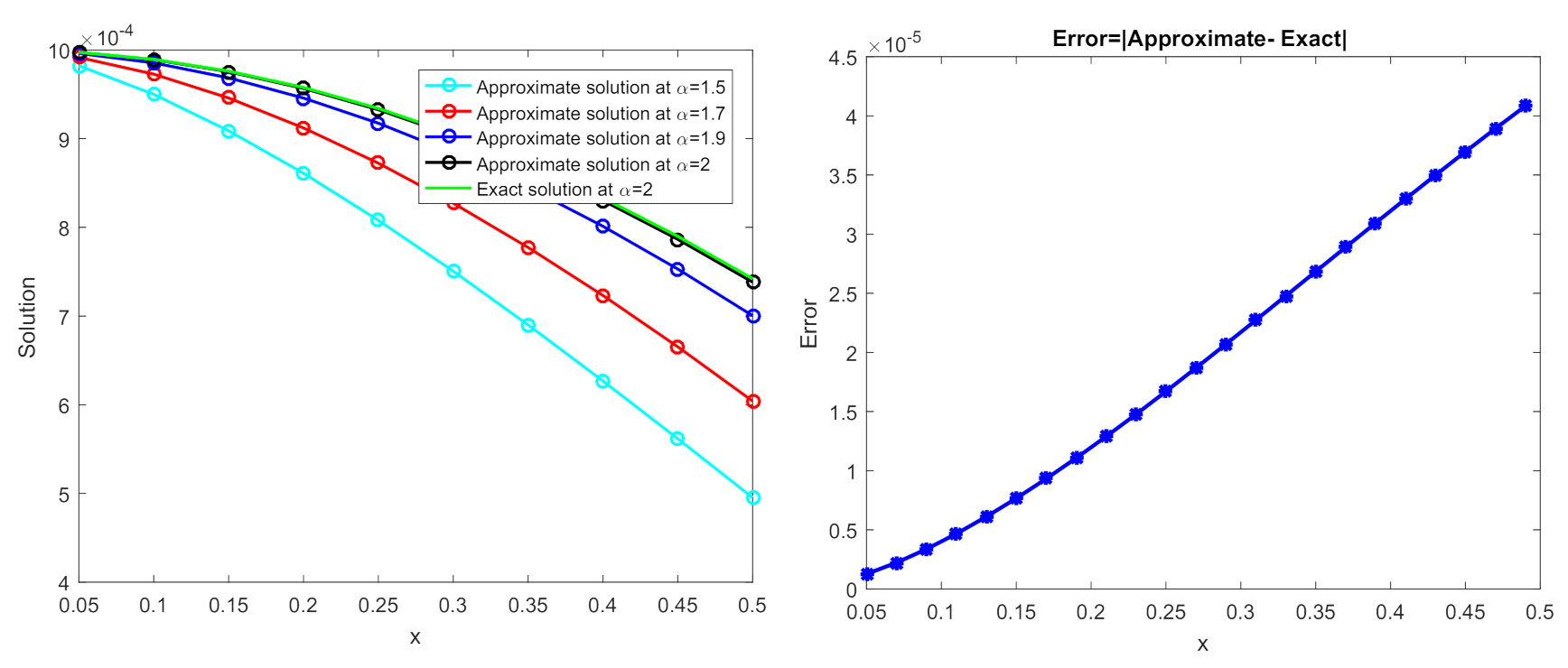
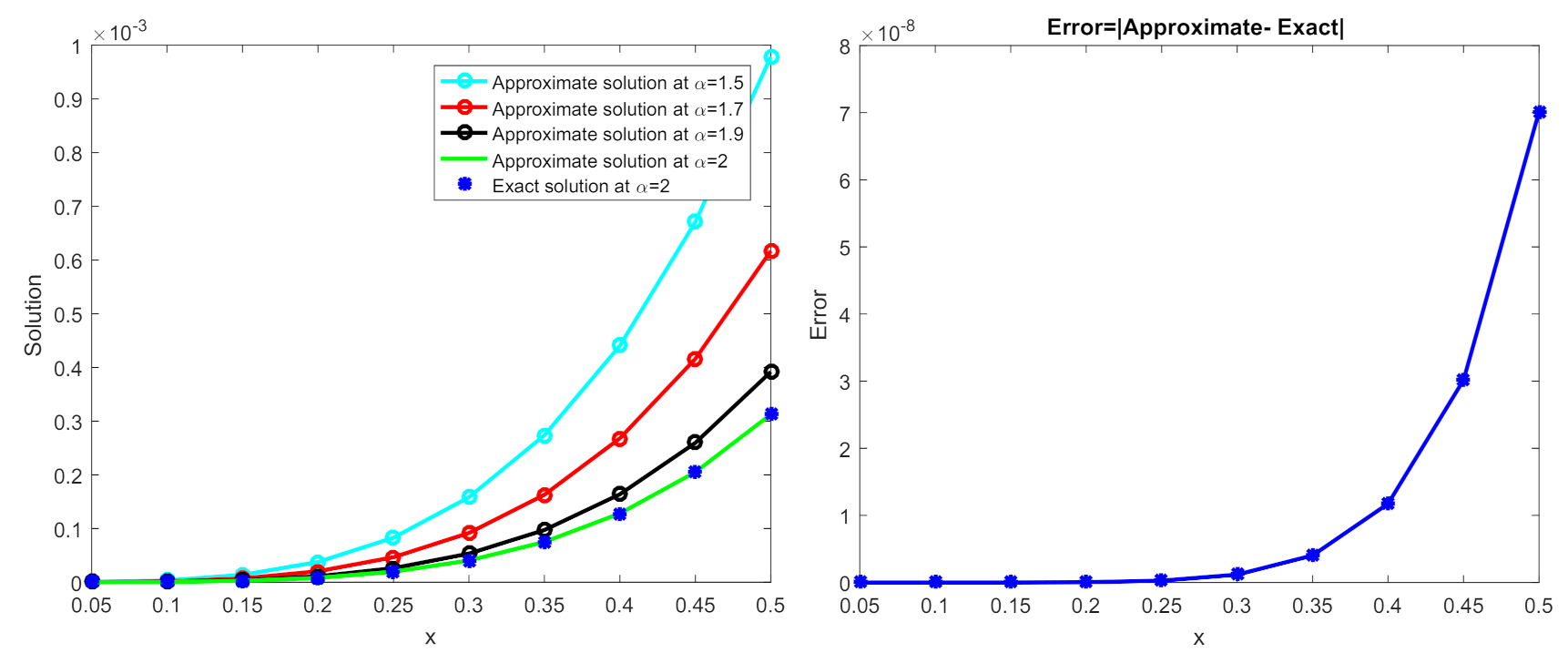
| x | |||
|---|---|---|---|
| [1]) | ||||
|---|---|---|---|---|
| x | |||
|---|---|---|---|
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 |
| x | |||
|---|---|---|---|
| e−04 | e−04 | e−06 | |
| e−04 | e−04 | e−05 | |
| e−04 | e−04 | e−05 | |
| e−04 | e−04 | e−05 | |
| e−04 | e−04 | e−05 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 |
| x | |||
|---|---|---|---|
| e−07 | e−07 | e−08 | |
| e−06 | e−06 | e−07 | |
| e−05 | e−06 | e−06 | |
| e−05 | e−05 | e−05 | |
| e−05 | e−05 | e−05 | |
| e−04 | e−05 | e−05 | |
| e−04 | e−04 | e−05 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 | |
| e−04 | e−04 | e−04 |
| x | |||
|---|---|---|---|
| e−08 | e−08 | e−16 | |
| e−07 | e−07 | e−13 | |
| e−06 | e−06 | e−12 | |
| e−06 | e−06 | e−11 | |
| e−05 | e−05 | e−10 | |
| e−05 | e−05 | e−09 | |
| e−05 | e−05 | e−09 | |
| e−04 | e−04 | e−08 | |
| e−04 | e−04 | e−08 | |
| e−04 | e−04 | e−08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gul, H.; Ali, S.; Shah, K.; Muhammad, S.; Sitthiwirattham, T.; Chasreechai, S. Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation. Symmetry 2021, 13, 2215. https://doi.org/10.3390/sym13112215
Gul H, Ali S, Shah K, Muhammad S, Sitthiwirattham T, Chasreechai S. Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation. Symmetry. 2021; 13(11):2215. https://doi.org/10.3390/sym13112215
Chicago/Turabian StyleGul, Haji, Sajjad Ali, Kamal Shah, Shakoor Muhammad, Thanin Sitthiwirattham, and Saowaluck Chasreechai. 2021. "Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation" Symmetry 13, no. 11: 2215. https://doi.org/10.3390/sym13112215
APA StyleGul, H., Ali, S., Shah, K., Muhammad, S., Sitthiwirattham, T., & Chasreechai, S. (2021). Application of Asymptotic Homotopy Perturbation Method to Fractional Order Partial Differential Equation. Symmetry, 13(11), 2215. https://doi.org/10.3390/sym13112215







