Non-Separable Linear Canonical Wavelet Transform
Abstract
:1. Introduction
2. Non-Separable Linear Canonical Wavelet Transform in
2.1. Non-Separable Linear Canonical Transform
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- .
2.2. Non-Separable Linear Canonical Wavelet Transform
2.3. Basic Properties of the Non-Separable Linear Canonical Wavelet Transform
- (i)
- Linearity:
- (ii)
- Anti-linearity:
- (iii)
- Translation:
- (iv)
- Scaling:
- (v)
- Conjugation: .
3. Uncertainty Principles for the Non-Separable Linear Canonical Wavelet Transform
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Moshinsky, M.; Quesne, C. Linear canonical transformations and their unitary representations. J. Math. Phys. 1971, 12, 1772–1780. [Google Scholar] [CrossRef]
- Xu, T.Z.; Li, B.Z. Linear Canonical Transform and Its Applications; Science Press: Beijing, China, 2013. [Google Scholar]
- Healy, J.J.; Kutay, M.A.; Ozaktas, H.M.; Sheridan, J.T. Linear Canonical Transforms: Theory and Applications; Springer: New York, NY, USA, 2016. [Google Scholar]
- Zhang, Z. Uncertainty principle of complex-valued functions in specic free metaplectic transformation domains. J. Fourier Anal. Appl. 2021, 27. [Google Scholar] [CrossRef]
- Zhang, Z. Uncertainty principle for real functions in free metaplectic transformation domains. J. Fourier Anal. Appl. 2019, 25, 2899–2922. [Google Scholar] [CrossRef]
- Gosson, M. Symplectic Geometry and Quantum Mechanics; Birkhäuser: Basel, Switzerland, 2006. [Google Scholar]
- Jing, R.; Liu, B.; Li, R.; Liu, R. The N-dimensional uncertainty principle for the free metaplectic transformation. Mathematics 2020, 8, 1685. [Google Scholar] [CrossRef]
- Debnath, L.; Shah, F.A. Lectuer Notes on Wavelet Transforms; Birkhäuser: Boston, MA, USA, 2017. [Google Scholar]
- Debnath, L.; Shah, F.A. Wavelet Transforms and Their Applications; Birkhäuser: New York, NY, USA, 2015. [Google Scholar]
- Dai, H.; Zheng, Z.; Wang, W. A new fractional wavelet transform. Commun. Nonlinear Sci. Numer. Simulat. 2017, 44, 19–36. [Google Scholar] [CrossRef]
- Wei, D.; Li, Y.M. Generalized wavelet transform based on the convolution operator in the linear canonical transform domain. Optik 2014, 125, 4491–4496. [Google Scholar] [CrossRef]
- Wang, J.; Wang, Y.; Wang, W.; Ren, S. Discrete linear canonical wavelet transform and its applications. EURASIP J. Adv. Sig. Process. 2018, 29, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Shah, F.A.; Teali, A.A.; Tantary, A.Y. Special affine wavelet transform and the corresponding Poisson summation formula. Int. J. Wavelets Multiresolut. Inf. Process. 2021, 19. [Google Scholar] [CrossRef]
- Shah, F.A.; Tantary, A.Y.; Zayed, A.I. A convolution-based special affine wavelet transforms. Integ. Trans. Special Funct. 2020, 1–21. [Google Scholar] [CrossRef]
- Shah, F.A.; Teali, A.A.; Tantary, A.Y. Linear canonical wavelet transforms in quaternion domains. Adv. Appl. Clifford Algebr. 2021, 31, 42. [Google Scholar] [CrossRef]
- Shah, F.A.; Lone, W.Z. Quadratic-phase wavelet transform with applications to generalized differential equations. Math. Methods Appl. Sci. 2021. accepted. [Google Scholar] [CrossRef]
- Antoine, J.P.; Murenzi, R.; Vandergheynst, P.; Ali, S.T. Two-Dimensional Wavelets and Their Relatives; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Pandey, J.N.; Pandey, J.S.; Upadhyay, S.K.; Srivastava, H.M. Continuous wavelet transform of Schwartz tempered distributions in S′(Rn). Symmetry 2019, 11, 235. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, H.M.; Shah, F.A.; Tantary, A.Y. A family of convolution-based generalized Stockwell transforms. J. Pseudo-Differ. Oper. Appl. 2020, 11, 1505–1536. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Singh, A.; Rawat, A.; Singh, S. A family of Mexican hat wavelet transforms associated with an isometry in the heat equation. Math. Methods Appl. Sci. 2021, 44, 11340–11349. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.P.; Gazeau, J.P. Coherent States, Wavelets, and Their Generalizations; Springer: New York, NY, USA, 2014. [Google Scholar]
- Pandey, J.N.; Jha, N.K.; Singh, O.P. The continuous wavelet transform in n-dimensions. Int. J. Wavelets Multiresolut. Inf. Process. 2016, 14, 1650037. [Google Scholar] [CrossRef]
- Folland, G.B.; Sitaram, A. The uncertainty principle: A mathematical survey. J. Fourier Anal. Appl. 1997, 3, 207–238. [Google Scholar] [CrossRef]
- Cowling, M.G.; Price, J.F. Bandwidth verses time concentration: The Heisenberg-Pauli-Weyl inequality. SIAM J. Math. Anal. 1994, 15, 151–165. [Google Scholar] [CrossRef]
- Beckner, W. Pitt’s inequality and the uncertainty principle. Proc. Am. Math. Soc. 1995, 123, 1897–1905. [Google Scholar]
- Wilczok, E. New uncertainty principles for the continuous Gabor transform and the continuous wavelet transform. Doc. Math. 2000, 5, 201–226. [Google Scholar]
- Shah, F.A.; Nisar, K.S.; Lone, W.Z.; Tantary, A.Y. Uncertainty principles for the quadratic-phase Fourier transforms. Math. Methods Appl. Sci. 2021, 44, 10416–10431. [Google Scholar] [CrossRef]
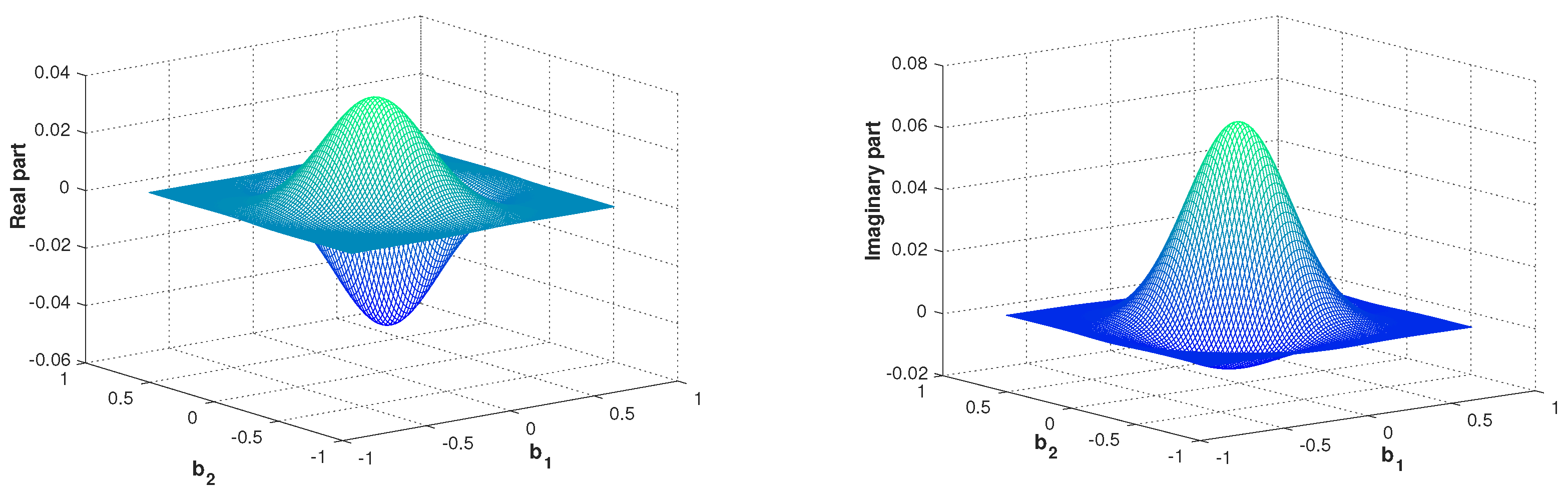
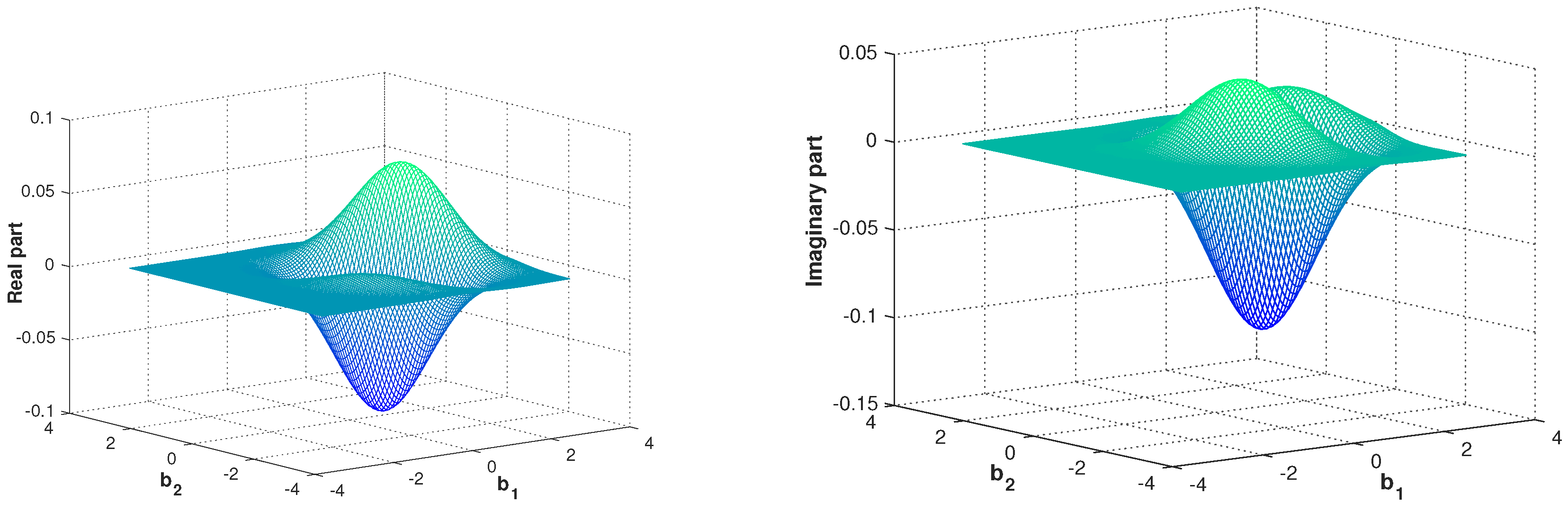
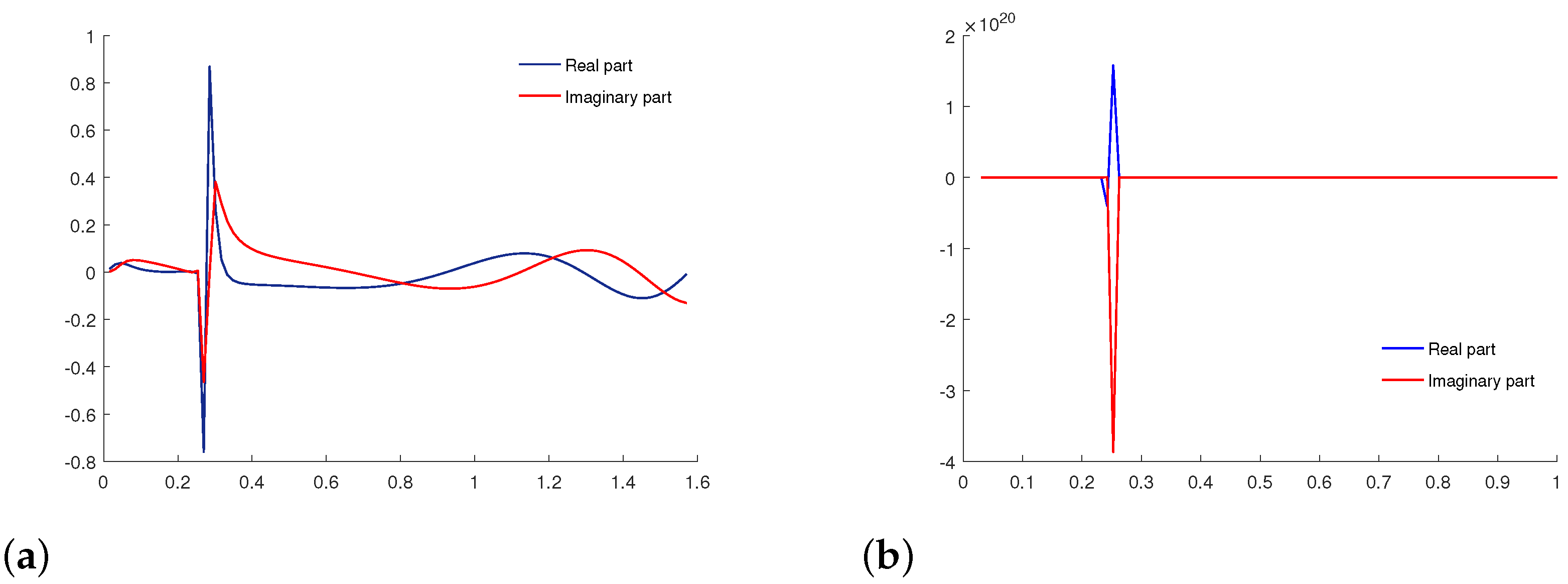
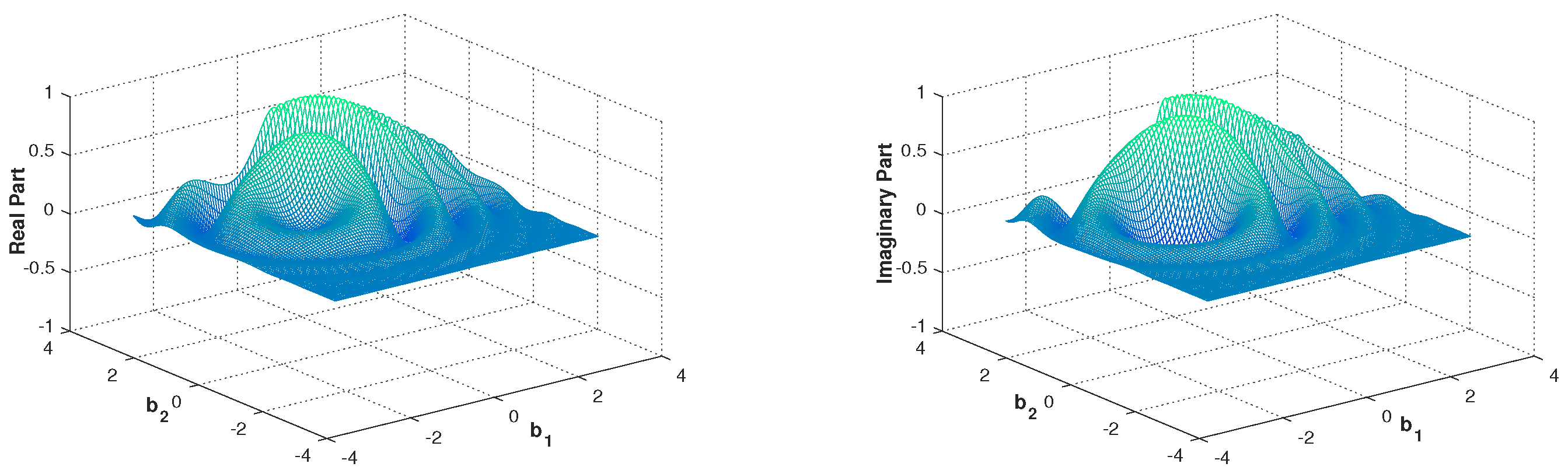
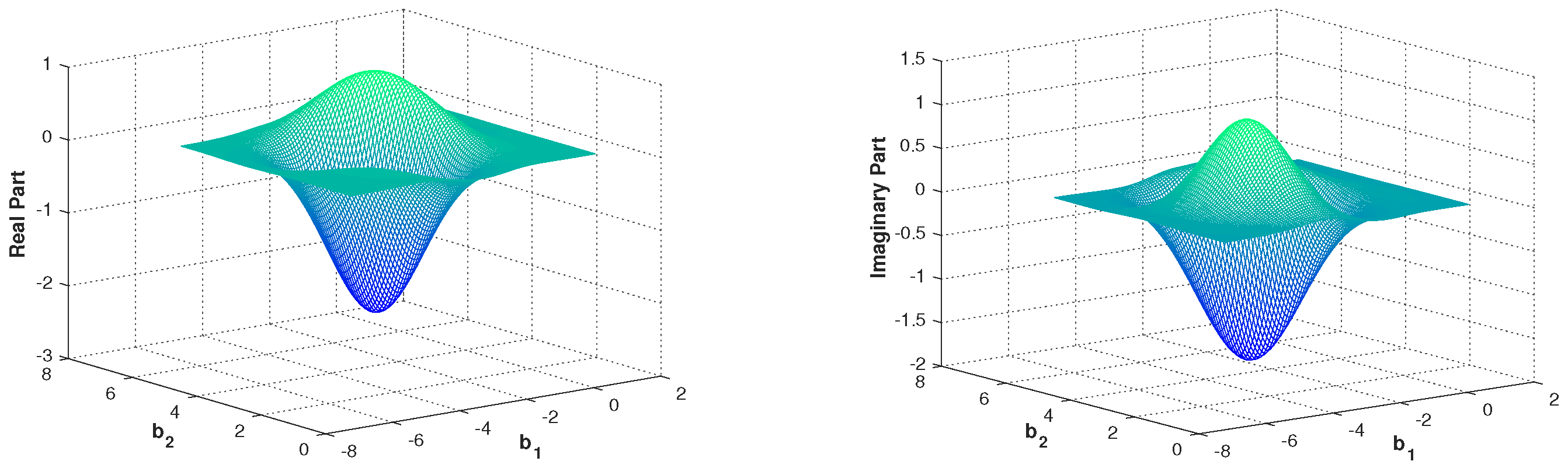
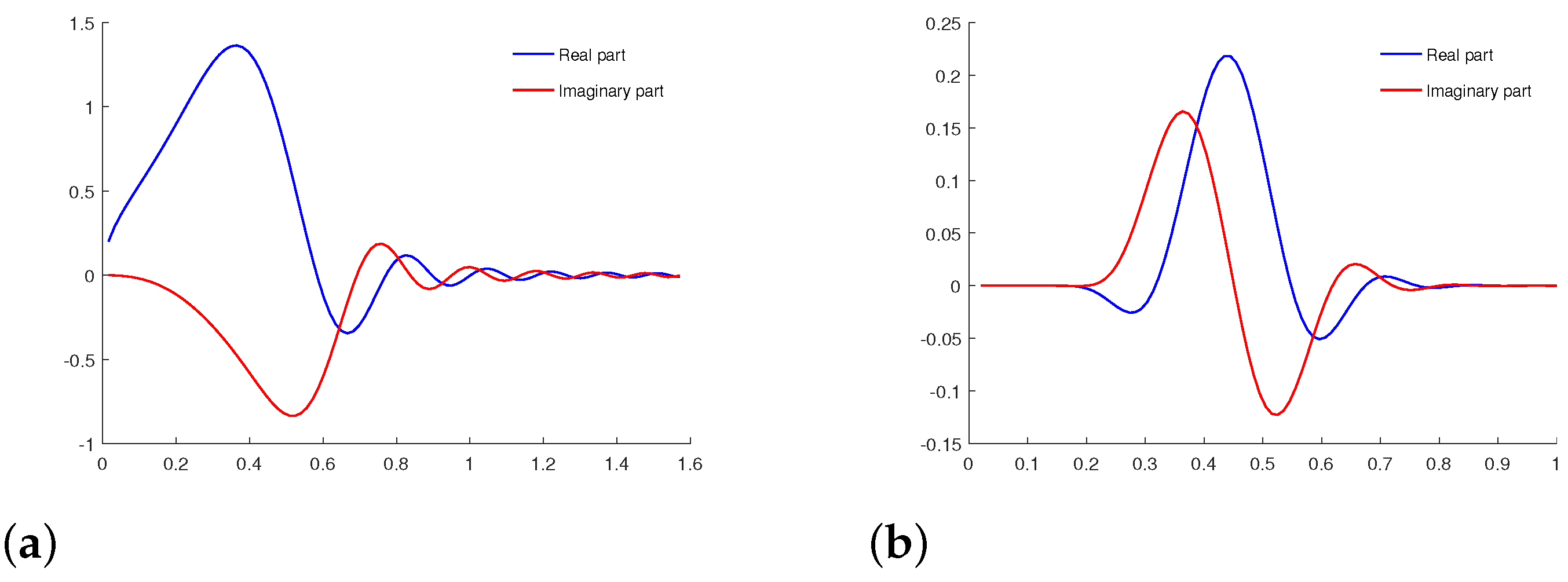
| Free Symplectic MATRIX | Free Metaplectic Transformation |
|---|---|
| • , | n-dimensional FT |
| • , , | |
| , | n-dimensional separable LCT |
| • , | |
| n-dimensional separable FrFT | |
| • , | n-dimensional non-separable FrFT |
| • , , | n-dimensional separable FrT |
| • , | n-dimensional non-separable FrT |
| Symplectic Matrix | Admissibility Constant | Lower Bound |
|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Shah, F.A.; Garg, T.K.; Lone, W.Z.; Qadri, H.L. Non-Separable Linear Canonical Wavelet Transform. Symmetry 2021, 13, 2182. https://doi.org/10.3390/sym13112182
Srivastava HM, Shah FA, Garg TK, Lone WZ, Qadri HL. Non-Separable Linear Canonical Wavelet Transform. Symmetry. 2021; 13(11):2182. https://doi.org/10.3390/sym13112182
Chicago/Turabian StyleSrivastava, Hari M., Firdous A. Shah, Tarun K. Garg, Waseem Z. Lone, and Huzaifa L. Qadri. 2021. "Non-Separable Linear Canonical Wavelet Transform" Symmetry 13, no. 11: 2182. https://doi.org/10.3390/sym13112182
APA StyleSrivastava, H. M., Shah, F. A., Garg, T. K., Lone, W. Z., & Qadri, H. L. (2021). Non-Separable Linear Canonical Wavelet Transform. Symmetry, 13(11), 2182. https://doi.org/10.3390/sym13112182







