Symmetric Oscillator: Special Features, Realization, and Combination Synchronization
Abstract
:1. Introduction
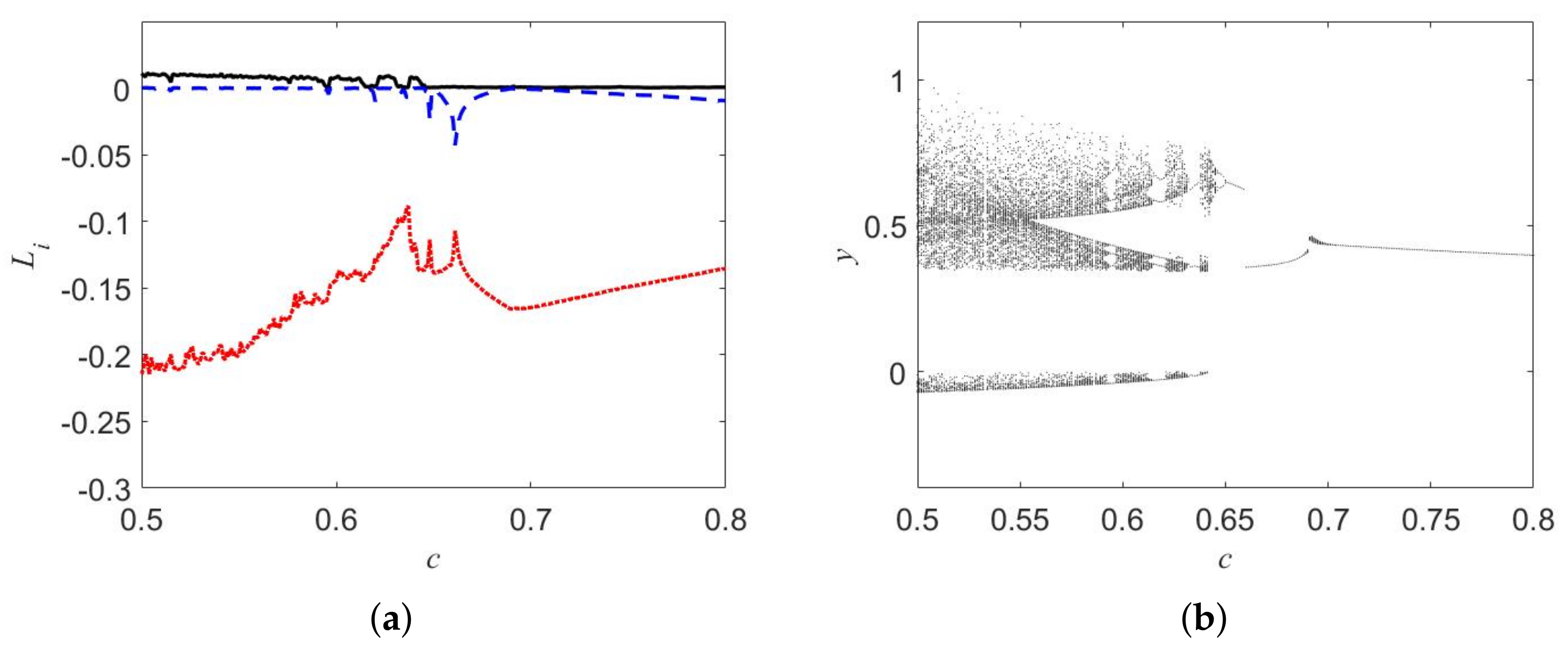
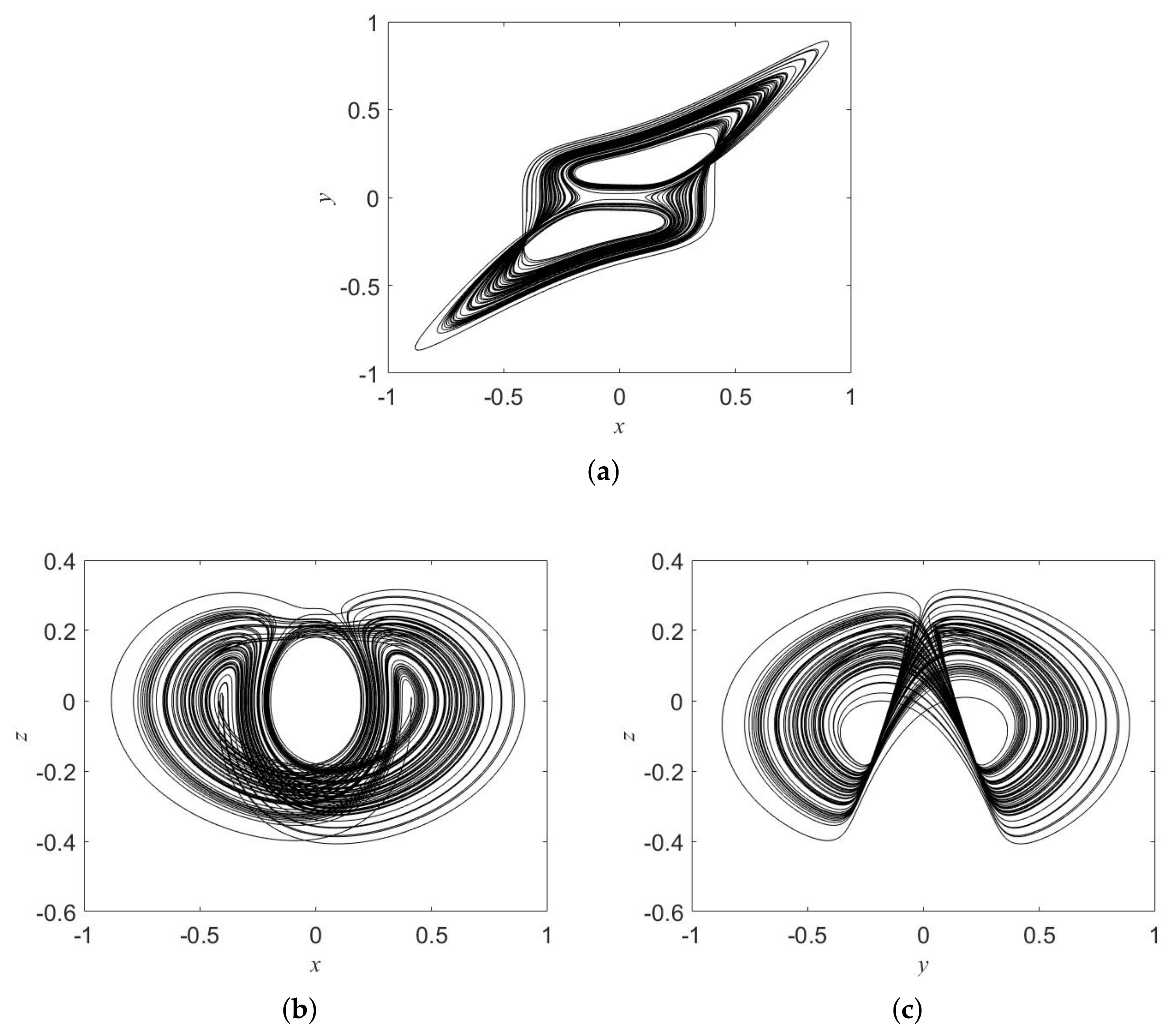
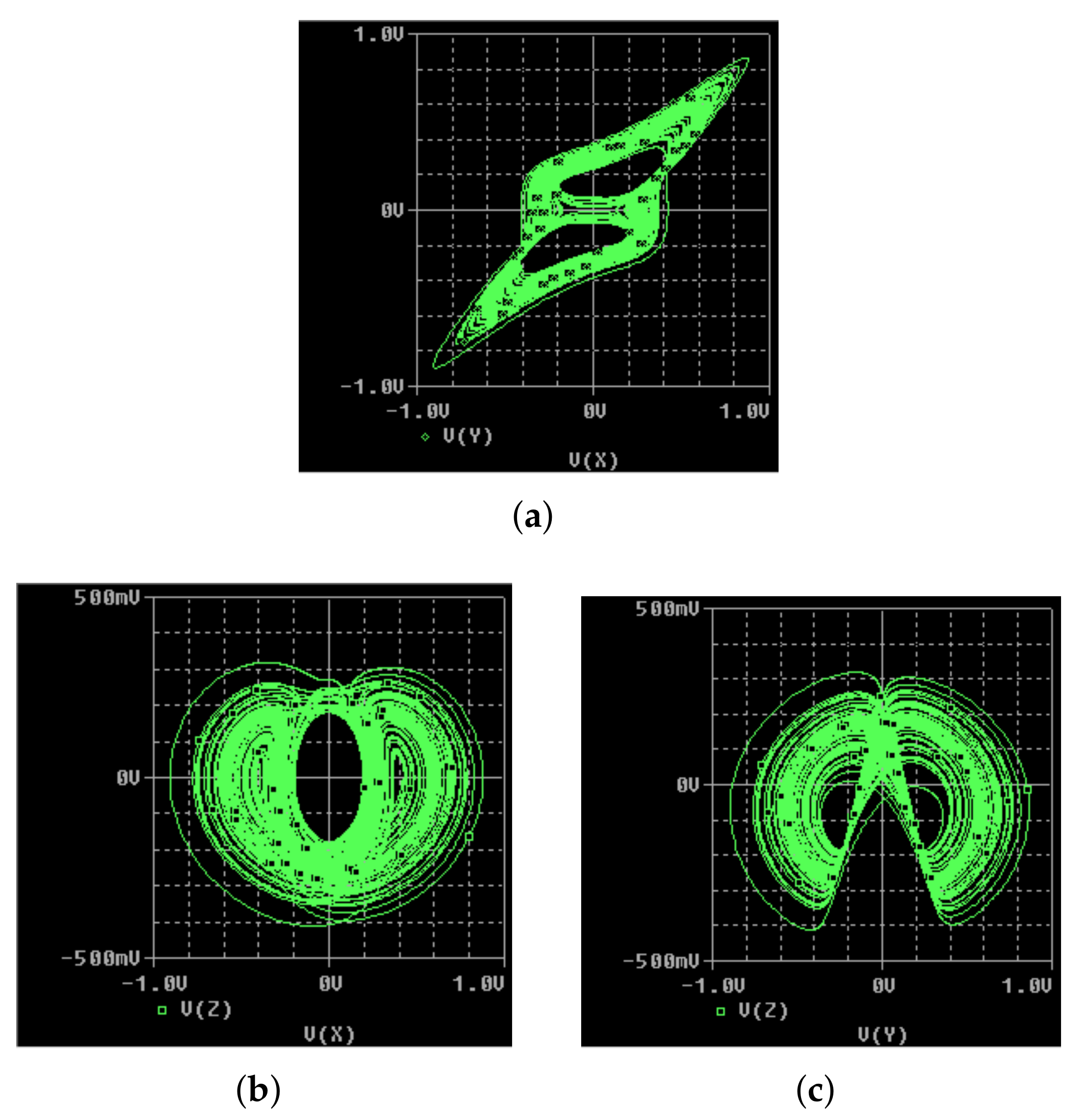
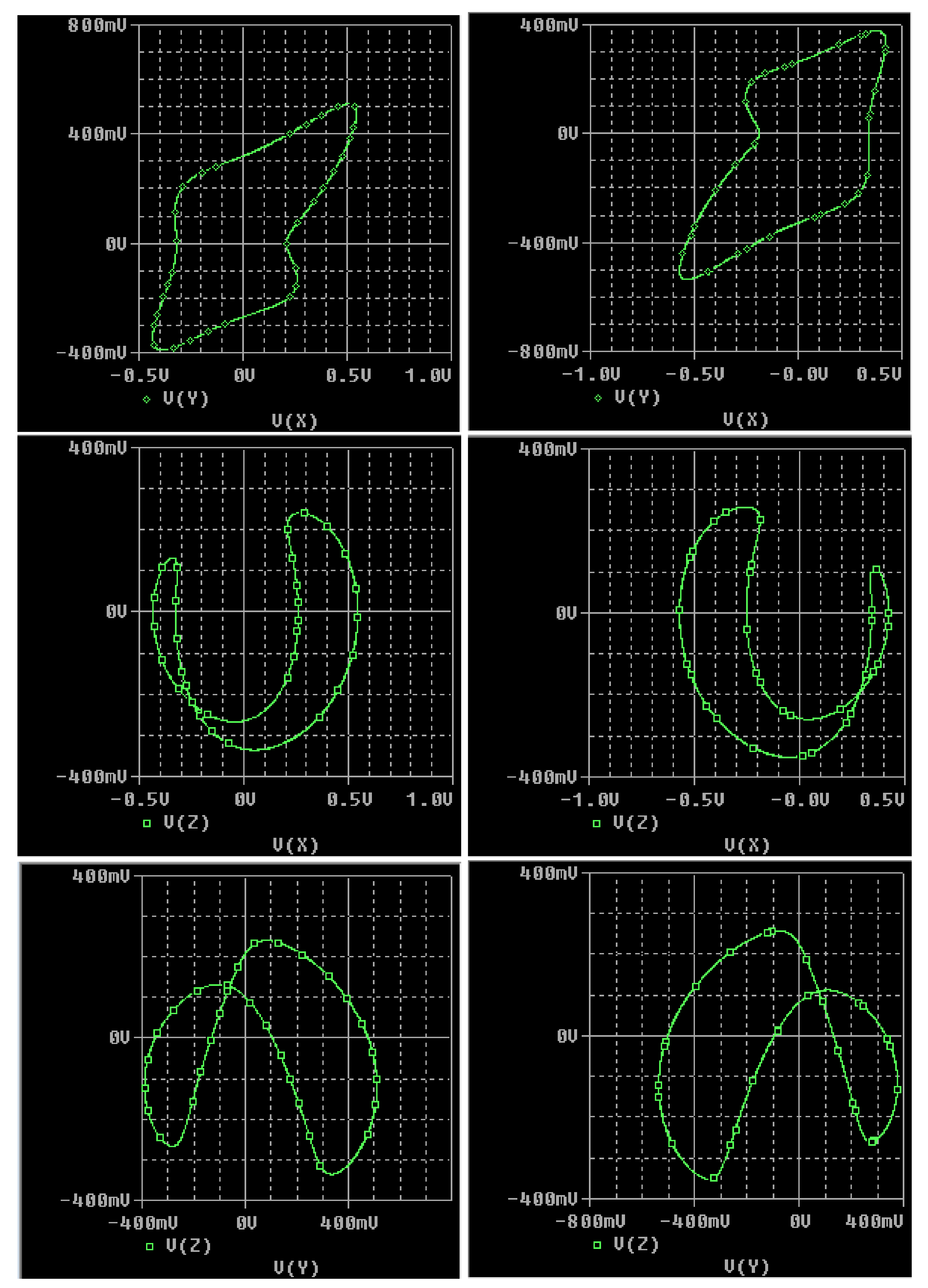
2. Features and Dynamics of the Oscillator
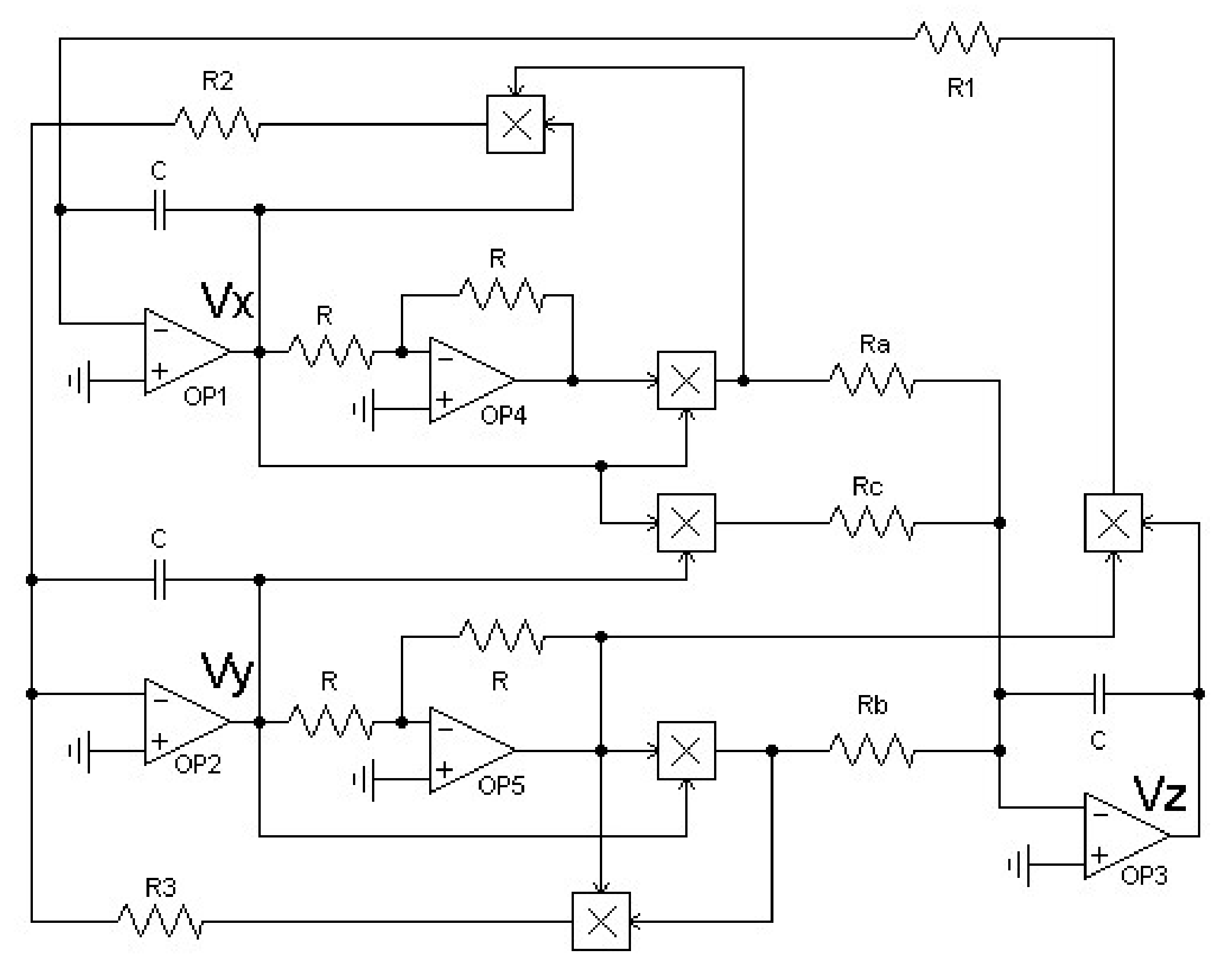
3. Oscillator Implementation
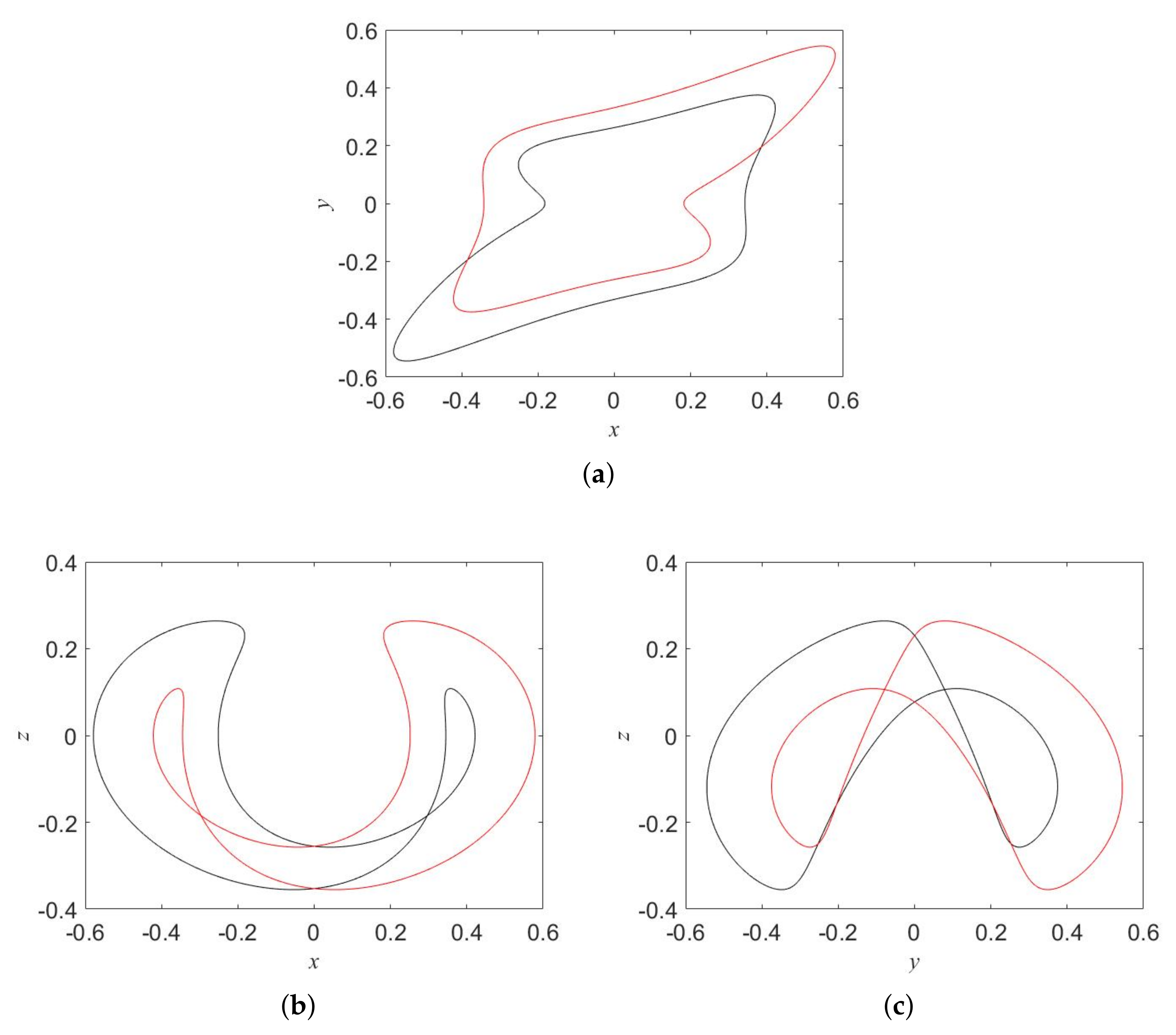
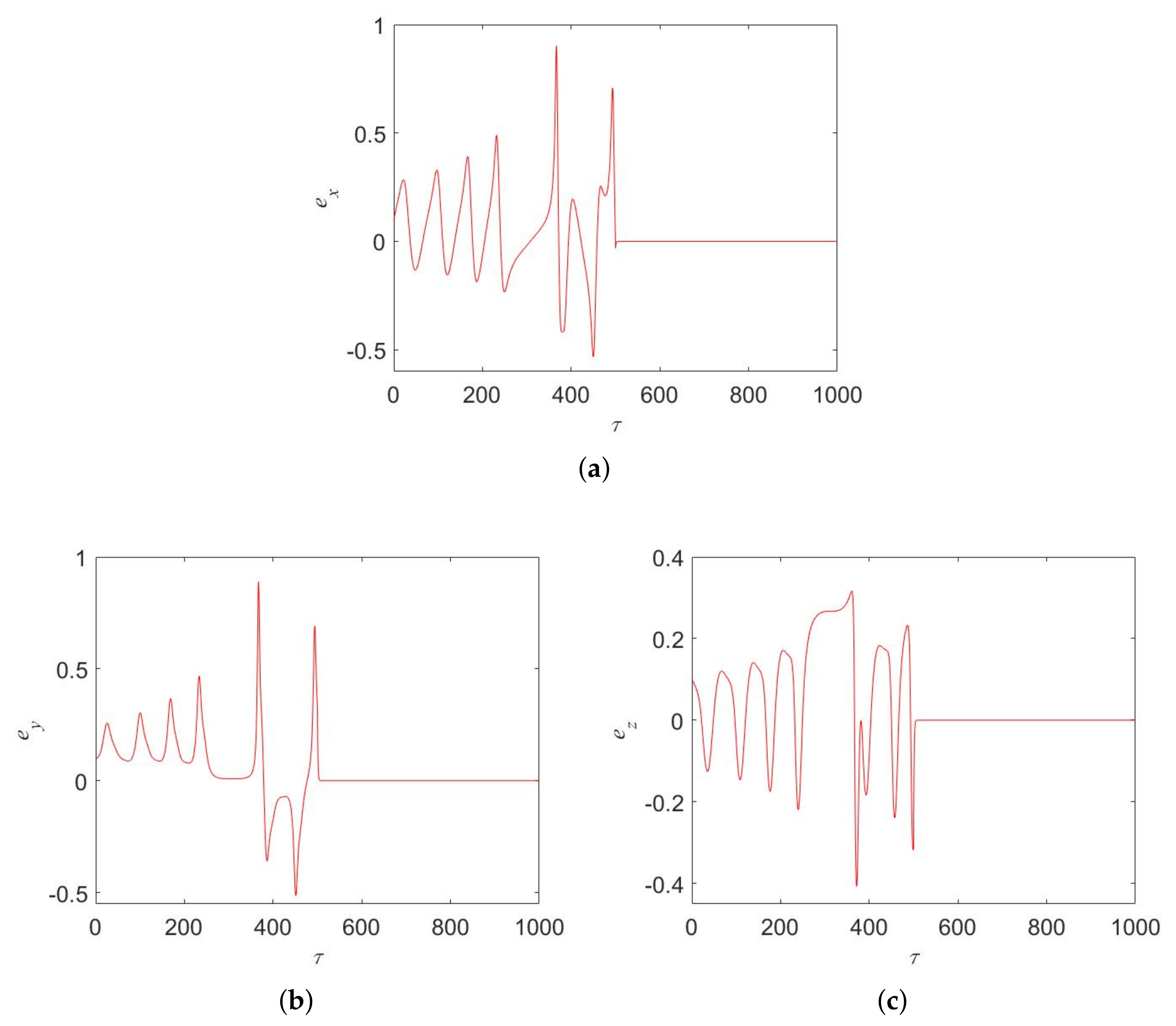
4. Combination Synchronization of Oscillator
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, B.; Jahanshahi, H.; Volos, C.; Bekiros, S.; Yusuf, A.; Agarwal, P.; Aly, A.A. Control of a Symmetric Chaotic Supply Chain System Using a New Fixed-Time Super-Twisting Sliding Mode Technique Subject to Control Input Limitations. Symmetry 2021, 13, 1257. [Google Scholar] [CrossRef]
- Wang, C.; Di, Y.; Tang, J.; Shuai, J.; Zhang, Y.; Lu, Q. The Dynamic Analysis of a Novel Reconfigurable Cubic Chaotic Map and Its Application in Finite Field. Symmetry 2021, 13, 1420. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, L.; Rajagopal, K.; Akgul, A.; Cicek, S.; Aricioglu, B. Fractional-Order Analysis of Modified Chua’s Circuit System with the Smooth Degree of 3 and Its Microcontroller-Based Implementation with Analog Circuit Design. Symmetry 2021, 13, 340. [Google Scholar] [CrossRef]
- Zang, H.; Gu, Z.; Lei, T.; Li, C.; Jafari, S. Coexisting chaotic attractors in a memristive system and their amplitude control. Pramana 2020, 94, 1–9. [Google Scholar] [CrossRef]
- Rajagopal, K.; Bayani, A.; Jafari, S.; Karthikeyan, A.; Hussain, I. Chaotic dynamics of a fractional order glucose-insulin regulatory system. Front. Inf. Technol. Electron. Eng. 2020, 21, 1108–1118. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Moysis, L.; Tutueva, A.; Volos, C.; Butusov, D.; Munoz-Pacheco, J.M.; Nistazakis, H. A two-parameter modified logistic map and its application to random bit generation. Symmetry 2020, 12, 829. [Google Scholar] [CrossRef]
- Panahi, S.; Shirzadian, T.; Jalili, M.; Jafari, S. A new chaotic network model for epilepsy. Appl. Math. Comput. 2020, 346, 395–407. [Google Scholar] [CrossRef]
- Parastesh, F.; Aram, Z.; Namazi, H.; Sprott, J.C.; Jafari, S. A simple chaotic model for development of HIV virus. Sci. Iran. 2021, 28, 1643–1652. [Google Scholar]
- Chen, X.; Qian, S.; Yu, F. Pseudorandom Number Generator Based on Three Kinds of Four-Wing Memristive Hyperchaotic System and Its Application in Image Encryption. Complexity 2020, 2020, 8274685. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. Dynamics analysis, hardware implementation and engineering applications of novel multi-style attractors in a neural network under electromagnetic radiation. Chaos Solitons Fractals 2021, 152, 111350. [Google Scholar] [CrossRef]
- Garcia-Guerrero, E.E.; Inzunza-Gonzalez, E.; Lopez-Bonilla, O.R.; Cardenas-Valdez, J.R.; Cuautle, E.T. Randomness improvement of chaotic maps for image encryption in a wireless communication scheme using PIC-microcontroller via Zigbee channels. Chaos Solitons Fractals 2020, 133, 109646. [Google Scholar] [CrossRef]
- Petavratzis, E.; Moysis, L.; Volos, C.; Stouboulos, I.; Nistazakis, H.; Valavanis, K. A chaotic path planning generator enhanced by a memory technique. Rob. Auton. Syst. 2021, 143, 103826. [Google Scholar] [CrossRef]
- La Fraga, L.G.D.; Mancillas-Lopez, C.; Tlelo-Cuautle, E. Designing an authenticated Hash function with a 2D chaotic map. Nonlinear Dyn. 2021, 104, 4569–4580. [Google Scholar] [CrossRef]
- Mobayen, S.; Volos, C.; Cavusoglu, U.; Kacar, S.S. A Simple Chaotic Flow with Hyperbolic Sinusoidal Function and Its Application to Voice Encryption. Symmetry 2020, 12, 2047. [Google Scholar] [CrossRef]
- Adeyemi, V.A.; Nunez-Perez, J.C.; Ibarra, Y.S.; Perez-Pinal, F.J.; Tlelo-Cuautle, E. FPGA Realization of the Parameter-Switching Method in the Chen Oscillator and Application in Image Transmission. Symmetry 2021, 13, 923. [Google Scholar] [CrossRef]
- Muhammad, A.S.; Ozkaynak, F. SIEA: Secure Image Encryption Algorithm Based on Chaotic Systems Optimization Algorithms and PUFs. Symmetry 2021, 13, 824. [Google Scholar] [CrossRef]
- Yu, F.; Shen, H.; Zhang, Z.; Huang, Y.; Cai, S.; Du, S. A new multi-scroll Chua’s circuit with composite hyperbolic tangent-cubic nonlinearity: Complex dynamics, Hardware implementation and Image encryption application. Integration 2021, 81, 71–83. [Google Scholar] [CrossRef]
- Yu, F.; Li, L.; He, B.; Liu, L.; Qian, S.; Zhang, Z.; Shen, H.; Cai, S.; Li, Y. Pseudorandom number generator based on a 5D hyperchaotic four-wing memristive system and its FPGA implementation. Eur. Phys. J. Spec. Top. 2021, 230, 1763–1772. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Jin, J.; Du, S. Design and FPGA implementation of a pseudo-random number generator based on a Hopfield neural network under electromagnetic radiation. Front. Phys. 2021, 9, 690651. [Google Scholar] [CrossRef]
- Tutueva, A.V.; Karimov, T.I.; Moysis, L.; Nepomuceno, E.G.; Volos, C.; Butusov, D.N. Improving chaos-based pseudo-random generators in finite-precision arithmetic. Nonlinear Dyn. 2021, 105, 727–737. [Google Scholar] [CrossRef]
- Sajad, S.; Kapitaniak, T. Special chaotic systems. Eur. Phys. J. Spec. Top. 2020, 229, 877–886. [Google Scholar]
- Xu, Y.; Yang, Y. A new chaotic system without linear term and its impulsive synchronization. Optik 2014, 125, 2526–2530. [Google Scholar] [CrossRef]
- Mobayen, S.; Kingni, S.; Pham, V.T.; Nazarimehr, F.; Jafari, S. Analysis, synchronisation and circuit design of a new highly nonlinear chaotic system. Int. J. Syst. Sci. 2018, 49, 617–630. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.; Li, Z. Chaos in a novel fractional order system without a linear term. Int. J. Nonlinear Mech. 2018, 106, 1–12. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 2002. [Google Scholar]
- Sprott, J.C. Elegant Chaos: Algebraically Simple Chaotic Flows; World Scientific: Singapore, 2010. [Google Scholar]
- Wang, X.; Chen, G. Constructing a chaotic system with any number of equilibria. Nonlinear Dyn. 2013, 71, 429–436. [Google Scholar] [CrossRef] [Green Version]
- Leonov, G.A.; Kuznetsov, N.V. Hidden attractors in dynamical systems: From hidden oscillation in Hilbert-Kolmogorov, Aizerman and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bif. Chaos 2013, 23, 1330002. [Google Scholar] [CrossRef] [Green Version]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Z.; Sun, K.; Shaobo He, H.W.; Xu, Q.; Chen, M. Chaotic flows with special equilibria. Eur. Phys. J. Spec. Top. 2020, 229, 905–919. [Google Scholar] [CrossRef]
- Hens, C.; Dana, S.K.; Feudel, U. Extreme multistability: Attractors manipulation and robustness. Chaos 2015, 25, 053112. [Google Scholar] [CrossRef] [Green Version]
- Bao, B.; Qian, H.; Xu, Q.; Chen, M.; Wang, J.; Yu, Y. Coexisting Behaviors of Asymmetric Attractors in Hyperbolic-Type Memristor based Hopfield Neural Network. Front. Comput. Neurosci. 2017, 11, 81. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Sun, J.; Lu, T.; Lei, T. Symmetry Evolution in Chaotic System. Symmetry 2020, 12, 574. [Google Scholar] [CrossRef] [Green Version]
- Thoai, V.P.; Kahkeshi, M.S.; Huynh, V.V.; Ouannas, A.; Pham, V.T. A Nonlinear Five-Term System: Symmetry, Chaos, and Prediction. Symmetry 2020, 12, 865. [Google Scholar] [CrossRef]
- Xu, Q.; Lin, Y.; Bao, B.; Chen, M. Multiple attractors in a non-ideal active voltage- controlled memristor based Chua’s circuit. Chaos Solitons Fractals 2016, 83, 186–200. [Google Scholar] [CrossRef]
- Xu, Q.; Cheng, S.; Ju, Z.; Chen, M.; Wu, H. Asymmetric coexisting bifurcations and multi-stability in an asymmetric memristive diode-bridge-based jerk circuit. Chin. J. Phys. 2021, 70, 69–81. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Physica D 1985, 16, 285–317. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Sprott, J.C. Variable-boostable chaotic fows. Opt. Int. J. Light Electron Opt. 2016, 27, 10389–10398. [Google Scholar] [CrossRef]
- Tamba, V.K.; Karthikeyan, R.; Pham, V.T.; Hoang, D.V. Chaos in a system with an absolute nonlinearity and chaos synchronization. Opt. Int. J. Light Electron Opt. 2018, 2018, 5985489. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.F.; Tan, Y.R.; Wang, Y.H.; Yang, H.J. Active backstepping control of combined projective synchronization among different nonlinear systems. Automatika 2018, 58, 295–301. [Google Scholar] [CrossRef]
- Runzi, L.; Yinglan, W.; Shucheng, D. Combination synchronization of three classic chaotic systems using active backstepping design. Chaos 2012, 22, 023109. [Google Scholar] [CrossRef]
- Pone, J.R.M.; Kingni, S.T.; Kol, G.R.; Pham, V.T. Hopf bifurcation, antimonotonicity and amplitude controls in the chaotic Toda jerk oscillator: Analysis, circuit realization and combination synchronization in its fractional-order form. Automatika 2019, 60, 149–161. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamba, V.K.; Ramadoss, J.; Pham, V.-T.; Grassi, G.; Almatroud, O.A.; Hussain, I. Symmetric Oscillator: Special Features, Realization, and Combination Synchronization. Symmetry 2021, 13, 2142. https://doi.org/10.3390/sym13112142
Tamba VK, Ramadoss J, Pham V-T, Grassi G, Almatroud OA, Hussain I. Symmetric Oscillator: Special Features, Realization, and Combination Synchronization. Symmetry. 2021; 13(11):2142. https://doi.org/10.3390/sym13112142
Chicago/Turabian StyleTamba, Victor Kamdoum, Janarthanan Ramadoss, Viet-Thanh Pham, Giuseppe Grassi, Othman Abdullah Almatroud, and Iqtadar Hussain. 2021. "Symmetric Oscillator: Special Features, Realization, and Combination Synchronization" Symmetry 13, no. 11: 2142. https://doi.org/10.3390/sym13112142
APA StyleTamba, V. K., Ramadoss, J., Pham, V.-T., Grassi, G., Almatroud, O. A., & Hussain, I. (2021). Symmetric Oscillator: Special Features, Realization, and Combination Synchronization. Symmetry, 13(11), 2142. https://doi.org/10.3390/sym13112142






