Abstract
Background: Some medical and technological tasks lead to the geometrical problem of how to cover the unit circle as much as possible by n congruent circles of given radius r, while r varies from the radius in the maximum packing to the radius in the minimum covering. Proven or conjectural solutions to this partial covering problem are known only for n = 2 to 5. In the present paper, numerical solutions are given to this problem for n = 6 and 7. Method: The method used transforms the geometrical problem to a mechanical one, where the solution to the geometrical problem is obtained by finding the self-stress positions of a generalised tensegrity structure. This method was developed by the authors and was published in an earlier publication. Results: The method applied results in locally optimal circle arrangements. The numerical data for the special circle arrangements are presented in a tabular form, and in drawings of the arrangements. Conclusion: It was found that the case of n = 6 is very complicated, whilst the case n = 7 is very simple. It is shown in this paper that locally optimal arrangements may exhibit different types of symmetry, and equilibrium paths may bifurcate.
1. Introduction
Let n congruent circles, that is, circles with the same radius, be given, and let r be their radius such that , where is the maximum radius of n congruent circles that can be packed in the unit circle without overlap and is the minimum radius of n congruent circles that can cover the unit circle without interstices. For congruent circles, Zahn [1] posed the following partial covering problem: how to arrange n congruent circles of radius r so that the area of the part of the unit circle covered by the congruent circles is a maximum? An important question is connected to this: how does the maximum-area arrangement of the congruent circles change if r varies from to ?
It turns out that physical realizations of partial coverings with congruent circles occur in different practical fields. Here, the mosaicplasty surgical method for repairing circular cartilaginous defects [2] is mentioned as one example (Figure 1).
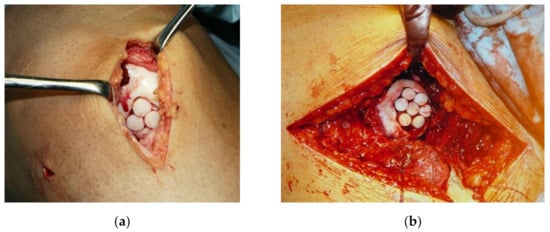
Figure 1.
Arrangements of equal grafts in the cartilage replacing surgery with mosaicplasty: (a) partial covering with three congruent circles; (b) packing of seven congruent circles. (Photo courtesy of László Hangody).
The above problems of maximum packing, minimum covering and maximum partial covering are problems of discrete geometry that, for different circle numbers, require independent solutions. Even in the case of packing and covering, the optimum has been proven for only a few values of n: for packing up to n = 14 and for 19 [3,4,5,6,7,8,9], for covering up to n = 10 [10,11,12]. However, many papers have been published that describe numerically determined, putatively optimal arrangements for different circle numbers, sometimes improving on former results. The best-known packings up to n = 65 are given by Ref. [13], and the data of the best-known coverings up to n = 35 are presented in Ref. [14]. Partial-covering problems are much more complicated than packing or covering problems, and results for the transition from the maximum packing to the minimum covering are known only for fewer than six circles.
The proven solution for n = 2 was provided by Zahn [1] and for n = 3 by Szalkai [15]. For n = 4 [16] and n = 5 [17], conjectured numerical solutions have been presented. In the cases of n = 6 to 10, Zahn [1] gave numerical results for some sporadic values of r. He thoroughly investigated the case n = 6 (for r = k/16, k = 6, 7, 8, 8.5, 8.625, 8.75) that he found particularly complicated. The maximum-area arrangements of the circles occurred in different forms that he called ring, central, triangular and diamond, which represented different kinds of symmetry (and sometimes broken symmetry). Because of the relatively low accuracy of calculation, and the small number of r values considered, he could not describe the complete transition of the maximum area arrangement of the circles from the maximum packing to the minimum covering. In the case of n = 7, he made calculations for r = k/16, k = 6 and 7, and found that the maximum-area arrangement of circles has sixfold symmetry.
The aim of this paper is to provide numerical solution to this partial covering problem in the cases of n = 6 and 7, when r varies from the maximum packing radius to the minimum covering radius. It will be shown that this geometrical problem can be solved with tools derived from mechanics. Point group symmetry [18,19] and catastrophe theory [20] will also be applied.
It is worth mentioning that closely related problems arise where n congruent circles are arranged on the spherical surface instead of the unit circle. Here, especially the maximum packing problem, also known as Tammes problem, has a vast literature. In the case of packing and covering, the optimum has been proven for only a few values of n: for packing up to n = 14 and for 24 [21,22,23,24,25,26], for covering up to n = 10 and for 14 [27,28,29,30]. The best known packings up to n = 130 are given in Ref. [31], and the best-known coverings up to n = 130 are presented in Ref. [32]. For partial coverings, much fewer results are known. The optimum has been proven for n = 2, 3, 4, 6, 12 [33,34], and conjectural results have been presented for n = 5, 7, 8, 9, 10, 11, 13 [35,36].
2. Method
First, some definitions and basic statements after Ref. [37] are presented. The network of the system of members in covering the unit circle by congruent circles is a bipartite graph. This is owing to the fact that the members are specifically connected with two kinds of joints. Joints of the first kind are the centres of the congruent circles. Joints of the second kind are common points of intersection of the boundaries of three or more circles, which are not internal points of any of the congruent circles.
A tensegrity structure is a framework that is composed of cables, struts and bars. Cables cannot increase their length (they are able to carry only tensile forces). Struts cannot decrease their length (they are able to carry only compressive forces). Bars can neither increase nor decrease their length (they are able to carry both tensional and compressive forces).
A generalised tensegrity constructed for partial covering is a framework built up from cables, struts and triangular elements. A cable joins the centre of one of the congruent circles to the centre of the unit circle, and the cable is active (a tension force appears in the cable) if the circle and the unit circle intersect. A strut joins the centres of two congruent circles, and the strut is active (a compression force appears in the strut) if the two congruent circles intersect. A triangular element forms a triangle whose vertices are centres of congruent circles, and the triangle element is active (a tension force appears at least in one edge of the triangle) if the intersection of the three congruent circles has an area different from zero.
In the calculations, the tensegrity structure is replaced by a bar-and-joint assembly where only the active elements are replaced by bars. (The length of a stress-free bar replacing a strut is 2r, and the length of a stress-free bar replacing a cable is 1 – r.) Here, the gradual change of the length of the radius (i.e., of the elements) is the load. For each new step, it must be checked whether the forces in bars have the correct sign (tensional force in a cable and compressive force in a strut), and none of the previous passive elements has exceeded the current valid length of the stress-free elements. If the opposite of any of these situations occurs, then an iteration procedure should be used to determine the value of r (the special value) at which one of the bars will just be stress-free, or a hitherto passive element will become active. In this way, the bar-and-joint structure will change significantly.
The quantity, where the area of the part of the unit circle covered by the congruent circles is divided by the area of the unit circle, is called coverage.
A circle in an arrangement is called a rattling circle, if it is not fixed by the neighbouring circles, and is able to translate freely in a domain with two degrees of freedom without changing the coverage. A rattling circle is either disconnected from the others and can move without overlapping other circles, or is connected to its neighbours and can move without making interstices.
Overlaps of circles define parts of the congruent circles that can be removed while the coverage of the unit circle remains unchanged. The sum of the areas of the removed parts is called the surplus area.
A framework is in a state of self-stress if it can have internal forces without external forces, and the internal forces are in equilibrium at every joint, and, consequently, the whole framework is in equilibrium.
Consider the surplus area A as the potential energy of a generalised tensegrity, which is in a state of self-stress at a point if the gradient of A is zero at that point. The generalised tensegrity is in a stable state of self-stress if the potential energy A has a local minimum at that point. According to this, the equilibrium is stable at a point, if the Hessian matrix, which in structural mechanics is called the tangent stiffness matrix (or, for short, the stiffness matrix), is positive definite, unstable if the Hessian matrix has a negative eigenvalue, and critical if the Hessian matrix is singular.
Csikós [38] established that the derivative of the overlapping area with respect to the distance between the centres of two intersecting circles is equal to the length of the chord that the two circles have in common. This simplifies the calculation of the gradient of the covered area, which should be equal to zero in the case of the maximum partial covering. Connelly [39] introduced a tensegrity structure analogous to the arrangement of the congruent circles and made a stress interpretation of Csikós´s result. Connelly´s model worked well if only double overlaps appeared, but for circle radii close to the minimum covering radius some triple overlaps occurred, for which it was not clear what the adequate model should be. In Ref. [37], we introduced a generalised tensegrity structure, which also contained triangle elements by which it is possible to model triple overlaps. By analogy, we transformed the geometrical problem to a problem of mechanics and worked out a method to solve the partial covering problem numerically. It is only outlined here, because earlier a complete paper [37] was dedicated to the description of the method, where the interested reader can find the details.
The main points of the method are the following. Instead of finding the maximum of the covered area of the unit circle, we are looking for the minimum of the surplus area A. The surplus area is considered as an internal potential energy. Since the external potential energy is zero, condition for vanishing of the gradient of A equates to the necessary condition for an extremum (expressing the equilibrium of forces), and the condition is obtained in the form of a set of homogeneous linear equations, which means that the equilibrium appears in the form of a state of self-stress of the generalised tensegrity. Stability of the equilibrium is decided by the eigenvalues of the Hessian matrix (tangent stiffness matrix) at the point where the generalised tensegrity is in equilibrium. In this way, the partial covering problem can be solved by finding the self-stress positions of a generalised tensegrity structure.
We introduce the concept of the equilibrium path, in which we plot a characteristic of the circle arrangements for which the associated structure is in a state of self-stress as a function of the radius of the congruent circles. Starting from an equilibrium arrangement and slightly changing the radius of the congruent circles, we can use an iteration procedure to determine another point of the equilibrium path using the tangent stiffness matrix. If all eigenvalues of the tangent stiffness matrix in a state are positive, then the arrangement is locally optimal. If the number of negative eigenvalues changes during a step, then the equilibrium path will bifurcate. The location of the bifurcation can be specified to arbitrary precision, via iteration by expediently changing the step size. We also try to find the points of the equilibrium paths where the number and/or type of active elements change. (At these points, due to the non-smoothness of the material equations, the eigenvalues can change abruptly.)
To simplify the notation, and will stand for and , respectively. and , denote cyclic and dihedral symmetry groups in the plane ( consists of rotations; of rotations and axial reflections) [18,19].
3. Optimal Packings of Six Circles
As known [3,4], without overlap up to six equal circles of radius can be packed into the unit circle. It is also true that seven of these circles can also be packed: one in the middle of the unit circle and six evenly distributed around it. At packing of six circles, one of these should be removed. Thus, two substantially different packings are possible (Figure 2). If the middle circle is removed (Figure 2a), then the packing has symmetry. If one of the outer circles is removed (Figure 2b–d), then the packing can be of or symmetry but typically is asymmetric (). The location of the outer circles can be given by a four-dimensional set. For giving the location, consider the symmetry packing (Figure 2c) and denote the angle of the gaps between the outer circles visible from the centre of the unit circle by α. In full symmetry, α = π/15. Starting from the lowest circle, denote by (i = 0,1,...,5) the angle by which the ith circle is rotated about the origin (centre of the unit circle) from the position that it had in the symmetry configuration. The lowest circle is supported against rotation, thus . So, a displaced position can be defined by the coordinates (i =1,...,4). The outer circles cannot overlap, that is, with the inequalities:
the space can be reduced to a simplex whose vertices are
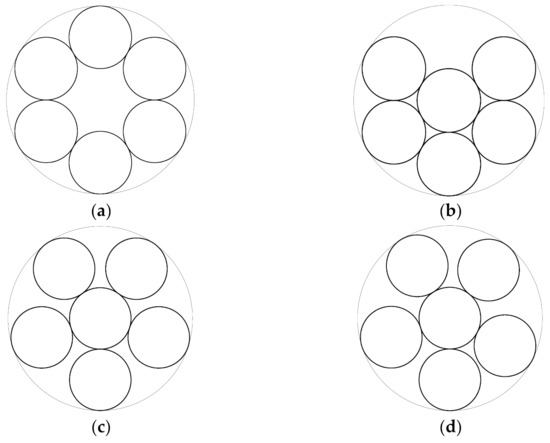
Figure 2.
Optimum packing of six equal circles in the unit circle () in symmetries: (a) , (b) , (c) and (d) .
At these points, the configurations have symmetry shown in Figure 2b.
The data of the special or investigated circle arrangements (radius, locus of the centre of the circles, and coverage) are presented in tabular form in Section 6.
4. Coverings by Six Circles
It is easy to see that the unit circle can be covered by circles of radius in symmetry (Figure 3a), and by circles of radius in symmetry (Figure 3b). According to Figure 3a, the boundary of the unit circle can be covered by five congruent circles, if the diameter of the circles is at least equal to the distance between the endpoints of an arc of length 2π/5. Using circles of this size, the sixth circle abundantly covers the area not yet covered by the five circles, so in symmetry the radius of the circles required for optimal covering is .
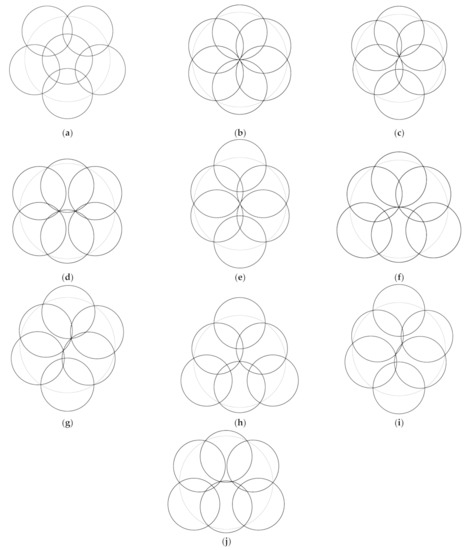
Figure 3.
Coverings of the unit circle (the subscript on R indicates the type of symmetry, if there are more types, then these are numbered in parentheses): (a) , (b) , (c) , (d) , (e) , (f) , (g) , (h) , (i) and (j) .
According to Figure 3b, for a covering of symmetry , each circle must cover a sector with a central angle π/3, that is, for the optimal covering, circumcircles of equilateral triangles of side length 1 should be applied, i.e., .
At the check of optimality, it should be established that there are not more than three bars connected to the joints of the second kind of the bar-and-joint assembly (structure) described in Ref. [37] (since in such a case the joint should be considered as a multiple joint, and it should be split (multiplied)); otherwise, in this position, the structure can be in a state of self-stress produced entirely by bars in tension (which can be considered as cables). The structures defined by the six circles can be in a state of self-stress in both configurations (Figure 3a,b).
Although the symmetric assembly associated only with the five outer circles in Figure 3a can be in a state of self-stress, the covering is locally optimal. Because the position of the middle circle is not fixed, it can be shifted to any position in which it covers the central region not covered by the other five circles. The permissible range of the centre of the middle circle is bounded by five circular arcs of radius r, the centre of which is the point of the common part of 2–2 outer circles, closest to the origin. If the middle circle is moved off the origin, the symmetry is lost. Generally, all symmetries disappear, but if the centre of the middle circle is fitted to one of the axes of symmetry of the arrangement shown in Figure 3a, the arrangement will remain of symmetry.
In the case of a covering of symmetry, six bars are also connected to the joint of the second kind in the centre, so the covering can be improved. The improvement will be achieved in steps to get to as many covering positions (allowing states of self-stress) as possible. (At each step, the unit circle can be covered by circles with a smaller radius than the previous one.) In the first step, one of the six bars can be omitted or, in the case of joint doubling, two bars lying on one of the straight lines can be doubled. In both cases, the structure slackens and we can return to a state of self-stress with even cooling. In the first case (Figure 3c), the covering will have symmetry, and in the second case (Figure 3d), symmetry.
Neither case is optimal, since in the first case five bars run into a joint of the second kind, while in the second case four bars run into two joints of the second kind, so the next step is to remove one bar again. Since we do not want to remove a neighbour of the previously removed bar, we have two substantially different options in the position shown in Figure 3c: one with symmetry (Figure 3e) and the other symmetry (Figure 3f). In the case of the covering shown in Figure 3d, there can be only one case due to symmetries (it is not possible to remove the previously doubled bars because among the remaining three bars one would have an angle of more than 180 degrees); also, according to Figure 3g, the covering has no symmetry. The three coverings thus obtained are not optimal since, at all the three ones, four bars meet at a joint of the second kind.
In the arrangement shown in Figure 3e, the middle joint and the bars along one of the straight lines must be doubled to obtain the covering of symmetry shown in Figure 3i. In the covering shown in Figure 3f, a bar can be removed to obtain an arrangement of symmetry as shown in Figure 3h, or the middle joint and the vertical cables can be doubled to obtain a covering of symmetry (Figure 3j). Note that arrangements presented in Figure 3i,j, are obtained even if the corresponding bar of the arrangement of symmetry shown in Figure 3g is removed. The coverings shown in Figure 3h–j meet the conditions for a local optimum.
So, we found a total of four coverings to be locally optimal. Of these, the circles in the covering shown in Figure 3j have the smallest radius, which represents the global optimum. The optimality of this covering has already been proven by Bezdek [10].
5. Equilibrium Paths in the Case of Six Circles
The position of the unit circle and the six congruent circles is determined by a total of 14 coordinates. Of these, three coordinates were prescribed to avoid rigid body displacement, so the order of the stiffness matrix is 11.
We have shown in Figure 2 that there are two substantially different optimal packings, which cannot be brought into coincidence by keeping the rules of packing and continuously changing the position of the circles. At first, we start with these packings and follow the equilibrium paths that start from them. Then, when we decide that we cannot reach the optimal covering in this way; we also determine the equilibrium path starting from this covering.
5.1. Equilibrium Path Starting from the Packing of Symmetry
The relationship between the different branches of the equilibrium path starting from the symmetry packing is illustrated in Figure 4. Above each branch we give the number of branches of that type and the symmetry of the circle arrangements. The type of line illustrates the number of negative eigenvalues of the stiffness matrix of the structure associated with the arrangement (0—solid, 1—dashed, 2—result and 3—dotted). For clarity, we drew only one of each type at the branches; the others are indicated only at their start. The symbols of the circle radii belonging to the special equilibrium positions are also given in Figure 4.
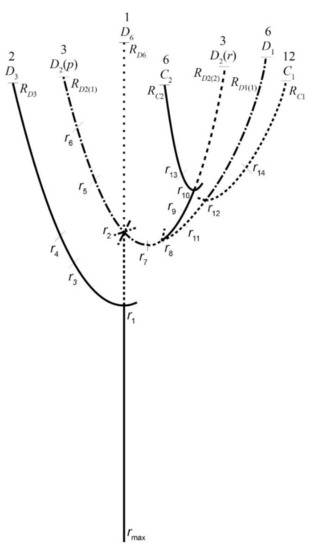
Figure 4.
Equilibrium path starting from the packing of symmetry .
5.1.1. The Branch of Symmetry
Starting from the configuration shown in Figure 2a and then increasing the radius in small steps, the tensegrity structure consists of six active cables and six struts in the interval (, ), and the stiffness matrix is positive definite. At radius (Figure 5a), the stiffness matrix has one zero eigenvalue. This point is a standard cusp catastrophe, where the equilibrium path has a stable symmetric bifurcation. The eigenvector corresponding to the zero eigenvalue shows that the “buckled” shape has symmetry.

Figure 5.
Arrangements in symmetry , (a) one zero eigenvalue, and (b) one negative and two zero eigenvalues.
If , then the stiffness matrix has one negative eigenvalue. If the magnitude of the radius is exactly (Figure 5b), then in addition to one negative eigenvalue, there will also be two zero eigenvalues. Since the number and type of the active elements do not change, the function describing the surplus area of congruent circles in a small neighbourhood of this point is smooth, so the elementary catastrophe theory can be applied. Similarly to the statement made in Ref. [17] for the five secondary paths (branches) for five congruent circles, we can say that in a suitable coordinate system the third truncation of the active part of the function describing the surplus area A can be transformed into the form
where . Examining this form, we can conclude that there is an elliptic umbilic catastrophe, that is, three secondary paths intersect the primary equilibrium path, and each secondary path increases the number of negative eigenvalues by one compared to the previous ones, i.e., there will be two negative eigenvalues. The three secondary equilibrium paths lie in the vertical planes , and gives their shape. The buckled shapes have symmetry. On the ascending branches, the circle centres fitting to axes of symmetry approach each other (pumpkin shape), while on the descending branches they move away from each other (rugby ball shape).
If , then the stiffness matrix has three negative eigenvalues throughout. Of course, in the meantime we also reach states where triple overlaps occur, but here the common part of two circles is completely enclosed by a third circle, so the forces generated in the newly formed struts are just equilibrated by the edge force of the triangle element, so these two elements can be ignored together. If the radius of the circles tends to , two positive eigenvalues tend to zero, but when complete covering is reached (Figure 3b), three new struts appear.
5.1.2. The Branch of Symmetry
In Section 5.1.1, we found that the equilibrium path bifurcates at point . We are now examining this branch. If , then the structure consists of six cables and six active struts. At point , the three inner circles pairwise just touch each other (Figure 6a), and thus three new struts become active. At , the common parts of the inner circles reach the outer circles (Figure 6b), so three triangle elements also appear. This model remains up to the radius , at which the unit circle is just covered by the six congruent circles (Figure 3h). The stiffness matrix is positive definite on the whole branch . Approaching the covering arrangement, five eigenvalues also tend to zero.
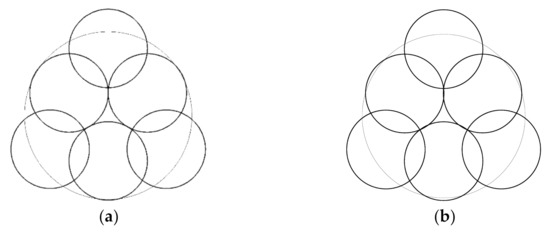
Figure 6.
Arrangements in symmetry: (a) three new struts appear, (b) three triangle elements appear.
5.1.3. The Branch of (Pumpkin) Symmetry
In Section 5.1.1, we found that the primary equilibrium path is obliquely intersected by three secondary equilibrium paths at point . We are now examining the ascending branch of these paths. The six circles form an arrangement with symmetry, whose convex hull resembles a pumpkin. If , then the structure consists of six cables and six active struts. At point , the two circles fitting the axis of symmetry just touch each other (Figure 7a), and thus a strut becomes active. At point , four circular contacts are formed, and by maintaining the symmetry, four new active struts and four triangle elements appear (Figure 7b), but these again quench the effect of each other. No significant change occurs until the covering shown in Figure 3d. The stiffness matrix has two negative eigenvalues over the entire pumpkin branch, so the arrangement is not even locally optimal. Approaching the covering configuration, five eigenvalues tend to zero.
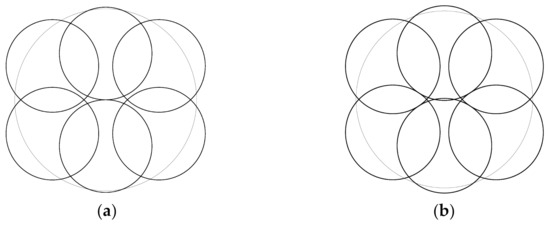
Figure 7.
Arrangements in (pumpkin) symmetry: (a) appearance of a new strut, (b) appearance of four struts and four triangle elements equilibrating each other.
5.1.4. The Branch of (Rugby Ball) Symmetry
We now consider the descending branch of the three secondary equilibrium paths intersecting equilibrium path at point . Here, too, the six circles form a symmetry arrangement; their convex hull is reminiscent of a rugby ball. If , then the tensegrity structure consists of six cables and six active struts. At (Figure 8a), one of the two negative eigenvalues of the stiffness matrix of the structure becomes zero, and at a limit point (fold catastrophe) the equilibrium path begins to rise (the active topology of the structure does not change). At the point (Figure 8b), two new struts become active. Thus, the stiffness matrix changes abruptly, and all its eigenvalues become positive. (Since the smallest eigenvalue changes sign at the jump, the equilibrium path may bifurcate. The side branches are analysed in Section 5.1.5).
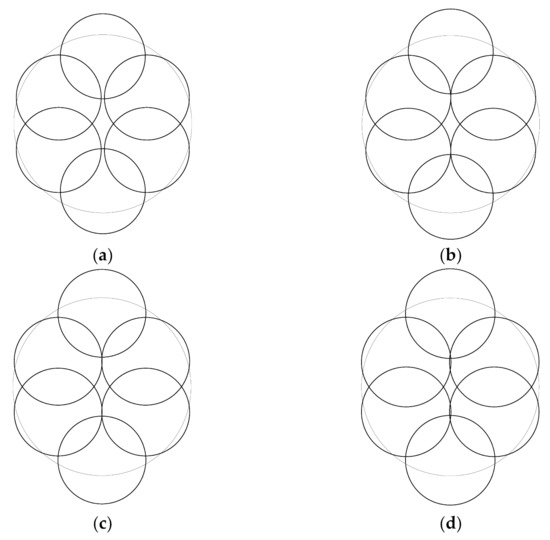
Figure 8.
Arrangements in (rugby ball) symmetry (a) limit point, (b) appearance of two new struts, (c) appearance of two triangle elements and (d) one zero eigenvalue.
In the interval the structure consists of six cables and eight active struts. At the point (Figure 8c), two triangle elements become active, but the stiffness matrix remains positive definite. This state lasts to the point (Figure 8d), at which the stiffness matrix has a zero eigenvalue, so bifurcation occurs. The two side branches remain stable; the stiffness matrix at the points of the (rugby ball) branch will have a negative eigenvalue in the following. So, at point there is a standard cusp catastrophe (stable symmetric bifurcation). There is no significant change along this branch until the covering shown in Figure 3e.
5.1.5. The Branch of Symmetry
In the previous section, we found that, on the rugby ball branch, at radius , 2–2 circles just touch each other. In the touching position, the respective strut can be considered both active and passive. The stiffness of the strut jumps at this point, so the type of bifurcation cannot be determined on the basis of catastrophe theory since it deals only with smooth functions. A similar case occurred in Ref. [17], where two asymmetric branches ran into a point of a branch of symmetry. Here, too, only one strut will be active on each of the two side branches, so the degree of symmetry decreases here as well; the arrangements on the rugby ball branch have symmetry and on the side branches have symmetry. From the point of bifurcation, these branches ascend, but the stiffness matrix of the structure containing six cables and seven active struts still has a negative eigenvalue.
At radius (Figure 9a), a triangle element becomes active, and then at radius (Figure 9b) the stiffness matrix also has a zero eigenvalue. Here, the energy function is smooth, and the classification of the catastrophe theory can be used: a standard cusp catastrophe (stable symmetric bifurcation) occurs. One negative eigenvalue remains on the side branches; however, in the rest of the branch , the stiffness matrix already has two negative eigenvalues. On this branch, the arrangement is essentially unchanged (the new struts and the triangle elements equilibrate each other) all the way to radius , covering the unit circle (Figure 3c), when five small circles intersect each other at the same point.
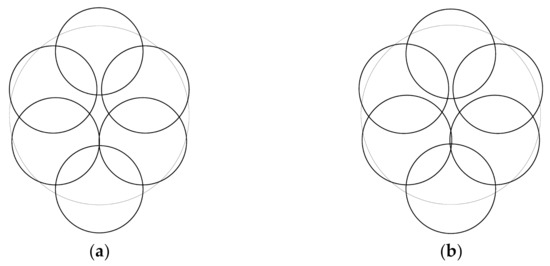
Figure 9.
Arrangements in symmetry: (a) appearance of a triangle element, (b) one zero eigenvalue.
5.1.6. The Branch of Symmetry
In Section 5.1.4, we found that the rugby ball branch has a stable symmetric bifurcation point at radius . The arrangements belonging to the side branches have symmetry, and the stiffness matrix is positive definite, i.e., the arrangements are locally optimal. In the interval the structure consists of six cables, eight active struts and two triangle elements. At radius (Figure 10), a third triangle also becomes active, but the branch remains stable until covering that occurs at radius (Figure 3i).
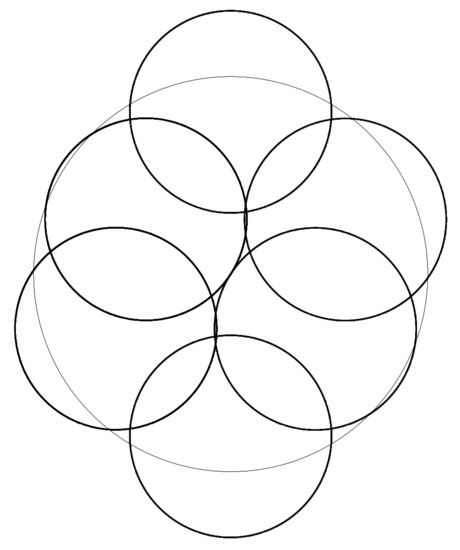
Figure 10.
Appearance of one new strut in symmetry, .
5.1.7. The Branch of Symmetry
In Section 5.1.5, we found that branch has a stable symmetric bifurcation point at radius . With buckling, the symmetry decreases, so the side branch has asymmetrical ( symmetry) arrangements. Branch has a passive negative eigenvalue at this point, so there will also be a negative eigenvalue on the side branch. At the radius two circles touch each other (Figure 11) and a new strut becomes active. The resulting structure composed of six cables, eight struts and one triangle element all the way to the covering (Figure 3g) is a suitable model, because the two struts that still appear are equilibrated by the new triangle elements.
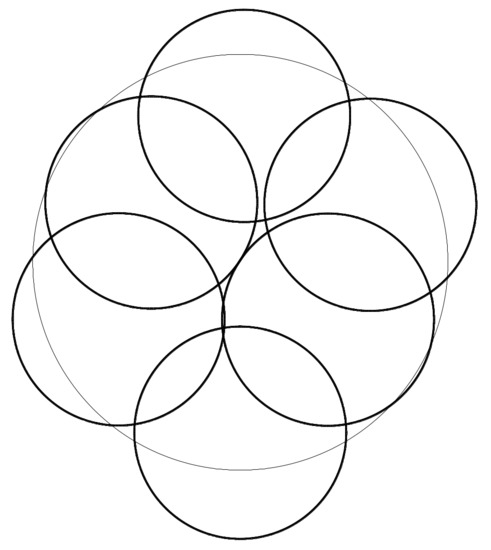
Figure 11.
Appearance of a new strut in symmetry, .
5.2. Equilibrium Path Starting from the Packing of Symmetry
The relationship between the different equilibrium paths starting from the symmetry packing is illustrated in Figure 12a. Above the branches, we give how many of that type of branch there are and what the symmetry of the arrangements is. The solid line indicates the locally optimal arrangements, and the line marked with short horizontal segments means that an equilibrium surface starts from each of its points.
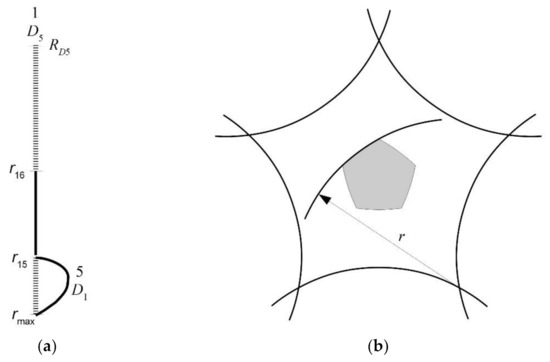
Figure 12.
(a) Equilibrium paths starting from the packing of symmetry, (b) shape of the cross-sections of the part associated with the interval .
5.2.1. The Branch of Symmetry
If the radius of the congruent circles is chosen to be slightly larger than and we start from the packing of symmetry shown in Figure 2c, the structure will have five active cables and five struts, but the stiffness matrix will have two negative and two zero eigenvalues. Zero eigenvalues indicate that there is a bifurcation at every point (of this segment) of the equilibrium path.
This strongly degenerate state lasts all the way to the radius , at which the five outer circles touch their neighbour (Figure 13a) and five new struts become active. The stiffness matrix of the structure changes abruptly, and all its eigenvalues will be positive, so the structure consisting of five cables and 10 active struts, from the radius , belongs to stable arrangements of symmetry.
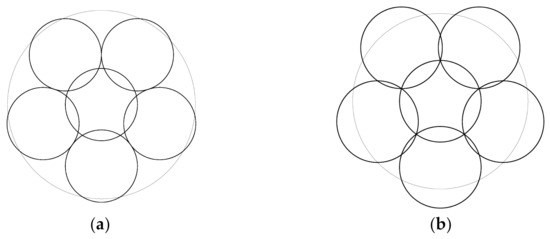
Figure 13.
Arrangements in symmetry: (a) the outer circles touch the neighbour, (b) appearance of five triangle elements.
This stable equilibrium path lasts up to the radius , at which the common part of the outer circles reaches the boundary of the inner circle, so that five triangle elements become active (Figure 13b). The eigenvalues of the stiffness matrix change abruptly again, and two zero eigenvalues also appear. The symmetry structure consists of five cables, 10 struts and five triangle elements; the stiffness matrix is singular until the radius is reached, that is, there is a bifurcation at every point of this segment as well. The symmetry arrangement for the radius is shown in Figure 3a.
5.2.2. The Segment
It has already been pointed out in Section 3 that, in the packings shown in Figure 2b–d, the permissible positions of the four outer circles can be given by a four-dimensional simplex. If the radius is increased, the angle introduced in Section 3 decreases:
However, not each point of the simplex corresponds to an equilibrium position. This is because if the radius is greater than , then equal forces are generated in the active struts, which are kept in equilibrium by the cable forces at the outer circles, but the middle circle is only in equilibrium if the following conditions are met:
Conditions (5) define a zero-measure part of the four-dimensional simplex. i.e., a part of a two-dimensional surface, which can be parametrised, for example, also with the coordinates , . Assigned the planar shape defined above to each point of the segment , a tree-trunk-like space is obtained (at point the cross-section shrinks to a point), the points of which define equilibrium positions. The “heart- and sapwood” of a tree trunk belong to arrangements in symmetry. In the “bark” of a tree trunk, at least one of the inequalities (1) is fulfilled in the form of an equality, i.e., two circles touch each other, that is, one strut becomes active and changes the stiffness matrix though with zero strut force but with infinitely large stiffness. At all points of a cross-section of a tree trunk, the coverage of the unit circle is the same.
5.2.3. The Segment
The phenomenon at is similar to the reverse of the phenomenon at . Equilibrium positions here also form a “tree trunk”; the “heart- and sapwood” are the equilibrium path of arrangements of symmetry. The cross-section of the trunk is illustrated by the shaded plane shape in Figure 12b, and its explanation (the middle circle is “rattling”) is given in Section 4. The points of the “bark” indicate the positions in which the line of the inner circle just passes through the point of the common domain of two outer circles closest to the centre of the unit circle. Then, the area of one triangle element, and thus its edge forces, will be zero, even its stiffness will be zero. Because of this, the stiffness matrix of the structure also changes; one of its zero eigenvalues becomes positive, since the centre of the middle circle can no longer move inside the tree trunk, i.e., in a plane in all directions but only on the bark. Five edges are also formed on the bark from the intersections of the circles. In the case of the structures associated with the edges, two triangle elements are also passive, and the corresponding arrangements are stable.
Note that during the iteration there are serious difficulties caused by the singularity. If we prescribe an upper bound for the norm of the vector of unequilibrated forces as a stopping condition, the inner circle may not completely cover the area that is not covered by the outer five circles, so the number of active triangle elements is unreliable.
5.2.4. The Branch of Symmetry
In Section 5.2.2, we determined the arrangements on the segment where the structure is in equilibrium. But what happens if we rotate the five outer circles about the origin so that the middle circle is not in equilibrium? The middle circle moves out from its position, and begins to widen one slot and closes the others. The coverage is improved, and we get to a locally optimal arrangement. This arrangement can also be reached by starting directly from the arrangement shown in Figure 2b; by moving the middle circle slightly upwards, five active cables and nine active struts are formed, and the stiffness matrix becomes positive definite.
In Figure 14, for the sake of comparability, we show the arrangements of different symmetries for the radius :
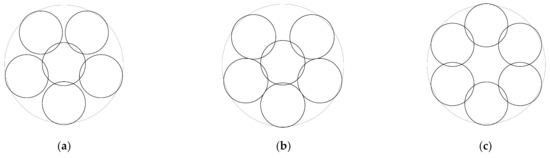
Figure 14.
Arrangements corresponding to the radius in (a) symmetry, (b) symmetry and (c) symmetry.
- (a)
- symmetry discussed in Section 5.2.1 (there is not even a local optimum, coverage: 0.7643588212),
- (b)
- symmetry (local optimum, coverage: 0.7651570086),
- (c)
- symmetry discussed in Section 5.1.1 (local optimum, coverage: 0.7582353854).
It can be stated that the arrangement of symmetry is optimal. If we increase the radius, starting from the value of , then
- (i)
- In the arrangement shown in Figure 14b, the gap visible at the top gradually decreases,
- (ii)
- The displacement of the middle circle increases, then begins to decrease, and finally it becomes zero at the radius , that is, the arrangement of symmetry passes into an arrangement of symmetry.
This means that if the arrangements are characterised by the coordinates of the centre of the middle circle, then the tree trunks discussed in Section 5.2.2 will shrink to a straight line lying on the axis. The branches just discussed (of which there are of course five different branches, since the initial gap between the outer circles can be considered between any two outer circles at start-up) show the shape of the wires of an old-fashioned whisk (or of air roots penetrating into the ground at the trunk) in the interval , (Figure 12a).
5.3. Equilibrium Path Starting from the Optimal Covering
The equilibrium path starting from the optimal covering is illustrated in Figure 15. There are six such paths since any of the six circles can be considered as closest to the origin. Each point of the equilibrium path corresponds to an arrangement of symmetry. The solid line indicates the locally optimal arrangements, and the stiffness matrix of the structure corresponding to the points of the dashed line has a negative eigenvalue.
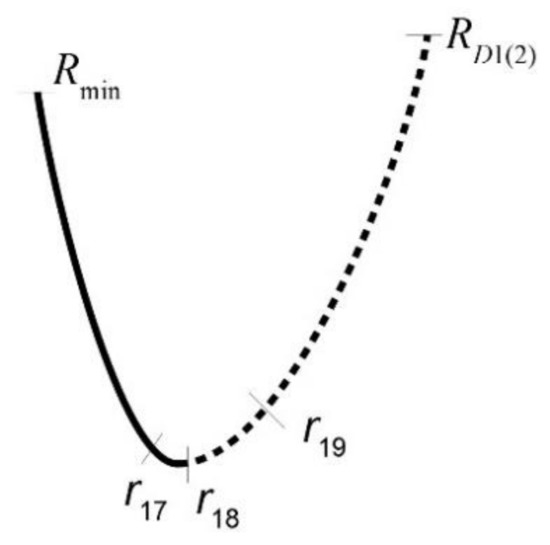
Figure 15.
Equilibrium path starting from the optimal covering.
Starting from the optimal covering shown in Figure 3j and reducing the radius, the generalised tensegrity structure consists of six cables, nine struts and two triangle elements. The equilibrium path is stable. However, at radius , the vertical strut will be passive (Figure 16a). The equilibrium path remains stable.
Figure 16.
Arrangements on the branch starting from the optimal covering (a) zero force in the vertical strut, (b) one zero eigenvalue and (c) zero force in a horizontal strut.
In the interval the structure consists of six cables, eight struts and two triangle elements. The equilibrium path is stable. However, at the radius , the smallest eigenvalue will be zero (Figure 16b), and the equilibrium path (at fold catastrophe) has a limit point loss of stability (minimum point).
There is a negative eigenvalue on the unstable branch, and until radius the eight struts remain, but then, according to Figure 16c, two circles in the second row from above touch; consequently, a new strut enters the generalised tensegrity structure. With nine struts, there is an unstable branch up to the covering, but close to the covering (with smaller radius than the covering radius) other covering arrangements can occur. The top of the branch maintaining symmetry is given by the arrangement, shown in Figure 3f, corresponding to radius .
6. Summary of the Results Concerning Six Circles
In the previous three sections, we have shown that in the case of six circles there are two significantly different types of optimal packing, and , , , , , , symmetry coverings are easily constructed (more can be constructed in some of these symmetries), so the equilibrium paths are much more complicated than the equilibrium paths for smaller number of circles.
Table 1 summarises the most important data for optimal packings and different types of coverings: the radii of the congruent circles and the coordinates of their centres; the magnitude of the coverage of the unit circle; and in the last column, the symbol (number) of the figure showing the respective circle arrangement. At covering, the radius is denoted by capital letters, with their subscript indicating the type of symmetry; if there is more than one type, it is numbered in parentheses.

Table 1.
Data for circle packings and coverings (radius , serial number of a circle, coordinates , of the centre of circle , coverage, and sign of figure).
Table 2 shows similar data for partial coverings. We gave a subscript to a radius when something special happens in its respective circle arrangement: the stiffness matrix becomes singular, or some element of the tensegrity structure is at the boundary between the active and passive range. We also selected a radius at which the arrangements of different symmetry were comparable.

Table 2.
Data of special and investigated points (types of data as in Table 1).
Based on the results obtained, we highlight that
- The equilibrium paths form three different systems that are unconnected to each other (systems starting from the packings of and symmetries and the optimal covering);
- For the branches associated with the equilibrium path of the symmetry arrangement, the product of the number of cycles and the number of branches, if there is an axis of symmetry (type ), then six, otherwise (type ), 12;
- The equilibrium path corresponding to the symmetry arrangement has two strongly degenerate segments, at each point of which the equilibrium path bifurcates in an infinite number of directions, i.e., in the neighbourhood of these segments the equilibrium positions form a three-dimensional set.
The examinations in Section 5 show that, in contrast to the case n = 3, 4, 5, there were several (essentially different) locally optimal arrangements for each value of r. To determine the global optimum, the values of the coverage for the local optima must be compared. (An example of this is shown in Section 5.2.4.) The global optimum is given:
- in the interval by the arrangement corresponding to ,
- in the interval by the arrangement corresponding to ,
- in the interval (0.47449, 0.54715) by the arrangement corresponding to ,
- in the interval by the arrangement corresponding to
symmetry branches (in the last interval, to the branch that starts from the optimum covering).
The optimal coverage is shown in Figure 17 as a function of radius.
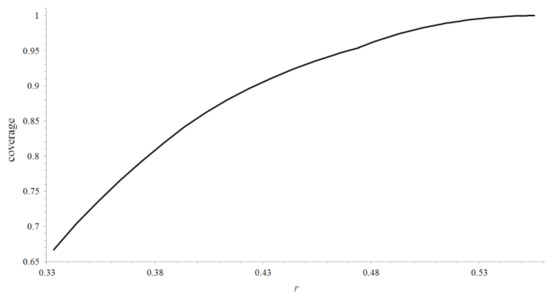
Figure 17.
The optimal coverage by six circles as a function of the radius.
7. Optimal Arrangements of 7 Circles
For n = 7, the problem is simple. An early publication where the picture of the maximum packing configuration appeared in a mathematical context was Pacioli´s [40] Summa de Arithmetica. In the case of seven congruent circles, the radius of the largest circle that can still be packed is , and the smallest radius at which the unit circle can already be covered is . Both arrangements have symmetry, and even the optimal arrangements between these two radii show this symmetry everywhere. If 1/3 < r < 1/2, then the centre of six circles is at a distance
from the centre of the unit circle, all strut forces are equal; their absolute value is just half of the cable forces. The packing, covering and an intermediate optimal arrangement of seven circles are illustrated in Figure 18.
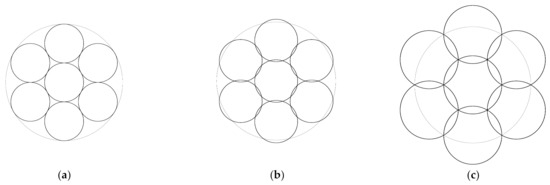
Figure 18.
In the case of seven circles, the optimal (a) packing, ; (b) partial covering for and (c) covering, .
The optimal coverage is shown in Figure 19 as a function of radius.
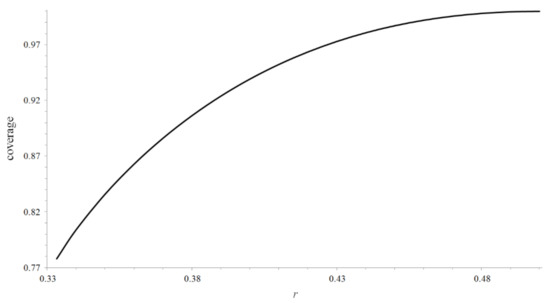
Figure 19.
For n = 7, the optimal coverage as a function of radius.
8. Conclusions
In Ref. [37], we have shown how to determine the position of n congruent circles by the tools of mechanics so that they cover the maximum area within the unit circle. In the present paper, we extended the range of n up to 7 to obtain results in this way.
We did not deal with the case of n = 1 since, trivially, the packing and covering are identical and there is no active element, and so we cannot define an equilibrium path (point).
We did not investigate the case n = 2, because it was solved already by Zahn [1], but it was easy to see that, between and , to the arrangement of symmetry, there corresponds a stable structure consisting of two cables and one strut all along.
In the case n = 3 [15], the types of optimal packing and optimal covering are identical, and even in the transition segment, the arrangement of symmetry is optimal.
In the case n = 4 [16], the types of optimal packing and optimal covering are identical, but the arrangement of symmetry is optimal only on the part of the transition segment. The equilibrium path bifurcates at a critical point, and afterwards the optimal arrangement is of symmetry.
In the case n = 5 [17], we found that the equilibrium path is very diversified; there was a degenerate double cusp catastrophe, a standard cusp catastrophe, and a degenerate bifurcation point at which the studied function was not smooth, so the elementary catastrophe theory could not be used. We have shown that only one substantially different stable equilibrium configuration corresponds to each radius, so that locally optimal arrangements are always globally optimal.
For n = 6, the situation is even more complicated. Two essentially different arrangements were obtained for optimal packing, and their types of symmetry ( and ) differ from the type of optimal covering (). We have shown that the equilibrium paths starting from these three arrangements
- Are not connected to each other;
- At each path, there is a branch corresponding to a locally optimal arrangement;
- The arrangements corresponding to the global optimum are divided between these three independent paths;
- Here, too, the bifurcation types experienced for n = 5 occur, in fact;
- Here were segments where the stiffness matrix was singular at each point of certain segments of the equilibrium path, so that the equilibrium path degenerated into equilibrium body.
In the case n = 7, we obtained an even simpler path than in the case of n = 3, which also consists of a stable branch, but here the active elements of the tensegrity structure did not change either.
Examining partial coverings by greater than seven circles may reveal further interesting cases.
Author Contributions
Z.G. carried out the main part of the theoretical and computational work, T.T. contributed to the collection of data and the writing of the manuscript and K.H. made the computer graphics and contributed to the numerical computations. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by OTKA, Grant No. K81146 and by NKFI under Grant No. K119440 and Grant No. K138615.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank P.W. Fowler for valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Zahn, C.T. Black box maximization of circular coverage. J. Res. Nat. Bur. Stand. B 1962, 66, 181–216. [Google Scholar] [CrossRef]
- Hangody, L.; Feczkó, P.; Bartha, L.; Bodó, G.; Kish, G. Mosaicplasty for the treatment of articular defects of the knee and ankle. Clic. Orthop. Relat. Res. 2001, 391, S328–S336. [Google Scholar] [CrossRef] [PubMed]
- Graham, R.L. Sets of points with given minimum separations (Solutions to Problem E 1921). Amer. Math. Mon. 1968, 75, 192–193. [Google Scholar]
- Pirl, U. Der Mindestabstand von n in der Einheitskreisscheibe gelagenen Punkten. Math. Nachr. 1969, 40, 111–124. [Google Scholar] [CrossRef]
- Melissen, H. Densest packing of eleven congruent circles in a circle. Geom. Dedicata. 1994, 50, 15–25. [Google Scholar] [CrossRef]
- Fodor, F. The densest packing of 19 congruent circles in a circle. Geom. Dedicata. 1999, 74, 139–145. [Google Scholar] [CrossRef]
- Fodor, F. The densest packing of 12 congruent circles in a circle. Beiträge Algebra Geom. 2000, 41, 401–409. [Google Scholar]
- Fodor, F. The densest packing of 13 congruent circles in a circle. Beiträge Algebra Geom. 2003, 44, 431–440. [Google Scholar]
- Fodor, F. Packing of 14 congruent circles in a circle. Stud. Univ. Žilina Math. Ser. 2003, 16, 25–34. [Google Scholar]
- Bezdek, K. Optimal Covering of Circles; Thesis: Budapest, Hungary, 1979. (In Hungarian) [Google Scholar]
- Bezdek, K. Über einige Kreisüberdeckungen. Beiträge Algebra Geom. 1983, 14, 7–13. [Google Scholar]
- Fejes Tóth, G. Thinnest covering of a circle by eight, nine, or ten congruent circles. In Combinatorial and Computational Geometry; Mathematical Sciences Research Institute Publications; Goodman, J.E., Pach, J., Welzl, E., Eds.; Cambridge University Press: Cambridge, UK, 2005; Volume 52, pp. 361–376. [Google Scholar]
- Graham, R.L.; Lubachevsky, B.D.; Nurmela, K.J.; Östergård, P.R.L. Dense packings of congruent circles in a circle. Discrete Math. 1998, 181, 139–154. [Google Scholar] [CrossRef]
- Nurmela, K.J. Covering a Circle by Congruent Circular Discs; Department of Computer Science and Engineering, Helsinki University of Technology: Espoo, Finland, 1998; preprint. [Google Scholar]
- Szalkai, B. Optimal cover of a disk with three smaller congruent disks. Adv. Geom. 2016, 16, 465–476. [Google Scholar] [CrossRef]
- Gáspár, Z.; Tarnai, T.; Hincz, K. Partial covering of the unit circle by four equal circles. Annales Univ. Sci. Budapest. 2017, 60, 137–144. [Google Scholar]
- Gáspár, Z.; Tarnai, T.; Hincz, K. Partial covering of a circle by equal circles, Part II: The case of 5 circles. J. Comput. Geom. 2014, 5, 126–149. [Google Scholar]
- Coxeter, H.S.M. Introduction to Geometry; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Weil, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Poston, T.; Stewart, I. Catastrophe Theory and Its Applications; Pitman: London, UK, 1978. [Google Scholar]
- Fejes Tóth, L. Über die Abschetzung des kürzesten Abstandes zweier Punkte eines auf einer Kugelfläche liegenden Punktsystems. Jber. Dtsch. Math.-Ver. 1943, 53, 66–68. [Google Scholar]
- Schütte, K.; van der Waerden, B.L. Auf welcher Kugel haben 5, 6, 7, 8 oder 9 Punkte mit Mindestabstand ein Platz? Math. Annln. 1951, 123, 96–124. [Google Scholar] [CrossRef]
- Danzer, L. Endliche Punktmengen auf der 2-Sphäre mit möglichst grossem Minimalabstand; Habilitationschrift: Universität Göttingen: Göttingen, Germany, 1963. [Google Scholar]
- Musin, O.R.; Tarasov, A.S. Enumeration of irreducible contact graphs on the sphere. J. Math. Sci. 2014, 203, 837–850. [Google Scholar] [CrossRef][Green Version]
- Musin, O.R.; Tarasov, A.S. The Tammes problem for N = 14. Experimental Math. 2015, 24, 460–468. [Google Scholar] [CrossRef]
- Robinson, R.M. Arrangement of 24 points on a sphere. Math. Annln. 1961, 144, 17–48. [Google Scholar] [CrossRef]
- Fejes Tóth, L. On covering the spherical surface with equal spherical caps. Matematikai Fiz. Lapok 1943, 50, 40–46. (In Hungarian) [Google Scholar]
- Schütte, K. Überdeckung der Kugel mit höchstens acht Kreisen. Math. Annln 1955, 129, 181–186. [Google Scholar] [CrossRef]
- Wimmer, L. Covering the sphere with equal circles. Discrete Comp. Geom. 2017, 57, 763–781. [Google Scholar] [CrossRef]
- Fejes Tóth, G. Kreisüberdeckungen der Sphäre. Studia Sci. Math. Hungar. 1969, 4, 225–247. [Google Scholar]
- Sloane, N.J.A.; Hardin, R.H.; Smith, W.D. Spherical Codes. Available online: NeilSloane.com/packings/ (accessed on 7 October 2021).
- Hardin, R.H.; Sloane, N.J.A.; Smith, W.D. Spherical Coverings. Available online: NeilSloane.com/coverings/ (accessed on 7 October 2021).
- Fejes Tóth, L. Regular Figures; Pergamon; Macmillan: New York, NY, USA, 1964. [Google Scholar]
- Fejes Tóth, L. Perfect distribution of points on a sphere. Periodica Math. Hungar. 1971, 1, 25–33. [Google Scholar] [CrossRef]
- Fowler, P.W.; Tarnai, T. Transition from spherical circle packing to covering: Geometrical analogues of chemical isomerization. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1996, 452, 2043–2064. [Google Scholar]
- Fowler, P.W.; Tarnai, T. Transition from circle packing to covering on a sphere: The odd case of 13 circles. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1999, 455, 4131–4143. [Google Scholar] [CrossRef]
- Gáspár, Z.; Tarnai, T.; Hincz, K. Partial covering of a circle by equal circles, Part I: The mechanical models. J. Comput. Geom. 2014, 5, 104–125. [Google Scholar]
- Csikós, B. On the volume of the union of balls. Discrete Comput. Geom. 1998, 20, 449–461. [Google Scholar] [CrossRef]
- Connelly, R. Maximizing the Area of Unions and Intersections of Discs. Lecture at the Discrete and Convex Geometry Workshop; Alfréd Rényi Institute of Mathematics: Budapest, Hungary, 2008. [Google Scholar]
- Pacioli, L. Summa de Arithmetica, Geometria, Proportioni et Proportionalita; Paganius de Paganinis: Venezia, Italy, 1494. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).