Interplay between Spacetime Curvature, Speed of Light and Quantum Deformations of Relativistic Symmetries
Abstract
1. Introduction
2. The -Poincaré Model
2.1. The -Poincaré Quantum Algebra
2.2. The -Poincaré Lie Bialgebra and -Minkowski Spacetime
2.3. Applications
- There is a vast literature on how to construct classical (in the sense of ) and quantum noncommutative field theories that are symmetric under the -Poincaré group and are based on different versions of -Minkowski spacetime. A non-exhaustive list is [79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104], and references therein.
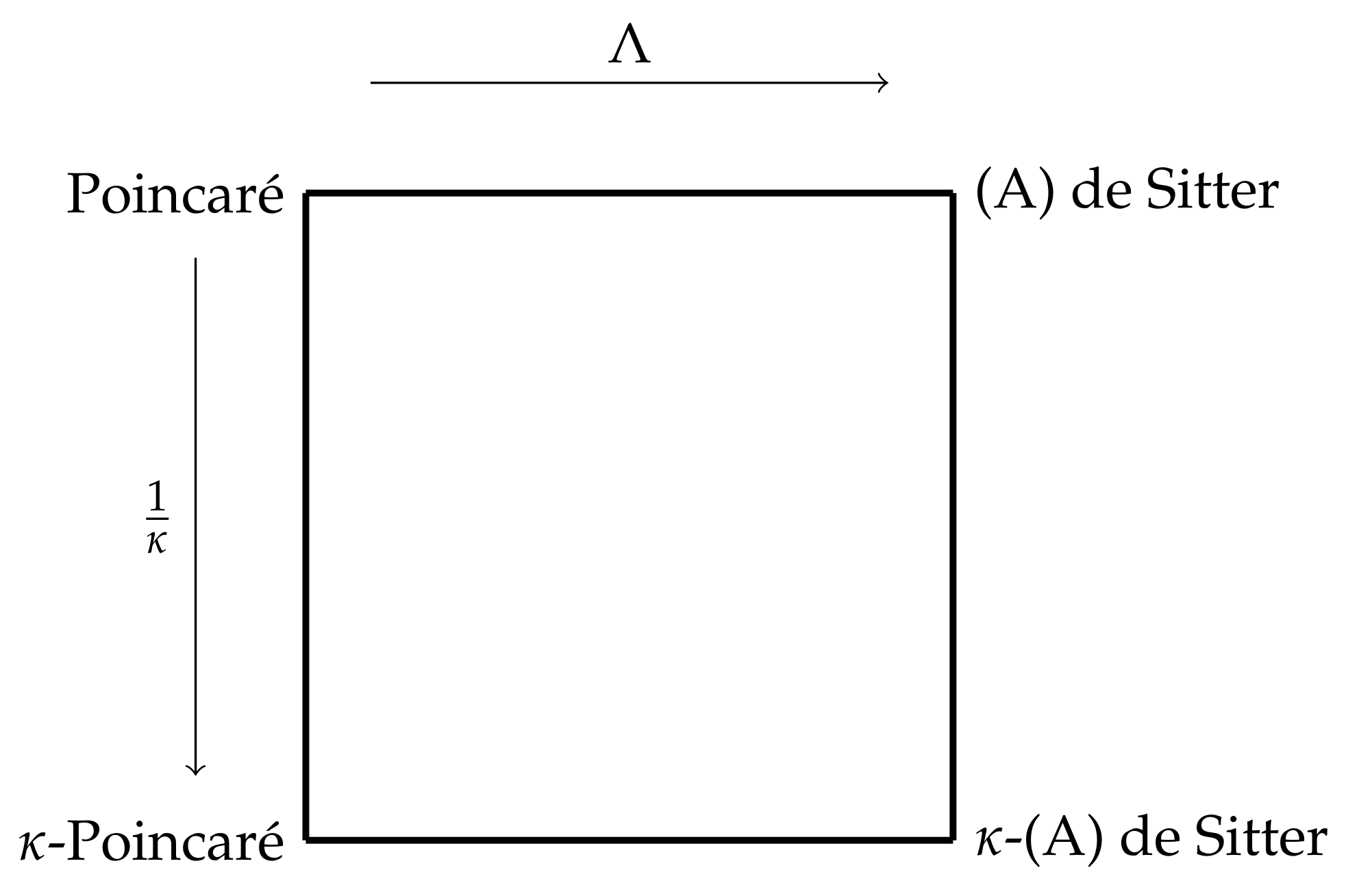
3. Interplay between Curvature and Quantum Effects
3.1. (Anti-)de Sitter Symmetries as a Classical Deformation of Poincaré Symmetries
- For we have the symmetry algebra and the AdS spacetime is obtained as the coset space .
- For we have the symmetry algebra that gives rise to the de Sitter spacetime .
- Finally, for we recover the Poincaré algebra, and Minkowski spacetime is .
3.2. The -(A)dS Model in (3 + 1) Dimensions
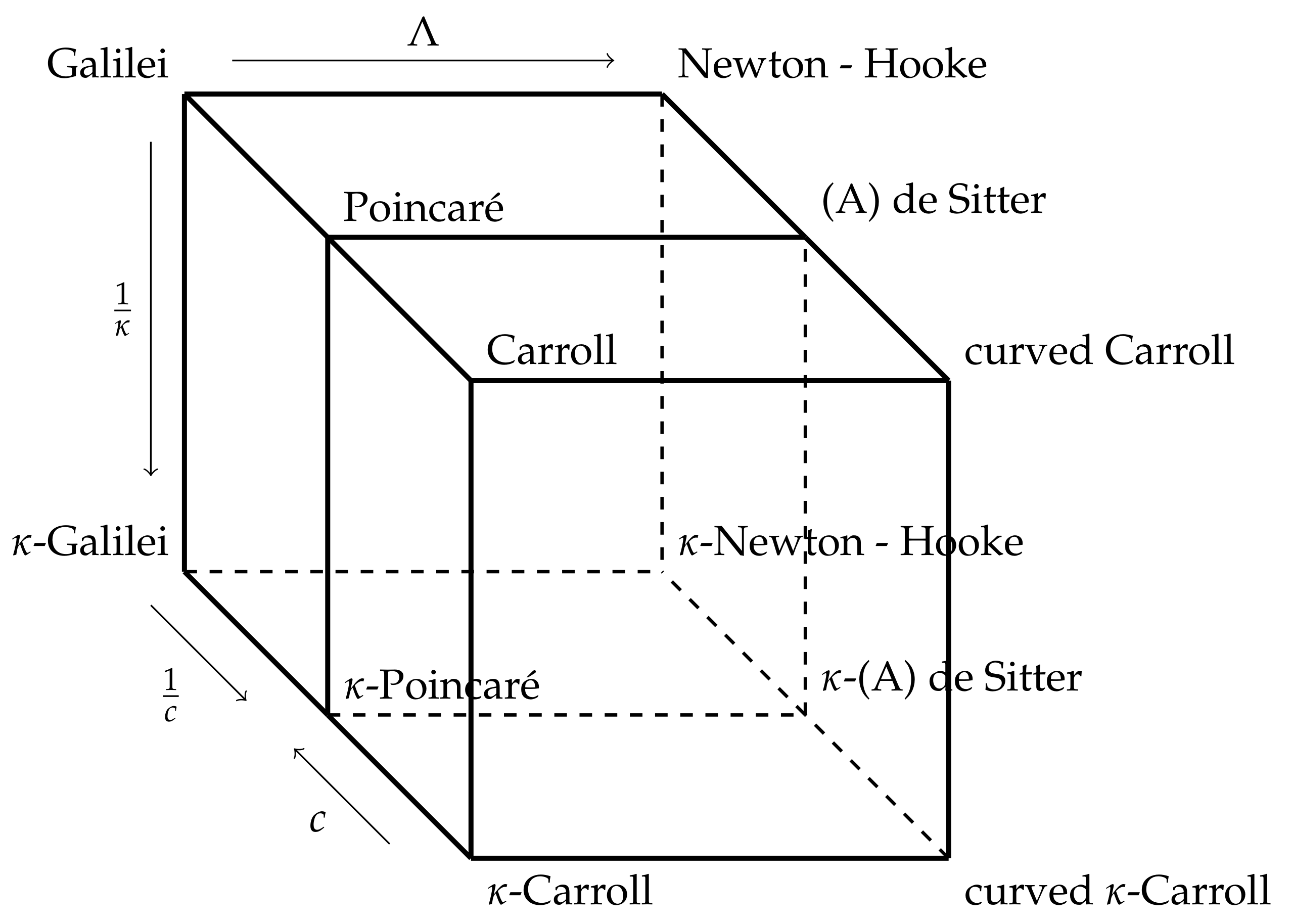
4. Interplay between Curvature and the Speed of Light
4.1. The Galilean Limit of (A)dS
4.2. The Carroll Limit of (A)dS
5. Interplay of the Three Parameters: Curvature, Speed of Light and Quantum Deformation
5.1. Zero Curvature Case: Galilei and Carroll Contraction of -Poincaré
5.2. With Curvature: Galilei and Carroll Contraction of -(A)dS
6. Noncommutative Spacetimes
6.1. The -(A)dS Spacetime
6.2. -Galilean and -Carrollian Spacetimes
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Amelino-Camelia, G.; Freidel, L.; Kowalski-Glikman, J.; Smolin, L. The principle of relative locality. Phys. Rev. D 2011, 84, 084010. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Freidel, L.; Kowalski-Glikman, J.; Smolin, L. Relative locality: A deepening of the relativity principle. Gen. Rel. Grav. 2011, 43, 2547–2553. [Google Scholar] [CrossRef]
- Lukierski, J.; Ruegg, H.; Nowicki, A.; Tolstoy, V.N. q-deformation of Poincaré algebra. Phys. Lett. B 1991, 264, 331–338. [Google Scholar] [CrossRef]
- Giller, S.; Kosinski, P.; Majewski, M.; Maslanka, P.; Kunz, J. More about the q-deformed Poincaré algebra. Phys. Lett. B 1992, 286, 57–62. [Google Scholar] [CrossRef]
- Lukierski, J.; Nowicki, A.; Ruegg, H. New quantum Poincaré algebra and κ-deformed field theory. Phys. Lett. B 1992, 293, 344–352. [Google Scholar] [CrossRef]
- Maslanka, P. The n-dimensional κ-Poincaré algebra and group. J. Phys. A Math. Gen. 1993, 26, L1251–L1253. [Google Scholar] [CrossRef]
- Zakrzewski, S. Quantum Poincaré group related to the κ-Poincaré algebra. J. Phys. A Math. Gen. 1994, 27, 2075–2082. [Google Scholar] [CrossRef]
- Majid, S.; Ruegg, H. Bicrossproduct structure of κ-Poincaré group and non-commutative geometry. Phys. Lett. B 1994, 334, 348–354. [Google Scholar] [CrossRef]
- Lukierski, J.; Ruegg, H. Quantum kappa-Poincaré in any dimension. Phys. Lett. 1994, B329, 189–194. [Google Scholar] [CrossRef]
- Lukierski, J. Kappa-Deformations: Historical Developments and Recent Results. J. Phys. Conf. Ser. 2017, 804, 012028. [Google Scholar] [CrossRef]
- Majid, S. Hopf algebras for physics at the Planck scale. Class. Quantum Gravity 1988, 5, 1587–1606. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Smolin, L.; Starodubtsev, A. Quantum symmetry, the cosmological constant and Planck-scale phenomenology. Class. Quantum Gravity 2004, 21, 3095–3110. [Google Scholar] [CrossRef]
- Marciano, A.; Amelino-Camelia, G.; Bruno, N.R.; Gubitosi, G.; Mandanici, G.; Melchiorri, A. Interplay between curvature and Planck-scale effects in astrophysics and cosmology. J. Cosmol. Astropart. Phys. 2010, 6, 30. [Google Scholar] [CrossRef]
- Bianchi, E.; Rovelli, C. A Note on the geometrical interpretation of quantum groups and non-commutative spaces in gravity. Phys. Rev. D 2011, 84, 027502. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Marciano, A.; Matassa, M.; Rosati, G. Deformed Lorentz symmetry and relative locality in a curved/expanding spacetime. Phys. Rev. D 2012, 86, 124035. [Google Scholar] [CrossRef]
- Rosati, G.; Amelino-Camelia, G.; Marciano, A.; Matassa, M. Planck-scale-modified dispersion relations in FRW spacetime. Phys. Rev. D 2015, 92, 124042. [Google Scholar] [CrossRef]
- Barcaroli, L.; Gubitosi, G. Kinematics of particles with quantum-de Sitter-inspired symmetries. Phys. Rev. D 2016, 93, 124063. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Rosati, G.; Bedić, S. Phenomenology of curvature-induced quantum-gravity effects. Phys. Lett. B 2021, 820, 136595. [Google Scholar] [CrossRef]
- Herranz, F.J.; Santander, M. (Anti)de Sitter/Poincaré symmetries and representations from Poincaré/Galilei through a classical deformation approach. J. Phys. A Math. Theor. 2008, 41, 015204. [Google Scholar] [CrossRef]
- Ballesteros, A.; Herranz, F.J.; del Olmo, M.A.; Santander, M. Quantum (2 + 1) kinematical algebras: A global approach. J. Phys. A Math. Gen. 1994, 27, 1283–1297. [Google Scholar] [CrossRef]
- Ballesteros, A.; Bruno, N.R.; Herranz, F.J. A non-commutative Minkowskian spacetime from a quantum AdS algebra. Phys. Lett. B 2003, 574, 276–282. [Google Scholar] [CrossRef]
- Ballesteros, A.; Herranz, F.J.; Meusburger, C. A (2 + 1) non-commutative Drinfel’d double spacetime with cosmological constant. Phys. Lett. B 2014, 732, 201–209. [Google Scholar] [CrossRef]
- Ballesteros, A.; Herranz, F.J.; Musso, F.; Naranjo, P. The κ-(A)dS quantum algebra in (3 + 1) dimensions. Phys. Lett. B 2017, 766, 205–211. [Google Scholar] [CrossRef]
- Rosati, G. κ-de Sitter and κ-Poincaré symmetries emerging from Chern-Simons (2 + 1)D gravity with a cosmological constant. Phys. Rev. D 2017, 96, 066027. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gutierrez-Sagredo, I.; Herranz, F.J. The κ-(A)dS noncommutative spacetime. Phys. Lett. B 2019, 796, 93–101. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.M. Une nouvelle limite non-relativiste du group de Poincaré. Ann. Inst. H. Poincaré 1965, 3, 1–12. [Google Scholar]
- Bacry, H.; Lévy-Leblond, J.M. Possible Kinematics. J. Math. Phys. 1968, 9, 1605–1614. [Google Scholar] [CrossRef]
- Aldrovandi, R.; Barbosa, A.L.; Crispino, L.C.B.; Pereira, J.G. Non-relativistic spacetimes with cosmological constant. Class. Quantum Gravity 1999, 16, 495–506. [Google Scholar] [CrossRef]
- Duval, C.; Gibbons, G.W.; Horvathy, P.A.; Zhang, P.M. Carroll versus Newton and Galilei: Two dual non-Einsteinian concepts of time. Class. Quantum Gravity 2014, 31, 085016. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gubitosi, G.; Gutierrez-Sagredo, I.; Herranz, F.J. The κ-Newtonian and κ-Carrollian algebras and their noncommutative spacetimes. Phys. Lett. B 2020, 805, 135461. [Google Scholar] [CrossRef]
- Tung, W.-K. Group Theory in Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Chari, V.; Pressley, A. A guide to Quantum Groups; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Majid, S. Foundations of Quantum Group Theory; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Zakrzewski, S. Poisson structures on the Poincaré group. Commun. Math. Phys. 1997, 185, 285–311. [Google Scholar] [CrossRef][Green Version]
- Podleś, P.; Woronowicz, S.L. On the classification of quantum Poincaré groups. Commun. Math. Phys. 1996, 178, 61–82. [Google Scholar] [CrossRef][Green Version]
- Celeghini, E.; Giachetti, R.; Sorace, E.; Tarlini, M. The quantum Heisenberg group H(1)q. J. Math. Phys. 1991, 32, 1155–1158. [Google Scholar] [CrossRef]
- Celeghini, E.; Giachetti, R.; Sorace, E.; Tarlini, M. Contractions of quantum groups. Lect. Notes Math. 1992, 1510, 221–244. [Google Scholar]
- Ballesteros, A.; Gromov, N.A.; Herranz, F.J.; del Olmo, M.A.; Santander, M. Lie bialgebra contractions and quantum deformations of quasi-orthogonal algebras. J. Math. Phys. 1995, 36, 5916–5937. [Google Scholar] [CrossRef]
- Drinfeld, V. Quantum groups. In Proceedings of the International Congress of Mathematicians (Berkeley 1986); American Mathematical Society: Providence, RI, USA, 1987; pp. 798–820. [Google Scholar]
- Jimbo, M. A q-difference analogue of U(g) and the Yang-Baxter equation. Lett. Math. Phys. 1985, 10, 63–69. [Google Scholar] [CrossRef]
- Kowalski-Glikman, J.; Nowak, S. Doubly special relativity theories as different bases of κ-Poincaré algebra. Phys. Lett. B 2002, 539, 126–132. [Google Scholar] [CrossRef]
- Gubitosi, G.; Mercati, F. Relative locality in κ-Poincaré. Class. Quantum Gravity 2013, 30, 145002. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Arzano, M.; Kowalski-Glikman, J.; Rosati, G.; Trevisan, G. Relative-locality distant observers and the phenomenology of momentum-space geometry. Class. Quantum Gravity 2012, 29, 075007. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly-special relativity: Facts, myths and some key open issues. Symmetry 2010, 2, 230–271. [Google Scholar] [CrossRef]
- Giller, S.; Gonera, C.; Kosinski, P.; Majewski, M.; Maslanka, P.; Kunz, J. On q covariant wave functions. Mod. Phys. Lett. A 1993, 8, 3785–3797. [Google Scholar] [CrossRef]
- Nowicki, A.; Sorace, E.; Tarlini, M. The Quantum deformed Dirac equation from the kappa Poincare algebra. Phys. Lett. B 1993, 302, 419–422. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gutierrez-Sagredo, I.; Herranz, F.J. Noncommutative (A)dS and Minkowski spacetimes from quantum Lorentz subgroups. arXiv 2021, arXiv:2108.02683. [Google Scholar]
- Gutierrez-Sagredo, I.; Herranz, F.J. Cayley–Klein Lie Bialgebras: Noncommutative Spaces, Drinfel’d Doubles and Kinematical Applications. Symmetry 2021, 13, 1249. [Google Scholar] [CrossRef]
- Kowalski-Glikman, J. de Sitter space as an arena for doubly special relativity. Phys. Lett. 2002, B547, 291–296. [Google Scholar] [CrossRef]
- Kowalski-Glikman, J.; Nowak, S. Doubly special relativity and de Sitter space. Class. Quantum Gravity 2003, 20, 4799–4816. [Google Scholar] [CrossRef]
- Kowalski-Glikman, J. Living in Curved Momentum Space. Int. J. Mod. Phys. A 2013, 28, 1330014. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Majid, S. Waves on noncommutative space–time and gamma-ray bursts. Int. J. Mod. Phys. A 2000, 15, 4301–4323. [Google Scholar] [CrossRef]
- Kowalski-Glikman, J.; Nowak, S. Noncommutative space–time of doubly special relativity theories. Int. J. Mod. Phys. 2003, D12, 299–316. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Quantum-Spacetime Phenomenology. Living Rev. Relativ. 2013, 16, 5. [Google Scholar] [CrossRef]
- Borowiec, A.; Pachol, A. κ-Minkowski spacetime as the result of Jordanian twist deformation. Phys. Rev. D 2009, 79, 04501. [Google Scholar] [CrossRef]
- Borowiec, A.; Pachol, A. κ-Minkowski spacetimes and DSR algebras: Fresh look and old problems. Symmetry Integr. Geom. Methods Appl. 2010, 6, 086. [Google Scholar] [CrossRef]
- Borowiec, A.; Gupta, K.S.; Meljanac, S.; Pachoł, A. Constraints on the quantum gravity scale from κ-Minkowski spacetime. Europhys. Lett. 2010, 92, 20006. [Google Scholar] [CrossRef]
- Aschieri, P.; Borowiec, A.; Pachol, A. Observables and dispersion relations in κ-Minkowski spacetime. J. High Energy Phys. 2017, 152, 2017. [Google Scholar] [CrossRef]
- Gubitosi, G.; Heefer, S. Relativistic compatibility of the interacting κ-Poincaré model and implications for the relative locality framework. Phys. Rev. D 2019, 99, 086019. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Loret, N.; Rosati, G. Speed of particles and a relativity of locality in κ-Minkowski quantum spacetime. Phys. Lett. B 2011, 700, 150–156. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Mazon, D.; Mercati, F. Locality and the Relativity Principle Beyond Special Relativity. Phys. Rev. 2011, D84, 085010. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Mercati, F. Relativistic kinematics beyond Special Relativity. Phys. Rev. 2012, D86, 084032. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortes, J.L.; Relancio, J.J. Spacetime from locality of interactions in deformations of special relativity: The example of κ-Poincaré Hopf algebra. Phys. Rev. D 2018, 97, 064025. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Bianco, S.; Brighenti, F.; Buonocore, R.J. Causality and momentum conservation from relative locality. Phys. Rev. D 2015, 91, 084045. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Bianco, S.; Rosati, G. Planck-Scale-Deformed Relativistic Symmetries and Diffeomorphisms on Momentum Space. Phys. Rev. D 2020, 101, 026018. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Gubitosi, G.; Palmisano, G. Pathways to relativistic curved momentum spaces: De Sitter case study. Int. J. Mod. Phys. D 2016, 25, 1650027. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Matassa, M.; Mercati, F.; Rosati, G. Taming Nonlocality in Theories with Planck-Scale Deformed Lorentz Symmetry. Phys. Rev. Lett. 2011, 106, 071301. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski, L.; Piacitelli, G. Canonical k-Minkowski Spacetime. arXiv 2010, arXiv:1004.5091. [Google Scholar]
- Agostini, A.; Lizzi, F.; Zampini, A. Generalized Weyl systems and kappa Minkowski space. Mod. Phys. Lett. 2002, A17, 2105–2126. [Google Scholar] [CrossRef]
- Agostini, A. κ-Minkowski representations on Hilbert spaces. J. Math. Phys. 2007, 48, 052305. [Google Scholar] [CrossRef]
- Lizzi, F.; Manfredonia, M.; Mercati, F.; Poulain, T. Localization and Reference Frames in κ-Minkowski Spacetime. Phys. Rev. D 2019, 99, 085003. [Google Scholar] [CrossRef]
- Carotenuto, A.; Lizzi, F.; Mercati, F.; Manfredonia, M. The Weyl-Mellin quantization map for κ-Minkowski Noncommutative Spacetime. arXiv 2020, arXiv:2011.10628. [Google Scholar]
- Sitarz, A. Noncommutative differential calculus on the κ-Minkowski space. Phys. Lett. B 1995, 349, 42–48. [Google Scholar] [CrossRef]
- De Azcárraga, J.A.; Pérez-Bueno, J.C. Relativistic and Newtonian kappa space–times. J. Math. Phys. 1995, 36, 6879–6896. [Google Scholar] [CrossRef]
- Mercati, F. Quantum κ-deformed differential geometry and field theory. Int. J. Mod. Phys. D 2016, 25, 1650053. [Google Scholar] [CrossRef]
- Mercati, F.; Sitarz, A. κ-Minkowski differential calculi and star product. arXiv 2011, arXiv:1105.1599. [Google Scholar]
- Durhuus, B.; Sitarz, A. Star product realizations of κ-Minkowski space. J. Noncommut. Geom. 2013, 7, 605–645. [Google Scholar] [CrossRef]
- Juric, T.; Meljanac, S.; Pikutić, D.; Štrajn, R. Toward the classification of differential calculi on κ-Minkowski space and related field theories. J. High Energy Phys. 2015, 2015, 55. [Google Scholar] [CrossRef][Green Version]
- Kosinski, P.; Lukierski, J.; Maslanka, P. Local D = 4 field theory on kappa deformed Minkowski space. Phys. Rev. D 2000, 62, 025004. [Google Scholar] [CrossRef]
- Kosinski, P.; Lukierski, J.; Maslanka, P. κ-deformed Wigner construction of relativistic wave functions and free fields on κ-Minkowski space. Nucl. Phys. B Proc. Suppl. 2001, 102, 161–168. [Google Scholar] [CrossRef]
- Agostini, A.; Amelino-Camelia, G.; Arzano, M. Dirac spinors for doubly special relativity and kappa Minkowski noncummutative space–time. Class. Quantum Gravity 2004, 21, 2179–2202. [Google Scholar] [CrossRef]
- Dimitrijević, M.; Jonke, L.; Möller, L.; Tsouchnika, E.; Wess, J.; Wohlgenannt, M. Deformed field theory on κ-spacetime. Eur. Phys. J. C 2003, 31, 129–138. [Google Scholar] [CrossRef]
- Kosinski, P.; Maslanka, P.; Lukierski, J.; Sitarz, A. Generalized kappa deformations and deformed relativistic scalar fields on noncommutative Minkowski space. In Conference on Topics in Mathematical Physics, General Relativity, and Cosmology on the Occasion of the 75th Birthday of Jerzy F. Plebanski; World Scientific: Singapore, 2006; pp. 255–277. [Google Scholar]
- Amelino-Camelia, G.; Gubitosi, G.; Marciano, A.; Martinetti, P.; Mercati, F. A No-pure-boost uncertainty principle from spacetime noncommutativity. Phys. Lett. B 2009, 671, 298–302. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Gubitosi, G.; Marciano, A.; Martinetti, P.; Mercati, F.; Pranzetti, D.; Tacchi, R.A. First results of the Noether theorem for Hopf-algebra spacetime symmetries. Prog. Theor. Phys. Suppl. 2007, 171, 65–78. [Google Scholar] [CrossRef]
- Freidel, L.; Kowalski-Glikman, J.; Nowak, S. From noncommutative κ-Minkowski to Minkowski space–time. Phys. Lett. B 2007, 648, 70–75. [Google Scholar] [CrossRef]
- Arzano, M.; Marciano, A. Fock space, quantum fields and kappa-Poincare symmetries. Phys. Rev. D 2007, 76, 125005. [Google Scholar] [CrossRef]
- Daszkiewicz, M.; Lukierski, J.; Woronowicz, M. κ–deformed statistics and classical fourmomentum addition law. Mod. Phys. Lett. A 2008, 23, 653–665. [Google Scholar] [CrossRef]
- Freidel, L.; Kowalski-Glikman, J.; Nowak, S. Field theory on κ-Minkowski space revisited: Noether charges and breaking of Lorentz symmetry. Int. J. Mod. Phys. 2008, A23, 2687–2718. [Google Scholar] [CrossRef]
- Arzano, M.; Kowalski-Glikman, J.; Walkus, A. Lorentz invariant field theory on κ-Minkowski space. Class. Quantum Gravity 2010, 27, 025012. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Loret, N.; Mandanici, G.; Mercati, F. Gravity in quantum spacetime. Int. J Mod. Phys. D 2010, 19, 2385–2392. [Google Scholar] [CrossRef]
- Dimitrijević, M.; Jonke, L.; Pachoł, A. Gauge theory on twisted κ-Minkowski: Old problems and possible solutions. Symmetry Integr. Geom. Methods Appl. 2014, 10, 063. [Google Scholar] [CrossRef][Green Version]
- Jurić, T.; Meljanac, S.; Samsarov, A. Light-like κ-deformations and scalar field theory via Drinfeld twist. J. Phys. Conf. Ser. 2015, 634, 012005. [Google Scholar] [CrossRef]
- Meljanac, S.; Meljanac, D.; Mercati, F.; Pikutić, D. Noncommutative spaces and Poincaré symmetry. Phys. Lett. 2017, B766, 181–185. [Google Scholar] [CrossRef]
- Loret, N.; Meljanac, S.; Mercati, F.; Pikutić, D. Vectorlike deformations of relativistic quantum phase-space and relativistic kinematics. Int. J. Mod. Phys. 2017, D26, 1750123. [Google Scholar] [CrossRef]
- Arzano, M.; Kowalski-Glikman, J. Non-commutative fields and the short-scale structure of spacetime. Phys. Lett. 2017, B771, 222–226. [Google Scholar] [CrossRef]
- Arzano, M. Anatomy of a deformed symmetry: Field quantization on curved momentum space. Phys. Rev. D 2011, 83, 025025. [Google Scholar] [CrossRef]
- Poulain, T.; Wallet, J.C. κ-Poincaré invariant quantum field theories with KMS weight. Phys. Rev. D 2018, 98, 025002. [Google Scholar] [CrossRef]
- Ballesteros, A.; Mercati, F. Extended noncommutative Minkowski spacetimes and hybrid gauge symmetries. Eur. Phys. J. C 2018, 78, 615. [Google Scholar] [CrossRef]
- Poulain, T.; Wallet, J.-C. κ-Poincaré invariant orientable field theories at one-loop. J. High Energy Phys. 2019, 1, 64. [Google Scholar] [CrossRef]
- Jurić, T.; Poulain, T.; Wallet, J.-C. Vacuum energy and the cosmological constant problem in κ-Poincaré invariant field theories. Phys. Rev. D 2019, 99, 045004. [Google Scholar] [CrossRef]
- Mercati, F.; Sergola, M. Pauli-Jordan function and scalar field quantization in κ-Minkowski noncommutative spacetime. Phys. Rev. 2018, D98, 045017. [Google Scholar] [CrossRef]
- Mathieu, P.; Wallet, J.-C. Gauge theories on κ-Minkowski spaces: Twist and modular operators. J. High Energy Phys. 2020, 5, 112. [Google Scholar] [CrossRef]
- Arzano, M.; Bevilacqua, A.; Kowalski-Glikman, J.; Rosati, G.; Unger, J. κ-deformed complex fields and discrete symmetries. Phys. Rev. D 2021, 103, 106015. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gubitosi, G.; Gutierrez-Sagredo, I.; Mercati, F. Fuzzy worldlines with κ-Poincaré symmetries. arXiv 2021, arXiv:2109.09699. [Google Scholar]
- Amelino-Camelia, G.; Astuti, V.; Rosati, G. Predictive description of Planck-scale-induced spacetime fuzziness. Phys. Rev. D 2013, 87, 084023. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Astuti, V.; Rosati, G. Relative locality in a quantum spacetime and the pregeometry of κ-Minkowski. Eur. Phys. J. C 2013, 73, 2521. [Google Scholar] [CrossRef]
- Mercati, F.; Sergola, M. Light cone in a quantum spacetime. Phys. Lett. B 2018, 787, 105–110. [Google Scholar] [CrossRef]
- Arzano, M.; Consoli, L.T. Signal propagation on κ-Minkowski spacetime and nonlocal two-point functions. Phys. Rev. D 2018, 98, 106018. [Google Scholar] [CrossRef]
- Blaut, A.; Daszkiewicz, M.; Kowalski-Glikman, J.; Nowak, S. Phase spaces of doubly special relativity. Phys. Lett. B 2004, 582, 82–85. [Google Scholar] [CrossRef]
- Lukierski, J.; Škoda, Z.; Woronowicz, M. κ-deformed covariant quantum phase spaces as Hopf algebroids. Phys. Lett. B 2015, 750, 401–406. [Google Scholar] [CrossRef]
- Lizzi, F.; Manfredonia, M.; Mercati, F. The momentum spaces of κ-Minkowski noncommutative spacetime. Nucl. Phys. B 2020, 958, 115117. [Google Scholar] [CrossRef]
- Carmona, J.M.; Cortés, J.L.; Relancio, J.J. Relativistic deformed kinematics from momentum space geometry. Phys. Rev. D 2019, 100, 104031. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gutierrez-Sagredo, I.; Herranz, F.J. Noncommutative spaces of worldlines. Phys. Lett. B 2019, 792, 175–181. [Google Scholar] [CrossRef]
- Lukierski, J.; Nowicki, A.; Ruegg, H. Real forms of complex quantum anti-de-Sitter algebra Uq(Sp(4;C) and their contraction schemes. Phys. Lett. B 1991, 271, 321–328. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gubitosi, G.; Gutiérrez-Sagredo, I.; Herranz, F.J. Curved momentum spaces from quantum (anti-)de Sitter groups in (3 + 1) dimensions. Phys. Rev. D 2018, 97, 106024. [Google Scholar] [CrossRef]
- Ballesteros, A.; Musso, F. Quantum algebras as quantizations of dual Poisson-Lie groups. J. Phys. A Math. Theor. 2013, 46, 195203. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gubitosi, G.; Gutiérrez-Sagredo, I.; Herranz, F.J. Curved momentum spaces from quantum groups with cosmological constant. Phys. Lett. B 2017, 773, 47–53. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gubitosi, G.; Herranz, F.J. Lorentzian Snyder spacetimes and their Galilei and Carroll limits from projective geometry. Class. Quantum Gravity 2020, 37, 195021. [Google Scholar] [CrossRef]
- Bergshoeff, E.; Gomis, J.; Rollier, B.; Rosseel, J.; Ter Veldhuis, T. Carroll versus Galilei Gravity. J. High Energy Phys. 2017, 2017, 165. [Google Scholar] [CrossRef]
- Dijkhuizen, M.S.; Koornwinder, T.H. Quantum homogeneous spaces, duality and quantum 2-spheres. Geom. Dedicata 1994, 52, 291–315. [Google Scholar] [CrossRef]
- Ciccoli, N. Quantum planes and quantum cylinders from Poisson homogeneous spaces. J. Phys. A Math. Gen. 1996, 29, 1487–1495. [Google Scholar] [CrossRef]
- Ballesteros, A.; Gutierrez-Sagredo, I.; Mercati, F. Coisotropic Lie bialgebras and complementary dual Poisson homogeneous spaces. J. Phys. A Math. Theor. 2021, 54, 315203. [Google Scholar] [CrossRef]
- Steinacker, H. Quantum anti-de Sitter space and sphere at roots of unity. Adv. Theor. Math. Phys. 2000, 4, 155–208. [Google Scholar] [CrossRef]
- Buric, M.; Madore, J. Noncommutative de Sitter and FRW spaces. Eur. Phys. J. C 2015, 75, 502. [Google Scholar] [CrossRef]
- Heckman, J.J.; Verlinde, H. Covariant non-commutative space–time. Nucl. Phys. B 2015, 894, 58–74. [Google Scholar] [CrossRef][Green Version]
- Manolakos, G.; Manousselis, P.; Zoupanos, G. Four-dimensional Gravity on a Covariant Noncommutative Space. J. High Energy Phys. 2020, 2020, 1. [Google Scholar] [CrossRef]
- Ballesteros, A.; Herranz, F.J.; Del Olmo, M.A.; Santander, M. Classical deformations, Poisson–Lie contractions, and quantization of dual Lie bialgebras. J. Math. Phys. 1995, 36, 631–640. [Google Scholar] [CrossRef]
- Snyder, H. Quantized space–time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]

| Galilean Limit | (A)dS | Carrollian Limit | |
|---|---|---|---|
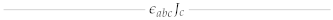 | |||
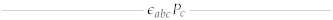 | |||
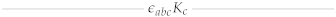 | |||
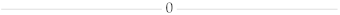 | |||
| 0 | 0 | ||
| 0 | |||
| 0 | |||
| 0 | |||
| -Galilei | -Poincaré | -Carroll | |
|---|---|---|---|
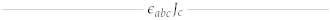 | |||
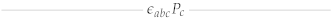 | |||
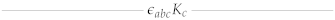 | |||
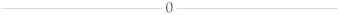 | |||
| 0 | 0 | ||
| 0 | |||
 | |||
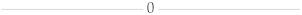 | |||
| (Curved) -Galilei | -(A)dS | (Curved) -Carroll | |
|---|---|---|---|
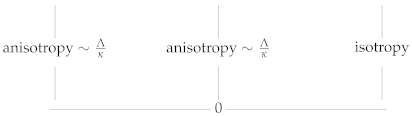 | |||
| 0 | |||
| 0 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballesteros, A.; Gubitosi, G.; Mercati, F. Interplay between Spacetime Curvature, Speed of Light and Quantum Deformations of Relativistic Symmetries. Symmetry 2021, 13, 2099. https://doi.org/10.3390/sym13112099
Ballesteros A, Gubitosi G, Mercati F. Interplay between Spacetime Curvature, Speed of Light and Quantum Deformations of Relativistic Symmetries. Symmetry. 2021; 13(11):2099. https://doi.org/10.3390/sym13112099
Chicago/Turabian StyleBallesteros, Angel, Giulia Gubitosi, and Flavio Mercati. 2021. "Interplay between Spacetime Curvature, Speed of Light and Quantum Deformations of Relativistic Symmetries" Symmetry 13, no. 11: 2099. https://doi.org/10.3390/sym13112099
APA StyleBallesteros, A., Gubitosi, G., & Mercati, F. (2021). Interplay between Spacetime Curvature, Speed of Light and Quantum Deformations of Relativistic Symmetries. Symmetry, 13(11), 2099. https://doi.org/10.3390/sym13112099






