Abstract
In this work, we present sufficient conditions in order to establish different types of Ulam stabilities for a class of higher order integro-differential equations. In particular, we consider a new kind of stability, the -semi-Hyers-Ulam stability, which is in some sense between the Hyers–Ulam and the Hyers–Ulam–Rassias stabilities. These new sufficient conditions result from the application of the Banach Fixed Point Theorem, and by applying a specific generalization of the Bielecki metric.
1. Introduction
In 1940, S. M. Ulam [1] proposed the well-known Ulam stability problem. The difficulty of this problem lies in the conditions to be imposed to guarantee the existence of a linear mapping near an approximately linear mapping. It is known that most of the time it is not possible to obtain exact solutions for some integro-differential equations. Therefore, special techniques are applied, allowing us to obtain approximate solutions. In this case, it is crucial to find error bounds to the approximations when replacing the exact solutions in practical problems.
In 1941, D. H. Hyers [2] gave a partial answer to the problem under the assumption that the groups are Banach spaces, considering the additive Cauchy equation . This contribution originated the naming Hyers–Ulam stability. Meanwhile some other approaches came to light, and later in 1978, new directions were introduced by Th. M. Rassias [3] aiming to solve the Ulam stability problem, which gave origin to the concept of Hyers–Ulam–Rassias stability. Furthermore, new developments were carried out involving different norms and other types of equations. We refer in particular to the works presented by T. Aoki [4], Z. Gajda [5] and Th. M. Rassias [6]. For more details on the subject, we refer to [7,8] and the references therein.
The work initiated by S. M. Ulam in the 1940s had relevant consequences in the field of applications as, for example, in chemical reactions, elasticity, fluid flows, semiconductors and population dynamics (see [9,10,11,12]). The study of problems involving differential, functional, integro-differential and integral equations, in particular their stability issues, has suffered greatly from the growing engagement over the years with a spread of interest among researchers, for example, see [2,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. Their applicability in mathematical models for which we cannot easily find exact solutions, namely those involving symmetry issues, the study of the stability of the approximate solutions is an open field of research. In particular, this work may be relevant in the study of the stability of the symmetrical flow of Newtonian and non-Newtonian fluids related to one-dimensional models obtained by Cosserat Theory associated with fluid dynamics (see [28,29]).
2. Notations and Preliminaries
Let us consider the higher order integro-differential equation defined by
with initial conditions
where , and , with fixed real numbers a and b. Moreover, we consider two continuous functions and .
Definition 1
(Hyers–Ulam stability). If for each continuously differentiable function φ satisfying
with and , the higher order integro-differential equation has a solution and there is a constant , independent of and φ, such that
for all , then we say that the given problem (1) and (2) has the Hyers–Ulam stability.
Definition 2
(Hyers–Ulam–Rassias stability). Let θ be a non-decreasing continuous function defined in the interval . If for each continuously differentiable function φ satisfying
with , the higher order integro-differential equation has a solution and there is a constant , independent of and φ, such that
for all , then we say that the given problem (1) and (2) has the Hyers–Ulam–Rassias stability.
Now, we will introduce a new kind of stability which was presented in [30].
Definition 3
(-semi-Hyers–Ulam stability). Let θ be a non-decreasing continuous function defined in the interval . If for each continuously differentiable function φ satisfying
where and , the higher order integro-differential equation has a solution and there is a constant , independent of and φ, such that
for all , then we say that the given problem (1) and (2) has the θ-semi-Hyers–Ulam stability.
In general, to study the stability of functional, integral and integro-differential equations, it is usual to consider fixed point arguments, for example, see [18,31,32,33,34,35,36,37,38]. Here, we consider the Banach fixed point theorem, which we recall next.
Theorem 1
(Banach fixed point theorem). Let be a generalized complete metric space and let a strictly contractive operator with a Lipschitz constant . If there exists a non-negative integer k such that for some , then the following three propositions hold true:
- 1.
- the sequence converges to a fixed point of T;
- 2.
- is the unique fixed point of T in ;
- 3.
- if , then
In the following, we consider the space of continuously differentiable functions in the interval , , endowed with a generalization of the Bielecki metric, given by
with a non-decreasing continuous function and is a complete metric space (see [39,40]).
3. Hyers-Ulam-Rassias Stability
In the following theorem we will present sufficient conditions for the Hyers–Ulam–Rassias stability relating to problem (1) and (2).
Theorem 2.
Let be a non-decreasing continuous function which fulfills the inequality
for all , where . Suppose also that the continuous function satisfies the condition
where is a Lipschitz constant, and the continuous kernel satisfies the condition
where is a Lipschitz constant. If is such that
where , and , then there is a unique function , solution of problem (1) and (2), such that
for all .
Proof.
Considering the initial conditions (2), i.e., , and using integration properties, Equation (1) is equivalent to
Let us define the continuous operator by
for all and . Indeed, for any continuous function , we have
when . Therefore, using condition (11), we have
Consequently, using conditions (17) and (18), we will prove that the operator T is strictly contractive to the Bielecki metric (10). In order to prove that, we have for all :
Therefore, by the fact that
we have that the operator T is strictly contractive. Thus, we can apply Theorem 1, which ensures that we have the Hyers–Ulam–Rassias stability for problem (1) and (2). Additionally, from (14), we have
where . Therefore, using integration, we obtain
Moreover, from (9) follows
4. -Semi-Hyers–Ulam and Hyers–Ulam Stabilities
Next theorems presents sufficient conditions for the -semi-Hyers–Ulam stability and for the Hyers–Ulam stability regarding problem (1) and (2).
Theorem 3.
Let be a non-decreasing continuous function which fulfills the inequality
for all , where . Suppose also that the continuous function satisfies the condition
where is a Lipschitz constant, and the continuous kernel satisfies the condition
where is a Lipschitz constant. If is such that
where , , and , then there exists a unique function , solution of the problem (1) and (2), such that
for all .
Proof.
Let us consider the operator , defined by
for all and .
Following the same ideas as in the proof of Theorem 2, we can prove that T is strictly contractive to the metric (10) due to the fact that
Theorem 4.
Let be a non-decreasing continuous function, which fulfills the inequality
for all , where . Suppose also that the continuous function satisfies the condition
where is a Lipschitz constant, and the continuous kernel satisfies the condition
where is a Lipschitz constant. If is such that
where , , and , then there exists a unique function , solution of the problem (1)–(2), such that
for all .
5. Examples
In this section, we present some examples in order to illustrate the results obtained throughout the work.
5.1. First Example: 2-Differentiable Function
Let us define the space
We consider the 2-differentiable functions on the space , and the integro-differential equation given by
with .
We also consider the continuous function defined by
which fulfills the inequality
with .
Thus, considering these assumptions all the conditions of Theorem 2 are satisfied.
Now, considering the continuous function defined by
we have
with .
Moreover, the kernel defined by
is a continuous function satisfying
with .
Consequently, by choosing , it follows
for all . Then, for any
we have .
Therefore, we have the Hyers–Ulam–Rassias stability of the integro-differential Equation (38).
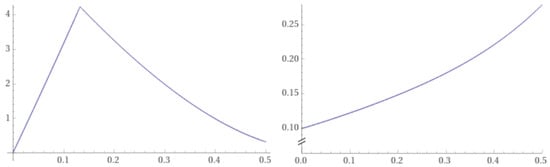
Moreover, if we consider the exact solution , we obtain
for all .
5.2. Second Example: 3-Differentiable Function
In this example, we consider the 3-differentiable functions , and the integro-differential equation given by
with . Moreover, we consider the continuous function defined by
which fulfills the inequality
with . Therefore, all conditions of Theorem 2 are satisfied.
Let us consider the continuous function defined by
which verifies
with . Furthermore, the kernel defined by
is a continuous function and verifies
with . Now, if we choose , it follows
for all . Additionally, for any we have . Consequently, we have the Hyers–Ulam–Rassias stability of the integro-differential Equation (44). If we consider the exact solution , we obtain
for all , which is in accordance with the presented results.
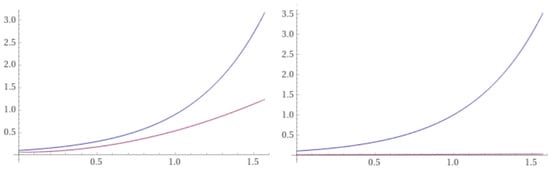
5.3. Third Example: 3-Differentiable Function and a Bigger Perturbation
We will consider the integro-differential Equation (44) but with another function and a bigger perturbation of the solution. Considering the continuous function defined by
we have
with .
Choosing , it follows
for all .
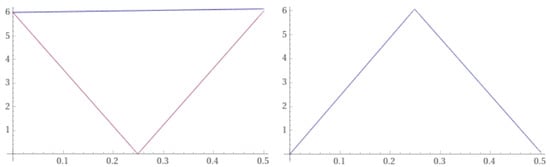
Figure 5.
On the left we have and . On the right, we have .
Therefore, this result exhibits the Hyers–Ulam–Rassias stability of the integro-differential Equation (44).
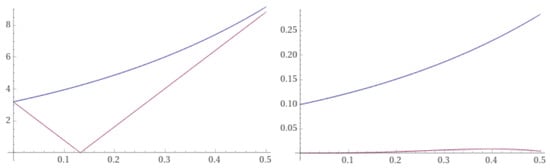
Moreover, by using the exact solution with
we obtain , and
for all .
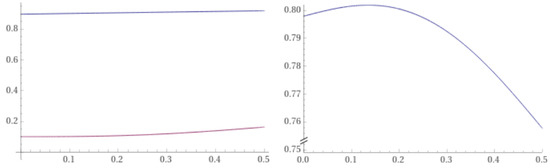
Figure 6.
On the left, we have with and . On the right, we have with .
6. Conclusions
In this work, we presented new sufficient conditions for the Hyers–Ulam–Rassias, the Hyers–Ulam and the -semi-Hyers–Ulam stabilities for a general higher order integro-differential equation by using the Banach fixed point theorem and a generalization of the Bielecki metric thus enabling the study of the stability of an expanding number of particular equations. Some examples were presented to illustrate the theoretical results.
Author Contributions
Conceptualization, A.M.S., F.C. and P.C.; formal analysis, A.M.S., F.C. and P.C.; investigation, A.M.S., F.C. and P.C.; methodology, A.M.S., F.C. and P.C.; project administration, A.M.S.; resources, A.M.S.; supervision, A.M.S.; writing—original draft, A.M.S.; writing—reviw and editing, A.M.S., F.C. and P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by FCT–Portuguese Foundation for Science and Technology through the Center of Mathematics and Applications of University of Beira Interior (CMA-UBI), within project UIDB/00212/2020, the Center for Research and Development in Mathematics and Applications (CIDMA) of University of Aveiro, within project UIDB/04106/2020 and the Research Center for Mathematics and Applications (CIMA) of University of Évora, within project UIDB/04674/2020.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ulam, S.M. A Collection of the Mathematical Problems; Interscience Publication: New York, NY, USA, 1960. [Google Scholar]
- Hyers, D.H. On the stability of linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27, 222–224. [Google Scholar] [CrossRef] [PubMed]
- Rassias, T.M. On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72, 297–300. [Google Scholar] [CrossRef]
- Aoki, T. On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2, 64–66. [Google Scholar] [CrossRef]
- Gajda, Z. On stability of additive mappings. Int. J. Math. Math. Sci. 1991, 14, 431–434. [Google Scholar] [CrossRef]
- Rassias, T.M. On a modified Hyers-Ulam sequence. J. Math. Anal. Appl. 1991, 158, 106–113. [Google Scholar] [CrossRef]
- Belluot, N.B.; Brzdęk, J.; Ciepliński, K. On some recent developments in Ulam’s type stability. Abstr. Appl. Anal. 2012, 2012, 41. [Google Scholar]
- Brzdęk, J.; Popa, D.; Rasa, I.; Xu, B. Ulam Stability of Operators; Elsevier Science Publishing Co Inc.: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Burton, T.A. Volterra Integral and Differential Equations, 2nd ed.; Mathematical in Science and Engineering; 202; Elseiver: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Corduneanu, C. Principles of Differential and Integral Equations, 2nd ed.; Chelsea: New York, NY, USA, 1988. [Google Scholar]
- Gripenberg, G.; Londen, S.O.; Staffans, O. Volterra Integral and Functional Equations; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Lakshmikantham, V.; Rao, M.R.M. Theory of Integro-Differential Equations, Stability and Control: Theory, Methods and Applications 1; Gordon and Breach Publisher: Lausanne, Switzerland, 1995. [Google Scholar]
- Alsulami, H.H.; Gülyaz, S.; Karapinar, E.; Erhan, I.M. An Ulam stability result on quasi-b-metric-like spaces. Open Math. 2016, 14, 1087–1103. [Google Scholar] [CrossRef]
- András, S.Z.; Kolumbán, J.J. On the Ulam-Hyers stability of first order differential systems with nonlocal initial conditions. Nonlinear Anal. Theory Methods Appl. 2013, 82, 1–11. [Google Scholar] [CrossRef]
- Bahyrycz, A.; Brzdęk, J.; Jablońska, E.; Malejki, R. Ulam’s stability of a generalization of the Fréchet functional equation. J. Math. Anal. Appl. 2016, 442, 537–553. [Google Scholar] [CrossRef]
- Brzdęk, J.; Popa, D.; Rassias, T.M. Ulam Type Stability; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Buşe, C.; O’Regan, D.; Saierli, O.; Tabassum, A. Hyers-Ulam stability and discrete dichotomy for difference periodic systems. Bull. Des Sci. MathéMatiques 2016, 140, 908–934. [Google Scholar] [CrossRef]
- Castro, L.P.; Simões, A.M. Hyers-Ulam and Hyers-Ulam-Rassias stability of a class of Hammerstein integral equations. In Proceedings of the AIP Conference Proceedings, ICNPAA 2016 WORLD CONGRESS: 11th International Conference on Mathematical Problems in Engineering, Aerospace and Sciences, La Rochelle, France, 4–8 July 2016; pp. 1–10. [Google Scholar]
- Castro, L.P.; Simões, A.M. Hyers-Ulam-Rassias stability of nonlinear integral equations through the Bielecki metric. Math. Methods Appl. Sci. 2018, 1–17. [Google Scholar] [CrossRef]
- Cho, Y.J.; Park, C.; Rassias, T.M.; Saadati, R. Stability of Functional Equations in Banach Algebras; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Du, W.S. A generalization of Diaz-Margolis’s fixed point theorem and its application to the stability of generalized Volterra integral equations. J. Inequal. Appl. 2015, 407, 1–15. [Google Scholar] [CrossRef][Green Version]
- Hassan, A.M.; Karapinar, E.; Alsulami, H.H. Ulam-Hyers stability for MKC mappings via fixed point theory. J. Funct. Spaces 2016, 2016, 11. [Google Scholar] [CrossRef]
- Hyers, D.H.; Isac, G.; Rassias, T.M. Stability of Functional Equations in Several Variables; Birkhäuser: Basel, Swizerland, 1998. [Google Scholar]
- Jun, K.W.; Kim, H.M. Ulam stability problem for quadratic mappings of Euler–Lagrange. Nonlinear Anal. Theory Methods Appl. 2005, 61, 1093–1104. [Google Scholar] [CrossRef]
- Jung, S.M. Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis; Hadronic Press: Palm Harbor, FL, USA, 2001. [Google Scholar]
- Park, D.W.; Lee, Y.H. The Hyers–Ulam–Rassias stability of the pexiderized equations. Nonlinear Anal. Theory Methods Appl. 2005, 63, 2503–2513. [Google Scholar] [CrossRef]
- Popa, D.; Raşa, I. On the best constant in Hyers-Ulam stability of some positive linear operators. J. Math. Anal. Appl. 2014, 412, 103–108. [Google Scholar] [CrossRef]
- Caulk, D.A.; Naghdi, P.M. Axisymmetric Motion of a Viscous Fluid Inside a Slender Surface of Revolution. J. Appl. Mech. 1987, 54, 190–196. [Google Scholar] [CrossRef]
- Carapau, F.; Correia, P. Numerical simulations of a third-grade fluid flow on a tube through a contraction. Eur. J. Mech. B/Fluids 2017, 65, 45–53. [Google Scholar] [CrossRef]
- Castro, L.P.; Simões, A.M. Different types of Hyers-Ulam-Rassias stabilities for a class of integro-differential equations. Filomat 2017, 31, 5379–5390. [Google Scholar] [CrossRef]
- Brzdęk, J.; Cădariu, L.; Ciepliński, K. Fixed point theory and the Ulam stability. J. Funct. Spaces 2014, 2014, 16. [Google Scholar] [CrossRef]
- Castro, L.P.; Guerra, R.C. Hyers-Ulam-Rassias stability of Volterra integral equations within weighted spaces. Lib. Math. 2013, 33, 21–35. [Google Scholar] [CrossRef]
- Castro, L.P.; Ramos, A. Hyers-Ulam and Hyers-Ulam-Rassias stability of Volterra integral equations with delay. In Integral Methods in Science and Engineering; Constanda, C., Pérez, M., Eds.; Birkhäuser: Boston, MA, USA, 2010; pp. 85–94. [Google Scholar]
- Castro, L.P.; Ramos, A. Hyers-Ulam-Rassias stability for a class of nonlinear Volterra integral equations. Banach J. Math. Anal. 2009, 3, 36–43. [Google Scholar] [CrossRef]
- Castro, L.P.; Ramos, A. Hyers-Ulam stability for a class of Fredholm integral equations. In Mathematical Problems in Engineering Aerospace and Sciences ICNPAA 2010; Sivasundaram, S., Ed.; Cambridge Scientific Publishers: Cambridge, UK, 2010; pp. 171–176. [Google Scholar]
- Castro, L.P.; Simões, A.M. Hyers-Ulam and Hyers-Ulam-Rassias stability of a class of integral equations on finite intervals. In Proceedings of the 17th International Conference on Computational and Mathematical Methods in Science and Engineering, Cádiz, Spain, 4–8 July 2017; pp. 507–515. [Google Scholar]
- Castro, L.P.; Simões, A.M. Hyers-Ulam and Hyers-Ulam-Rassias stability for a class of integro-differential equations. In Mathematical Methods in Engineering: Theoretical Aspects; Tas, K., Baleanu, D., Machado, J.A.T., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Castro, L.P.; Simões, A.M. Stabilities for a class of higher order integro-differential equations. AIP Conf. Proc. 2018, 2046. [Google Scholar] [CrossRef]
- Cădariu, L.; Găvruţa, L.; Găvruça, P. Weighted space method for the stability of some nonlinear equations. Appl. Anal. Discrete Math. 2012, 6, 126–139. [Google Scholar] [CrossRef]
- Tisdell, C.C.; Zaidi, A. Basic qualitative and quantitative results for solutions to nonlinear, dynamic equations on time scales with an application to economic modelling. Nonlinear Anal. 2008, 68, 3504–3524. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).