Aboodh Transform Iterative Method for Solving Fractional Partial Differential Equation with Mittag–Leffler Kernel
Abstract
:1. Introduction
2. Preliminaries
3. Aboodh Transform Iterative Method
Basic Idea of Aboodh Transform Iterative Method
Convergence Analysis
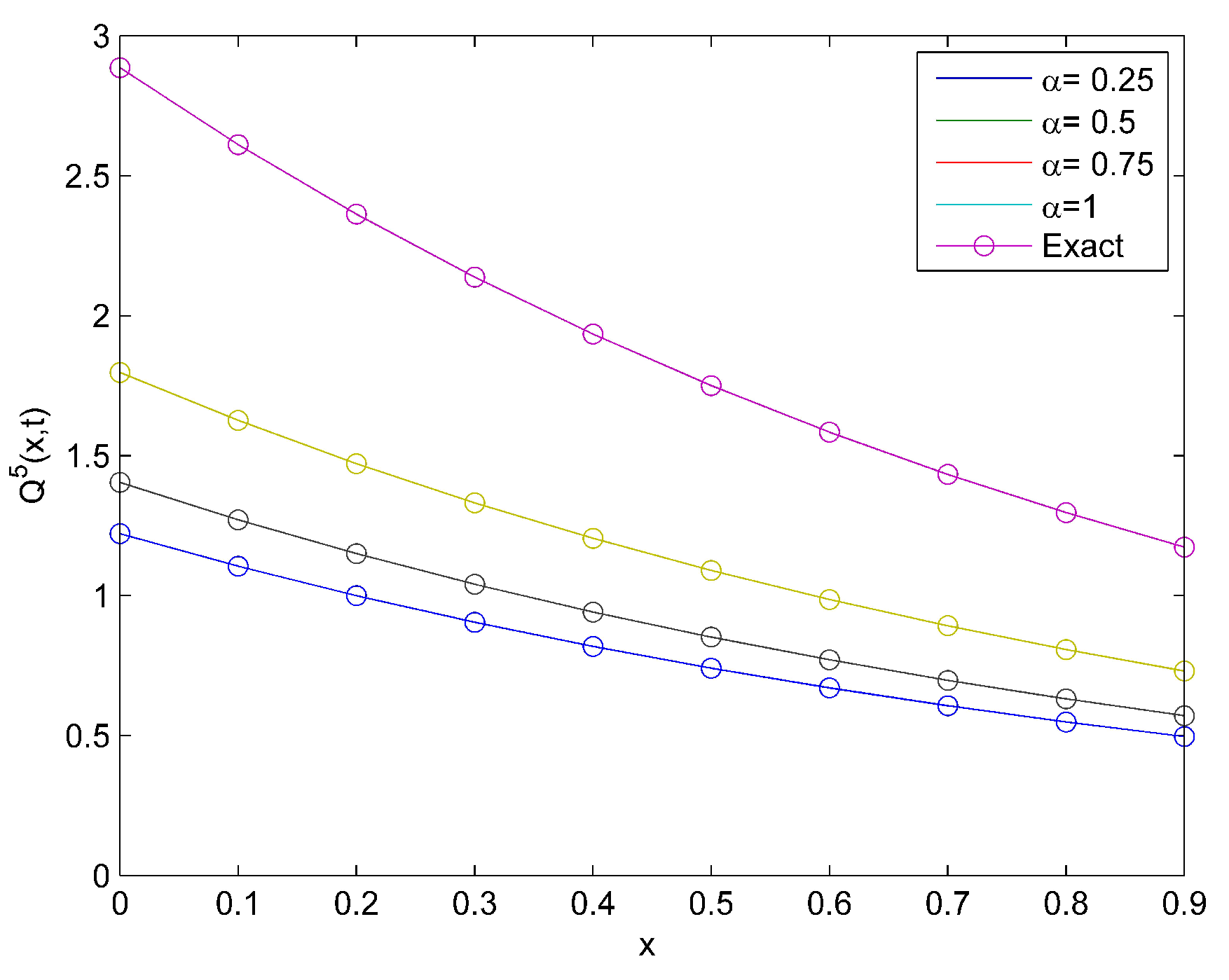
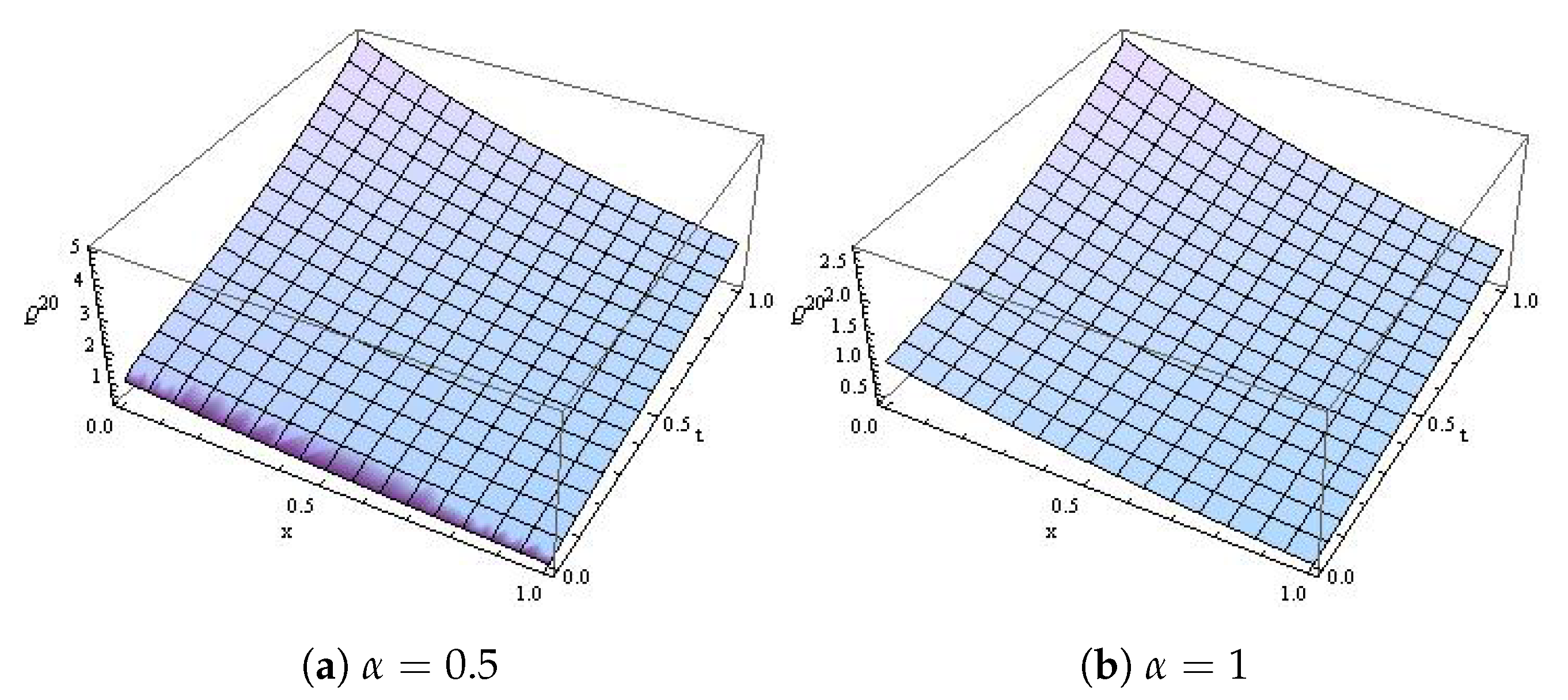
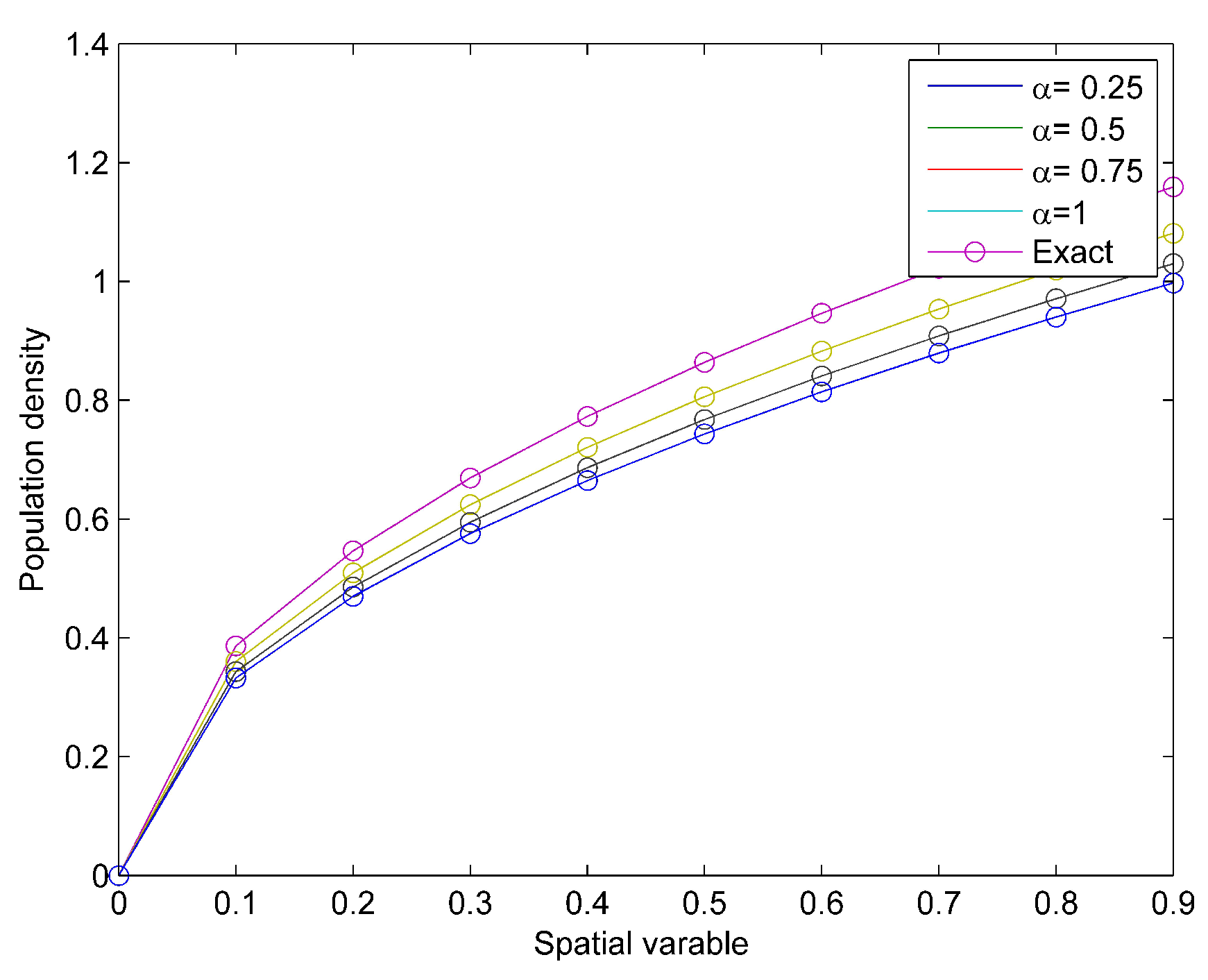
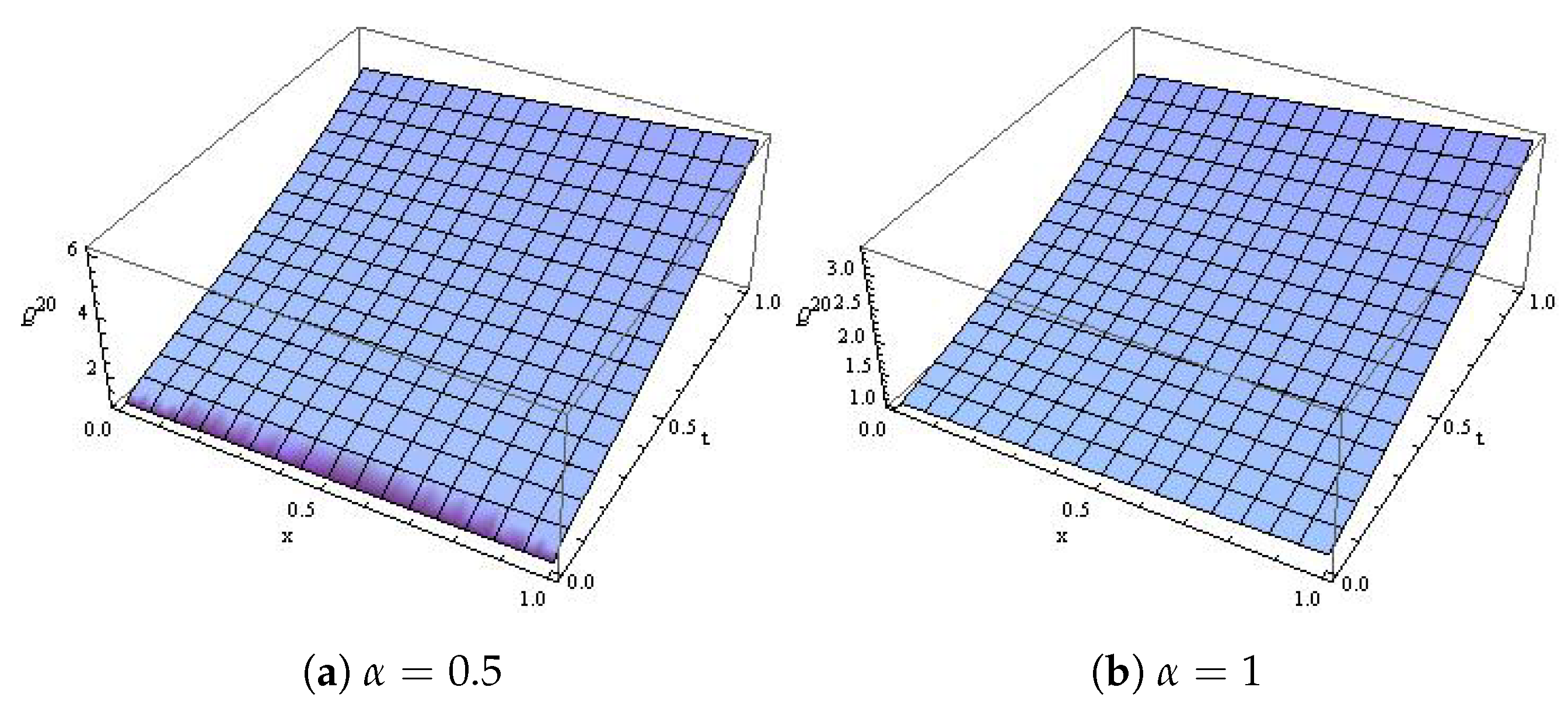
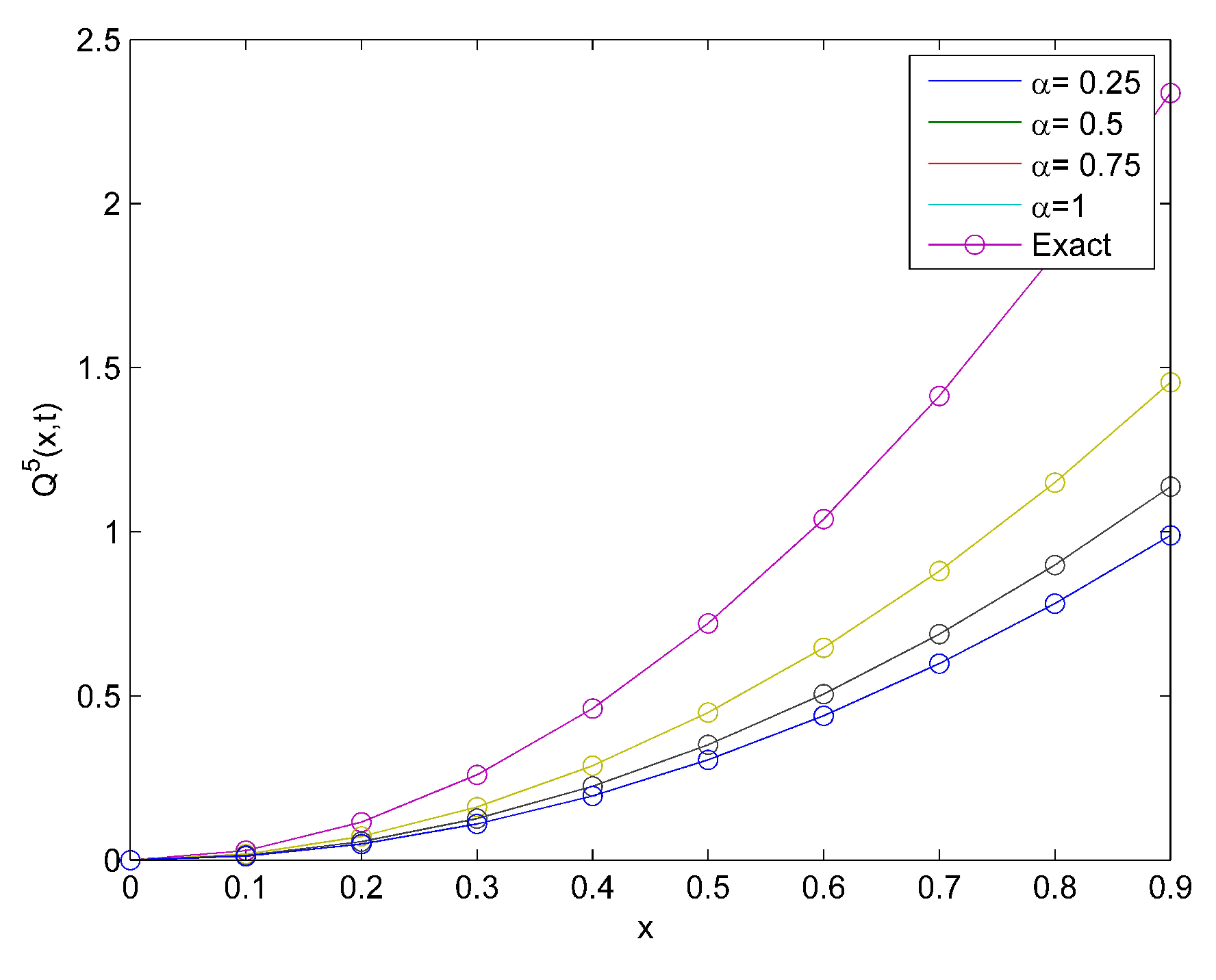
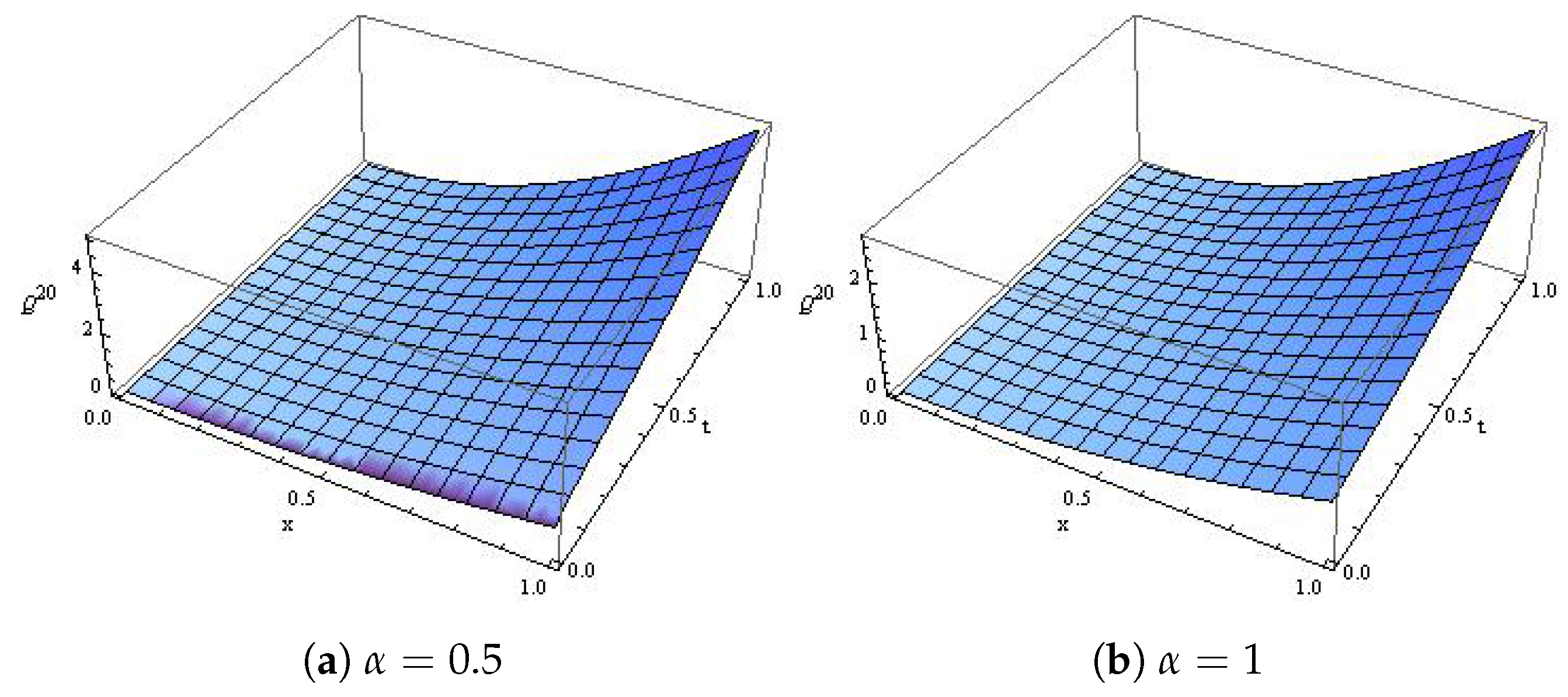
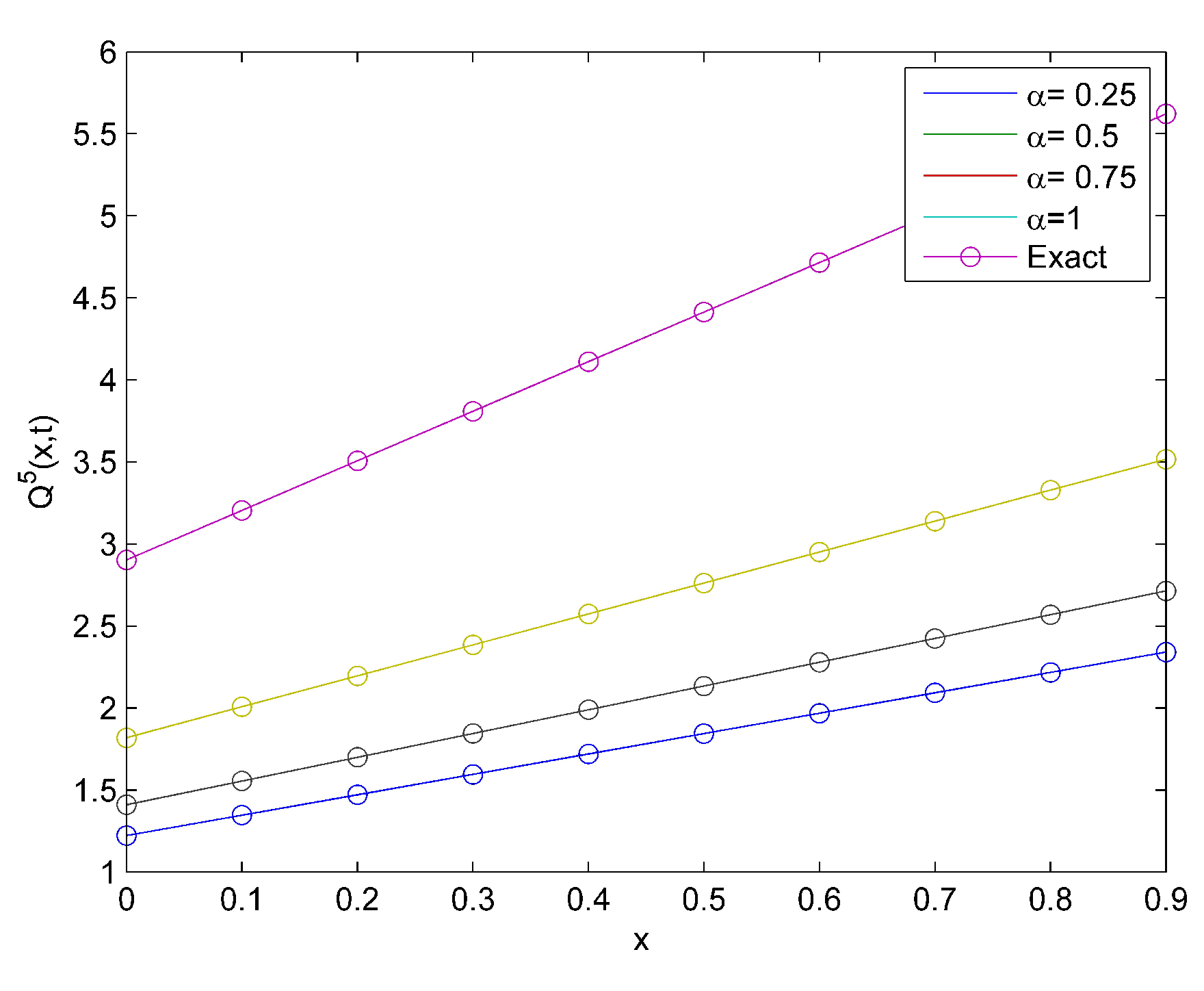
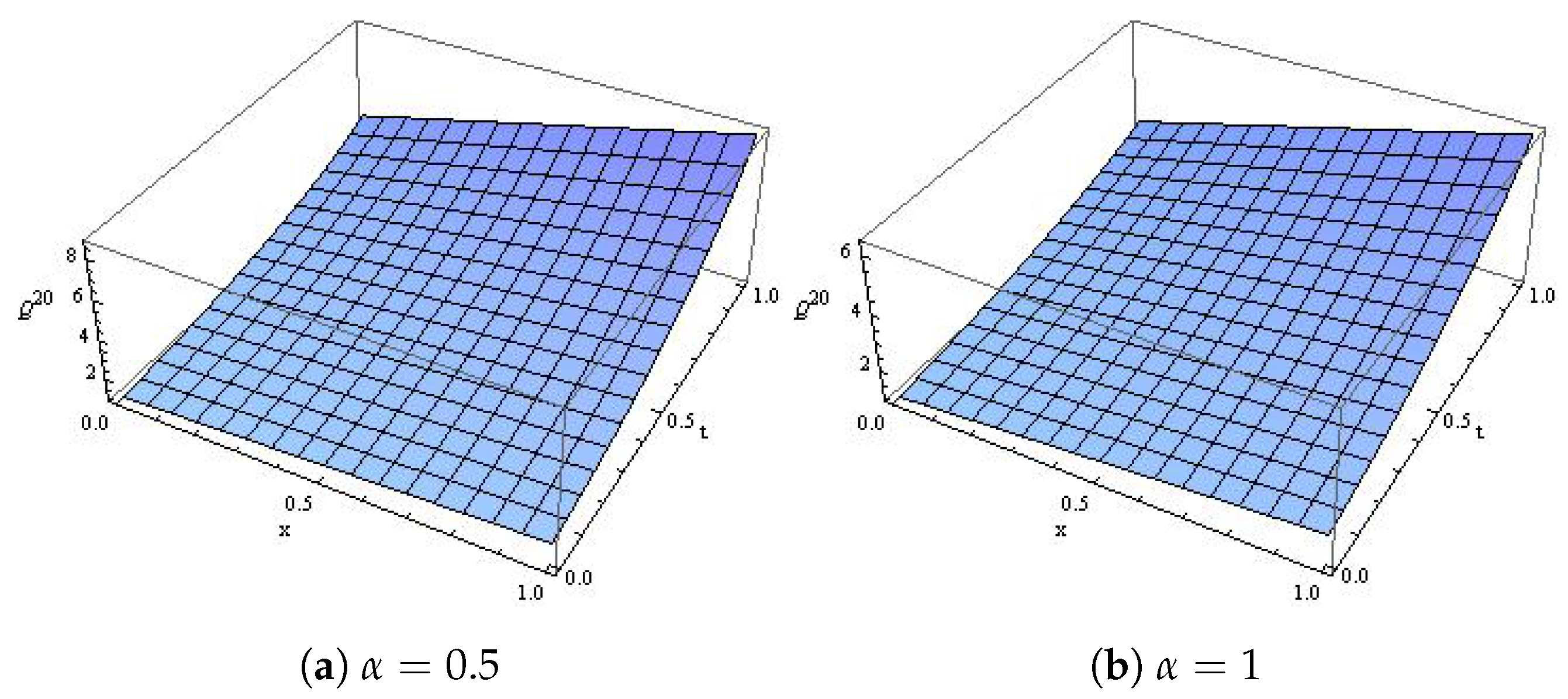
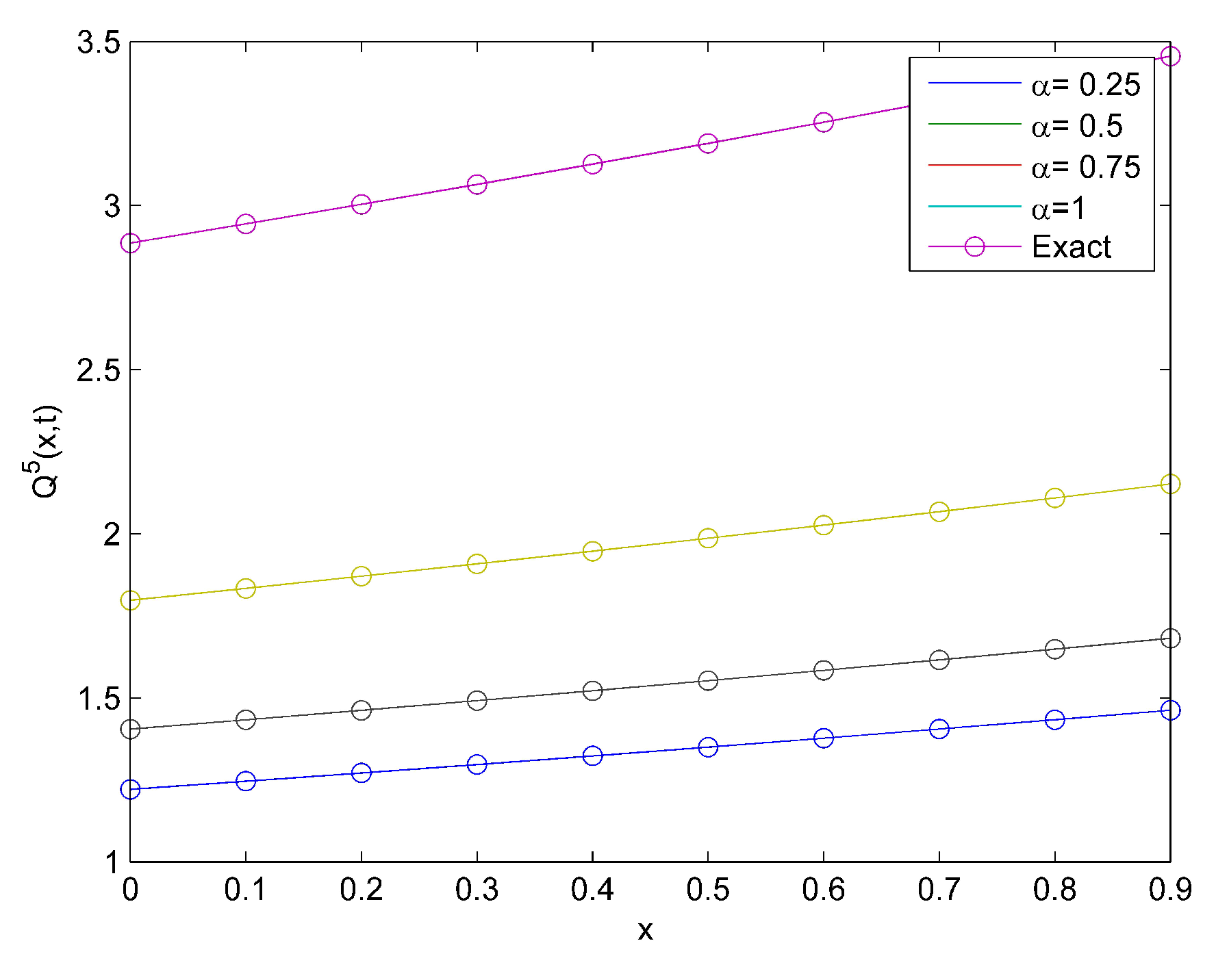
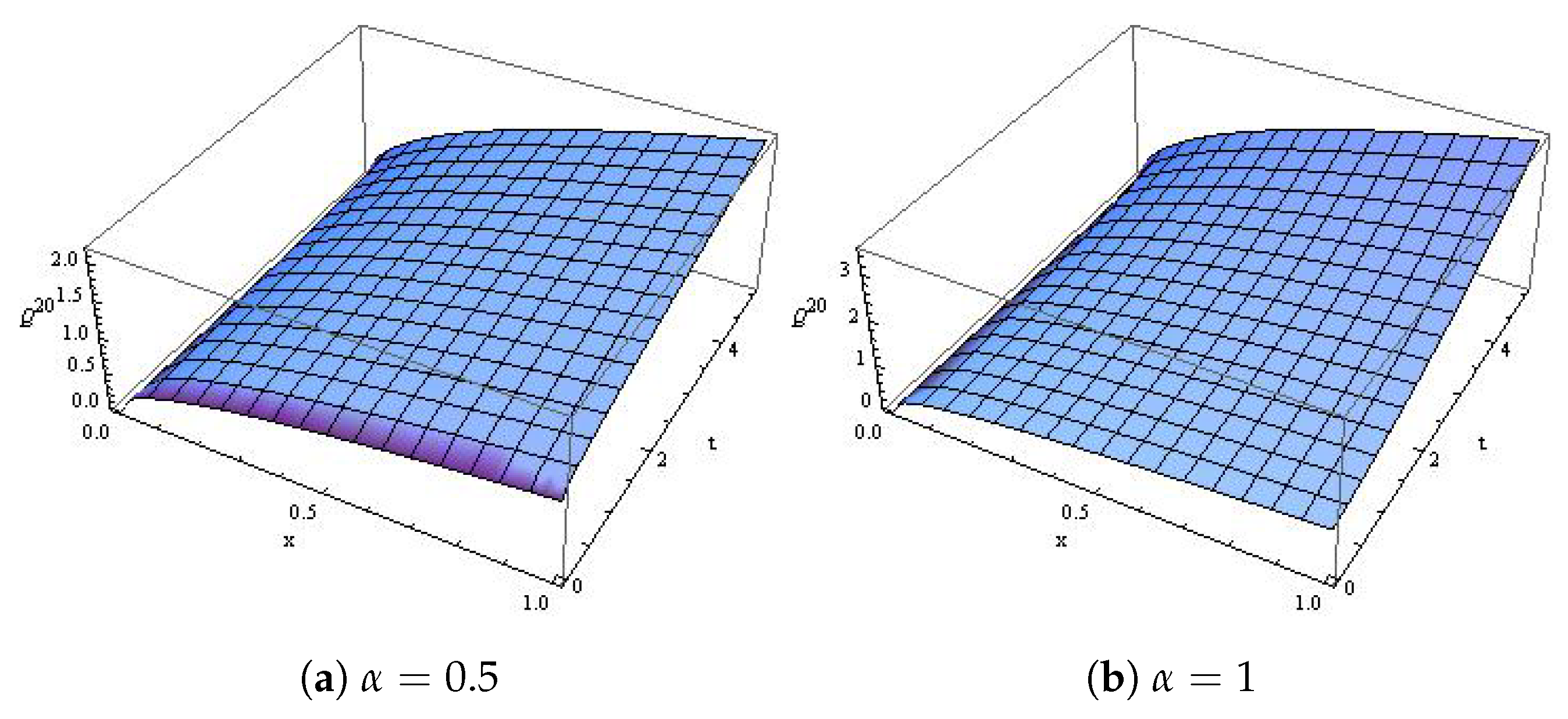
4. Applications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Iyiola, O.S.; Ojo, G.O. On the analytical solution of Fornberg–Whitham equation with the new fractional derivative. Pramana 2015, 85, 567–575. [Google Scholar] [CrossRef]
- Akinyemi, L.; Iyiola, O.S. Exact and approximate solutions of time-fractional models arising from physics via Shehu transform. Math. Methods Appl. Sci. 2020, 43, 7442–7464. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Ojo, G.O.; Mmaduabuchi, O. The fractional Rosenau–Hyman model and its approximate solution. Alex. Eng. J. 2016, 55, 1655–1659. [Google Scholar] [CrossRef] [Green Version]
- Ojo, G.O.; Mahmudov, N.I. Aboodh Transform Iterative Method for Spatial Diffusion of a Biological Population with Fractional-Order. Mathematics 2021, 9, 155. [Google Scholar] [CrossRef]
- Iyiola, O.S.; Ojo, G.O.; Audu, J.D. A Comparison Results of Some Analytical Solutions of Model in Double Phase Flow through Porous Media. J. Math. Syst. Sci. 2014, 4, 275–284. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer Science and Business Media: Heidelberg, Germany, 2010. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Gondal, M.A.; Arife, A.S.; Khan, M.; Hussain, I. An efficient numerical method for solving linear and nonlinear partial differential equations by combining homotopy analysis and transform method. World Appl. Sci. J. 2011, 15, 1786–1791. [Google Scholar]
- Arafa, A.A.; Hagag, A.M.S. Q-homotopy analysis transform method applied to fractional Kundu–Eckhaus equation and fractional massive Thirring model arising in quantum field theory. Asian-Eur. J. Math. 2019, 12, 1950045. [Google Scholar] [CrossRef]
- Arafa, A.A.; Hagag, A.M.S. A new analytic solution of fractional coupled Ramani equation. Chin. J. Phys. 2019, 60, 388–406. [Google Scholar] [CrossRef]
- Saad, K.M.; AL-Shareef, E.H.; Alomari, A.K.; Baleanu, D.; Gómez-Aguilar, J.F. On exact solutions for time-fractional Korteweg-de Vries and Korteweg-de Vries-Burger’s equations using homotopy analysis transform method. Chin. J. Phys. 2020, 63, 149–162. [Google Scholar] [CrossRef]
- Enyi, C.D. Efficacious Analytical Technique Applied to Fractional Fornberg–Whitham Model and Two-Dimensional Fractional Population Model. Symmetry 2020, 12, 1976. [Google Scholar] [CrossRef]
- Baleanu, D.; Mohammadi, H.; Rezapour, S. Analysis of the model of HIV-1 infection of CD4+ T-cell with a new approach of fractional derivative. Adv. Differ. Equ. 2020, 71, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Aydogan, M.S.; Baleanu, D.; Mousalou, A.; Rezapour, S. On high order fractional integro-differential equations including the Caputo–Fabrizio derivative. Bound. Value Probl. 2018, 2018, 90. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Shehu transform to Atangana-Baleanu derivatives. J. Math. Comput. Sci. 2020, 20, 101–107. [Google Scholar] [CrossRef] [Green Version]
- Debnath, I.; Bhatta, D. Integral Transforms and Their Application; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Aboodh, K.S.; Idris, A.; Nuruddeen, R.I. On the Aboodh transform connections with some famous integral transforms. Int. J. Eng. Inform. Syst. 2017, 1, 143–151. [Google Scholar]
- Mittag-Leffler, M.G. Sur La nonvelle Fonction Eα(x). Comptes Rendus Acad. Sci. Paris 1903, 2, 1003. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef] [Green Version]
- Gurtin, M.E.; MacCamy, R.C. On the diffusion of biological populations. Math. Biosci. 1977, 33, 35–49. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awuya, M.A.; Subasi, D. Aboodh Transform Iterative Method for Solving Fractional Partial Differential Equation with Mittag–Leffler Kernel. Symmetry 2021, 13, 2055. https://doi.org/10.3390/sym13112055
Awuya MA, Subasi D. Aboodh Transform Iterative Method for Solving Fractional Partial Differential Equation with Mittag–Leffler Kernel. Symmetry. 2021; 13(11):2055. https://doi.org/10.3390/sym13112055
Chicago/Turabian StyleAwuya, Michael A., and Dervis Subasi. 2021. "Aboodh Transform Iterative Method for Solving Fractional Partial Differential Equation with Mittag–Leffler Kernel" Symmetry 13, no. 11: 2055. https://doi.org/10.3390/sym13112055
APA StyleAwuya, M. A., & Subasi, D. (2021). Aboodh Transform Iterative Method for Solving Fractional Partial Differential Equation with Mittag–Leffler Kernel. Symmetry, 13(11), 2055. https://doi.org/10.3390/sym13112055




